Percentile ranks and benchmark estimates of change for the Health Education Impact Questionnaire: Normative data from an Australian sample

Abstract

Objective:

Participant self-report data play an essential role in the evaluation of health education activities, programmes and policies. When questionnaire items do not have a clear mapping to a performance-based continuum, percentile norms are useful for communicating individual test results to users. Similarly, when assessing programme impact, the comparison of effect sizes for group differences or baseline to follow-up change with effect sizes observed in relevant normative data provides more directly useful information compared with statistical tests of mean differences and the evaluation of effect sizes for substantive significance using universal rule-of-thumb such as those for Cohen’s ‘d’. This article aims to assist managers, programme staff and clinicians of healthcare organisations who use the Health Education Impact Questionnaire interpret their results using percentile norms for individual baseline and follow-up scores together with group effect sizes for change across the duration of typical chronic disease self-management and support programme.

Methods:

Percentile norms for individual Health Education Impact Questionnaire scale scores and effect sizes for group change were calculated using freely available software for each of the eight Health Education Impact Questionnaire scales. Data used were archived responses of 2157 participants of chronic disease self-management programmes conducted by a wide range of organisations in Australia between July 2007 and March 2013.

Results:

Tables of percentile norms and three possible effect size benchmarks for baseline to follow-up change are provided together with two worked examples to assist interpretation.

Conclusion:

While the norms and benchmarks presented will be particularly relevant for Australian organisations and others using the English-language version of the Health Education Impact Questionnaire, they will also be useful for translated versions as a guide to the sensitivity of the scales and the extent of the changes that might be anticipated from attendance at a typical chronic disease self-management or health education programme.

Introduction

Participant self-report data play an essential role in the evaluation of health education activities, programmes and policies. These data, frequently included under the rubric of patient-reported outcome measures (PROMs), are used across the healthcare system for performance assessment and monitoring, benchmarking and quality improvement, and individual diagnosis and needs assessment.¹ Quantitative self-report measures typically consist of multiple questionnaire items that are grouped into scales. These scales are constructed to measure hypothetical or ‘latent’ constructs that are assumed to underlie more-or-less consistent patterns of health-related cognitions, emotional responses or behaviours across varying contexts. Multiple items, differing in content, are used to measure each construct to achieve a satisfactory representation of situations and/or occasions.²

Two different statistical models are typically used to develop multiple item self-report scales: classical test theory (CTT) and item-response theory (IRT). Based on contrasting statistical assumptions and methods, each generates distinctly different data to inform recommendations regarding item selection, scale evaluation, and, of particular interest here, scale scoring and interpretation. The use of CTT scale development approaches usually entails items with common ordinal response options arranged into scales of fixed length that are scored by assigning consecutive numerals to the response options, summing the chosen options across the items in the scale and (often) dividing the sum by the number of items. In contrast, as the respondents’ locations on the latent score continuum (their ‘ability’) is a parameter in the statistical model itself, scales developed with IRT procedures are scored using algorithms that are incorporated within the model estimation software applied to the overall pattern of response to the items in the scale³ and are typically standardised, for example, to a mean of zero and a standard deviation (SD) of 1.0 or, as in the Patient-Reported Outcomes Measurement System (PROMIS; http://www.nihpromis.org), to a mean of 50 and a SD of 10.

While a plausible theoretical case can be made for the superior accuracy of IRT-based scoring,^2,3 in practice, there is typically a very high correlation between IRT scores derived from different estimation algorithms and simple unweighted or weighted summed scores.³ Additionally, for either approach, the resulting scores have an arbitrary metric. It is invariably a challenge to give a substantive meaning to individual or group-average scores based on this metric.^2,4 Using the valuable attribute of IRT modelling that persons and items are mapped onto the same latent dimension, Embretson² demonstrated how additional meaning might be achieved with one specific scale, the Functional Independence Measure (FIM), a widely used index of the severity of a disability. But this demonstration relied on the fact that the items in the FIM have a clear intuitive meaning relative to a person’s level of disability for any experienced healthcare provider. Thus, using Embretson’s example, consider a person whose score on the 13-item motor scale of the FIM locates them on the continuum of everyday self-care tasks at a 0.5 probability of ‘success’ at a similar level to ‘bathing’. This person will be clearly understood by professional (and most lay) interpreters to be experiencing a substantively lower level of disability compared to one who is located with a 0.5 probability of success mid-way between the ‘dressing upper-body’ and ‘toileting’ items of the scale. It is, however, unlikely that this approach would be particularly helpful when the items do not have such a clear mapping to a performance-based continuum and refer, for example, to self-reports of psychological attributes such as the attitudes, cognitions, or emotional states of the respondent (so called ‘perception’ and ‘evaluation’-based measures^5–7).

Within the CTT tradition of scale development, population norms, either in the form of percentiles or summary statistics of standardised scores including effect sizes (ES) for socio-demographic group differences, have traditionally been used to provide additional meaning for arbitrary scale scores.⁸ While these strategies have often been criticised from various perspectives, for example, Blanton and Jaccard⁴ and Crawford and Garthwaite,⁹ percentile norms in particular are argued to be appropriate for communicating test results to users because they ‘… tell us directly how common or uncommon such scores are in the normative population’.⁹ This direct interpretation of the likelihood of occurrence in a reference population of an otherwise-arbitrary score would seem to be particularly valuable for use in understanding individual scale scores and profiles that entail a high level of subjectivity in response generation and are not clearly indexed to observable behaviours.⁷

From an analogous viewpoint, when assessing programme impact, the comparison of ES for intervention versus comparison group or baseline to follow-up differences with the ES observed in relevant normative data yields a similar advantage compared with the evaluation of the statistical significance of mean differences and/or the evaluation of ES for substantive significance using universal rule-of-thumb such as the guidelines of approximately 0.2, 0.5 and 0.8, respectively, for ‘small’, ‘medium’ and ‘large’ ES recommended for Cohen’s ‘d’.^10,11 The interpretation of ES derived from a specific intervention within the context of ES derived from a range of studies of comparable interventions arguably provides better and more directly useful guidance for policy makers and programme personnel.¹¹

This article is designed to assist managers, programme staff and clinicians of healthcare organisations who use the Health Education Impact Questionnaire (heiQ) to interpret their results using percentile norms for individual baseline and follow-up scores together with group ES for change across the duration of a range of typical chronic disease self-management and support programmes. The percentile norms for individual heiQ scale scores and benchmarks for group change are based on the responses of 2157 participants of chronic disease self-management programmes conducted by a wide range of organisations in Australia between July 2007 and March 2013.

The data presented include the following: (1) baseline and follow-up average scores on the eight heiQ scales, (2) percentile norms for both baseline and follow-up responses, (3) average gain between baseline and follow-up and (4) ES for group gain from baseline to follow-up.

The heiQ

The heiQ is a self-report patient outcomes measure that was developed 10 years ago to be a user-friendly, relevant and psychometrically sound instrument for the comprehensive evaluation of patient education programmes and activities.¹² The present version (Version 3) measures eight constructs by multi-item composite scales: (1) Health-Directed Activities (HDA), (2) Positive and Active Engagement in Life (PAEL), (3) Emotional Distress (ED), (4) Self-monitoring and Insight (SMI), (5) Constructive Attitudes and Approaches (CAA), (6) Skill and Technique Acquisition (STA), (7) Social Integration and Support (SIS) and (8) Health Services Navigation (HSN). Further brief details of the heiQ scales (including number of items and construct descriptions) are provided in the Online Supplementary Material.

The heiQ was developed following a grounded approach that included the generation of a programme logic model for health education interventions and concept-mapping workshops to identify relevant constructs.¹² Based on the results of the workshops, candidate items were written and tested on a large construction sample drawn from potential participants of patient education programmes and persons who had recently completed a programme. The number of items was reduced to a 42-item questionnaire measuring eight constructs and again tested on a replication sample drawn from a broader population of attendees at a general hospital outpatient clinic and community-based self-management programmes. Confirmatory factor analysis (CFA) supported by IRT analysis was used for item selection and scale refinement. In subsequent revisions leading to Version 3, the number of response options was reduced from 6 to 4 on advice from users (they are now strongly disagree, disagree, agree and strongly agree with slightly options removed) and the number of items was reduced to 40.

The general eight-factor structure of the original version of the heiQ was replicated by Nolte¹³ who investigated its factorial invariance (equivalence)^14–17 across a traditional baseline to follow-up (pre-test and post-test) design, as well as across a post-test compared with a retrospective pre-test (‘then-test’) design. Nolte’s results supported the stability of the factor structure across measurement occasions and questionnaire formats (configural invariance) and the equivalence of item factor loadings (metric invariance) and intercepts/thresholds (scalar invariance) of the heiQ when used in the traditional pre-post design. More recently, the factor structure and factorial invariance of the 40 items that constitute Version 3 of the heiQ were investigated using a large sample of 3221 archived responses.⁷ The original eight-factor structure was again replicated and all but one of the scales (SMI) was found to consist of unifactorial items with reliability of ≥0.8 and satisfactory discriminant validity. Nolte’s findings of satisfactory measurement equivalence were replicated across baseline to follow-up for all scales, and strict measurement equivalence was also strongly supported across important population sub-groups (sex, age, education and ethnic background). Furthermore, it has also recently been demonstrated that change scores on the heiQ scales are relatively free from social desirability bias.¹⁸

The heiQ has become a widely used tool to measure the proximal outcomes of patient education programmes. Current licencing information held by Deakin University that reflects usage over the last 6 years indicates that the questionnaire is being employed in projects in 23 countries encompassing all continents. The heiQ is particularly widely used in England (15 registered projects), Canada (23) and the United States (10), and northern Europe (a total of 32 projects in Denmark, The Netherlands and Norway), as well as in Australia (31).

The validation and measurement equivalence studies summarised above support this high level of interest in the heiQ in the evaluation of health education and self-management programmes, particularly for use as a baseline to follow-up measure in experimental studies, other evaluation designs and for system-level monitoring and evaluation. In particular, they give users confidence that all heiQ scales are providing relatively unbiased and equivalent measures across baseline to follow-up data. The norms and benchmarks provided in this article are designed to support the practical but appropriate interpretation of both individual and group data from studies of this kind.

Methods

Data

The data were derived from 2157 participants in a range of programmes whose responses were archived on a dedicated heiQ website between July 2007 and March 2013. The participants were selected from the larger data set used for the recent replication and measurement equivalence study⁷ using only those organisations that could be clearly identified by name as an Australian health-supporting organisation (N = 64 organisations with between 4 and 212 respondents per organisation), thus deleting from the database organisations that were not clearly identified and those from outside Australia. All respondents had been participants in a chronic disease self-management or similar health support programme (typically a 6-week duration programme meeting weekly, but longer and more intensive programmes were also represented); had completed both baseline and follow-up versions of the heiQ; and provided responses to at least 50% of the questions that constitute the heiQ scales at both baseline and follow-up.

These data were gathered by the individual organisations for their own monitoring and evaluation purposes using an ‘opt-in’ consent process. The de-identified data were provided to the heiQ research team specifically for on-going validation studies. Some archived data were also gathered as part of a pilot health education quality assurance study funded by the Australian Government Department of Health and Ageing. Ethical approval for the use of these data for scale validation purposes was obtained from the University of Melbourne Human Research Ethics Committee. (The University of Melbourne was the original copyright owner of the heiQ, and in 2010, this was transferred to Deakin University, Australia. Information on how to access the full questionnaire for research, course evaluation and translation into languages other than English is available from the authors.)

In relation to data quality, there were relatively small amounts of missing data in the heiQ item responses in the larger data set from which the current sample was derived. For example, at baseline, all data were present for 84.7% of participants, while for a further 10.8%, there were between 1 and 3 data points missing. Missing data patterns were similar for the follow-up where 86.8% of cases had all data on the heiQ items present. Furthermore, despite the items requiring only four response options, skewness and kurtosis of item responses and scale scores were modest. No item demonstrated a skewness estimate of >1.0, whereas 30 of the 80 baseline and follow-up items had kurtosis >1.0 and only 3 of these had a kurtosis estimate >2.0. All kurtosis estimates >1.0 were positive, suggesting there was an acceptable distribution over the four available response options for all but a very small number of items. Similarly, while the majority of heiQ scale scores showed some evidence of negative skew, none had a skewness estimate >1.0, whereas 8 of the 16 had a kurtosis estimate >1.0 but <2.0, and 3 had a kurtosis estimate >2.0.

In calculating the percentile norms and benchmarks, the small amounts of missing data on individual heiQ questions were replaced with point estimates (rounded to the nearest whole number) generated by the ‘EM’ algorithm in the IBM Corp Statistical Package for the Social Sciences (SPSS Version 21.0).¹⁹ Equally weighted summed item scores on the eight heiQ domains were then calculated. These raw-scale scores were also rescaled (averaged across the number of items in the scale) to range from 1 to 4 to parallel the question response options. Scale scores on ED are typically not reversed, and this practice has been followed here; unless otherwise indicated, higher scores on this scale refer to self-reports of more negative affect and a decrease in scores on this scale would be regarded as a desirable outcome of a self-management programme.

Preliminary calculations

Summary statistics for demographic data and heiQ scale scores at baseline and follow-up were calculated using standard routines in IBM Corp SPSS Version 21.0.¹⁹ Additionally, relationships between a selected sample of demographic variables and the heiQ scale scores at baseline were studied by computing the mean scores across sex, age (recoded to two groups: younger, <65, and older, ≥65), education (recoded to completed schooling up to year 8 and completed schooling beyond year 8) and country of birth (Australia and overseas). Given that heiQ scale scores show some skewness and (particularly) kurtosis, the statistical significance of the apparent differences between means was assessed using robust (Brown–Forsythe) one-way analysis of variance. Additionally, robust estimates of the ES (Cohen’s d for a between-subject design) together with bootstrapped 95% confidence intervals (CIs) were computed using software developed by Professor James Algina and colleagues (ESBootstrapIndependent1; available at http://plaza.ufl.edu/algina/index.programs.html).

Percentile ranks

Percentile ranks (PRs) were constructed according to the reporting standards advocated by Crawford et al.²⁰ and calculated using the programme Percentile_Norms_Int_Est.exe described in their paper. The programme is available from Professor John Crawford’s personal web pages (http://homepages.abdn.ac.uk/j.crawford/pages/dept/). It is important to note that the programme uses the ‘mid-p variant’ method for calculating the PR in data where there are ties (i.e. where there is more than one respondent with the same raw score). The mid-p variant approach bases the PR on the proportion of respondents who achieved a result lower that the observed score plus 50% of the proportion of respondents who achieved the observed score (in contrast to the more commonly used method that utilises just the proportion of respondents who achieved a result below the specified score²⁰).

CIs were also calculated for each PR. These CIs express the uncertainty associated with the use of the point estimate of the PR in the normative sample as an estimate of the PR in the population that the sample was (theoretically) derived from.²¹ The 95% CIs provided here were calculated using the Bayesian option in Crawford et al.’s²⁰ computer programme, for example, the 95% CI for the PR of a raw score of 10 on HDA at baseline is 29 with 95% CI = 23.4–34.5. The Bayesian interpretation is that there is a 95% probability that the PR of this raw score in the population lies between 23.4 and 34.5, or, alternatively, that there is a 2.5% probability that the PR of a raw score of 10 lies below 23.4 in the population and a corresponding 2.5% probability that this PR lies above 34.5 in the population.

Baseline to follow-up ES

An ES is a standardised estimate of the magnitude of the difference between two measures, either across two comparison groups or between baseline and follow-up measures. Typically, an ES is calculated as the difference between the two means divided by the pooled SD of the two sets of scores. Point and interval estimates of the baseline to follow-up ES in this study were calculated using the robust ES estimator with pooled variance and bootstrapped CIs described by Algina and colleagues.^22,23 Calculations were conducted using the computer programme ESBootstrapCorrelated3 described by Algina et al.²² The robust pooled variance option is recommended for data that are skewed and where baseline and follow-up variances are unequal as is typically the case with heiQ scale scores.

Results

Sample characteristics

Broad characteristics of the normative sample are shown in Table 1. It should be noted that all people in the sample were participants in a chronic disease self-management programme or related health education or health support activity. Also, somewhat fewer respondents provided demographic data than heiQ scale scores. This was particularly the case with the respondents’ age. The demographic profile in Table 1 should therefore be regarded as an estimate only of the characteristics of the full sample. The average age of the participants for whom the data were available was over 61 years, but there was a wide spread of ages (e.g. the age range was 19–97 years, while approximately 25% of the sample were 72 years or older and a similar percentage were aged ≤53 years). Approximately 46% were aged 65 years or older. There were more women (58.3%) than men. Approximately three-fourths of the respondents had completed some form of education or trade training beyond year 8, whereas 43% had a non-school educational qualification and 23% had a university degree or higher. A very small proportion of the sample identified themselves as either Aboriginal or Torres-Strait Islander, whereas a little below one-fourth were born in a country other than Australia. The majority (approximately 59%) of the sample for whom employment data were available was retired and/or a pensioner, and approximately 43% had private health insurance.

Table 1.

Sample characteristics.

Respondent characteristics	Mean (SD), %	Total N
Age (years)	61.78 (13.43)	994
Sex
Female	58.3%	1628
Education		1583
None, or some primary school	1.0%
Primary school	8.0%
High school to year 8	24.5%
High school to year 12	23.5%
TAFE/trade qualification	20.3%
University degree	22.7%
Aboriginal or Torres-Strait Islander		1572
Yes	1.0%
Country of birth		1646
Australia	76.1%
Home Language		1646
English	93.4%
Current paid employment		1578
Full-time employed	14.3%
Part-time employed	9.7%
Unemployed	5.4%
Home duties	7.5%
Retired/pensioner	59.4%
Other	3.7%
Private health insurance		1593
Yes	42.6%

SD: standard deviation.

Summary statistics and reliability of the heiQ scales

Summary statistics (mean, SD, median, minimum, maximum and interquartile range) of the responses of the sample of 2157 participants to the eight heiQ scales at baseline and follow-up are shown in Table 2. These statistics are shown for both the raw summed totals of the items that constitute each scale and for these totals divided by the number of items in the scale (rescaled total scores). Based on these mean scores, it appears that, overall, there were only quite modest increases in the positively oriented heiQ scales from baseline to follow-up (and a modest decrease in ED). Composite scale reliability²⁴ with 95% CIs (italicised) based on robust standard errors and, for comparison with other studies, Cronbach’s α (in parenthesis) for the heiQ scales estimated from the baseline data of the larger sample of 3221 respondents that included the present ‘known Australian’ sample are as follows – (1) HDA: 0.83/0.82–0.84 (0.83), (2) PAEL: 0.83/0.82–0.84 (0.83), (3) ED: 0.86/0.86–0.87 (0.86), (4) SMI: 0.74/0.72–0.76 (0.74), (5) CAA: 0.88/0.87–0.89 (0.87), (6) STA: 0.80/0.78 0.81 (0.80), (7) SIS: 0.88/0.88–0.89 (0.88) and (8) HSN: 0.85/0.84–0.86 (0.85).⁷ All reliability estimates were ≥0.8 with the exception of that for SMI.

Table 2.

Summary of heiQ raw and rescaled scores.

Scale	Mean	SD	Median	Min.	Max.	IQ range
Health-directed activities
Baseline	11.32	2.60	12.0	4.0	16.0	10.0–13.0
Baseline rescaled	2.83	0.65	3.0	1.0	4.0	3.3–2.5
Follow-up	12.34	2.28	12.0	4.0	16.0	11.0–14.0
Follow-up rescaled	3.08	0.57	3.0	1.0	4.0	2.8–3.5
Positive and active engagement in life
Baseline	14.75	2.56	15.0	5.0	20.0	13.0–16.0
Baseline rescaled	2.95	0.51	3.0	1.0	4.0	2.6–3.2
Follow-up	15.65	2.33	15.0	5.0	20.0	15.0–17.0
Follow-up rescaled	3.13	0.47	3.0	1.0	4.0	3.0–3.4
Emotional distress
Baseline	13.99	3.77	14.0	6.0	24.0	12.0–17.0
Baseline rescaled	2.33	0.63	2.33	1.0	4.0	2.0–2.8
Follow-up	13.23	3.63	13.0	6.0	24.0	11.0–16.0
Follow-up rescaled	2.21	0.60	2.33	1.0	4.0	2.0–2.8
Self-monitoring and insight
Baseline	18.23	2.34	18.0	6.0	24.0	17.0–20.0
Baseline rescaled	3.04	0.39	3.0	1.0	4.0	2.8–3.3
Follow-up	19.06	2.20	19.0	6.0	24.0	18.0–20.0
Follow-up rescaled	3.18	0.37	3.2	1.0	4.0	3.0–3.3
Constructive attitudes and approaches
Baseline	15.24	2.61	15.0	5.0	20.0	14.0–16.0
Baseline rescaled	3.05	0.52	3.0	1.0	4.0	2.8–3.2
Follow-up	15.78	2.44	15.0	5.0	20.0	15.0–17.0
Follow-up rescaled	3.16	0.49	3.0	1.0	4.0	3.0–3.4
Skill and technique acquisition
Baseline	11.36	1.92	12.0	4.0	16.0	10.0–12.0
Baseline rescaled	2.84	0.48	3.0	1.0	4.0	2.5–3.0
Follow-up	12.21	1.62	12.0	5.0	16.0	12.0–13.0
Follow-up rescaled	3.05	0.41	3.0	1.3	4.0	3.0–3.23
Social integration and support
Baseline	14.63	2.83	15.0	5.0	20.0	13.0–16.0
Baseline rescaled	2.93	0.57	3.0	1.0	4.0	2.6–3.2
Follow-up	15.11	2.68	15.0	5.0	20.0	14.0–17.0
Follow-up rescaled	3.02	0.54	3.0	1.0	4.0	2.8–3.4
Health service navigation
Baseline	15.54	2.34	15.0	5.0	20.0	15.0–17.0
Baseline rescaled	3.11	0.47	3.0	1.0	4.0	0–3.4
Follow-up	15.97	2.33	15.0	5.0	20.0	5.0–18.0
Follow-up rescaled	3.19	0.47	3.0	1.0	4.0	3.0–3.6

heiQ: Health Education Impact Questionnaire; SD: standard deviation.

Relationships between demographic variables and baseline heiQ scale scores

Despite being drawn from a range of diverse organisations, the strong measurement equivalence of the data across the sex, age, education and ethnic background of the respondents was demonstrated in the recently published study.⁷ Given this finding, it can be concluded that the heiQ items yield equivalent measurement parameters across these critical socio-demographic groups and, when combined into the eight scales, result in unbiased scores that can justifiably be compared across these groups. Relationships between the heiQ scale scores at baseline and these socio-demographic groups are presented in Table 3.

Table 3.

Relationships between selected socio-demographic variables and raw baseline heiQ scores.

Socio-demographic factor		Health-directed activities	Positive and active engagement in life	Emotional distress	Self-monitoring and insight	Constructive attitudes and approaches	Skill and technique acquisition	Social integration and support	Health service navigation
Sex	Female, mean (SD)	11.19 (2.59)	14.93 (2.53)	14.18 (3.77)	8.29 (2.35)	15.34 (2.61)	11.40 (1.97)	14.52 (2.87)	15.50 (2.39)
	Male, mean (SD)	11.65 (2.48)	14.69 (2.51)	13.43 (3.71)	18.23 (2.35)	15.31 (2.56)	11.41 (1.87)	15.00 (2.65)	15.66 (2.31)
	Robust ANOVA	F = 12.99; 1, 1495.5 d.f.; p < 0.00	F = 3.61; 1, 1467.9 d.f.; p = 0.06	F = 16.13; 1, 1474.4 d.f.; p < 0.00	F = 0.25; 1, 1460.3 d.f.; p = 0.62	F = 0. 05; 1, 1475.9 d.f.; p = 0.82	F = 0.01; 1, 1503.5 d.f.; p = 0.92	F=12.37; 1, 1525.2 d.f.; p < 0.00	F = 1.84; 1, 1489.5 d.f.; p = 0.18
	ES (95% CI)	0.22 (0.12–0.31)	−0.07 (–0.16–0.04)	−0.22 (–0.32–−0.11)	−0.04 (–0.14–0.06)	0.01 (–0.09–0.12)	0.06 (–0.04–0.16)	0.19 (0.11–0.31)	0.05 (–0.05–0.16)
Age (years)	<65, mean (SD)	11.43 (2.77)	14.87 (2.59)	13.85 (3.85)	18.09 (2.49)	15.42 (2.66)	11.27 (2.05)	14.65 (2.88)	15.30 (2.47)
	≥65, mean (SD)	11.73 (2.29)	15.26 (2.25)	13.26 (3.54)	18.57 (2.18)	15.61 (2.33)	11.76 (1.78)	15.24 (2.48)	15.87 (2.29)
	Robust ANOVA	F = 3.51; 1, 991.5 d.f.; p = 0.061	F = 6.69; 1, 991.1 d.f.; p = 0.010	F = 6.34; 1, 984.9 d.f.; p = 0.012	F = 10.32; 1, 990.6 d.f.; p < 0.00	F = 1.38; 1, 990.7 d.f.; p. = 0.24	F = 16.05; 1, 991.1 d.f.; p < 0.00	F = 11.99; 1, 991.5 d.f.; p < 0.00	F = 14.34; 1, 983.0 d.f.; p < 0.00
	ES (95% CI)	0.09 (−0.05–0.21)	0.15 (0.02–0.28)	−0.17 (−0.30–−0.02)	0.21 (0.08–34)	0.02 (−0.11–0.15)	0.30 (0.16–0.41)	0.20 (0.06–0.30)	0.19 (0.05–0.30)
Education (years)	≤10, mean (SD)	11.44 (2.39)	14.64 (2.47)	14.41 (3.60)	18.31 (2.36)	15.19 (2.42)	11.50 (1.88)	14.95 (2.56)	15.67 (2.21)
	>10, mean (SD)	11.33 (2.63)	14.90 (2.55)	13.61 (3.81)	18.23 (2.34)	15.37 (2.67)	11.36 (1.96)	14.59 (2.88)	15.49 (2.44)
	Robust ANOVA	F = 0.72; 1, 1151.8 d.f.; p = 0.395	F = 4.07; 1, 1093.6 d.f.; p = 0.044	F = 16.69; 1, 1115.3 d.f.; p < 0.00	F = 0.36; 1, 1050.2 d.f.; p = 0.551	F = 1.92; 1, 1157.1 d.f.; p = 0.166	F = 1.98; 1, 1104.3 d.f.; p = 0.159	F = 6.61; 1, 1175.1 d.f.; p = 0.010	F = 2.16; 1, 1158.8 d.f.; p = 0.142
	ES (95% CI)	−0.07 (−0.17–0.04)	0.10 (−0.02–0.21)	−0.22 (−0.33–−0.11)	−0.01 (−0.12–0.09)	0.09 (−0.01–0.19)	−0.14 (−0.24–−0.03)	−0.10 (−0.22–0.01)	−0.01 (−0.11–0.09)
Country of birth	Australia, mean (SD)	11.33 (2.56)	14.85 (2.55)	13.89 (3.72)	18.27 (2.37)	15.31 (2.60)	11.44 (1.93)	14.72 (2.83)	15.56 (2.33)
	O’seas, mean (SD)	11.53 (2.52)	14.76 (2.48)	13.84 (3.83)	18.22 (2.26)	15.36 (2.57)	11.28 (1.94)	14.72 (2.64)	15.60 (2.41)
	Robust ANOVA	F = 1.99; 1, 665.5 d.f.; p = 0.159	F = 0.361; 1, 673.1 d.f.; p = 0.548	F = 0.043; 1, 640.6 d.f.; p = 0.835	F = 0.184; 1, 683.9 d.f.; p = 0.668	F = 0.105; 1, 662.1 d.f.; p = 0.746	F = 2.17; 1, 652.8 d.f.; p = 0.141	F = 0.00; 1, 697.1 d.f.; p = 0.993	F = 0.10; 1, 639.6 d.f.; p = 0.749
	ES (95% CI)	0.10 (−0.03–0.21)	−0.09 (−0.20–0.03)	−0.02 (−0.15–0.10)	−0.02 (−0.16–0.11)	0.00 (−0.11–0.14)	−0.11 (−0.25–0.01)	−0.05 (−0.17–0.08)	0.03 (−0.09–0.15)

heiQ: Health Education Impact Questionnaire; SD: standard deviation; CI: confidence interval; ANOVA: analysis of variance; ES: effect size.

Overall, there were statistically significant differences between age groups, educational level and country of birth across a number of heiQ scales, but these significant differences were associated with ES for comparison groups that were always ≤0.3 (while the upper 95% CI was always <0.5). By the conventional rule-of-thumb, these ES are ‘small’ (>0.2 but <0.5) or trivial (<0.2). It might be noted, however, that while the ES are small at best, a general pattern emerges from the data for comparisons over sex and age. Mean HDA and SIS scores for males are higher than those for females, whereas mean ED scores are lower. Older respondents scored higher than those who are younger on PAEL, SMI, STA, SIS and HSN and lower on ED. Additionally, respondents with more formal education scored higher on PAEL, but lower on STA and SIS, and ED. As strong measurement equivalence has previously been demonstrated and as the ES for these across-group comparisons were, at their largest, small, it was considered acceptable to compute percentile ranks and ES for change on the basis of the full undifferentiated sample.

Percentile ranks for individual heiQ scale scores

PRs for the eight heiQ scales at baseline and follow-up are presented in full in the Online Supplementary Material. Both the raw summed score and its equivalent rescaled to the range of an individual item are presented in the tables together with the PR equivalent to the heiQ scale score and its lower and upper 95% CIs. Note that the PRs for the scores at the extremes of the distribution (<5 and >95) are tabled to one decimal place, whereas those further towards the centre of the score distribution are tabled in integers. This format follows the reporting standards suggested by Crawford et al.,²⁰ who argue that while greater precision towards the centre of the distribution may be distracting for the user, finer discriminations in PRs are useful for respondents whose raw scores are more extreme (particularly, in the case of heiQ scores, with the exception of ED, scores that are at the lower end of the distribution).

Note also that the CIs express the uncertainty associated with the use of the PR of the normative sample as an estimate of the PR of the normative population.²⁰ Due to the increased number of ties in the score distribution, the CIs will be broader with smaller samples and, for any given sample size, for scales with a relatively smaller range of scores. For example, compare the CIs for the four-item HDA scale for the PR associated with the raw-score mid-point of 10 (PR = 29, 95% CI = 23.4–34.5) to the narrower CI for the six-item SMI scale for the raw-score mid-point of 15 (PR = 8, 95% CI = 4.8–10.5). Both estimates are based on the same sized sample, but while there are 228 respondents with a HDA scale mid-point score of 10, there are only 113 respondents with a parallel SMI score of 15.

Using the PRs in the tables for each heiQ scale in the Online Supplementary Material to convert a course participant’s baseline heiQ raw or rescaled scores to percentiles for each heiQ scale can give insight into the characteristics of the participants who are being recruited for the course, relative to the characteristics of those who are typically recruited to self-management courses in Australia. Furthermore, inspection of the profile of an individual participant’s baseline percentile scores across the eight scales will provide insight into those domains where the participant might benefit most from a planned or individually targeted intervention. It is much preferable to use the percentiles for this comparison rather than the raw or rescaled scores as the use of PRs takes into account the relative ‘difficulty’ of the items that constitute the specific heiQ scales, whereas the use of, particularly, rescaled scores obscures the confounding influence of varying scale difficulties. (By ‘difficulty’ we mean the relative tendency people have to respond ‘strongly agree’ or ‘agree’ to the heiQ items that make up a particular scale.)

Similarly, converting a participant’s follow-up raw or rescaled heiQ scores to percentiles using the follow-up PRs in the tables gives insight into the extent to which the participant, post-intervention, is achieving levels of response to the particular scale and the domain of health-related behaviour the scale is referencing that are comparable with the post-intervention responses of the normative population. Additionally, comparison of a course participant’s follow-up profile with their baseline will provide an indication of the extent to which they have achieved gains across the heiQ domains, relative to gains achieved by the normative population. Finally, the percentile scores for individuals can be evaluated for the uncertainty that the point estimate of the sample PR is an accurate estimate of the population PR using the 95% CIs. This serves both as a useful reminder to users that test results such as the self-report scale scores from the heiQ are fallible estimates and giving one specific indicator of the extent of that fallibility.⁹

Baseline to follow-up ES

Estimates of the ES for the eight heiQ scales from baseline to follow-up together with their 95% CIs are shown in Table 4. ES range from approximately 0.50 to 0.15 (changing the sign of the ED ES to reflect a ‘positive’ result for this scale). The strongest impact of chronic disease self-management programmes in the normative sample is observed for STA, HDA and SMI (all ES >0.35), whereas the weakest effects were observed for SIS, HSN and ED (all ES <0.2).

Table 4.

Baseline to follow-up ES estimates for eight heiQ scales: full sample.

	ES (robust estimate, pooled variances)
	Estimate	Lower 95% CI	Upper 95% CI
HDA	0.40	0.36	0.47
PAEL	0.31	0.27	0.37
ED	−0.20	−0.23	−0.15
SMI	0.36	0.30	0.40
CAA	0.21	0.15	0.25
STA	0.50	0.45	0.55
SIS	0.15	0.10	0.21
HSN	0.18	0.14	0.22

ES: effect size; heiQ: Health Education Impact Questionnaire; HDA: Health-Directed Activities; PAEL: Positive and Active Engagement in Life; ED: Emotional Distress; SMI: Self-monitoring and Insight; CAA: Constructive Attitudes and Approaches; STA: Skill and Technique Acquisition; SIS: Social Integration and Support; HSN: Health Services Navigation.

There are a number of possible reasons for these apparent differences in standardised mean change across the heiQ scales. It is possible that the items in those scales where less change is observed were, on average, less ‘difficult’ for respondents to assert to (i.e. to ‘agree’ or to ‘strongly agree’) resulting in stronger ceiling effects at follow-up. Equally, however, it is possible that the differences observed across the scales reflect a predominant focus on practical health management and behavioural issues in the self-management programmes offered across Australia over the years from which the data were gathered. Either way these differences highlight the importance of interpreting the change profile achieved by a self-management programme against norms and benchmarks such as those presented in this article, rather than interpreting un-normed change score means.

These ES should be particularly useful at the level of individual self-management course groups by providing a comparison benchmark for anticipated change. Similarly, data might be aggregated across course groups and compared with the benchmarks to support the evaluation, for example, of the relative effectiveness of different course content or modes of delivery. Organisations might also find comparison of their overall performance in the delivery of self-management programmes against the benchmarks useful in reporting to government agencies, funding providers and so on.

ES for the larger organisations

There were 67 healthcare organisations represented in the database. The number of participants in these individual organisations ranged from 3 to 212 (mean = 33; median = 13). These contrasting values for the average indicate that the distribution was markedly skewed to the right, with a large number of organisations having small numbers of study participants (50% with 12 participants or fewer) and, conversely, a very small number of organisations having a large group of participants (6 organisations with >100 participants). This uneven distribution of the numbers of participants across organisations will potentially bias the ES calculated from the total sample in favour of the relative effectiveness (or otherwise) in bringing about the changes measured by the heiQ of those organisations with very large numbers of clients. However, it might be anticipated that these organisations may have the better established self-management programmes possibly resulting in stronger and more stable outcomes. In an attempt to balance better these potentially competing sources of bias, the ES achieved by organisations with more than 50 participants (14 organisations) were calculated for each programme separately (Table 5; Figure 1).

Table 5.

Baseline to follow-up ES estimates for eight heiQ scales: individual organisations with >50 respondents (N = 1352).

Org.	Org. N	HDA	PAEL	ED	SMI	CAA	STA	SIS	HSN
A	74	0.27	0.45	−0.35	0.43	0.20	0.49	−0.03	0.17
B	83	0.23	0.43	−0.20	0.25	0.18	0.78	0.24	0.15
C	122	0.27	0.37	0.04	0.59	0.10	0.64	0.18	0.32
D	157	0.61	0.49	−0.46	0.62	0.20	0.71	0.23	0.03
E	51	0.70	0.48	−0.22	0.42	−0.10	0.53	−0.15	0.08
F	120	0.61	0.46	−0.21	0.43	0.20	0.42	0.19	0.33
G	74	0.55	0.41	−0.04	0.29	0.11	0.15	0.05	0.08
H	56	0.81	0.35	−0.07	0.25	0.03	0.40	0.17	0.09
I	68	0.25	0.22	0.14	0.18	−0.12	0.32	0.08	0.03
J	64	0.45	0.27	−0.33	0.42	0.07	0.29	0.25	0.36
K	55	0.34	0.29	−0.13	0.36	0.22	0.36	0.14	0.17
L	77	0.43	0.32	−0.14	0.42	0.52	0.57	0.28	0.09
M	140	0.46	0.13	−0.15	0.28	0.23	0.48	0.19	0.05
N	212	0.48	0.59	−0.33	0.48	0.35	0.56	0.41	0.31
Median		0.45	0.39	0.14	0.42	0.19	0.48	0.18	0.12
75th percentile		0.59	0.46	0.30	0.43	0.21	0.57	0.24	0.28

Org: Organisation; Org N: Number of respondents in organisation; ES: effect size; heiQ: Health Education Impact Questionnaire; HDA: Health-Directed Activities; PAEL: Positive and Active Engagement in Life; ED: Emotional Distress; SMI: Self-monitoring and Insight; CAA: Constructive Attitudes and Approaches; STA: Skill and Technique Acquisition; SIS: Social Integration and Support; HSN: Health Services Navigation.

Smallest and largest ES values on each heiQ scale are given in bold.

Figure 1.

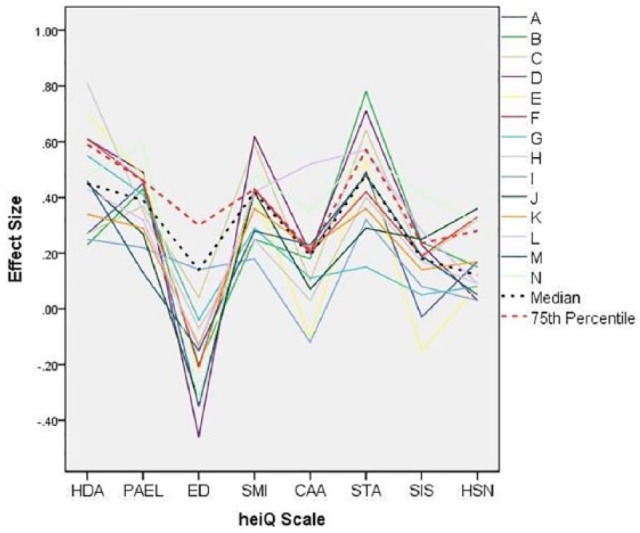
Effect size estimates for 14 organisations with >50 course participants.

It can be seen in Figure 1 that while there was a considerable variation in the ES achieved by the various organisations, there was some consistency in those scales on which the organisations achieved the higher standardised gains (HDA, PAEL, SMI and, particularly, STA). Similarly, consistent smaller improvements (or, indeed, declines) were observed on ED, CAA, SIS and HSN. These data mirror the patterns seen in the ES for data pooled across all participating organisations. Conversely, there appears to be little consistency in the relative achievement of organisations across the eight heiQ scales. The largest and smallest ES values for each scale are given in bold in Table 5. While organisation 1 has the smallest positive ES for SMI and shows the largest decline for CAA, and the largest gain for ED, no single organisation stands out as consistently achieving the largest positive changes. This pattern not only highlights the multi-dimensional nature of the desired proximal outcomes of self-management education programmes but also appears to reflect clearly differential success across organisations in achieving these outcomes.

A number of possible benchmarks for change on the heiQ scales might be derived from these data on individual organisations. We consider below the possibility of using the median of the ES estimates for the 14 organisations and the 75th percentile of the distribution of these estimates.

Which benchmark?

Three possible benchmarks against which the gains on the heiQ achieved by a self-management programme in Australia might be compared are suggested, derived from the following: (1) the baseline to follow-up ES achieved across the full normative sample, (2) the median ES achieved by the 14 organisations with >50 participants represented in the database and (3) the 75th percentile of the ES achieved by these 14 organisations (Table 6). In the absence of a ‘gold standard’ for change on the heiQ, it is not possible to offer a single recommendation for an organisation about which set of benchmarks to choose. As the estimates based on the group of larger organisations are possibly more stable than those based on the full sample that includes the large number of organisations with very small numbers of participants, we tentatively recommend the median ES achieved by the organisations for which samples of >50 are available for general use. Organisations wishing to evaluate the performance of a small sample of participants could choose to use the benchmarks derived from the full normative sample. If, however, an organisation wished to judge its performance against a more demanding standard, the 75th percentile of the ES achieved by the larger organisations might be used.

Table 6.

Three possible benchmarks for change on the heiQ scales.

Benchmark	HDA	PAEL	ED	SMI	CAA	STA	SIS	HSN
ES: full sample	0.40	0.31	−0.20	0.36	0.21	0.50	0.15	0.18
Median ES: large organisations	0.46	0.39	−0.14	0.42	0.19	0.48	0.18	0.12
75th percentile ES: large organisations	0.59	0.46	−0.30	0.43	0.21	0.57	0.24	0.28

ES: effect size; heiQ: Health Education Impact Questionnaire; HDA: Health-Directed Activities; PAEL: Positive and Active Engagement in Life; ED: Emotional Distress; SMI: Self-monitoring and Insight; CAA: Constructive Attitudes and Approaches; STA: Skill and Technique Acquisition; SIS: Social Integration and Support; HSN: Health Services Navigation.

Two worked examples

Percentile norms

As an example of the use of the percentile norms tables for individuals, consider a participant whose baseline and follow-up heiQ scores were as follows: HDA = 5, 14; PAEL = 16, 17; ED = 10, 18; SMI = 13, 20; CAA = 16, 15; STA = 9, 12; SIS = 17, 15; and HSN = 11, 14. (These data are from an actual participant in the database.) Using the percentile tables in the Online Supplementary Material, these raw summed scores were converted to their equivalent PRs and plotted in Figure 2. Looking first at the baseline PRs for this participant, we can see that they have very low scores, relative to the normative sample, on HDA, SMI, STA and HSN. Conversely, they are relatively high on PAEL, CAA and SIS. Broadly, this profile might be interpreted as suggesting this participant, prior to their course attendance, reported low levels of health focussed behaviours, perceived ability to monitor their physical and/or emotional health and the consequent insight into appropriate self-management activities, skills to help them cope with their condition and a self-perceived low level of ability to engage with the healthcare system. Conversely, the participant indicated a relatively high level of motivation to engage with life-fulfilling activities, a positive attitude towards the impact of their health problem and strong social engagement and support. Also, the participant indicated they had a relatively low level of emotional distress. After course participation, compared with the normative sample at follow-up, the participant reported a high level of health-supporting behaviours, a considerable relative increase in this domain. However, the participant was now, relative to the normative sample, reporting a high level of emotional distress and relatively lower levels than previously of social integration and support and constructive attitudes and approaches. It might be speculated that this person participated in a programme that had a strong focus on developing health-supporting behaviours (exercise, quitting smoking, appropriate diet, etc.) but that the programme (or the course environment) had the unanticipated impact, for them, of generating considerable emotional distress and somewhat diminished self-perceived social interaction and positive attitudes to life – a possible result of ‘response shift’ (a change in the response perspective) from baseline to follow-up.²⁵

Figure 2.

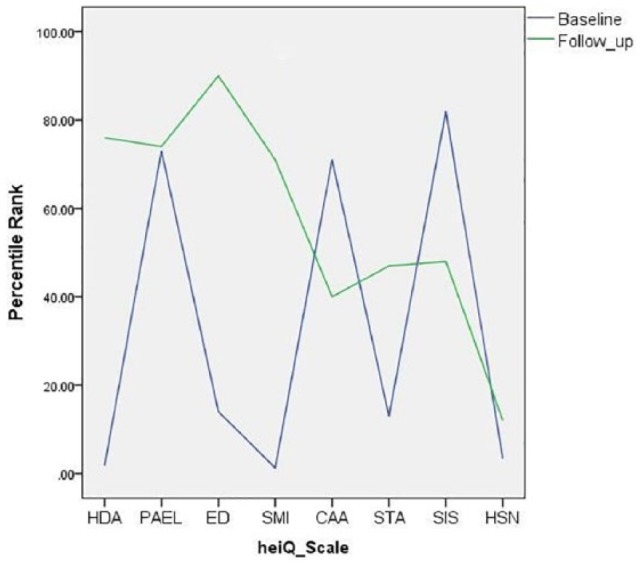
Baseline and follow-up heiQ percentile scores of a single course participant.

Group benchmarks for change

Date provided by one of the large organisations (N = 212) were extracted from the archive. The ES and accompanying CIs were calculated and plotted against the three proposed benchmarks in Figure 3. It can be seen that the ES estimates for this organisation exceed all three benchmarks for PAEL, SMI, CAA and SIS and the ES is lower than all three benchmarks for ED. Additionally, the organisation’s ES is higher than the overall ES for the normative sample and the median ES for the larger organisations for HDA, STA and HSN. As an organisation with a large pool of course participants, it is appropriate to compare its performance against the other large organisations in the database. It is clearly achieving significant change in this respect, performing better that 75% of the large organisations on 5 heiQ domains and better than the median on the other 3. As a caveat to these observations, however, it should be noted that the lower 95% CI for the ES estimates for this organisation exceeds the lower two benchmarks for only PAEL and SIS and is below the 75th percentile benchmark for all scales. While it is a relatively large organisation, the 95% CIs of the ES estimates are still relatively wide, thus introducing a clear element of caution into the interpretation of these results. It would be prudent for this organisation to accumulate additional data on the performance of their self-management programmes over a number of years before drawing unequivocal conclusions about the success of these programmes.

Figure 3.

Effect size estimates for a sample programme (N=288) compared against the three proposed benchmarks.

Discussion and conclusion

The percentile norms and benchmark ES presented in this article have been prepared to assist healthcare organisations interpret the scores they obtain from the heiQ, particularly when the questionnaire is used in a study design that includes baseline and follow-up administrations. While the data will be particularly relevant for Australian organisations and others using the English-language version of the heiQ, they could also be used by those using translated versions as a guide to the sensitivity of the scales and the extent of the changes that might be anticipated from attendance at a typical chronic disease self-management or similar health education programme.

The percentile norms will allow organisations and clinicians to interpret the scale scores of individual clients by facilitating the direct comparison of these scores with those obtained from the large normative sample. These individual normed heiQ scores at baseline might be used in a needs assessment prior to recommendations about the specific course that might be of most benefit to the client or for tailoring individual course experiences. Alternatively, they might simply be used as baseline data to facilitate charting individual improvement across course attendance. At follow-up, the percentile norms can be used to provide information on how the gains achieved by an individual client compare with those achieved by the normative sample. If the follow-up percentile equivalent of the client’s follow-up heiQ score is, for example, notably higher than their baseline percentile score, it might be concluded that they have gained more than would be anticipated compared with the gains in the normative sample (and, similarly, gained less than the normative sample if their follow-up percentile score is notably lower than their baseline percentile).

Considering the heiQ gains potentially achieved by groups of clients (e.g. individual course groups, year cohorts enrolled in similar courses and the organisation’s complete year cohort), we have provided three possible benchmark ES estimates for each heiQ scale. An organisation can calculate the baseline to follow-up ES for the heiQ scores of their group data using Keselman et al.’s software (robust, pooled variance option) for comparison against any one of these sets of estimates (selected a priori to provide an argued hypothesis for the size of the gain anticipated). The full sample estimate also has CIs available (Table 4). These can be used along with the CIs of the sample estimates to assess (conservatively at the 95% level of confidence if the CIs don’t overlap) whether or not the estimated ES for the organisation’s sample is significantly different (in a statistical sense) from the benchmark estimate. More generally, the provision of CIs for both the PRs and the ES remind organisations and individual health workers that the estimates are fallible²⁶ being susceptible to not only sampling error as for the CIs used here but also errors associated with the unreliability of the measurements used.

We recommend that judgements about the relative effectiveness of programmes and organisations be made by direct comparison of aggregated course heiQ scores with the benchmarks and caution against the ‘algorithmic’ application of Cohen’s¹⁰ rule-of-thumb values of 0.2, 0.5 and 0.8 to, respectively, establish ‘small’, ‘medium’ and ‘large’ ES for these baseline to follow-up data. This is particularly the case as Cohen’s ‘d’ was initially derived for the comparison of two independent groups, not the comparison of follow-up scores with a baseline. The ES derived from cross-sectional group comparisons and longitudinal data are not a priori directly comparable.²⁷ It is possible that the ES derived from a baseline to follow-up study will be inflated compared to an across-group study, partly according to the manner in which the ES is calculated and also due to the potential biases and threats to validity inherent in one-group baseline to follow-up designs.²⁸ For example, a large ‘meta-meta-analysis’ of the impact of psychological, educational and behavioural interventions reported a mean ES for randomised and non-randomised comparison-group research of 0.47 (with non-randomised designs yielding just a slightly lower ES than randomised designs) compared with a mean ES for one-group pre- and post-test research of 0.76.²⁹ This suggests that Cohen’s ES guidelines may not be appropriate for baseline to follow-up data, providing an upwardly biased intuition about the meaningfulness of the observed impact.

Finally, we emphasise that the ES presented here as benchmarks for change on the heiQ scales are not benchmarks for clinically significant change. Establishing clinically significant change for the heiQ scales would require either a study that involved independently socially validated judgements about the amount of self-reported change on the scales or data from comparison samples of ‘dysfunctional’ and ‘functional’ groups.³⁰ A possible alternative would be to benchmark heiQ change results against an indicator of ‘reliable change’.^31,32 This would have the advantage of building into the index of change estimates of the (un)reliability of the heiQ scales and the opportunity to move beyond benchmark values to the statistically-based classification of individuals as achieving heiQ results that are above a statistically-based threshold for achieving ‘success’ from the self-management programme.

Implications for practice

As noted in the ‘Introduction’ section, the principal aim of this article was to assist users to interpret the heiQ responses of their clients using percentile norms for individual baseline and follow-up scores and group ES for change over the duration of a range of typical chronic disease self-management and support programmes. We argued that norms and benchmarks can play an important role in assisting managers of healthcare organisations, their programme staff and clinicians interpret and use heiQ scores from monitoring and evaluation studies by drawing direct and meaningful conclusions about programme impact from them. In the absence of a comparison-group study, the ‘raw’ responses of an individual or group to subjective self-report scales are very difficult to interpret alone. As these ‘no intervention’ data are rarely available, norms and benchmarks derived from a defined population that is of similar composition to the one being evaluated can offer a valid and useful alternative.

We suggest that the percentile norms for individual baseline and follow-up heiQ scores can be used in a number of ways as illustrated in the first worked example. When baseline scores are converted to percentiles, a direct comparison can be made between the heiQ scores of an individual and those of the normative group, thus indicating how common among similar respondents that score is. This information might, for example, be used to evaluate where an individual’s self-management strengths and weaknesses lie and to suggest where best to focus their work in the course or, if available, what options might be best for them. A similar interpretation can be given to the individual’s follow-up scores where an assessment can be made of the extent to which scores have changed in comparison with those of the normative group. Has this person changed less than might be expected had they responded ‘on average’ to similar health education programmes, changed about the same as might be expected or exceeded what might be expected? Similar normative comparisons might also be made for a small course group if the heiQ data are summarised as median scores across the group. We recommend, particularly, that users focus on the pattern of the normed scores across the eight scales to provide insights as to where the individual or group of clients has benefited most and least. The use of individual or group median scores in this manner will suggest where follow-up interventions for individual clients might be focussed after an initial course experience, and where the organisation’s clients might benefit from a change in course content or emphasis.

The benchmarks for change provide similar information at the group level and will be useful for data derived from larger samples of clients, both for internal monitoring and course improvement and for public reporting, for example, to funding or accreditation agencies. Comparisons against the benchmarks might be particularly useful for monitoring programmes offered by organisations over a number of years where improvements (or declines) in course performance can be compared with those observed over the 6-year period encompassed by the benchmarks in similar organisations. For this purpose, we have offered the choice of three possible benchmarks, only one of which might be chosen according to the size and aspirations of the organisation. Thus, this article provides programme managers, staff and clinicians in organisations that use the heiQ with a range of strategies, that we believe, will enhance their ability to usefully interpret their data and to draw useful conclusions and recommendations from them.