Spectral CT of the Extremities with a Silicon Strip Photon Counting Detector

Abstract

Purpose

Photon counting x-ray detectors (PCXDs) are an important emerging technology for spectral imaging and material differentiation with numerous potential applications in diagnostic imaging. We report development of a Si-strip PCXD system originally developed for mammography with potential application to spectral CT of musculoskeletal extremities, including challenges associated with sparse sampling, spectral calibration, and optimization for higher energy x-ray beams.

Methods

A bench-top CT system was developed incorporating a Si-strip PCXD, fixed anode x-ray source, and rotational and translational motions to execute complex acquisition trajectories. Trajectories involving rotation and translation combined with iterative reconstruction were investigated, including single and multiple axial scans and longitudinal helical scans. The system was calibrated to provide accurate spectral separation in dual-energy three-material decomposition of soft-tissue, bone, and iodine. Image quality and decomposition accuracy were assessed in experiments using a phantom with pairs of bone and iodine inserts (3, 5, 15 and 20 mm) and an anthropomorphic wrist.

Results

The designed trajectories improved the sampling distribution from 56% minimum sampling of voxels to 75%. Use of iterative reconstruction (viz., penalized likelihood with edge preserving regularization) in combination with such trajectories resulted in a very low level of artifacts in images of the wrist. For large bone or iodine inserts (>5 mm diameter), the error in the estimated material concentration was <16% for (50 mg/mL) bone and <8% for (5 mg/mL) iodine with strong regularization. For smaller inserts, errors of 20-40% were observed and motivate improved methods for spectral calibration and optimization of the edge-preserving regularizer.

Conclusion

Use of PCXDs for three-material decomposition in joint imaging proved feasible through a combination of rotation-translation acquisition trajectories and iterative reconstruction with optimized regularization.

1. INTRODUCTION

Material discrimination capabilities offered by spectral x-ray techniques, such as dual-energy (DE) imaging, are of increasing interest in diagnostic CT for applications involving detection of contrast agents (e.g., iodine in blood vessels [1]) or endogenous materials (e.g., renal stones [2]). In the context of musculoskeletal extremities imaging, DE radiography has been commonplace for bone densitometry, while DE CT has recently been found to provide superior performance for detection of uric acid crystals in gout [3] or detection of bone marrow edema.

Photon counting x-ray detectors (PCXDs) can benefit material separation in spectral CT mainly due to the elimination of electronic noise and the ability to discriminate the energy of incoming photons and group them into energy bins [4]. Several PCXD configurations have been proposed using CZT, CdTe, or edge-on silicon strips (Si-strip) as the detection medium. Among the different PCXD technologies, edge-on Si-strip sensors provide count rates appropriate for x-ray imaging owing to the fast photon transport and relative purity of the high-quality Si crystals. Si-strip PCXDs have entered clinical use in scanning slot mammography [5] but their adaptation in CT imaging is challenged by the edge-on sensor configuration that typically involves sparse arrangement of sensor banks with gaps to accommodate detector electronics. In scanning slot mammography, complete sampling is achieved by motion of the source-detector assembly; however, extension of this concept to CT imaging requires dedicated acquisition trajectories. Iterative reconstruction approaches with appropriate regularization can help to achieve volumetric CT imaging for such sparse detector configurations. Application of Si-strip PCXDs to spectral imaging is also challenged by the relatively low absorption efficiency of silicon and the larger fraction of Compton interactions that degrade energy resolution and necessitate careful system calibration.

In this work we investigate the potential of Si-strip PCXDs for spectral imaging of the extremities. We present a bench-top CT system based on a Si-strip detector (Philips Microdose, Solna, Sweden), optimize detector calibration methods, evaluate a variety of acquisition orbits and iterative reconstruction approaches, and quantify performance in three-material DE decomposition in a context pertinent to application in joint arthrography.

2. METHODS

2.1. Silicon Strip Detector and Experimental Bench

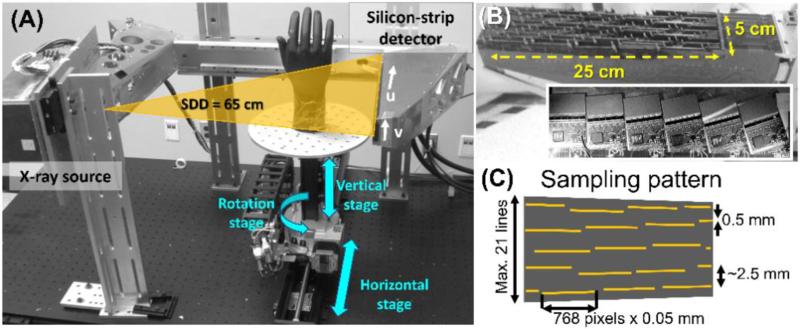
Fig. 1 (A) shows the CT imaging platform for the Si-strip PCXD. The detector [Fig. 1 (B)] consists of an array of line sensors with 0.05 × 0.5 mm² pixel pitch in edge-on configuration (thickness of 3.6 mm). Each pixel implements two energy thresholds, with the counts below the low threshold rejected as electronic noise, and a second threshold used for low- and high-energy bins in DE imaging. Coincident events are identified when two adjacent pixels are triggered within a ~20 ns time window. The coincident photons are assigned to the pixel that detected the higher signal. The sensors are slightly tilted to avoid interaction on the detector edges and focused on the x-ray source. As a consequence of the line tilt and accommodation of detector electronics, the sensors are arranged in a sparse array, with gaps as large as ~2.5 mm, as shown in Fig 1 (C). A pre-patient collimator matched to the detector grid ensures that the detector sparsity does not imply wasted dose to the patient, although the pre-patient collimator was removed for convenience in the phantom studies below. The complete detection area, including dead zones, spans a rectangular region of 25 cm in the long (u) axis, and 5 cm in the short (v) axis. For CT acquisition, the long axis of the detector, u, is placed perpendicular to the axis of rotation, providing ~10 cm axial field-of-view (FOV) and ~2.5 cm longitudinal FOV.

Figure 1.

(A) CT imaging bench. (B) Photograph and close-up of the PCXD. (C) Illustration of the sparse detector sampling pattern.

The CT bench employs a pulsed, fixed anode x-ray source (SourceRay, Rokonkoma, NY) mounted with the PCXD on a rigid arm to ensure proper focusing of the detector array. The source-to-detector distance is 65 cm in a half-fan configuration [see Fig. 1 (A)]. Two motorized linear stages combined with a motorized rotation stage for the object allow flexible selection of rotation-translation acquisition trajectories. Geometric calibration was achieved with a method developed specifically for the sparse detector. A planar arrangement of two thin wires parallel to the axis of rotation and intersected by an angled wire was imaged. The system geometry was estimated from the sinogram of two virtual points created by the intersection of the projections of the wires, which are easier to track in the sparsely sampled frames than projections of spheres typically employed in CBCT geometric calibration.

Data acquisition was performed at 60 kVp with 2 mm Al equivalent inherent filtration (as reported by the manufacturer) and no additional filtration. Projections were acquired at 1° steps with 30 ms pulses and 2 mA / pulse.

2.2 Acquisition Orbits for Improved Sampling

The sparse pattern of the sensors in the PCXD does not yield sufficient sampling for high quality CT reconstruction in a single axial circular scanning trajectory, motivating the design of modified acquisition trajectories. For acquisition of a single 2D axial slice, we developed a trajectory in which the center of rotation is translated by 6 mm in the u direction for alternating projections. The proposed trajectory yields two sinograms with 180 projections combined in reconstruction.

For full volumetric imaging, sparse sampling in the v direction was compensated by the addition of vertical translation to the trajectory. We investigated the modified sampling and reduction in artifacts for a set of trajectories involving six vertical axial steps (0.5 mm increment) and angular acquisition range of 180°, 270° and 360°. Acquisition with continuous helical motion is in progress. The orbits were evaluated in simulation studies involving a test phantom consisting of a random arrangement of hypo-dense spheres of 2 - 10 mm diameter embedded in a cylindrical background (88 mm diameter), as well as in an experimental study with an anthropomorphic wrist phantom. The sampling density was quantified as the number of rays passing through each voxel in the acquisition.

As shown below, the modified trajectories improved the sampling density significantly but did not yield complete volumetric sampling. To improve robustness to undersampling effects in the reconstruction, an iterative reconstruction method was implemented to permit arbitrary system geometries and regularization that reduced deleterious effects of projection gaps on image quality. We used penalized likelihood (PL) statistical reconstruction with a monochromatic Poisson signal model [6]:

$$L(\mu ;y)=\sum _i{y}_i\log I_{0i}{e}^{-l_i}-I_{0i}{e}^{-l_i}$$ (1)

where μ is the reconstructed attenuation and y the measured projection values with i sweeping through all the projection pixels and I_0i is the bare beam signal. The line integral through the volume for the ith ray is denoted by l_i = [Aμ]_i, where the matrix A represents the linear projection operator. Reconstruction was performed minimizing the following objective function:

$$\widehat{\mu }=\arg {\max }_{\mu }L(\mu ;y)-\beta \cdot R\left(\mu \right)$$ (2)

where R(μ) is a regularization function with strength β. We set the I_0i term in positions corresponding to the gaps to 0 to let the regularization term compensate for the lack of projection data. A Huber penalty function was used. Reconstructions were obtained with 50 iterations (30 subsets) at 0.3 × 0.3 × 0.5 mm³ voxels.

2.3 Detector Calibration and Dual-Energy Decomposition

Material decomposition in spectral CT imaging requires calibration of the threshold values to equalize the response of the pixels across the detector area. Low-energy (noise) threshold variations were reduced by tuning the threshold position to obtain a uniform ratio of coincidence to primary events across the detector in the bare beam. The ratio of pixel variance to mean pixel signal was used to estimate the upper limits for the low energy threshold, where some pixels enter saturation and noise no longer follows a Poisson distribution. In the second calibration stage, the attenuation behind a 0.5 mm thick silver sheet was measured as a function of the high energy threshold. Threshold trims where adjusted to obtain the best match of the positions of the silver K-edge (25.5 keV) across pixels.

Three-material decomposition was performed in the reconstruction domain using bone, iodine, and soft tissue as basis materials. We followed the approach in [7] that assumes that the concentration of the three materials in each voxel adds to unity, thus providing the third equation to solve the decomposition problem using only two energy bins. Optimal high- and low-energy thresholds for material decomposition were estimated using the phantom depicted in Fig. 2(A) consisting of an acrylic cylinder with four tissue-equivalent plastic inserts (Gammex, Middleton WI): calcium (100 mg/mL), iodine (5 mg/mL and 10 mg/mL), and adipose tissue with 0.9 g/cm³ density. The phantom was imaged with low-energy threshold values of 60 and 100 and high-energy threshold values of 120, 130, 140 and 150. Threshold values are expressed in internal detector units (DU) that are nonlinearly related to photon energy. The mean attenuation for the low- and high-energy bins was measured in 20×20 pixel ROIs in the two iodine inserts, in the bone insert, and background. Separation between materials was estimated as the angle between the line connecting soft-tissue attenuation to iodine attenuation and the line connecting soft-tissue to bone. The performance of material decomposition was assessed in a phantom consisting of pairs of iodine (5 mg/mL) and bone (50 mg/mL) inserts (Gammex, Middleton, WI) with diameters of 3, 5, 15 and 20 mm, shown in Fig. 2(B). Material classification accuracy was quantified by measuring the ratio of voxels with concentration above 50 % of the nominal value to the total number of voxels in the insert.

Figure 2.

(A) Calibration phantom with inserts of bone, iodine and adipose in an acrylic background and (B) evaluation phantom containing pairs of bone iodine inserts of matched size submerged in water.

3. RESULTS AND BREAKTHROUGH WORK

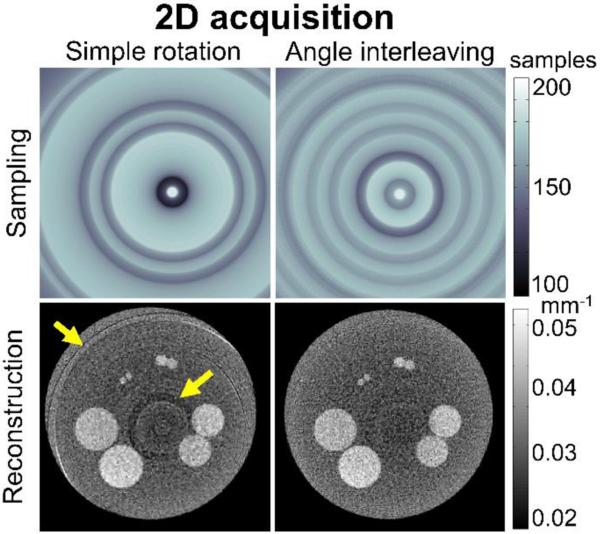
Fig. 3 shows the result of using the modified sampling pattern for 2D axial slice acquisition. The image acquired using a simple circular trajectory shows artifacts due to the detector gaps that are only partly mitigated by the penalty term in the PL reconstruction (Eq. 2). The modified trajectory (angle interleaving) showed the same mean sampling density as the circular scan (87% of full sampling, defined as that obtained with a continuous detector), but with larger homogeneity (minimum density of 75%, compared to 56 % for the original case) that resulted in a significant reduction of artifacts.

Figure 3.

Effects of various acquisition trajectories for 2D axial slice imaging. A simple circular trajectory yields artifacts due to detector gaps (partly alleviated by regularization in PL) that are greatly reduced using the rotation-translation orbit as shown in the right column.

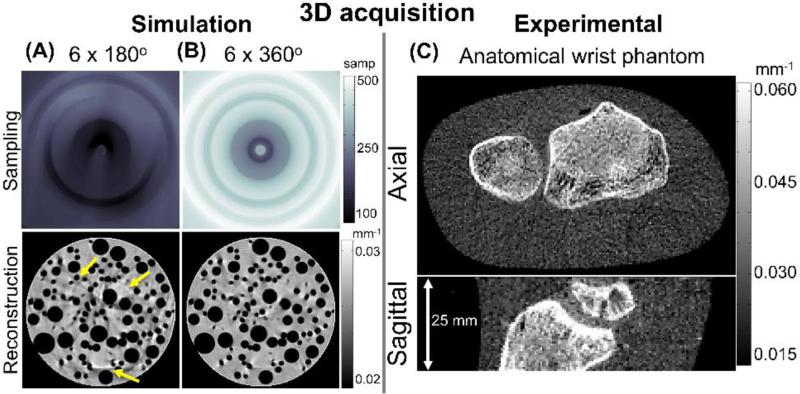
Figs. 4 (A) and (B) show the results of a simulation study of two 3D imaging orbits combining vertical translation (6 positions, 0.5 mm increment) with rotation (180° and 360° angular range). The images exhibit nearly complete elimination of sampling artifacts when the vertical motion is combined with full rotation (360°). Fig. 4 (C) shows a reconstructed volume of a wrist phantom (natural bone embedded in soft tissue mimicking plastic) exhibiting only marginal artifacts and fairly high quality in visualization of bone details.

Figure 4.

(A, B) Sampling patterns and reconstructions of simulated projections of a test phantom for two examples of 3D rotation-translation orbits for 3D imaging (C) Images of a wrist phantom acquired on the PCXD test bench with the improved sampling trajectory.

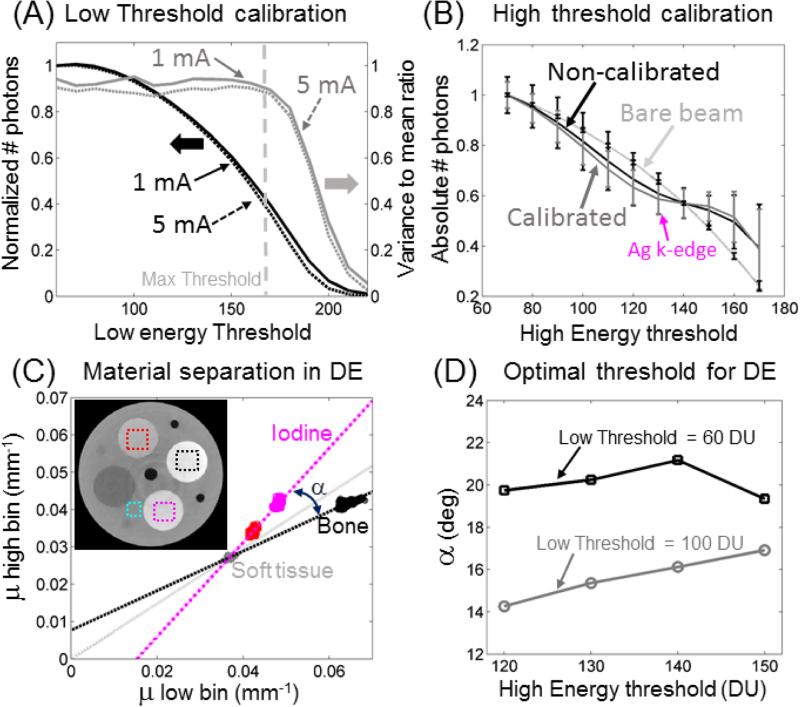
Figure 5 (A) shows variance proportional to mean signal with a ratio of around 0.9 (gray line) for thresholds below 150, above which some pixels start to show effects of saturation. The ratio remains constant for exposures from 0.5 mA to 5 mA, indicating that pile-up is not an issue in this exposure range.

Figure 5.

(A) Low threshold calibration. (B) High threshold calibration. (C) Material separation in μ_low-μ_high for bone and iodine. (D) Maximum material separation was observed for low threshold of 60 DU and high threshold of 140 DU.

Fig. 5 (B) shows that after calibration of the high energy threshold (gray line), the K-edge of silver becomes more conspicuous than before calibration (black line), indicating reduced variability of pixel response. This is also signified by a reduction of 40 % in standard deviation computed over all detector pixels. Study of optimal threshold position [Fig. 5 (C) and (D)] yielded a value of 60 DU for low and 140 DU for high threshold to maximize the dual-energy separation between iodine and calcium.

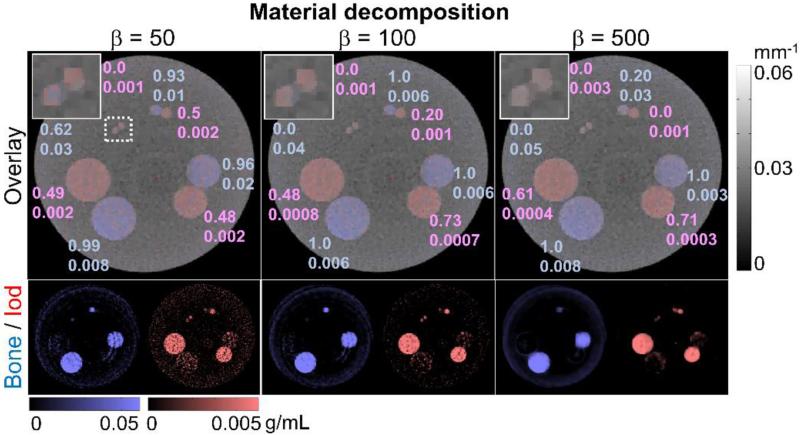
Figure 6 shows the material decomposition for the evaluation phantom for low (β = 50), medium (β = 100) and strong (β = 500) regularization. Material decomposition images overlaid over the conventional CT images (reconstructions of the sum of low and high energy bin projections) show that areas of the phantom containing iodine are properly separated from bone areas despite their very similar attenuation value in the conventional CT. Estimated concentration values of iodine showed root mean squared errors (RMSE) between 0.001 and 0.002 (nominal concentration of 0.005 g/mL) for β = 50. When the threshold for classifying a voxel to one of the base materials was set at 50 % of the nominal concentration, the resulting classification was successful for ≥50 % of the voxel for the 5, 15, and 20 mm regions. The performance in the smallest region (3 mm) was significantly poorer due to a reduction of the reconstructed values caused by the smoothing effect introduced by the regularization process, hampering the classification of the iodine pixels. Larger values of β improved the decomposition performance in the larger regions (15 and 20 mm), reducing RMSE to 3×10⁻⁴ and 4×10⁻⁴, for β = 500, and increasing classification accuracy to 71% and 61%, respectively. However the better performance in the larger regions was accompanied by increased classification errors and no improvement in RMSE in the 5 mm region compared to weaker regularization. Bone regions showed a similar behavior but with lower error values. For low β (β = 50), very high classification accuracy (> 93 %) was achieved in bone for the 5, 10, and 15 mm regions, whereas the 3 mm insert exhibited a somewhat less successful classification with accuracy of 62 %. RMSE of 0.008, 0.02, 0.01, and 0.03 (nominal concentration 0.05 g/mL) was found in the 3, 5, 15 and 20 mm regions, respectively. Increasing β to 100 reduced the RMSE, permitted the correct classification of all pixels (classification accuracy=100%) in all areas except the 3 mm region, in which the RMSE increased from 0.03 to 0.04 and the fraction of pixels correctly classified was reduced from 0.62 to 0. For β = 500 the same trend was observed, with a reduction in RMSE value in the two larger regions, but an increase of RMSE and reduction of the classification accuracy (to 20 %) in the 5 mm region.

Figure 6.

Material decomposition for the evaluation phantom for low (β = 50), medium (β = 100) and strong (β = 500) regularization. Top row shows the overlay of the composite reconstruction (low-energy bin plus high-energy bin) with material decomposition (Calcium in blue, Iodine in red), and the bottom row shows individual materials. Numerical values show classification accuracy using a detection threshold at 50% of the nominal concentration (top number) and RMSE (bottom number) of the estimated concentration in g/mL. Larger β provided better RMSE values for large inserts but in the case of small inserts, the use of a large β spread the background into the inserts, degrading the performance of the algorithm and decreasing the estimated material concentration.

4. CONCLUSIONS

Three-material decomposition of soft-tissue, iodine, and calcium was achieved with Si-strip PCXDs in a spectral CT imaging arrangement. The use of modified acquisition trajectories helped to overcome undersampling effects when combined with strong (TV-like) regularization. True helical trajectories combined with translation motion could provide better performance and is a subject of ongoing research.