Abstract
Opinions are rarely binary; they can be held with different degrees of conviction, and this expanded attitude spectrum can affect the influence one opinion has on others. Our goal is to understand how different aspects of influence lead to recognizable spatio-temporal patterns of opinions and their strengths. To do this, we introduce a stochastic spatial agent-based model of opinion dynamics that includes a spectrum of opinion strengths and various possible rules for how the opinion strength of one individual affects the influence that this individual has on others. Through simulations, we find that even a small amount of amplification of opinion strength through interaction with like-minded neighbors can tip the scales in favor of polarization and deadlock.
Keywords: Echo chamber, influence, opinion dynamics, opinion reinforcement, opinion strength, polarization, spatial, voter model
1. Introduction
Opinion dynamics are often modeled under the assumption that there are just two options, such as “yes or no,” “candidate 1 or candidate 2,” or “vaccinate or not.” While at voting time issues are often presented in this binary way, the opinions people hold generally occupy a wider spectrum. Even in cases where an issue has only two sides, strength of opinion can play an important role in both behavior (voting vs. not voting) and the likelihood of influencing or being influenced by the opinions of others. Gridlock can occur when political parties become polarized, with most influence being held by individuals with more extreme opinions and little tolerance for moderate voices “in the middle.” Concurrent with this influence of extremes is often an “echo chamber” dynamic in which opinions are hardened through one-sided interactions even in the absence of any new evidence to support a particular opinion. In alter-native scenarios, a more diverse spectrum of opinions might be maintained, or moderation might triumph over extreme views.
In this article we introduce a spatial agent-based model that allows us to explore these population-level behaviors, and how they are driven by local interactions. Each agent in the model can have one of two basic opinions; these opinions are further subdivided according to how strongly they are held. In addition, the model includes state-dependent influence functions that mediate “imitation dynamics,” as well as a mechanism for “hardening of opinions” through an amplification of confidence that is based on agreement with neighbors. Amplification means that an individual expresses a type of confirmation bias, interacting with another individual with the same opinion increases the entrenchment of the first individual’s opinion. This is consistent with empirical findings (Lord, Ross, & Lepper, 1979; Miller, McHoskey, Bane, & Dowd, 1993; Munro et al., 2002; Taber & Lodge, 2006). We analyze spatial and temporal aspects of the opinion dynamics that arise in response to these features, and we explore conditions leading to polarization, centrality, and uniform (flat) distributions of opinions.
Our model has some behaviors reminiscent of the (linear) voter model and the threshold voter model (Holley & Liggett, 1975; Clifford & Sudbury, 1973; Durrett, 1988; Liggett, 1999), with clustering of like opinions and the absence or presence of surface tension (Castellano, Fortunato, & Loreto, 2009; Dall’Asta & Castellano, 2007). It also exhibits features observed in other models of opinion dynamics and cultural dynamics. Especially important among these is polarization (Schelling, 1971; Nowak, Szamrej, & Latané, 1997; Axelrod, 1997; DeGroot, 1974; Horowitz, 1962; Deffuant, Neau, Amblard, & Weisbuch, 2000; Weisbuch, Deffuant, Amblard, & Nadal, 2003; Hegselmann & Krause, 2002; Flache & Macy, 2011; Dandekar, Goel, & Lee, 2013; Friedkin & Johnsen, 2011; Friedkin, 2015), though the mechanisms that give rise to polarization vary across models, and the mechanism we explore here is different from those studied previously (see Discussion).
An interesting feature of our model is that adding a small tendency for hardening of opinions results in qualitatively different behavior at the population level. Models in social sciences teach us how small changes at the micro-level can sometimes produce large changes at the macro-level. For example, in the Schelling segregation model (1971), a small preference for having neighbors of the same type can produce strong segregation patterns. In our model, we show how a small probability for hardening of opinions is magnified at the macro-level, producing ever larger clusters of opinions with fairly well-defined boundaries, eventually leading to polarization in the spectrum of opinions.
We proceed first with a description of our opinion model and its associated simulations in Section 2. In Section 3, we describe the behaviors of the model as (1) spatial configurations that develop over time, and (2) global frequencies of opinions. After presenting our simulation results, we discuss the implications of our findings in Section 4 and compare our model to others that aim to capture similar phenomena.
2. Mathematical model
Our simulations are based on a discrete-time stochastic spatial model, or agent-based model. Individuals reside at sites on a 2-dimensional square grid, one individual per site. Each individual is characterized by an attitude from the attitude spectrum
This value encodes the individual’s opinion as well as its strength. Positive values all correspond to the intensities with which one opinion is held, while negative values correspond to the intensities with which the opposing opinion is held. The larger the absolute value, the stronger the opinion held, with ±L representing the strongest opinions. Thus, individuals with the same opinion can have different attitudes (i.e., strengths of opinion). Note that there is no 0 attitude, and so no individual can hold a position that is completely neutral. This constraint is consistent with the binary voter model (Holley & Liggett, 1975; Clifford & Sudbury, 1973), which was one of the inspirations for this work.
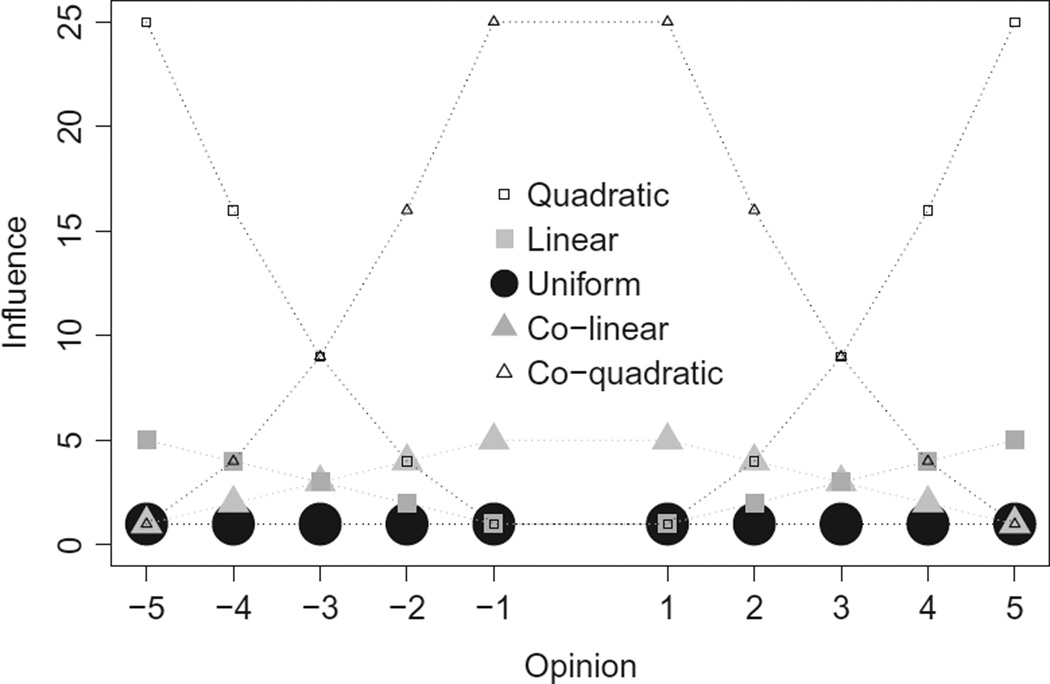
To account for the notion that the strength of an individual’s opinion can affect the probability that that individual influences another, we define an influence function 1(a), a ∈ 𝒜, that gives the influence exerted by an individual with attitude a. We consider five different influence functions (cf. Figure 1) as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
The linear and quadratic functions give more influence to individuals with strongly held opinions; the co-linear and co-quadratic functions give more influence to moderately held opinions; and the uniform function gives everyone the same influence.
Figure 1.
Plot of the five influence functions we consider, shown here for L = 5. For the linear and quadratic influence functions, influence increases with the absolute value of the opinion. For the co-linear and co-quadratic influence functions, influence increases for more moderate opinions. Note that influence functions are only defined for integers. Connecting lines are provided as guides for the eye.
The entire grid of attitudes is updated simultaneously as follows: Given the current configuration of attitudes on the grid, the attitude value for each site at the next time step is computed and stored, and then the entire grid is updated at once. For a particular site, say x, the new attitude is computed in two steps. A neighbor must first be chosen according to probabilities that depend on the influence function, and then the attitude at x is adjusted accordingly. For the first step, let us denote the 8 nearest sites in the “local neighborhood” of x as 𝒩(x). Then neighbor z ∈ 𝒩(x) is chosen with probability
where each value y is the attitude value from the current generation. In other words, a single neighbor is chosen with probability proportional to its influence (relative to the other neighbors).
For the second step, the individual at site x adjusts its attitude based on the attitude observed at the chosen neighboring site z. Here we allow two types of interactions that differ in their response to agreement; i.e., when the interacting individuals are on the same side of the attitude spectrum. A fraction pa of the interactions result in a hardening of the opinion of the individual at the focal site x when the selected neighbor at site z has the same opinion; a fraction 1 − pa of these interactions result in no change when the neighbors agree. We refer to pa as the probability of “opinion amplification.” More formally, at a given time step, the attitude at site x is updated according to one of the following:
No opinion amplification: With probability 1 − pa, A(x) is moved one allowable step toward the value of A(z). Note that since there is no zero state in 𝒜, a move to the left from +1 involves a jump to −1, and vice versa. If A(z) = A(x), then A(x) will not change.
Opinion amplification: With probability pa, A(x) is moved one step to the right if A(z) > 0 and one step to the left if A(z) < 0, regardless of where the value of A(z) lies in relation to A(x).
To illustrate these two processes, consider the situation where 1 ≤ A(z) < A(x) < L. Both individual x and neighbor z have opinions on the positive side of the spectrum, but neighbor z’s attitude lies to the left (more neutral) of individual x’s attitude. Under no opinion amplification, A(x) will move one step toward A(z), that is, A(x) becomes A(x) − 1. The interaction of x with a more neutral neighbor moderates x’s opinion. Under opinion amplification, however, the opposite change is observed. Since the attitude of neighbor z lies on the same side as the attitude of individual x, A(x) becomes more positive, that is A(x) + 1. In this case, the interaction of x with a neighbor sharing the same opinion, no matter how moderate or extreme, leads to an echo chamber effect where individual x moves toward a more extreme opinion.
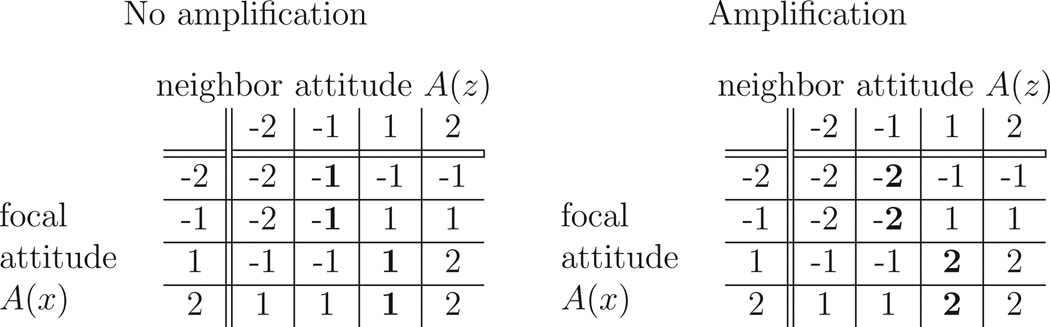
In some cases, both attitude adjustment processes result in the same shift at x. It is thus important not to confuse entrenchment with amplification; entrenchment is a change towards a more extreme attitude, while amplification is the disposition to become more extreme when interacting with any like-minded individuals (even less extreme ones). For the case where L = 2, all possible interactions and their result are shown in Figure 2.
Figure 2.
These tables show how a focal individual’s attitude, A(x), is updated given the selected neighbor’s attitude, A(z), where the attitude spectrum ranges from −2 to 2. Numbers in boldface highlight the difference between no amplification and amplification.
Note that simultaneous updating means that attitudes are updated based on the spatial attitude configuration from the previous generation. The interactions with neighbors need not be reciprocal; even if the individual at x chooses neighbor z, z gets to choose its own neighbor from 𝒩(z) when deciding how to update.
This model was coded in NetLogo (Wilensky & Evanston, 1999) and is available in the NetLogo Modeling Commons at http://modelingcommons.org/browse/one_model/4530
For the model to work, the user also needs to download the rnd extension https://github.com/NetLogo/Rnd-Extension
3. Model behavior
In the special case of only two attitude states, 𝒜 = {−1, 1} (and hence no influence function effect) and no amplification, pa = 0, our model behaves like the (discrete time) voter model. Over time, opinions begin to cluster, i.e., regions form where sites all have the same opinion. As with the voter model, there is no “surface tension” to form smooth boundaries (like water droplets), and so boundaries between opposing clusters remain rough (more on surface tension below in 3.1). The smooth boundaries that are characteristic of surface tension appear with other parameter settings, discussed below, and are similar to those in the threshold voter model (Liggett, 1999; Durrett & Steif, 1993).
New behaviors arise when we expand the attitude spectrum (L ≥ 2) and introduce amplification (pa > 0) and/or attitude-dependent influence. These new behaviors appear even for L = 2 and low values of pa. Below, we group the behaviors of our model in two ways, one focusing on spatial aspects, the other on the global frequencies of attitudes.
3.1. Spatial behaviors
One of the common behaviors we see across all influence functions, as long as there exists some amplification, is “surface tension,” similar to behavior in the threshold voter model, where boundaries between clusters of different opinions are fairly smooth compared to the noisy boundaries in the voter model. This surface tension leads to “motion by mean curvature” (Castellano et al., 2009; Dall’Asta & Castellano, 2007) (see Figures 3 and 5). Roughly, this means that a region that is more or less surrounded by opposing opinions is more likely to be converted to the surrounding opinion. This behavior leads to the gradual removal of “dents”; circular shapes and straight lines tend to keep their shape, with circular regions tending to decrease in size and straight line boundaries being very stable. Surface tension and motion by mean curvature are concepts that are defined for continuous (reaction diffusion equation) models and are only approximate in our model, which has discrete space and stochastic dynamics, but they do lend some insight. Surface tension occurs in our model with linear or quadratic influence, even without opinion amplification, and for equal, co-linear, and co-quadratic influence provided that opinion amplification is sufficiently large. In these cases, surface tension behavior develops in three phases as follower (see Figure 4):
Boundary formation. In very early stages of the simulations, starting from a completely random configuration, small clusters begin to form. These clusters quickly aggregate into larger clusters and form rough boundaries.
Boundary smoothing and cluster homogenization. As clusters increase in size, their interiors are not exposed to contrary opinions; any amplification will tend to push these attitudes toward the extreme end of that side of the spectrum. With this homogenization and extremization, sites at the boundary between two clusters (the only ones that can change their opinions) become more resistant to change, with most changes occurring at sites that are “outnumbered” by neighbors of the opposite opinion. This promotes smoothing of boundaries on a small scale and is the precursor of the next phase.
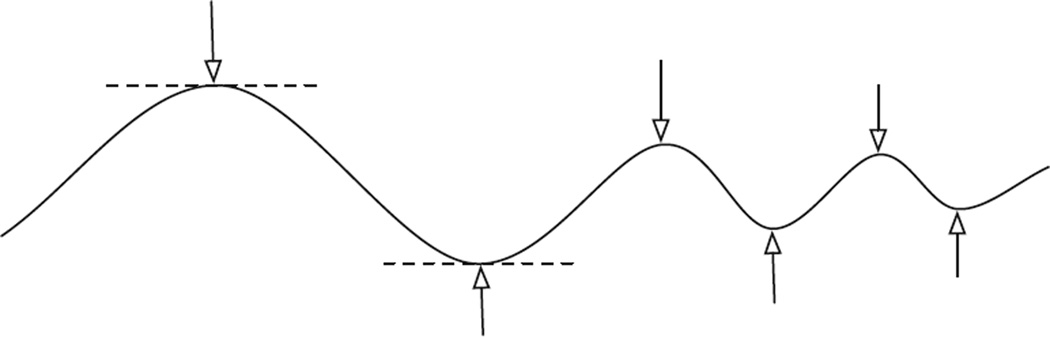
Boundary contraction. Once boundaries have become smoother, few opinions spread into regions with opposing opinions. However, where the boundary is curved, the opinions on the side of the curve that contains the tangent have an advantage and the opinions on the opposite side tend to be changed (see Figure 3).
Figure 3.
Boundary contraction: Opinions on the side of the curve that contain the tangent (dotted line) will tend to spread in the direction of the arrow.
Figure 5.
Evolution of attitudes from three different initial configurations on a 65×65 lattice with uniform influence and amplification probability pa= 0.1. The top row has an attitude spectrum with L = 5, while the other two rows have L = 2. These sequences illustrate that when one kind of opinion (here, black) is surrounded by another (here, white), the inside opinion eventually disappears, regardless of the initial black:white opinion ratio. While the ultimate outcome is known, the rate at which consensus is reached depends on the initial size of the clusters (compare rows 2 and 3), and on the size of the attitude spectrum (compare rows 1 and 2). With a larger attitude spectrum (row 1), the clusters have higher surface tension. While this tension slows down the rate at which the clusters disappear, it also makes the emergence of isthmus structures (see the 2nd panel in row 2) less likely. The initial black:white opinion ratio is approximately 1.3:1 (significantly more black than white). Snapshots are taken at times 0, 200, 400, and 800.
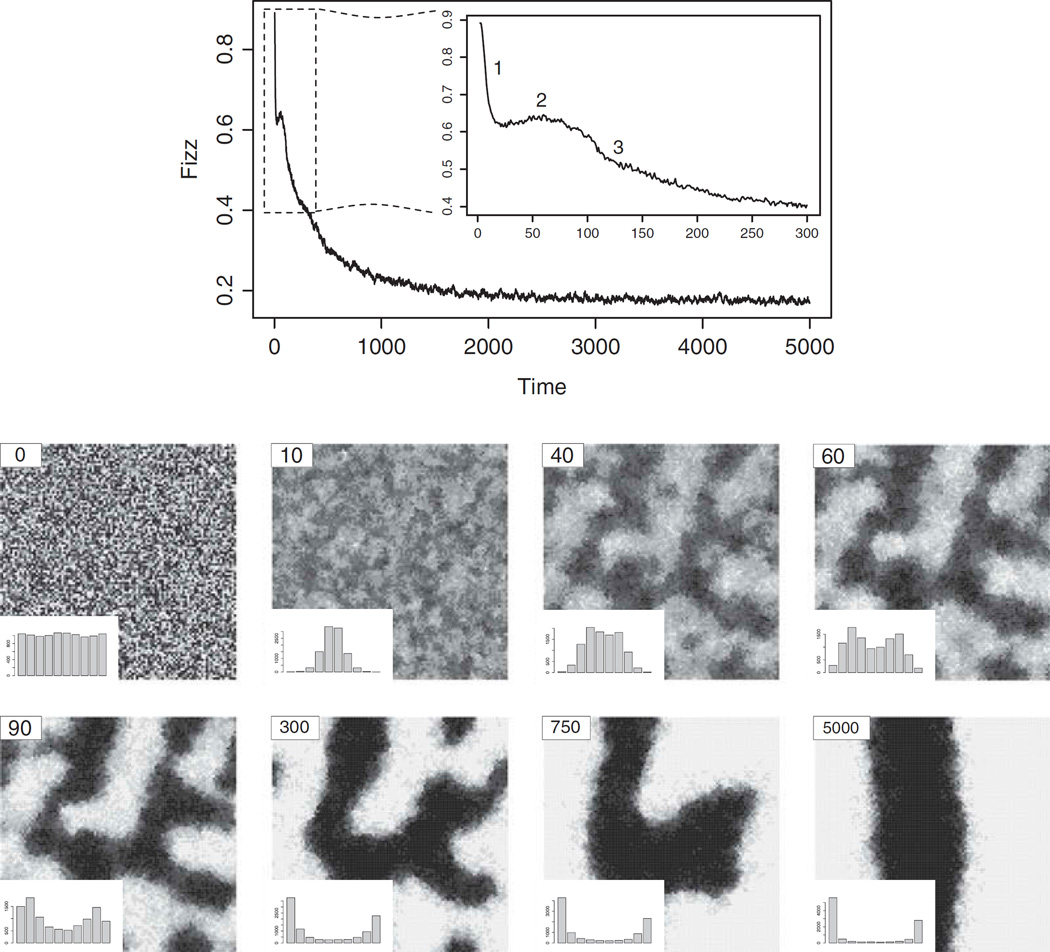
Figure 4.
Snapshots of a simulation on a 101×101 grid, with low amplification (pa = .07) and uniform influence. Inserts in the bottom left corners show the distribution of attitudes between −5 and 5 at the respective times, indicated in the top left corners. The time plot tracks fizz, the fraction of sites where an attitude has changed. Notice the relationship between the distribution of attitudes, spatial patterns, and fizz. The simulation begins with a uniform distribution of attitudes. Within 40 time steps there is significant clustering and boundary formation. The first period of high but rapidly decreasing activity (indicated by “1” in the time plot) is followed by a brief period where fizz increases slightly (see “2”; this corresponds to a widening of attitude distribution from a more centered distribution). Spatially, we observe the smoothing and sharpening of boundaries. This next period leads into a more gradual decrease in fizz (see “3”) and the contraction of boundaries via motion by mean curvature. These three periods correspond to changes in the frequencies of attitudes, where we first observe centering, and then a gradual increase in polarization.
These three phases correlate with change in a quantity we call fizz, the global fraction of attitudes that change at each time step. Fizz represents changes in opinion (e.g., from 1 to –1) as well as changes in intensity of opinion (e.g., from 1 to 2). Visually, these changes in attitude and how they spread in the vicinity of boundaries produce an effect that looks like carbonation.
Some levels of fizz or its rate of change can be associated with different spatial patterns. Consider the simulation depicted in Figure 4, where the initial configuration was completely random. Boundary formation occurs over approximately the first 25 time steps, boundary smoothing over approximately the next 75 time steps, and then boundary contraction for the remaining time. The first phase of boundary formation leads to the appearance of many small clusters and corresponds to fizz dropping rapidly from an initially high level. Over the next two phases, cluster interiors become more resistant to change, boundaries become smoother, and total boundary length declines. This leads to a gradual drop in fizz.
Note that the spatial process of boundary contraction can introduce a bias in the distribution of attitudes. Both amplification and influence functions are symmetric in that they do not bias the frequency of attitudes on one side of the spectrum or the other. However, when clusters form, their spatial configuration itself can favor one side of the attitude spectrum, even if opinions on that side are held by fewer sites. This is effectively motion by mean curvature. In Figure 5 we show how consensus in one direction can be biased by the topology of clusters.
3.2. Frequency behaviors
Another set of behaviors exhibited by the model appear in the frequencies of attitudes. These include polarization, centering, and consensus, which are related to the boundary behaviors just discussed. A population is polarized when the majority of the population is roughly balanced on the extreme ends of the attitude spectrum. A population is centered when most attitudes reside in the center of the spectrum (e.g., on −1 and 1). A population reaches consensus when everyone has the same opinion (i.e., attitudes on the same side of the spectrum). There is no mechanism in the model for reconstituting an opinion that has been lost to the population, so the two types of consensus represent “absorbing states.” Since our grid is finite, a population will eventually reach consensus given enough time. We are interested in the dynamics of how consensus is reached. In particular, what are the frequency behaviors in the interim period before consensus, especially in the early stages, and is the approach to consensus slow or fast?
To simplify the analysis, ‘we restrict our presentation to the case L = 2, which corresponds to the smallest attitude spectrum wherein influence functions and opinion amplification are relevant. Simulations with this spectrum exhibit all the behaviors seen in simulations with larger spectra, although the time scales are affected, with a larger spectrum of attitudes requiring a longer time for opinion shifts.
Given 𝒜 = {−2, −1, 1, 2}, we define the population center as the proportion of the population with A(x) = ±1, population left as the proportion with A(x) = −2, and population right as the proportion with A(x) = 2 (where there is no confusion, we drop the term “population”). We say a population is polarized when the population center is low and both left and right are high. A population is centered when center is high and both left and right are low. We define population center to include both −1 and 1, so a uniform distribution of attitudes would have center at a frequency of 0.5, and left and right at a frequency of 0.25 each (see time 0 in Figures 6 and 7). Hence, polarization is indicated when both left and right are above 0.25 and center drops below 0.5.
Figure 6.
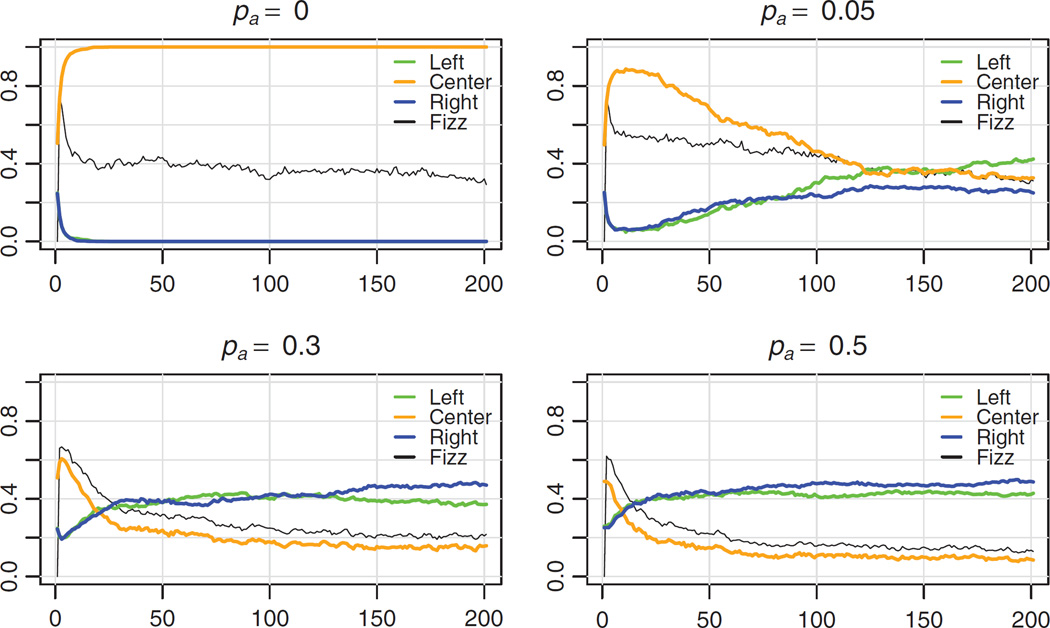
Temporal plots of the frequencies of left (green), right (blue), and center (orange), along with fizz, for different values of amplification probability (pa) when the influence function is uniform. The top left figure indicates rapid centering of attitudes. In the top right figure, equal frequencies of the four attitudes is reached around 80 time steps; following this point, the attitudes on the left and right begin to dominate, with the left being more prominent. In the two bottom figures, polarization emerges. (Note that because center includes both −1 and 1, an equal distribution would have center at 0.5 and left and right at 0.25, as seen at time 0.) Notice that some centering occurs in each plot, except when pa = 0.5. The case where pa = 0.05 is similar to the case depicted in Figure 4, where there is an initial trend to the center of the attitude spectrum before polarization emerges. In general, as amplification increases, we see a decrease in the height of centering (orange) and the time spent in it.
Figure 7.
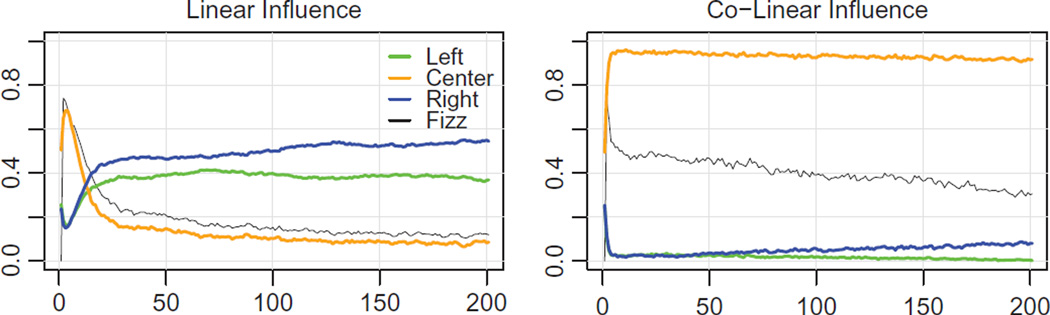
When opinion amplification is sufficiently low (here shown with pa = 0.05), influence functions can produce qualitatively different behavior. The left plot shows polarization as a result of linear influence, while the right plot shows that co-linear influence produces centering. The intermediate case with uniform influence is shown above in Figure 6.
To describe the frequency behaviors of our model, we begin by establishing a baseline case: With no amplification, pa = 0.1, and a uniform influence function, we observe a rapid transition to centering (Figure 6, top left panel). In what follows, we will observe how this baseline behavior is altered by the addition of amplification, and/or changes in the influence function. These two factors give us three ways in which the model can be made to deviate from the baseline.
The first way to deviate from the baseline is to change the influence function to be linear or quadratic, which means that neighbors with more extreme opinions have a higher probability of being selected for an exchange. In these scenarios we observe polarization—center attitudes become scarce, and most of the population holds attitudes at the far left or right. Results (not shown) are similar to those presented in Figure 4 and the left panel in Figure 7.
The second way to deviate from the baseline is to introduce amplification. When we add to the baseline a small probability of amplification, e.g., pa = 0.05, we observe a short period of centering, which is then proceeded by polarization (see top right panel of Figure 6). As amplification is gradually increased, the period of time during which centering is observed decreases, and the population rapidly becomes polarized (roughly evenly divided between the most extreme left and right attitudes).
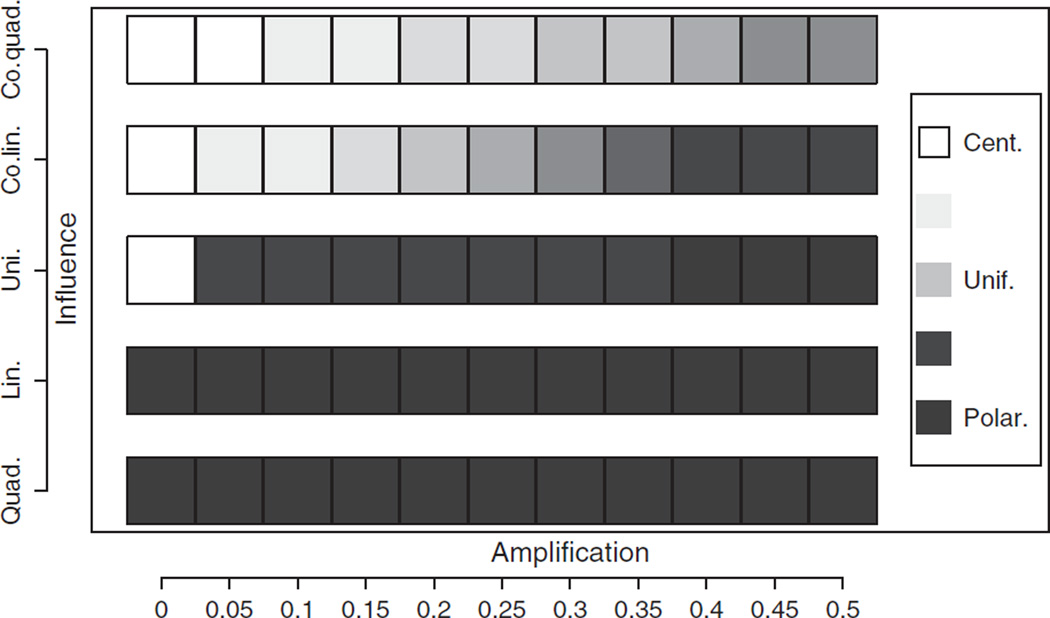
The third way to deviate from the baseline is to have combinations of amplification levels and influence functions. For example, when amplification is low, a linear influence function acts as a catalyst for polarization, but a co-linear influence function produces centering (see Figure 7). A co-influence function means that individuals with moderate opinions have a higher probability of being selected for an attitude update. This selection bias can offset the effects of amplification, up to a point. As amplification increases, co-linear influence needs to be replaced by co-quadratic influence in order to offset the polarization effects of amplification. However, once amplification is high enough, the co-influence functions lose their inhibitory effect. Figure 8 shows the effects of combinations of influence functions and amplification levels.
Figure 8.
Effects of combining influence functions with different amplification levels. Notice that each can independently affect the behavior of the system. Even when amplification is zero, a linear influence function produces polarization. Likewise, a small amount of amplification under uniform influence produces polarization. Co-linear influence and co-quadratic influence can help offset the polarization effects of amplification, but only follower levels of amplification. The behaviors are measured by taking the average difference between the frequency of center and the frequency of left or right, whichever is higher. Simulations were carried out for 200 steps.
Thus, influence functions and amplification can independently change the qualitative behavior of the system, reversing an early transition towards centering into polarization. However, the timing of the two effects differ. Influence functions have an effect earlier on because they largely determine the initial configuration of clusters. Once small clusters have formed, amplification produces a reinforcement effect that results in the formation and smoothing of longer and more definite boundaries, as shown above in the discussion of spatial behaviors. If we increase amplification, reinforcement is stronger as more individuals move to the extreme attitudes more quickly, and consequently the time period and magnitude of centering diminishes. Very little amplification, however, is required to achieve this effect. Co-influence functions can only offset amplification up to a point; amplification is a powerful process (Figure 8).
Several other factors affect the timing of frequency behaviors. First, the rate at which consensus is reached decreases with increasing L (compare rows 1 and 2 in Figure 5).
Second, the rate at which the frequencies change depends on the size of the clusters that form. Consider two idealized cases, depicted in rows 2 and 3 in Figure 5. In one case we have a large circle whose area is slightly larger than half of the area of the entire grid. Even though the frequency of the positive opinions (black) is greater than the negative opinions (white), the entire population eventually reaches consensus on negative opinions because of the curvature of the spatial arrangement of opinions. We observe the same effect in a second idealized case where we have four circles in the grid with, again, a combined area that is just over half the total area of the grid. As before, the entire population eventually reaches consensus on negative opinions, but at a faster rate (compare the last two plots in rows 2 and 3 of Figure 5).
Finally, some cluster configurations will maintain polarization for a very long time. This is especially true when boundaries become straight. In this configuration, surface tension no longer has any effect other than that of maintaining the straight boundary. Consequently, the frequency of opinions on either side is maintained. We see an example of this situation in the last panel of Figure 4 where a vertical band has formed.
4. Discussion
Our model includes an expanded spectrum of attitudes, unlike the binary opinion spectrum of voter models, the Schelling model (1971), and the Nowak–Latané model (Nowak, Szamrej, & Latané, 1997). Other models with an expanded spectrum include Axelrod’s model of dissemination of culture and variations thereof (Axelrod, 1997; Lanchier, 2012). However, these deal with multiple cultural features, each with a given number of trait levels. Lanchier (2010) also has a related model that combines voter and Axelrod model dynamics to produce an opinion model with continuous state space [0, 1]. Bounded confidence models and variations thereof are also examples of models that use a continuous opinion spectrum (Deffuant, Neau, Amblard, & Weisbuch, 2000; Weisbuch, Deffuant, Amblard, & Nadal, 2003; Hegselmann & Krause, 2002). In these models, an agent considers whether to update their opinion and confidence (and by how much) by taking into account both the opinion and confidence of the other agent. If the first agent is highly confident or the other opinion is too different, the first agent does not update. In our model an agent is “open” to any opinion regardless of what it is or how entrenched it is. Nonetheless, we retain a form of interaction bias through the use of influence functions.
The expanded spectrum allows us to explore the effects of unequal influences and the hardening of opinions. These effects include features that are shared by binary processes as well as other expanded spectrum models. For example, several mechanisms that produce polarization have been modeled, including stubbornness (Friedkin, 2015), extremist agents with high persuasiveness (Lanchier, 2010), high levels of confidence (Hegselmann & Krause, 2002), network structure (Deffuant et al., 2000; Flache & Macy, 2011), and diverging opinions (Dandekar, Goel, & Lee, 2013). The main mechanism that we study, amplification, complements the work of Dandekar et al. (2013). Most opinion dynamics models study how some relevant mechanism (e.g., network structure) hinders the convergence of opinions towards consensus, which can produce polarization and the fragmentation of opinions. Dandekar et al. (2013) however, argue that a more satisfactory explanation of polarization is one where divergence of opinion can increase, which leads them to study the role that biased assimilation has in producing polarization. Our model includes both a mechanism that hinders consensus and a mechanism that allows for divergence of opinions. The linear and quadratic influence functions polarize the population by preserving more entrenched opinions through biased interactions which prevents consensus. Without amplification, however, extreme opinions cannot be produced once they are lost. Amplification makes it possible for opinions to diverge and become more extreme.
Similar to bounded confidence models, the hallmark of Axelrod-type models is that individuals only interact with each other if they are sufficiently similar, which leads to an eventual freezing of the configuration of types into clusters of like-minded individuals who do not interact with their cross-border neighbors (Nowak et al., 1997; Axelrod, 1997; Lanchier, 2012; Lanchier, 2010). Threshold voter models with sufficiently high thresholds also produce polarization, effectively causing the system to freeze.
Our model does not completely freeze when there is polarization, but the change in time scale would essentially render the dynamics frozen if one were to add other dynamics with faster time scales. These observations lead us to focus our attention on the different timescales at play in the model behaviors. The amount of delay in our model can be varied by either changing levels of amplification, influence functions, or the size of the spectrum (L). Changes in delay can, for example, change consensus rates: the rate at which consensus is reached decreases with increasing L (compare rows 1 and 2 in Figure 5).
Moreover, changes in delay can also affect the “sharpness” of boundaries. For example, looking at the contrast between row 1 and row 2 in Figure 5, we notice that increasing the spectrum L makes boundaries evolve more smoothly, and clusters are thereby less likely to form an isthmus. However, in the event that one or more isthmuses form and evolve into a band with straight boundaries, as depicted in Figure 4, then the time to consensus is dramatically increased. This is because neither side of the boundary has an advantage when the boundary is straight.
Note that our model reduces to a discrete-time voter model when the attitude spectrum is 𝒜 = {−1, 1}. In this case, there can be no effects of influence or amplification due to the limited spectrum of attitudes. If we do not allow opinion amplification in our model (pa = 0), we can say more about the fate of some states, even if the attitude spectrum has L ≥ 2. Without amplification, there is no mechanism for generating an opinion that is more extreme than whatever happens to be the most extreme opinion in the population. For example, if the attitude spectrum is 𝒜 = {−3, −2, −1, 1, 2, 3} but no instances of −3 or 2 or 3 exist, then the absence of amplification implies that there is no way to generate a −3 or 2 or 3. Hence, without amplification, all “exterior” zero frequencies act as traps. Moreover, once an opinion is lost (i.e., all positive or all negative attitude values disappear), it can never be regained, regardless of influence settings. At this point, any loss of an outer value will be permanent. For example, if the only attitudes present are 1, 2, and 3, then 2s can be reconstituted if lost as long as 1s and 3s are still present. If 1s or 3s are lost, however, they are gone forever. The existence of such trap states leads to a one-sided spectrum converging on a single value.
These considerations suggest that, even if the attitude spectrum has L ≥ 2, in the absence of opinion amplification our model will either converge on a single value of one opinion (the other opinion going extinct) or will converge to the voter model on 𝒜 = {−1, 1}. A co-influence function would encourage the tendency to reduce the active spectrum to {−1, 1}, while a linear or quadratic influence function would make fixation of one opinion more likely. For example, if the active spectrum is {−2, −1, 1}, linear influence would create favorable conditions for opinions in the negative part of the spectrum, similar to—but not quite—a biased voter model.
However, if we do include even a small amount of amplification, we see a large effect at the macro-scale. Instead of converging to the voter model, or reaching consensus in the short term, we see the emergence of polarization. This polarization is realized spatially in the form of boundaries, which dramatically slows down the time to consensus. This might help explain why there is a tendency for political parties to become extreme in their views. It may also explain the geographical contiguity of like-minded voters. The spatial constraints on interactions between people in our model are, of course, overly simplistic, as they are in all spatial models of social interactions. They do, however, capture some of the features that limit interactions and slow the propagation of influence. In this sense, our model is another example of how small changes in the micro-level (in our case a small amount of amplification) can produce a large effect at the macro-level.
Finally, we remark that we chose a discrete-time implementation of our model with synchronous updates because we thought it was the simplest way to represent changes in attitude without pretending to know behavioral details on a finer time scale. We did, however, also run simulations with an asynchronously updating version of model and observed similar behavior.
Acknowledgments
Funding
Support for this research comes from NIH grant P20GM104420 (BB and SK) and the University of Idaho CLASS Excellence in Teaching the Humanities Endowment (BB). RT was supported by NSERC.
Footnotes
Color versions of one or more of the figures in the article can be found online at www.tandfonline.com/GMAS.
References
- Axelrod R. The dissemination of culture: A model with local convergence and global polarization. Journal of Conflict Resolution. 1997;41(2):203–226. [Google Scholar]
- Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamic. Reviews of Modern Physics. 2009;81(2):591–646. [Google Scholar]
- Clifford P, Sudbury A. A model for spatial conflict. Biometrika. 1973;60(3):581–588. [Google Scholar]
- Dall’Asta L, Castellano C. Effective surface-tension in the noise-reduced voter model. EPL (Europhysics Letters) 2007;77(6):60005. [Google Scholar]
- Dandekar P, Goel A, Lee DT. Biased assimilation, homophily, and the dynamics of polarization. Proceedings of the National Academy of Science. 2013;110(15):5791–5796. doi: 10.1073/pnas.1217220110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deffuant G, Amblard F, Weisbuch G, Faure T. How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation. 2002;5(4) [Google Scholar]
- Deffuant G, Neau D, Amblard F, Weisuch G. Mixing beliefs among interacting agents. Advances in Complex Systems. 2000;3(01n04):87–98. [Google Scholar]
- DeGroot MH. Reaching a consensus. Journal of the American Statistical Association. 1974;69(345):118–121. [Google Scholar]
- Durrett R. Lecture notes on particle systems and percolation. Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software; 1988. [Google Scholar]
- Durrett R, Steif JE. Fixation results for threshold voter systems. Annals of Probability. 1993;21(1):232–247. [Google Scholar]
- Flache A, Macy MW. Small worlds and cultural polarization. The Journal of Mathematical Sociology. 2011;35(1–3):146–176. [Google Scholar]
- Friedkin NE, Johnsen EC. Social influence network theory: A sociological examination of small group dynamics. Vol. 33. Cambridge, UK: Cambridge University Press; 2011. [Google Scholar]
- Friedkin NE. The problem of social control and coordination of complex systems in sociology: A look at the community cleavage problem. Control Systems, IEEE. 2015;35(3):40–51. [Google Scholar]
- Hegselmann R, Krause U. Opinion dynamics and bounded confidence: Models, analysis and simulation. Journal of Artificial Societies and Social Simulation. 2002;5:1–24. [Google Scholar]
- Holley RA, Liggett TM. Ergodic theorems for weakly interacting infinite systems and the voter model. Annals of Probability. 1975;3(4):643–663. [Google Scholar]
- Horowitz IL. Consensus, conflict and cooperation: A sociological inventory. Social Forces. 1962;41(2):177–188. [Google Scholar]
- Lanchier N. The Axelrod model for the dissemination of culture revisited. Annals of Applied Probability. 2012;22(2):860–880. [Google Scholar]
- Lanchier N. Opinion dynamics with confidence threshold: An alternative to the Axelrod model. ALEA. 2010;(7):1–18. [Google Scholar]
- Liggett TM. Stochastic interacting systems: Contact, voter, and exclusion processes. Berlin, Germany: Springer-Verlag; 1999. [Google Scholar]
- Lord CG, Ross L, Lepper MR. Biased assimilation and attitude polarization: The effects of prior theories on subsequently considered evidence. Journal of Personality and Social Psychology. 1979;37(11):2098–2109. [Google Scholar]
- Miller AG, McHoskey JW, Bane CM, Dowd TG. The attitude polarization phenomenon: Role of response measure, attitude extremity, and behavioral consequences of reported attitude change. Journal of Personality and Social Psychology. 1993;64(4):561–574. [Google Scholar]
- Munro GD, Ditto PH, Lockhart LK, Fagerlin A, Gready M, Peterson E. Biased assimilation of sociopolitical arguments: Evaluating the 1996 us presidential debate. Basic and Applied Social Psychology. 2002;24(1):15–26. [Google Scholar]
- Nowak A, Szamrej J, Latané B. From private attitude to public opinion: A dynamic theory of social impact. Psychological Review. 1997;97(3):362. [Google Scholar]
- Schelling T. Dynamic models of segregation. Journal of Mathematical Sociology. 1971;1:143–146. [Google Scholar]
- Taber CS, Lodge M. Motivated skepticism in the evaluation of political beliefs. American Journal of Political Science. 2006;50(3):755–769. [Google Scholar]
- Weisbuch G, Deffuant G, Amblard F, Nadal J-P. Heterogenous Agents, Interactions and Economic Performance. Berlin, Germany: Springer-Verlag; 2003. Interacting agents and continuous opinions dynamics; pp. 225–242. [Google Scholar]
- Wilensky U, Evanston I. Netlogo: Center for connected learning and computer-based modelling. Evanston, IL: Northwestern University; 1999. pp. 49–52. [Google Scholar]