Patch-Based Discrete Registration of Clinical Brain Images

Abstract

We introduce a method for registration of brain images acquired in clinical settings. The algorithm relies on three-dimensional patches in a discrete registration framework to estimate correspondences. Clinical images present significant challenges for computational analysis. Fast acquisition often results in images with sparse slices, severe artifacts, and variable fields of view. Yet, large clinical datasets hold a wealth of clinically relevant information. Despite significant progress in image registration, most algorithms make strong assumptions about the continuity of image data, failing when presented with clinical images that violate these assumptions. In this paper, we demonstrate a non-rigid registration method for aligning such images. The method explicitly models the sparsely available image information to achieve robust registration. We demonstrate the algorithm on clinical images of stroke patients. The proposed method outperforms state of the art registration algorithms and avoids catastrophic failures often caused by these images. We provide a freely available open source implementation of the algorithm.

1 Introduction

We propose a robust non-linear registration method for images with sparse slice acquisition. Medical image registration is a fundamental step in population studies and atlas-based analyses, and has been a topic of active research for many years. Most registration algorithms require research quality images with sufficiently high resolution. Unfortunately in many clinical settings the acquired images have extremely sparse slices. The proposed method enables explicit modeling of spatially sparse images and facilitates analyses in a large class of image data. Such analyses are currently unavailable to clinical research due to challenges in alignment.

Throughout this paper we use the motivating example of a clinical imaging study of stroke patients where thousands of brain MR scans are acquired within 48 h of stroke onset. The in-plane resolution in these images is 0.85 mm, while the slice spacing is 5–7 mm, as illustrated in Fig. 1. The study aims to quantify the white matter disease burden and to analyze population trends, necessitating non-linear registration to a common coordinate frame, and segmentation of healthy tissue and pathology near the ventricles [13]. Analyses of such images are hindered by the wide slice spacing, presenting significant challenges for basic tasks such as registration, skull stripping, and bias correction. In this work, we focus on registration.

Fig. 1.

An example clinical T2-FLAIR MRI of a stroke patient in axial (left), sagittal (center) and coronal (right) views. The slice spacing is much larger than is usually encountered in research scans, making registration a challenging task.

Non-linear registration methods developed for high resolution images often make continuity and smoothness assumptions [7] that are violated by clinically acquired images, as illustrated in Fig. 1. Specifically, most algorithms operate on image gradients. However, in volumes with wide slice spacing, the volume is no longer smooth, and the anatomical structure may change dramatically between subsequent slices. While for some images the registration may be adequate, in many cases it fails catastrophically. Some methods attempt to directly address this problem by designing processing pipelines and tuning respective parameters specific to a particular dataset [14]. Instead, we explicitly account for the sparse nature of the slices and avoid anatomical continuity assumptions.

Feature-based methods [8,11,15] present an alternative approach to voxel-wise registration algorithms by extracting sparse features or region summaries and using these features to guide the registration. Point set representations [3] use a representative selection of voxels to direct the registration. Unfortunately, the spatial sparseness of clinical images makes it difficult to extract meaningful and consistent features or point sets.

Our algorithm builds on discrete registration methods [5,6] that have been demonstrated recently as an alternative to gradient-based methods. The discrete registration approach models voxels of a moving image as nodes of a discrete Markov Random Field (MRF). Each node can move to a pre-specified number of voxels in each direction. Node potentials capture the agreement of intensities between the voxel in the moving image and the target voxel in the fixed image. Neighbouring voxels are encouraged to move together through pairwise potentials. The optimal registration is obtained via minimizing the energy of the MRF [5,6,12]. Since the same optimization can be used for a wide variety of potentials, the framework provides significant flexibility in adapting these terms to specific tasks. Discrete registration algorithms typically achieve similar results to state of the art gradient-based methods for research quality high resolution scans, and offer an alternative framework when image gradients cannot be computed reliably.

To address the challenges of clinical data, we design a general and robust patch-based discrete registration algorithm that captures the sparse structure characteristic of our problem. While most methods use single voxels to asses data similarity, we design an appropriate 3D patch-based similarity function surrounding each voxel. We demonstrate our approach on real clinical data from a study of stroke.

While a large number of software packages is available for continuous registration, very few tools have been developed for discrete registration, and are generally task-specific or proprietary [5,6]. To motivate and facilitate further research, we provide a flexible, fast, and open-source implementation of discrete deformable registration, and provide several voxel-based and patch-based data similarity functions at http://github.com/adalca/patchRegistration.

2 Methods

We let Ω be the set of all spatial locations, and aim to non-rigidly register a moving image M = {M_x}_x∊Ω to a fixed image F = {F_x}_x∊Ω. For simplicity we assume both images have been interpolated to isotropic resolution and are of the same size. In our experiments we use affine registration with linear interpolation to align images into a common space as a pre-processing step. Although the method we develop below applies to the registration of data with any spatially missing data, in this paper we focus on registering a moving image with sparse slice acquisition to a high resolution atlas. In this section, we first review discrete deformable registration, then describe our treatment of sparse data within this framework, and finally discuss important implementation details.

2.1 Discrete Deformable Registration

Discrete registration is often modeled as a labeling problem using a Markov Random Field (MRF) [5,6]. Control points x ∊ Ω of the moving image M are viewed as nodes arranged on a grid. For each node x, a finite set of states 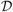_x = {d_x} represent discrete displacements d_x ∊ ℤ³ that node x can take. For example, a node could be allowed to move at most one voxel in each direction, resulting in 27 possible states.

The node potential Φ_x(d_x) measures the quality of each displacement d_x, most often in terms of similarity of image intensities M(x) and F(x + d_x). The pairwise potential Ψ_x,x′(d_x, d_x′) encourages similar displacements for neighbouring nodes x and x′. Registration aims to find the optimal displacement field by minimizing the MRF energy function

$$E(\mathcal{D})=\sum _{\mathbf{x}}{\Phi }_{\mathbf{x}}({\mathbf{d}}_{\mathbf{x}})+\lambda \sum _{\mathbf{x},{\mathbf{x}}^{\prime }\in \mathcal{N}(\mathbf{x})}{\Psi }_{\mathbf{x},{\mathbf{x}}^{\prime }}({\mathbf{d}}_{\mathbf{x}},{\mathbf{d}}_{\mathbf{x}\prime }),$$ (1)

where λ is a parameter that trades off between the data and smoothness terms, and 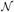(x) is the set of neighbors of node x. While efficient MRF optimization methods have been a topic of active research [4,5,9], we find that using Loopy Belief Propagation [12] is sufficiently fast and accurate for our application.

2.2 Patch Based Discrete Registration

The node potential is most often based on a difference between image intensities M(x) and F(x + d_x):

$${\Phi }_{\mathbf{x}}({\mathbf{d}}_{\mathbf{x}})={(M(\mathbf{x})-F(\mathbf{x}+{\mathbf{d}}_{\mathbf{x}}))}^2.$$ (2)

In clinical datasets, where known voxels are sparse, we instead use patches to aggregate information from available voxels.

We introduce masks W_M = {W_Mx ∊ [0, 1]}_x∊Ω and W_F = {W_Fx ∊ [0, 1]}_x∊Ω that define the confidence in image intensities for each voxel. For example, in our clinical dataset, the moving weight mask describes the original locations of the original high-resolution slices in the interpolated clinical image (Fig. 2). Mask values vary between 0 and 1 due to interpolation effects of the affine transformations of the moving image M and the fixed image F.

Fig. 2.

Overview of the information captured by the unary potentials using 3D patches.

All patches in our method share the same shape and size. We let {I(x + z)}_z∊Ωx define a patch of image I centered at voxel x with patch footprint Ω_x. We define the unary potential as the weighted patch distance

$${\Phi }_{\mathbf{x}}({\mathbf{d}}_{\mathbf{x}})=\frac{{\sum }_{\mathbf{z}\in \Omega \mathbf{x}}W(\mathbf{x},{\mathbf{d}}_{\mathbf{x}},\mathbf{z}){(M(\mathbf{x}+\mathbf{z})-F(\mathbf{x}+{\mathbf{d}}_{\mathbf{x}}+\mathbf{z}))}^2,}{{\sum }_{\mathbf{z}\in \Omega \mathbf{x}}W(\mathbf{x},{\mathbf{d}}_{\mathbf{x}},\mathbf{z})},$$ (3)

where

$$W(\mathbf{x},{\mathbf{d}}_{\mathbf{x}},\mathbf{z})=W_M(\mathbf{x}+\mathbf{z})W_F(\mathbf{x}+{\mathbf{d}}_{\mathbf{x}}+\mathbf{z}).$$ (4)

The classical node potential (2) uses a single pair of potentially interpolated intensities at M(x) and F(x + d_x), forcing implementations to either limit control points to only available high-resolution planes, or use interpolated intensities to drive the registration, resulting in sub-optimal alignment. Instead, our patch-based potential (3) relies more heavily on voxels whose intensity was observed directly and downweights the interpolated values (Fig. 2). This approach provides a robust measure of the quality of displacement d_x for voxel x, capturing context for voxel x using known data.

We do not explicitly model slice thickness [10], as in many clinical datasets the slice thickness is unknown or varies by site, scanner or acquisition. Instead, we simply treat the original data as thin high resolution planes. When known, slice thickness can be easily modeled by modifying the sampling mask W.

We use the ℓ₂ distance as the pairwise potential:

$$\Psi ({\mathbf{d}}_{\mathbf{x}},{\mathbf{d}}_{\mathbf{x}}^{\prime })=\parallel {\mathbf{d}}_{\mathbf{x}}-{\mathbf{d}}_{\mathbf{x}}^{\prime }{\parallel }_2^2\cdot$$ (5)

Once Φ(d_x) and $\Psi ({\mathbf{d}}_{\mathbf{x}},{\mathbf{d}}_{\mathbf{x}}^{\prime })$ are defined and the parameter λ is set, we seek the optimal MRF labeling to obtain the desired displacement of each image voxel.

2.3 Implementation

We implemented a multi-resolution variant of the discrete registration algorithm described above. We prepare the moving clinical images at different scales by first down-sampling the original acquired slices for each scale, and then interpolating the data between slices. This approach maximizes the use of voxels with known intensity values.

To improve runtime, we implement several approximations. Specifically, we limit the number of states for each node to the top few states based on unary potentials, and remove nodes from the MRF based on the variance among their state potentials. Both pruning steps are controlled by model parameters. At the end of the registration step at each scale, the displacement field is linearly interpolated between nodes. We optimize parameter settings on a held-out subset of images described below. In this experiment, we varied the parameter λ to trade off the importance of the data and smoothness terms, as well as the spacing of the control points.

We use Loopy Belief Propagation to minimize energy function (1). When run on a single quad-code 2.7 GHz, 32 Gb of RAM registering two images takes approximately 120 min. Our implementation accepts for any patch definition and weight pattern and includes several built-in patch similarities. Developed to be highly modifiable and extensible, the code is freely available at http://github. com/adalca/patchRegistration.

3 Results

We demonstrate the performance of our algorithm on clinically acquired stroke images. The stroke study aims to quantify periventricular white matter disease burden, requiring particularly accurate registration around the ventricles.

Data and Processing

To evaluate the algorithm, we randomly selected 100 T2-FLAIR brain MR scans from the stroke patient cohort for evaluation. Our clinical scans are severely anisotropic (0.85 × 0.85 mm in-plane, slice separation of 6mm, variable TR and TE). All subjects are linearly interpolated to isotropic resolution and intensity corrected by matching the intensity of the white matter across subjects. Finally, the subjects are affinely registered to a T2-FLAIR atlas. All subjects have manual delineation of the ventricles created for this evaluation.

Parameters

We choose patch registration parameters found to be optimal in a subset of 18 held-out scans, separate from those used in the experiments. We varied the parameter λ and the spacing of the control points. We set λ = 0.1 and an optimal grid spacing of 3 mm, but find little variation in the results when using wider spacing. At each scale, each node can only move up to two voxels in each dimension. We keep the top 50 states (out of 125 possible states) for each node, and keep the top 50 % of nodes. We use a patch size large enough to include at least two observed slices in every patch, which for our experiments is 9 mm in the highest resolution scale and 3 mm in the lowest.

Experiments

We register each scan in the evaluation set to the atlas. We evaluate registrations by propagating manual segmentations of the ventricles from the atlas to each subject through resulting warps and measuring volume overlap via the Dice metric [2]. We use the state of the art ANTs registration algorithm [1] as the baseline method for evaluation. Throughout our work with the clinical study, we found ANTs to be the most consistent at tackling the sparse data among all existing algorithms. We run ANTs with the default parameters, as well as parameters we identified by optimizing ANTs for stroke clinical images.

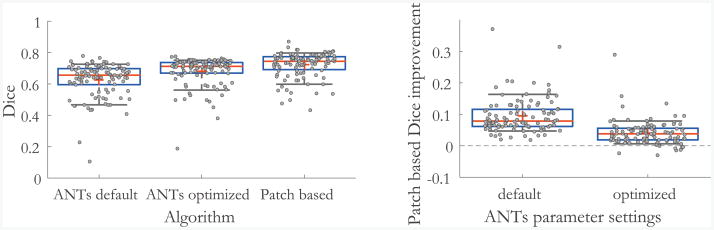
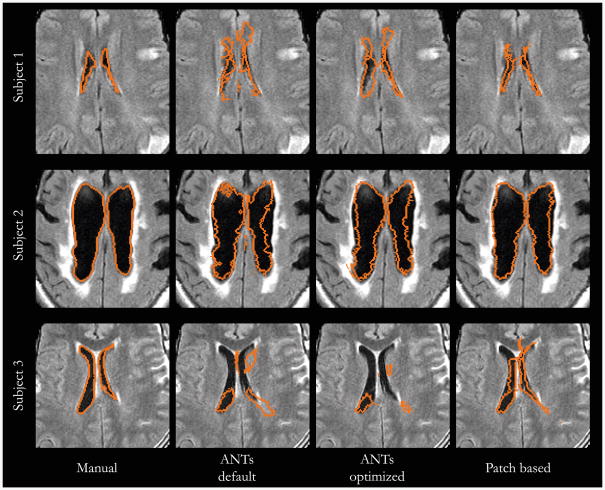
Patch based registration outperforms substantially the baseline ANTs algorithms in most subjects. Since the Dice measure varies significantly among subjects due to variable ventricle shape and cerebral pathology, we also report statistics of patch based registration improvement over ANTs results (Fig. 3). Patch based registration yields an improved Dice score in 92 % of the subjects compared to optimized ANTs results, with a mean improvement of 4.1 dice points. It also yields significant improvement (more than 5 Dice points) in 31 % of the subjects where ANTs often resulted in serious registration errors (Fig. 4). Overall, the presented algorithm shows consistent improvement across the dataset.

Fig. 3.

Results on the stroke clinical dataset. For each setting, the measurements are shown in gray. The red line and cross represent the median and mean value respectively, box edges show 25th and 75th percentiles, and black whiskers show 10th and 90th percentiles. Left: Ventricle Dice measure for the ANTs algorithm with default and optimized parameters, and the patch based method. Right: Dice improvement achieved by patch based registration compared to ANTs, for both default and optimized parameters, respectively. Our method improves registration for all subjects when compared to default ANTs settings, and for 92 % of the subjects when compared to optimized ANTs settings. (Color figure online)

Fig. 4.

Examples of serious registration failures of the ANTs algorithm. For the first two subjects, that patch based registration recovers successful registrations. For the third subject, the patch based registration yields dramatic improvement, but several areas can still be improved. Aside from low resolution, the image exhibits significant pathology, imperfect skull stripping, and suboptimal affine registration, all common in stroke subjects.

4 Conclusion

Clinical images present significant challenges for many computational analyses, yet hold the wealth of clinically relevant information. We combine three- dimensional patch information with the discrete registration framework to robustly drive registration of such images. The three-dimensional patches explicitly model the sparsely available image information to achieve robust registration. We demonstrate the algorithm on images with sparsely acquired slices in clinical scans of stroke patients. The proposed method outperforms the state of the art registration algorithms and avoids significant failures often observed in the alignment of these images. Our implementation is freely available and accepts images of varying resolution.