Experimental investigation of trailing edge noise from stationary and rotating airfoils

Abstract

Trailing edge noise from stationary and rotating NACA 0012 airfoils is characterised and compared with a noise prediction based on the semi-empirical Brooks, Pope, and Marcolini (BPM) model. The NACA 0012 is symmetrical airfoil with no camber and 12% thickness to chord length ratio. Acoustic measurements were conducted in an anechoic wind tunnel using a stationary NACA 0012 airfoil at 0° pitch angle. Airfoil self-noise emissions from rotating NACA 0012 airfoils mounted at 0° and 10° pitch angles on a rotor-rig are studied in an anechoic room. The measurements were carried out using microphone arrays for noise localisation and magnitude estimation using beamforming post-processing. Results show good agreement between peak radiating trailing edge noise emissions of stationary and rotating NACA 0012 airfoils in terms of the Strouhal number. Furthermore, it is shown that noise predictions based on the BPM model considering only two dimensional flow effects, are in good agreement with measurements for rotating airfoils, at these particular conditions.

I. INTRODUCTION

Trailing edge noise is the dominant noise source on modern wind turbines at close proximity. Since wind farm noise represents an important hindrance to the development of wind energy, mainly due to annoyance, it is important to be able to accurately predict and control this noise.

Trailing edge noise is generated when the turbulent boundary layer on the surface of an airfoil encounters its sharp trailing edge. Since turbulent flow consists of energy-containing eddies of various sizes, the resulting noise is broadband, which reflects the random nature of the pressure variations inside the turbulent boundary layer. An important characteristic of trailing edge noise is the so called “low-frequency” peak, which represents the maximum sound pressure level. In a review of trailing edge noise by Doolan and Moreau,¹ a comparison between several experimental data sets of trailing edge noise for a stationary NACA 0012 airfoil at 0° angle of attack and a range of Reynolds numbers, Re, is presented. Reynolds number is a dimensionless quantity used for characterise flow regimes defined as $\text{Re}=vL/\nu$, where v is the fluid velocity, L is the characteristic linear dimension (for example chord length), and ν is the kinematic viscosity. Doolan and Moreau¹ found a consistent “low-frequency” peak at a non-dimensional Strouhal number (${\text{St}}_{{\delta }^{*}}=f{\delta }^{*}/U_{\infty }$, where f is frequency, δ* is the boundary layer displacement thickness and U_∞ is the free stream velocity) of ∼0.069, which they believe is a true characteristic of trailing edge noise. The peak has been observed in several experimental investigations² and numerical simulations.^3,4 However, some researchers^5,6 attribute the “low-frequency” peak to the facility scattering effects and/or data processing effects and thus the origin of this peak is debatable.

Throughout the history of trailing edge noise experimental investigation, testing was predominantly done on blades fixed in a wind tunnel for practical reasons. In comparison to a rotating airfoil system, aerodynamic data are easier to obtain from a stationary airfoil, which, in general, can have a larger chord length, higher Reynolds number and improved spatial resolution. However, important differences exist between the stationary and rotating blades, since the latter experience spanwise varying inflow conditions and thus spanwise varying blade aerodynamic capabilities and trailing edge noise generation. Only a few rotating airfoil acoustic data sets are available which were obtained on scaled rotors/wind turbines. Oerlemans et al.⁷ performed beamforming measurements on a scaled wind turbine, whose purpose was to evaluate the noise reduction capabilities of optimised airfoil designs. Tests were done on a two-bladed 4.48 m diameter rotor wind turbine. Cho et al.⁸ conducted a wind tunnel beamforming study in which they studied noise sources on a 12% scale NREL wind turbine model. Cho et al.⁸ showed, that the source location in the rotor plane moved outboard as the frequency increased. Ryi et al.⁹ proposed a method for scaling small wind turbine noise data in a way to predict full scale wind turbine noise. Experiments were conducted in a wind tunnel on a three-bladed rotor-rig with a 1.4 m rotor diameter and the results showed that large scale wind turbine noise can be accurately predicted from data obtained on a small-scale wind turbine. No literature has been found that compares the trailing edge noise produced by rotating NACA 0012 airfoils to well-studied trailing edge noise from a stationary NACA 0012 airfoil at similar flow conditions.

For predicting trailing edge noise from rotating airfoil systems, the semi-empirical Brooks, Pope and Marcolini (BPM) model by Brooks et al.¹⁰ is commonly used.^11–13 This model was developed based on NACA 0012 airfoil experimental data at various angles of attack and Reynolds numbers ranging from 0.069 × 10⁶ to 1.47 × 10⁶. Interestingly, despite the model simplicity, the experimental data obtained across various facilities compare well with the BPM model as observed by Doolan and Moreau.¹ What this indicates is that the BPM model is of significant importance in the investigation of trailing edge noise since it allows wide comparison and validation of experimental data. However, the model has not yet been validated on rotating NACA 0012 airfoils, although it is commonly used for predicting trailing edge noise from rotating airfoil systems.

In summary, the main purpose of this paper is, therefore, to examine trailing edge noise of rotating NACA 0012 airfoils mounted at 0° and 10° pitch angles in a controlled environment and to compare the results to the BPM model, which is based on two dimensional aerodynamic data input. The BPM model has not yet been validated on rotating NACA 0012 airfoils despite its application to complicated rotating blade systems such as wind turbines¹⁴ and hence such comparison is of great interest.

II. METHODOLOGY

A. Stationary NACA 0012 airfoil

Acoustic experiments on a stationary NACA 0012 airfoil were conducted in the anechoic wind tunnel (AWT) at the University of Adelaide. The wind tunnel contraction outlet has dimensions of 75 mm × 275 mm and the turbulence intensity in the outlet plane was measured to be 0.3%. The anechoic room surrounding the wind tunnel outlet, which is 8 m³ in volume, is shown in Fig. 1. The anechoic room provides a near-reflection free acoustic environment down to a frequency of ∼200 Hz.¹⁵

FIG. 1.

(Color online) Photograph showing anechoic room of the anechoic wind tunnel. In the photograph, the wind tunnel contraction outlet and microphone array located on the ceiling, can also be seen.

The NACA 0012 airfoil used in experiments has a chord of 70 mm, span of 450 mm, ∼0.8 mm thick trailing edge (measured with a vernier caliper). The airfoil is made out of extruded aluminium and has a polished surface and a flat (square) tip. In order to guarantee a turbulent boundary layer at the trailing edge, the airfoil was tripped at 10% of the chord length using 0.4 mm thick serrated tripping tape. Tripping of the airfoil was necessary to create a turbulent boundary layer at the trailing edge since natural transition was not anticipated due to the low Reynolds number and smooth airfoil surface. The trip performance was assessed via measuring the velocity profile (with a hot-wire probe) of the boundary layer in the wake of trailing edge. The measured boundary layer velocity profile is in broad agreement with the 1/7 power law profile which implies that the trip produces a turbulent boundary layer at the trailing edge in this particular configuration. The experiments were conducted at flow speed of 30 and 37 m/s which corresponds to a Reynolds number based on chord of 147 814 and 182 304.

The far-field spectra and background noise were recorded with the central microphone of the microphone array, which was positioned on the ceiling of the anechoic wind tunnel (see Fig. 1 for the microphone array mounting). The central microphone was positioned at an angle (θ_e) of 70° and radial distance, r₀, of 0.54 m from the trailing edge. The angle θ_e is an angle between the airfoil chord line and location of the microphone (observer) as shown in Fig. 5.

FIG. 5.

Directivity angles defined with respect to the blade-fixed coordinate system. The blade segment is represented as a flat plate moving in the −y direction.

The mounting arrangement of the NACA 0012 airfoil in the AWT was such that the airfoil was secured to the aluminium housing which was then attached to the outlet contraction of the wind tunnel (see outlet contraction in Fig. 1). The positioning of the airfoil in the housing is shown in Fig. 2.

FIG. 2.

Schematic diagram of the NACA 0012 airfoil mounted in the aluminium housing showing front and side view.

From Fig. 2(a), it is evident that the span of the airfoil extends beyond the width of the wind tunnel contraction outlet. This is to eliminate noise due to side plate boundary layer interaction with the airfoil leading edge. However, this does not prevent noise from the shear layer interaction with the airfoil. The housing was secured to the wind tunnel contraction outlet, which is shown in Figs. 1 and 2.

The microphone array is located on the ceiling of the anechoic room (see Fig. 1) and was used for beamforming measurements. The array consists of 31 G.R.A.S. 40PH 1/4 in. phase matched microphones arranged in an Underbrink design.¹⁶ The microphones are firmly attached to a 12 mm MDF board with an EchoSorb 25 (25 mm thickness) sound absorption layer. The array is located 520 mm above the centre of the contraction outlet and has a minimum radius of 400 mm and a maximum radius of 490 mm. The microphones were protected against wind contamination using 30 mm spherical windshields. The microphone array was connected to a National Instruments PXIe-8106 data acquisition system containing 4 PXI-4496 24-bit sound cards. The data on this device were recorded at a sampling rate of 65 536 Hz for a duration of 60 s for each measurement.

The spatial resolution of the circular array at a frequency, f, to a point source located at ${\overrightarrow{x}}_s=(0,0)$, was investigated using the following identity for calculating the response of the array, Y, to a point source:

$$Y(f,{\overrightarrow{x}}_p,{\overrightarrow{x}}_s)=\left(\sum _{m=1}^{m_0}\frac{r_s}{r_m}\right)\sum _{m=1}^{m_0}\frac{r_s}{r_m}\hspace{0.17em}\text{exp}\left(2\pi fj\left[\frac{(r_s-r_p)-(r_m-r_m^{\prime })}{c_0}\right]\right),$$ (1)

where m₀ is the number of microphones, r_s is the distance from the source to the origin of the array, r_p is the distance from the origin to the focus point, r_m is the distance from the source to the mth microphone, $r_m^{\prime }$ is the distance from the mth microphone to the focus point, and c₀ is the speed of sound. In the calculation of the microphone response, the source plane was positioned 0.54 m away from the array, since this is the location of the trailing edge of the stationary airfoil. The beamwidth, or the microphone array spatial resolution, is the width at a point 3 dB down from the maxima at the focusing point. Table I shows the beamwidth at selected frequencies. The beamwidth is inversely proportional to frequency and ranges from 72 mm at 3.2 kHz to 12 mm at 12.5 kHz. Since the beamwidth is larger than the airfoil chord for frequencies below 4 kHz, the trailing edge noise localisation is expected to be poor below this frequency.

TABLE I.

Beamwidth of the circular microphone array used for noise source localisation on the stationary airfoil at selected one-third-octave band frequencies.

Freq.1/3, kHz	3.2	4	5	6.3	8	10	12.5
BW, m	0.072	0.056	0.044	0.032	0.024	0.02	0.012

The narrow-band power spectral density (PSD) estimation was calculated using Welch's averaged modified periodogram method of spectral estimation with a Hanning window and 50% overlap.

B. Rotating NACA 0012 airfoils

Acoustic measurements on rotating NACA 0012 airfoils were conducted in the anechoic room at the University of Adelaide, on a rotor rig as shown in Fig. 3, using large circular microphone array. The rotor was positioned with its centre at 1.42 m height above the ground and has diameter of a 1.04 m. The spacing between the rotor plane and the tower was 70 mm. It was observed via beamforming noise maps, that a change in spacing has only a minor effect on the amount of reflected noise from the tower and, therefore, results in this paper are presented for only one spacing. Three NACA 0012 airfoils with specifications and tripping details identical to the airfoil used in AWT, were mounted on the rotor with 0° and 10° pitch angle, no twist angle and no taper. A Kistler torque sensor type 4502ARA with inbuilt shaft encoder was used for measuring airfoil azimuth position, θ, as defined in Fig. 4. The accuracy of the azimuthal angle measurements was 1.5°. Guy wires were used to secure the rotor to the floor. During the measurement phase the microphone array in Fig. 3 was positioned further away from the rotor at a distance of 1.5 m.

FIG. 3.

(Color online) Photograph of the rotor and large circular microphone array in the anechoic room.

FIG. 4.

Schematic showing rotor centered (X, Y, Z) coordinate system, blade-fixed coordinate system (x, y, z), and the geometrical relationship between the rotating blade segment, S, and the observer, O.

The large circular microphone array used in the anechoic room has 64 G.R.A.S. 40PH phase and magnitude matched microphones, which were accurately attached to the aluminium frame with cable glands. The microphone locations were optimised so that the array has the smallest beamwidth possible at the largest aperture possible.¹⁷ The microphone array was connected to a National Instruments PXIe-8106 data acquisition system containing 4 PXI-4496 24-bit sound cards on which the data were recorded at a sampling rate of 65 536 Hz for a duration of 60 s. The spatial resolution of this microphone array for a source plane located 1.5 m away at selected frequencies is presented in Table II.

TABLE II.

Beamwidth of the large circular microphone array used for noise source localisation on the rotor at selected one-third-octave band frequencies.

Freq.1/3, kHz	3.2	4	5	6.3	8	10	12.5
BW, m	0.12	0.1	0.08	0.06	0.04	0.036	0.024

The anechoic room has dimensions of 4.79 m × 3.9 m × 3.94 m (73.6 m³) and provides a near-reflection free environment down to a frequency of ∼100 Hz. The centre of the microphone array was aligned with the rotor axis of rotation. Blade position as determined by the blade azimuth angle, θ, is measured from the 9 o'clock position (see Fig. 4). The rotor was run at the blade-pass frequencies of 32 and 45 Hz, which gives a blade tip speed of 38 and 48 m/s, respectively, and Reynolds number based on chord at the blade tip of approximately 172 232 and 236 503, respectively.

C. Noise prediction

The calculation method described in this section was used to predict trailing edge noise from the rotating NACA 0012 airfoils (rotor). Presented are also formulations for trailing edge bluntness noise and tip vortex formation noise as these noise sources are present when the blades are mounted under an angle of attack. Since these noise sources radiate from the whole span of the blade, the blade must be divided into segments, S₁, S₂, S₃,…,S_N, where each segment can be seen as an independent noise source. Figure 4 defines the geometry and coordinate system used to describe the rotor and its relationship to a fixed observer, O.

The observer location, O, in terms of the rotor centred coordinate system is given by the position vector

$$O(X,Y,Z)=\overrightarrow{R}(R_0,\Psi ,\Phi ),$$ (2)

with the polar to Cartesian transformation:

$$\begin{array}{c}X=R_0\hspace{0.17em}\text{sin}\hspace{0.17em}\Psi \hspace{0.17em}\text{cos}\hspace{0.17em}\Phi ,\\ Y=R_0\hspace{0.17em}\text{sin}\hspace{0.17em}\Psi \hspace{0.17em}\text{sin}\hspace{0.17em}\Phi ,\\ Z=R_0\hspace{0.17em}\text{cos}\hspace{0.17em}\Psi .\end{array}$$ (3)

A blade segment position, S, in the rotor is given by the vector $\overrightarrow{S}(x,y,z)=\overrightarrow{S}(r_0,\theta ,\Psi )=90°)$ whose Cartesian components are

$$\begin{array}{c}x=R_S\hspace{0.17em}\text{cos}\hspace{0.17em}\theta ,\\ y=R_S\hspace{0.17em}\text{sin}\hspace{0.17em}\theta ,\\ z=0.\end{array}$$ (4)

The observer position, O, can now be expressed in the blade-fixed coordinate system (x, y, z) with the vector $\overrightarrow{r}(x,\hspace{0.17em}y,\hspace{0.17em}z)=\overrightarrow{R}-\overrightarrow{S}$. The blade segment, S, directivity angles in terms of the blade-fixed coordinate system, are shown in Fig. 5.

With respect to the blade segment, S, directivity angles are defined as

$$\begin{array}{c}{\Psi }_e={\text{tan}}^{-1}\frac{z}{x},\\ {\theta }_e={\text{cos}}^{-1}\frac{y}{r_0},\\ r_0=\sqrt{{\left(x\right)}^2+{\left(y\right)}^2+{\left(z\right)}^2}.\end{array}$$ (5)

The trailing edge noise sound pressure level at the observer location, which is given by the positioning vector $\overrightarrow{R}$, is an average of one complete rotor revolution and is given by

$$\begin{array}{c}\text{SPL}\left(\overrightarrow{R}\right)\\ =10\hspace{0.17em}{\text{log}}_{10}\left[\frac{1}{N}\sum _{j=1}^N\sum _{i=1}^{B}10^{L_{{\text{CA}}_i}\left({\theta }_j\right)/10}\left({10}^{{\text{SPL}}_{{\text{TOT}}_i}\left({\theta }_j\right)/10}\right)\right]\\ +10\hspace{0.17em}{\text{log}}_{10}\left[N_B\right],\end{array}$$ (6)

where N is the number of discrete blade azimuthal positions, B is the number of blade segments, N_B is the number of blades on the rotor and L_CA is the correction for convective amplification defined as¹⁸

$$L_{\text{CA}}=10\hspace{0.17em}{\text{log}}_{10}\left[\frac{1}{{(1-M\hspace{0.17em}\text{cos}\hspace{0.17em}{\theta }_e)}^4}\right],$$ (7)

where M is the Mach number. The total sound pressure level, ${\text{SPL}}_{{\text{TOT}}_i}$, which consist of trailing edge noise (${\text{SPL}}_{{\text{TE}}_i}$) and a directivity correction ($L_{{\text{DTE}}_i}$) for the ith blade segment is

$${\text{SPL}}_{{\text{TOT}}_i}\left({\Theta }_{\mathrm{s}}\right)={\text{SPL}}_{{\text{TE}}_i}{+\text{SPL}}_{{\text{BTE}}_i}{+\text{SPL}}_{{\text{TIP}}_i}+L_{{\text{DTE}}_i},$$ (8)

where the sound pressure level due to trailing edge noise from a blade element is

$${\text{SPL}}_{{\text{TE}}_i}=10\hspace{0.17em}\text{log}\hspace{0.17em}10({10}^{{\text{SPL}}_{\alpha }/10}{+10}^{{\text{SPL}}_s/10}{+10}^{{\text{SPL}}_p/10}).$$ (9)

Parameters sound pressure level (SPL)_α, SPL_s and SPL_p are a function of boundary layer displacement thickness (δ*), Mach number, airfoil length (or airfoil element length), distance from the observer, Strouhal number and spectral functions. These parameters are part of the BPM model and are calculated using Brooks et al.¹⁰ Bluntness trailing edge noise is calculated as follows according to Brooks et al.:¹⁰

$${\text{SPL}}_{{\text{BTE}}_i}=10\hspace{0.17em}{\text{log}}_{10}\left(\frac{h{M}^{5.5}L\overline{D}h}{r_e^2}\right)+D,$$ (10)

where h is the thickness of the trailing edge, M is the Mach number, L is the length of the blade element, ${\overline{D}}_h$ is the directivity function, and r_e is the distance between the source and the observer and the spectral function D is described in Brooks et al.¹⁰ The sound pressure level due to blade tip vortex formation noise, ${\text{SPL}}_{{\text{TIP}}_i}$, is stated as follows:

$${\text{SPL}}_{{\text{TIP}}_i}=10\hspace{0.17em}{\text{log}}_{10}\left(\frac{M^5{\ell }^2{\overline{D}}_h}{r_e^2}\right)+C,$$ (11)

where ℓ is the separation over the trailing edge due to the tip vortex and C is the spectral function. Both the spectral function, C, and the separation distance, ℓ, are calculated according to Brooks et al.¹⁰ The directivity correction, $L_{{\text{DTE}}_i}$, was calculated according to Boorsma and Schepers¹⁸ as follows:

$$L_{\text{DTE}}=10\hspace{0.17em}{\text{log}}_{10}\left[2\hspace{0.17em}{\text{sin}}^2\left(\frac{{\theta }_e}{2}\right)\hspace{0.17em}{\text{sin}}^2{\Psi }_e\right].$$ (12)

The observer position in the prediction was set to equal the array centre microphone position; that is on the axis of rotation at a distance of 1.5 m from the rotor. In the prediction, the blade was divided into 40 segments since the predicted sound pressure level converges towards a constant value at this number of blade segments. XFOIL was used to calculate the boundary layer displacement thickness, δ*, at the trailing edge of each blade segment. It is assumed that the use of XFOIL is valid in this particular case since its prediction of boundary layer properties on the stationary airfoil are in reasonable agreement with the measurements. The XFOIL predictions of boundary layer displacement thickness (δ*), momentum thickness (Θ), and shape factor (H) and measured values of these quantities are shown in Table III.

TABLE III.

Measured and predicted boundary layer properties for stationary airfoil at 0° angle of attack at Re_c = 147 814.

	δ*, mm	Θ, mm	H
Measured	1	0.6	2
XFOIL	0.7	0.4	1.8

D. Aerodynamic analysis

In order to establish the state of the turbulent boundary layer on rotating NACA 0012 airfoils used for the BPM noise prediction, the blade angle of attack must be first determined. The angle of attack varies with radial distance from the axis of rotation due to; (a) variations in the inflow velocity with radial distance and (b) the rotor blade tip effect.¹⁹ A way to obtain blade segment angle of attack and thus aerodynamic conditions, is to use blade-element-momentum theory (BEMT),¹⁹ in which the rotating NACA 0012 airfoils on a rotor-rig can be analytically treated as a rotor in hover. Blade inflow velocity across rotor in hover varies azimuthally axisymmetric and radially linear. According to Fig. 6, the resulting flow velocity at any blade element has an out-of-plane component U_p = v_c + v_i normal to the rotor plane and in-plane component U_T = Ωr, where V_c is the climb velocity, v_i is the local induced velocity, Ω is the rotational frequency of the rotor, and r is the blade segment radial distance from the axis of rotation.

FIG. 6.

Schematic of aerodynamic environment at a blade segment at radius r for a rotor in hover.

The inflow velocity, U_T, which serves to modify the direction of the relative flow velocity field vector, U, will alter the pitch angle, θ, and will thus give a rise to an angle of attack, α. The relationship between these two angles and the local inflow angle, $\varphi$, is as follows:

$$\alpha =\theta -\varphi ,$$ (13)

where

$$\varphi =\left(\frac{\overline{r}\sigma C_{l\alpha }}{16F_{\mathit{t}\mathit{i}\mathit{p}}}\right)\left(\sqrt{1+\frac{32F_{\mathit{t}\mathit{i}\mathit{p}}}{\sigma C_{l\alpha }}\theta \overline{r}}-1\right),$$ (14)

where σ is the solidity ($\sigma =N_{b}c/R\pi$, where N_b is the number of blades, c is the chord of the local blade element, and R is the rotor radius), C_lα is the local aerodynamic loading defined as $\partial C_l/\partial \alpha$, F_tip is Prandtl's tip loss factor and $\overline{r}$ is the non-dimensional radial position. Prandtl's tip loss factor, F_tip, takes into account the loss in momentum over the rotor and is defined as

$$F_{\text{tip}}=\left(\frac{2}{\pi }\right)\arccos \left[\text{exp}(-f)\right],$$ (15)

where

$$f=\frac{N_b}{2}\left(\frac{1-\overline{r}}{\overline{r}\varphi }\right).$$ (16)

Because F_tip is a function of $\varphi$, the Eq. (14) cannot be solved analytically since $\varphi$ is initially unknown; Eq. (14) must, therefore, be solved iteratively by using F_tip = 1 in the first iteration, and then finding F_tip from Eq. (15) and recalculating $\varphi$ from the numerical solution to Eq. (14). The convergence of the numerical solution is rapid and it is usually obtained in less than four iterations. In the calculations, $\partial C_l/\partial \alpha$ was assumed to be 2π, which is an assumption valid for thin airfoils.

E. Beamforming technique

For trailing edge noise localisation and power estimation on stationary and rotating NACA 0012 airfoils, the conventional beamforming technique was used.¹⁶ This technique is a proven^20,21 and powerful spatial filtering process technique for extracting noise source location and magnitude in aeroacoustic applications.

To map the noise generation of a rotating source at different angles of that source, a hybrid time delaying scheme with modified ensemble averaging to estimate the cross-spectrum matrix was used in phase-averaged beamforming. Consider a rotational source in front of sparse array of microphones, such that Doppler shift of the source is negligible. If the position (angle) of a source (blade) is known, for example as recorded using an encoder, then instead of averaging over the entire pressure record to generate the cross-spectrum matrix as for conventional beamforming, the averaging is performed over segments centred about a rotor angle of interest, θ₀. However, for even modest rotor speeds this algorithm will suffer from having to trade off the size of the angle to plot, or the coherence between channels drops as the time delay between a single source and multiple microphones becomes significant relative to window length. For example, for a rotational source running at blade tip speed of 48 m/s and a microphone sample rate of F_s = 65 536 Hz, the number of samples per degree rotation is only 12, which corresponds to a path length difference of only 63 mm before total coherence between segments is lost. This can be overcome by delaying signals between channels, however shifting the time signal by intra-sample delays requires either interpolation, which performs poorly at higher frequencies, or upsampling, which can be slow. Instead, the pressure records can be shifted by the closest number of samples, and adjust the residual time difference in the frequency domain, as a phase shift in the steering vectors. The algorithm, in more detail is as follows. For each focus point, j in the scanning grid, the time delays to each microphone, m, t_j,m are calculated as per standard beamforming. An integer number of samples, I, to delay each channel is then calculated by rounding:

$$I_{j,m}=\lfloor F_s{t}_{j,m}\rceil$$ (17)

from which the residual time can be calculated to be

$$t_{\text{res}.,j,m}=t_{j,m}-\frac{I_{j,m}}{F_s}.$$ (18)

The cross-spectrum matrix, G(f), for each scanning grid point is then calculated using a segment centred about each time the rotor angle, θ(t), passes through the phase angle of interest, θ₀:

$$\begin{array}{c}{G}_{j,m_a,m_b}\left(f\right)=\frac{2}{K{F}_s\sum _{l=0}^{L-1}\overrightarrow{w}{\left(l\right)}^2}\sum _{k=0}^{K-1}{\left(F\left\{\overrightarrow{w}\circ p_{m_a}(I_{j,m_a}+kD)\right\}\right)}^{†}\left(F\left\{\overrightarrow{w}\circ p_{m_b}(I_{j,m_b}+kD)\right\}\right),\\ I_{j,m_a}=I_{m_a,j}+\left[-L-L+1\hspace{0.17em}\dots \hspace{0.17em}L-2\hspace{0.17em}L-1\right],\\ I_{j,m_b}=I_{m_b,j}+\left[-L-L+1\hspace{0.17em}\dots \hspace{0.17em}L-2\hspace{0.17em}L-1\right],\end{array}$$ (19)

where p_m is the recorded pressure at mth microphone, L is the length of the time segment, ${(•)}^{†}$ is the conjugate transpose, $\overrightarrow{w}$ is the tapering function (a Hanning window), F_s is the sampling rate, ∘ denotes the Hadamard product, K is the number of times θ(t) = θ₀, D is the offset in samples and F{•} stands for Fourier transform.

Conventional frequency-domain beamforming was then used with the cross-spectrum matrix from Eq. (19), and modified steering vectors using the residual times for each microphone. Specifically, the forward propagation function is modified to be

$$a_{j,m}\left(f\right)=\frac{r_{j,0}}{r_{j,m}}{e}^{-2\pi f{t}_{\text{res}.,j,m}},$$ (20)

from which the Sarradj's²² “formulation 4” steering vectors are

$$e_{j,m}=\frac{1}{\sqrt{M}}\frac{a_{j,m}\left(f\right)}{\left|\right|{\overrightarrow{a}}_j\left(f\right)\left|\right|},$$ (21)

where M is the number of microphones. The power density at each point is then

$$Y_j(f)=e_{j,m}^{†}(f)G(f)e_{j,m}(f).$$ (22)

Phase-averaged beamforming was calculated over ∼1 ms time blocks, which is the time that it takes for the blade tip to travel over a ∼5° arc. Since the sampling frequency was 65 536 Hz, 1 ms of time corresponds to ∼60 samples. This value of samples when used for calculating the cross-spectral matrix was zero-padded to a length of 256 samples and thus providing a frequency resolution of 256 Hz. Although the zero padding does not increase the effective frequency resolution, it provides a smoother spectral estimate.

Measured noise sound pressure level was obtained using the beamforming integration technique as described by Brooks and Humphreys.²³ Using this integration approach, the trailing edge noise source can be isolated from other noise sources on the airfoil by integrating the conventional beamforming noise map over the trailing edge region only. Integration regions are marked in beamforming source maps later in the paper.

The measured rotor noise is the mean noise from 72 azimuthal phase-averaged beamforming noise maps. The integration zone at each azimuthal position was 210 × 300 mm.

III. RESULTS

A. Stationary NACA 0012 airfoil

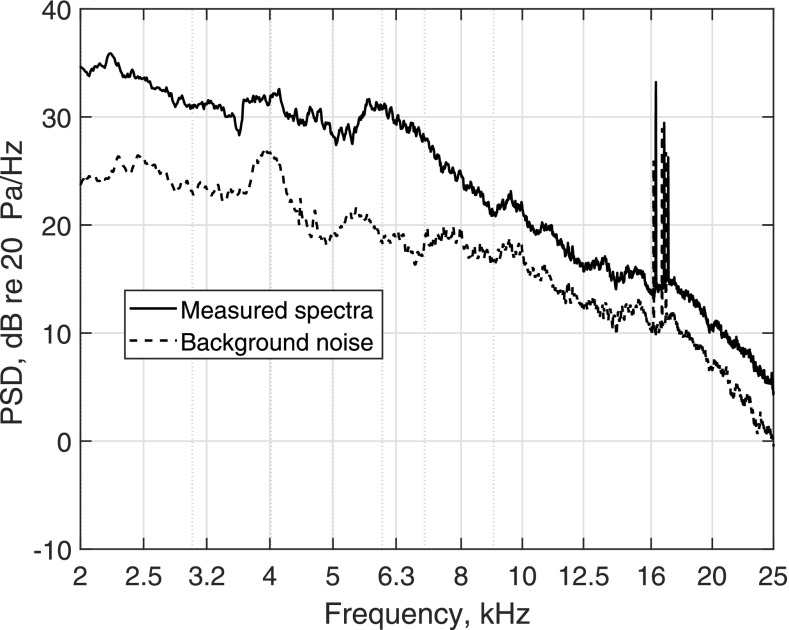
Figure 7 shows the comparison between the anechoic wind tunnel background noise at a flow speed of 37 m/s and the far-field acoustic spectrum of the stationary NACA 0012 airfoil recorded at the microphone center location. As can be seen, the measured spectrum lies well above the background noise over the whole frequency range. Tonal components around 16 kHz are attributed to the facility noise since they appear in both spectra.

FIG. 7.

Far-field acoustic spectra for a stationary NACA 0012 airfoil at Re_c = 182 304 and background noise.

To identify the frequency range of trailing edge noise, an M⁵ velocity scaling was used. According to Ffowcs-Williams and Hawkings,²⁴ the far-field acoustic spectra obtained at different free-stream velocities (30 and 37 m/s) must collapse over the trailing edge frequency range after being scaled by an M⁵ factor because trailing edge noise radiation is proportional to M⁵. This scaling is only valid for frequencies whose acoustic wavelength, λ, is significantly larger than the airfoil chord, c, (λ > 4 c); that is for frequencies above ∼2 kHz since the chord length of the airfoil is 70 mm. The one-third-octave band far-field spectra are scaled as follows:

$$L{p}_{\text{Scaled},1/3}=L{p}_{1/3}-10\hspace{0.17em}\text{log}\left(M^5\frac{{\delta }^{*}L}{r_e^2}\right),$$ (23)

where Lp_Scaled,1/3 is the far-field spectrum, M is the Mach number, L is the wetted airfoil span and r_e is the distance from the trailing edge to the microphone. The boundary layer displacement thickness, δ*, at both Mach numbers was determined using XFOIL. Figure 8 shows a good collapse of the noise spectra between ${\text{St}}_{{\delta }^{*}}=0.15$ and ${\text{St}}_{{\delta }^{*}}=0.24$, indicating that the trailing edge noise is the dominant noise source in this region. The differences in scaled noise spectra below ${\text{St}}_{{\delta }^{*}}=0.15$ are attributed to shear layer noise which is observed in Fig. 9.

FIG. 8.

Stationary NACA 0012 airfoil one-third-octave band frequency spectra scaled with M⁵. Strouhal number, ${\text{St}}_{{\delta }^{*}}$, is based on δ* at the trailing edge as estimated by XFOIL.

FIG. 9.

(Color online) Beamforming noise maps at selected Strouhal numbers for a stationary NACA 0012 airfoil at Re_c = 182,304. The red rectangle represents the beamforming integration zone. (a) ${\text{St}}_{{\delta }^{*}}=0.088$ (f_1/3 = 5 kHz) and (b) ${\text{St}}_{{\delta }^{*}}=0.111$ (f_1/3 = 6.3 kHz).

In Fig. 9, conventional beamforming noise maps at selected Strouhal numbers for the stationary NACA 0012 airfoil, are shown for Re_c = 182 304. Strouhal number is based on the free stream velocity of 37 m/s and δ* at the trailing edge of 0.65 mm as estimated by XFOIL. As can be seen in this figure, the dominant source is located at the trailing edge.

Figure 10 shows a comparison between the measured one-third-octave band trailing edge noise spectrum and BPM model prediction. The trailing edge noise spectrum was obtained by integrating over the trailing edge region which is marked by the 40 mm × 200 mm red square in Fig. 9. The trailing edge noise prediction was performed for the microphone positioned 0.54 m away from the airfoil trailing edge at an angle θ_e = 70°. This position corresponds to the location of the array centre microphone. The boundary layer displacement thickness, δ*, input into the prediction procedure was calculated using XFOIL and the span length was set to 200 mm. The solid angle of the sloping surface upstream of the trailing edge (Ψ) was set to be 14° in the BPM bluntness trailing edge noise calculations, as this angle is expected for NACA 0012 airfoil.

FIG. 10.

Comparison between predicted and measured noise for stationary NACA 0012 airfoil at Re_c = 182 304. Strouhal number, ${\text{St}}_{{\delta }^{*}}$, is based on U_∞ = 37 m/s and δ^*= 0.65 mm at the trailing edge (estimated by XFOIL).

Excellent agreement between the measured noise and the BPM trailing edge prediction is observed in Fig. 10. The peak trailing edge noise occurs at $\mathrm{S}{\mathrm{t}}_{{\delta }^{*}}=0.07$, which is in general agreement with previously published experimental and numerical data for a NACA 0012 airfoil at 0° angle of attack according to Doolan and Moreau.¹ These authors found the mean peak trailing edge noise at 0° angle of attack to occur at ${\text{St}}_{{\delta }^{*}}=0.069\pm 0.02$. As can be seen in Fig. 10, the BPM model over predicts the bluntness trailing edge noise. This could partially be due to the differences between the current airfoil and the airfoils on which the BPM model is based. Brooks et al.¹⁰ used blunt extension plates attached to the airfoil trailing edge while in the experiments presented here a truncated airfoil is used. Furthermore, in comparison of the BPM bluntness trailing edge model by Brooks et al.¹⁰ against experimental data for NACA 0012 by Schlinker,²⁵ the authors set the trailing edge solid angle, Ψ, to be 23° because this yields the best agreement with experimental data. In contrast, the trailing edge solid angle for bluntness trailing edge noise predictions in this paper is set to be 14°, as expected for NACA 0012 airfoil. This suggests an uncertainty about the value of trailing edge solid angle for 0° angle of attack.

B. Rotating NACA 0012 airfoils

Figure 11 shows the far-field PSD for rotating NACA 0012 airfoils at approximately Re_c = 236 503 and 172 232 (Reynolds numbers based on chord at U_TIP = 48 and 38 m/s) and 10° pitch angle, against the background noise. Data were measured on the axis of rotation at distance 1.5 m away from the rotor. The background noise was measured at these two rotational speeds without the blades being attached. From Fig. 11 it is evident that the measured spectra at both speeds sit well above the background noise. A strong peak at 7.5 kHz is attributed to slip ring noise, and this is conformed in the beamforming results. The PSD for 0° pitch angle is also well above the background noise and is not shown here.

FIG. 11.

Far-field acoustic spectra of rotating NACA 0012 airfoils at 10° pitch angle against background noise for blade tip speed, U_TIP, of 48 and 38 m/s.

In Fig. 12, M⁵ scaling results for rotating NACA 0012 airfoils at Re_c = 236 503 and 172 232, are shown. In that figure is shown a good collapse of spectra with M⁵ for the majority of Strouhal number range. The scaling is based on M and δ* (and ${\delta }_{\text{avg}}^{*}$ for 10° pitch angle) estimated at the blade tip since the majority of noise emits from there as shown in Figs. 13. The averaged boundary layer displacement thickness, ${\delta }_{\text{avg}}^{*}$, is estimated based on pressure and suction side value as in Brooks et al.¹⁰

FIG. 12.

Rotating NACA 0012 airfoil one-third-octave band frequency spectra scaled with M⁵. Strouhal numbers are based on the U_TIP velocity and δ* at the trailing edge estimated by XFOIL. (a) 0° pitch angle (δ^*= 0.6 mm) and (b) 10° pitch angle (${\delta }_{\text{avg}}^{*}=1.05\hspace{0.17em}\text{mm}$).

FIG. 13.

(Color online) Conventional beamforming noise maps for rotating NACA 0012 airfoils at selected Strouhal number, which is based on blade chord, blade tip speed of 48 m/s and 0° pitch angle. Strouhal number is based on δ* at the blade tip of 0.6 mm as estimated by XFOIL. The white circle represents the rotor edge and the white dashed square represent the support tower. The blades are rotating in a clockwise direction. (a) ${\text{St}}_{{\delta }^{*}}=0.046$ (f_1/3 = 4 kHz) and (b) ${\text{St}}_{{\delta }^{*}}=0.072$ (f_1/3 = 6.3 kHz).

In Fig. 13, beamforming noise maps at selected Strouhal numbers for rotating NACA 0012 airfoils at 0° pitch angle are shown. This figure shows that the noise sources are concentrated on the outer part of the rotor at all Strouhal numbers. At Strouhal numbers of 0.041 shown in Fig. 13(a), the noise is emitted from the outer ∼25% of the rotor region while at higher Strouhal numbers, shown in Figs. 13(b), the noise region reduces to ∼18% (${\text{St}}_{{\delta }^{*}}=0.082$) of the rotor radius. This reduction of the noise source area with increasing frequency is likely due to the decreasing beamwidth of beamforming with increasing frequency. The noise source observed in the middle of the rotor disk (x, y = 0) at various frequencies is attributed to the slip ring noise. Beamforming results for 10° pitch angle are similar to the ones shown in Fig. 13 and are hence not shown here.

The variations in sound pressure level around the rotor azimuth are attributed to the reflections mainly from the rotor-rig base plate and nacelle (motor, torque sensor and slip ring). This conclusion is based on; (a) the random nature of sound pressure variations around the azimuth and (b) axisymmetric aerodynamic capabilities and thus constant trailing edge noise generation at all azimuthal positions. However, at the location of the support tower in Figs. 13(a) and 13(b), the increased sound pressure level is attributed to reflections from the support tower. These reflections increase the noise level by less than 6 dB and thus indicate that the addition of sound rays at the observer is non-coherent. Some sound rays originate from the trailing edge when the blade is on front of the tower and pass directly to the observer. Others are generated at different times and are reflected by the tower and thus arrive at the observer with a delay, which causes a non-coherent addition; as the signal is broadband it is essentially incoherent from one blade position to the next. Additionally, the curvature of the tower increases the scattering of sound rays in directions other than the observer direction and this also adds to the variation in time delay between rays that are being scattered from the tower.

In Fig. 14, phase-averaged beamforming noise maps at selected Strouhal numbers for rotating NACA 0012 airfoils at 0° pitch angle at θ = 270° azimuthal position and Re_c = 246 000 at the blade tip, are presented. At this blade azimuthal position, the blade is directly in-front of the support tower. In comparison to the conventional beamforming noise maps shown in Fig. 13, the phase-averaged beamforming reveals the location of the noise sources on the airfoil in the chord wise direction. In terms of the span wise noise source distribution, the conventional and phase-averaged beamforming noise maps are in good agreement. Results for blades mounted at 10° pitch angle are not shown due to their similarity with the ones for 0° pitch angle.

FIG. 14.

(Color online) Phase-averaged beamforming noise maps for rotating NACA 0012 airfoils at selected Strouhal numbers, θ = 270° azimuthal position and 0° pitch angle. Strouhal number is based on δ* at the blade tip of 0.6 mm as estimated by XFOIL. The solid white square represents the airfoil (blade). The blades are rotating in a clockwise direction. The red square represents the beamforming integration zone. (a) ${\text{St}}_{{\delta }^{*}}=0.046$ (f_1/3 = 4 kHz) and (b) ${\text{St}}_{{\delta }^{*}}=0.072$ (f_1/3 = 6.3 kHz).

In Fig. 14(a), the noise source is located in the centre of the airfoil surface with respect to the chord wise direction. At this Strouhal number (frequency of 4 kHz) the wavelength of the source is in the order of the blade chord and hence the noise emits from the whole surface of the airfoil. The source of this noise, known as leading-edge interaction noise, is the unsteady lift caused by the turbulent gust interacting with the leading edge. At higher Strouhal number shown in Fig. 14(b), the noise source region is located at the trailing edge.

Figure 15 shows a comparison between the one-third-octave band frequency measured noise and noise predictions based on the BPM models. Measured data were obtained with beamforming integration and it, therefore, represents the spectra which would be measured with the central microphone of the array.

FIG. 15.

Comparison between predicted and measured noise for rotating NACA 0012 airfoils at Re_c = 256 000 at the blade tip. Strouhal numbers are based on the blade tip speed of 48 m/s and δ* at the blade tip as estimated by XFOIL and trailing edge thickness, h, of 0.8 mm. (a) 0° pitch angle (δ^*= 0.6 mm) and (b) 10° pitch angle (${\delta }_{\text{avg}}^{*}=1.05\hspace{0.17em}\text{mm}$).

Excellent agreement between the predicted trailing edge noise and measured noise is observed above 5 kHz in Fig. 15(a). Again, the BPM model over predicts the bluntness trailing edge noise most likely for reasons discussed in Sec. III A. The peak radiating noise is not clearly evident and it occurs between ${\text{St}}_{{\delta }^{*}}=0.057$ and 0.072 which is in broad agreement with the trailing edge noise peak (${\text{St}}_{{\delta }^{*}}=0.07$) of the stationary NACA 0012 airfoil. This is also in agreement with Fig. 14(b) which show noise source located at the trailing edge at ${\text{St}}_{{\delta }^{*}}=0.072$. The difference between prediction and measurement is less than ∼2 dB at all Strouhal numbers.

In Fig. 15(b), a comparison between measured noise and prediction at 10° pitch angle, is shown. The agreement between prediction and measured noise is good at all one-third-octave band frequencies with a maximum difference of ∼3 dB at 3.2 kHz. The dominating noise source at frequencies below 5 kHz appears to be trailing edge noise. The peak measured trailing edge noise ranges from ${\text{St}}_{d_{\text{avg}}^{*}}=0.067$ and 0.084. The difference in sound pressure level in this Strouhal number range is ∼0.1 dB and is considered to be insignificant. On the other hand, at frequencies above 5 kHz the contribution from bluntness trailing edge noise is the most significant. The peak bluntness trailing edge noise occurs at St_h of 0.128, as evident from Fig. 15(b) [${\text{St}}_h=x(fh/U_{\infty })$]. This is in broad agreement with expected bluntness trailing edge peak Strouhal number, ${\text{St}}_{\text{peak}}^{″\prime }$, which is to occur at 0.137 according to Brooks et al.¹⁰ [${\text{St}}_{\text{peak}}^{″\prime }=0.1(h/{\delta }_{\text{avg}}^{*})+0.095-0.00243\Psi$]. The tip vortex formation noise appears to have no influence in the frequency range of interest since the peak predicted tip vortex formation noise is at approximately 20 kHz (not shown). Recently Moreau et al.²⁶ developed an empirical model based on wall-mounted finite airfoil measurements for predicting tip vortex formation noise. According to that model, the peak tip vortex formation noise is expected to occur around Strouhal number based on chord of 22. For the current case with 70 mm chord length this yields a peak frequency at 15 kHz, which is lower than the BPM peak predicted frequency. This difference is due to the differences in flow around the airfoil on which the models are based. The Moreau et al.²⁶ model is based on span varying flow conditions while the BPM model assumes uniform flow characteristics across the span. According to these flow characteristics, the model by Moreau et al.²⁶ appears to be more suited for predicting tip vortex formation noise of rotating airfoils at 10° pitch angle. However, the validity of either tip vortex noise prediction model cannot be confirmed due to the high frequency limitations of the microphone array used in this study.

IV. CONCLUSIONS

The results of an experimental acoustic investigation of trailing edge noise from stationary and rotating NACA 0012 airfoils at 0° and 10° pitch angle has been presented. The results are important because rotating airfoil data have been obtained under controlled laboratory conditions.

The acoustic analysis showed excellent agreement between stationary airfoil trailing edge noise at Re_c = 182 304 and the trailing edge noise prediction based on the BPM trailing edge noise model for 0° pitch angle. Peak trailing edge noise was observed to occur at ${\text{St}}_{{\delta }^{*}}=0.07,$ which is in broad agreement with previously published data. The BPM model was found to over predict bluntness trailing edge noise. This discrepancy is attributed to the uncertainties of the empirical BPM model.

The acoustic investigation of trailing edge noise from rotating NACA 0012 airfoils at Re_c = 236 503 based on the blade tip speed, showed that trailing edge noise is radiated from the outer part of the rotor. Excellent agreement was observed between the measured trailing edge noise and prediction based on two dimensional flow characteristics at 0° and 10° pitch angles, where the peak trailing edge noise was found to be at comparable Strouhal numbers. Furthermore, it was found that the peak radiating trailing edge noise from rotating airfoils at 0° and 10° pitch angles agrees well with the peak trailing edge noise from stationary airfoils at 0° pitch angle and literature. Although the results based on limited data suggest that peak trailing edge noise from rotating airfoils is independent of the pitch angle, more research is warranted. Bluntness trailing edge noise was found to be the dominant noise source at higher frequencies for 10° pitch angle and in good agreement with the prediction. On the other hand, the model over predicted the bluntness trailing edge noise for rotating airfoil at 0° pitch angle.