Abstract
Background
Humeral retroversion is variable among individuals, and there are several measurement methods. This study was conducted to compare the concordance and reliability between the standard method and 5 other measurement methods on two-dimensional (2D) computed tomography (CT) scans.
Methods
CT scans from 21 patients who underwent shoulder arthroplasty (19 women and 2 men; mean age, 70.1 years [range, 42 to 81 years]) were analyzed. The elbow transepicondylar axis was used as a distal reference. Proximal reference points included the central humeral head axis (standard method), the axis of the humeral center to 9 mm posterior to the posterior margin of the bicipital groove (method 1), the central axis of the bicipital groove –30° (method 2), the base axis of the triangular shaped metaphysis +2.5° (method 3), the distal humeral head central axis +2.4° (method 4), and contralateral humeral head retroversion (method 5). Measurements were conducted independently by two orthopedic surgeons.
Results
The mean humeral retroversion was 31.42° ± 12.10° using the standard method, and 29.70° ± 11.66° (method 1), 30.64° ± 11.24° (method 2), 30.41° ± 11.17° (method 3), 32.14° ± 11.70° (method 4), and 34.15° ± 11.47° (method 5) for the other methods. Interobserver reliability and intraobserver reliability exceeded 0.75 for all methods. On the test to evaluate the equality of the standard method to the other methods, the intraclass correlation coefficients (ICCs) of method 2 and method 4 were different from the ICC of the standard method in surgeon A (p < 0.05), and the ICCs of method 2 and method 3 were different form the ICC of the standard method in surgeon B (p < 0.05).
Conclusions
Humeral version measurement using the posterior margin of the bicipital groove (method 1) would be most concordant with the standard method even though all 5 methods showed excellent agreements.
Keywords: Humerus, Version, Computed tomography
Humeral retroversion is generally defined as the angular difference between the orientation of the proximal humeral head and the axis of the elbow at the distal humerus.1) The degree of humeral head retroversion is important in various clinical situations such as hemiarthroplasty, total shoulder arthroplasty, or reverse total shoulder arthroplasty.2,3) Several biomechanical studies have shown that if the prosthetic geometry deviates even by a small amount from the normal anatomy, there may be a marked decrease in available range of motion.2,4) Hence, correct retroversion of the humeral component is important because it affects the position of the instant center of rotation, the stability of the joint, and the amount of internal or external rotation.
The retroversion angle of the humeral head has a wide range of variability, from –6° to 60°.1) Numerous studies have investigated the degree of humeral head retroversion by using various methods (e.g., direct anatomic measurements, radiography, computed tomography [CT], magnetic resonance imaging [MRI], ultrasonography, and computer-assisted methods).1,5,6,7,8,9) Some studies demonstrated that retroversion of the proximal part of the humerus can be reliably measured on CT scans.1,10) On CT scans, the orientation of the humeral head is defined as the perpendicular axis of the boundaries of the articular surface determined by using the limits of the subchondral bone in the largest circle of the humeral head. However, the humeral head articular surface is not always intact because of humeral head fracture, arthritis, or avascular necrosis. Accordingly, some authors have found some useful anatomic landmarks of the humeral head for guiding anatomic recreation of retroversion such as the posterior margin of the bicipital groove, the bicipital groove center, the metaphysis of the proximal humerus, or the distal part of an osteoarthritic humeral head.10,11,12,13) In addition, some authors have found a considerable difference between contralateral measurements, whereas others have found no difference.10,14) These differences and variability make surgeons reconsider which landmark is most reliable and concordant for humeral retroversion measurement.
Therefore, the current study was conducted to evaluate the concordance of various methods for measuring humeral retroversion, especially between the standard method and other methods using five landmarks (the bicipital tuberosity, bicipital groove center, metaphysis, distal part of the humeral head, and contralateral humeral head) on two-dimensional (2D) CT scans. The null hypothesis was that the 5 measurement methods would demonstrate no differences with the standard measurement method.
METHODS
Patients
We retrospectively reviewed the CT scans of 21 patients (19 women and 2 men: 28 humeri [9 right and 19 left]) who underwent reverse total shoulder arthroplasty for cuff tear arthropathy between March 2013 and March 2015. After obtaining Institutional Review Board approval from Seoul National University Bundang Hospital to review the patients' chart, a retrospective study was initiated (No. B-1508/312-112). The patients' mean age was 70.1 years (range, 42 to 81 years). Bilateral CT for patients undergoing arthroplasty is a routine protocol in the Seoul National University Bundang Hospital. To minimize radiation exposure, CT was performed separately for the proximal and distal humeri instead of the entire humerus. Reconstruction of the CT scans was performed perpendicular to the humeral diaphysis to obtain true axial slices and the truest retroversion angle.15) All measurements were conducted twice with an 1-week interval, independently by 2 orthopedic surgeons.
Technique
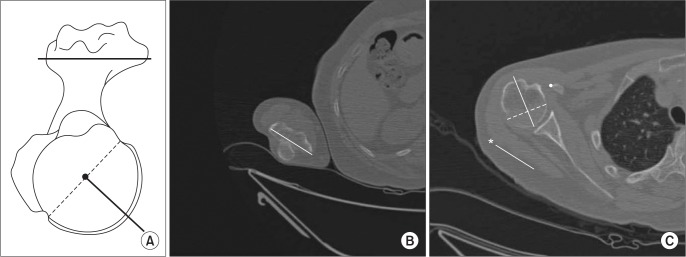
We defined the standard method as a measurement of the angle between the central axis of the humeral head and the elbow transepicondylar axis.1) The central axis of the humeral head was defined on axial 2D CT scans as the perpendicular axis of the boundaries of the articular surface of the humeral head determined by using the limits of the subchondral bone in the largest circle of the humeral head. The elbow transepicondylar axis was defined as a line between the most medial and most lateral extension of the distal humerus (Fig. 1). This transepicondylar axis was also used in the other methods.
Fig. 1. (A) Schematic drawing of the standard method. (B) The transepicondylar axis is defined as a line between the most medial and most lateral extension of the distal humerus. (C) The angle between the central axis of the humeral head and the elbow transepicondylar axis (asterisk) is shown. The central axis is a perpendicular axis of the boundaries of the articular surface determined by using the limits of the subchondral bone in the largest circle of the humeral head.
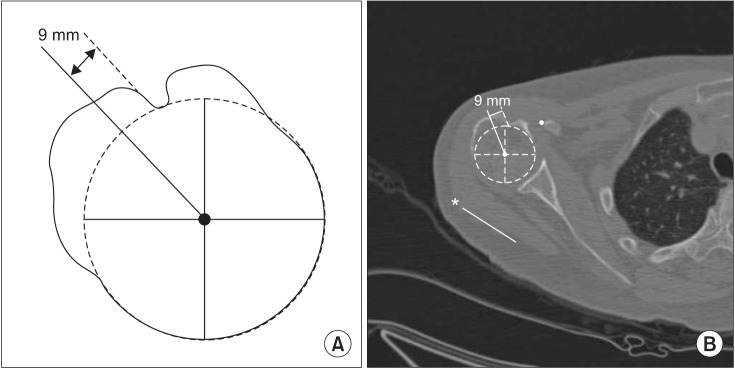
We defined method 1 as a measurement of the angle between the 9 mm posterior point of the bicipital groove axis and the elbow transepicondylar axis, as suggested by Tillett et al.12) The 9 mm posterior point of the bicipital groove axis was determined as the axis drawn from the humeral head center to 9 mm posterior to the posterior margin of the bicipital groove (Fig. 2).
Fig. 2. (A) Schematic drawing of method 1. (B) The angle between the 9 mm posterior margin of the bicipital groove axis and the elbow transepicondylar axis (asterisk) is shown.
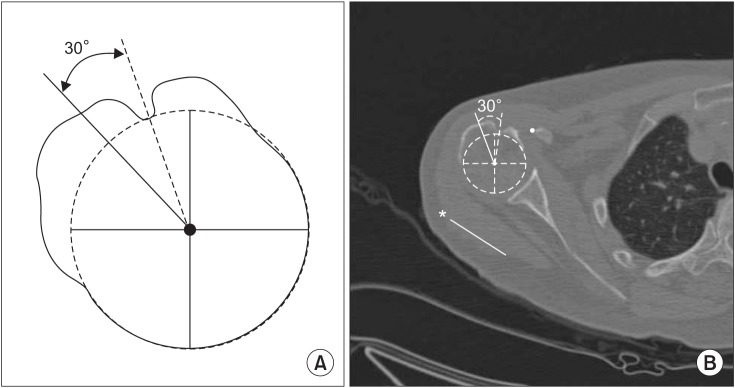
Kummer et al.11) suggested that the bicipital groove can be used as a landmark for prosthetic stem positioning in shoulder arthroplasty if the center of the lateral aspect of the stem is posteriorly offset by approximately 30° from the center of the groove. Accordingly, method 2 was defined as a measurement of the angle between the bicipital groove center axis and the elbow transepicondylar axis –30°. The bicipital groove center axis was defined as the axis extending from the humeral head center to the bicipital groove center (Fig. 3).
Fig. 3. (A) Schematic drawing of method 2. (B) The angle between the bicipital groove center axis and the elbow transepicondylar axis (asterisk) –30° is shown.
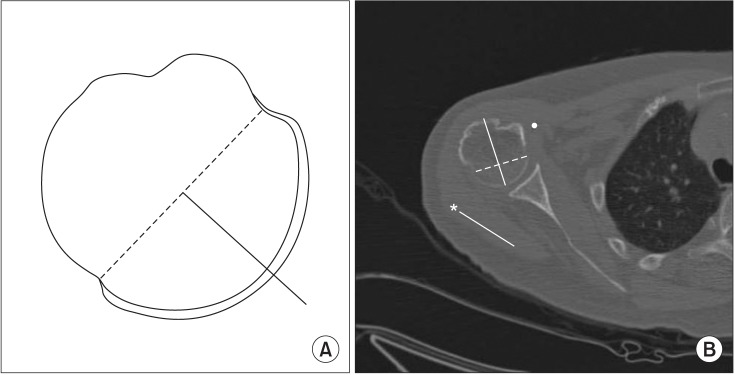
Athwal et al.13) reported that the mean difference between metaversion and humeral head retroversion was 2.5°. Hence, we defined method 3 as a measurement of the angle between the metaphyseal axis and the elbow transepicondylar axis +2.5°. The metaphyseal axis was determined as the axis of the medial apex of the metaphyseal zone connected to a midway point at the base of the triangular shaped metaphysis (Fig. 4).
Fig. 4. Method 3 measures the angle between the metaphyseal axis and the elbow transepicondylar axis (asterisk) +2.5°.
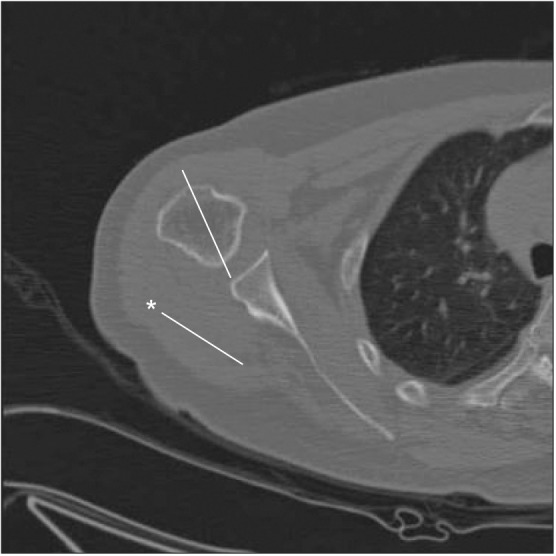
Hernigou et al.10) calculated the mean side-to-side difference in the torsion angle to be 2.4° in unilateral patients by measuring retroversion on the pathological side at the limits of the osteophytes in the distal part of the humeral head using the epicondylar axis. We defined method 4 as a measurement of the angle between the distal humeral head central axis and the elbow transepicondylar axis +2.4°. The distal humeral head central axis was defined as the axis perpendicular to the boundaries of the articular surface determined by using the limits of the subchondral bone on 2 slices (6 mm) below the largest circle of the humeral head on axial slices (Fig. 5).
Fig. 5. (A) Schematic drawing of method 4. (B) The angle between the axis through the distal humeral head central axis and the elbow transepicondylar axis (asterisk) +2.4° is shown. The distal humeral head central axis is the axis perpendicular to the boundaries of the articular surface determined by using the limits of the subchondral bone on 2 slices (6 mm) below the largest circle of the humeral head on axial slices.
Method 5 was defined as contralateral humeral head retroversion measured by using the standard method.
Statistical Analysis
All statistical analyses were conducted using SPSS ver. 18.0 (SPSS Inc., Chicago, IL, USA) and R (R Development Core Team, 2015; https://www.r-project.org/).
We evaluated the mean and standard deviation of the humeral retroversion angle. The interobserver reliability and intraobserver reliability were calculated using the intraclass correlation coefficient (ICC) of Shrout and Fleiss16) The ICCs can range from 0 (no agreement) to 1 (perfect agreement): a value of 0.00–0.39 was considered poor agreement; 0.40–0.74, moderate agreement; and 0.75–1.00, excellent agreement. Finally, we verified the concordance between the standard method and the other methods. The null hypothesis that 5 other measurement methods would demonstrate no differences with the standard method was evaluated by means of modified form of Fisher transformation to test the equality of two ICCs as proposed by Donner et al.17)
RESULTS
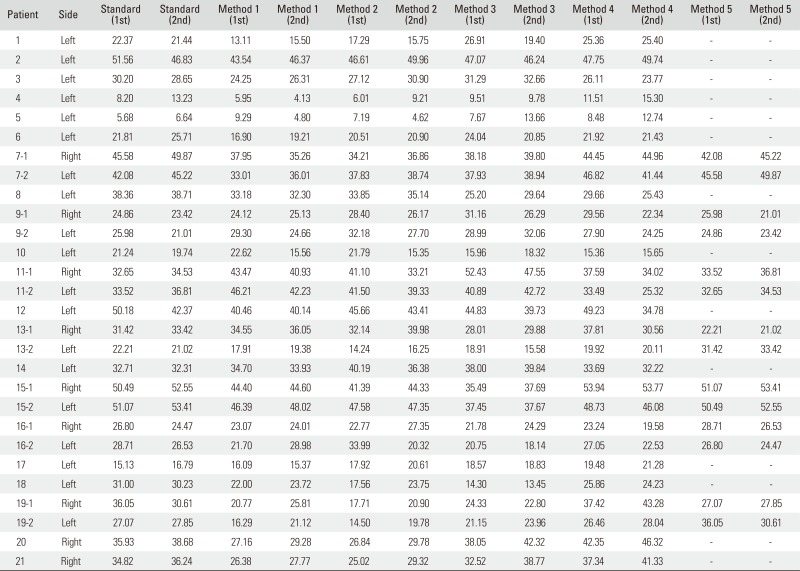
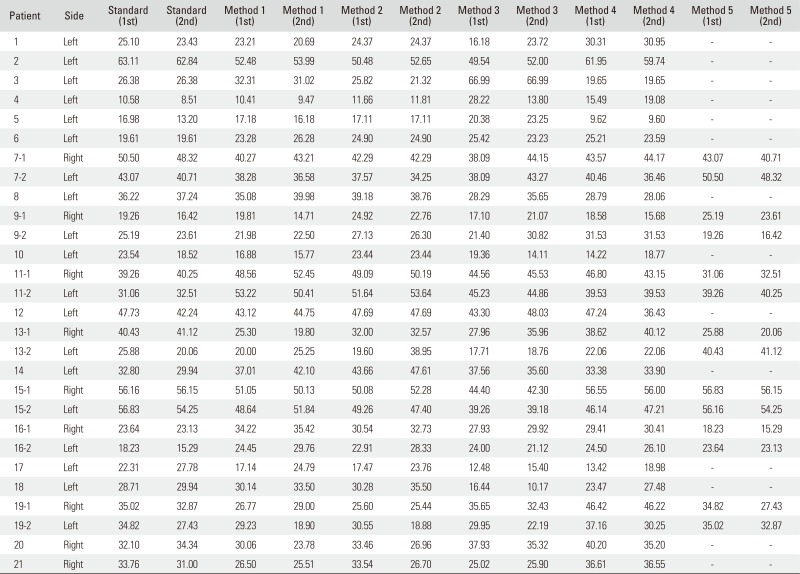
The values of humeral head retroversion were widely distributed from 10.63° to 56.09°. The mean humeral retroversion of the standard method was 31.42° ± 12.10°. We presented all measurements for all 21 patients (Appendices 1 and 2). The mean humeral retroversion of the other methods was 29.70° ± 11.66° (method 1), 30.64° ± 11.24° (method 2), 30.41° ± 11.17° (method 3), 32.14° ± 11.70° (method 4), and 34.15° ± 11.47° (method 5). The closest mean humeral retroversion values were observed between the standard method and method 4 (Table 1).
Table 1. Humeral Retroversion Measured Using Standard and Five Methods by Surgeon A and B.
| Method (°) | Surgeon A | Surgeon B | Surgeon A and B |
|---|---|---|---|
| Standard | 31.63 ± 12.99 | 31.21 ± 11.79 | 31.42 ± 12.10 |
| 1 | 31.53 ± 12.48 | 27.88 ± 11.43 | 29.70 ± 11.66 |
| 2 | 32.75 ± 11.73 | 28.51 ± 11.50 | 30.64 ± 11.24 |
| 3 | 31.66 ± 12.75 | 29.16 ± 11.04 | 30.41 ± 11.17 |
| 4 | 32.60 ± 12.54 | 31.66 ± 11.50 | 32.14 ± 11.70 |
| 5 | 34.34 ± 12.94 | 33.98 ± 10.54 | 34.15 ± 11.47 |
Values are presented as mean ± standard deviation.
The ICCs for Interobserver reliability and intraobserver reliability exceeded 0.75 in all methods showing the excellent agreement (Table 2).
Table 2. Intraclass Correlation Coefficients (95% Confidence Interval) of Interobserver Reliability and Intraobserver Reliability.
| Method | Interobserver reliability | Intraobserver reliability | |
|---|---|---|---|
| Surgeon A | Surgeon B | ||
| Standard | 0.912 (0.819–0.958) | 0.979 (0.954–0.990) | 0.965 (0.926–0.984) |
| 1 | 0.897 (0.790–0.951) | 0.947 (0.888–0.975) | 0.962 (0.920–0.982) |
| 2 | 0.890 (0.777–0.948) | 0.899 (0.793–0.952) | 0.920 (0.834–0.962) |
| 3 | 0.754 (0.534–0.878) | 0.917 (0.829–0.961) | 0.952 (0.900–0.978) |
| 4 | 0.907 (0.809–0.956) | 0.964 (0.923–0.983) | 0.926 (0.846–0.965) |
| 5 | 0.909 (0.742–0.970) | 0.983 (0.947–0.994) | 0.958 (0.900–0.978) |
On the equality of two ICCs17) (ICC of the standard method vs. ICCs of the other methods) (Table 3), the ICCs of method 2 and method 4 were statistically significantly different from the ICC of the standard method in surgeon A (p < 0.05). In surgeon B, ICCs of method 2 and method 3 were significantly different from the ICC of the standard method (p < 0.05). This meant that method 1 and method 5 were more concordance with the standard method than the other methods; however, statistical significance could not be demonstrated with method 5 due to the small number of cases.
Table 3. Test to Evaluate the Equality of Two Intraclass Correlation Coefficients (ICCs) Proposed by Donner et al.17).
| Method | Surgeon A | Surgeon B | ||
|---|---|---|---|---|
| Statistic | p-value | Statistic | p-value | |
| 1 | 0.251 | 0.802 | 1.787 | 0.074 |
| 2 | 2.056 | 0.040* | 3.372 | 0.001* |
| 3 | 0.732 | 0.464 | 2.462 | 0.014* |
| 4 | 2.197 | 0.028* | 0.666 | 0.505 |
| 5 | < 0.001 | 1.000 | −0.029 | 0.977 |
*p-value < 0.05 means that ICC of the standard method and that of other method were different.
DISCUSSION
In the current study, we evaluated humeral head retroversion by using 5 different landmarks (posterior margin of the bicipital groove, bicipital groove center, proximal humeral metaphysis, distal humeral head, and contralateral humeral head). The method using the posterior margin of the bicipital groove as a landmark (method 1) demonstrated the highest concordance with the standard method.
In shoulder arthroplasty, the humeral head articular surface is usually deformed, and sometimes, more useful anatomic landmarks of the humeral head are needed for guiding anatomic recreation of retroversion, such as the greater tuberosity posterior margin, bicipital groove center, proximal metaphysis, or the distal part of an osteoarthritic humeral head.10,11,12,13) The bicipital groove center and the posterior margin of the bicipital groove are known local landmarks that assist with the determination of humeral head retroversion.11,12) However, the method using the bicipital groove center showed lower concordance with the standard method in this study, whereas the method using the posterior margin of the bicipital groove demonstrated higher concordance. These findings may be attributable to the bicipital tuberosity. The posterior margin of the bicipital groove was measured somewhat clearly on 2D CT. In contrast, the bicipital groove center was measured subjectively for the variation of bicipital tuberosity.18)
Proximal humeral metaphyseal version has been considered to be reliable and accurately predict true humeral head version.13) However, the present study has found that proximal humeral metaphyseal version has lower concordance with humeral head version measured using the standard method. This may be attributed to the fact that it is difficult to exactly bisect the metaphyseal zone. The apex of the metaphysis is not always triangular and sometimes the apex of the metaphysis is more circular than triangular as observed in this study.
Distal humeral head retroversion had lower concordance in this study. This finding may be attributed to the difference in humeral head size and the vague cartilage and metaphyseal interface. Some authors also reported the variation in retroversion at each level of the humeral head.10,19) The size of humeral head was different from person to person. Therefore, the distal humeral head central axis in a small size humeral head was measured at a more distal humeral level. The cartilage and metaphyseal interface was more vague at the more distal humeral level.
The present study had some limitations. First, CT scans were used to calculate humeral head retroversion. CT scans are usually used to assess osseous anatomy, not true articular cartilage, which is radiolucent. Nevertheless, CT scans can be used to accurately measure humeral head retroversion.1,10) Second, patient positioning was different in the CT scanner. To decrease the effect of patient position and to obtain true axial slices, we reconstructed CT scans perpendicular to the humeral diaphysis. This reconstruction could be used to obtain the true axial slices and the truest retroversion angle.15) Third, the humeri of some patients showed osteoarthritis. This was unavoidable considering that the enrolled patients were scheduled to undergo shoulder arthroplasty and a certain degree of osteoarthritis would inevitably be present. However, we excluded patients with moderate to severe osteoarthritis (Samilson-Prieto grade II and III); hence, we believe that arthritis had a minimal effect considering the current data. Finally, other landmarks, such as the lesser tuberosity, pectoralis insertion, and glenoid version were not measured in this study. Accordingly, in future studies, other landmarks should be evaluated and normal controls who are not scheduled to undergo arthroplasty should also be included.
The mean retroversion was between 29.7° and 34.2° in this study. Clinically, 5° of difference in retroversion might not be significant. Although the current study could not suggest an absolute standard to predict humeral retroversion, we believe that this study might help surgeons in predicting humeral head retroversion preoperatively when head deformity is considerable and the standard method cannot be used. Since method 1 was most concordant with the standard method, it could be used in patients with deformed humeral head even though all the 5 methods also showed excellent agreements.
In conclusions, humeral version measurement using the posterior margin of the bicipital groove was most concordant with the standard method even though all the other methods also showed excellent agreements.
Appendix 1
Retroversion (°) of All Measurements in All Patients by Surgeon A
Appendix 2
Retroversion (°) of All Measurements in All Patients by Surgeon B
Footnotes
CONFLICT OF INTEREST: No potential conflict of interest relevant to this article was reported.
References
- 1.Boileau P, Bicknell RT, Mazzoleni N, Walch G, Urien JP. CT scan method accurately assesses humeral head retroversion. Clin Orthop Relat Res. 2008;466(3):661–669. doi: 10.1007/s11999-007-0089-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Favre P, Sussmann PS, Gerber C. The effect of component positioning on intrinsic stability of the reverse shoulder arthroplasty. J Shoulder Elbow Surg. 2010;19(4):550–556. doi: 10.1016/j.jse.2009.11.044. [DOI] [PubMed] [Google Scholar]
- 3.Hasan SS, Leith JM, Campbell B, Kapil R, Smith KL, Matsen FA., 3rd Characteristics of unsatisfactory shoulder arthroplasties. J Shoulder Elbow Surg. 2002;11(5):431–441. doi: 10.1067/mse.2002.125806. [DOI] [PubMed] [Google Scholar]
- 4.Pearl ML, Volk AG. Retroversion of the proximal humerus in relationship to prosthetic replacement arthroplasty. J Shoulder Elbow Surg. 1995;4(4):286–289. doi: 10.1016/s1058-2746(05)80022-9. [DOI] [PubMed] [Google Scholar]
- 5.Krahl VE. An apparatus for measuring the torsion angle in long bones. Science. 1944;99(2581):498. doi: 10.1126/science.99.2581.498. [DOI] [PubMed] [Google Scholar]
- 6.Cyprien JM, Vasey HM, Burdet A, Bonvin JC, Kritsikis N, Vuagnat P. Humeral retrotorsion and glenohumeral relationship in the normal shoulder and in recurrent anterior dislocation (scapulometry) Clin Orthop Relat Res. 1983;(175):8–17. [PubMed] [Google Scholar]
- 7.Tellioglu AM, Karakas S, Taskin F. Determining torsion angle of humerus head using MRI method. Turk J Med Sci. 2014;44(4):639–642. [PubMed] [Google Scholar]
- 8.Ito N, Eto M, Maeda K, Rabbi ME, Iwasaki K. Ultrasonographic measurement of humeral torsion. J Shoulder Elbow Surg. 1995;4(3):157–161. doi: 10.1016/s1058-2746(05)80045-x. [DOI] [PubMed] [Google Scholar]
- 9.Robertson DD, Yuan J, Bigliani LU, Flatow EL, Yamaguchi K. Three-dimensional analysis of the proximal part of the humerus: relevance to arthroplasty. J Bone Joint Surg Am. 2000;82(11):1594–1602. doi: 10.2106/00004623-200011000-00013. [DOI] [PubMed] [Google Scholar]
- 10.Hernigou P, Duparc F, Hernigou A. Determining humeral retroversion with computed tomography. J Bone Joint Surg Am. 2002;84(10):1753–1762. doi: 10.2106/00004623-200210000-00003. [DOI] [PubMed] [Google Scholar]
- 11.Kummer FJ, Perkins R, Zuckerman JD. The use of the bicipital groove for alignment of the humeral stem in shoulder arthroplasty. J Shoulder Elbow Surg. 1998;7(2):144–146. doi: 10.1016/s1058-2746(98)90225-7. [DOI] [PubMed] [Google Scholar]
- 12.Tillett E, Smith M, Fulcher M, Shanklin J. Anatomic determination of humeral head retroversion: the relationship of the central axis of the humeral head to the bicipital groove. J Shoulder Elbow Surg. 1993;2(5):255–256. doi: 10.1016/S1058-2746(09)80085-2. [DOI] [PubMed] [Google Scholar]
- 13.Athwal GS, MacDermid JC, Goel DP. Metaversion can reliably predict humeral head version: a computed tomography-based validation study. J Shoulder Elbow Surg. 2010;19(8):1145–1149. doi: 10.1016/j.jse.2010.04.047. [DOI] [PubMed] [Google Scholar]
- 14.DeLude JA, Bicknell RT, MacKenzie GA, et al. An anthropometric study of the bilateral anatomy of the humerus. J Shoulder Elbow Surg. 2007;16(4):477–483. doi: 10.1016/j.jse.2006.09.016. [DOI] [PubMed] [Google Scholar]
- 15.Farrokh D, Fabeck L, Descamps PY, Hardy D, Delince P. Computed tomography measurement of humeral head retroversion: influence of patient positioning. J Shoulder Elbow Surg. 2001;10(6):550–553. doi: 10.1067/mse.2001.118412. [DOI] [PubMed] [Google Scholar]
- 16.Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86(2):420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- 17.Donner A, Shoukri MM, Klar N, Bartfay E. Testing the equality of two dependent kappa statistics. Stat Med. 2000;19(3):373–387. doi: 10.1002/(sici)1097-0258(20000215)19:3<373::aid-sim337>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- 18.Dashottar A, Borstad JD. Validity of measuring humeral torsion using palpation of bicipital tuberosities. Physiother Theory Pract. 2013;29(1):67–74. doi: 10.3109/09593985.2012.675416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Harrold F, Wigderowitz C. A three-dimensional analysis of humeral head retroversion. J Shoulder Elbow Surg. 2012;21(5):612–617. doi: 10.1016/j.jse.2011.04.005. [DOI] [PubMed] [Google Scholar]