Insights into Watson–Crick/Hoogsteen breathing dynamics and damage repair from the solution structure and dynamic ensemble of DNA duplexes containing m¹A

Abstract

In the canonical DNA double helix, Watson–Crick (WC) base pairs (bps) exist in dynamic equilibrium with sparsely populated (∼0.02–0.4%) and short-lived (lifetimes ∼0.2–2.5 ms) Hoogsteen (HG) bps. To gain insights into transient HG bps, we used solution-state nuclear magnetic resonance spectroscopy, including measurements of residual dipolar couplings and molecular dynamics simulations, to examine how a single HG bp trapped using the N1-methylated adenine (m¹A) lesion affects the structural and dynamic properties of two duplexes. The solution structure and dynamic ensembles of the duplexes reveals that in both cases, m¹A forms a m¹A•T HG bp, which is accompanied by local and global structural and dynamic perturbations in the double helix. These include a bias toward the BI backbone conformation; sugar repuckering, major-groove directed kinking (∼9°); and local melting of neighboring WC bps. These results provide atomic insights into WC/HG breathing dynamics in unmodified DNA duplexes as well as identify structural and dynamic signatures that could play roles in m¹A recognition and repair.

INTRODUCTION

Soon after the discovery of the double helix (1), a crystal structure of 9-methyladenine and 1-methylthymine revealed an unusual pairing now referred to as a ‘Hoogsteen’ (HG) base pair (bp) (2) in which the purine base was flipped 180° to adopt a syn conformation forming a unique set of hydrogen bonds that bring the paired bases into closer proximity by ∼2.0–2.5 Å (Figure 1A). In the ensuing years, A(syn)•T and analogous G(syn)•C⁺ HG bps (Figure 1A) continued to surface (reviewed in (3)) in X-ray structures of AT-rich sequences that form duplexes entirely composed of HG bps (4–7); in structures of DNA bound to small molecules (8–12) and proteins (13–15) where HG bps contribute to DNA recognition; and in DNA duplexes bearing lesions such as N²-propanoguanine (16,17), 1,N²-ethylguanine (18), N¹-methyladenine (m¹A) (19–22) where they are speculated to contribute toward damage accommodation (19,23,24), recognition (23) and repair (25). In addition, there is now strong evidence that some members of the Y-family low fidelity polymerases replicate DNA using HG pairing as a means of bypassing lesions on the Watson-Crick (WC) face during replication (26–29).

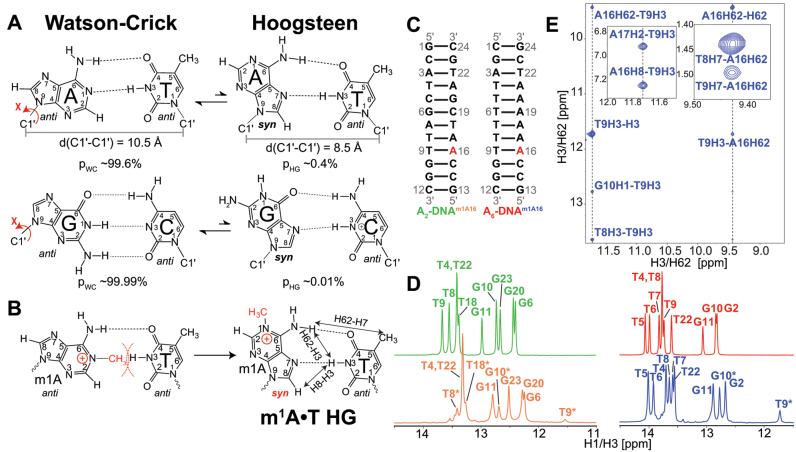
Figure 1.

(A) Watson–Crick (WC) base pairs (bps) exists in dynamic equilibrium with transient low-abundance Hoogsteen (HG) bps through flipping of the purine base 180° about the glycosidic bond from anti to syn conformation. This is also accompanied by a net reduction of C1΄–C1΄ distance by ∼2.0–2.5 Å. Shown are the average populations (p_WC/p_HG) for WC and HG bps as measured by nuclear magnetic resonance (NMR) relaxation dispersion (RD) methods (33,35). (B) m¹A stabilizes HG bp due to steric clash between the methyl group at m¹A-N1 position and T-H3. Nuclear Overhauser effect (NOE) distance connectivity between complementary nucleotides that help in distinguishing HG, WC and reverse-HG pairing modes are indicated using arrows. (C) A₂- and A₆-DNA duplexes used in this study. (D) 1D imino ¹H spectra of A₂-DNA (green), A₂-DNA^m1A16 (orange), A₆-DNA (red) and A₆-DNA^m1A16 (blue). Spectra for for A₂-DNA/A₆-DNA and A₂-DNA^m1A16/A₆-DNA^m1A16 were recorded at 25 and 9°C, respectively. Sites experiencing exchange broadening are denoted with an asterisk (*). (E) T9-H3–A16-H8, T9-H3–A-H62 and T9-H7–A-H62 NOE connectivity distinguishes the formation of HG bp from other pairing modes in A₆-DNA^m1A16 (19) (see Supplementary Figure S3 for A₂-DNA^m1A16). Sequential imino NOEs between T9-H3 with T8-H3 and G10-H1 indicate the formation of a stable duplex.

Recently, studies based on nuclear magnetic resonance (NMR) relaxation dispersion (RD) (30–32) showed that in the canonical DNA double helix, A–T and G–C WC bps exist in dynamic equilibrium with shorter lived (lifetimes of 0.2–2.5 ms) and more sparsely populated (∼0.02–0.4%) HG counterparts (33–35) (Figure 1A). Dynamic transitions toward HG bps occur ubiquitously across a wide range of sequences and positional contexts (35). The abundance and lifetimes of transient HG bps strongly depend on sequence (∼10-fold variations), tending to be more populated and longer lived in unstable dinucleotide steps (35). WC-HG breathing defines a new form of duplex DNA dynamics that could play important roles in DNA biochemical processes. For example, it was recently proposed that WC-HG breathing dynamics can explain how amino nitrogen groups of cytosine in duplex DNA become accessible to hydroxymethylation by formaldehyde, a byproduct of oxidative damage (36).

There are presently no high-resolution structures for transient HG bps in canonical duplex DNA. Therefore, it remains unclear if and how dynamic changes in base pairing affect other structural features of the DNA double helix. Some insights into the potential consequence of HG bps on duplex DNA structure can be obtained from analysis of X-ray and NMR structures of duplex DNA bound to proteins (13–15) and small molecules (8–12); or containing chemically modified nucleotides trapped in HG configurations (16–20,37–39). A recent survey of these structures revealed major-groove directed local kinking at the HG bp along with local backbone perturbations in the neighboring WC bps (40). While this raises the possibility that transient HG bps are coupled to transient kinking of the double helix, one cannot rule out that inter-molecular interactions in these complexes or crystal packing forces also contribute to the observed structural perturbations (40). It is therefore of interest to characterize the structure and dynamic properties of HG bps in unbound DNA duplexes under solution conditions.

In this study, we used solution-state NMR, including measurements of residual dipolar couplings (RDCs) (41–44), in concert with molecular dynamics (MD) simulations to examine how HG bps that are trapped using the lesion m¹A affect the structural and dynamic properties of duplex DNA. m¹A is a non-mutagenic cytotoxic DNA lesion that acts as a strong replication blocker (45). It is generated by external and endogenous alkylating agents that modify single- and double-stranded DNA (46). The N1-methyl group knocks out a WC H-bond and sterically destabilizes WC pairing (Figure 1B) (19,22,33,34). However, flipping of the adenine base by 180° about the glycosidic bond to adopt a syn rather than anti conformation allows formation of relatively stable HG bps (Figure 1B) (19–21,33). Damage repair enzymes such as α-ketoglutyrate dependent dioxygenases (e.g. AlkB, ABH2, ABH3, etc.) repair m¹A by flipping out of the modified base extrahelically into the catalytic domain of the enzyme for direct reversal repair (23,47,48).

Our results show that the trapped m¹A•T HG bp induce local backbone perturbations as well as major-groove DNA kinking (by ∼9°) while partially destabilizing neighboring WC bps. These results provide new insights into WC-HG breathing dynamics as well as identify unique DNA signatures that may be employed during recognition and repair of m¹A.

MATERIALS AND METHODS

Sample preparation

Unmodified DNA samples were purchased as single-stranded oligonucleotides from Integrated DNA Technologies with standard desalting purification. N¹-methyladenosine-modified single-stranded DNA was obtained from Midland DNA Technologies with deprotection of groups performed under mildly basic conditions to avoid the Dimroth rearrangement (49). Samples were purified using reverse-phase HPLC. The DNA oligos were resuspended in water to a concentration of ∼500 μM and subsequently annealed by mixing an equimolar ratio of the complementary DNA single-strands, heating at 95°C for 10 min followed by gradual cooling at room temperature for 60 min. Duplexes were then washed four times in NMR buffer (15 mM sodium phosphate buffer pH 6.8, 25 mM NaCl, 0.1 mM ethylenediaminetetraacetic acid) by microcentrifugation using an Amicon Ultra-15 centrifugal filter with a 3-kDa cutoff, concentrated to 2–3 mM and ∼250–275 μl and then supplied with 10% D₂O. For m¹A-modified DNA duplexes, additional NMR resonances corresponding to m¹A-modified single-strand were observed. These samples were titrated with their respective unmodified complementary single-strand until the single-stranded peaks disappeared, which was monitored using 2D aromatic [¹³C, ¹H] SOFAST-HMQC (50). Pf1 phage ordering medium (51,52) (stock concentration 50–55 mg/ml) was purchased from ASLA Biotech Limited in the NMR buffer and was used without further purification. The DNA samples were concentrated to 2X and Pf1 phage co-solvent (final concentration ∼20–25 mg/ml) and D₂O (final concentration 10%) added. The aligned samples yielded a ²H quadrupolar coupling splitting ²Q_HD ∼28–32 Hz.

NMR spectroscopy

Resonance assignments

The chemical shift assignments for all constructs were obtained using [¹⁵N, ¹H] SOFAST-HMQC (53) (32/58 ms, 77 × 1024 real points), [¹³C, ¹H] SOFAST-HMQC (50) (100/64 ms, 200 × 512), [¹³C, ¹H] HSQC (54) (25/58 ms, 220 × 1024), [¹H, ¹H] TOCSY (54) (115 ms mixing time, 8 kHz spin-lock, 85/170 ms, 512 × 1024) and [¹H, ¹H] WATERGATE-NOESY experiment (54) (100, 150 and 200 ms mixing time, 43/89 ms, 750 × 1536, inter-scan delay 3 s). Splittings to measure RDCs were obtained using the 2D [¹³C, ¹H] sugar (49/80 ms, 74 × 512) and aromatic (50/80 ms, 102 × 512) TROSY experiments (54) that yield individual multiplets for isotropic and phage-aligned samples. Data were obtained using 18.8 T Agilent spectrometer equipped with a DirectDrive 2 console and a triple-resonance HCN cryogenic probe. [¹H, ¹H] 3-9-19 WATERGATE DQF-COSY (54) (85/170 ms, 512 × 1024) and 2D [³¹P, ¹H] HSQC (55) (198/107 ms, 48 × 1024) experiments were performed on 14.1 T Agilent spectrometer equipped with a Bruker HCPN cryogenic probe. Data were acquired at 25°C unless otherwise stated. ¹H and ³¹P chemical shifts were referenced with external standards 50 μM 4,4-dimethyl-4-silapentane-1-sulfonic acid (DSS) and 85% phosphoric acid samples. All spectra were processed using NMRPipe (56) and were zero-filled appropriately to obtain high digital resolution for precise frequency and intensity measurements. Spectra were analyzed using the program SPARKY (T. D. Goddard and D. G. Kneller, SPARKY 3, University of California, San Francisco) and NMRFAM-SPARKY (57).

RDC measurements

RDCs were measured using two different frequency-domain experiments in which the splitting is encoded either along the ¹³C or ¹H dimension in 2D TROSY spectra as described previously (58,59). The uncertainty in RDC measurement was estimated based on the root-mean-square-deviation (RMSD) difference between the two experiments (RMSD ∼ 2 Hz).

NMR data analysis

Chemical shift perturbations

Chemical shift perturbations for each residue (Δω_residue, in ppm) was calculated as described previously (22), 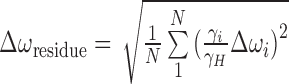, where N is the number of measurements per residue, γ_i and γ_H the gyromagnetic ratio of spin ‘i’ (¹H, ³¹P, ¹³C or ¹⁵N) and proton and Δω_i (in ppm) the chemical shift difference for spin ‘i’ observed between the unmodified duplex (A₂- or A₆-DNA) and the m¹A16-modified duplex (A₂- or A₆-DNA^m1A16).

Intensity measurements

Intensity measurements were performed using the 2D [¹³C, ¹H] aliphatic and aromatic TROSY spectra acquired for all samples at 25°C as previously described (60,61). Intensity ratios were obtained from the ratio of signal-to-noise ratio (S/N) of each peak to the S/N of a reference helical residue in 2D [¹³C, ¹H] aliphatic and aromatic TROSY spectra. The resonance intensities were then normalized with the reference residues set to 1.0 unit. Noise for S/N measurement was obtained from a representation 2D plane in the spectra that contained no peaks and was calculated using 2.5× the RMSD of this noise floor. Error for the normalized intensity was propagated using one S/N unit for each peak and the reference helix peak.

Analysis of NOESY spectra

2D NOESY experiments were acquired at three different mixing times (100, 150 and 200 ms) and the intensity from each experiment was calibrated using cytosine H5–H6 distance (2.45 Å) and thymine H7–H6 (3.00 Å) for methyl groups using the r^–6 distance dependence. The distance extrapolation method (62) was then used to determine the inter-proton distance from the nuclear Overhauser effect (NOE) build-up curves at different mixing times to minimize the effects of spin-diffusion and more accurately determine the distances. NOE cross-peaks from m¹A modified methyl group were also included in the structure refinement of A₆-DNA^m1A16.

Analysis of RDCs

Singular value decomposition implemented in the module calcTensor present in XPLOR-NIH was used to fit experimental RDCs to static structures of DNA. Sugar RDCs of A₂-DNA^m1A16, A₆-DNA and A₆-DNA^m1A16 were normalized prior to comparison with A₂-DNA. Normalized RDCs were obtained by scaling down the RDCs by a factor of 0.90, 0.85 and 0.90 for A₂-DNA^m1A16, A₆-DNA and A₆-DNA^m1A16, respectively. This uniform factor was determined by minimizing the RMSD for the RDC datasets being compared.

Structure refinement

Structure refinement starting from an idealized B-form geometry was performed using XPLOR-NIH version 2.41 (63). Distances (251–284 in total) obtained from the NOESY spectra were used with a 15% (20–30%) tolerance for resolved (overlapped) cross-peaks. A total of 52–67 ¹D_CH RDCs measured for sugar (18–20 C1΄-H1΄, 17–20 C4΄-H4΄) and base (25–29 C2-H2/C5-H5 and C6-H6/C8-H8) bond-vectors (excluding the terminal bps) were used for structure refinement. The experimental data were supplemented with 72 H-bond, 164 dihedral angle and 26 planarity constraints as described previously (64). For m¹A•T HG bp H-bond distances were set to the average values calculated for HG bps in crystal structures: A-N7•T-N3 2.86 Å; A-N7•T-H3 1.89 Å; A-N6•T-O4 1.87 Å; A-H8•T-O2 2.81 Å; A-N7•T-O4 3.75 Å; A-N7•T-O2 3.46 Å; with a uniform ±0.4 Å distance tolerance). The χ dihedral angle for m¹A16 was set to 61° ± 40° (±180° from anti conformation dihedral of −119°) in order to satisfy the syn conformation. Planarity constraints were modified for the m¹A•T HG bp, such that m¹A-N7/C5/C8 atoms remain in plane instead of the default A-N1/C6/C2 atoms for a WC bp.

Force-field parameters for the m¹A group were adapted from the preexisting parameters from the XPLOR-NIH library and the net total charge of +1 was conserved within the modified adenine group (see Supplementary Data). Simulated annealing was performed with force constants for NOEs and RDCs set to 50 kcal Å⁻² and 0.3 kcal Hz⁻², respectively. The amplitude (D_a) and the rhombicity (R_h) of the alignment tensor were arrayed between the values 10–50 units and 0.025–0.400 units, respectively, and the refinement was performed with distance, dihedral angles, H-bond, planarity and RDCs restraints as described previously (65,66). Ten lowest energy structures that yield no NOE violations (>0.40 Å), dihedral angle violations (>6°) and RDC RMSD (<2.5 Hz) were selected for analysis. Overview of structure statistics can be found in supplementary information (Supplementary Table S1).

MD simulations

All simulations were performed using the AMBER ff99 force fields (67) with bsc0 corrections (68) and using standard periodic boundary conditions as implemented in the AMBER MD package (69). Starting structures for unmodified duplexes were obtained by generating idealized B-form duplexes using 3DNA (70). Starting structures for the corresponding m¹A containing duplexes were constructed by superimposing the HG bp from lowest energy XPLOR structures of A₆-DNA^m1A16 onto the backbone of an idealized B-form double helix. The helices were then solvated using an truncated octahedral box of SPC/E (71) waters molecules, with box size chosen such that the boundary was at least 10 Å away from any of the DNA atoms. Na⁺ ions treated using the Joung Cheatham parameters (72) were then added to neutralize the charge of the system. The system was then energy minimized in two stages with the solute (excluding the HG bp) being fixed during the first stage. This was followed by gradual heating of the system (at constant volume) for 100 ps with harmonic restraints on the solute, to a temperature of 298 K. The system was then allowed to equilibrate for 1 ns followed by a production run of 1 μs with a time step of 2 fs. A Langevin thermostat (73) with a collision frequency of 3 ps⁻¹ and a Berendsen barostat (74) with a time constant of 2 ps were used to maintain the temperature (298 K) and pressure (1 bar). The Particle mesh Ewald (PME) method (75) and a non-bonded cutoff of 9 Å were used to treat non-bonded interactions. A set of 10 000 equally spaced snapshots was used for subsequent analysis.

Ensemble determination

Sample and select

The ensembles were generated using the sample and select (SAS) approach as described previously (76–78) using the same RDC dataset used for XPLOR structure determination. In the SAS approach, the measured RDCs are used to guide selection of conformers from a pool generated using MD simulations to construct an ensemble with size N that best satisfies the RDC data. A Monte Carlo sampling scheme was used to search for the ensemble that minimizes the differences between the measured RDCs and values back-calculated for a given trial ensemble using the program PALES (79). We have previously validated the use of PALES in the generation of nucleic acid ensembles (78). The initial effective temperature used in the Monte Carlo scheme was set to 1 K and decreased by multiplying a factor of 0.9 every 10⁵ steps. Several SAS calculations were performed starting from sampling N = 1, and incrementally increasing the ensemble size until the RMSD agreement between predicted and measured RDCs was comparable to the combined RDC measurement and PALES prediction uncertainty (<2.5 Hz, Supplementary Figure S1). The optimal N values were 6, 10, 10 and 15 for A₂-DNA, A₂-DNA^m1A16, A₆-DNA and A₆-DNA^m1A16, respectively.

Cross-validation

Cross-validation was used to evaluate the accuracy of the determined ensemble as described previously (78). In this approach, 25% of the total RDCs data were removed from the SAS analysis; and the generated ensembles were evaluated based on their ability to predict the left-out RDCs data. This procedure was repeated four times and the resulting RDC RMSD was averaged.

Chemical shift prediction

Chemical shifts for H1΄, H2΄, H4΄, H1, H2, H3, H5, H6, H7# and H8 excluding 2 bp from each terminal end were computed for the generated ensembles using SHIFTS (80).

Testing ensemble determination using simulated data

We performed simulations, as described previously (78), to evaluate how well the measured RDC datasets can define specific structural features of interest in the ensembles. Three distinct ‘target’ ensembles (N = 2000) were generated from the A₂-DNA MD pool (N = 10 000) using Gaussian probabilities (average ± standard deviation) as acceptance criteria (i) local inter-helical angles (vide infra) α_h = −20° ± 30°; β_h = 30° ± 8°; γ_h = 20° ± 30° at the A16–T9 junction bp (3D Gaussian) (ii) ε-ζ = −90° ± 150° at G10pG11 (1D Gaussian) (iii) T9 sugar phase angle = 60° ± 30° (1D Gaussian) (Supplementary Figure S2). Synthetic ensemble average RDCs datasets corresponding to the experimentally measured RDCs were computed for each ensemble using PALES. The synthetic RDCs were then noise corrupted (2.5 Hz) and used to perform SAS analysis (N = 2000) using the initial MD pool. The RDC-generated ensembles were then compared with the target ensembles (Supplementary Figure S2).

Ensemble NOE analysis

Average inter-proton distances were computed for a given ensemble and then compared to the experimentally derived distances. In this analysis, NOE-derived distances were used as an upper limit for the inter-proton distance rather than as a strict distance range between protons. Deviations from the NOE-derived upper limit distances that are farther by more than 0.4 Å were adjudged as a violation. Inter-atomic distances for each conformer were generated using an in-house python script.

Structure and ensemble analysis

Local torsion parameters

Base pair, step and helical parameters were computed for all residues except for HG bps (which change the reference frame) using X3DNA-DSSR (81) and groove widths using Curves+ (82).

Kinking and global bending

We used an Euler angle approach to quantify DNA kinking (40,83,84). Here, the two idealized B-form helices (H1 and H2) that are each 2 bps long are superimposed on the DNA structure immediately above and below a specific junction (J) bp. The resulting orientation of the two helices is then specified using three inter-helical Euler angles (α_h, β_h, γ_h) relative to a reference helix, in which the two helices are coaxially aligned in an idealized B-form geometry (40). The inter-helical Euler angle β_h (0° ≤ β_h ≤ 180°) defines the kink angle about the junction bp, while γ_h (−180° ≤ γ_h ≤ 180°) defines the directionality of kinking, with γ_h (−90° ≤ γ_h ≤ 90°) indicating major groove and γ_h (−180° ≤ γ_h ≤ −90° or 90° ≤ γ_h ≤ 180°) indicating minor groove directed kinking, respectively (40). The inter-helical Euler angles (α_h, β_h, γ_h) are then computed for various junction bps along the DNA (J varied from T4–A21 to T9–A16 1 bp at a time). Global bending analysis was performed with Curves+ excluding terminal bps. Euler angles were calculated with H1 and H2 being 2 bp each from the ends of the helix, with the intermediate 6 bp serving as the junction.

RESULTS

m¹A forms a Hoogsteen base pair and induces duplex perturbations and micro-to-millisecond conformational exchange

We examined the impact of introducing single m¹A nucleotide at the same position (A16) in two well characterized duplexes (33,34); A₆-DNA contains a rigid and intrinsically bent A-tract (85–90) while A₂-DNA contains a more scrambled sequence (Figure 1C). Prior NMR studies of these unmodified duplexes showed that the A16–T9 WC bp transiently forms a HG bp with 2-fold greater abundance in A₆-DNA (population ∼0.39 ± 0.02%) as compared to A₂-DNA (population ∼0.17 ± 0.01%) (33). Examining the impact of m¹A on the double helix structure for two distinct sequence contexts helps to assess the robustness of any observed perturbation.

NMR analysis reveals that m¹A16 forms HG bps in both A₆-DNA^m1A16 and A₂-DNA^m1A16 while all remaining residues are WC consistent with previous studies (22,33) (Figure 1D and E; Supplementary Figure S3). The NMR evidence for m¹A16•T9 HG bps includes significantly upfield shifted imino T9-N3/H3 resonances (11,19,22,33,34,91) (Figure 1D and Supplementary Figure S3); several inter-proton NOE distance connectivities (Figure 1E and Supplementary Figure S3) involving complementary (e.g. T9-H7# and m¹A16-H62) and sequential (e.g. C15-H6–m¹A16-H2) nucleotides that confirm HG and rule out reverse-HG pairing (19); and significantly downfield shifted (>3 ppm) m¹A16-C8 (22,33) and m¹A16-C1΄ (Figure 2A and D; Supplementary Table S2) along with strong intra-nucleotide m¹A16-H1΄–H8 NOE cross-peaks that are consistent with a syn conformation for m¹A16 nucleobase (Figure 1E and Supplementary Figure S3) (33,34). Interestingly, many of the base, sugar and backbone resonances belonging to m¹A16•T9 HG bp resonances including T9 (H3), m¹A (C2, C1΄, C2΄, C4΄), and backbone-³¹P (Figure 2C) are significantly broadened, indicating that the HG bp experiences conformational exchange at the micro-to-millisecond timescale (Figure 2A, C and E). This could reflect partial melting of the HG bp to form an open state or distorted WC-like bp (34).

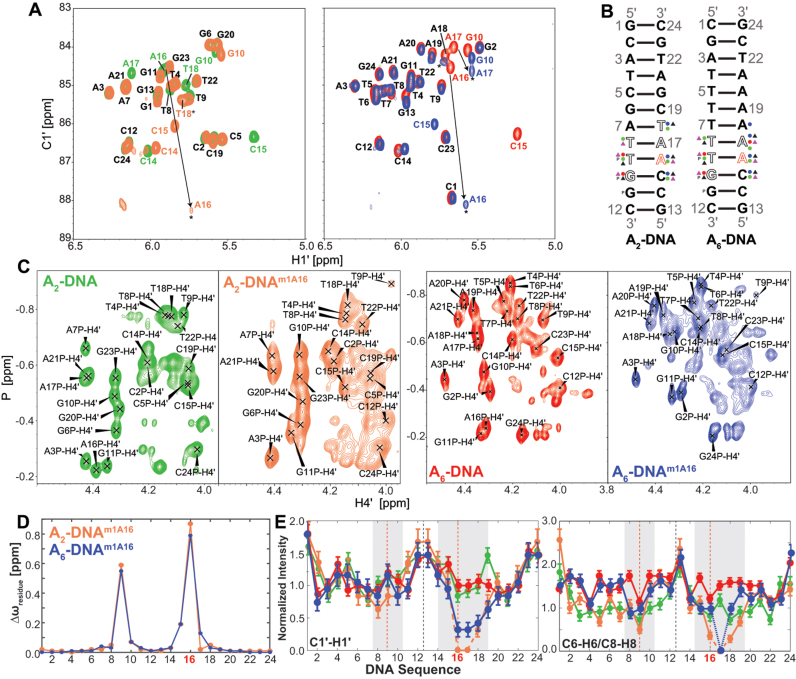
Figure 2.

(A) 2D [¹³C, ¹H] HSQC spectra (54) acquired for A₂-DNA (green), A₂-DNA^m1A16 (orange), A₆-DNA (red) and A₆-DNA^m1A16 (blue) depicting the chemical shift perturbations in the C1΄-H1΄ region. Residues that remain unperturbed are labeled in black; colored labels are for the respective samples and exchange broadened resonances are indicated with an asterisk (*). (B) Chemical shift perturbations observed for sugar (circle) C1΄-H1΄ (blue), C2΄-H2΄/H2″ (red), C4΄-H4΄ (green), base (triangle) C6-H6/C8-H8 (black), N1-H1/C2-H2/N3-H3/C5-H5 (purple) and with backbone (P) ³¹P resonances in A₂- and A₆-DNA upon incorporation of m1A16 residue is shown. Residues that exhibit exchange broadening are indicated as open alphabets. (C) 2D [³¹P, ¹H] HSQC (55) acquired for A₂-, A₆-DNA and their m1A16 counterparts are shown. Phosphorus atom shared between the residues ‘i’ and ‘j’ is given the label jP i.e. T9P indicates T8pT9. (D) Chemical shift perturbation quantitatively plotted as Δω_residue (see ‘Materials and Methods’ section) as a function of DNA sequence for A₂- (orange) and A₆-DNA^m1A16 (blue). (E) Normalized resonance intensities (see ‘Materials and Methods’ section) measured in sugar C1΄-H1΄ (left) and base C6-H6/C8-H8 2D heteronuclear spectra for A₂-DNA (green), A₂-DNA^m1A16 (orange), A₆-DNA (red) and A₆-DNA^m1A16 (blue) as a function of residues, with regions highlighted in gray showing significant intensity perturbation.

m¹A also induced significant chemical shift perturbations in the immediately neighboring bps (Figure 2 and Supplementary Table S2). These include up-field ³¹P perturbations (−0.10 to −0.17 ppm) at the complementary strand (T8pT9, T9pG10 and G10pG11) that suggest an increase in the BI population by ∼12–20% (92); and sugar perturbations (>0.5 ppm) at T9 (C4΄), A16 (C2΄) and A17 (C1΄) in A₆-DNA and G10 (C2΄), C15 (C4΄) and A16 (C1΄, C4΄) in both duplexes that suggest changes in sugar pucker; as supported by ³J_H1΄-H2΄ coupling constant measurements (Supplementary Table S3). Line-broadening is also observed at residues 3΄-end of m¹A which are more significant in A₂-DNA^m1A16 as compared to A₆-DNA^m1A16 (Figure 2E). This could reflect increased WC-HG dynamics and/or partial melting of the WC bps. Interestingly, a prior X-ray structure shows that the m¹A•T HG bp displaces the 3΄-end neighbor WC bp toward the major-groove while minimally affecting the 5΄-neighbor (21).

m¹A•T Hoogsteen base pair perturbs the local and global structure of duplex DNA

To further characterize the impact of the m¹A•T HG bp on both the local and global structural and dynamic properties of the DNA duplexes, we measured RDCs (41–44) in A₂- and A₆-DNA and their m¹A16 counterparts. RDCs provide long-range information regarding the orientation of individual ¹⁵N-¹H and ¹³C-¹H bond vectors relative to the principal axis system of an order tensor frame that is typically oriented along the long axis of the nucleic acid (41–44,93–95). RDCs have been used to determine high-resolution structures of RNA (58,96–99) and DNA (65,66,88,89,100–107). They are also sensitive to internal motions occurring over a broad range of timescales (from picoseconds up to milliseconds) that generally cause a reduction in the magnitude of the measured RDCs (41,43,107–110). Bax et al. have previously demonstrated the utility of natural abundance RDC measurements to examine the perturbations induced by modifications that lock the sugar pucker in the less favored C2΄-exo configuration resulting in bending of the helix toward the major groove (106).

One-bond ¹³C-¹H RDCs (¹D_CH) were measured at natural abundance at 25°C for bond vectors in sugar (C1΄-H1΄, C4΄-H4΄) and base (C2-H2, C5-H5, C6-H6, C8-H8) moieties as the difference between splittings measured in the presence (¹D_CH + ¹J_CH) and absence (¹J_CH) of 20–25 mg/ml of Pf1 phage (51,52). Due to severe line broadening and spectral overlap, it was not feasible to measure RDCs for A17 and T18 as well as for T8(C4΄-H4΄) and G10(C4΄-H4΄) in A₂-DNA^m1A16. In all cases, RDCs were measured in duplicate using TROSY-based experiments in which ¹³C-¹H splittings are encoded either along the direct (¹H) or indirect (¹³C) dimension (see ‘Materials and Methods’ section). A representative example showing the agreement (RMSD = 1.7–2.2 Hz) between the RDCs measured using these two approaches is shown in Figure 3A.

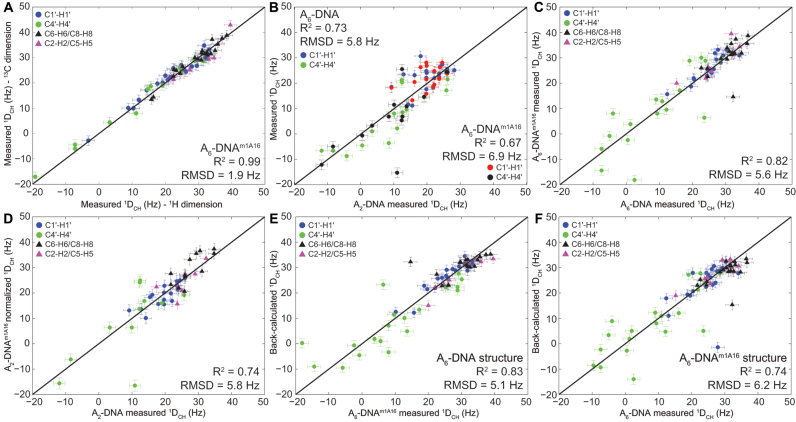
Figure 3.

(A) Comparison of residual dipolar couplings (RDCs) measured by encoding C-H splittings along the ¹³C or ¹H dimension. Shown is the root-mean-square-deviation (RMSD) and Pearson's correlation coefficient (R²). (B) Correlation plot between sugar RDCs measured in A₂-DNA and ¹D_CH A₆-DNA (blue/green) or A₆-DNA^m1A16 (red/black). The A₆-DNA and A₆-DNA^m1A16 RDCs are normalized by scaling factors of 0.85 and 0.90 units, respectively, to account for differences in alignment. (C and D) Correlation plot between RDCs measured in unmodified and m¹A16 modified duplexes: (C) A₆-DNA versus A₆-DNA^m1A16 and (D) A₂-DNA versus A₂-DNA^m1A16, with the different bond vectors colored as shown in the inset. The A₂-DNA^m1A16 data are normalized by scaling factor of 0.90 units to account for differences in alignment. (E) Best-fitting A₆-DNA^m1A16 RDCs to the refined A₆-DNA structure and (F) A₆-DNA RDCs to the refined A₆-DNA^m1A16 structure. Error bar denotes one-standard deviation in RDC measurement.

Significant differences (RMSD ∼ 6 Hz) are observed when comparing sugar RDCs measured in A₂- and A₆-DNA (note that comparison of base RDCs is not possible due to differences in sequence) (Figure 3B). These differences are not surprising given the unique structural features of the A-tract in A₆-DNA (85–90). Interestingly, significant differences (RMSD ∼ 6 Hz) are also observed when comparing RDCs measured in A₂-DNA or A₆-DNA and their m¹A counterparts (Figure 3C and D). Large RDC differences (>6 Hz) are observed not only at the m¹A•T HG bp, but also at neighboring residues, particularly at sugar bond vectors of T8(C4΄-H4΄), T9(C4΄-H4΄), G10(C4΄-H4΄), C15(C4΄-H4΄) and A18(C4΄-H4΄) in A₆-DNA^m1A16. Sizeable RDC deviations (>3 Hz) are also observed at sites >2 bp away from m¹A site that show little to no chemical shift perturbations; this potentially implies changes in global structure. These results suggest that m¹A primarily affects the local conformation of neighboring residues but leaves open the possibility that it also causes significant changes in global structure that affect RDCs measured at a distance.

Solution structure of DNA duplexes with and without m¹A

To gain further insights into the structural changes accompanying formation of the m¹A16•T9 HG bp, we solved the NMR solution structures (see ‘Materials and Methods’ section) of A₂-DNA, A₂-DNA^m1A16, A₆-DNA and A₆-DNA^m1A16 using the measured RDCs and NOEs, supplemented by H-bonding and dihedral angle constraints and the XPLOR-NIH program v 2.41 (63).

All four structures form a B-form double helix with bp parameters (shear, stretch, stagger, buckle, propeller twist, opening); backbone (α,β,γ,δ,ε,ζ,χ); and sugar (ν₀-ν₄) dihedral angles (70) that fall within the distributions of canonical B-form DNA duplexes (40) (Supplementary Figure S4). The A₆-DNA structure (Figure 4A) captures well known A-tract features (A_n•T_n, n ≥ 4) (88,89,104), including the narrowing of the minor groove width (Supplementary Figure S5) and minor-groove directed bending on the order of ∼12° (Table 1 and Supplementary Figure S5), local kinking at 5΄-CAA junctions and lower kinking within the A-tract, and greater roll and inclination in 5΄-CAA junctions (Supplementary Figure S5) (88,89,104).

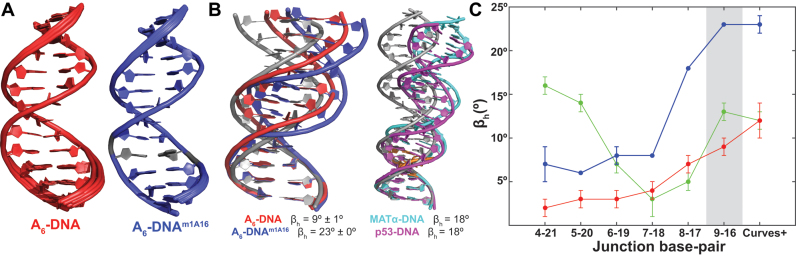
Figure 4.

(A) Lowest energy conformers obtained from XPLOR refinement of idealized B-form DNA using experimental distance constraints and RDCs (see ‘Materials and Methods’ section) for A₆-DNA (red, PDB ID: 5UZF, BMRB ID: 30254) and A₆-DNA^m1A16 (blue, PDB ID: 5UZI, BMRB ID: 30255). The single m¹A•T HG bp is in gray for A₆-DNA^m1A16. (B) Cartoon representation of A₆-DNA (red), A₆-DNA^m1A16 (blue), DNA-p53 (cyan) and MATα2-homeodomain (magenta) complexes depicting major-groove kinking at the HG bp. An idealized B-form DNA helix (in gray) is overlaid for reference (HG bps shown in orange). (C) Local kink angle (β_h) as a function of the junction position and global bending calculated for A₂-DNA (green), A₆-DNA (red) and A₆-DNA^m1A16 (blue).

Table 1. Global bending and local kink angles determined using curves+ and Euler angles.

		Global bending (°)	Local kinking (βh, °)
Type	Structure	Curves+	4–21	5–20	6–19	7–18	8–17	9–16
XPLOR structures	A2-DNA	12 ± 1	16 ± 1	14 ± 1	7 ± 1	3 ± 2	5 ± 1	13 ± 1
	A2-DNAm1A16	17 ± 4	9 ± 2	8 ± 2	4 ± 1	3 ± 1	12 ± 1	19 ± 1
	A6-DNA	12 ± 2	2 ± 1	3 ± 1	3 ± 1	4 ± 1	7 ± 1	9 ± 1
	A6-DNAm1A16	23 ± 1	7 ± 2	6 ± 0	8 ± 1	8 ± 0	18 ± 0	23 ± 0
RDC-selected ensembles	A2-DNA	11 ± 5	21 ± 8	22 ± 6	21 ± 8	19 ± 10	19 ± 8	17 ± 7
	A2-DNAm1A16	15 ± 8	23 ± 8	21 ± 7	18 ± 8	17 ± 9	22 ± 8	26 ± 9
	A6-DNA	14 ± 8	11 ± 7	10 ± 6	12 ± 7	14 ± 9	17 ± 9	15 ± 8
	A6-DNAm1A16	22 ± 10	12 ± 8	13 ± 8	13 ± 6	13 ± 7	18 ± 8	23 ± 10

Terminal bps were excluded for global bending analysis. Bold numbers indicate kinking at T9•A16 bp for the unmodified and the m¹A modified site.

The structures of A₆-DNA (PDB ID: 5UZF) and A₆-DNA^m1A16 (PDB ID: 5UZI) are well defined by the NMR data (Figure 4A); the bundle of lowest energy structures superimposed with all heavy atoms excluding terminal bps yields an RMSD of 0.22–0.39 Å and 0.05–0.25 Å for A₆-DNA and A₆-DNA^m1A16, respectively. The overall RMSD when superimposing heavy atoms of A₆-DNA and A₆-DNA^m1A16 excluding terminal bps is ∼1 Å. However, there are significant differences between the two structures that are sensed by the RDCs as evidenced by the poor agreement (RMSD ∼ 5–6 Hz) when fitting RDCs measured in A₆-DNA^m1A16 to the NMR structure of A₆-DNA and vice versa (Figure 3E and F).

Indeed, visual comparison of the structures immediately reveals increased major-groove directed kinking at the m¹A•T HG bp in A₆-DNA^m1A16 (β_h ∼ 23°) as compared to A₆-DNA (β_h ∼ 9°) (Figure 4B and C; Supplementary Figure S6). The observed ∼14° increase in major-groove kinking induced by m¹A in the NMR structures is in excellent agreement with the major groove kinking induced by HG bp observed in X-ray structures including DNA duplexes containing m¹A•T bps (PDB ID: 3H8O, β_h = 19°) (21) and DNA–protein complexes containing unmodified HG bps (e.g. PDB ID: 1K61 and 3KZ8, β_h ∼ 18°) (Figure 4B). In both the current solution NMR and previous X-ray structures (40), the kink is localized at the HG bp itself and 3΄-neighbor with no significant added kinking is observed further away from the m¹A site (Figure 4C). The global bend angle (see ‘Materials and Methods’ section) measured for A₆-DNA (12 ± 2°) is in good agreement with values reported previously (3–14°, PDB ID: 1FZX) (40,88,90). However, the corresponding global bend angle is significantly larger (23 ± 1°) for A₆-DNA^m1A16 (Table 1). Together, these data indicate that m¹A•T HG bps promote major-groove directed kinking of the DNA helix under solution conditions.

Comparison of the structures also reveals that m¹A induces local perturbations in sugar phase angle (111) in and around the m¹A16•T9 HG bp; with minor deviations seen at sites that are >2 bp away consistent with the minimal chemical shift perturbations observed at these sites (Figure 2B and D). The perturbations in sugar phase angle are associated with alternative sugar ring puckers for residues above and below the HG bp; including T8 (C1΄-exo/O4΄-endo to C2΄-endo), T9 (more C3΄-endo), C15 (O4΄-endo to C2΄-endo) and m¹A16 (C2΄-endo to O4΄-endo) in good agreement with prior solution NMR studies (19). These variations are driven by the differences in the measured sugar RDCs and NOEs and are in good agreement with measured ³J_H1΄-H2΄ scalar couplings (Table 1) and sugar chemical shift perturbations (Figure 2A and B; Supplementary Table S2). For example, the upfield shift in C4΄ in m¹A16 (0.7–1 ppm) and T9 (0.4–0.5 ppm) are consistent with deviations toward C3΄-endo while the downfield shift in C15 C4΄ (0.5–0.7 ppm) is consistent with deviations toward C2΄-endo (112). Interestingly, all the residues adopt the BI conformation and similar ε and ζ angles are observed in structures with and without m¹A. This is inconsistent with the ³¹P chemical shift perturbations, which suggest changes in the BI/BII populations at several residues in the complementary strand. Such deviations in fractional populations are difficult to capture when solving average single structures and are better addressed using the ensemble analysis described below.

Due to line broadening, fewer NMR constraints were available in and around the m¹A16•T9 HG bp for solving the structure of A₂-DNA^m1A16. Due to the lack of constraints, we observed distortions in these regions including an increase in bp rise by 1 Å and local unstacking between m¹A16•T9 and A17–T8 bp step. In addition, we observe significant differences in kink angles (>5°) when comparing A₂-DNA (PDB ID: 5UZD, BMRB ID: 30253) and A₂-DNA^m1A16 at sites >2 bp away from the m¹A, which show little to no m¹A induced chemical shift perturbations. As we discuss in the ensemble analysis below, these deviations could in part arise due to motional average and/or lack of NMR constraints particularly at the HG bp. Notwithstanding the above limitations, many of the m¹A induced perturbations observed in A₆-DNA^m1A16 are also observed in A₂-DNA^m1A16, including increased local kinking (6°) at the HG bp and global bending (5°) albeit by a smaller amount relative to A₆-DNA^m1A16.

Generating and evaluating duplex ensembles

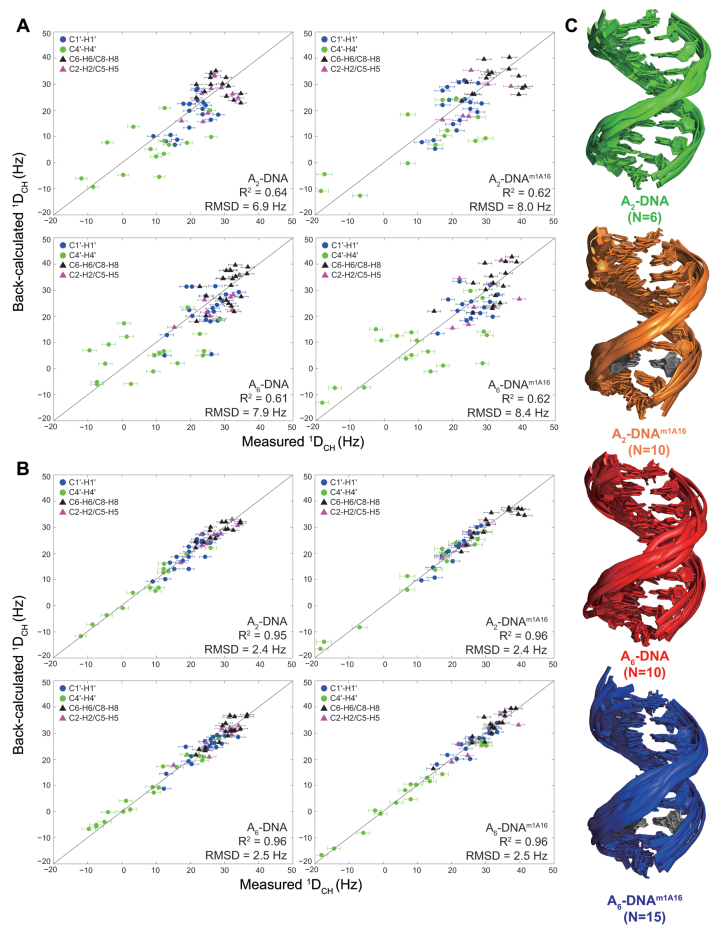
We carried out an ensemble-based analysis of the RDC data to identify potential dynamic perturbations induced by m¹A that are not readily apparent in the XPLOR structures. Using the SAS approach (76,77), the RDC data were used to guide selection of an ensemble of conformations from a pool of conformations generated using 1 μs MD simulations (see ‘Materials and Methods’ section). For all four duplexes, the agreement between the measured RDCs and values predicted by ensembles generated using the full MD trajectories (RMSD = 6.8–8.5 Hz and Pearson's correlation coefficient R² = 0.61–0.64) exceeded the estimated uncertainty (∼2.5 Hz) in RDC measurement (Figure 5A). Poor agreement (RMSD = 9.7–9.9 Hz and R² = 0.38–0.45) was also observed when using a more recent DNA force field, Parmbsc1 (113). Such discrepancies with MD-ensembles have previously been reported in HIV-1 TAR RNA (78) and could arise from insufficient sampling in the MD simulations, given that the simulation time remains short (1 μs) compared to the RDC timescale sensitivity (less than milliseconds) and/or due to force-field imperfections. Comparison of the MD-generated and RDC-selected ensembles reveals increased levels of kinking in the RDC-selected ensembles as compared to the MD trajectories (Supplementary Figure S7). Changes in inter-helical angles have previously shown to be the major source of discrepancy between RDCs and MD simulations of HIV-1 TAR (78,114).

Figure 5.

(A) Comparison of measured RDCs and values back-predicted RDCs using molecular dynamics (MD) trajectories. (B) Comparison of measured RDCs and values predicted for the RDC-selected ensembles. (C) Cartoon representation of a bundle of structures in RDC-selected ensembles of A₂-DNA (green), A₂-DNA^m1A16 (orange), A₆-DNA (red), A₆-DNA^m1A16 (blue) where m¹A•T HG bp is colored gray.

RDC-generated SAS ensembles with size N = 6, 10, 10 and 15 for A₂-DNA, A₂-DNA^m1A16, A₆-DNA and A₆-DNA^m1A16, respectively, reproduce the RDCs to within experimental error (∼2.5 Hz) (Figure 5B and C). Cross-validation analysis (see ‘Materials and Methods’ section) indicates that the ensembles are underdetermined when removing 25% of RDC data in SAS but suggest that they are nevertheless more accurate than the ensembles generated using the entire MD trajectories (Supplementary Figure S1). Several SAS runs were then carried out to generate final ensembles with 2400 structures. The final RDC-generated ensembles predict the ¹H chemicals shifts within estimated calculation error of shifts (<0.26 ppm) (115) and exhibit minimal NOE violations (<2%). Furthermore, simulations establish that many key features of the ensembles discussed below, including local kinking and BI/BII population, are well defined by the RDC data (Supplementary Figure S2).

m¹A-induced structural and dynamic perturbations from ensemble analysis of RDCs

The ensembles reproduce many of the key features observed in the XPLOR structures, including the characteristics of the A-tract in A₆-DNA (Supplementary Figure S5). The average local kink angles throughout the helix in all four duplex ensembles are in good agreement with the XPLOR structures though they tend to be slightly larger (11–26° in ensembles versus 2–23° in XPLOR structures, Table 1, Figure 4C and Supplementary Figure S6). The ensembles also have larger standard deviations in the kink angle (6–10°) as compared to the bundle of XPLOR structures (0–3°) (Supplementary Figure S6) and superimpose with larger all heavy-atom RMSD (0.61–2.63 Å compared to 0.05–0.53 Å). This suggests a potentially greater level of motion than implied by the XPLOR structures.

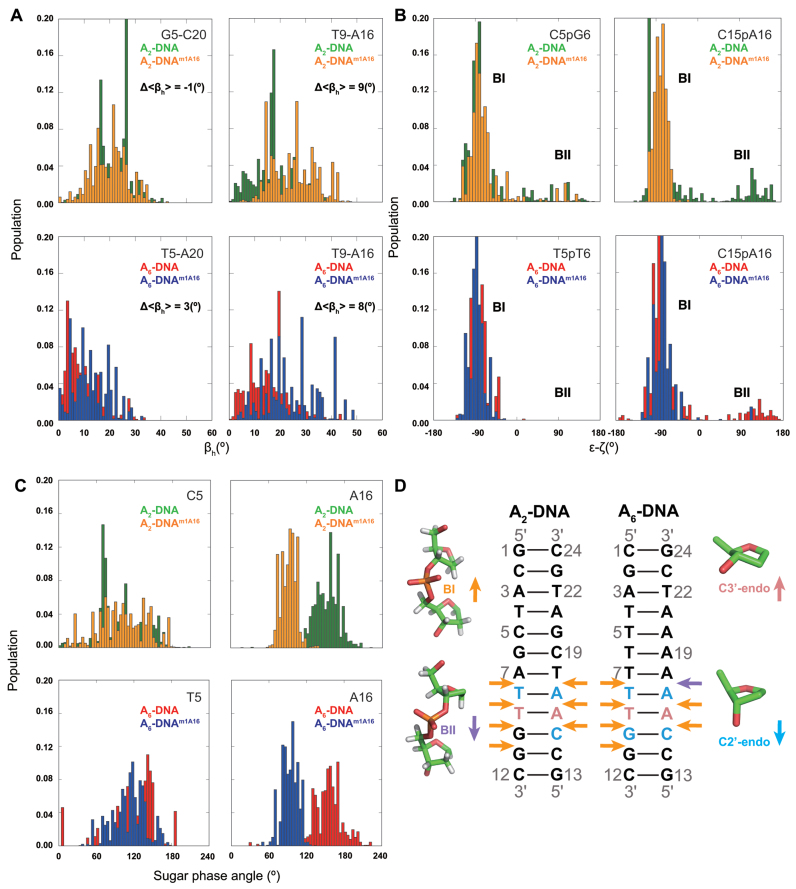
Comparison of the ensembles also reveals increased major-groove directed kinking (by ∼9°) at the m¹A•T HG bp relative to the control A16–T9 WC bp for both A₂- and A₆-DNA, in good agreement with the XPLOR structures (6–14°) (Table 1 and Figure 6A). The increased HG-directed major groove kinking was robustly observed when varying ensemble size or number of input RDCs (Supplementary Tables S4 and 5). Simulations establish that these trends in kink angles can be well determined by single RDC data (Supplementary Figure S2). The RDC-selected ensemble of A₂- and A₆-DNA^m1A16 also display larger global bending angles (see ‘Materials and Methods’ section) than A₂- and A₆-DNA consistent with the XPLOR structures (Table 1). Interestingly, in contrast to the XPLOR structures, we did not observe significant (>3°) m¹A induced kinking in the A₂-DNA ensemble at sites >2 bp from the m¹A residue consistent with chemical shift perturbations (Table 1 and Figure 2). In the ensembles, the m¹A-induced kinking is more localized around the HG bp as compared to the XPLOR structures for both A₂- and A₆-DNA (Table 1), possibly reflecting the influence of motional averaging in the experimentally measured RDCs. These results reinforce the findings that single HG bp induces major-groove directed kinking under solution conditions.

Figure 6.

(A) Ensemble distribution of local kink angle (β_h) in the RDC-selected ensembles (N = 2400) at the m¹A16•T9 HG and control C5–G20 (A₂-DNA) and T5–A20 (A₆-DNA) WC bp. Δ<β_h> denotes the difference between the average kink angles. (B) Ensemble distribution of BI/BII population (ε-ζ) in the RDC-selected ensembles (N = 2400) at the C15pA16 and control C5pG6 (A₂-DNA) and T5pT6 (A₆-DNA). (C) Ensemble distribution of sugar phase angle in the RDC-selected ensembles (N = 2400) at the m¹A16 and control C5 (A₂-DNA) and T5 (A₆-DNA). (D) Duplexes depicting m¹A induced changes in ensemble distributions of sugar pucker toward C3΄-endo (pink) or C2΄-endo (light blue), and backbone torsion angles toward BI (orange) or BII (purple) in A₂- and A₆-DNA as inferred from ensemble, structure and other NMR data.

Comparison of the ensemble with REsemble to facilitate analysis (114) reveals m¹A-induced dynamic perturbations in BI/BII backbone conformations not seen in the XPLOR structures. These deviations are well defined by the RDC data (Supplementary Figure S7). In particular, the m¹A ensembles show enrichment in BI at G10pG11, C15pm¹A16, m¹A16pA17 in and around the m¹A•T HG bp due to perturbations in the backbone angles ε and ζ (Figure 6B and D). These deviations can help explain the observed m¹A-induced ³¹P chemical shift perturbations, specifically at G10pG11. While spectral overlap and line broadening did not allow us to resolve ³¹P resonances for C15pm¹A16 and m¹A16pA17, the observed enrichment of BI population at these sites in the ensembles is in agreement with previous NMR studies of m¹A containing duplexes inferred based on ³J_H3΄-P coupling constants (19). Interestingly, analysis of the MD simulation shows that an increase in the local kink angle is accompanied by a correlated reduction in the BII population for residues around the junction bps (Supplementary Figure S8). However, these features are driven by the MD simulations and need to be further verified experimentally.

As expected, minor local perturbations are observed for sites >2 bp away from m¹A for the ensembles as well (Supplementary Figure S7). The ensembles also feature changes in sugar pucker at m¹A16 (toward O4΄-endo), C15 (more C2΄-endo) and T9 (more C3΄-endo) (Figure 6C and D). While these variations in the ensemble are purely driven by MD and not well defined by the RDC data (Supplementary Figure S2), they are consistent with the XPLOR structure, sugar chemical shift (Figure 2A) and ³J coupling constants (see Supplementary Table S3).

DISCUSSION

NMR studies have shown that in canonical duplex DNA, WC bps exist in dynamic equilibrium with sparsely populated (∼0.02–0.4%) and short-lived (lifetimes of milliseconds) HG bps (33–35). Very little structural information is available regarding these transient HG bps given the challenges in structurally characterizing such fleeting states. In this work, we sought to obtain insights into WC-HG breathing dynamics by using m¹A and pursue in depth NMR analysis on the resulting trapped m¹A•T HG bps.

Several lines of evidences indicate that the m¹A•T HG bp mimic the transient A•T HG bp in unmodified DNA duplexes including the similarities in chemical shifts (33) and formation of HG type H-bonds in both cases (34,35). In addition, the perturbations induced by m¹A•T HG bps observed in our study are also observed in X-ray structures of unmodified DNA duplexes containing HG bps bound to proteins (40). Nevertheless, we cannot entirely rule out that the methyl group in m¹A•T could affect HG pairing as compared to unmodified HG bps due to presence of the methyl group and/or the positive charge on the adenine base which can also affect electronic properties and stacking interactions (21).

A recent survey of X-ray structures revealed that HG bps are correlated with increased duplex kinking at the HG site (40). Such major groove kinking (6–19°) was robustly observed for a variety of sequences and structural contexts, including single A•T HG bps within triplet sequences TAA, GAA, TAC, TAT and including CAA probed in this study; however, in these X-ray structures, the duplex DNA was bound to a protein or small molecule. Our results show that HG bps induce significant major-groove kinking of the double helix under solution conditions in the absence of any binding partner.

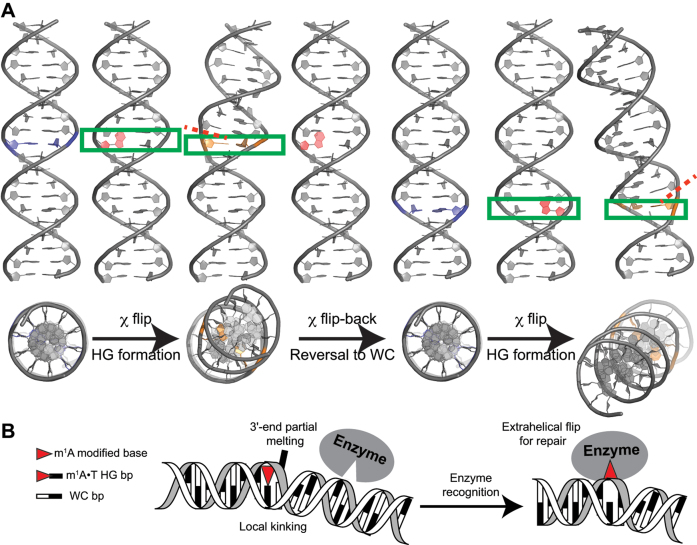
Since transient HG bps in unmodified DNA have been shown to be stabilized by HG-type H-bonds (34), we can expect that they also will feature constricted C1΄-C1΄ distances and duplex kinking. A dynamic picture emerges in which transient formation of HG bps is coupled to major-grove DNA kinking (Figure 7A). These kinks will be phase-shifted by the periodicity of the double helix as depicted in Figure 7A. In this regard, it is interesting to note that c7-deazaadenine, which inhibits formation of transient HG bps (34), also reduces macroscopic bending in A-tract DNA duplexes (116). Likewise, A-form RNA shows little to no signs of transient HG bps (22), and correspondingly shows reduced kinking (117) and other biophysical studies indicate A-form RNA to be relatively rigid (118–120) and thus more linear. Note that this does not rule out major-groove directed kinking in the absence of HG; rather, the analysis indicates that HG bps are likely to be enriched at sites of major-groove directed kinking.

Figure 7.

(A) Proposed model for Watson–Crick/Hoogsteen breathing dynamics. Shown is major-groove directed DNA kinking (∼18°) upon transient formation of HG bps. Base pairs undergoing WC to HG transition are labeled blue, with the purine-ring undergoing flip denoted in red and the final HG bps denoted in orange. A red-dashed line indicates the directionality of partial local melting occurring at the 3΄-end of the HG bp. (B) Proposed mode of m¹A recognition in duplex DNA by damage repair enzymes (e.g. ABH2) that probe for a local kink and partial melting at the 3΄-end, in addition to the positive charge on m¹A modification and HG H-bonds.

Our results also indicate that formation of HG bps induce partial melting of neighboring WC bps at the 3΄-end of the m¹A. This partial melting of neighbors may help to explain the proposed weaker dependence of HG stability on sequence context as compared to stable WC bps (35). Such a dynamic behavior is interesting as ‘kink-and-melt’ dynamics are frequently invoked in DNA transactions, including transcriptional activation (14,121) and damage/mismatch-repair (23,122,123). Whether HG bps play roles in these processes remains to be seen.

The unique structural and dynamic features of m¹A•T HG bps might play roles in the recognition mechanism of enzymes that repair m¹A lesion in double-stranded DNA (Figure 7B). Direct damage reversal by these enzymes is known to proceed by extrahelically flipping out the damaged base (23,124). While AlkB is marginally more efficient for single-stranded DNA, its homolog ABH2 repairs m¹A damage in double-stranded DNA and involves kinking of the DNA helix following extrahelical flipping of damaged base (23). Prior studies have demonstrated that poor base stacking (125), altered dynamics of neighboring bps at damaged/mismatch site (126,127), weakened bp stability (128) at the lesion may initiate recognition by repair proteins. Following recognition, enzymes kink the DNA helix to flip bases into the active site for repair (122,129). The pre-kinked m¹A•T HG bp along with flexible neighboring bps, could help facilitate damage recognition in the search for m¹A lesions, while simultaneously creating a structure with weakened stacking interactions that is primed for extra-helical base flipping (Figure 7B).

ACCESSION NUMBERS

PDB IDs: 3H8O, 1K61, 3KZ8, 1FZX, 5UZD, 5UZF and 5UZI. BMRB accession codes: 30253, 30254 and 30255.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

US National Institute for General Medical Sciences [GM103297 to H.M.A]. Funding for open access charge: US National Institute for General Medical Sciences [GM103297 to H.M.A].

Conflict of interest statement. None declared.