Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2017 Apr 28;31(3):601–614. doi: 10.1111/cobi.12856

Extrapolating cetacean densities to quantitatively assess human impacts on populations in the high seas

Laura Mannocci 1,✉, Jason J Roberts 1, David L Miller 2,3,4, Patrick N Halpin 1
PMCID: PMC5435923  PMID: 27775847

Abstract

As human activities expand beyond national jurisdictions to the high seas, there is an increasing need to consider anthropogenic impacts to species inhabiting these waters. The current scarcity of scientific observations of cetaceans in the high seas impedes the assessment of population‐level impacts of these activities. We developed plausible density estimates to facilitate a quantitative assessment of anthropogenic impacts on cetacean populations in these waters. Our study region extended from a well‐surveyed region within the U.S. Exclusive Economic Zone into a large region of the western North Atlantic sparsely surveyed for cetaceans. We modeled densities of 15 cetacean taxa with available line transect survey data and habitat covariates and extrapolated predictions to sparsely surveyed regions. We formulated models to reduce the extent of extrapolation beyond covariate ranges, and constrained them to model simple and generalizable relationships. To evaluate confidence in the predictions, we mapped where predictions were made outside sampled covariate ranges, examined alternate models, and compared predicted densities with maps of sightings from sources that could not be integrated into our models. Confidence levels in model results depended on the taxon and geographic area and highlighted the need for additional surveying in environmentally distinct areas. With application of necessary caution, our density estimates can inform management needs in the high seas, such as the quantification of potential cetacean interactions with military training exercises, shipping, fisheries, and deep‐sea mining and be used to delineate areas of special biological significance in international waters. Our approach is generally applicable to other marine taxa and geographic regions for which management will be implemented but data are sparse.

Keywords: extrapolation, habitat‐based density models, survey coverage, cobertura de censo, extrapolación, modelos de densidad basados en el hábitat

Introduction

During the past century, technological developments have allowed humans to exploit ocean waters farther from shore. Offshore waters beyond national jurisdiction, known as the high seas, are increasingly used for fishing, shipping, military training, and other purposes (Ramirez‐Llodra et al. 2011). These activities can be incidentally harmful to cetaceans, but cetacean abundance and density data for the high seas are often very sparse; thus, population‐level impacts are poorly known.

Line transect surveys (LTSs) are frequently used to estimate the abundance and density of cetacean populations. Observers onboard a ship or aircraft record sightings with a distance sampling protocol to control for the decrease in detection probability as distance from the transect line increases (Buckland et al. 2001). Line transect methods are traditionally used to provide stratified estimates for a surveyed area (e.g., Hammond et al. 2013) or to develop habitat‐based density models that relate cetacean densities to environmental covariates (e.g., Ferguson et al. 2006). Modeled relationships can then be used to predict cetacean densities in fine‐resolution spatial grids spanning surveyed areas (Miller et al. 2013). Line transect surveys have been conducted in the Exclusive Economic Zones (EEZs) of many countries (extending 200 nautical miles from shore), but comparatively few have occurred in the high seas (Kaschner et al. 2012).

Density estimates may be derived for unsurveyed areas by fitting habitat models in extensively surveyed areas and extrapolating them (Conn et al. 2015; Mannocci et al. 2015). But extrapolation is inherently risky because of the lack of observations for evaluating model predictions. Extrapolation in geographic space (i.e., beyond surveyed areas but within the sampled ranges of covariate values) can lead to accurate predictions if relationships between species densities and covariates hold in extrapolated areas (Wenger & Olden 2012). Extrapolation in environmental space (i.e., beyond the ranges of covariate values sampled in the surveyed areas) may lead to more speculative predictions because relationships between species densities and covariates are unknown in extrapolated areas (Elith et al. 2010).

Despite these risks, the spatiotemporal coverage of LTSs for cetaceans is likely to remain patchy for the foreseeable future, owing to high logistical and financial costs (Kaschner et al. 2012). As expanding use of the high seas is negotiated, more decisions are likely to be based on extrapolative models. We considered the development of extrapolated density estimates to facilitate a quantitative assessment of the impacts of naval training exercises on cetacean populations.

Active sonar and other in‐water devices used in military training are of particular concern for cetaceans. The intense sounds they produce can disrupt diving behavior (DeRuiter et al. 2013), alter acoustic communication (Henderson et al. 2014), and cause displacements from productive habitats (Goldbogen et al. 2013). There is also evidence of a link between military sonar exercises and atypical mass strandings of cetaceans (Jepson et al. 2003). In the United States, the Marine Mammal Protection Act regulates the take (defined as “to harass, hunt, capture, or kill, or attempt to harass, hunt, capture, or kill”) of marine mammals by U.S.‐based organizations anywhere in the world, including the high seas. The U.S. Navy is required to estimate incidental takes resulting from naval training exercises and seek permits to conduct these activities. To do so, the U.S. Navy developed a model that simulates propagation of sound from planned exercises across cetacean density maps and tallies the individual cetaceans affected (Ciminello et al. 2013).

Using as our area of interest the U.S. Navy Atlantic Fleet Training and Testing area, spanning large regions of the western North Atlantic never surveyed for cetaceans, we modeled densities of 15 taxa with available LTS data and habitat‐based covariates and extrapolated predictions to unsurveyed regions. We formulated and constrained models to reduce the chance of errant extrapolations and evaluated confidence in the predictions.

Methods

Study Area and LTS Data

The spatial extent of our study corresponded to the U.S. Navy Atlantic Fleet Training and Testing (AFTT) area. The AFTT area spans 11 million km2 of the western North Atlantic Ocean, extending from the coast of North America to 45°W and from approximately 20°N to 65°N. It includes the Gulf of Mexico and U.S. waters surrounding Puerto Rico and spans 7 biogeographical provinces and 4 biomes (Longhurst 2007) (Fig. 1a). Major oceanographic features include the Loop Current, Gulf Stream, Labrador Current, and North Atlantic gyre (Fig. 1b). The study area was projected to an Albers equal‐area projection to minimize spatial error and gridded into 10 × 10 km cells, the requested spatial resolution for this management application.

Figure 1.

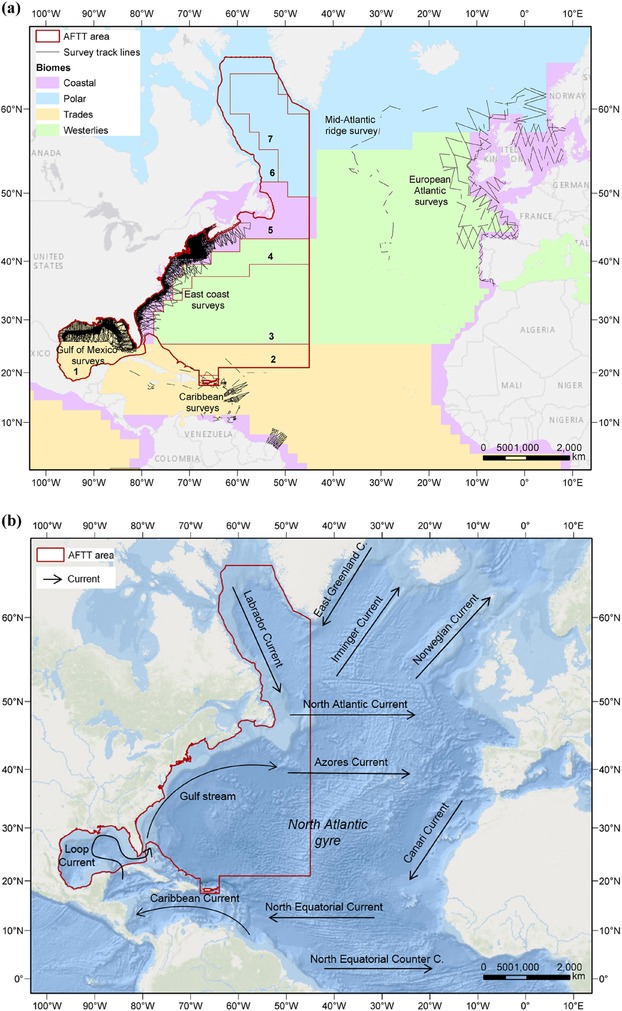
Figure 1

Open in a new tab

Maps of (a) the North Atlantic basin showing the U.S. Navy Atlantic Fleet Training and Testing (AFTT) area, line transect surveys for cetaceans included in this study, and Longhurst's (2007) biomes (color‐coded) and biogeographical provinces within the study area(1, Caribbean; 2, North Atlantic tropical gyre; 3, North Atlantic subtropical gyre; 4, Gulf Stream; 5, northwest Atlantic shelves; 6, Atlantic Arctic; 7, boreal polar) and (b) the North Atlantic basin showing major surface currents. The AFTT area excludes territorial waters (<12 nautical miles from shore) outside of the United States.

We considered LTSs that used 2 or more observers and met the assumptions of the distance sampling methodology (Buckland et al. 2001). We included data from shipboard and aerial surveys conducted from 1992 to 2014 along the U.S. East Coast (887,963 km of effort) and in the northern Gulf of Mexico (194,715 km) by multiple U.S. organizations (details in Roberts et al. [2016]) and data from surveys in the Caribbean, European Atlantic, and along the mid‐Atlantic ridge (Table 1). Incorporating surveys from these other North Atlantic regions increased the representativeness of biomes in the study area that were poorly covered by U.S. surveys (Fig. 1a) and increased sample sizes available for fitting detection functions and developing density models.

Table 1.

Line transect survey data incorporated in habitat‐based density models of cetaceans.*

Region Platform Surveyor Effort (km) Number of segments Survey years Reference
U.S. East Coast (EC) Shipboard and aerial NEFSC, NJDEP, SEFSC, UNCW, VAMSC 887,963 89,426 1992–2014 Roberts et al. 2016 (contains complete list)
Gulf of Mexico (GOM) Shipboard and aerial SEFSC 194,715 19,988 1992–2009 Roberts et al. 2016 (contains complete list)
Caribbean (CAR) Shipboard SEFSC 8,975 914 2000, 1995 Swartz et al. 2002
Aerial University of La Rochelle 15,289 1,528 2008 Mannocci et al. 2013
European Atlantic (EU) Shipboard Partners of the CODA Program 9,584 957 2007 Hammond et al. 2009
Mid Atlantic Ridge (MAR) Shipboard Partners of the SCANS‐II Program 17,942 1,805 2005 Hammond et al. 2013
Shipboard Partners of the MAR‐ECO Program 2,424 243 2004 Waring et al. 2008
TOTAL 1,136,892 114,861
Open in a new tab

*Surveyors: NEFSC, NMFS Northeast Fisheries Science Center; NJDEP, New Jersey Department of Environmental Protection; SEFSC, NMFS Southeast Fisheries Science Center; UNCW, University of North Carolina at Wilmington; VAMSC, Virginia Aquarium & Marine Science Center; SCANS‐II, Small Cetacean Abundance in the North Sea and adjacent waters‐II; CODA, Cetacean Offshore Distribution and Abundance in the European Atlantic; MAR‐ECO, Mid‐Atlantic Ridge Ecology Program.

Group size (number of sighted individuals), taxonomic identification, perpendicular distance to sighted groups, and the observer's assessment of detection conditions (e.g., Beaufort sea state) were available for all the surveys. We divided survey transects into (approximately) 10‐km segments following Roberts et al. (2016). This segment length corresponded to the requested spatial resolution of predictions and was a reasonable compromise between the resolutions of environmental data available (4 km to 0.25°) (Supporting Information).

Environmental Covariates

To reduce the extent of environmental extrapolation, we used covariates for which broad ranges of values were sampled by the surveys. Hence, we excluded longitude, latitude, distances to the shore, and ecologically relevant isobaths. These covariates are commonly used in cetacean habitat modeling (e.g., Ferguson et al. 2006), but would result in extrapolating far beyond the range of sampled values in the study area. To increase the success of model transferability to new regions, we considered biological covariates expected to be related directly to cetacean densities (Wenger & Olden 2012), namely biomass and production of epipelagic micronekton and zooplankton predicted with the Spatial Ecosystem and Population DYnamics Model (SEAPODYM) (Lehodey et al. 2010). Zooplankton and epipelagic micronekton (i.e., squid, crustaceans, and fish) constitute potential prey for many of the cetaceans we considered, in particular dolphins and mysticetes (Pauly et al. 1998). All these covariates correlate with cetacean distributions (e.g., Ferguson et al. 2006; Doniol‐Valcroze et al. 2007; Lambert et al. 2014).

We derived covariates from remote sensing and ocean models (Supporting Information) and projected them to the 10 × 10 km grid of the study area. For dynamic covariates, we prepared monthly climatologies by aggregating and summarizing the available time series. Although monthly climatologies smoothed out interannual variations in oceanographic conditions, they successfully captured important seasonal variations. We obtained covariate values for the survey segments by interpolating the 10 × 10 km grid at the segment centroids. We used ArcGIS (version 10.2.2) and the Marine Geospatial Ecology Tools software (Roberts et al. 2010) to prepare all covariates.

Detection‐Function Fitting And Per‐Segment Abundance Estimation

We relied on a 2‐stage density modeling approach (Hedley & Buckland 2004; Miller et al. 2013) to extrapolate densities of 15 cetacean taxa (comprising 12 species and 3 guilds) to unsurveyed regions in the western North Atlantic.

We used the single‐observer methodology to fit taxon‐specific detection functions (Buckland et al. 2001). For each taxon, we pooled multiple surveys with similar observation platforms and protocols or used proxy species with similar detectability to obtain sufficient sightings (Roberts et al. 2016). Before fitting each detection function, we right‐truncated the most distant sightings and applied left truncation for aerial surveys that had an inadequate view of the survey track line (Buckland et al. 2001). We compared a number of detection‐function formulations with both conventional distance sampling (Buckland et al. 2001) and multiple covariate distance sampling (Marques & Buckland 2004) and selected the model with the lowest Akaike information criterion (AIC) (Roberts et al. 2016). We fitted all detection functions in R using the mrds package (version 2.1.10) (Laake et al. 2014).

The probability of detecting an animal on the track line, or g(0), is affected by both availability bias (i.e., observers fail to detect animals because they are submerged) and perception bias (i.e., observers fail to detect animals present at the surface) (Pollock et al. 2006). We corrected for availability and perception bias by obtaining estimates of g(0) from the literature that incorporated these biases. We obtained separate g(0) estimates for aircraft and shipboard platforms and, where possible, for different group sizes (to account for large groups being easier to detect than small groups) (Roberts et al. 2016). We then scaled the estimated abundance of each sighting with the inverse of g(0) appropriate for that sighting based on the platform and group size. Details on detection function fitting and g(0) estimates are in Roberts et al. (2016).

For each taxon, we estimated the abundance in segment j, N^j, by using the Horvitz–Thompson‐like estimator:

N^j=∑r=1Rjsjr/p^(zjr), (1)

where Rj is the number of observed groups in segment j, sjr is the size of the rth group in segment j, and p^(z jr) is the estimated probability of detection given observation level covariates, zjr (Marques et al. 2007).

Generalized Additive Model Fitting, Predictions, And Uncertainty

We fitted generalized additive model (GAMs) with the following structure:

EN^j=Aj exp β0+∑kfkzjk, (2)

where N^ j is the response variable assumed to follow a Tweedie distribution (e.g., Foster & Bravington 2013) and E indicates expectation; Aj, the model offset, is the area of segment j calculated as 2(w R − w L)lj, where w R is the right‐truncation distance, w L is the left‐truncation distance (0 if data were not left truncated), and lj is the segment length; fk are smooth functions of the environmental covariates zk; and β0 is the model intercept.

We considered survey segments from the U.S. East Coast, Gulf of Mexico, Caribbean, mid‐Atlantic ridge, and European Atlantic to fit the models depending on the taxon. When different density–environment relationships were expected in different seasons (e.g., for baleen whales that forage in summer and breed and calve in winter) and there were sufficient sightings in each season, we fitted separate seasonal models. Otherwise, we fitted a year‐round model. Modeling decisions for individual taxon are detailed in reports available from the Ocean Biogeographic Information System Spatial Ecological Analysis of Megavertebrate Populations (OBIS‐SEAMAP) repository (http://seamap.env.duke.edu/models/AFTT-2015/).

Is it important to constrain model complexity based on the study objectives (Merow et al. 2014). Consistent with our objective of extrapolating cetacean densities beyond surveyed areas, we developed simple habitat models that captured dominant cetacean–environment relationships but did not reproduce details present in the data (Elith et al. 2010). Simple models (i.e., models characterized by few parameters and smooth species–environment relationships) can achieve higher transferability and are highly recommended for extrapolation (Wenger & Olden 2012; Merow et al. 2014). Authier et al. (2016) found that models with a large number of covariates lead to widespread environmental extrapolation. In line with these findings, we considered models with a maximum of 4 covariates (models including 5 or more covariates led to an excessively large extent of environmental extrapolation). We fitted GAMs with all possible combinations of 4 covariates, after eliminating the pairs of covariates for which the Spearman's rank correlation coefficient (Hollander & Wolfe 1973) calculated on segments was ≥0.6 or ≤−0.6. We used thin‐plate regression splines with shrinkage to allow smooth term effects to be removed from the model during fitting. To model simple density‐environment relationships and mitigate overfitting, which is known to limit model transferability (Wenger & Olden 2012), we restricted the basis size to 4 for each smooth term. We used restricted maximum likelihood as the criterion for estimating smooth parameters because it penalizes overfitting and leads to more pronounced optima (Wood 2011). We selected the models with the lowest AIC as the best models. Model selection based on AIC effectively reduces overfitting by penalizing models with excessive complexity (Wenger & Olden 2012). We fitted all GAMs in R with the mgcv package (version 1.8.4) (Wood 2014).

We produced maps of mean predicted densities (individuals per 100 km2) by averaging monthly predictions seasonally (if a seasonal model was fitted) or annually (if a year‐round model was fitted) on a per‐cell basis. To visualize parameter uncertainty from the spatial part of the model, we produced maps of the mean (seasonal or year‐round) coefficients of variation (CVs) for each cell in the prediction grid by applying the approach described in Miller et al. (2013) (details in their Appendix S2).

Our inference was based on a single best supported model; however, different models can lead to widely different predictions beyond predictor ranges (Pearson et al. 2006). We further assessed uncertainty in the model‐selection process by examining, in each of Longhurst's biogeographical provinces, mean densities predicted by statistically supported models (sensu Burnham & Anderson 2002) (Δ AIC<2). (See reports available from the OBIS‐SEAMAP repository.)

Confidence in Extrapolations

For each taxon, we evaluated confidence in predictions by examining maps of sampled covariate ranges (i.e., so‐called environmental envelopes) to visualize where the model was extrapolated and by comparing predicted densities with maps of cetacean sightings available in the OBIS‐SEAMAP repository (Halpin et al. 2009) that could not be integrated into our models (e.g., opportunistic sightings, telemetry data). These results and a discussion of our relative levels of confidence in extrapolations are presented in the reports available from the OBIS‐SEAMAP repository.

Results

The most commonly selected predictors were depth, distance to the nearest sea surface temperature (SST) front, and production of epipelagic micronekton. Explained deviances ranged from 22.9% (fin whale [Balaenoptera physalus]) to 57.2% (striped dolphin [Stenella coeruleoalba]) (Table 2). The extent of extrapolation beyond the sampled covariate ranges varied from 4% (harbor porpoise [Phocoena phocoena]) to 50% (Globicephala spp.) (Table 2). Extrapolation mostly occurred in the westerlies biome (lower chlorophyll‐a concentration, lower zooplankton production, and larger distances from SST fronts in summer) and in the polar biome (lower sea surface temperature in winter). Extrapolations beyond sampled covariate ranges (horizontal lines on Figs. 2, 3, and 4) are largely speculative and should be considered with due caution.

Table 2.

Overview of density‐modeling results of cetaceans. a

Species or guild Season Number of sightings Predictors (listed in decreasing order of importance according to F scores)b Explained deviance (%) Extent of environmental extrapolation (%) Described range
Mysticetes
fin whale (Balaenoptera physalus) year‐round 1785 EpiMnkPB, Slope, SST, DistToFront 22.9 29 cosmopolitan
humpback whale (Megaptera novaeangliae) summer 2578 Depth, CHL, SLAStDev, DistToFront 36.6 44 cold temperate and subpolar waters (summer)
minke whale (Balaenoptera acutorostrata) year‐round 1109 PkPB, Depth, DistToFront 23.6 20 cosmopolitan
Sei whale (Balaenoptera borealis) summer 852 Depth, SLAStDev, SST, EpiMnkPP 38.5 40 cold temperate and subpolar waters (summer)
Odontocetes
Atlantic spotted dolphin (Stenella frontalis) year‐round 1150 SST, Depth, PkPP, EKE 41.8 50 tropical and warm temperate waters
Atlantic white‐sided dolphin (Lagenorhynchus acutus) year‐round 2329 SST, Depth, EpiMnkPP, DistToFront 35.2 28 cold temperate and subpolar waters
Beaked whalesc year‐round 395 Depth, DistToCanyonOrSeamount, CHL, CurrentSpeed 42.8 34 cosmopolitan
Bottlenose dolphin (Tursiops truncatus) year‐round 6524 PkPB, Depth, EpiMnkPP, DistToFront 25.7 20 tropical and warm temperate waters
Globicephala spp.d year‐round 1058 Depth, PkPP, SLAStDev, EpiMnkPP 23.3 50 cosmopolitan
Harbor porpoise (Phocoena phocoena)c year‐round 2018 PkPB, Depth, EpiMnkPP, SLAStDev 46.5 4 cold temperate and subpolar waters
Kogia spp.ce year‐round 256 SST, Depth, EpiMnkPP 41.8 9 tropical and warm temperate waters
Risso's dolphin (Grampus griseus) year‐round 1002 Depth, PkPB, EpiMnkPP, DistToFront 38.4 20 tropical and temperate waters
Short‐beaked common dolphin (Delphinus delphis) year‐round 1428 Slope, SLAStDev, CHL, DistToFront 36.6 34 temperate waters
Sperm whale (Physeter macrocephalus) year‐round 941 Depth, DistToCanyonOrSeamount, CHL 42.0 33 cosmopolitan
Striped dolphin (Stenella coeruleoalba) year‐round 336 Depth, EpiMnkPP, CHL, DistToFront 57.2 34 tropical and temperate waters
Open in a new tab

aDetailed results are presented in the taxon‐specific reports available from the OBIS‐SEAMAP repository.

bAbbreviations: DistToCanyonOrSeamount, distance to the nearest submarine canyon or seamount; SST, sea surface temperature; DistToFront, distance to the nearest sea surface temperature front; CurrentSpeed, absolute current speed; SLAStDev, standard deviation of sea level anomaly; EKE, eddy kinetic energy; CHL, chlorophyll‐a concentration; EpiMnkPB, biomass of epipelagic micronekton; EpiMnkPP, production of epipelagic micronekton; PkPB, biomass of zooplankton; PkPP, production of zooplankton. For dynamic predictors, climatological monthly means were used.

cIncludes Blainville's beaked whale (Mesoplodon densirostris), Cuvier's beaked whale (Ziphius cavirostris), Gervais' beaked whale (Mesoplodon europaeus), Sowerby's beaked whale (Mesoplodon bidens), True's beaked whale (Mesoplodon mirus), and unidentified Mesoplodon.

dIncludes long‐finned pilot whale (Globicephala melas) and short‐fined pilot whale (Globicephala macrorhynchus).

eIncludes dwarf sperm whale (Kogia sima) and pygmy sperm whale (Kogia breviceps).

Figure 2.

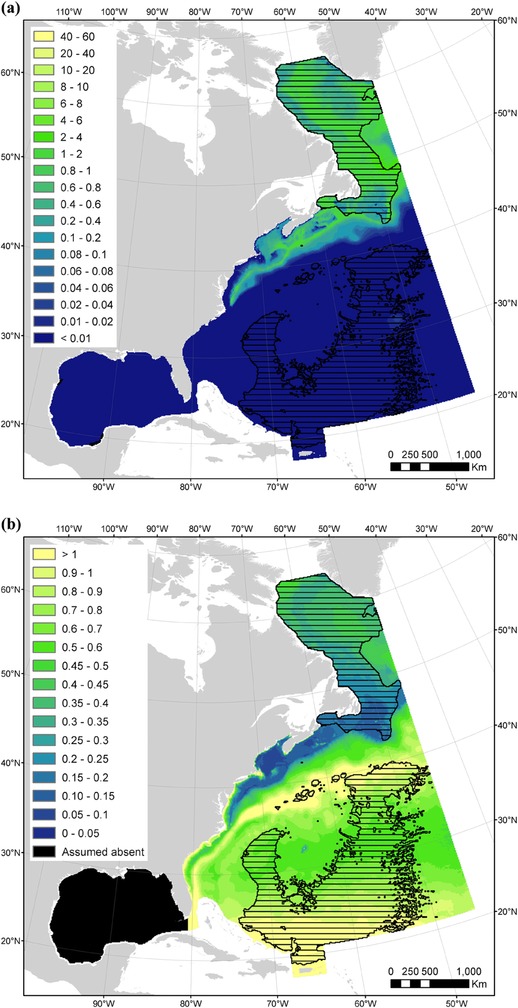
Figure 2

Open in a new tab

Maps of (a) mean summer predicted densities (individuals per 100 km2) and (b) mean summer coefficients of variation from the spatial part of the density model for sei whale (black horizontal lines, extrapolations beyond the sampled covariate ranges [these predicted densities should be considered with extreme caution]). An Albers equal‐area projection is used for the study area.

Figure 3.

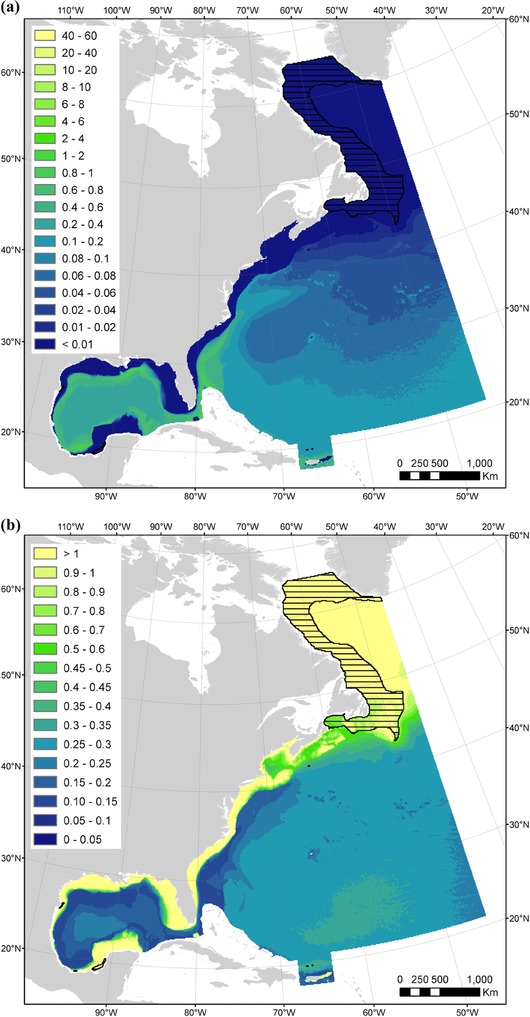
Figure 3

Open in a new tab

Maps of (a) mean year‐round predicted densities (individuals per 100 km2) and (b) mean year‐round coefficients of variation from the spatial part of the density model for Kogia spp. (black horizontal lines, extrapolations beyond the predictor ranges [these predicted densities should be considered with extreme caution]). An Albers equal area projection is used for the study area.

Figure 4.

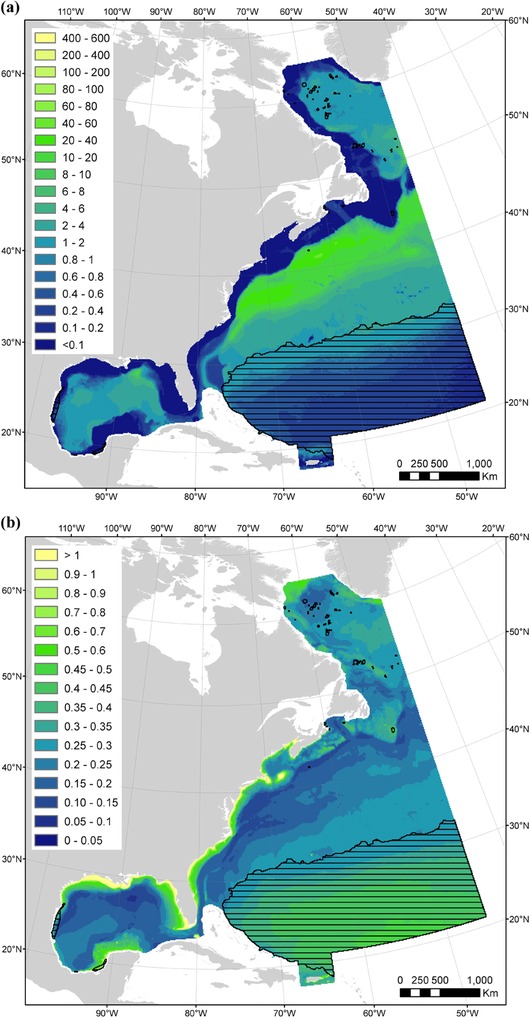
Figure 4

Open in a new tab

Maps of (a) mean year‐round predicted densities (individuals per 100 km2) and (b) mean year‐round coefficients of variation from the spatial part of the density model for striped dolphin (black horizontal lines, extrapolations beyond the predictor ranges [these predicted densities should be considered with extreme caution]). An Albers equal area projection is used for the study area.

Overall, mean predicted densities in Longhurst's biogeographical provinces based on statistically supported models were not widely different. Notable exceptions were mean predicted densities of sperm whale (Physeter macrocephalus) in the Atlantic Arctic and boreal polar provinces (differing by a factor of 5) and mean predicted densities of striped dolphin in the Atlantic Arctic province (differing by a factor of 4.5) (see results and discussions in taxon‐specific reports).

We present density‐modeling results for a migratory mysticete (sei whale [Balaenoptera borealis]), a deep‐diving odontocete (Kogia spp., including K. sima and K. breviceps), and an oceanic dolphin (striped dolphin) representing 3 ecologically distinct cetacean families (Prieto et al. 2012). Predicted density maps, CV maps, and detailed modeling results for all taxa are freely available from the OBIS‐SEAMAP repository.

Sei Whale

Sei whale summer densities were predicted to increase in deep, cold waters where mesoscale activity is low and epipelagic micronekton production is high. To predict densities in the entire study area, we extrapolated to deeper waters in the North Atlantic gyre, to colder waters in the polar biome, and to a lesser extent to waters of higher mesoscale activity in the Gulf Stream. These extrapolations comprised 40% of the cells of the study area (Table 2 & Fig. 2a). Sei whales were predicted to occur in temperate and subpolar waters, primarily on the continental slope and offshore. Predicted densities were the highest on the continental slope north of Cape Hatteras (U.S. East Coast) and in offshore waters of the Labrador Current (Fig. 2a). Coefficients of variation were the highest in waters of high mesoscale activity in the Gulf Stream, shallow waters along the U.S. coast, and warm waters in the North Atlantic gyre (Fig. 2b).

Kogia spp

Densities of Kogia spp. were predicted to increase in warm waters of intermediate depth and high micronekton production. To predict densities in the entire study area, we extrapolated to colder waters in the polar biome (9% of the cells) (Table 2 & Fig. 3a). Kogia spp. were predicted to occur in tropical and warm offshore temperate waters. Predicted densities were the highest on the continental slope in the Gulf of Mexico and south of Cape Hatteras (Fig. 3a). Coefficients of variation were the highest in shallow waters on continental shelves, and in cold waters throughout the polar biome (Fig. 3b).

Striped Dolphin

Striped dolphin densities were predicted to increase in deep waters of high epipelagic micronekton production, intermediate chlorophyll concentration (CHL), and near SST fronts. In order to predict densities in the entire study area, we extrapolated to lower CHL and further from fronts in the North Atlantic gyre (these extrapolations comprised 34% of the cells) (Table 2 & Fig. 4a). Striped dolphins were predicted to occur in offshore waters throughout most of the study area. Predicted densities were the highest in the northern part of the Gulf Stream (Fig. 4a). Coefficients of variation were the highest in shallow waters of the continental shelves (Fig. 4b).

Discussion

Confidence in Extrapolations

Overall, we have a reasonable confidence in predictions for tropical and warm‐temperate taxa for which survey data were available within most of the distributional range (Atlantic spotted dolphin [Stenella frontalis], Kogia spp., and bottlenose dolphin [Tursiops truncatus]) and a relatively lower confidence in predictions for cold‐temperate and subpolar taxa for which survey data covered only the southern part of their ranges (Atlantic white‐sided dolphin [Lagenorhynchus acutus], harbor porpoise, and all species of mysticetes). Although the models correctly predicted the occurrence of these taxa in northern waters, predicted densities were largely speculative and should be interpreted cautiously. The incorporation of LTSs from Canada (Lawson & Gosselin 2009) and Greenland (Heide‐Jørgensen et al. 2007) would have increased the reliability of these models. Unfortunately, we were unable to obtain permission to incorporate these surveys in the current models but we hope they will be incorporated in future iterations. We call for increased collaboration and data sharing in order to better model cetaceans in international waters.

Caveats of the Approach

The geographical distribution of LTSs available for this study was heterogeneous with the highest concentration of effort in the U.S. EEZ. Despite our efforts to incorporate surveys external to the study area to increase the coverage of the westerlies and polar biomes poorly covered by U.S. surveys, these ecological biomes remained largely underrepresented. In Supporting Information, we discuss the sensitivity of density‐modeling results to heterogeneity in survey coverage by splitting the available survey data into 11 geographical regions, excluding each region, and examining predictions of the resulting models. We found that our models were generally capable of showing overall interregional patterns in taxa distributions when data from one region were withheld. This suggests that predictions in underrepresented regions are overall plausible, but we urge caution regarding the absolute accuracy of density estimates in certain situations.

Some unsurveyed regions (e.g., the Labrador Sea and the North Atlantic gyre) have oceanographic conditions that are very different from conditions in surveyed regions despite some overlap with sampled covariate ranges. Intercovariate correlations may also be expected to differ between unsurveyed and surveyed regions. Changing correlations between the sample and prediction data sets may lead to unreliable predictions in areas where they differ the most (Elith et al. 2010). In Supporting Information, we compared covariate correlations in the sample and prediction data and found that covariates that were moderately correlated in one direction in the sample data were always correlated in this same direction in the prediction data.

By design, our models were simple and not tightly fitted to the data. Complex models do not transfer well to new regions because species–environment relationships apply specifically to the sample data but do not generalize well (Elith et al. 2010; Wenger & Olden 2012; Merow et al. 2014). In contrast, in a related study limited to U.S. waters, we were less concerned with model transferability and developed more complex models to accurately map cetacean densities within extensively surveyed areas (Roberts et al. 2016). In our study, limiting the basis size of smooth terms prevented overfitting and helped model general relationships that likely transfer better to unsurveyed regions. Of course, underfitting also limits model transferability because it can lead to misunderstandings of the drivers of species distributions and to potentially biased predictions (Merow et al. 2014). To ensure our models did not result in severe bias in extrapolation, we always assessed predictions against ecological knowledge. However, bias in predicted densities beyond predictor ranges cannot be ruled out, and we once again urge caution in their interpretation.

It is important to monitor the shapes of fitted relationships at the edges of sampled covariate ranges to prevent spurious extrapolation (Elith et al. 2010; Merow et al. 2014). For thin‐plate regression splines (Wood 2003), fitted relationships outside the observed data tend to extreme values as the distance from observed values increases. Steeply increasing relationships may be particularly problematic because they result in unrealistically high density predictions when extrapolated beyond the sampled covariate ranges. Such situations did not occur in our study, and the shapes of relationships at the edges of sampled covariate ranges appeared ecologically plausible. However, for some cold‐water taxa (e.g., sei whale and fin whale), the relatively steep decrease of densities at the lower edge of the sampled sea surface temperature range may have resulted in an underestimation in northern waters.

We advise caution when interpreting our maps of CVs because they document a single source of uncertainty (the spatial model) and do not reflect the uncertainty associated with predicted densities beyond covariate ranges, the detection functions, g(0) estimates, or model covariates. Covariate uncertainty may be highest for biological covariates derived from the SEAPODYM model. Thanks to the incorporation of in situ acoustic data for parameter optimization (Lehodey et al. 2014), SEAPODYM outputs are becoming increasingly accurate, making their use as covariates in cetacean extrapolation models promising. The development of statistical methods propagating these various sources of uncertainty to final density estimates constitutes an area of active research (e.g., Foster et al. 2012).

Applications

Our results provide baseline density predictions for 15 cetacean taxa in a very large portion of the western North Atlantic. Our confidence in the predictions depends on the taxon and region. We strongly advise users of these predictions to review taxon‐specific supplementary reports available from the OBIS‐SEAMAP repository and proceed with caution where indicated. In the future, the predictions may be improved by incorporating new LTS data in underrepresented regions. To facilitate this, we call for expanded collaboration that would allow incorporation of extant data (e.g., Heide‐Jørgensen et al. 2007; Lawson & Gosselin 2009) and urge increased surveying in underrepresented regions.

Beyond the example application of facilitating a quantitative assessment of military training impacts on cetacean populations, our density estimates can inform a variety of management needs in the high seas. Management applications include quantifying the impacts of industrial activities that generate underwater noise, including deep‐sea mining and seismic surveying; quantifying cetacean interactions with offshore fisheries and transoceanic shipping; and informing the delineation of areas of special biological significance in international waters (e.g., the Sargasso Sea, recently proposed as a potential UNESCO World Heritage site). Finally, our approach is generally applicable to other geographic regions, marine taxa, and management needs in areas of sparse data.

Supporting information

Environmental covariates used to fit habitat‐based density models (Appendix S1), model sensitivity to heterogeneity in survey coverage for sei whale, striped dolphin and Kogia spp. assessed with a cross‐validation approach (Appendix S2), and Spearman's rank correlation coefficients between covariates calculated on surveyed segments and cells of the prediction area (Appendix S3) are available online. The authors are solely responsible for the content and functionality of these materials. Queries (other than absence of the material) should be directed to the corresponding author.

Click here for additional data file. (20.1KB, docx)

Supplementary Material

Click here for additional data file. (515.6KB, docx)

Supplementary Material

Click here for additional data file. (48.9KB, docx)

Acknowledgments

We thank the numerous researchers who collected and shared line transect data with us. D. Palka and T. Cole contributed the NEFSC surveys; L. Garrison contributed the SEFSC surveys; A. Whitt, S. Bates, and G. Buchanan contributed the NJDEP surveys; G. Lockhart contributed the VAMSC surveys; B. McLellan and colleagues contributed the UNCW surveys; V. Ridoux contributed the University of La Rochelle surveys; P. Hammond and C. Lacey contributed the SCANS‐II and CODA surveys; O. A. Bergstad, T. de Lange Wenneck, L. Nøttestad, and G. Waring contributed the MAR‐ECO survey under the Norwegian License for Open Government data (NLOD). We are grateful to P. Lehodey, who provided the micronekton and zooplankton outputs from SEAPODYM, and S. Maritorena and E. Fields, who provided chlorophyll data from the Ocean Color MEaSUREs project. For providing advice and reviewing results, we thank especially E. Becker, D. Cholewiak, P. Corkeron, A. DiMatteo, K. Forney, J. Harrison, L. Hatch, D. Johnston, B. Josephson, D. Nowacek, J. Ortega‐Ortiz, A. Read, D. Risch, J. Robbins, M. Soldevilla, J. Stanistreet, L. Thomas, S. Van Parijs, D. Waples, and S. Wood. We are grateful to J. Cleary for his help with map automation in Python and E. Fujioka for his help extracting sightings from OBIS‐SEAMAP. This study benefited from discussion during meetings of the PELAGIC project funded by the Fondation pour la Recherche sur la Biodiversité and Fondation Total and hosted by the Centre for the Synthesis and Analysis of Biodiversity. Funding for this study came from the U.S. Fleet Forces Command (cooperative agreement N62470‐13‐2‐8008), NASA (NNX08AK73G) and NOAA/NMFS (EE‐133F‐14‐SE‐3558).

Literature cited

  1. Authier M, Saraux C, Péron C. 2016. Variable selection and accurate predictions in habitat modelling: a shrinkage approach. Ecography 40:549–560. [Google Scholar]
  2. Buckland ST, Anderson DR, Burnham KP, Laake JL, Borchers DL, Thomas L. 2001. Introduction to distance sampling: estimating abundance of biological populations. Oxford University Press, Oxford, United Kingdom. [Google Scholar]
  3. Burnham KP, Anderson DR. 2002. Model selection and multimodel inference: a practical information‐theoretic approach. Springer Science & Business Media, New York. [Google Scholar]
  4. Ciminello CA, et al. 2013. Determination of acoustic effects on marine mammals and sea turtles for the atlantic fleet training and testing environmental impact statement/overseas environmental impact statement (technical report). Naval Undersea Warfare Center Division Newport, Rhode Island. [Google Scholar]
  5. Conn PB, Johnson DS, Boveng PL. 2015. On Extrapolating past the range of observed data when making statistical predictions in ecology. PLOS ONE 10 (e0141416) DOI: 10.1371/journal.pone.0141416. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. DeRuiter SL, et al. 2013. First direct measurements of behavioural responses by Cuvier's beaked whales to mid‐frequency active sonar. Biology Letters 9:20130223. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Doniol‐Valcroze T, Berteaux D, Larouche P, Sears R. 2007. Influence of thermal fronts on habitat selection by four rorqual whale species in the Gulf of St. Lawrence. Marine Ecology Progress Series 335:207–216. [Google Scholar]
  8. Elith J, Kearney M, Phillips S. 2010. The art of modelling range‐shifting species. Methods in ecology and evolution 1:330–342. [Google Scholar]
  9. Ferguson MC, Barlow J, Fiedler P, Reilly SB, Gerrodette T. 2006. Spatial models of delphinid (family Delphinidae) encounter rate and group size in the eastern tropical Pacific Ocean. Ecological Modelling 193:645–662. [Google Scholar]
  10. Foster SD, Bravington MV. 2013. A Poisson–Gamma model for analysis of ecological non‐negative continuous data. Environmental and Ecological Statistics 20:533–552. [Google Scholar]
  11. Foster SD, Shimadzu H, Darnell R. 2012. Uncertainty in spatially predicted covariates: Is it ignorable? Journal of the Royal Statistical Society: Series C (Applied Statistics) 61:637–652. [Google Scholar]
  12. Goldbogen JA, et al. 2013. Blue whales respond to simulated mid‐frequency military sonar. Proceedings of the Royal Society B: Biological Sciences 280:20130657–20130657. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Halpin P, et al. 2009. OBIS‐SEAMAP: The World Data Center for Marine Mammal, Sea Bird, and Sea Turtle Distributions. Oceanography 22:104–115. [Google Scholar]
  14. Hammond PS, et al. 2009. Cetacean offshore distribution and abundance in the European Atlantic (CODA). Final Report. University of St Andrews, St Andrews, United Kingdom. [Google Scholar]
  15. Hammond PS, et al. 2013. Cetacean abundance and distribution in European Atlantic shelf waters to inform conservation and management. Biological Conservation 164:107–122. [Google Scholar]
  16. Hedley SL, Buckland ST. 2004. Spatial models for line transect sampling. Journal of Agricultural, Biological, and Environmental Statistics 9:181–199. [Google Scholar]
  17. Heide‐Jørgensen MP, Borchers DL, Witting L, Simon MJ, Laidre KL, Rosing‐Asvid A, Pike D. 2007. Final estimates of large whale abundance in West Greenland waters from an aerial survey in 2005. Journal of Cetacean Research and Management 10:119–129. [Google Scholar]
  18. Henderson EE, Smith MH, Gassmann M, Wiggins SM, Douglas AB, Hildebrand JA. 2014. Delphinid behavioral responses to incidental mid‐frequency active sonar. The Journal of the Acoustical Society of America 136:2003–2014. [DOI] [PubMed] [Google Scholar]
  19. Hollander M, Wolfe D. 1973. Non parametric statistical methods. Wiley, New York. [Google Scholar]
  20. Jepson PD, et al. 2003. Gas‐bubble lesions in stranded cetaceans. Nature 425:575–576. [DOI] [PubMed] [Google Scholar]
  21. Kaschner K, Quick NJ, Jewell R, Williams R, Harris CM. 2012. Global coverage of cetacean line‐transect surveys: status quo, data gaps and future challenges. PLOS ONE 7 (e44075) DOI: 10.1371/journal.pone.0044075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Laake JL, Borchers DL, Thomas L, Miller D, Bishop JR. 2014. Mark‐recapture distance sampling (mrds) package. Version 2.1.10. Available from http://CRAN.R-project.org/package=mrds (accessed March 1, 2014).
  23. Lambert C, Mannocci L, Lehodey P, Ridoux V. 2014. Predicting cetacean habitats from their energetic needs and the distribution of their prey in two contrasted tropical regions. PLOS ONE 9 (e105958) DOI: 10.1371/journal.pone.0105958. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lawson JW, Gosselin J‐F. 2009. Distribution and preliminary abundance estimates for cetaceans seen during Canada's Marine Megafauna Survey—a component of the 2007 TNASS. Canadian Science Advisory Secretariat, Ottawa: Available from http://biblio.uqar.qc.ca/archives/30125408.pdf (accessed March 2014). [Google Scholar]
  25. Lehodey P, Conchon A, Senina I, Domokos R, Calmettes B, Jouanno J, Hernandez O, Kloser R. 2014. Optimization of a micronekton model with acoustic data. ICES Journal of Marine Science 72:1399–1412 DOI: 10.1093/icesjms/fsu233. [Google Scholar]
  26. Lehodey P, Murtugudde R, Senina I. 2010. Bridging the gap from ocean models to population dynamics of large marine predators: a model of mid‐trophic functional groups. Progress in Oceanography 84:69–84. [Google Scholar]
  27. Longhurst AR. 2007. Ecological geography of the sea. Academic Press, Oxford. [Google Scholar]
  28. Mannocci L, Monestiez P, Bolaños‐Jiménez J, Dorémus G, Jeremie S, Laran S, Rinaldi R, Van Canneyt O, Ridoux V. 2013. Megavertebrate communities from two contrasting ecosystems in the western tropical Atlantic. Journal of Marine Systems 111:208–222. [Google Scholar]
  29. Mannocci L, Monestiez P, Spitz J, Ridoux V. 2015. Extrapolating cetacean densities beyond surveyed regions: habitat‐based predictions in the circumtropical belt. Journal of Biogeography 42:1267–1280. [Google Scholar]
  30. Marques FFC, Buckland ST. 2004. Covariate models for the detection function. Pages 31–47 in Buckland ST, Anderson DR, Burnham KP, Laake JL, Borchers DL, Thomas L, editors. Advanced Distance Sampling. Oxford, New York. [Google Scholar]
  31. Marques TA, Thomas L, Fancy SG, Buckland ST. 2007. Improving estimates of bird density using multiple‐ covariate distance sampling. The Auk 124:1229–1243. [Google Scholar]
  32. Merow C, Smith MJ, Edwards TC, Guisan A, McMahon SM, Normand S, Thuiller W, Wüest RO, Zimmermann NE, Elith J. 2014. What do we gain from simplicity versus complexity in species distribution models? Ecography 37:1267–1281. [Google Scholar]
  33. Miller DL, Burt ML, Rexstad EA, Thomas L. 2013. Spatial models for distance sampling data: recent developments and future directions. Methods in Ecology and Evolution 4:1001–1010. [Google Scholar]
  34. Pauly D, Christensen V, Trites AW. 1998. Diet composition and trophic levels of marine mammals. ICES Journal of Marine Science 55:467–481. [Google Scholar]
  35. Pearson RG, Thuiller W, Araújo MB, Martinez‐Meyer E, Brotons L, McClean C, Miles L, Segurado P, Dawson TP, Lees DC. 2006. Model‐based uncertainty in species range prediction. Journal of Biogeography 33:1704–1711. [Google Scholar]
  36. Pollock KH, Marsh HD, Lawler IR, Allderdge M. 2006. Estimating animal abundance in heterogeneous environments: an application to aerial surveys for dugongs. Journal of Wildlife Management 70:255–262. [Google Scholar]
  37. Prieto R, Janiger D, Silva MA, Waring GT, GonçAlves JM. 2012. The forgotten whale: a bibliometric analysis and literature review of the North Atlantic sei whale Balaenoptera borealis: North Atlantic sei whale review. Mammal Review 42:235–272. [Google Scholar]
  38. Ramirez‐Llodra E, et al. 2011. Man and the last great wilderness: human impact on the deep sea. PLOS ONE 6 (e22588) DOI: 10.1371/journal.pone.0022588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Roberts JJ, et al. 2016. Habitat‐based cetacean density models for the U.S. Atlantic and Gulf of Mexico. Scientific Reports 6:22615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Roberts JJ, Best BD, Dunn DC, Treml EA, Halpin PN. 2010. Marine geospatial ecology tools: An integrated framework for ecological geoprocessing with ArcGIS, Python, R, MATLAB, and C++. Environmental Modelling & Software 25:1197–1207. [Google Scholar]
  41. Swartz SL, Martinez A, Stamates J, Burks C, Mignucci‐Giannoni AA. 2002. Acoustic and visual survey of cetaceans in the waters of Puerto Rico and the Virgin Islands, February‐March 2001. Technical memorandum NMFS‐SEFSC‐ 463. U.S. National Oceanic and Atmospheric Administration, Southeast Fisheries Science Center, Miami. Available from http://manatipr.org/wp-content/uploads/2010/01/Swartz2001NOAA.pdf (accessed October 2014).
  42. Waring GT, Nøttestad L, Olsen E, Skov H, Vikingsson G. 2008. Distribution and density estimates of cetaceans along the mid‐Atlantic Ridge during summer 2004. Journal of Cetacean Research and Management 10:137–146. [Google Scholar]
  43. Wenger SJ, Olden JD. 2012. Assessing transferability of ecological models: an underappreciated aspect of statistical validation. Methods in Ecology and Evolution 3:260–267. [Google Scholar]
  44. Wood S. 2014. Mixed GAM computation vehicle with GCV/AIC/REML smoothness estimation (mgcv) package. Version 18–4. Available from http://CRAN.R-project.org/package=mgcv (accessed March 1, 2014). [Google Scholar]
  45. Wood SN. 2003. Thin plate regression splines. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 65:95–114. [Google Scholar]
  46. Wood SN. 2011. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 73:3–36. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Environmental covariates used to fit habitat‐based density models (Appendix S1), model sensitivity to heterogeneity in survey coverage for sei whale, striped dolphin and Kogia spp. assessed with a cross‐validation approach (Appendix S2), and Spearman's rank correlation coefficients between covariates calculated on surveyed segments and cells of the prediction area (Appendix S3) are available online. The authors are solely responsible for the content and functionality of these materials. Queries (other than absence of the material) should be directed to the corresponding author.

Click here for additional data file. (20.1KB, docx)

Supplementary Material

Click here for additional data file. (515.6KB, docx)

Supplementary Material

Click here for additional data file. (48.9KB, docx)

Articles from Conservation Biology are provided here courtesy of Wiley

RESOURCES