Visualizing single-stranded nucleic acids in solution

Abstract

Single-stranded nucleic acids (ssNAs) are ubiquitous in many key cellular functions. Their flexibility limits both the number of high-resolution structures available, leaving only a small number of protein–ssNA crystal structures, while forcing solution investigations to report ensemble averages. A description of the conformational distributions of ssNAs is essential to more fully characterize biologically relevant interactions. We combine small angle X-ray scattering (SAXS) with ensemble-optimization methods (EOM) to dynamically build and refine sets of ssNA structures. By constructing candidate chains in representative dinucleotide steps and refining the models against SAXS data, a broad array of structures can be obtained to match varying solution conditions and strand sequences. In addition to the distribution of large scale structural parameters, this approach reveals, for the first time, intricate details of the phosphate backbone and underlying strand conformations. Such information on unperturbed strands will critically inform a detailed understanding of an array of problems including protein–ssNA binding, RNA folding and the polymer nature of NAs. In addition, this scheme, which couples EOM selection with an iteratively refining pool to give confidence in the underlying structures, is likely extendable to the study of other flexible systems.

INTRODUCTION

For biological macromolecules, knowledge of structure can be critical for establishing function. A rigid one-to-one view of biology is however far removed from the true cellular picture, where molecules sample an array of possible conformations (1–4). Motions can vary from small fluctuations of proteins about their native state, to bulk movements of domains conferred by linkers or hinges. An extreme example is the case of single-stranded nucleic acids (ssNAs), which exist in a broad range of unfolded and highly flexible conformations (5–8). In the cell, ssNAs are found in a variety of locations, such as in telomeric overhangs at the end of chromosomes, at double stranded DNA breaks and at replication forks (9,10). Given these diverse contexts, and their critical biological roles, ssNAs are a prime target for structural investigation. Unfortunately, capturing the conformations and properties of ssNAs challenges traditional techniques. Fluorescence measurements such as single-molecule FRET report both dynamics and inter-dye distances of ssNAs with unmatched resolution (7); however, the technique offers limited global structural information, making the results difficult to interpret. Atomic force microscopy (AFM) and similar ‘pulling’ experiments provide mechanical data, but fail to report detailed molecular conformations (11,12). Nuclear magnetic resonance (NMR) can reveal intricate dynamics and structures for complex RNA molecules (13–15), however its application to isolated single-strands is both challenging and length limited (16–18).

Small angle X-ray scattering (SAXS) reports the global shape and size of molecules in solution, and is sensitive to the full ensemble of populated conformations (19,20). Uniquely, SAXS can capture the richness of such highly flexible systems without added perturbations through dyes or mechanical linkages, and is therefore ideally suited to the study of ssNAs. In spite of this, the conformational averaging of the measurement makes detailed analysis of the data troublesome. Past interpretations have therefore relied on assumptions that reduce the ensemble statistics to means, masking pertinent features. For example, studies on the stiffness of rU₄₀ and dT₄₀ assumed a worm-like chain (WLC) model and constrained the fit with end-to-end distance measurements from FRET experiments (8). While self-consistent, this method sacrifices information gleaned from distributions of parameters. Furthermore, the WLC assumptions were found to be invalid in certain salt regimes. Improved schemes model the phosphate backbone in terms of virtual bonds, trading bulk assumptions in the WLC model for a coarse-grained view of the ssDNA chains (6). Although this latter approach has advantages, providing distributions of some conformational parameters and adding interaction terms missing from the WLC model, structural information applicable to real chains is restricted due to the simplified representation of the backbone. The assumptions required to model the interaction potentials also bring additional complexity and uncertainty to the analysis.

Recent advances in ensemble methods have made it possible to fit sets of models to experimental SAXS data (21,22), deconvolving the conformational averaging of the measurement into individual conformers. This approach grants both a representation of the underlying states and provides distributions of structural parameters. These ensemble optimization methods (EOM) work by selecting structures from a pool containing thousands of possible candidates, with the scattering profiles computed from the selected models together reconstituting the experimentally measured curve. The generation of a large and realistic pool is crucial to obtaining meaningful results. This method has been applied with great success to multi-domain proteins (23–26), and RNA molecules with well-defined secondary structure (27), but has yet to be applied to ssNAs. In contrast to proteins and RNA, very few structures of ssNAs are available to build an extensive pool around. While crystal structures of bound ssNAs exist, their numbers are few and may be unrepresentative of the solution state of the molecule. Theoretical alternatives to chain generation such as molecular dynamics, coarse-grained models and fragment analysis have been applied to predict ssNA conformations and binding (28–30), but are computationally intensive and not suited to the on-demand generation of thousands of conformers. Commonly used approaches and pipelines for RNA model construction (31–34), while providing viable structures for complex RNAs, cannot currently provide realistic conformers for molecules completely lacking base-pairing interactions, such as ssNAs.

Here we present a dynamic pool generation and refinement method that enables ensemble optimization of ssNA structures using SAXS data. The particular challenge encountered in modeling ssNAs compared with disordered proteins is that many more interrelated torsion angles are involved, and their conformational preferences are expected to vary significantly depending on base sequence and solution conditions. For a general sample however, these preferences are unknown. The main innovation in our approach allowing us to circumvent this difficulty, is that the torsion angle preferences are empirically refined during multiple rounds of ensemble optimization. By challenging this scheme using several test cases, we find that the method can recover structural motifs and ensemble properties from ssNA distributions. Additionally, we apply the method to experimental SAXS data from ssDNA homopolymers with juxtaposing conformations and stacking propensities, dA₃₀ and dT₃₀ (5,35,36). These test cases and experimental examples show the method to be a robust and versatile way to determine otherwise unobtainable distributions of conformational parameters in ssNA systems. Furthermore, by pairing EOM selection with an iteratively refining pool, parameters from the underlying structures can be inferred that are beyond the current standard for ensemble methods. These points highlight SAXS and EOM as the ideal partnership for studying the solution structure of ssNAs.

Overview of the method

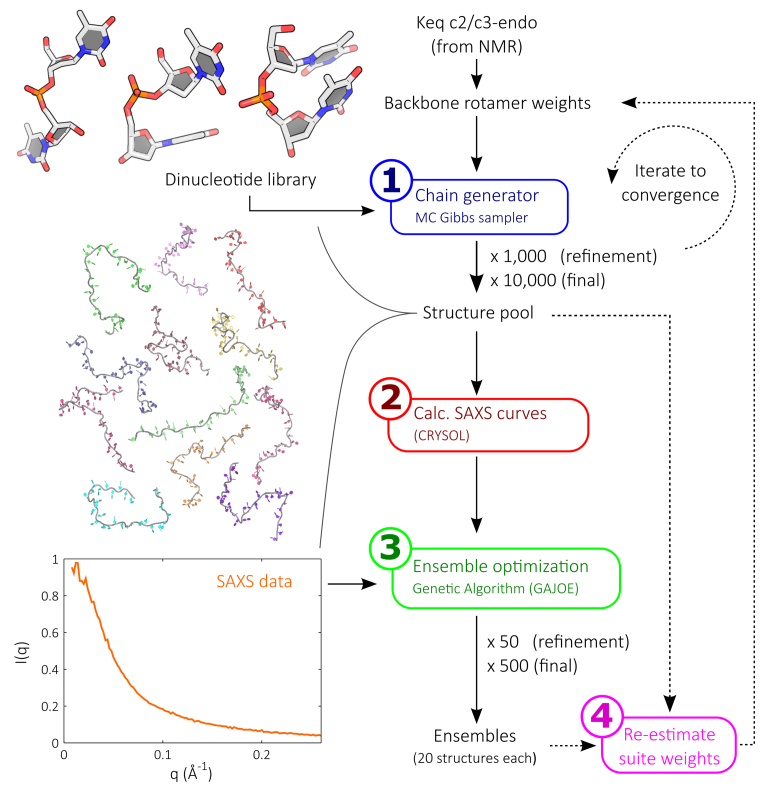
Before providing an in-depth (fully referenced) description of the method, we give a general overview outlining the key steps and ideas of the iterative refinement scheme. To begin, single ssNA chains are constructed from a sequence of discrete, dinucleotide steps, referred to as suites. Each suite is drawn from a pre-defined library with an initial statistical weight. The library we have assembled is based on known dinucleotide steps derived from both DNA and RNA crystal structure surveys, and is tailored for a specific base. By drawing steps probabilistically from this library, individual ssNA chains can be built. Once the chain is checked for steric clashes, it is added to the structure pool. Iteration of this procedure populates the pool with a large number of potential candidates of varying shapes, sizes and suite compositions. After calculating the theoretical SAXS profiles of each chain, we fit the pool to experimental scattering data using ensemble optimization. This step identifies sets of models in the pool that best reconstruct the true scattering profile of the ssNA under study. Once we have identified the models that best reconstitute the experimental data, we compare the frequency of each suite in the selected models to the frequency of suites in the overall pool. Based on this comparison, the weights of the suites in the library are adjusted and a new pool of models subsequently built from the updated library. This procedure is iterated until convergence is achieved, at which point a final round of selection yields the interpreted results.

MATERIALS AND METHODS

Ensemble concept in SAXS

We begin by briefly reviewing EOM applied to SAXS. In solution, conformational fluctuations result in the existence of an ensemble of possible states for any given molecule. These variations are reflected in the associated SAXS profiles at any snapshot in time. The experimental scattering curve therefore encompasses the many thousands of conformations sampled by the molecule during the measurement interval. The ensemble method decomposes the total scattering curve I(q) into the sum of profiles for each frequented state I_n(q), such that:

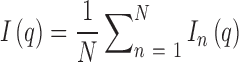where N is the number of states representing the number of underlying conformations (counting degeneracies separately). To keep the problem tractable, the number of states is kept small (generally N < 50). If the scattering profiles of potential conformations are known or calculable, a genetic algorithm can be used to derive sets of structures that best recapitulate the experimental data. These structures are therefore representative of the solution states of the molecule. For this method to give meaningful results, a large pool of potential, but realistic conformers must be supplied for the genetic algorithm to select from. The generation of a pool of models from which the scattering profiles are calculated is thus critical.

Overview of chain generation

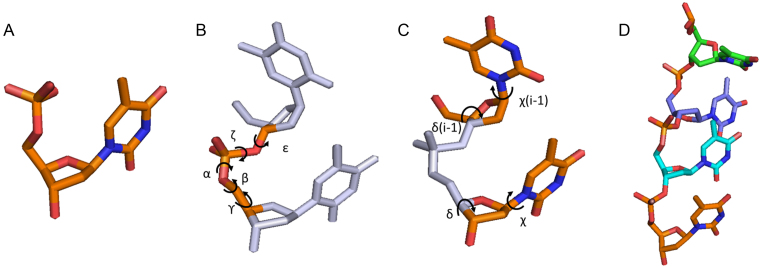
To build pools of ssNA structures, we begin with the most basic building block for all nucleic acids: the single nucleotide (Figure 1A). Single nucleotides bind together to form dinucleotides, which can be described by two parameter sets: the torsion angle set which defines the phosphate backbone (Figure 1B) and the angles defining the two associated sugars and bases (Figure 1C). The chain building method we describe is based on the long standing observation that the torsion angles between adjacent nucleotides tend to be correlated with one another: in RNA, 46 distinct sets account for the majority of conformations measured in high-resolution structures (37–42). While DNA is more conformationally plastic than RNA, similar clustering exists for DNA torsion angles (43). Our method uses these distinct angle sets as the framework for chain generation in units referred to as suites (37,44). In each suite, a torsion angle set defining the phosphate backbone is specified, as well as the sugar pucker and base torsion angles of the two accompanying bases. Chains of varying size, sequence and geometries are then built by drawing individual steps probabilistically from a library of representative suites (Figure 1D).

Figure 1.

(A) The basis for all DNA and RNA structures is the single nucleotide. (B) Torsion angles defining the phosphate backbone in a dinucleotide (α, β, ϒ, ζ, ε). (C) Torsion angles defining the two sugar puckers (δ) and base orientations (χ) in a dinucleotide. (D) A chain built from a series of dinucleotide steps. Rendered using Pymol version 1.2 (DeLano Scientific LLC).

Constructing a library of suites

In contrast to proteins, where the backbone and side chains have a more uniform molecular composition, the global shape and scattering of ssNAs is largely determined by the relatively electron-dense phosphate backbone, rather than the orientation of the bases. It is therefore especially critical to select a variety of torsion angle sets when modeling ssNA data acquired by a low-resolution technique such as SAXS. To this end we used 12 torsion angle sets with the goal of capturing conformations readily found in DNA crystal structures (such as stacked conformations), as well as sampling extended conformations that may rarely be found in high resolution structures, but are likely present in solution. The latter we derive from RNA rotamers (37). This assumption is reasonable; given that RNA is more sterically hindered than DNA, the conformations that RNA can assume presumably represent a subset of those that DNA can form. This fact is readily observed in nature: DNA can adopt both A and B-form helices, while RNA can only adopt the former.

Each torsion angle set was assigned a 2-3-character mnemonic, as specified in Supplementary Table S1. For the unstacked, RNA-derived conformations, the first two characters define the region of α/ζ space that the given torsion sets fall in, as in reference (45), while the third specifies the range of ϒ (p = gauche+, m = gauche- and t = trans) (46). For the stacked conformations, the mnemonic reflects the specific geometry of stack formed, i.e. A1 is canonical A-form (following (43)). In RNA, the precise values in each torsion angle set are correlated with the sugar pucker (δ) of consecutive bases. For simplicity, we use a single torsion angle set for all allowed values of δ. These values were taken as the average for RNA suites belonging to a particular (α/ζ,ϒ) group, but having different sugar puckers. This is not a severe approximation, as the dinucleotides were identified as the correct RNA suites by the program suitename (37).

Having established a framework for describing torsion angle sets, we construct a library of suites around these sets and weight each to define a probability distribution from which steps of a chain may be drawn. The chain building technique is very general, and may be applied to give libraries of RNA or DNA suites for constructing models of arbitrary sequence. For simplicity, we began with libraries for DNA homopolymers with T or A bases. To extend the torsion angle sets to suite libraries, we need only determine the possible values of both sugar puckers and base torsion angles appropriate for each homopolymer. We can reduce the number of possible suites in the libraries by looking to NMR data on dinucleotides. The NMR derived equilibrium constant between C2’ and C3’ endo sugar puckers 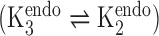for dTpdT dinucleotides is 1.9, while for dApdA it is 24 (47). Such a high sugar pucker constant for dA dinucleotides implies that the C3’ sugar pucker will be exceedingly rare. Therefore, suites featuring C3’-endo sugar puckers were not included in the dA libraries. Furthermore, in accordance with known preferences for purines and pyrimidines (48), both anti and syn bases were modeled in poly dA suites, while poly dT suites feature only anti conformers. Similarly, a single sugar pucker pair was modeled for each stacked suite, with the base angle always anti (43). Therefore, before removal of sterically hindered suites, we arrive at four suites for each non-stacked torsion angle set and one suite for each stacked torsion set.

To determine steric clashes in the suites, atoms were assigned Van der Waals radii of 1.52 (O), 1.7 (C), 1.8 (P) and 1.55Å (N) as in previous discrete models for nucleic acids (49). A steric clash was defined as a Van der Waals overlap >0.42Å for non-bonded atoms (this value was relaxed slightly from the overlap cutoff of 0.4Å defined in the nucleic acid model validation tool MolProbity (50) to accommodate imperfect stacking geometry resulting from binning sugar pucker and base torsion angles in our reduced suite definitions). Bond angles and distances were taken from the XPLOR high-resolution parameter set (51). Steric clashes in suites were checked between all non-bonded atoms and suites showing overlap were removed from the libraries. When building chains with suites, the gamma angle of the 5΄-terminal sugar is undefined, and was therefore assigned the canonical values of 52.5 degrees. Base torsion angles were adjusted slightly within their allowed ranges to prevent steric clashes in the stacked dTpdT suites. After removing steric clashes from the libraries, dTpdT suites totaled 35 (1 suite removed due to steric clashes), while dApdA totaled 32 (2 suites removed due to steric clashes). The torsion angle sets and base/sugar parameters used to build the suite libraries are summarized in Supplementary Tables S1 and 2. To help visualize these angle-sets, we provide representations of each of the suites in Supplementary Figures S1–3.

Chain building

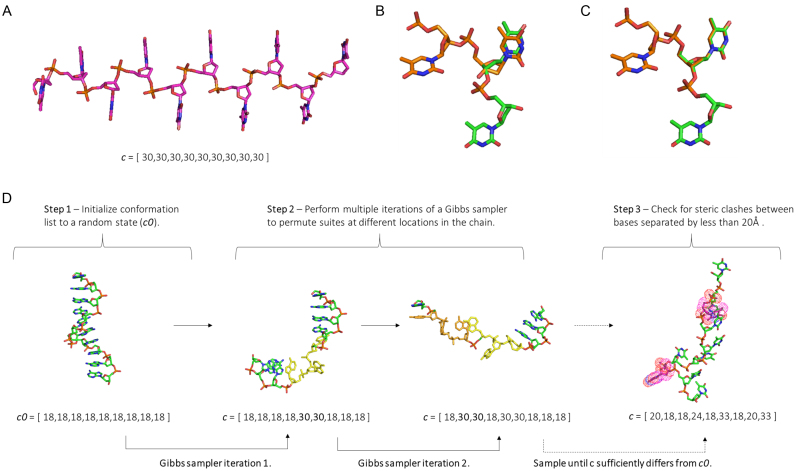
In our chain generator, a set of M suites specify all possible dinucleotide steps, with a chain of length N defined by a list c of N-1 integers between 1 and M, as illustrated in Figure 2A. As each suite defines both 5΄ and 3΄ sugars, adjacent suites overlap. Therefore, neighboring suites must obey adjacency rules with regards to the sugars and bases (a 5΄ C3΄ endo suite cannot follow a 3΄ C2΄ endo suite, Figure 2B and C). A combination of steric clashes and adjacency rules severely limit the number of possible suite permutations. Thus to accelerate structure generation, all chains of length 5 (4 suites) are precomputed and checked for steric clashes and adjacency rule violations. All possible suite combinations are then stored in a (MxMxMxM) logical matrix L₄ which identifies if a given suite permutation is allowed. Next, each suite in the library is assigned an initial statistical weight t_i, equal to the probability for it to occur as an isolated dinucleotide. These probabilities are generally unknown, but may be constrained by the frequency each appears in consensus survey data (37,43). These statistical weights are stored in a vector w of length M, and are collectively rescaled in order to obtain the correct NMR derived sugar pucker constants, as in previous work (47). We express this process as w = w(t,K), where K is the sugar-pucker equilibrium constant and t a vector containing the suite weights (the t_i's). Having laid out the definitions of relevant objects, we now proceed to explain the chain building algorithm. The procedure to build a single chain consists of 3 steps and is illustrated in Figure 2D.

Figure 2.

(A) A chain of length N is defined by a vector c of length N-1, containing integers between 1 and M which define a suite in the library. The simplest case is illustrated, 9 of the same suite in a row (suite 30) to give a chain of 10 bases. (B) Adjacency rule violation: a 5΄ C3’ endo sugar pucker suite (orange) cannot follow a 3΄ C2’ endo sugar pucker suite (green). (C) Correctly overlapping suites with no adjacency rule violation. (D) Illustration of the procedure to build a single chain. In the first step, an initial conformation is set at random. For simplicity, we chose a ‘random’ conformation consisting of all the same suite in a row. In step two, multiple iterations of a Gibbs sampler are performed. In each iteration, a random position in the conformation list is selected and permuted based on statistical weights (first change to c₀ is highlighted in yellow, the second orange). Enough iterations are performed to make the new state c significantly different from the initial state c₀. In the third step, the PDB is built and checked for steric clashes.

A Monte Carlo procedure is applied to generate chains of arbitrary length that are free of steric clashes and consistent with the equilibrium constants for each dinucleotide step. Initially, a chain conformation c₀ is set randomly. To make c₀ consistent with adjacency rules and steric clashes (defined by L₄), changes to a single position in c₀ are proposed at random and accepted if the total number of violations, V_tot, decreases or stays the same. V_tot is computed by scanning L₄ across c₀:

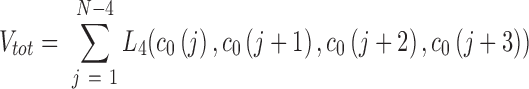this process is repeated until the number of violations is zero. Next, a Gibbs sampler is used to modify the chain at random locations according to the probability derived from the dinucleotide weights. In each iteration, a location in c₀ is chosen at random (a random integer n between 1 and N-2). Two adjacent suites are permuted at a time to allow suites of any sugar pucker or base torsion angle to be inserted into the chains. For example, it would be impossible to insert a C2’-endo sugar pucker suite into a stretch of C3’-endo sugar pucker suites without permuting two positions simultaneously. The sampler generates new values for positions n and n + 1 in c₀ based on the adjacent and the statistical weights. To begin, all pairs allowed by L₄ are enumerated. The statistical weight for each pair is computed from the product of its statistical weight divided by the sum of the weights for all possible pairs (this is the Gibbs sampling step (52)). The sampler is iterated until the new trial state c is sufficiently different from the initial state c₀. An appropriate number of iterations will depend on the length and complexity of the chain being generated. We found that 50 iterations were sufficient for 30-mer homopolymer chain (N = 30).

At this stage, c represents a proposed move, however it may contain long-ranged steric clashes that were not captured by the L₄ matrix. The 3D model is computed from c using the geometric rules for nucleic acid bond angles and distances. Because c is guaranteed to have no steric clashes between nucleotides separated by <5 bases, and because nucleotides have a known maximum size, it is not necessary to compute the pairwise distance between all atoms. First, pairwise distances between all C1’ atoms are computed for all pairs of nucleotides separated by more than 5 bases along the chain. Next, those nucleotides whose C1’ atoms are within a cutoff distance of 20Å (49) are checked for clashes. If one or more clashes are found, c is rejected, and the Gibbs sampler is re-run from the previous state, c₀. Finally, after a burn-in period of 10 successful iterations, the 3D models are saved in PDB format.

Ensemble optimization and iterative refinement of suite weights

Chains constructed from the initial suite weights likely do not yet represent the true solution structure of a given ssNA in a particular salt condition. Multiple rounds of chain building and suite weight refinement based on fitting experimental SAXS data to the constructed models are required to achieve good agreement. Each round of refinement (Figure 3) consists of four steps:

1. Build chains with steps drawn probabilistically from the suite library to populate a pool of models.

2. Calculate the theoretical SAXS profile for each model in the pool.

3. Identify the most representative structures by fitting input experimental data using the pool by EOM.

4. Re-estimate the suite weights in the library based on the frequency of suites in the selected models compared to the pool.

Figure 3.

Our ssNA modeling strategy consists of four steps. The first involves iterating the chain building procedure using a statistically-weighted dinucleotide suite library to populate a large structure pool. The pool is populated with 1000 models in each refinement round, while the final round utilizes 10 000 structures. In the next step, the SAXS profiles for all models in the pool are calculated. In step 3, the structure pool is fitted to input experimental SAXS data using ensemble optimization. This step selects sets of 20 structures from the pool whose calculated scattering profiles reconstitute the experimental data. This process is repeated 50 times in each refinement round, and 500 times in the final round. Finally, the selected structures are examined against the pool and a new set of suite weights is defined. This process is iterated until convergence.

This loop iterates until the selections converge, at which point a final round of selection is run to provide interpreted results.

The particular implementation of each step during refinement is as follows. In the first step, the chain-building algorithm is iterated to generate a pool 1000 structures. In step 2, each structure's SAXS profile is computed using CRYSOL (53), with a maximum harmonic order of 15, Fibonacci grid of order 18 and default hydration parameters. Due to its extensive application to flexible intrinsically disordered proteins (21,22,54–58), the reduced contrast of proteins emphasizing hydration models compared to nucleic acids (59), and the low q-range we utilize, the use of CRYSOL to hydrate and compute theoretical scattering profiles for these flexible ssNAs is well justified. In step 3, EOM is implemented as a genetic algorithm by the program GAJOE 1.3 (21), which fits theoretical SAXS profiles to the input experimental curve. We use 20 structures per ensemble with repeat selections allowed to reconstitute the data. For each refinement round, the algorithm is run for 50 generations. The EOM process is repeated 50 times to accumulate statistics.

In step 4, the frequency of each suite in the pool (h_pool) and in the selected ensembles (h_ens) is calculated. A new estimate for the suite weights (t_new) is found that minimizes the discrepancy between the observed suite frequencies (h_ens) and an expected value for h_ens assuming that the frequencies are proportional to the underlying weights (47):

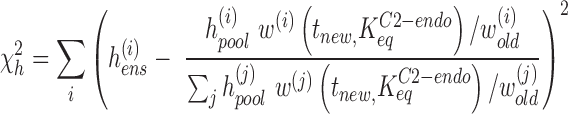where w_old is the vector of suite weights used by the chain generator to create the pool (the NMR rescaled vector of t). A vector t_new that minimizes χ_h² is found using the lsqnonlin function in MATLAB. Having re-weighted the suites in the library, we can now proceed back to step 1 and start the next round of refinement.

In general, we run 15 refinements in preparation for the final round of the loop. The final round differs from the refinement rounds in that 10 000 structures are built in step 1, EOM is run for 500 generations and is repeated 500 times in step 3. The results of this final round of selection are interpreted as the conformations adopted by the ssNA of interest.

Metrics for convergence

To determine whether the refinements effectively increase the quality of models in the pool, and to check for convergence, we monitor two metrics at each stage of the refinement. First, the goodness of fit χ² of each individual ensemble is assessed by comparing the ensemble (I_ens) and experimentally derived (I_exp) SAXS curves:

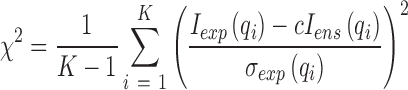where K is the total number of points in q-space, σ_exp is the experimental error at each q point and c is a scaling factor. The reduced chi-square is then used to judge the global fit of all ensembles to the experimental data:

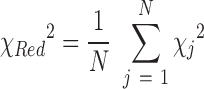here, the summation is over all generated ensembles (N equals 50 for each refinement stage and 500 for the final round of selection). Second, to assess convergence of the refinement procedure, we compare the populations of suites in the pool and ensembles by evaluating the Jensen Shannon Divergence (JSD) (60). This metric enables the similarity of two probability distributions to be assessed. In terms of two probability distributions p₁ and p₂, the JSD is defined as:

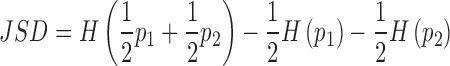H(p) is the Shannon entropy for a discrete probability distribution p with states p_i:

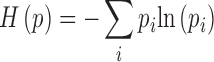The use of two metrics allows us to assess convergence and increased model quality in complementary ways.

Experimental methods

HPLC-purified DNA oligomers of dT₃₀ and dA₃₀ were purchased from Integrated DNA Technologies (Coralville, IA, USA). Lyophilized powders were resuspended in STE buffer (10mM TRIS, 50mM NaCl, 1mM EDTA, pH 8.0) and dialyzed four times with 20 mM NaCl, 1 mM Na MOPS pH 7.0 using Amicon Ultra-0.5 10 kDa concentrators (EMD Millipore, Billerica, MA, USA). SAXS profiles were measured at the Cornell High Energy Synchrotron Source (CHESS) beamline G1, at three strand concentrations: 200, 100 and 50 μM. Buffer subtracted curves were matched in the range 0.15Å⁻¹ < q, for accurate concentration normalization and were linearly extrapolated to zero-concentration to remove any inter-particle interference effects observed at low q. The zero-concentration curves were joined at q = 0.15Å⁻¹ to the high concentration curve to provide the final, structure-factor free SAXS profiles. Due to a slight over-estimation of errors during the SAXS integration step, a rescaling of the uncertainties was performed. The inverse fourier transform (IFT) of the experimental data was calculated with GNOM (61), after which the uncertainties on the experimental curves were rescaled so that the chi-square for the IFT fits were equal to 1. All data analysis was performed with MATLAB using in-house code.

Generation of test cases

Test cases were generated by building structures with the chain-generating algorithm as described above. Each structures’ SAXS curve was computed with CRYSOL and, unless stated otherwise, the average of at least 2000 structures was used to provide the synthetic data to test our iterative refinement scheme.

RESULTS AND DISCUSSION

Sampling of conformational space and ensemble size

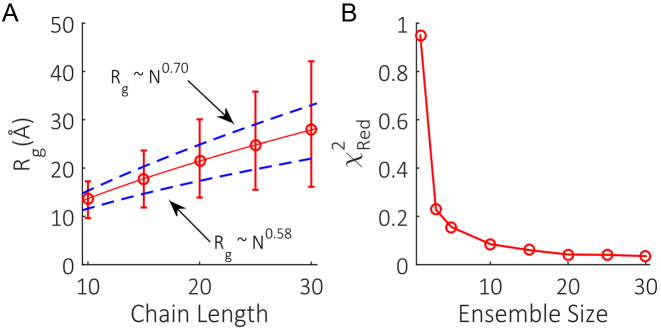
To correctly implement EOM, two basic criteria must be met. First, it is crucial that the pool of models is conformationally broad and adheres to known distribution statistics. Second, the ensemble size must be large enough to capture the underlying number of accessible states. These conditions ensure GAJOE is given realistic conformational variety and sufficient structure selections to adequately recapitulate the SAXS data. To test the first requirement, unrefined pools of dT chains with a variety of lengths were generated. The mean R_g of the pools were fit with a power law of the form R_g ∼ N^ν, which has been previously used to analyze experimental SAXS data on ssDNA homopolymers of varying lengths (35). This work showed that ν falls in between a self-avoiding walk (ν∼0.58) under high-screening conditions, while displaying stiffer behavior (ν∼0.70) under low-screening conditions. We checked whether our initial unrefined pool of structures could capture this range of behavior. The derived power law shown in Figure 4A falls in between these limits, illustrating that the initial pool of structures is physically reasonable. Furthermore, the range of structures generated in the initial pools at each length is broad enough to provide coverage of both extreme chain conformations. The unrefined pools are therefore well positioned to match any ionic condition ssNA chains may be in upon subsequent refinements.

Figure 4.

(A) Mean R_g (red circles) and range (red bars) of unrefined dT pools of varying chain lengths. The mean R_g of the pools were fit with a power law of the form R_g ∼ N^ν (solid red line) that falls in between the scaling behavior expected for self-avoiding chains (ν∼0.58) and stiffer chains (ν∼0.70). (B) Effect of ensemble size on the quality of data fitting.

To check the second requirement, the whole iterative refinement scheme was run multiple times on synthetic input data with a 2% uncertainty included on the intensity values. Each separate implementation utilized a differing ensemble size. The reduced χ² of the ensembles in the final rounds of selection were used to assess the minimum number of structures per ensemble required to best fit the data. The fits (Figure 4B) show a decrease in χ_Red² from a maximum of 0.95 with one structure per ensemble, before plateauing at a χ_Red² of 0.04 for an ensemble consisting of 20 members. These low chi-square values even for one-member ensembles are a result of the synthetic input, and are not realistically achievable when applied to experimental data. Nevertheless, this test shows that the minimum number of structures per ensemble required to fit free nucleic acid systems is around 20.

Recovery of conformational distributions

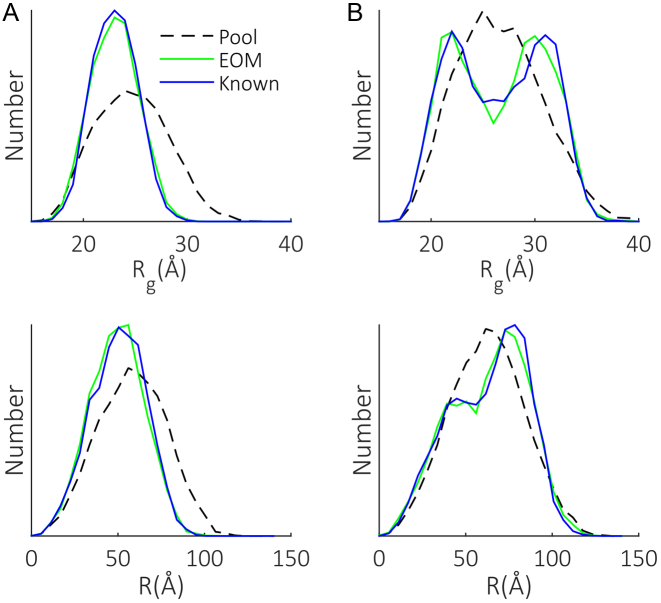
The use of EOM to produce R_g distributions for multi-domain and intrinsically-disordered proteins is well established (21,22). Such behavior however, has not been demonstrated for flexible linker type molecules such as ssNAs. Another intriguing possibility is the extraction of additional parameters useful in the study of nucleic acids, in particular the end-to-end distance R. To illustrate that the refinement method is capable of capturing and reporting these parameters, two test cases with known R_g and R distributions were simulated and used as the input for our scheme. The results (Figure 5) show the good agreement obtained between known and EOM-derived distributions, with both the shape and extent of conformational space recovered. It is somewhat surprising that the R distributions are reproduced, given that EOM only indirectly constrains this metric. These examples establish that the use of the pool refinement mechanism paired with EOM is applicable to the study ssNAs conformations.

Figure 5.

Demonstration of the applicability of EOM to the study of ssNAs. Two test cases (A and B) with known R_g and R distributions (blue) were generated and fed to the iterative refinement scheme. The pools generated in the final chain building rounds are shown (dotted black) along with the distributions associated with the models selected from these pools (green) by GAJOE.

Recovery of model parameters

While details of individual models are certainly far from discernable in a low-resolution technique such as SAXS, ensemble generalizations relating to specific torsion sets are extractable. As SAXS is sensitive to the overall shape of molecules in solution, and because the shape of the chain is governed by specific sets of torsion angles defining the phosphate backbone, some global information about these angles should be recoverable. The refinements in our method allow us to reconstruct the mean shape and suite composition of chains defining the input SAXS curve. To quantify the directional persistence of the chain, we calculate the orientation correlation function (OCF), defined as:

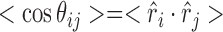Here, 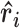is the normalized bond vector between the ith and ith+1 phosphate in the chain. The average dot product between bond vectors is computed as a function of separation along the chain (|i-j|). The average OCF of all members in the selected ensembles are used to interpret the mean shape of the molecule for a given condition.

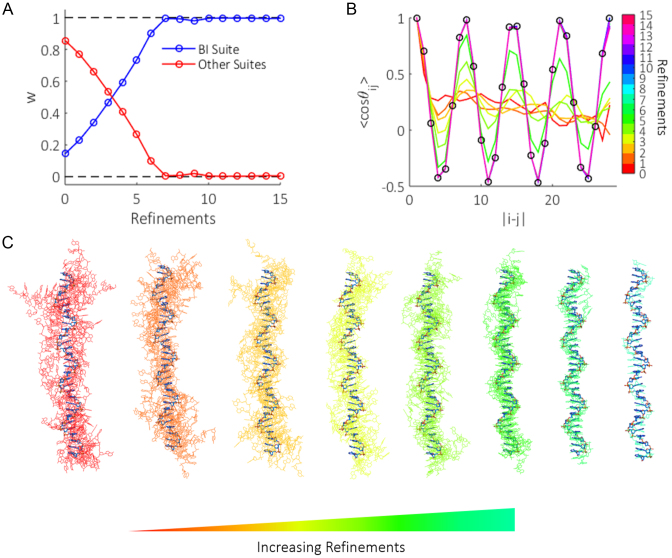
To demonstrate the refinement scheme's ability to recover mean chain composition and shape, we generated the most ordered ssDNA structure one can imagine, a half-canonical B-form helix (29 instances of dA suite B1) and used the theoretical SAXS profile from this conformation as input for our method. Figure 6A and C show the evolution of suite weights and selected ensemble structures with refinements when solving this test case. For presentation purposes, the ensemble structures shown in Figure 6C were aligned with DAMSUP (62). Initially, the suite weights are far from representing a structure pool containing canonical B-form helices. GAJOE therefore identifies conformers from the pool that best approximate this state, selecting models that by chance have a larger composition of the B1 suite than the pool average (Figure 6C, red-yellow structures). Suite B1 is thus re-weighted more heavily in later refinement rounds. This procedure results in a gradual increase in the weight of suite B1, until the scheme converges after refinement round seven, where full B1 helices are represented in the pool (Figure 6C, blue-cyan). This test provides a further example of the effect of ensemble size as shown in Figure 4A. While the input test case is a sole conformation, and our ensemble size consists of 20 structures, the allowance of repeat selections results in the same model being chosen multiple times. Hence the quality of the fit is unaffected as long as the ensemble size is sufficiently large.

Figure 6.

(A) The effect of refinements on the weight (w) of suite B1 compared to all other suite weights. With each round of selection from the pool by GAJOE, models are identified which contain a higher content of suite B1 than the pool average. This suites weight is subsequently increased for the proceeding round of structure building. This trend continues until the scheme converges. (B) The mean OCF of ensemble structures (solid colored lines), is initially far from representing the known half B-form helix (black circles). Refinements to the suite weights allow structures whose backbone shape more closely resemble the input data to be generated in the pool. Eventually the route of the backbone is matched. (C) Evolution of ensemble structures (solid colors) compared with the known input structure (bold blue) as refinements progress. Structures were aligned with DAMSUP (62) with enantiomorphs allowed. Note that near the latter refinements, perfect overlap of input and ensemble structures occur, and therefore fewer structures are ‘seen’ as the refinements progress.

The mean OCFs of the selected structures for each refinement round are shown in Figure 6B. The early rounds of ensemble optimization yield structures that poorly represent the true shape of the input backbone (black circles), displaying no clear oscillatory features characteristic of strong base stacking. Upon subsequent refinements, oscillations in the OCFs emerge that increase in amplitude as a higher composition of suite B1 appears in the ensemble structures. After round seven, the OCF remains mostly static (as expected from the convergence of suite weights) and matches the input B-form helix. Slight variations at the largest phosphate separations are however still seen, as the end bases make little contribution to the global shape of the molecule. Regardless, by employing an iteratively refining structure pool, additional model parameters relating to the mean suite composition and backbone shape can be reconstructed. This is beyond the standard limitations of traditional EOM, where the selected models solely provide distributions of R_g and D_max.

We note however, that due to the limited resolution of SAXS, our method is sensitive to the global shapes and sizes of the chains under study, as well as the presence of repeating structural motifs (such as base stacking, chain stiffening and ion binding pockets) in the phosphate backbone. As such, the OCF and strongly weighted suite selections are the safely extractable parameters from this analysis. Less frequently selected suites present in the refined structures act to contort the chain into the correct global shape. No deeper interpretation is given to these subsidiary suites. A possible extension to improve this resolution would incorporate wide angle X-ray scattering (WAXS) data to further refine the selected ensemble structures, as is routinely applied in other works (63,64). In this case however, special care would need to be taken in calculating the theoretical scattering profiles at high-q, where hydration models become influential (65).

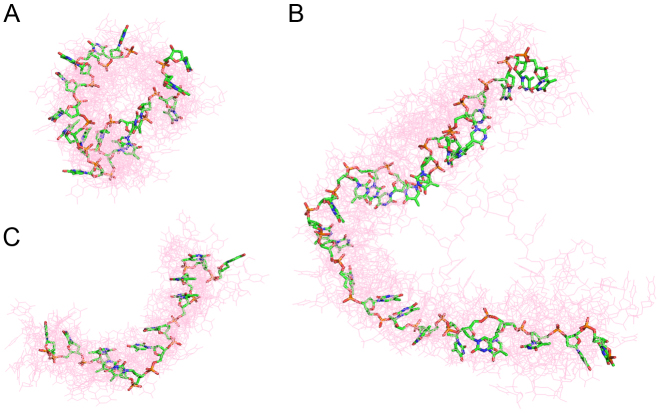
As a second check, three dT chains derived from crystal structures (PDB: 2C62, 4GNX and 4GOP) were used to provide test cases for the refinement scheme. Figure 7 shows the final selected ensembles (light red) for each case, together with the input structures (green). Good agreement is obtained between the selected ensemble structures and the input for all cases, confirming the refinements are having the desired effect of recreating the mean backbone shape when viewed together. Additionally, this confirms that our method is not just self-consistent, but is flexible enough to reconstruct real chain geometries that are not defined in terms of the suites in our library.

Figure 7.

Three poly dT chains derived from crystal structures were used as test cases for the refinement scheme (solid green sticks) (A) PDB: 2C62 (B) PDB: 4GNX (C) PDB: 4GOP. The EOM derived ensembles (red lines) clearly show that the mean shape of the backbone is reproduced for each case. All structures were aligned with DAMSUP with enantiomorphs allowed.

Application to dT₃₀ and dA₃₀

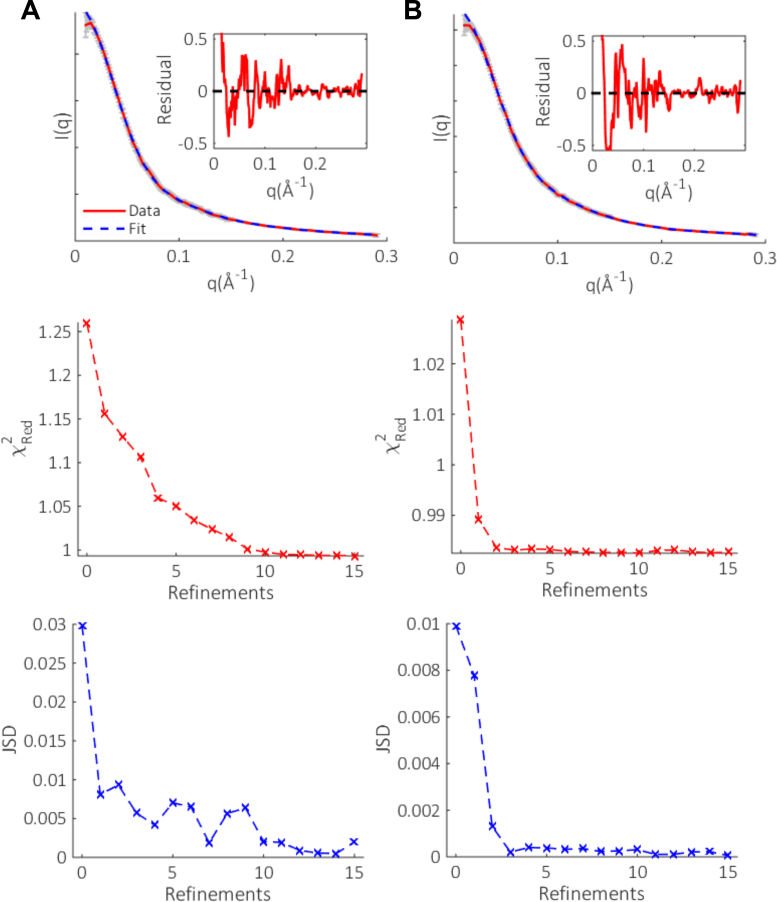
To experimentally test the method, we chose to focus on the conformations of dT₃₀ and dA₃₀ at low salt (20mM NaCl). These molecules display distinct conformational preferences and have been widely investigated, hence they are the ideal test subjects for the iterative refinement scheme. After fifteen rounds of refinement, the final selection resulted in excellent fits to the experimental SAXS data, as shown in Figure 8. The selected ensembles fit the data with χ_Red² values of 1.00 and 0.98 for dT₃₀ and dA₃₀ respectively, improved from the initial round of selection using the unrefined pools. The evolution of chi-square with refinements show a gradual improvement of the fits for both homopolymers, followed by a plateau after which the fits to the data do not improve. This trend is echoed in the JSD, which is initially large when the pool and selected ensembles suite distributions are disparate. Subsequent refinements decrease this distance, eventually remaining constant when the scheme has converged. These metrics indicate that the refinements have the desired effect of increasing the quality of models in the pool, and that the method has converged on a solution well before round 15 of refinement.

Figure 8.

The EOM fits (dashed blue) to the experimental SAXS data (solid red) with associated experimental errors (gray) and residuals (inset) for (A) dT₃₀ and (B) dA₃₀. In the residual plots, we limit the y-axis to enable the high-q agreement to be easily seen. The effect of refinements on the reduced chi-square (χ²_Red) and Jensen Shannon Divergence (JSD) of the selected ensembles for each molecule are also shown. The SAXS data and additional information, such as Kratky and Guinier plots, are available on SASDBD (dT₃₀: SASDBD6, dA₃₀: SASDBE6), and are reproduced in Supplementary Figure S4.

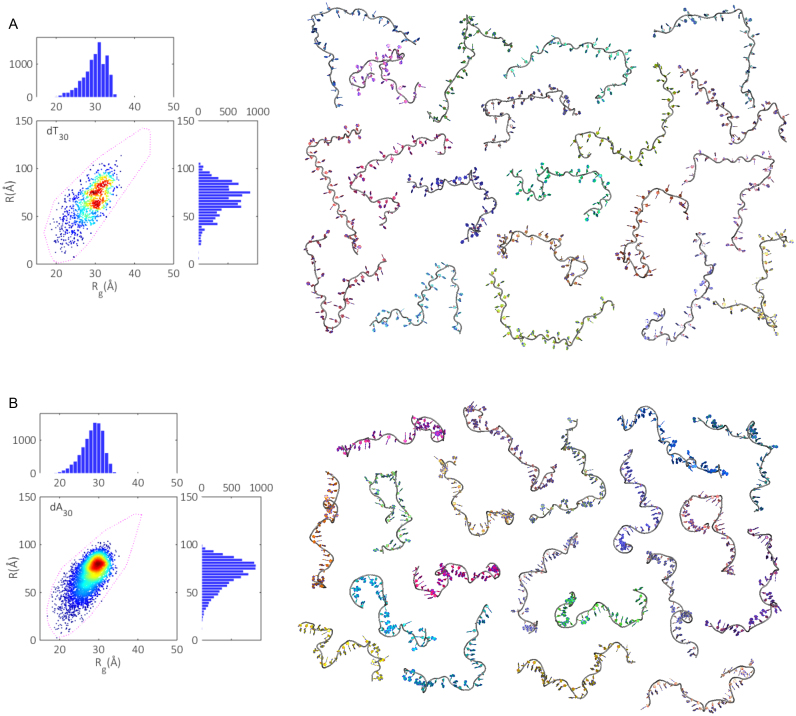
From the SAXS curves, the mean radii of gyration for dT₃₀ and dA₃₀ are measured to be (29.6 ± 0.3)Å and (27.2 ± 0.3)Å respectively (Supplementary Figure S4). Using the iterative refinement scheme, we can further mine these curves to obtain the distributions of both R_g and R for each homopolymer. To aid in visualizing these distributions with respect to individual models in the ensembles, we move from the 1d representation of R_g and R histograms previously introduced, to a 2d heat map (Figure 9). In these plots, each model in the ensembles defines a point in space, located by its R_g and R value. The heat on the map is determined by calculating the number of states within a 2Å circle centered about each point. The bounding models in the pool are now represented by the purple dashed contours. By comparing the populated region of conformation space to the extreme states of the pool, it is clear that both dT₃₀ and dA₃₀ are only moderately flexible at these low salt conditions; with the largest structures in the pools not selected. The extent of coverage in conformational space (EoC) also appears to be roughly equal for both polymers, indicating each is as flexible as the other in terms of accessible states. This finding is surprising, given that dA₃₀ is generally considered a more rigid polymer than dT₃₀ (5). While the EoC is comparable, the density of structures in R_g-R space is far higher for dA₃₀ than dT₃₀, suggesting that the former has a stronger preference for certain conformations than the latter. Despite differences in the global size of each polymer as reported by R_g, the mean end-to-end distance for both is 70Å. Thus, while dA₃₀ is on average more compact, its length remains roughly equivalent to that of dT₃₀. The associated R distributions echo the conformational preferences as noted earlier, with dT₃₀ much more smeared over many length scales than the more constrained dA₃₀.

Figure 9.

Conformational spaces (R_g and R) were formed from every selected model in the (A) dT₃₀ ensembles and (B) dA₃₀ ensembles (500 sets of 20 models for a total of 10 000 points) (left). Projections onto 1d R_g and R histograms are also shown. On the right, one of the 500 sets of 20 member ensembles reconstituting the experimental curves are displayed. These ensemble structures are available on SASBDB, (dT₃₀: SASDBD6, dA₃₀: SASDBE6). The repeatability of the conformational spaces is demonstrated in Supplementary Figure S5.

To pictorially represent the above conformational spaces, we show one ensemble of structures for each polymer (Figure 9, right). The most striking difference between the two is seen in the route of the phosphate backbone. In dA₃₀, the strong propensity for base-stacking sets the backbone in a tortuous wind, juxtaposed to dT₃₀ where a lack of stacking interactions yields straighter conformations. The ensembles reveal that while there is a large variety in chains required to represent the SAXS data, the structures themselves are distinctly non-globular, in agreement with previous ab initio methods of structure determination for DNA homopolymers (35).

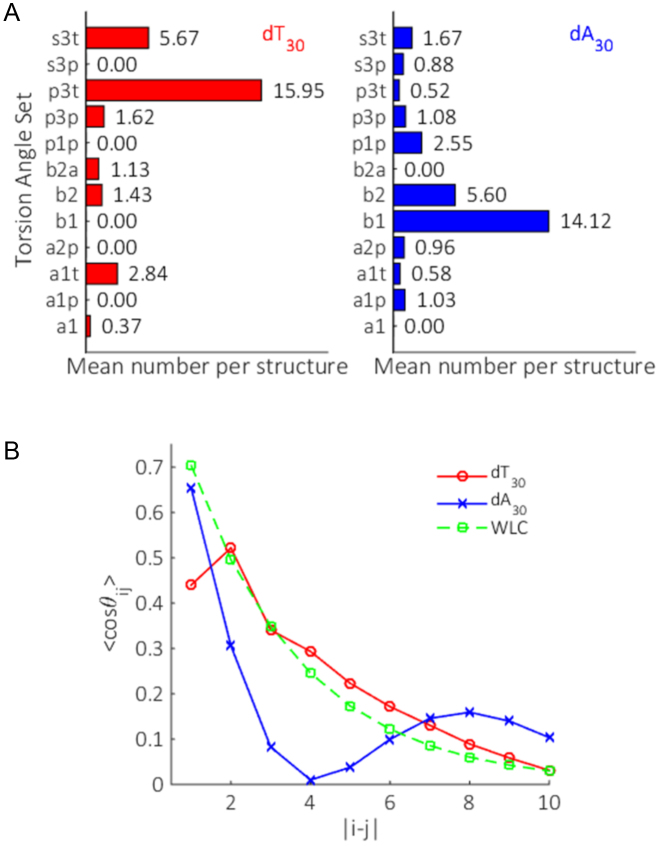
To quantify these observations, we examine the mean number of a given torsion set per structure (Figure 10A). In this view, dA₃₀ features a high degree of base-stacking, with large population of the B-form suites B2 and B1. The latter canonical B-form suite is more favored. In contrast, dT₃₀ shows a strong bias for suites which straighten the phosphate backbone, such as the p3 family, with only marginal base-stacking present through suites B2 and hybrid B2A. These results agree well with AFM pulling experiments on dA₃₀ and dT₃₀, where there is little sign of any base-stacking in dT₃₀, but extensive stacking in dA₃₀ (66). Unlike these experiments, we obtain these metrics for the molecules in their natural, unextended states at low salt and can quantify the mean number of stacked bases per chain without referring to the other for a baseline. While on average, dT₃₀ and dA₃₀ show strong preferences for particular suites, the range of subsidiary torsion sets selected in both polymers emphasizes the plasticity of these systems.

Figure 10.

The mean suite composition (A) and OCF (B) of all selected models in the ensembles for dT₃₀ (red) and dA₃₀ (blue). We additionally plot the OCF predicted for a WLC model (dashed green), fit using the parameters derived from the dT₃₀ ensemble structures and the measured persistence length from (8). The repeatability of both these metrics is demonstrated in Supplementary Figures S6 and S7.

Finally, we assess the directional persistence of the phosphate backbone for all ensemble structures by looking at the OCF (Figure 10B). This metric is useful for both identifying structural motifs in the backbone of a collection of models, and for testing polymer theories. To our knowledge, this is the first time an OCF has been experimentally derived. The OCFs clearly emphasize the differences in backbone shape and suite selection between dA₃₀ and dT₃₀. A gradual decay is observed for dT₃₀ with increased separation, consistent with theories on charged polyelectrolytes where the chain gradually ‘forgets’ its orientation with increasing number of monomer steps (67). The trend however is not well described through a simple exponential decay, as would be predicted by a WLC model (shown as the dashed green line). This is unsurprising; given the low ionic strength (20 mM monovalent salt) we would expect repulsion between distant chain elements to stiffen the polymer at large base separations, an effect that is neglected in a WLC. dA₃₀ on the other hand features an oscillatory OCF, a result of the helical nature of the polymer, where the backbone returns to its original direction after one helical period. Referring back to the mean number of suites per structure, we see that the two stacked conformations B2 and B1 are far more prevalent than any other suite selected. This results in long runs of B1 stacks in the selected structures, with occasional breaks likely being B2 suites. In this way, there is a correlation at large base separations which exceeds that expected in the conventional polyelectrolyte theory. The fact that most suites in dA₃₀ are involved in stacks of B1 also explains the sharper decay of OCF seen at small separations relative to dT₃₀. The sharp wind of the backbone in extended B1 runs results in a greater decay of the OCF when compared to the straighter nature of dT₃₀ suite selections.

CONCLUSION

Here we have outlined a dynamic pool generation and iterative refinement scheme for fitting ssDNA structures to experimental SAXS data. Through test cases and experimental examples, we have shown that the method is a promising and flexible way to determine conformational distributions associated with ssDNA's in solution. Furthermore, by pairing EOM selection with an iteratively refining pool, we have shown that differences in mean backbone shape and chain composition are distinguishable when applied to homopolymers with disparate stacking propensities. While this work focused on homopolymers of ssDNA, future efforts will extend the modeling technique to mixed sequence ssNAs (RNA or DNA). Additionally, the scheme could naturally be reworked to incorporate WAXS data, enabling further refining of the model structures. This style of EOM led structure selection and refinement may also be applicable to modeling more complex RNA structures and flexible proteins.

ACCESSION NUMBERS

The data and ensemble structures are available on SASBDB, as: SASDBD6 and SASDBE6.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [R01-GM085062 to L.P.]; National Science Foundation and the National Institutes of Health/National Institute of General Medical Sciences under NSF award [DMR-1332208 to CHESS]. Funding for open access charge: National Institutes of Health R01-GM085062.

Conflict of interest statement. None declared.