Structured Sparse Low-Rank Regression Model for Brain-Wide and Genome-Wide Associations

Abstract

With the advances of neuroimaging techniques and genome sequences understanding, the phenotype and genotype data have been utilized to study the brain diseases (known as imaging genetics). One of the most important topics in image genetics is to discover the genetic basis of phenotypic markers and their associations. In such studies, the linear regression models have been playing an important role by providing interpretable results. However, due to their modeling characteristics, it is limited to effectively utilize inherent information among the phenotypes and genotypes, which are helpful for better understanding their associations. In this work, we propose a structured sparse low-rank regression method to explicitly consider the correlations within the imaging phenotypes and the genotypes simultaneously for Brain-Wide and Genome-Wide Association (BW-GWA) study. Specifically, we impose the low-rank constraint as well as the structured sparse constraint on both phenotypes and phenotypes. By using the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset, we conducted experiments of predicting the phenotype data from genotype data and achieved performance improvement by 12.75 % on average in terms of the root-mean-square error over the state-of-the-art methods.

1 Introduction

Recently, it has been of great interest to identify the genetic basis (e.g., Single Nucleotide Polymorphisms: SNPs) of phenotypic neuroimaging markers (e.g., features in Magnetic Resonance Imaging: MRI) and study the associations between them, known as imaging-genetic analysis. In the previous work, Vounou et al. categorized the association studies between neuroimaging phenotypes and genotypes into four classes depending on both the dimensionality of the phenotype being investigated and the size of genomic regions being searched for association [13]. In this work, we focus on the Brain-Wide and Genome-Wide Association (BW-GWA) study, in which we search non-random associations for both the whole brain and the entire genome.

The BW-GWA study has a potential benefit to help discover important associations between neuroimaging based phenotypic markers and genotypes from a different perspective. For example, by identifying high associations between specific SNPs and some brain regions related to Alzheimer’s Disease (AD), one can utilize the information of the corresponding SNPs to predict the risk of incident AD much earlier, even before pathological changes begin. This will help clinicians have much time to track the progress of AD and find potential treatments to prevent the AD. Due to the high-dimensional nature of brain phenotypes and genotypes, there were only a few studies for BW-GWA [3,8]. Conventional methods formulated the problem as Multi-output Linear Regression (MLR) to estimate the coefficients independently, thus resulting in unsatisfactory performance. Recent studies were mostly devoted to conduct dimensionality reduction while the results should be still interpretable at the end. For example, Stein et al. [8] and Vounou et al. [13], separately, employed t-test and sparse reduced-rank regression to conduct association study between voxel-based neuroimaging phenotypes and SNP genotypes.

In this paper, we propose a novel structured sparse low-rank regression model for the BW-GWA study with MRI features of a whole brain as phenotypes and the SNP genotypes. To do this, we first impose a low-rank constraint on the coefficient matrix of the MLR. With a low-rank constraint, we can think of the coefficient matrix decomposed by two low-rank matrices, i.e., two transformation subspaces, each of which separately transfers high-dimensional phenotypes and genotypes into their own low-rank representations via considering the correlations among the response variables and the features. We then introduce a structured sparsity-inducing penalty (i.e., an l_2,1-norm regularizer) on each of transformation matrices to conduct biomarker selection on both phenotypes and genotypes by taking the correlations among the features into account. The structured sparsity constraint allows the low-rank regression to select highly predictive genotypes and phenotypes, as a large number of them are not expected to be important and involved in the BW-GWA study [14]. In this way, our new method integrates low-rank constraint with structured sparsity constraints in a unified framework. We apply the proposed method to study the genotype-phenotype associations using the Alzheimer’s Disease Neuroimaging Initiative (ADNI) data. Our experimental results show that our new model consistently outperforms the competing methods in term of the prediction accuracy.

2 Methodology

2.1 Notations

In this paper, we denote matrices, vectors, and scalars as boldface uppercase letters, boldface lowercase letters, and normal italic letters, respectively. For a matrix X = [x_ij], its i-th row and the j-th column are denoted as xⁱ and x_j, respectively. Also, we denote the Frobenius norm and the l_2,1-norm of a matrix X as ${\Vert \mathbf{X}\Vert }_F=\sqrt{{\sum }_i{\Vert {\mathbf{x}}^i\Vert }_2^2}=\sqrt{{\sum }_j{\Vert {\mathbf{x}}^j\Vert }_2^2}$ and ${\Vert \mathbf{X}\Vert }_{2,1}={\sum }_i{\Vert {\mathbf{x}}^i\Vert }_2$, respectively. We further denote the transpose operator, the trace operator, the rank, and the inverse of a matrix X as X^T, tr(X), rank(X), and X⁻¹, respectively.

2.2 Low-Rank Multi-output Linear Regression

We denote $\mathbf{X}\in {\mathbb{R}}^{n\times d}$ and $\mathbf{Y}\in {\mathbb{R}}^{n\times c}$ matrices as n samples of d SNPs and c MRI features, respectively. We assume that there exists a linear relationship between them and thus formulate as follows:

$$\mathbf{Y}=\mathbf{XW}+\mathbf{eb}$$ (1)

where $\mathbf{W}\in {\mathbb{R}}^{d\times c}$ is a coefficient matrix, $\mathbf{b}\in {\mathbb{R}}^{1\times c}$ is a bias term, and $\mathbf{e}\in {\mathbb{R}}^{n\times 1}$ denotes a column vector with all ones. If the covariance matrix X^TX has full rank, i.e., rank(X^TX) = d, the solution of W in Eq. (1) can be obtained by the Ordinary Least Square (OLS) estimation [4] as:

$$\widehat{\mathbf{W}}={\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}^T(\mathbf{Y}-\mathbf{eb}).$$ (2)

However, the MLR illustrated in Fig. 1(a) with the OLS estimation in Eq. (2) has at least two limitations. First, Eq. (2) is equivalent to conduct mass-univariate linear models, which fit each of c univariate response variables, independently. This obviously doesn’t make use of possible relations among the response variables (i.e., ROIs). Second, neither X nor Y in MLR are ensured to have a full-rank due to noise, outliers, correlations in the data [13]. For the non-full rank (or low-rank) case of X^TX, Eq. (2) is not applicable.

Fig. 1.

Illustration of multi-output linear regression and low-rank regression.

The principle of parsimony in many areas of science and engineering, especially in machine learning, justifies to hypothesize low-rankness of the data, i.e., the MRI phenotypes and the SNP genotypes in our work. The low-rankness leads to the inequality rank(W) ≤ min(d, c) or even rank(W) ≤ min(n, d, c) in the case with limited samples. It thus allows to decompose the coefficient matrix W by the product of two low-rank matrices, i.e., W = BA^T, where $\mathbf{B}\in {\mathbb{R}}^{d\times r}$, $\mathbf{A}\in {\mathbb{R}}^{c\times r}$, and r is the rank of W. For a fixed r, a low-rank MLR model illustrated in Fig. 1(b) is formulated as:

$$\underset{\mathbf{A},\mathbf{B},\mathbf{b}}{\min }{\Vert \mathbf{Y}-{\mathbf{XBA}}^T-\mathbf{eb}\Vert }_F^2.$$ (3)

The assumption of the existence of latent factors in either phenotypes or genotypes has been reported, making imaging-genetic analysis gain accurate estimation [1,15]. Equation (3) may achieve by seeking the low-rank representation of phenotypes and genotypes, but not producing interpretable results and also not touching the issues of non-invertible X^TX and over-fitting. Naturally, a regularizer is preferred.

2.3 Structured Sparse Low-Rank Multi-output Linear Regression

From a statistical point of view, a well-defined regularizer may produce a generalized solution, and thus resulting in stable estimation. In this section, we devise new regularizers for identifying statistically interpretable BW-GWA.

The high-dimensional feature matrix often suffers from multi-collinearity, i.e., lack of orthogonality among features, which may lead to the singular problem and the inflation of variance of coefficients [13]. In order to circumvent this problem, we introduce an orthogonality constraint on A to Eq. (3). In the BWGWA study, there are a large number of SNP genotypes or MRI phenotypes, some of them may not be related to the association analysis between them. The unuseful SNP genotypes (or MRI phenotypes) may affect the extraction of r latent factors of X (or Y). In these cases, it is not known with certainty which quantitative phenotypes or genotypes provide good estimation to the model.

As human brain is a complex system, brain regions may be dependently related to each other [3,14]. This motivates us to conduct feature selection via structured sparsity constraints on both X (i.e., SNPs) and Y (i.e., brain regions) while conducting subspace learning via the low-rank constraint. The rationale of using a structured sparsity constraint (e.g., an l_2,1-norm regularizer on A, i.e., ∥A∥_2,1) is that it effectively selects highly predictive features (i.e., discard ing the unimportant features from the model) by considering the correlations among the features. Such a process implies to extract latent vectors from ‘purified data’ (i.e., the data after removing unuseful features by conducting feature selection) or conduct feature selection with the help of the low-rank constraint.

By applying the constraints of orthogonality and structured sparsity, Eq. (3) can be rewritten as follows:

$$\underset{\mathbf{A},\mathbf{B},\mathbf{b},r}{\min }{\Vert \mathbf{Y}-{\mathbf{XBA}}^T-\mathbf{eb}\Vert }_F^2+\alpha {\Vert \mathbf{B}\Vert }_{2,1}+\beta {\Vert \mathbf{A}\Vert }_{2,1},\mathrm{s}.\mathrm{t}.,{\mathbf{A}}^T\mathbf{A}=\mathbf{I}.$$ (4)

Clearly, the l_2,1-norm regularizers on B and A penalize coefficients of B and A in a row-wise manner for joint selection or un-selection of the features and the response variables, respectively.

Compared to sparse Reduced-Rank Regression (RRR) [13] that exploits regularization terms of l₁-norm on B and A to sequentially output a vector of either B or A, thus leading to suboptimal solutions of B and A, our method panelizes l_2,1-norm on BA^T and A to explicitly conduct feature selection on X and Y. Furthermore, the orthogonality constraint on A helps avoid the multi-collinearity problem, and thus simplifies the objective function to only optimize B (instead of BA^T) and A.

Finally, after optimizing Eq. (4), we conduct feature selection by discarding the features (or the response variables) whose corresponding coefficients (i.e., in B or A) are zeros in the rows.

3 Experimental Analysis

We conducted various experiments on the ADNI dataset (‘www.adni-info.org’) by comparing the proposed method with the state-of-the-art methods.

3.1 Preprocessing and Feature Extraction

By following the literatures [9,11,20], we used baseline MRI images of 737 subjects including 171 AD, 362 mild cognitive impairments, and 204 normal controls. We preprocessed the MRI images by sequentially applying spatial distortion correction, skull-stripping, and cerebellum removal. We then segmented images into gray matter, white matter, and cerebrospinal fluid, and further warped them into 93 Regions Of Interest (ROIs). We computed the gray matter tissue volume in each ROI by integrating the gray matter segmentation result of each subject. Finally, we acquired 93 features for one MRI image.

The genotype data of all participants were first obtained from the ADNI 1 and then genotyped using the Human 610-Quad BeadChip. In our experiments, 2,098 SNPs, from 153 AD candidate genes (boundary: 20 KB) listed on the AlzGene database (www.alzgene.org) as of 4/18/2011, were selected by the standard quality control (QC) and imputation steps. The QC criteria includes (1) call rate check per subject and per SNP marker, (2) gender check, (3) sibling pair identification, (4) the Hardy-Weinberg equilibrium test, (5) marker removal by the minor allele frequency, and (6) population stratification. The imputation step imputed the QC?ed SNPs using the MaCH software.

3.2 Experimental Setting

The comparison methods include the standard regularized Multi-output Linear Regression (MLR) [4], sparse feature selection with an l_2,1-norm regularizer (L21 for short) [2], Group sparse Feature Selection (GFS) [14], sparse Canonical Correlation Analysis (CCA) [6,17], and sparse Reduced-Rank Regression (RRR) [13]. The former two are the most widely used methods in both statistical learning and medical image analysis, while the last three are the state-of-the-art methods in imaging-genetic analysis. Besides, we define the method ‘Baseline’ by removing the third term (i.e., β∥A∥_2,1) in Eq. (4) to only select SNPs using our model.

We conducted a 5-fold Cross Validation (CV) on all methods, and then repeated the whole process 10 times. The final result was computed by averaging results of all 50 experiments. We also used a 5-fold nested CV to tune the parameters (such as α and β in Eq. (4)) in the space of {10⁻⁵, 10₋₄, …, 10⁴, 10⁵} for all methods in our experiments. As for the rank of the coefficient matrix W, we varied the values of r in {1, 2, …, 10} for our method.

By following the previous work [3,14], we picked up the top {20, 40, …, 200} SNPs to predict test data. The performance of each experiment was assessed by Root-Mean-Square Error (RMSE), a widely used measurement for regression analysis, and ‘Frequency’ (∈ [0, 1]) defined as the ratio of the features selected in 50 experiments. The larger the value of ‘Frequency’, the more likely the corresponding SNP (or ROI) is selected.

3.3 Experimental Results

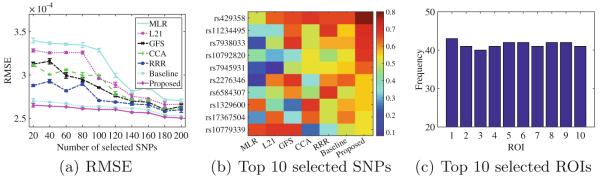
We summarized the RMSE performances of all methods in Fig. 2(a), where the mean and standard deviation of the RMSEs were obtained from the 50 (5-fold CV × 10 repetition) experiments. Figure 2(b) and (c) showed, respectively, the values of ‘Frequency’ of the top 10 selected SNPs by the competing methods and the frequency of the top 10 selected ROIs by our method.

Fig. 2.

(a) RMSE with respect to different number of selected SNPs of all methods; (b) Frequency of top 10 selected SNPs by all methods; and (c) Frequency of the top 10 selected ROIs by our method in our 50 experiments. The name of the ROIs (indexed from 1 to 10) are middle temporal gyrus left, perirhinal cortex left, temporal pole left, middle temporal gyrus right, amygdala right, hippocampal formation right, middle temporal gyrus left, amygdala left, inferior temporal gyrus right, and hippocampal formation left.

Figure 2(a) discovered the following observations: (i) The RMSE values of all methods decreased with the increase of the number of selected SNPs. This is because the more the SNPs, the better performance the BW-GWA study is, in our experiments. (ii) The proposed method obtained the best performance, followed by the Baseline, RRR, GFS, CCA, L21, and MLR. Specifically, our method improved by on average 12.75 % compared to the other competing methods. In the paired-sample t-test at 95 % confidence level, all p-values between the proposed method and the comparison methods were less than 0.00001. Moreover, our method was considerably stable than the comparison methods. This clearly manifested the advantage of the proposed method integrating a low-rank constraint with structured sparsity constraints in a unified framework. (iii) The Baseline method improved by on average 8.26 % compared to the comparison methods and the p-values were less than 0.001 in the paired-sample t-tests at 95 % confidence level. This manifested that our model without selecting ROIs (i.e., Baseline) still outperformed all comparison methods. It is noteworthy that our proposed method improved by on average 4.49 % over the Baseline method and the paired-sample t-tests also indicated the improvements were statistically significant difference. This verified again that it is essential to simultaneously select a subset of ROIs and a subset of SNPs.

Figure 2(b) indicated that phenotypes could be affected by genotypes in different degrees: (i) The selected SNPs in Fig. 2(b) belonged to the genes, such as PICALM, APOE, SORL1, ENTPD7, DAPK1, MTHFR, and CR1, which have been reported as the top AD-related genes in the AlzGene website. (ii) Although we know little about the underlying mechanisms of genotypes in relation to AD, but Fig. 2(b) enabled a potential to gain biological insights from the BW-GWA study. (iii) The selected ROIs by the proposed method in Fig. 2(c) were known to be highly related to AD in previous studies [10,12,19]. It should be noteworthy that all methods selected ROIs in Fig. 2(c) as their top ROIs but with different probability.

Finally, our method conducted the BW-GWA study to select a subset of SNPs and a subset of ROIs, which were also known in relation to AD by the previous state-of-the-art methods. The consistent performance of our methods clearly demonstrated that the proposed method enabled to conduct more statistically meaningful BW-GWA study, compared to the comparison methods.

4 Conclusion

In this paper, we proposed an efficient structured sparse low-rank regression method to select highly associated MRI phenotypes and SNP genotypes in a BW-GWA study. The experimental results on the association study between neuroimaging data and genetic information verified the effectiveness of the proposed method, by comparing with the state-of-the-art methods.

Our method considered SNPs (or ROIs) evenly. However, SNPs are naturally connected via different pathways, while ROIs have various functional or structural relations to each other [6,7]. In our future work, we will extend our model to take the interlinked structures within both genotypes and incomplete multi-modality phenotypes [5,16,18] into account for further improving the performance of the BW-GWA study.