Laser particle stimulated emission (LASE) microscopy

Abstract

We introduce an optical microscopy technique that utilizes micro- or nano-lasers embedded in a sample as imaging probes. The narrow spectra and nonlinear power dependence of stimulated emission from the laser particles yield optical sectioning, sub-diffraction resolution, and low out-of-focus background. A proof-of-concept is demonstrated using perovskite nanowires.

Stimulated emission allows light amplification and build-up of cavity modes in lasers. While numerous types of lasers are available, recent advances in micro-fabrications and gain materials made it possible to realize lasers with micro- or nano-sized cavities. Stand-alone lasers, such as micro-spheres containing optically excitable gain elements, may be injected or embedded in other materials [1,2]. For example, micro-lasers have been recently incorporated in biological cells [3,4]. Moreover, exploiting plasmonic resonance, nanoscale lasers have been demonstrated [5–7]. These micro- and nano-lasers may serve as internal light sources, generating coherent stimulated emission with distinct properties from spontaneous emission. Here we describe the measurement of the output emission from such laser particles using laser-scanning optical microscopy. We demonstrate that such a system offers a unique set of capabilities including super resolution, 3-dimensional optical sectioning, and low out-of-focus background, all of which are desirable for imaging thick samples such as biological tissues.

Fluorescence microscopy is an established, powerful tool for studying biological samples, such as cells and tissues. This technique uses a pump beam that excites fluorescent probes, such as organic dyes or semiconductor quantum dots, and their spontaneous emission (fluorescence) is detected. The principle of stimulated emission has been implemented in optical microscopy in two schemes. First, stimulated emission depletion (STED) microscopy [8] employs an intense doughnut-shaped beam that depletes the excited fluorophores via stimulated emission transition to the ground state. This allows only un-depleted fluorophores at the null center of the depletion beam to generate fluorescence, which results in sub-diffraction resolution. Second, pump-and-probe techniques are used to measure the amplification of a probe beam via stimulated emission processes. This scheme has been implemented in stimulated emission microscopy to visualize chromophores with low fluorescence quantum yields [9]. Stimulated Raman scattering microscopy measures the optical gain in a Stokes probe beam from the pump via stimulated Raman effects [10].

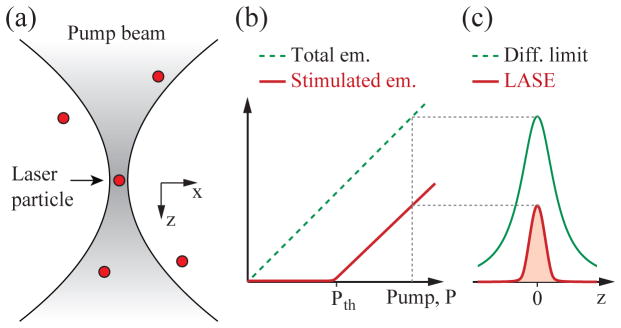
Our proposed microscopy is different from these schemes in that it uses laser particles and stimulated emission from them within a sample. We refer to this technique as Laser pArticle Stimulated Emission (LASE) microscopy. The signal, background noise, and resolution of LASE microscopy are different from any existing microscopy techniques, as described below. Consider, as illustrated in Fig. 1(a), an excitation beam with numerical aperture, NA, illuminating laser particles that are distributed in space and have a size smaller than the optical wavelength, λ. For a Gaussian-profile beam, the 1/e beam radius is given by w(z) = w₀(1 + (z/z_R)²)^1/2, where w₀ = λ/(π ·NA) is the spot size at the focus at z = 0, and z_R = w₀/NA is the Rayleigh length. The pump intensity is expressed as I_p(x, y, z) = I₀{w₀/w(z)}² ·exp[−(x² + y²)/w²(z)]·exp(−εz), where ε is an attenuation coefficient of the pump beam in the sample.

FIG. 1.

The principe of LASE microscopy (a) Laser particles excited by a tightly focused optical pump beam. (b) Output energy from a laser particle as a function of pump intensity. The laser output increases steeply at pump energy above the threshold (P_th). (c) The PSF of laser emission (red line) in comparison to the traditional diffraction-limited PSF of fluorescence detection (green line). Both the resolution and signal-to-background contrast is superior in LASE microscopy.

The number of photons in the laser cavity modes of the laser as a function of a pump rate, P, follows a typical nonlinear threshold curve, as illustrated in Fig. 1(b) (red curve). Figure 1(c) plots the stimulated emission output from a laser particle as a function of the particle position along z. This output profile represents the axial-scan point spread function (PSF) of signal generation, and indicates that lasing is achieved only at a narrow region along z, providing depth sectioning. The axial resolution is below the diffraction limit, due to nonlinearity of signal generation given by lasing threshold. Since the lasing cavity modes exhibit defined spectral peaks, it is possible to determine the magnitude of the stimulated emission output. Outside the focus, the magnitude of stimulated emission is negligible, which yields a low out-of-focus background.

These features compare favorably with two representative optical sectioning techniques: confocal and two-photon microscopy. Confocal laser scanning microscopy uses single-photon absorption and generates fluorescence both in and outside the focal volume, but detects only the signal generated from the focus by using a pinhole. Two-photon microscopy uses nonlinear two-photon absorption to generate fluorescence primarily at the focal volume [11]. LASE microscopy uses single-photon absorption (although two-photon pumping is also possible), can generate stimulated emission only at the focal volume, and does not require a tight pinhole. This combination of advantageous features can allow efficient generation and collection of signals with sub-diffraction limit resolution. Another advantageous feature is the low out-of-focus background, which may offer enhanced imaging depths in scattering samples [12].

Imagine an infinitely small laser located at x = y = z = 0. The general rate equations of a 3- or 4-level system can be written as [13]:

$$\frac{{dN}_1(t)}{dt}=P(t)-\frac{\beta N_1(t)q(t)}{\tau }-\frac{N_1(t)}{\tau }$$ (1)

$$\frac{dq(t)}{dt}=\frac{\beta N_1(t)q(t)}{\tau }+\frac{\beta N_1(t)}{\tau }-\frac{q(t)}{{\tau }_c}$$ (2)

where N₁(t) is the number of excited fluorophores (or atoms), q(t) the number of photons in the cavity modes, and P(t) the pump rate. τ is the spontaneous emission lifetime, and τ_c the cavity lifetime (or inverse of cavity decay rate). β is the spontaneous emission factor that corresponds to the fraction of spontaneous emission coupled into the cavity modes [14,15]. The pump rate can be expressed as P(t) = QY σ_aI_p(t)N₀(t), where QY, σ_a, and N₀(t) are the quantum yield, absorption cross-section, and number of fluorophores in the ground state, respectively. In a steady state (i.e. dN₁/dt = dq/dt = 0), the emission rate of the cavity modes is given by:

$$P_l=q/{\tau }_c=P_{th}·(p-1+\sqrt{{(p-1)}^2+4\beta p})/2$$ (3)

where P_th ≡ (β τ _c)⁻¹ is the threshold pump rate and p ≡ P/P_th is the normalized pump power at the laser. The laser output curve is depicted schematically in Fig. 1b. A smaller β value results in a sharper kink at the threshold.

As the focus of a pump beam is scanned laterally (x, y) or axially (z), the laser output power is changed. The axial-scan profile calculated from (3) is plotted in Fig. 2(a) at two pump levels, p = 1.05 and 3, respectively, for a specific β of 10⁻⁵. The scan profile of fluorescence emission, which is identical to the pump profile, is also shown for comparison. We define a resolution enhancement factor, Δ_LASE/Δ₀, where Δ_LASE and Δ₀ are the full-width half-maximum (FWHM) values of the laser output and fluorescence profiles, respectively. Figure 2(b) plots the normalized resolution, Δ_LASE/Δ₀, as a function of p for β = 10⁻² and 10⁻⁵ for axial resolution. Lateral resolution is similar (not shown). A heuristic approximate form of the exact solutions for both axial and lateral resolutions is:

$${\mathrm{\Delta }}_{\mathit{LASE}}/{\mathrm{\Delta }}_0\approx \sqrt{1-\frac{2}{p+1}(1-\sqrt{\beta })}(p>1).$$ (4)

FIG. 2.

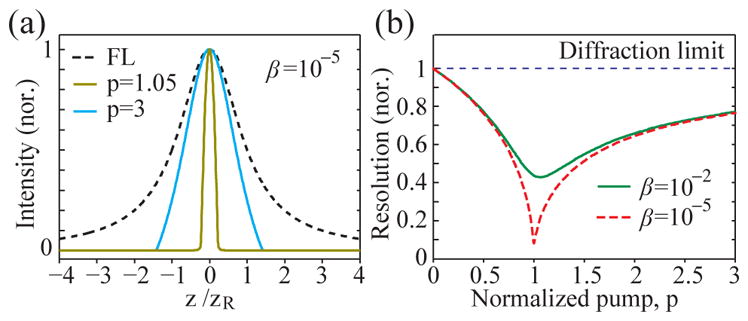
Numerical simulation of LASE microscopy (a) Axial PSF of wide-field fluorescence (FL) versus LASE microscopy at pump rates at the lasing threshold (p=1) and of 300% higher than lasing threshold (p=3). (b) Normalized axial resolution, Δ_LASE/Δ₀, for β = 10⁻² (green, solid) and 10⁻⁵ (red, dashed).

The enhancement is the maximum just above the threshold at p = 1, where Δ_LASE/Δ₀ ≈ β^0.25. As p increases, the enhancement decreases and the resolution converges to the diffraction limit. At β → 0, ${\mathrm{\Delta }}_{\mathit{LASE}}/{\mathrm{\Delta }}_0\to {(\frac{p-1}{P+1})}^{0.5}$. As β approaches to 1 (i.e. threshold-less laser), the resolution becomes the same as the diffraction limit.

Far from the focus the pump intensity is below the threshold, and the output rate of the laser modes is given by P_l( p≪1) ≈ βP_th[ p + (1− β )p²]. The laser output below threshold is predominantly spontaneous emission. We define a stimulated emission output rate, P_SE = P_l − βN₁/τ, where the contribution of spontaneous emission to the cavity modes was subtracted from the laser emission rate. In the steady state, P_SE = P − N₁/τ. The left side of this equation describes P_l the output rate of the cavity modes minus the contribution of spontaneous emission to the cavity modes and; this corresponds to a stimulated emission output rate, P_SE. Outside the focus where p ≪ 1, the stimulated emission background, P_SE,b, below threshold scales with P² (q ∝ P, N₁ ∝ P)

$$P_{SE,b}\equiv P_l-\frac{\beta N_1}{\tau }\approx \beta P_{th}{p}^2.$$ (5)

When the excitation beam is focused with high NA, the stimulated emission from lasers located outside the focus decreases with the square of the pump beam area, resulting in a low out-of-focus background. The ratio of the background at z to the laser signal at z = 0 or a depth-resolved background-to-signal ratio, BSR(z), is given by

$$\mathit{BSR}(z)\equiv \frac{\int P_{SE,b}(x,y,z)dxdy}{\int P_l(z=0)dxdy}\approx \frac{\beta P_{th}{p}^2}{P_l}\frac{w_0^2}{w^2(z)}{\mathrm{e}}^{-2\epsilon z},$$ (6)

where p is measured at the focus, z = 0. For small β, we find the ratio to be minimized for all depths at p = 2, where $\mathit{BSR}=4\beta ·w_0^2/w^2(z){\mathrm{e}}^{-2\epsilon z}$.

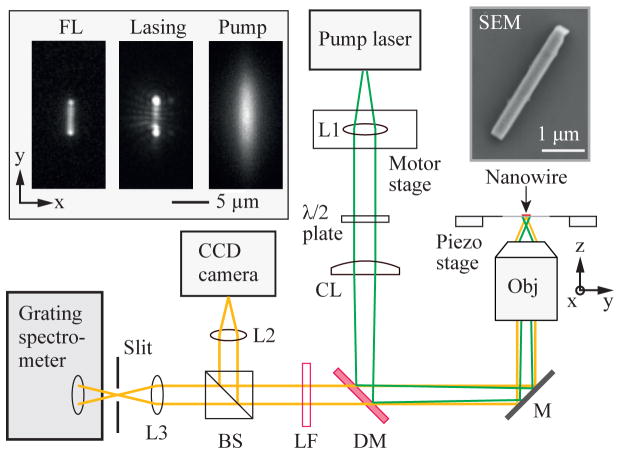
We constructed an inverted imaging setup similar to a line-confocal hyperspectral fluorescence microscope, as depicted in Fig. 3. As laser particles, we used lead iodide perovskite (CH₃NH₃PbI₃) nanowires that were grown to typical widths of 300–500 nm and lengths of 3–7 μm [16]. The samples were transferred to a slide glass and sealed from air with a cover glass optical epoxy to prevent degradation by moisture and oxygen.

FIG. 3.

Schematic of the experimental setup. L1, L2, L3: spherical lenses, λ/2: half-wave plate, CL: cylindrical lens, DM: dichroic mirror, M: mirror, Obj: objective lens (NA=0.8, water immersion), LF: long pass filter, and BS: Beam splitter. SEM: a scanning-electron-microscope image of a typical lead iodide perovskite nanowire. Insets (from left to right): a typical fluorescence image of a perovskite nanowire below threshold, a stimulated emission image above threshold of the nanowire, and a pump beam profile recorded in the CCD camera.

Given the long shape of nanowires, we configured a pump beam to have a matching elongated shape and measured scan profiles across the short axes of nanowires. The pump light source was a microchip laser emitting at 532 nm with a repetition rate of 5 kHz and a pulse duration of ~2.5 ns, slightly longer than the fluorescence lifetime (τ ≈ 2 ns) of perovskite [16]. The objective lens was a 0.8-NA, 40× water immersion lens (Nikon). The back aperture of the objective lens was under-filled, and a cylindrical lens (CL; f = 500 mm) was employed to make an elliptical pump beam profile at the focus with a FWHM of 2.4 μm along the x-axis and 9.5 μm in the y-axis, which illuminates the entire nanowire. The nanowire on a sample stage was oriented parallel to the major (y) axis of the pump beam. The polarization axis of the pump beam was aligned orthogonal to the long (y) axis of the nanowire, at which the threshold intensity was the lowest. The pump beam was scanned along the x-axis by translating a collimation lens (L1) resulting to a 35-nm step resolution in the imaging plane. The output emission was directed, through a dichroic filter, to a charge-coupled device (CCD) camera (Luca, Andor) for wide-field imaging and a diffraction-grating-based CCD spectrometer (Shamrock, Andor) for spectral analysis. The entrance slit of the spectrometer was oriented along the long-axis (y) of the nanowire so that the emission from the entire nanowire was collected by the spectrometer. The spectral resolution was ~ 1 nm.

The inset of Fig. 3 shows a pump beam profile imaged on the CCD, and fluorescence and laser emission images from a 5–μm-long nanowire, collected through a long-pass filter (LF) on the CCD, at pump energy levels below and above threshold, respectively. The laser emission profile exhibits bright spots at both ends, indicating longitudinal laser oscillation, and characteristic interference patterns of coherent laser emission. The polarization states of the laser output at the detector plane were nearly parallel to the short (x) axis [17].

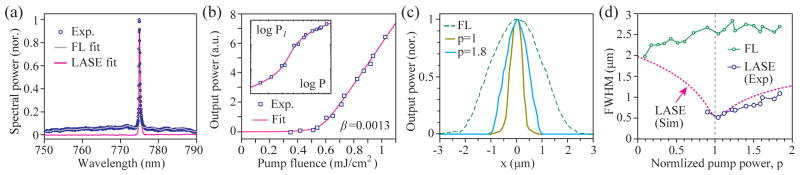
Figure 4(a) shows a typical output spectrum from the nanowire above threshold. The spectrum was decomposed into broadband fluorescence background (grey curve in Fig. 4a), which has the same profile as the fluorescence spectrum obtained at a low pump power, and a narrowband stimulated emission component (magenta curve). The laser power was measured by integrating the stimulated emission spectrum. Figure 4(b) shows the measured output as a function of pump energy. The data reveals a well-defined lasing threshold at a pump pulse energy of 0.58 mJ/cm². The best curve fit based on (3) was obtained with β = 1.3×10⁻³.

FIG. 4.

LASE imaging of a nanowire laser. (a) A typical laser output spectrum (circles). Curves: the curve fit for fluorescence background (gray) and the stimulated-emission laser output spectrum (magenta) calculated by subtracting the fluorescence background from the measured spectrum. (b) The stimulated emission output power (squares) measured as a function of the pump pulse fluence level. Line: a curve fit based on Eq. (3). Inset: same plot in a log-log scale. (c) Representative pump-beam scan profiles of the nanowire, for fluorescence background at p < 1 (green dashed line) and stimulated emission at p = 1 (gold) and p = 1.8 (cyan). (d) Measured FWHM of laser emission profiles (blue circles) and fluorescence profiles (green circles), and numerical simulation data (magenta, dotted line).

Figure 4(c) shows the x-scan profile of the nanowire at two different pump levels, p = 1 and 1.8. Significant narrowing of the laser profiles compared to the fluorescence scan profile are evident. The FWHM of laser emission Δ_LASE is about 520 nm at p = 1 and 1.1 μm at p = 1.8, which are about 5 and 2.3 times, respectively, smaller than the diffraction-limited resolution (FWHM: ~2.5 μm) measured from the scan profile of fluorescence emission at p = 1. The measured FWHM of stimulated emission had the minimum indeed at p ≈ 1 and increased modestly with pump pulse energy, as shown in Fig. 4(d). The stimulated emission profile is given by the convolution of optical resolution and the lasing cavity mode profiles. Assuming a cavity mode size of 300 nm, Δ_LASE = ~420 nm and thus Δ_LASE/Δ₀ = ~5.9 at p = 1, and Δ_LASE/Δ₀ = ~2.3 at p = 1.8. A fit curve based on numerical simulation using the actual pump profile and an assumed cavity mode size (5 μm × 0.3 μm) showed good agreement with the experimental data. The slight increase of the fluorescence FWHM with increasing pump is presumably due to pump-induced fluorescence saturation or gain depletion (i.e. N₀ decreases with q).

Similar resolution enhancements by a factor ~5 were measured consistently from numerous different nanowires, with similar lengths and β values. The opening width of the confocal slit in front of the spectrometer affected resolution only modestly, through its influence on the laser output measurement leading to slightly different β values [17].

Furthermore, to test different light collection geometry we changed the orientations of nanowires and the pump beam and translated the sample stage (along the y-axis) with respect to a fixed pump beam (major axis along the x-axis). The emission from nanowires was projected horizontally onto the spectrometer, through the slit either widely open (100–300 μm) to collect the entire emission or narrowly closed (10 μm) to image only a small segment along the nanowire. For all cases, we obtained similar experimental results. For example, the smallest β value we obtained was ~1.4 × 10⁻⁴, for which the FWHM of stimulated emission was 310 nm at p = 1 and 490 nm for p = 1.4, whereas the fluorescence profile had a FWHM of ~2.2 μm.

We have demonstrated the principle and experimental proof-of-concept of LASE microscopy based on the detection of stimulated emission from standalone submicron-size lasers. The optical system does not need of a pinhole or complex illumination or detection schemes. Besides perovskite nanowires, other types of semiconductor photonic lasers and plasmonic lasers are candidates for laser particles [18–19]. Nano-lasers are desirable due to their sub-resolution sizes and in fact essential for super resolution nanoscopy. For deep tissue imaging, however, micron-sized lasers may be more attractive because of the stronger signals they can generate and relatively easy spectral tunability. In addition to stimulated emission, the principle of LASE microscopy can apply to other spontaneous emission particles with nonlinear responses to the pump energy, such as exciton-polariton lasers [20]. Our work warrants the development of various stand-alone, photonic, plasmonic, and polariton laser particles. We note that LASE microscopy is not well suited to determine the physical structure of micro- and nano-lasers, although it may be useful to investigate laser modes. The idea behind future applications of LASE microscopy is to use laser particles smaller than sub-diffraction resolution, where they act as nearly point light sources (like single quantum dots [21]). The output characteristics of laser particles within a sample, such as in intracellular space, are generally sensitive to variations in the local environment, which is useful for local sensing as well as imaging. Furthermore, the narrowband nature of laser emission should allow a large number of laser particles with different output spectra to be multiplexed for labeling and tracking. With the advance of laser particles, we expect LASE microscopy may prove useful in a wide range of applications in deep tissue imaging, biomedical investigations, and material sciences.