Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Apr 11.
Published in final edited form as: J Biomech. 2017 Feb 21;55:71–77. doi: 10.1016/j.jbiomech.2017.02.008

Contribution of muscle short-range stiffness to initial changes in joint kinetics and kinematics during perturbations to standing balance: a simulation study

Friedl De Groote 1,*, Jessica L Allen 2, Lena H Ting 2,3
PMCID: PMC5436583  NIHMSID: NIHMS857909  PMID: 28259465

Abstract

Simulating realistic musculoskeletal dynamics is critical to understanding neural control of muscle activity evoked in sensorimotor feedback responses that have inherent neural transmission delays. Thus, the initial mechanical response of muscles to perturbations in the absence of any change in muscle activity determines which corrective neural responses are required to stabilize body posture. Muscle short-range stiffness, a history-dependent property of muscle that causes a rapid and transient rise in muscle force upon stretch, likely affects musculoskeletal dynamics in the initial mechanical response to perturbations. Here we identified the contributions of short-range stiffness to joint torques and angles in the initial mechanical response to support surface translations using dynamic simulation, respectively. We developed a dynamic model of muscle short-range stiffness to augment a Hill-type muscle model. Our simulations show that short-range stiffness can provide stability against external perturbations during the neuromechanical response delay. Assuming constant muscle activation during the initial mechanical response, including muscle short-range stiffness was necessary to account for the rapid rise in experimental sagittal plane knee and hip joint torques that occurs simultaneously with very small changes in joint angles and reduced root mean square errors between simulated and experimental torques by 56% and 47%, respectively. Moreover, forward simulations lacking short-range stiffness produced unreasonably large joint angle changes during the initial response. Using muscle models accounting for short-range stiffness along with other aspects of history-dependent muscle dynamics may be important to advance our ability to simulate inherently unstable human movements based on principles of neural control and biomechanics.

Keywords: posture, muscle dynamics, musculoskeletal modeling, dynamic optimization, forward simulations

INTRODUCTION

Simulating realistic musculoskeletal dynamics is critical to understanding neural control of muscle activity in sensorimotor feedback responses. Musculoskeletal responses to external perturbations are influenced by the initial mechanical response of the musculoskeletal system that precedes neurally-mediated changes in muscle activity (Horak and Macpherson, 1999; Ting et al., 2009). In particular, muscle short-range stiffness, a history-dependent property of muscles that is absent in Hill-type muscle models, likely plays an important role, yet its contributions to stabilizing musculoskeletal dynamics are not well understood.

In perturbed standing balance where baseline muscle activity is constant, the initial response to perturbations can be attributed solely to intrinsic mechanical properties of the body. Joint torques generated during the initial mechanical response to perturbations of standing are substantial despite minimal joint angle changes (Runge et al., 1999). However, the first small change in muscle activity due to spinal reflexes only occurs at ~50ms (Carpenter et al., 1999), and much larger balance-correcting effects are evoked ~100ms after perturbation onset (Horak and Macpherson, 1996). We refer to the period preceding neural changes in muscle activity at 50ms as the initial mechanical response.

Short-range stiffness causes a rapid increase in muscle force upon muscle fiber stretch (Nichols and Houk, 1976), but its contributions to perturbed standing cannot be easily studied through experimentation. Short-range stiffness is observed when activated isometric muscle fibers are stretched and has been attributed to deformation of attached muscle cross-bridges (Campbell and Lakie, 1998). Due to actin-myosin overlap, short-range stiffness is highest at optimal fiber length (Campbell, 2014). In isolated muscle fibers, a stretch of less than a nanometer per half sarcomere length rapidly increases force to at least twice the pre-stretch isometric force, followed by a force plateau (Getz et al., 1998). Consistent with the effects of short-range stiffness, substantial increases in ankle joint torques in the absence of change in muscle activity are observed for joint angle perturbations smaller than 1° (Loram et al., 2007a–b).

We currently lack dynamic simulations of whole-body movement that can be used to identify the functional role of short-range stiffness in perturbation responses. A phenomenological model in which short-range stiffness was proportional to the initial isometric force in each muscle (Cui et al., 2008) has been used to identify contributions of short-range stiffness to instantaneous arm endpoint stiffness in static postures using a musculoskeletal model of the arm (Hu et al. 2011). However, to our knowledge, models of short-range stiffness have yet to be implemented in dynamic musculoskeletal simulations of movement. Simulating muscle dynamics is computationally challenging and expensive, and therefore often neglected when computing muscle inputs that reproduce observed joint torques (Crowninshield and Brand, 1981).

Our recently-published dynamic optimization method based on direct collocation reduces the sensitivity of simulations to forward integration errors, allowing more efficient simulations of muscle dynamics in solving the muscle redundancy problem (De Groote et al., 2016). Solving skeletal and muscle dynamics independently further facilitates the rapid exploration of dynamic models of muscle force generation.

Here we identified the contributions of short-range stiffness to joint torques and angles in the initial mechanical response to perturbed standing using dynamic simulation. We developed a dynamic model of muscle short-range stiffness to augment a Hill-type muscle model. Dynamic optimization was used to assess whether a feasible set of muscle activations could reproduce the experimental joint torques. Joint torques during the initial mechanical response could only be reproduced with the addition of muscle short-range stiffness if muscle activations were assumed constant. Further, forward simulations were used to assess the effect of different models of muscle dynamics on joint kinematics. Forward simulations lacking short-range stiffness exhibit unrealistically large changes in joint angles in the initial mechanical responses. Our simulations provide evidence that short-range stiffness provides stability against perturbations before long-latency balance-correcting responses can intervene.

METHODS

To assess the contribution of short-range stiffness to changes in joint torques during the initial mechanical response to perturbation, we first performed inverse dynamics (ID) analyses of perturbed standing balance during forward and backward translations of the support surface using a lower-limb musculoskeletal model in OpenSim (Delp et al., 2007; Fig. 1, gray boxes). We then identified constant muscle activation levels that accounted for the ID torques during the initial mechanical response using simulations of Hill-type muscle models without and with short-range stiffness (Fig. 1). To assess the effect of short-range stiffness on joint angle changes, we performed forward dynamics simulations driven by the computed muscle activations.

Figure 1.

Figure 1

Open in a new tab

Procedure for computing constant muscle activations that account for inverse dynamics joint torques during the initial mechanical response. OpenSim (Delp et al., 2007; gray blocks) was used to generate inverse dynamics joint torques and muscle-tendon lengths, velocities, and moment arms from measured data. We then used dynamic optimization to minimize a cost function consisting of a weighted sum of sum-squared joint torque tracking error and sum-squared muscle activity. During the optimizations, muscle dynamics were imposed using Hill-type muscle models both with and without the addition of short-range stiffness.

Data collection

Two healthy subjects participated in the study (S1: male, 34y; S2: male, 24y). The experimental protocol was approved by the Institutional Review Boards of Emory University and Georgia Institute of Technology. Subjects provided written, informed consent prior to participating. We analyzed perturbed standing in response to forward and backward ramp-and-hold translations (12 cm total excursion, 30 cm/s peak velocity, 0.45g peak acceleration, total duration of 500ms) administered within a block of randomized perturbations spanning multiple directions in the horizontal plane (similar to Torres-Oviedo and Ting, 2007). Subjects stood at a stance width equal to their hip width. To examine the sensitivity of our model to different initial biomechanical contexts, we also examined the response when standing at narrow (50% hip width) and wide (150% hip width) stance widths for S2 (similar to Torres-Oviedo and Ting, 2010). A total of 19 trials were analyzed across both subjects (S1: 4 forward and 3 backward, S2: 2 forward and 2 backward at each stance width).

Kinematic, kinetic, and electromyographic (EMG) data were collected. Whole-body motion was recorded at 120Hz using an 8-camera Vicon motion capture system and a custom 25 marker set. Ground reaction forces (GRFs) were collected at 1,080 Hz from two force plates (AMTI OR6-6) embedded in the platform. EMG data was collected at 1080Hz from respectively 13 and 9 surface EMG electrodes for S1 and S2. Raw EMG data were high-pass filtered at 40 Hz (4th order, zero-lag Butterworth filter), rectified, low-pass filtered 35 Hz (4th order, zero-lag Butterworth filter), and normalized to peak activity over all trials.

Data processing

Experimental data was processed using a musculoskeletal model with five degrees of freedom (three at the hip and one at the knee and ankle) and 43 muscles per leg (Delp et al., 1990). This model was scaled to the subjects’ dimensions based on marker information collected during a static trial using OpenSim’s Scale tool. Joint kinematics were calculated from the measured marker coordinates using a Kalman smoothing algorithm (De Groote et al., 2008). ID torques were calculated from joint kinematics and measured ground reaction forces using OpenSim’s Inverse Dynamics tool. Muscle-tendon lengths and moment arms were calculated from joint kinematics using OpenSim’s Muscle Analysis tool.

Computation of baseline muscle activations

Based on the assumption that changes in muscle activity are absent during the initial mechanical response to a perturbation, we computed constant baseline muscle activations that reproduce the ID torques during this period. We used a dynamic optimization approach based on direct collocation (De Groote et al., 2016) to reproduce ID torques at the ankle, knee, and hip while penalizing high levels of muscle activation by minimizing the following cost function:

minabm∫t0tf∑k=1K‖TID,k(t)−Tk(t)‖22dt+w∑m=1Mabm2, (1)

where abm is baseline activation of muscle m, M is the number of muscles in the model, t0 and tf are initial and final times of the simulation, TID,k and Tk are the ID and simulated joint torque for the kth degree of freedom, k is the number of degrees of freedom in the model, and w is a constant factor weighting the two terms in the cost function. Baseline muscle activities were bounded between 0 and 0.3 to avoid unrealistically high activity. Muscle activation and tendon force were constrained by muscle dynamics, which were determined by baseline muscle activation and recorded muscle-tendon lengths, as described below. To account for measurement errors, small deviations (<0.5mm) from the experimental muscle-tendon lengths were allowed. Simulated joint torques were obtained by multiplying and summing tendon forces and muscle moment arms:

Tk(t)=∑m=1Mdmk(t)FTm(t), (2)

where dmk is the moment arm of muscle m with respect to the kth degree of freedom and FTm is tendon force of muscle m. Note that we omitted muscle activation dynamics, since muscle activations were assumed to be constant and therefore equal muscle excitations.

Dynamic model of short-range stiffness

To create a short-range stiffness model for dynamic simulations of motion, we added a passive force component FSRS to the Hill-type model described in De Groote et al. (2016). In accordance with Cui et al. (2008), we modeled short-range stiffness to be proportional to the isometric force prior to the perturbation. In order to use this model in dynamic simulations, we also accounted for the critical stretch, i.e. the stretch at which the slope of force build-up sharply decreases (Getz et al., 2008). FSRS was defined only during muscle lengthening where the magnitude of force generation was proportional to muscle length change up to the critical stretch, δ:

FSRS={0ifΔl∼M<0γFM0abfact(l∼M)Δl∼Mif0<Δl∼M<δγFM0abfact(l∼M)δifΔl∼M>δ (3)

where γ=280 is the short-range stiffness constant, FM0 is maximal isometric muscle force, fact(l∼M) is muscle force-length relation, l∼M is fiber length normalized by optimal fiber length lMo, Δl∼M is normalized fiber stretch, and δ=5.7×10−3 is the normalized critical stretch. A smooth approximation of this model was implemented to allow the use of a gradient-based optimization method. The short range stiffness constant and critical stretch were calculated based on the stiffness (normalized force change to imposed stretch ratio of 0.208 per nm stretch per half sarcomere length) and critical stretch (7.7 nm per half sarcomere length) reported by Getz et al. (1998) using an optimal sarcomere length of 2.7 μm.

To evaluate our phenomenological model, we simulated the response to a ramp and hold muscle-tendon stretch with a duration of 50ms at a fast (0.8lMo/s) and slow (0.4lMo/s) speed. Consistent with the findings of Getz et al. (1998), the two phases of the force response were clearly observable for fast but not for slow stretches (Fig. 2).

Figure 2.

Figure 2

Open in a new tab

Example of muscle-tendon stretch responses of soleus muscle simulated with a Hill-type model augmented with short-range stiffness. (A) Imposed ramp-and-hold musculotendon stretch for at a fast speed of 0.8lM0/s (solid lines) and a slow speed of 0.4lM0/s (dashed lines) (B) Simulated tendon and (C) muscle fiber stretch. (D) Simulated ratio of tendon force with respect to pre-stretch tendon force.

Forward simulation of kinematic response

To assess the effect of short-range stiffness on the kinematic response to perturbed standing, we performed forward dynamics simulations of the initial mechanical response. A simplified musculoskeletal model was used to avoid the need for a foot-ground contact model, whose parameters would be hard to determine and might influence the results. To remove indeterminacy due to multiple ground connections, we simulated a one-legged, two-dimensional model consisting of a foot, lower leg, upper leg, and head-arms-trunk segment connected with hinge joints and actuated by nine muscles. The foot was rigidly connected to a platform that could translate with respect to the ground. Musculoskeletal geometry and muscle-tendon parameters were obtained from OpenSim’s gait10dof18musc model. Inertial parameters of the single leg’s segments were adapted to represent both legs and maximal isometric muscle forces were doubled. The model was driven by constant baseline activations calculated following the method described above using the simple model. To simulate perturbations, measured platform accelerations were applied to the platform.

Outcome measures

We first validated our assumption that muscle activity does not change during the initial mechanical response. Changes in EMG were computed with respect to the mean EMG level recorded during quiet standing in the 50ms preceding the onset of the perturbation. We quantified changes in mean EMG at three time bins during the response to perturbation (Fig. 3A): (1) the first 50ms after perturbation onset (Fig. 3A, gray shaded area), (2) 50ms to 100ms after the perturbation onset (Fig. 3A, pink shaded area), and (3) during a 50ms time bin centered around the time of peak total EMG activity 100 to 1500 ms after perturbation onset (Fig. 3A, blue vertical line).

Figure 3.

Figure 3

Open in a new tab

Experimental changes in muscle activity, joint torques, and joint angles during perturbed standing. (A) Example of EMG (top), joint torque (middle), and joint angle (bottom) trajectories during a forward support-surface perturbation in S1. Perturbation onset is at 0ms. The initial mechanical response, i.e. the period during which EMG activity does not change, is denoted by the gray and pink bars, corresponding to the responses (B) 0–50 and (C) 50–100 ms after onset of perturbation. The red line depicts the peak EMG magnitude corresponding to (D) the active response magnitudes. Changes in EMG were analyzed thirteen and nine muscles for respectively S1 and S2: gluteus medius (Gme), tensor fasciae latae (TFL), rectus femoris (RF), vastus medialis (VM), vastus lateralis (VL), semitendinosus (ST), adductor magnus (ADm), biceps femoris long head (BFl), gastrocnemius lateralis (GL), gastrocnemius medialis (GM), soleus (SOL), peroneus (PER), and tibialis anterior (TA). Absolute changes in joint torques and angles were analyzed for the five degrees of freedom of the right leg: ankle dorsiflexion (AD), knee extension (KE), hip flexion (HF), hip abduction (HA), hip endorotation (HE).

Absolute joint torque and angle changes were computed with respect to their initial value at the time of perturbation onset, and evaluated at 50ms after the perturbation onset (Fig. 3BC, end of gray shaded area), 100ms after the perturbation onset (Fig. 3BC, end of pink shaded area), and 50ms after the time of peak EMG activity to account for the electromechanical delay (Fig. 3BC, blue vertical line).

Root mean square errors (RMSE) were computed between ID joint torques and simulated joint torques based on constant muscle activation of Hill-type muscles both with and without short-range stiffness (Eq. 2). We selected constant muscle activation levels based on the optimization procedure described above that reflected an optimal tradeoff between reducing muscle effort and tracking ID torques. Therefore, we generated an optimal trade-off curve by solving the optimization problem for a series of weights, w, in the objective function (Eq. 1). We initially used the weight values at the point of highest curvature, such that any further decreases in muscle effort would have resulted in large increases in ID torque tracking errors (Boyd and Vandenberghe, 2004).

RMSE were computed between the joint angles obtained from the experimental data using the simple model and those obtained from the forward dynamic simulations using Hill-type muscles without and with short-range stiffness. To test whether increased tendon stiffness could account for the observed changes in joint torques and angles, we repeated the simulations using tendon stiffness values that were twice as large as standard values. To test the validity of the rigid connection between the feet and the platform, center of pressure locations with respect to the ankle were evaluated.

RESULTS

During the initial mechanical response, joint torques changed substantially as a result of the support surface translation whereas changes in muscle activity were absent and changes in joint kinematics were small (Fig. 3). For subject 1, mean change in normalized EMG from baseline levels was less than 5% of the maximum observed EMG value for all muscles during both the 0–50 and 50–100ms time bins after perturbation onset (Fig. 3B–C, top row). In contrast, increases of 16±5% of the maximum observed EMG value were observed across muscles during the balance correcting responses. However, relatively large changes in hip and knee sagittal plane torques were observed during the initial mechanical response 0–100ms after perturbation onset (Fig. 3B–C, middle row). For example, the changes in hip flexion torque were of comparable magnitude across all three time points. Joint angle changes were below 0.12° and 1° during respectively the first 50 and 100ms following perturbation onset, but up to several degrees in the active response (Fig. 3B–C, bottom row). Similar trends were observed in subject 2 (Fig. 3, gray bars).

Assuming constant muscle activations, a Hill-type muscle model with short-range stiffness could explain the ID torques during the initial mechanical response, whereas a Hill-type muscle model without short-range stiffness could not. During the initial mechanical response to both backward (Fig. 4A top row) and forward (Fig. 4A bottom row) perturbations, the simulated sagittal hip and knee torques were closer to experimental ID joint torques (Fig. 4A, black traces) using a Hill type model with short range stiffness (Fig. 4A, purple traces) as compared to a Hill type model without short-range stiffness (Fig. 4A, green traces). In the remaining three degrees of freedom, both models performed equally well, as only small changes in joint torque were observed (Fig. 4A). Accordingly, RMSE values averaged over all trials for both subjects were largest for the sagittal plane hip and knee torques when short-range stiffness was omitted (Fig. 4B, green bars) and were lowest when short-range stiffness was included (Fig. 4B, purple bars), regardless of the tendon stiffness value. However, extending simulation time from 50 to 100ms increased RMSE averaged over all trials and degrees of freedom by 80% to 105% for all models and subjects.

Figure 4.

Figure 4

Open in a new tab

Simulated and experimental (ID) torques during the initial mechanical response (0–50ms after perturbation onset). (A) Example of simulated and experimental torques in a backward (top) and forward (bottom) support surface translation for S1. (B) Root mean square errors (RMSE) between simulated and ID torques during the initial mechanical response for S1 (top) and S2 (bottom). RMSE were averaged over all analyzed trials and are shown along with the standard deviations. Results for the model without (green) and with (purple) short-range stiffness are shown for the simulation with Pareto optimal trade-off between ID joint torque tracking errors and muscle effort (wopt). Either the standard or high tendon stiffness kT was used. RMS errors for simulations with zero weight on minimizing muscle effort (w0) in combination with standard tendon stiffness are also shown.

Assuming constant muscle excitations to drive Hill-type muscle models in forward simulations resulted in large joint motions in the initial mechanical response, which were greatly reduced and more closely resembled recorded values when short-range stiffness was included. In subject 1, simulations without short-range stiffness exhibited joint angle changes up to 5° and 15° at 50ms and 100ms, respectively (Fig. 5A, green traces). In contrast, adding short-range stiffness reduced the changes in joint angles by half (Fig. 5A, purple traces), more similar to those observed experimentally (Fig 5A, black traces), except for hip joint angles changes during forward perturbations which were small for both models. RMSE values were lower in simulations including short-range stiffness (Fig. 5B, purple bars) compared to those without short-range stiffness (Fig. 5B, green bars). For the nominal model with short-range stiffness, simulated center of pressure locations were always within 3 to 12cm anterior to the ankle. However, the models without short-range stiffness and with double tendon stiffness often resulted in center of pressure locations outside the base of support (ranging from 5cm posterior to 27cm anterior of the ankle).

Figure 5.

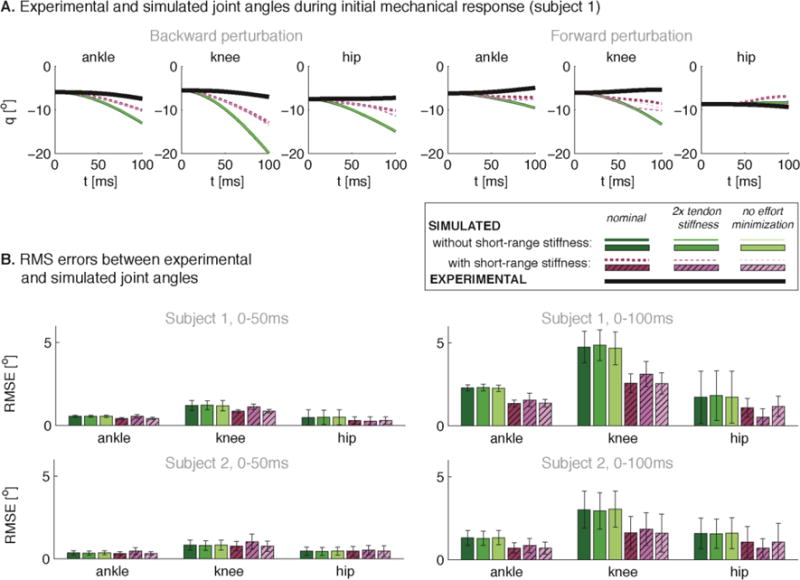
Figure 5

Open in a new tab

Simulated and experimental joint kinematics during the initial mechanical response. Example of simulated and experimental joint angles during a backward (A, left) and forward (A, right) support surface translation for S1. (B) Root mean square errors (RMSE) between simulated and experimental joint kinematics during the first 50ms (left) and 100ms (right) following perturbation onset for S1 (top) and S2 (bottom). RMSE were averaged over all analyzed trials and are shown with the standard deviations. Results for the model without (green) and with (purple) short-range stiffness are shown as in Figure 4.

While the contractile element contributed substantially to the simulated muscle forces during the initial mechanical response, the changes in force during the initial mechanical response were mainly due to short-range stiffness. In the nominal simulations, short-range stiffness contributed on average 6% to overall force and 97% to change in force. In contrast, the contractile element contributed on average 86% to overall force and only 3% to change in force.

Allowing baseline muscle activity to be greater than the optimal levels did not significantly alter ID joint torque tracking errors (Fig. 4) or forward simulation results (Fig. 5). Due to musculoskeletal redundancy, many different baseline muscle activation patterns could satisfy the conditions of static stability prior to perturbation onset. We explicitly tested the effects of increasing baseline muscle activity by eliminating the muscle effort term in the cost function (w = 0). In the inverse-dynamics simulations without short-range stiffness, mean baseline activity approximately doubled (S1: 0.10±0.02 vs 0.22±0.02, S2: 0.11±0.02 vs 0.22±0.02; mean and standard deviation over all trials), with only a slight improvement in tracking errors, (S1: 0.86±0.15Nm vs 0.83±0.17Nm, S2: 1.06±0.22Nm vs 1.06±0.23Nm). Similarly, when short-range stiffness was included, mean baseline activity increased (S1: 0.08±0.01 vs. 0.20±0.04, S2: 0.10±0.02 vs. 0.18±0.03) without affecting mean tracking error (S1: 0.58Nm±0.18Nm vs. 0.56Nm±0.14Nm, S2: 0.74Nm±0.31Nm vs. 0.74Nm±0.31Nm). In our forward dynamics simulations, mean muscle activity increased by less than 5% without significantly altering the simulated joint angle changes (Fig. 5).

DISCUSSION

Our musculoskeletal simulations demonstrate that short-range stiffness plays a substantial role in perturbed standing. In the initial 50ms following a perturbation where muscle activity cannot be modified through sensorimotor feedback, we were only able to account for the rapid rise in joint torques by incorporating a dynamic model of muscle short-range stiffness. Moreover, forward simulations lacking short-range stiffness produced unrealistically large joint angle changes in the first 50ms, many times those observed experimentally. Our dynamic optimization approach for identifying muscle activations that reproduce experimental joint torques was crucial to efficiently explore the influence of augmenting a Hill-type muscle model with a model of muscle short-range stiffness.

Based on physiological data from muscle fiber experiments, we extended the muscle short-range stiffness model of Cui et al. (2008) such that it could be implemented in dynamic musculoskeletal simulations. Our model includes the transient behavior of short-range stiffness by accounting for the critical stretch. While our approach was simple and does not describe all physiological mechanisms underlying short-range stiffness, it proved to be a robust first step to simulating the dynamic effects of muscle short-range stiffness under behaviorally-relevant whole-body movements. We used a short-range stiffness constant based on single muscle fiber stretches (Getz et al., 1998), which was about ten times higher than that derived previously from whole muscle-tendon stretches; we were unable to reproduce ID torques using the previously reported value (Cui et al., 1998). Differences in the physiological activation of electrically-stimulated cat muscle versus naturally-activated human muscle and experimental conditions (e.g. perturbation acceleration) may affect short-range stiffness. Without tuning the short-range stiffness parameters, we were able to robustly reproduce experimental joint torques and angles in simulation. However, muscle-tendon stiffness is determined by the combined effect of tendon and muscle stiffness and it is possible that different combinations of tendon and short-range stiffness parameters may explain the experimental observations equally well. While further refinements will improve the fidelity of the model, they are unlikely to qualitatively influence our results and would increase the computational complexity.

Other musculoskeletal properties likely cannot adequately reproduce the instantaneous and rapid rise in muscle force that we modeled as muscle short-range stiffness. As muscle-tendon length and velocity changes are near zero during the initial mechanical response, it is impossible to reproduce observed joint torques based solely on muscle force-length or force-velocity properties. The passive force component of a Hill-type mode forces would only be high enough at extreme joint angles. We further showed that increasing tendon stiffness did not improve joint torque and joint angle fits in the simulations with or without short-range stiffness (Fig. 4, 5). In addition, altered muscle coordination strategies cannot account for the rapid rise in experimental joint torques. Our simulations both with and without effort minimization, which produced different levels of muscle co-contraction, led to similar conclusions about the necessity to model short-range stiffness (Fig. 4, 5).

Spinal reflexes may contribute to later joint torques, 50ms to 100ms after perturbation, where our simulations deviated from observed responses. Although we were not able to identify significant changes in EMG 50ms to 100ms after the perturbation onset, it is possible that the changes were too small to be reflected in the EMG signal. The changes in muscle activity required to account for ID joint torques changes 50–100ms after perturbation onset would be small in comparison to the changes in muscle activity during the balance correcting response evoked after 100ms.

We believe our main finding that short-range stiffness contributes significantly to the initial mechanical response to perturbations is robust to variations in model parameters. Increasing the complexity and accuracy of our short-range stiffness augmented Hill-model may allow us to reduce the background muscle activity necessary in our model to reproduce experimental observations. However, we are unlikely to account for experimental observations with a more accurate muscle model in the absence of short-range stiffness. Although we verified the realism of the center of pressure locations for the nominal simulations with short-range stiffness, including foot-ground contact dynamics in the forward dynamics model could possibly influence the quantitative contributions of short-range stiffness. While the simulated joint torques at perturbation onset differ from the experimental ID torques, a better fit of these initial torques would increase RMSE for the model without short-range stiffness and only modestly affect RMSE for the model with short-range stiffness, further strengthening our conclusions.

Using muscle models accounting for history-dependent muscle dynamics may be important to advance our understanding of neural and biomechanical factors contributing to human movement through simulations. In particular, short-range stiffness is an important consideration in simulations of perturbed movements where changes in muscle activity in response to perturbations only occur after significant sensorimotor feedback delays. The effects of short-range stiffness are highest when muscles are isometric and active, as in quiet standing and the stance phase of walking and running. Other aspects of history-dependent muscle dynamics that may influence neural control of movement and are not typically simulated include force depression after muscle shortening (De Ruiter et al., 1998) and force enhancement after muscle lengthening (Herzog, 2014).

Acknowledgments

We gratefully acknowledge the support of FWO-V430116N, NIH HD046922 and F32-NS087775.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of Interest Statement

We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no financial support for this work that could have influenced its outcome.

References

  1. Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; Cambridge: 2004. pp. 177–187. [Google Scholar]
  2. Bunderson NE, Burkholder TJ, Ting LH. Reduction of neuromuscular redundancy for postural force generation using an intrinsic stability criterion. Journal of Biomechanics. 2008;41(7):1537–1544. doi: 10.1016/j.jbiomech.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Campbell KS, Lakie M. A cross-bridge mechanism can explain the thixotropic short-range elastic component of relaxed frog skeletal muscle. Journal of Physiology. 1998;510(3):941–962. doi: 10.1111/j.1469-7793.1998.941bj.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Campbell KS. Dynamic coupling of regulated binding sites and cycling myosin heads in striated muscle. The Journal of General Physiology. 2014;143(3):387–399. doi: 10.1085/jgp.201311078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Carpenter MG, Allum JHJ, Honegger F. Directional sensitivity of stretch reflexes and balance corrections for normal subjects in the roll and pitch planes. Experimental Brain Research. 1999;129:93–113. doi: 10.1007/s002210050940. [DOI] [PubMed] [Google Scholar]
  6. Crowninshield RD, Brand RA. A physiologically based criterion of muscle force prediction in locomotion. Journal of Biomechanics. 1981;14(11):793–801. doi: 10.1016/0021-9290(81)90035-x. [DOI] [PubMed] [Google Scholar]
  7. Cui L, Perreault EJ, Maas H, Sandercock TG. Modeling short-range stiffness of feline lower hindlimb muscles. Journal of Biomechanics. 2008;41:1945–1952. doi: 10.1016/j.jbiomech.2008.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. De Groote F, Kinney AL, Rao AV, Fregly BJ. Evaluation of direct collocation optimal control problem formulations for solving the muscle redundancy problem. Annals of Biomedical Engineering. :2016. doi: 10.1007/s10439-016-1591-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. De Groote F, De Laet T, Jonkers I, De Schutter J. Kalman smoothing improves the estimation of joint kinematics and kinetics in marker-based human gait analysis. Journal of Biomechanics. 2008;41:3390–8. doi: 10.1016/j.jbiomech.2008.09.035. [DOI] [PubMed] [Google Scholar]
  10. Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Transactions in Biomedical Engineering. 2007;54:1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
  11. Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM, Rosen ANDJM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Transactions in Biomedical Engineering. 1990;37:757–67. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
  12. De Ruiter CJ, De Haan A, Jones DA, Sargeant AJ. Shortening-induced force depression in human adductor pollicis muscle. Journal of Physiology. 1998;507(2):583–591. doi: 10.1111/j.1469-7793.1998.583bt.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Getz EB, Cooke R, Lehman SL. Phase transition in force during ramp stretches of skeletal muscle. Biophysical Journal. 1998;75:2971–2983. doi: 10.1016/S0006-3495(98)77738-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Herzog W. Mechanisms of enhanced force production in lengthening (eccentric) muscle contractions. Journal of Applied Physiology. 2014;116:1407–1417. doi: 10.1152/japplphysiol.00069.2013. [DOI] [PubMed] [Google Scholar]
  15. Horak FB, Macpherson JM. Handbook of Physiology. American Physiological Society; New York: 1996. pp. 255–292. [Google Scholar]
  16. Hu X, Murray WM, Perreault EJ. Muscle short-range stiffness can be used to estimate the endpoint stiffness of the human arm. Journal of Neurophysiology. 2011;105:1633–1641. doi: 10.1152/jn.00537.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Loram ID, Maganaris CN, Lakie M. The passive, human calf muscles in relation to standing: the non-linear decrease from short range to long range stiffness. Journal of Physiology. 2007a;584(2):661–675. doi: 10.1113/jphysiol.2007.140046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Loram ID, Maganaris CN, Lakie M. The passive, human calf muscles in relation to standing: the short range stiffness lies in the contractile component. Journal of Physiology. 2007b;584(2):677–692. doi: 10.1113/jphysiol.2007.140053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Nichols TR, Houk JC. Improvement in linearity and regulation of stiffness that results from actions of stretch reflex. Journal of Neurophysiology. 1976;39(1):119–142. doi: 10.1152/jn.1976.39.1.119. [DOI] [PubMed] [Google Scholar]
  20. Runge CF, Shupert CL, Horank FB, Zajac FE. Ankle and hip postural strategies defined by joint torques. Gait & Posture. 1999;10:161–70. doi: 10.1016/s0966-6362(99)00032-6. [DOI] [PubMed] [Google Scholar]
  21. Ting LH, van Antwerp KW, Scrivens JE, McKay JL, Welch TDJ, Bingham JT, DeWeerth SP. Neuromechanical tuning of nonlinear postural control dynamics. Chaos. 2009;19(2):026111. doi: 10.1063/1.3142245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Torres-Oviedo G, Ting LH. Muscle synergies characterizing human postural responses. Journal of Neurophysiology. 2007;98(4):2144–2156. doi: 10.1152/jn.01360.2006. [DOI] [PubMed] [Google Scholar]
  23. Torres-Oviedo G, Ting LH. Subject-specific muscle synergies in human balance control are consistent across different biomechanical contexts. Journal of Neurophysiology. 2010;103(6):3084–3098. doi: 10.1152/jn.00960.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES