Abstract
Objective
This project contributes to the emerging research that aims to identify distinct body mass index (BMI) trajectory types in the population. We identify clusters of long-term BMI curves among older adults and determine how the clusters differ with respect to initial health.
Method
Health and Retirement Study cohort (N = 9,893) with BMI information collected in up to 10 waves (1992–2010) is analyzed using a powerful cutting-edge approach: hierarchical clustering of BMI functions estimated via the Principal Analysis by Conditional Expectations (PACE) algorithm.
Results
Three BMI trajectory clusters emerged for each gender: stable, gaining, and losing. The initial health of the gaining and stable groups in both genders was comparable; the losing cluster experienced significantly poorer health at baseline.
Discussion
BMI trajectories among older adults cluster into distinct types in both genders, and the clusters vary substantially in initial health. Weight loss but not gain is associated with poor initial health in this age group.
Keywords: BMI trajectories, BMI trajectory clusters, health, older adults, functional data analysis
The relationship between body weight and health evolves gradually over the course of life (Preston, Mehta, & Stokes, 2013). In recognition of the importance of this ongoing development, researchers are increasingly aiming to examine long-term weight changes using longitudinal data with multiple body mass index (BMI) data points. Given the steep increase in obesity in the U.S. population in recent decades (Reither, Hauser, & Yang, 2009) and the high health and economic costs associated with obesity (Allison, Fontaine, Manson, Stevens, & VanItallie, 1999; Wolf & Colditz, 1998), understanding how long-term BMI trajectories are linked to health among U.S. adults is critical for public health. We analyze long-term BMI trajectories in an 18-year longitudinal study of a nationally representative cohort of older adults, using a flexible powerful nonparametric methodology: hierarchical clustering of functional curves.
Most studies focusing on BMI change over time use approaches that require a priori categorization of initial BMI level and BMI change. Researchers often create multiple categories of BMI change, categories such as “gaining from normal weight to overweight” or “losing weight from obese to overweight,” to capture both level and change in weight (Lee et al., 2011; Myrskylä & Chang, 2009; Newman et al., 2001; Stevens, Juhaeri, & Cai, 2001; Strandberg et al., 2013; Strandberg et al., 2009). Although this approach allows for a nuanced study of the initial level and change in BMI, the results can vary depending on the selected thresholds. Another approach is to model an average BMI trajectory for the sample and examine how individual variation around the average is associated with health or other individual characteristics (Botoseneanu & Liang, 2011; Walsemann & Ailshire, 2011).
However, these “variable-centered” approaches (Laursen & Hoff, 2006; Muthén & Muthén, 2000) do not reveal the actual patterns of typical weight trajectories that occur in the population. Discovering such qualitative latent variation in BMI trajectories is important for classification of individuals into various risk levels and for targeting interventions accordingly. Several studies, using a latent class approach (Muthén, 2002; Nagin & Odgers, 2010), have identified distinct BMI trajectory classes exist among older adults (Botoseneanu & Liang, 2013; Kuchibhatla, Fillenbaum, Kraus, Cohen, & Blazer, 2013; Walsemann & Ailshire, 2011) and at younger ages (C. Li, Goran, Kaur, Nollen, & Ahluwalia, 2007; Nonnemaker, Morgan-Lopez, Pais, & Finkelstein, 2009). However, the findings from these emerging studies on BMI trajectory classes differ regarding the optimal number of the BMI trajectory classes, their shapes, and their health correlates.
For instance, two recent studies (Zajacova & Ailshire, 2013; Zheng, Tumin, & Qian, 2013) used the same data on older adults from the Health and Retirement Study. Both estimated latent growth mixture models to determine BMI trajectory groups in the older population. However, the two studies made different assumptions in the models—in particular, Zheng et al. (2013) restricted the residual variance of the growth factors in the trajectory groups to zero, whereas Zajacova and Ailshire (2013) imposed no such restriction. These different approaches resulted in fundamentally different findings. The first study reported five BMI trajectory classes with relatively modest change over time; the second study found three BMI trajectory classes with one group that had relatively stable BMI over time, whereas the other two were marked by pronounced weight gain and loss, respectively. Such conflicting findings indicate that the BMI data are sensitive to model assumption and many open questions remain about the actual underlying trajectory groups. In addition, the conflicting findings also show that there is room for innovative approaches to modeling weight trajectories.
The present analysis uses hierarchical clustering of functional curves estimated using the Principal Analysis by Conditional Expectations (PACE) algorithm, a powerful, cutting-edge, nonparametric approach to analyzing longitudinal data. The methodology was developed in the statistical literature over the past decade (Chen & Müller, 2012; Hitchcock & Greenwood, in press; Müller, 2005; Ramsay, Hooker, & Graves, 2009; Ramsay & Silverman, 2005; Yao, Müller, & Wang, 2005) with applications primarily in environmental sciences research (Haggarty, Miller, Scott, Wyllie, & Smith, 2012; Henderson, 2006; Huzurbazar & Humphrey, 2008). To the best of our knowledge, the present study is its first application in a public health area. Using repeated observations from older adults over almost 20 years, BMI curves are estimated using PACE and then clustered to identify typical BMI “trajectories” in the sample. We then characterize the clusters and describe the initial sociodemographic and health differences across the clusters. The findings thus provide a clear, data-driven, and empirically grounded analysis of typical patterns of body weight trajectories in older adults, patterns that can help inform public health and clinical recommendations.
Method
Data
We used data from the Health and Retirement Survey (HRS; Hodes & Suzman, 2007). The HRS, one of the leading sources of data on the health of older Americans, is a nationally representative panel survey of U.S. adults born between 1931 and 1941. The sample cohort was first interviewed in 1992 when respondents were between 51 and 61 years old, and reinterviewed every 2 years thereafter. We used data collected from this group through the 2010 interview, which provides up to 10 measures of BMI over 18 years of the study period. The information was downloaded from Version M of the data set available from the RAND Corporation (2011).
Sample definition
We defined the sample as all individuals included in the original HRS sample who were born between 1931 and 1941 and interviewed first in 1992. After excluding 3 individuals who had no BMI information at any wave and 286 individuals (2.8%) who had BMI values considered to be outliers (above 45 or below 15 at any interview wave), the final sample size was N = 9,893.
Variables
BMI
BMI was calculated as weight (kg)/height (m) squared. Height was self-reported at the first interview; weight was self-reported at every interview. For each individual, all available BMI data points are included to define the BMI curves.
Baseline characteristics
Baseline characteristics included sociodemographic and health information. Age was included as a time-varying measure and served as the time axis for the BMI curves. Sex was dichotomized, and all analyses were conducted independently for men and women. Race was coded White versus non-White and marital status married (includes cohabiting respondents) versus not married. Educational attainment was included in completed years of schooling as a continuous covariate. Three baseline measures of general health were included: self-rated health (SRH), count of chronic conditions, and limitations in Activities of Daily Living (ADL). SRH, measured on the standard 5-point scale from excellent (1) to poor (5), was dichotomized as excellent to good versus poor or fair. The number of chronic conditions, which included highly prevalent conditions such as hypertension, arthritis, cancer, and diabetes, was a count variable ranging from 0 up to 7 and was also dichotomized as 0 to 1 versus 2 to 7 conditions. The individual health conditions were also analyzed separately and compared across the BMI trajectory clusters.
Approach
Our approach was to estimate the individual BMI curves (or functions) from observed BMI data points, and to then use the estimated functions as the units of further analysis. Specifically, functional BMI curves are estimated by applying the PACE algorithm; then hierarchical clustering of the functional curves is used to identify groups with similar BMI patterns. We describe the method in a broad conceptual way and include references for readers interested in additional information about the methodology.
Functional data analysis (FDA) and functional principal components analysis (FPCA)
FDA is a flexible, nonparametric approach to modeling longitudinal data. FDA was originally developed for dense data with thousands of measurements over time as may be available with temperature measurements or from functional magnetic resonance imaging (fMRI; Ramsay et al., 2009; Ramsay & Silverman, 2005). For dense data, measurement error is viewed as minimal and basis functions such as splines are used to estimate curves as functions of time for each unit of observation. FPCA is the core dimension-reduction tool in FDA (Y. Li, Wang, & Carroll, 2013). Analogous to multivariate principal components analysis, FPCA decomposes the covariance surface into eigenvalues and eigenfunctions, which are then used to obtain FPCA scores for further analyses (Yao, 2007). The mean function (M BMI function by age in our case) is estimated with a local linear scatterplot smoother fitted to the aggregated BMI data plotted against age. The mean function is combined with the raw data to calculate raw covariances of pairwise time points of BMI measurements for each individual. A final smooth covariance surface is estimated by fitting a two-dimensional smoother over the combination of the raw covariances for all individuals, and the covariance surface is decomposed into eigenvalues with corresponding eigenfunctions. For dimension reduction, a small number of eigenfunctions are chosen such that a high percentage of the variation, as given by the eigenvalues, is explained and FPCA scores for each individual are obtained using the mean function and the retained eigenfunctions. The FPCA scores for each individual are used in further analyses.
PACE
In contrast to the densely observed data that motivated the original FDA methods and applications, social research longitudinal data, including the repeated BMI measurements in the Health and Retirement Study, are sparse (up to 10 observations per individual) and direct application of basis functions to estimate each individual’s BMI function and FPCA scores is not possible. The statistical theory and computing algorithms for sparse functional data were developed in recent years (Müller, 2005, 2009; Yao et al., 2005). An approach to overcoming sparsity is to include an additional modeling step, namely, PACE (Müller & Wang, 2012; Yao et al., 2005), while combining the available individual data points with data from the whole sample. Specifically, this requires an assumption that the FPCA scores and the errors are jointly normal so that the conditional expectations of the FPCA scores are estimated based on the estimated mean and eigenfunctions (Hall, Müller, & Wang, 2006). As with dense data, these predicted FPCA scores can be used in other analyses.
Hierarchical clustering for sparse functional data
Cluster analysis is an exploratory approach for sorting objects into meaningful groups. In general, any clustering procedure comprises two steps: First, a dissimilarity matrix is calculated, then clustering algorithms are used to group the observations, ideally, resulting in meaningful patterns. For dense functional data, when using the estimated functions, dissimilarity is defined using the L2 distance, the functional analogue of Euclidean distance for multivariate data (Peng & Müller, 2008; see Huzurbazar & Humphrey, 2008, for one such application). In other applications, especially with sparse data, the FPCA scores are clustered (Y. Li et al., 2013). In this analysis, we use the univariate scores from the second principal component (PC) to obtain the dissimilarity matrix. The first PC captures the main source of variability in the data, which is the variation in the average BMI level over time across individuals. In other words, the variability in average BMIs across individuals is large compared with within-individual changes in BMI. However, it is precisely those within-individual changes in BMI we are interested in capturing. This variability is captured primarily in the second PC and thus clustering is performed on the second PC.
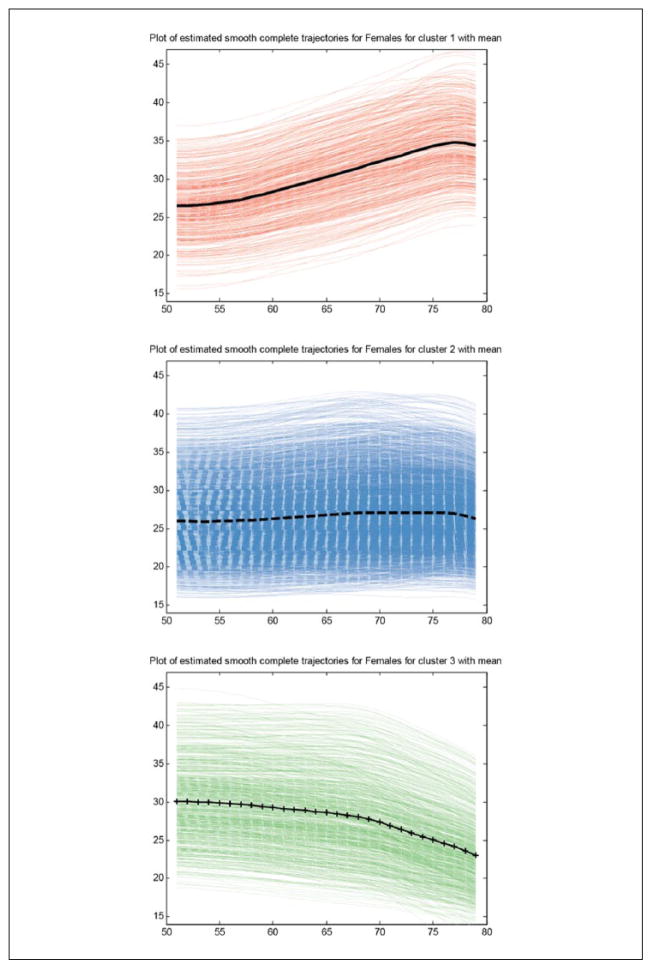
We use Ward’s (1963) linkage and Euclidean distance to obtain a solution with the optimal number of clusters. Matlab hierarchical clustering supports an agglomerative method (bottom-up) in which smaller clusters are joined to create larger clusters as the algorithm proceeds. The process is usually visualized by a dendrogram, a branching diagram where clusters at one level are grouped into larger clusters at a higher level, to represent the dissimilarity across clusters or arrangement of clusters produced by hierarchical clustering. The dendrogram can be used to select the number of cluster. Documentation for the hierarchical clustering in Matlab is available online (MathWorks, 2013). Figure 2 shows the result of the cluster analysis: the mean BMI trajectory and the estimated individual BMI trajectories for each cluster.
Figure 2.
Individual BMI curves in each cluster and mean cluster trajectory, females.
Note. BMI = body mass index.
Finally, we compare the baseline health characteristics across the clusters. All analyses are stratified by gender. Stata 13.0 (StataCorp, 2013) was used for descriptives and for comparing the characteristics of the clusters; PACE 2.16 package in Matlab (Müller & Wang, 2012) was used for FDA.
Results
Table 1 summarizes sample characteristics weighted to represent the population. There are slightly more women (52%) than men, and the mean year of birth for both genders is 1936, meaning they were 56 years old at the start of the survey. Men had a mean BMI of 27 at the baseline, and women started the study with a BMI of 26.4. Both genders gained 0.9 BMI points on average during the 18 years of follow-up. About 19% of men and 20% of women reported poor or fair health; 25% of men and 29% of women reported having been diagnosed with two or more chronic conditions, and 9% of men (10% of women) had any ADL limitations.
Table 1.
Characteristics of the HRS Cohort 1992–2010, by Sex (N = 9,893).
| Men | Women | |
|---|---|---|
| Proportion of sample at baseline | 48.3% | 51.7% |
| BMI at 1992 baseline | 27.0 | 26.4 |
| BMI in 2010 | 27.9 | 27.3 |
| Year of birth | 1936.2 | 1936.2 |
| Non-White | 18.0% | 19.4% |
| Not married | 21.2% | 29.7% |
| Educational attainment | 12.5 | 12.2 |
| Poor or fair self-rated health | 18.9% | 20.1% |
| Two or more conditions | 25.0% | 28.7% |
| Any ADL limitations | 9.2% | 9.7% |
| Specific health conditions | ||
| Hypertension | 39.0% | 35.7% |
| Heart condition | 14.9% | 10.3% |
| Diabetes | 9.9% | 9.0% |
| Arthritis | 30.5% | 42.8% |
| Cancer | 3.1% | 7.7% |
| Respiratory condition | 7.9% | 8.3% |
| Stroke | 3.0% | 2.2% |
| Psychiatric disorder | 7.9% | 13.3% |
| n | 4,764 | 5,129 |
Note. Adjusted for the complex sampling design of the HRS. HRS = Health and Retirement Survey; BMI = body mass index.
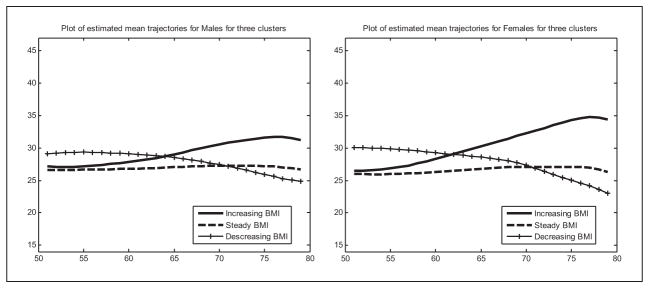
Figure 1 shows the mean of the original continuous BMI curves in each cluster for men and women. In both genders, the optimal number of clusters is three, and their overall shapes are rather similar. One group retained a relatively stable BMI. Among men, this group comprised 69% of the sample (as shown in Table 2). The mean BMI trajectory in this cluster started at about 26.4 and increases slightly by about 1 BMI point by age 75. Among women, this group, comprising 78% of the sample, started at about 26 BMI points and also increases by about 1 point. The second group is characterized by weight gain. Among men, this group that included 16% of the respondents started at about 27 BMI points and increased about 4 points to the obese range, at about 31 BMI points. Among women where the increasing cluster comprised 8% of the sample, the starting BMI was also nearly 27, and the increase was even steeper—8 points—to a BMI of nearly 35. The third cluster is characterized by weight loss. For men, this cluster included 15% of the sample. The mean BMI trajectory in this group started at about 29 BMI points and after some stability, dropped to about BMI of 25 by age 80, a drop of about 4 BMI points. Among women where this group included 14% of the sample, there was an even steeper decline from BMI of 30 at age 50 to below 24 BMI points by age 80, a drop of more than 6 BMI points.
Figure 1.
Mean BMI trajectories in the three clusters, by sex.
Table 2.
Three-Cluster Solution for BMI Curves: Sample Means and Group Comparison Tests.
| Stable | Gaining | Losing | Gaining vs. Stable | Losing vs. Stable | Losing vs. Gaining | Overall group comparison | |
|---|---|---|---|---|---|---|---|
| Men | |||||||
| % in each class | 69.1 | 16.0 | 14.9 | — | — | — | — |
| BMI at 1992 baseline | 26.6 | 26.8 | 29.7 | .130 | <.001 | <.001 | <.001 |
| BMI in 2010 | 27.2 | 32.0 | 25.7 | <.001 | <.001 | <.001 | <.001 |
| Sociodemographic characteristics | |||||||
| Year of birth | 1936.1 | 1936.5 | 1936.1 | .001 | .839 | .008 | .003 |
| Non-White | 26.3 | 23.4 | 32.1 | .102 | .002 | <.001 | <.001 |
| Not married | 19.6 | 20.7 | 20.8 | .537 | .497 | .952 | .701 |
| Educational attainment | 12.3 | 12.1 | 11.6 | .254 | <.001 | .009 | <.001 |
| General health measures | |||||||
| Poor or fair self-rated health | 19.8 | 17.9 | 28.3 | .234 | <.001 | <.001 | <.001 |
| Two or more conditions | 25.3 | 23.9 | 31.3 | .429 | <.001 | .002 | <.001 |
| Any ADL limitations | 9.7 | 7.6 | 14.3 | .087 | <.001 | <.001 | <.001 |
| Specific health conditions | |||||||
| Hypertension | 37.8 | 39.9 | 47.8 | .292 | <.001 | .003 | .002 |
| Heart condition | 14.7 | 13.3 | 17.7 | .341 | .049 | .023 | .058 |
| Diabetes | 10.3 | 8.0 | 14.8 | .072 | .001 | <.001 | <.001 |
| Arthritis | 30.1 | 29.4 | 35.7 | .727 | .004 | .012 | .011 |
| Cancer | 3.4 | 2.4 | 3.1 | .146 | .674 | .395 | .340 |
| Respiratory condition | 7.3 | 8.5 | 8.0 | .308 | .580 | .736 | .558 |
| Stroke | 3.2 | 3.0 | 4.4 | .877 | .100 | .175 | .227 |
| Psychiatric disorder | 7.4 | 7.2 | 10.3 | .876 | .010 | .039 | .028 |
| Women | |||||||
| % in each class | 77.8 | 7.9 | 14.3 | — | — | — | — |
| BMI at 1992 baseline | 26.0 | 26.5 | 30.2 | .030 | <.001 | <.001 | <.001 |
| BMI in 2010 | 27.1 | 33.7 | 25.0 | <.001 | <.001 | <.001 | <.001 |
| Sociodemographic characteristics | |||||||
| Year of birth | 1936.2 | 1936.9 | 1936.3 | <.001 | .453 | .001 | <.001 |
| Non-White | 28.7 | 25.3 | 38.6 | .139 | <.001 | <.001 | <.001 |
| Not married | 31.4 | 34.0 | 37.8 | .290 | <.001 | .214 | .003 |
| Educational attainment | 12.0 | 12.2 | 11.4 | .186 | <.001 | <.001 | <.001 |
| General health measures | |||||||
| Poor or fair self-rated health | 21.2 | 21.3 | 33.7 | .943 | <.001 | <.001 | <.001 |
| Two or more conditions | 28.2 | 30.7 | 43.5 | .295 | <.001 | <.001 | <.001 |
| Any ADL limitations | 10.3 | 10.7 | 14.8 | .809 | <.001 | .051 | .002 |
| Specific health conditions | |||||||
| Hypertension | 36.2 | 36.8 | 50.9 | .803 | <.001 | <.001 | <.001 |
| Heart condition | 10.2 | 11.2 | 14.1 | .544 | .002 | .162 | .008 |
| Diabetes | 8.8 | 8.9 | 18.7 | .963 | <.001 | <.001 | <.001 |
| Arthritis | 41.4 | 48.0 | 52.2 | .012 | <.001 | .181 | <.001 |
| Cancer | 7.2 | 7.9 | 10.1 | .614 | .007 | .227 | .028 |
| Respiratory condition | 7.9 | 7.1 | 11.8 | .575 | <.001 | .014 | .002 |
| Stroke | 2.4 | 2.3 | 3.8 | .894 | .033 | .180 | .093 |
| Psychiatric disorder | 12.7 | 14.2 | 17.2 | .406 | <.001 | .195 | .005 |
Note. The first three columns summarize characteristics within each BMI cluster. The next three columns show p values from pairwise comparisons of the groups using t tests and chi-square tests. The last column shows the p value for the test of hypothesis that the three groups are identical with respect to each characteristic using chi-square tests for categorical variables and ANOVA F tests for continuous variables. BMI = body mass index.
p < .05.
p < .01.
p < .001.
Table 2 compares the sociodemographic characteristics and initial health of the three BMI trajectory clusters for men and women. Chi-square and ANOVA F tests were used to test for overall differences across the three clusters; two-sample t tests and chi-square tests assessed pairwise differences between clusters. Among men, the three BMI trajectory clusters differed in all sociodemographic characteristics except marital status: In particular, the men in the losing cluster had the highest proportion of non-Whites and the lowest education. Significant differences appeared in all three baseline general health measures: The losing cluster had a significantly higher proportion of respondents in fair or poor health, with two or more chronic conditions, and with any ADL limitations, compared with the stable and gaining clusters. These differences were substantively large. For instance, in the stable and gaining clusters, fewer than 20% of the members reported fair or poor health and fewer than 10% reported activity limitations, whereas the corresponding proportions were more than 14% and 28% in the losing cluster. There were differences with respect to specific conditions as well: The losing cluster had the highest prevalence of hypertension, heart condition, diabetes, arthritis, and psychiatric conditions; the prevalence was significantly higher than in the stable or gaining clusters. In all health measures and all but one sociodemographic measures (year of birth), the stable and gaining clusters were not statistically different.
Among women, the three BMI trajectory clusters differed significantly in all sociodemographic characteristics: The women in the losing cluster had the highest proportion of non-Whites and non-married, as well as the lowest education. Significant differences also appeared in all baseline health correlates: The losing cluster had the highest proportion of respondents in fair or poor health, with two or more chronic conditions, with any ADL limitations, as well as with all eight measured chronic conditions. As for men, the differences were substantively large: For instance, about 30% of women in the stable and gaining clusters reported two or more conditions, but more than 43% in the losing cluster did. The gaining cluster did not differ from the stable one in any general condition and only in one (arthritis) specific health problem and in the year of birth; in contrast, the gaining cluster has significantly lower prevalence of general health problems, compared with the losing cluster.
Discussion
The aim of this study was to determine typical BMI trajectory groups among older adults and to assess the initial health of the different groups. The analysis used a novel nonparametric approach—hierarchical clustering of functional curves estimated via the PACE algorithm for sparse longitudinal data. To the best of our knowledge, this is the first applied study using this approach in any health-related research.
We found that BMI curves among older adults fall into three groups, with relatively similar shapes in both men and women: The largest cluster is mostly in the low-overweight range and remains fairly stable or increases moderately across age, as shown in Figure 1. A second cluster is also partly in the overweight range but is characterized by gradual weight gain that pushes the average BMI in this group into the obese range in the later years. A third cluster is also mostly in the overweight range but is characterized by a steady weight loss that accelerates after about age 60. Interestingly, both the optimal number of clusters and the mean BMI trajectories in each cluster were similar for men and women, which suggests common underlying biological determinants for these three different BMI patterns.
The three BMI trajectory groups differed significantly and substantially in terms of sociodemographic characteristics and initial health. Again, the results were largely similar in men and women. For both genders, the stable and gaining clusters were rather similar in initial health—there was no evidence of a difference with respect to all three general health measures and all eight specific conditions except for a higher level of arthritis in the gaining cluster among women. In contrast, the losing cluster had much worse initial health: men and women in this cluster had significantly lower self-ratings of health, more chronic conditions, and more activity limitations. Among women, the losing cluster respondents had about 30% to 50% higher probability of reporting any specific conditions compared with women in the stable cluster; among men, the corresponding percentage points ranged from 0% to about 40%.
The worse health in the losing clusters corroborates the broad understanding in the literature that weight loss among older adults is associated with more health problems and higher mortality (Alley et al., 2010; Bamia et al., 2010; Richman & Stampfer, 2010). However, our results indicate that the typical weight loss patterns among older adults occur at relatively high BMI levels, from overweight/obese levels toward the normal weight range. This is an important factor because weight loss from overweight levels could be viewed as a positive change from the perspective of clinicians or the individuals themselves. This paradox, therefore, needs to be further examined because it is a particularly important link between population-health research on BMI trajectories and potential clinical interventions among older adults.
The similarity between those with stable weight and those with weight gain in terms of initial health and most sociodemographic characteristics is an interesting new finding. One explanation posits that continued weight gain signifies substantial physiological reserve that allows older adults to function over the long-term (Rowe & Kahn, 1997; Topinková, 2008). That is, perhaps the weight gain during the transition into older adulthood tends to occur among individuals with relatively robust health; the finding also dovetails nicely with the relatively low mortality among heavier older adults, especially when compared with those with low body weight or those who experienced weight loss (Mehta & Chang, 2009; Monteverde, Noronha, Palloni, & Novak, 2010; Strandberg et al., 2013; Zajacova & Burgard, 2011).
Our results also corroborate findings from one of the recent studies that modeled heterogeneity in BMI trajectories among older adults and associated health and/or mortality (Zajacova & Ailshire, 2013). That study used a joint growth mixture–survival (proportional hazard) model. Despite the different methodologies used, with fundamentally different assumptions (in particular, the FDA approach makes no parametric assumptions about the age effects, whereas the growth mixture analysis was parametric—linear—with respect to age), the findings of these two studies were substantively similar, which strengthens the validity of both sets of results. However, we argue that the FDA approach should be used in future analysis, as it is more responsive to data patterns and less restrictive in its assumptions.
Several caveats should be noted. First, we did not distinguish between voluntary and involuntary weight loss as we did not have this information. However, given the modest (at best) success rates of voluntary weight loss programs in the United States (Heshka et al., 2003; Levy, Finch, Crowell, Talley, & Jeffery, 2007), we can safely assume that the bulk of the weight loss observed in our data was involuntary. Second, all BMI information was self-reported, potentially biasing the results. Although we can expect that respondents tend to underreport their body weight (Gorber, Tremblay, Moher, & Gorber, 2007; Rowland, 1990), the underreporting tendencies are likely to remain relatively unchanged over the multiple interviews. Thus, the shape of the described trajectories is likely unbiased, although their overall levels may be biased slightly downward. Third, the FDA approaches developed so far do not include sampling weights. However, clustering does not require sampling weight adjustments as it tries to detect groups within the responses regardless of the number of individuals in the population each sample member represents. Thus, the shape of the BMI trajectories in the sample is not affected, even if the proportion of the population represented in each cluster may be somewhat different if weights were available. Finally, our approach, like other methods to characterize BMI trajectories, does not explicitly deal with attrition. Our sparse FDA methods assume a smooth path across the points that were observed. This assumption is akin to missing at random (MAR) missingness, that is, missing data points are assumed to be MAR conditional on the points observed—in other words, the trajectory is assumed to “continue” in the way it is observed in the data after an individual ceases to be observed, whether due to mortality attrition or nonmortality attrition. In our analysis, all three trajectory clusters contained enough observations to be estimated precisely and without bias in the surviving cohort. Moreover, our focus was to determine the characteristics of each sample at the baseline, before mortality and nonmortality attrition affected the sample during follow-up. For our question, therefore, attrition should have limited impact on the findings.
There is growing interest in examining heterogeneity in BMI trajectories—that is, identifying distinct BMI trajectory types. The growth mixture methodology used in the available studies, however, depends heavily on assumptions and modeling decisions, sometimes yielding contradictory results. We introduced a functional data approach as a compelling alternative methodology to identify such BMI trajectory types. The approach can be used for a wide variety of substantive issues, from physical and mental development in early life to health changes across the life course or health declines among the elderly. The nonparametric nature of the FDA allows the detection of subtle but possibly important features of the data, such as acceleration or deceleration of changes at specific ages or time points. For instance, in supplementary analyses (not shown), we found a systematic acceleration of weight loss starting at least several years prior to death, a pattern that is difficult to capture in parametric models. New tools and applications for FDA for sparse longitudinal data are being developed. We urge researchers to explore FDA to examine diverse substantive questions because its flexibility and assumptions that differ from most standard approaches can reveal new and important findings.
Acknowledgments
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This project was supported in part by grants from the National Center for Research Resources (P20RR016474) and the National Institute of General Medical Sciences (P20GM103432) from the National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Declaration of Conflicting Interests
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- Alley DE, Metter EJ, Griswold ME, Harris TB, Simonsick EM, Longo DL, Ferrucci L. Changes in weight at the end of life: Characterizing weight loss by time to death in a cohort study of older men. American Journal of Epidemiology. 2010;172:558–565. doi: 10.1093/aje/kwq168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison DB, Fontaine KR, Manson JE, Stevens J, VanItallie TB. Annual deaths attributable to obesity in the United States. Journal of the American Medical Association. 1999;282:1530–1538. doi: 10.1001/jama.282.16.1530. [DOI] [PubMed] [Google Scholar]
- Bamia C, Halkjaer J, Lagiou P, Trichopoulos D, Tjonneland A, Berentzen T. Weight change in later life and risk of death amongst the elderly: The European Prospective Investigation into Cancer and Nutrition–Elderly Network on Ageing and Health study. Journal of Internal Medicine. 2010;268:133–144. doi: 10.1111/j.1365-2796.2010.02219.x. [DOI] [PubMed] [Google Scholar]
- Botoseneanu A, Liang J. Social stratification of body weight trajectory in middle-age and older Americans: Results from a 14-year longitudinal study. Journal of Aging and Health. 2011;23:454–480. doi: 10.1177/0898264310385930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botoseneanu A, Liang J. Latent heterogeneity in long-term trajectories of body mass index in older adults. Journal of Aging and Health. 2013;25:342–363. doi: 10.1177/0898264312468593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen K, Müller HG. Modeling repeated functional observations. Journal of the American Statistical Association. 2012;107:1599–1609. doi: 10.1080/01621459.2012.734196. [DOI] [Google Scholar]
- Gorber SC, Tremblay M, Moher D, Gorber B. A comparison of direct vs. self-report measures for assessing height, weight, and body mass index: A systematic review. Obesity Reviews. 2007;8:307–326. doi: 10.1111/j.1467-789X.2007.00347.x. [DOI] [PubMed] [Google Scholar]
- Haggarty RA, Miller CA, Scott EM, Wyllie F, Smith M. Functional clustering of water quality data in Scotland. Environmetrics. 2012;23:685–695. doi: 10.1002/env.2185. [DOI] [Google Scholar]
- Hall P, Müller HG, Wang JL. Properties of principal component methods for functional and longitudinal data analysis. The Annals of Statistics. 2006;34:1493–1517. doi: 10.2307/25463465. [DOI] [Google Scholar]
- Henderson B. Exploring between site differences in water quality trends: A functional data analysis approach. Environmetrics. 2006;17:65–80. doi: 10.1002/env.750. [DOI] [Google Scholar]
- Heshka S, Anderson JW, Atkinson RL, Greenway FL, Hill JO, Phinney SD, … Xavier P-SF. Weight loss with self-help compared with a structured commercial program: A randomized trial. Journal of the American Medical Association. 2003;289:1792–1798. doi: 10.1001/jama.289.14.1792. [DOI] [PubMed] [Google Scholar]
- Hitchcock DB, Greenwood MC. Clustering functional data. In: Hennig CM, Meila M, Murtagh F, Rocci R, editors. Handbook of cluster analysis. Boca Raton, FL: Chapman and Hall/CRC Press; in press. [Google Scholar]
- Hodes RJ, Suzman R. Growing older in America: The health and retirement study. Bethesda, MD: National Institute on Aging, National Institute of Health, U.S. Department of Health and Human Services; 2007. [Google Scholar]
- Huzurbazar S, Humphrey NF. Functional clustering of time series: An insight into length scales in subglacial water flow. Water Resources Research. 2008;44(11):W11420. doi: 10.1029/2007wr006612. [DOI] [Google Scholar]
- Kuchibhatla MN, Fillenbaum GG, Kraus WE, Cohen HJ, Blazer DG. Trajectory classes of body mass index in a representative elderly community sample. The Journals of Gerontology Series A: Biological Sciences and Medical Sciences. 2013;68:699–704. doi: 10.1093/gerona/gls215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laursen B, Hoff E. Person-centered and variable-centered approaches to longitudinal data. Merrill-Palmer Quarterly. 2006;52:377–389. [Google Scholar]
- Lee CG, Boyko EJ, Nielson CM, Stefanick ML, Bauer DC, Hoffman A … Osteoporotic Fractures Men Study Group. Mortality risk in older men associated with changes in weight, lean mass, and fat mass. Journal of the American Geriatrics Society. 2011;59:233–240. doi: 10.1111/j.1532-5415.2010.03245.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy RL, Finch EA, Crowell MD, Talley NJ, Jeffery RW. Behavioral intervention for the treatment of obesity: Strategies and effectiveness data. The American Journal of Gastroenterology. 2007;102:2314–2321. doi: 10.1111/j.1572-0241.2007.01342.x. [DOI] [PubMed] [Google Scholar]
- Li C, Goran MI, Kaur H, Nollen N, Ahluwalia JS. Developmental trajectories of overweight during childhood: Role of early life factors. Obesity. 2007;15:760–771. doi: 10.1038/oby.2007.585. [DOI] [PubMed] [Google Scholar]
- Li Y, Wang N, Carroll RJ. Selecting the number of principal components in functional data. Journal of the American Statistical Association. 2013;108:1284–1294. doi: 10.1080/01621459.2013.788980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MathWorks. Hierarchical clustering (R2013a documentation) 2013 Retrieved from http://www.mathworks.com/help/stats/hierarchical-clustering.html.
- Mehta NK, Chang VW. Mortality attributable to obesity among middle-aged adults in the United States. Demography. 2009;46:851–872. doi: 10.1353/dem.0.0077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monteverde M, Noronha K, Palloni A, Novak B. Obesity and excess mortality among the elderly in the United States and Mexico. Demography. 2010;47(1):79–96. doi: 10.1353/dem.0.0085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller HG. Functional modelling and classification of longitudinal data. Scandinavian Journal of Statistics. 2005;32:223–240. [Google Scholar]
- Müller H-G. Functional modeling of longitudinal data. In: Fitzmaurice GM, Davidian M, Verbeke G, Molenberghs G, editors. Handbooks of Modern Statistical Methods: Longitudinal data analysis. Boca Raton, FL: Chapman & Hall; 2009. pp. 223–252. [Google Scholar]
- Müller H-G, Wang J-L. PACE: Principal analysis by conditional expectation, version 2.16. 2012 Retrieved from http://anson.ucdavis.edu/PACE/
- Muthén BO. Beyond SEM: General latent variable modeling. Behaviormetrika. 2002;29:81–117. [Google Scholar]
- Muthén BO, Muthén LK. Integrating person-centered and variable-centered analyses: Growth mixture modeling with latent trajectory classes. Alcoholism: Clinical & Experimental Research. 2000;24:882–891. [PubMed] [Google Scholar]
- Myrskylä M, Chang VW. Weight change, initial BMI, and mortality among middle- and older-aged adults. Epidemiology. 2009;20:840–848. doi: 10.1097/EDE.0b013e3181b5f520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagin DS, Odgers CL. Group-based trajectory modeling in clinical research. Annual Review of Clinical Psychology. 2010;6:109–138. doi: 10.1146/annurev.clinpsy.121208.131413. [DOI] [PubMed] [Google Scholar]
- Newman AB, Yanez D, Harris T, Duxbury A, Enright PL, Fried LP Cardiovascular Study Research Group. Weight change in old age and its association with mortality. Journal of the American Geriatrics Society. 2001;49:1309–1318. doi: 10.1046/j.1532-5415.2001.49258.x. [DOI] [PubMed] [Google Scholar]
- Nonnemaker JM, Morgan-Lopez AA, Pais JM, Finkelstein EA. Youth BMI trajectories: Evidence from the NLSY97. Obesity. 2009;17:1274–1280. doi: 10.1038/oby.2009.5. [DOI] [PubMed] [Google Scholar]
- Peng J, Müller HG. Distance-based clustering of sparsely observed stochastic processes, with applications to online auctions. The Annals of Applied Statistics. 2008;2:1056–1077. doi: 10.2307/30245120. [DOI] [Google Scholar]
- Preston SH, Mehta NK, Stokes A. Modeling obesity histories in cohort analyses of health and mortality. Epidemiology. 2013;24:158–166. doi: 10.1097/EDE.0b013e3182770217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay JO, Hooker G, Graves S. Functional data analysis with R and MATLAB. New York, NY: Springer; 2009. [Google Scholar]
- Ramsay JO, Silverman BW. Functional data analysis. New York, NY: Springer; 2005. [Google Scholar]
- RAND Corporation. RAND HRS Data, Version L [Data file] Santa Monica, CA: Author; 2011. Dec, (Vol. 2012) (Produced by the RAND Center for the Study of Aging, with funding from the National Institute on Aging and the Social Security Administration) [Google Scholar]
- Reither EN, Hauser RM, Yang Y. Do birth cohorts matter? Age–period–cohort analyses of the obesity epidemic in the United States. Social Science & Medicine. 2009;69:1439–1448. doi: 10.1016/j.socscimed.2009.08.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richman EL, Stampfer MJ. Weight loss and mortality in the elderly: Separating cause and effect. Journal of Internal Medicine. 2010;268:103–105. doi: 10.1111/j.1365-2796.2010.02227.x. [DOI] [PubMed] [Google Scholar]
- Rowe JW, Kahn RL. Successful aging. The Gerontologist. 1997;37:433–440. doi: 10.1093/geront/37.4.433. [DOI] [PubMed] [Google Scholar]
- Rowland ML. Self-reported weight and height. The American Journal of Clinical Nutrition. 1990;52:1125–1133. doi: 10.1093/ajcn/52.6.1125. [DOI] [PubMed] [Google Scholar]
- StataCorp. Stata statistical software: Release 13. College Station, TX: Author; 2013. [Google Scholar]
- Stevens J, Juhaeri J, Cai J. Changes in body mass index prior to baseline among participants who are ill or who die during the early years of follow-up. American Journal of Epidemiology. 2001;153:946–953. doi: 10.1093/aje/153.10.946. [DOI] [PubMed] [Google Scholar]
- Strandberg TE, Stenholm S, Strandberg AY, Salomaa VV, Pitkälä KH, Tilvis RS. The “obesity paradox,” frailty, disability, and mortality in older men: A prospective, longitudinal cohort study. American Journal of Epidemiology. 2013;178:1452–1460. doi: 10.1093/aje/kwt157. [DOI] [PubMed] [Google Scholar]
- Strandberg TE, Strandberg AY, Salomaa VV, Pitkälä KH, Tilvis RS, Sirola J, Miettinen TA. Explaining the obesity paradox: Cardiovascular risk, weight change, and mortality during long-term follow-up in men. European Heart Journal. 2009;30:1720–1727. doi: 10.1093/eurheartj/ehp162. [DOI] [PubMed] [Google Scholar]
- Topinková E. Aging, disability and frailty. Annals of Nutrition and Metabolism. 2008;52(Suppl 1):6–11. doi: 10.1159/000115340. [DOI] [PubMed] [Google Scholar]
- Walsemann KM, Ailshire JA. BMI trajectories during the transition to older adulthood: Persistent, widening, or diminishing disparities by ethnicity and education? Research on Aging. 2011;33:286–311. doi: 10.1177/0164027511399104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward JH., Jr Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association. 1963;58:236–244. doi: 10.2307/2282967. [DOI] [Google Scholar]
- Wolf AM, Colditz GA. Current estimates of the economic cost of obesity in the United States. Obesity Research. 1998;6:173–175. doi: 10.1002/j.1550-8528.1998.tb00322.x. [DOI] [PubMed] [Google Scholar]
- Yao F. Functional principal component analysis for longitudinal and survival data. Statistica Sinica. 2007;17:965–983. [Google Scholar]
- Yao F, Müller HG, Wang JL. Functional data analysis for sparse longitudinal data. Journal of the American Statistical Association. 2005;100:577–590. [Google Scholar]
- Zajacova A, Ailshire J. Body mass trajectories and mortality among older adults: A joint growth mixture-discrete-time survival analysis. The Gerontologist. 2013;54:221–231. doi: 10.1093/geront/gns164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zajacova A, Burgard SA. Shape of the BMI–mortality association by cause of death, using generalized additive models: NHIS 1986–2002. Journal of Aging and Health. 2011;24:191–211. doi: 10.1177/0898264311406268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng H, Tumin D, Qian Z. Obesity and mortality risk: New findings from body mass index trajectories. American Journal of Epidemiology. 2013;178:1591–1599. doi: 10.1093/aje/kwt179. [DOI] [PMC free article] [PubMed] [Google Scholar]