Abstract
This work presents an acoustofluidic device for manipulating coated microbubbles, designed for the simultaneous use of optical and acoustical tweezers. A comprehensive characterization of the acoustic pressure in the device is presented, obtained by the synergic use of different techniques in the range of acoustic frequencies where visual observations showed aggregation of polymer-coated microbubbles. In absence of bubbles, the combined use of laser vibrometry and finite element modelling supported a non-invasive measurement of the acoustic pressure and an enhanced understanding of the system resonances. Calibrated holographic optical tweezers were used for direct measurements of the acoustic forces acting on an isolated microbubble, at low driving pressures, and to confirm the spatial distribution of the acoustic field. This allowed quantitative acoustic pressure measurements by particle tracking, using polystyrene beads, and an evaluation of the related uncertainties. This process facilitated the extension of tracking to microbubbles, which have a negative acoustophoretic contrast factor, allowing acoustic force measurements on bubbles at higher pressures than optical tweezers, highlighting four peaks in the acoustic response of the device. Results and methodologies are relevant to acoustofluidic applications requiring a precise characterization of the acoustic field and, in general, to biomedical applications with microbubbles or deformable particles.
I. INTRODUCTION
Current medical applications that exploit micron-sized lipid-coated microbubbles require, in addition to number concentration and size distribution of the bubbles, an accurate knowledge of their acoustic emission, dictated by the bubble coating parameters (i.e., shell viscosity, stiffness, thickness). The acoustic fingerprint of the selected bubbles is then used as input for scanning systems and procedures.1 For current diagnostic applications, however, precise knowledge of bubble parameters is not strictly necessary: contrast enhanced ultrasound in the detection of liver cancer or heart diseases relies on large statistical populations of bubbles and is successful with a binary response, i.e., an area brighter/darker than the background indicates a change in the blood distribution and therefore a potential metastasis.2,3 Precise characterization of the acoustical behaviour of bubble populations becomes crucial when extending diagnostic applications to areas with less blood (e.g., prostate, breast) or for therapeutic developments such as drug delivery and targeted microbubbles.4–6 In these emerging applications ligands and drugs are introduced into the bubble coating and, consequently, knowing how this will affect bubble behaviour under acoustic excitation will be necessary for dosimetry and quantitative imaging.7
Additionally, if the acoustic emission is sufficiently well known, the non-linear response of bubbles to environmental changes makes them potentially sensitive bio-sensors.8 With these aims, it is advantageous to devise a metrological environment where bubbles can be manipulated, isolated and delivered into specific positions, to be probed by an acoustic beam to calibrate their acoustic behaviour.
This work presents an acoustofluidic device operating at 150–180 kHz, for the simultaneous optical and acoustical manipulation of microbubbles. This study focuses on the acoustic characterization of the device, both in terms of how energy is transferred to its microchannels and of the acoustic forces acting on polymer-coated bubbles, with the aim of designing a protocol to determine the acoustic pressure in a generic microfluidic chip, as a function of the driving parameters and with the lowest possible uncertainty. In order to avoid direct measurements of the pressure using a needle hydrophone, which would greatly perturb the field within the comparably-sized microchannel, two different methods have been used giving complementary information: finite elements (FE) calibrated laser vibrometry and particle tracking. In addition to this, a calibrated Laguerre-Gaussian optical trap was used to directly measure the acoustic forces acting on the bubbles as a function of their position in the device. The experimental procedure allowed the use of polymer coated microbubbles themselves as tracers, so that direct force measurements were possible on them at higher driving pressures and as a function of frequency.
A. Advantages of a hybrid manipulation tool
Optical tweezers seem the perfect micro-manipulation tool, as they have demonstrated their potential to manipulate microbubbles.9,10 In some studies,11–14 lipid-coated microbubbles were manipulated by optical tweezers to a fixed distance from a wall or from another bubble and then an acoustic pulse train was sent to excite volume oscillations.
Variations in high-speed dynamics11,12 or in the acoustic emission13,14 were then observed and analyzed, inferring from them changes in the involved forces. In these studies, bubble shell characteristics were taken as input parameters known with high precision and, since the acoustic field was generated from a transducer in the far field, there was little control on the local value of the acoustic pressure acting on the bubble. In all these studies, moreover, the laser light was removed before the arrival of the exciting acoustic pulses and the bubble was recaptured in the optical trap after each experiment.
A possible reason for this modus operandi is the different scale of the acoustical and optical forces near bubble resonance: primary Bjerknes forces can easily reach the nano-newton range,15 while the maximum optical trapping force is often on the order of a few piconewtons.16,17 The optical field is therefore not sufficient to maintain the bubbles in place during near-resonance excitation. Bubble manipulation, in the presence of an acoustic probe in the 1–10 MHz range (i.e., where bubbles with diameters between 0.6 and 4 μm have their resonance), therefore requires stronger forces than those exerted by optical trapping, and these can be offered by acoustic manipulation.18 Acoustic forces on micron-sized particles of nano-newton order can be estimated, for instance, from the data presented by Barnkob et al.19 and by Sitters et al.20
Acoustic manipulation of micron-sized bubbles in an acoustofluidic device has been achieved by Rabaud et al.,21,22 who worked with 20–50 μm diameter bubbles and frequencies between 20 and 140 kHz to study bubble dynamics and interactions below bubbles' acoustic resonance. These authors report the squeezing of their bubbles on the coverslip and the generation of surface waves on the bubble surface.
Acoustical tweezers, however, offer a much lower spatial resolution than their optical counterpart due to the wavelength being larger, so a hybrid system is desirable. Simultaneous optical and acoustical trapping in a microfluidic device has been successfully realised using solid particles,23,24 thus allowing the direct measurement of acoustic forces.20,24,25 Hybrid manipulation of microbubbles, however, presents additional challenges: not only they are low-optical index particles, and therefore require non-conventional laser configurations for optical tweezing, but can acoustically be treated as particles only when the trapping frequency is below the bubble resonance frequency () and at pressures where shape/volume oscillations and bubble-bubble interactions (i.e., secondary Bjerknes forces26) can be neglected.27
II. MATERIALS AND METHODS
Three different experimental set-ups have been used in this work, one for each of the measurement techniques detailed below (see supplementary material S128). The core of each experimental set-up is a glass microfluidic chip [W: 25 mm, H: 2 mm, L: 20 mm], designed at the National Physical Laboratory (NPL) and manufactured by Dolomite Microfluidics (Royston, UK). The microfluidic chip (Fig. 1) is made from four different glass layers fused together (by Dolomite) and presents a K-shaped manifold of etched microchannels (330 μm × 430 μm section) and a trapezoidal window for lateral illumination of the central area (see section S2 of the supplementary information28). The chip is mounted on a glass base [W: 40 mm, H: 1 mm, L: 25 mm], which provides fluidic connection to the in/out ports, and the base itself is mounted on a metallic holder, that can in turn be inserted in the optical tweezers set-up or used outside it. The dimensions of the base+chip assembly are constrained by the necessity of mounting it under the optical microscope and the holder's design allowed quick insertion/extraction from the optical tweezers set-up.
FIG. 1.
(Color online) The microfluidic chip described in this work. Also highlighted (bottom-right) are the directions of the reference axes, with the along the main channel and the perpendicular to it. The origin of the coordinates was set at the start of the channel, on the side where the piezo transducer sits. (See supplementary figure S2 for a technical drawing; Ref. 28).
Optical access to each channel was guaranteed by a 100 μm wide optically polished flat surface on its top and bottom, to eliminate lensing effects on the laser beams used for optical tweezing.17 The thickness of the polished at surface above the trapping region (“coverslip,” in the following text) was 0.17 mm. The use of multiple layers allowed the channels and the window to have a rectangular section with rounded edges (see schematic28). The K-shaped geometry has been chosen to facilitate future studies, where the two inclined channels will be used for monitoring acoustic emission from the bubbles in spectroscopy experiments.20,29 The angle of inclination of the side channels is (almost) arbitrary and has no effect on the operation of the device as described in this study.
A. Acoustic manipulation
The acoustic field is generated using a 5.9 mm × 5.9 mm × 13 mm Lead Zirconate Titanate (PZT) transducer (Morgan Ceramics Ltd., Southampton, UK, nominal resonance in air: ∼154 kHz), bonded on the device's top surface using conductive epoxy (Circuit works, CW2400). The voltage driving the PZT transducer was amplified using a chain formed by a signal generator (Agilent 33250A), a power amplifier (E&I, model A300) and a 1:25 step-up transformer. The latter reduced the impedance mismatch in the range 130–180 kHz, which was used for the experiments.
In isothermal and inviscid conditions, an isolated microsphere in an acoustic standing wave experiences a force (Gor'kov model),30,31
| (1) |
where is the particle radius, and are the pressure and the velocity in the inviscid fluid due to the input acoustic wave, is the ratio between the compressibilities of the particle () and the liquid () and is the ratio of their densities. In the simple case of a sinusoidal standing wave in the direction, Eq. (1) gives19,30
| (2) |
where is the amplitude of the impinging unperturbed wave (i.e., in absence of scattering), , is the speed of sound in the liquid medium, k is the wave number and is also known as acoustophoretic contrast factor. The fact that the force depends on diameter and on physical properties allows sorting, mixing and counting applications, often achieved using acoustic frequencies in the MHz range.18
A limited number of the experiments described here used carboxylated polystyrene beads (IZON, model CPC4000, nominal mode diameter: 3850 nm, nominal average diameter: 4000 nm): mono-disperse particles with (calculated using physical properties from the literature32) which would move toward acoustic nodes. In this study, however, has been corrected considering the more complete thermo-viscous conditions,33 to become (calculated at 160 kHz and using the average particle size).
Polymer-coated microbubbles (ExpancelTM WU-20, gas: iso-butane, coating: copolymer, diameter: 6–20 μm, manufactured by Akzo Nobel, Amsterdam, NL) starred in most of the experiments described in this study, after being expanded by leaving them for 10 min in boiled water. Given that in inviscid and isothermal conditions, these bubbles should therefore move toward antinodes (thermos-viscous effects are negligible, as in the worst possible case treated here). However, this is only true when the trapping frequency is below the bubble resonance frequency () and at pressures where shape/volume oscillations can be neglected, i.e., when they can be treated as particles.27
For a polymeric-shelled bubble,34 the resonance frequency depends on the stiffness χ of the shell, which in turn is given by with and , respectively, Young modulus and Poisson's ratio of the material in the shell and its thickness. Using the Hoff model [see Eq. (S1)28] and typical properties from the literature (ambient pressure = 101 kPa, specific heat ratio = 1.07, surface tension = 0.72 N m–1, Young Modulus: = 3 GPa, Poisson's ratio = 0.3, shell thickness 3 nm),32,35 the resonant frequency for the range of Expancel diameters utilised in this study was calculated to be above 1 MHz.
The choice of 130–180 kHz as trapping range, far below the resonant frequency of Expancel, therefore allowed sub-resonant trapping of the selected microbubbles. In future studies, it will allow simultaneous trapping and near-resonance probing of commercial ultrasound contrast agents microbubbles (typically resonant at 2–10 MHz).1,2
B. Frequency range selection: Electric impedance and visualization
Impedance spectroscopy can be used as a first technique to identify the natural modes of the system and select the operational regions where trapping of microbubbles in the device may occur.18,36 In this work, the electrical response of the whole system (i.e., PZT + glass chip + chip holder) was monitored using an impedance analyzer (Agilent, model 4294A), after filling the chip with a diluted solution containing 10% sodium dodecyl sulfate (SDS). Once the candidate frequencies had been identified, the microfluidic chip was inserted (with its holder) into the microscope set-up and filled with a diluted solution containing 10% sodium dodecyl sulfate (SDS) and polymer-coated Expancel microbubbles (300–500 bubbles/mL).
A quick check confirmed that the impedance did not change significantly when the chip was inserted under the microscope.
In presence of the SDS, the number of bubbles stuck on the coverslip was negligible. The acoustic field was then switched on and its frequency scanned over the range 100–180 kHz in 100 Hz steps.
Different cases were encountered: at some frequencies, there was quick aggregation in specific locations, at others aggregation was achieved over longer periods, at others no aggregation was observed, but instead a movement of the particles/bubbles away from the transducer. When aggregation was observed, the experiment was run until the formed a “stable aggregation,” whose centre of mass fluctuated very little (compared to its overall size).
A CCD camera (Thorlabs, model DCU223M) was used to monitor microbubble dynamics through an InfiniProbe TS-160 objective (Infinity, USA) in a bright field microscopy set-up, in order to visually determine which frequencies were more effective for trapping. Particular care was exercised to avoid pressure gradients across the microchannel manifold, as these would cause a background flow. In particular, the channels were first checked for the presence of air pockets, that were eliminated by flushing before sealing the chip sides. In order to avoid any capillary flow in the channels, in all the experiments described in this study the inlet/outlet pipes were filled with the same amount of water + SDS solution and the NanoportTM fittings were sealed before operation. When present, the only observed movement of bubbles/particles was due to the acoustic field.
C. Finite elements modelling and laser vibrometer
A Finite Element (FE) model of the PZT + chip system was developed using the PAFEC vibro-acoustics software37 and used to explore the acoustic pressure distributions in the trapping range. The total acoustic energy, proportional to the sum of the squared pressure over all the mesh nodes in the fluid, was used to identify potential resonances of the system in the acoustic spectrum.18,36 In the presence of standing waves, the FE model establishes a relationship between the displacement of the top surface and the pressure in the channel.
In this work, this relationship was exploited to derive a non-invasive estimate of the acoustic pressure in the channel by measuring the displacement of the glass surface 0.17 mm above the channel (i.e., on the top of the chip) with a laser vibrometer and calibrating the model.
For vibrometry measurements, the glass chip was filled with deionised water and maintained at room temperature. The top surface of the glass chip was masked with paper tape and scanned with a laser vibrometer (Polytec, PSV-400), while the PZT was driven across the frequency range of interest with 0.5 kHz resolution. With this analysis, it was possible to identify whether peaks in the impedance spectrum potentially corresponded to standing waves in the microfluidic channels.38 Measurements of the velocity normal to the surface of the chip over the range 150–180 kHz were used to get a deeper understanding of how the vibrational energy is transferred to the microfluidic channel at different frequencies, through comparison with classical wave-propagation theories. This analysis, previously discussed elsewhere39 and presented in a more comprehensive form here, highlighted frequencies where the acoustic field in the channel is due to refraction of Lamb waves at the interface and others where vibrational resonances of the chip dominated.
D. Tracking of polystyrene beads and polymer-coated microbubbles
For these experiments, CPC4000 particles or Expancel bubbles were diluted in water-SDS solution (10% SDS) and injected into the chip, where the acoustic field was activated. Then the trajectories of isolated particles/bubbles moving toward the aggregation point were recorded, at a single frequency but for different transducer voltages, using the MTrackJ plugin in ImageJ (Fiji distribution40). Calibration of the images was obtained using a 400 μm NPL graticule (National Physical Laboratory, UK) and a basic thresholding method was used to establish the diameter of each tracked particle, thus allowing an independent measurement of their size distribution. Uncertainties on diameter measurements are due to pixel resolution, but the images may be affected by defocusing: an uncertainty of ±0.2 μm was assigned to this method, taking into account both effects. Since an excellent agreement was observed between the statistical parameters given by the manufacturer and those measured optically in the case of CPC 4000 (measured mode diameter: 3.9 μm, measured average diameter: 3.7 μm, 90% percentile: 4.2 μm; see supplementary figure S3),28 the same uncertainty was assumed in this study for size measurements with the (larger) bubbles.
As demonstrated by Barnkob et al.,19,30 who pioneered the technique, a balance between [Eq. (2)] and Stokes drag (where is the viscosity of the liquid, the radius of the particle and its velocity) leads to a model of the velocity that can be fitted to tracking measurements, with being the only unknown. In this study, particles/bubbles were tracked until they were isolated (i.e., their trajectories were linear toward the aggregation point and at least ten diameters away from other tracers) and in absence of capillary flow. The aggregation point was well defined, and could then be selected by the operator at the start of the tracking, while was part of the fitting procedure for Barnkob et al. (see Secs. III H and IV A for more details on the practical application).
This method is well established in the literature when particles are involved,19,30 but the key assumptions (i.e., low Reynolds number, constant spherical shape of the traced particle/bubble, 1D planar wave) needed a review before bubbles could be used as tracers.
Equally important was to establish the potential effects on drag of bubble deformability,41,42 of walls presence,22,41,43,44 of temperature changes,33 of interparticle forces.45 As discussed in the supplementary section S4, the cumulative effect of these factors is lower than 0.5% in our set-up—as used in this study—and was therefore neglected. Like detailed above for the particles, threshold measurements allowed a measurement of the size distribution of the used sample of Expancel after expansion (measured mode diameter: 10.1 μm, measured average diameter: 12.4 μm, 90% percentile: 18.1 μm; see supplementary figure S3).28
Direct acoustic force measurements on Expancel bubbles were conducted in two different realisations of the chip in Fig. 1, named “C” and “K,” as a way to test the robustness of this method when microbubbles are involved. The known differences between chip C and chip K were the type of nanofluidic ports utilised (F-122-H for chip C and F-125-H for chip K, both from Upchurch Scientific) and, potentially, the bonding of the PZT (made in-house).
E. Optical tweezers
For these experiments, the glass chip (with its holder) was mounted in the optical tweezers set-up, fully detailed elsewhere.46 The trapping laser was a single mode Nd:YAG laser (Laser Quantum, Ventus, wavelength: λ = 1064 nm, used at fixed output power in this study: Plaser = 300 mW, measured at the laser output). A Laguerre-Gaussian (LG) laser mode was holographically generated via imprinting a helical phase, ( is the topological charge in this study, and is the azimuthal angle), on to the beam via a nematic liquid crystal spatial light modulator (SLM) (Boulder Non-Linear Systems Inc., XY Series, 256 × 256 pixels). The focusing was provided by a high numerical aperture objective lens (Nikon, PLAN APO IR, 60 x, 1.27 NA, water immersion), corrected for the 0.17 mm thickness of glass above the channel. A CCD camera (Thorlabs, model DCU223M) was used for visualisation during optical trapping.
These parameter gave a laser power at the trap mW, estimated assuming of the input power into the diffracted first order, transmittance for the objective, and a trap diameter of , measured at the focus as the distance between two opposite intensity peaks in the LG mode.
For each measurement, the trapped bubble was positioned at 30 μm below the coverslip and at a fixed position along the main channel (X axis). The position fluctuations of the bubble were measured by back-focal plane (BFP) interferometry.20,47,48 While the forward-scattered light from the trapping beam is abundantly available for high-refractive index particles, the interference pattern was either weak or not observable for a microbubble trapped in the dark core of a Laguerre-Gaussian beam. A second, Gaussian probe laser beam (He-Ne, 2mW peak power) was therefore necessary: forward scattered light was captured by an aspheric condenser (Thorlabs ACL2520) and recorded by a quadrant photodiode (QPD) manufactured by Thorlabs (model PQD80A).17 Calibration of the QPD signal was obtained for each bubble size by moving the trapped bubble in the X and Y directions and comparing the recorded QPD voltage with the displacement observed by the camera: for a 12.4 μm bubble, this gave a calibration factor of . The position fluctuations of the bubble within the optical trap were recorded for 10 s at 20 000 samples/s and then fitted with a normal distribution (mean: , standard deviation: ). While was used to check that no drift was present, was used to determine the trap stiffness , where kB is the Boltzmann constant and T is the temperature.49 At this point, the acoustic field was switched on and the displacement of the average bubble position was used to determine the applied force. Displacements used in this study were in the linear range of the force-displacement relationship (Hooke's law).50
III. CHARACTERIZATION OF THE ACOUSTOFLUIDIC DEVICE
In order to identify the most effective operational conditions for acoustofluidic manipulation and for metrological purposes, a number of different techniques have been used to investigate the acoustical response of the device. Each step in the procedure allowed a reduction in the number of frequencies potentially identified for acoustic trapping, until only four remained. Direct force measurements by optical tweezers were also used to check the main assumptions behind particle/bubble tracking methods.
A. Visual analysis of peaks in the impedance spectrum
An impedance scan in the range 100–180 kHz, conducted across the impedance matching circuit after filling the chip with deionised water, showed 15 peaks, each potentially corresponding to a resonance of the system (see supplementary section S6).28 Not all of these peaks, however, would necessarily result in good trapping conditions: for some of these candidate frequencies energy is confined in parts of the chip not easily exploitable. For this part of the study, the chip was filled with Expancel, the input voltage was set (e.g., 20 mV peak-to-peak, also reported as 20 mVpp) and bubble dynamics was visually monitored in the range 100–180 kHz (100 Hz steps), with particular attention paid close to the peak frequencies identified by the impedance spectrum. With the exception of 105 kHz, most of the movement was observed in the range 130–176 kHz (i.e., where the impedance is better matched), but stable aggregation of Expancel microbubbles was observed only in discrete ranges: 142.5 ± 0.5 kHz, 163 ± 3 kHz (see Mm. 1 at 164.5 kHz and Mm. 2 at 166.0 kHz), 170 ± 1 kHz (see Mm. 3 for 170.0 kHz), and 174.5 ± 0.5 kHz (see Mm. 4 for 174.5 kHz). For all these frequencies, microbubbles moved towards an aggregation area (whose position depended on the specific frequency range), where they formed an ellipsoidal structure (see Fig. 2 and related videos28).
FIG. 2.
(Color online) Composite images showing aggregation positions at the different frequencies, after 30 s of operation, for a fixed input voltage of 20 mVpp. For scaling purposes, the width of each channel is 430 μm. See multimedia material for 30 fps movies at different frequencies: 164.5 kHz (Mm. 1 for 164.5 kHz), 166.0 kHz (Mm. 2 for 166.0 kHz), 170.0 kHz (Mm. 3 for 170 kHz), 174.5 kHz (Mm. 4 for 174.5 kHz).
Mm. 1.
Movement of Expancel in the chip at 164.5 kHz, 20 mVpp on the transducer. At this frequency, bubbles aggregated in the centre of the chip, where they formed a spherical cloud. While aggregating, they formed structures perpendicular to the direction of motion, due to bubble-bubble interactions (secondary Bjerknes forces). The video shows the central part of the chip, one side of the main channel and one of the angled channels and has been taken at 30 frames per second (fps). This is a file of type “mov” (1.4 Mb).
Mm. 2.
Movement of Expancel in the chip at 166.0 kHz, 20 mVpp on the transducer. At 166–168 kHz, bubbles still aggregated in the central part of the microfluidic chip, but closer to the joining with the side channel, highlighting a potential change in the field. The final shape of the cloud appeared similar to the one observed in Mm. 1. The video shows the central part of the chip, one side of the main channel and one of the angled channels and has been taken at 30 frames per second (fps). This is a file of type “mov” (1.1 Mb).
Mm. 3.
Movement of Expancel in the chip at 170.0 kHz, 20 mVpp on the transducer. Also at this frequency bubbles aggregated in the centre of the chip, but at a lower speed than in Mm. 1, pointing to a less strong trap. The video shows the central part of the chip, one side of the main channel and one of the angled channels and has been taken at 30 frames per second (fps). This is a file of type “mov” (0.9 Mb).
Mm. 4.
Movement of Expancel in the chip at 174.5 kHz, 20 mVpp on the transducer. At this frequency, bubbles did not aggregate in the central part of the microfluidic chip, but repeatedly in one of the side channels. Both bubble velocities and the shape of the trap appear different from Mm. 1. All these changes point to a net change in the acoustic field. At the start of the video the acoustic field is OFF: the bubbles had been moved away from a previous aggregation using 164.5 kHz. The video zooms on the part of the chip where the main channel joins one of the angled channels and has been taken at 30 frames per second (fps). A similar aggregation was observed at the opposite side of the chip, in a symmetrical position. This is a file of type “mov” (2.0 Mb).
Within each of these ranges, the velocity of the microbubbles in the recorded videos showed a maximum and then decreased as frequency was increased, until the next aggregation-frequency range was entered, but the method did not allow to resolve whether the largest ranges (e.g., had a multiple peak structure (bubbles aggregated in a slightly different position at 166.0 kHz; see Mm. 2 at 166.0 kHz). Microbubbles aggregated most quickly in the range (see Mm. 4 at 174.5 kHz), but in a position away from the central region of the chip (Fig. 2). Trapping in the central region was observed instead at and (see Mm. 1 and Mm. 3). The central area of the chip is particularly important, as this is the region where the optical tweezers operate, so these two frequency ranges were the most promising for operation.
Within the two ranges, aggregation in the center of the chip (i.e., at the very center of the K-shaped manifold, 12.5 mm from either edge of the main microchannel) could be repeatedly observed at (see Mm. 1) in different realisations of the chip. This frequency subset will be investigated with more detail than others in the text below.
B. Results of the FE model
Figure 3 reports results of the finite element model (FEM) in terms of the RMS value of the displacement normal to the top surface of the chip, simulated along the length of the main microfluidic channel, for different values of the driving frequency in the range 70–180 kHz (1 V excitation on the piezo). According to the FEM, different frequencies generate a standing wave pattern on the top surface of the chip. Looking in particular at the range 130–180 kHz, there are five candidate frequencies: 134, 142.5, 164, 171, and 173 kHz.
FIG. 3.
(Color online) Predicted RMS value of the normal displacement on the top surface of the glass chip along the channel (i.e., X direction, where the origin sits on the side of the PZT; see also Fig. 1) as a function of frequency, according to the FE model. Particularly interesting for this study are the results at 143 kHz, 164 kHz, and 173 kHz, which show a standing wave pattern. Results reported here are in absence of damping.
These peaks are fewer in number than those identified via impedance scans (see Table I) and point to additional excitation frequencies when compared to those where aggregation was experimentally observed (Fig. 2). Passing from a real system to a FE model, however, required a certain degree of simplification, so a discrepancy between theory and experiment is usually expected.51,52 In our case, the FE model was accurate in terms of the glass material properties—the speed of sound in glass was measured using 5 MHz pulses and a sample piece of glass from Dolomite, obtaining for longitudinal waves and for shear waves; density of the glass was measured as 2639.5 ± 0.5 kg m–3—but did not consider other factors, e.g., the bonding between the PZT crystal and the glass chip or any absorption in the glass/fluid.
TABLE I.
Pairing between the peak frequencies in measurements and in modelling. The right hand side of the table reports the “useful” frequency ranges, as determined by the method detailed in the first column.
| Method | Frequency / kHz | |||||
|---|---|---|---|---|---|---|
| Electric impedance | 134 ± 1 | 140 | 153 ± 7 | 163 | n.a. | 174 |
| Visual aggregation | n.a.a | 142.5 ± 0.5 | n.a. | 163 ± 3 | 170 ± 1 | 174.5 ± 0.5 |
| FEM (Fig. 3) | 134 | 141.5 | n.a. | 164 | 171 | 173.5 |
| FEM (with damping) | n.a. | 141.5 | n.a. | 164 | Merged | |
| Laser vibrometer (Fig. 5) | n.a. | 163 ± 3 | 169 ± 1 | 174.5 ± 0.5 | ||
Not available (n.a.).
Furthermore, the piezoelectric and dielectric constants associated with the crystal were obtained from the PAFEC material properties library and were therefore not measured directly. In order to test the robustness of the FE simulations, an arbitrary damping factor was therefore added in both the glass and the water: this affected the width and amplitude of some of the resonances, leaving the peaks at 142 kHz and 164 kHz unchanged and completely cancelling the peak at 134 kHz.
C. Characterization of the chip by laser vibrometer
For these measurements, the chip was held perpendicular to a laser vibrometer beam and the laser beam was scanned across the device's top surface. In order to avoid effects due to multiple reflections within the glass chip, which would influence the signal to noise ratio, a thin masking tape (∼0.08 mm thickness) was placed on the top surface of the chip. The effect of the tape on the dynamics measured by the vibrometer was checked by comparing displacements measured with multiple masks and without a mask, and no difference was observed in the maximum displacements. Figure 4 shows a typical laser vibrometer scan (162 kHz), highlighting the position of the driving PZT [an animated version of Fig. 4(a), highlighting the standing wave nature of the excitation at 162 kHz, can be found in Mm. 5].
FIG. 4.
(Color online) Results of the laser vibrometer scan at 162 kHz, 40 mVpp, with vertical scale identifying the velocity normal to the scanned surface. Also highlighted are the transducer (1), the in/out ports (2), different directions of measurement (dotted lines) and, in particular, the portion of the glass surface on top of the main channel. See Mm. 5 for an animated version of (a).
Mm. 5.
Laser vibrometer scan at 162 kHz. The video reports the velocity of vibration perpendicular to the surface (colour scale in Fig. 4). Also highlighted in the picture are the position of the PZT generating the field (top left), the illumination window (center-top), the main channel (horizontal blue-dotted line), and one of the side channels (angled red-dotted line). At this frequency, a standing wave pattern could be observed both in the illumination window and in the main channel. The main channel presented two maxima-minima and its size was highlighted by a trapped air bubble, which oscillates in counter-phase. This is a file of type “mov” (1.2 Mb).
Figure 4 shows a different modal structure between the vibrations of the trapezoidal window and the rest of the chip. It also reports a front view taken at the same frequency, showing a modal pattern in the direction perpendicular to the side face and suggesting that a vibrational mode of the whole structure was excited. Finally, Fig. 4 reports three potential directions of measurement, and in particular (with the horizontal dotted line) the 0.17 mm thin portion of glass above the main channel. Depending on the frequency, the sinusoidal pattern along this line appeared as a travelling or a standing wave, so that the RMS value of the displacement could be used to identify standing waves, as previously done in the FEM case.
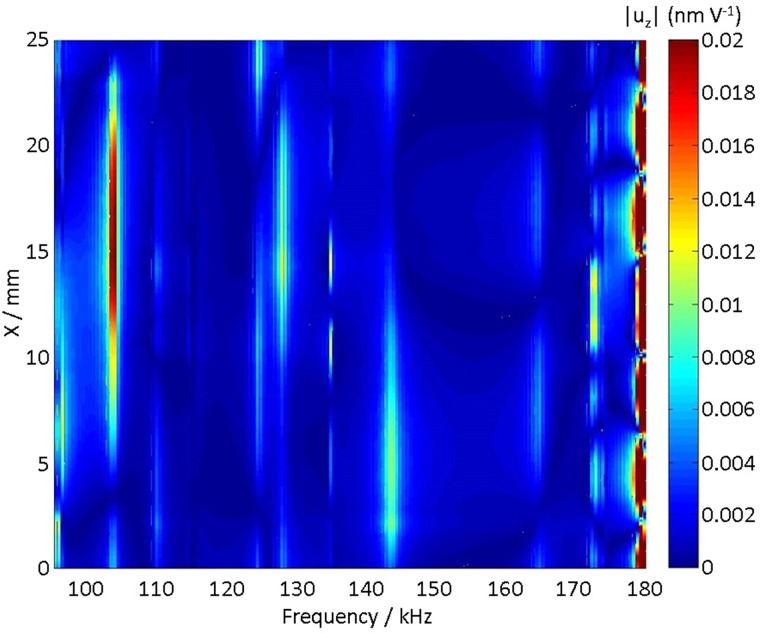
Figure 5 reports the results of vibrometer scans in the range 160–175 kHz (500 Hz step) across 24 mm (chip length: 25 mm, 70 points/mm), interpolated over a 0.2 mm × 0.5 kHz grid using cubic splines in MATLAB (The Mathworks, Natick, MA). In the range 160–175 kHz, Fig. 5 shows three active ranges of frequency (160–165 kHz, 168–170 kHz, 174–175 kHz) where areas of stable displacement appear along the chip. According to the measurements on the coverslip, there is a node at the center of the K-shaped manifold (X = 12.5 mm) both at 160–165 kHz and at 174–175 kHz, while the locations which appear as antinodes at 162–165 kHz (e.g., 5 mm and 17.5 mm) become nodes at 174–175 kHz.
FIG. 5.
(Color online) Spatial variation of the RMS value of the vertical displacement measured on the top surface of the chip, along the direction of the main channel, as reported by the laser vibrometer: (a) as a function of the input frequency (40 mVpp fixed input voltage) and (b) as a function of voltage at 164.33 kHz.
D. Comparing model and experiments
Table I presents a comparison of the experimental findings discussed so far with the FEM results. Impedance measurements show the larger number of potential frequencies where the transducer-chip system could be excited (15 peaks between 130 and 180 kHz), although it was possible to observe a stable aggregation in the chip for only a subset of these. Excitation frequencies predicted by FEM are within 1% from those where aggregation was observed. Selecting which theoretical frequency corresponds to each observed one was achieved by comparing the experimental vibration pattern on the whole top surface (i.e., data like those in Fig. 4), measured with the laser vibrometer at frequencies where aggregation was observed, with the displacement patterns predicted by theory in the range 130–180 kHz (0.5 kHz steps). For each given experimental profile, the “pairing” condition (i.e., the FEM frequency whose displacement pattern is closest to the experimentally measured one) was achieved by the cross-correlation method, commonly used in automated vision for matching two or more images. In this work, this method was used to compare the vibrational pattern detected on the top surface of the acoustofluidic chip with the displacements simulated by the finite elements model at different frequencies.
For the experimental frequency of 164.3 kHz, a difference of 300 Hz was found between the position of the peak in the experimental spectrum and the “best fit” FEM profile: 164 kHz. Similar comparisons through cross-correlation demonstrated that the profile measured at 174.3 kHz was best fitted by the FE-predicted profile at 173.5 kHz, leading to the comparison in Table I. In the rest of the paper, to avoid confusion, only the active frequencies observed in the experiments will be reported (e.g., 164.33 kHz), but the theoretical results will be those of the corresponding “best fit” frequency, from Table I.
E. Energy transfer to the channel
The use of a laser vibrometer to characterise acoustofluidic devices has previously been reported in the literature.1,5,52 Previous studies, however, were conducted mainly at MHz frequencies and often reported difficulties in comparing laser vibrometer results to FEM or visualisation results. Even in our case, when only a slight discrepancy was observed between model and experiment—also thanks to the glass thickness between the top surface and the channel being much smaller than the wavelength in both materials—uncertainties remained in whether it was possible, using what was detected on the top surface, to infer the acoustic pressure distribution in the channel. With the 1 order of magnitude change of impedance between glass (1.46 × 107 Pa s m–1, measured in our case) and water (1.48 × 106 Pa s m−1 at 20 °C, calculated from literature data32), if energy were transferred from PZT to the channel through Lamb waves, their refraction at the glass-water boundary would need to be taken into account.53 In this case, there would not be a direct relationship between the pressure distribution inside the main channel and the vertical displacement of the thin glass wall above it, as measured by laser vibrometry: part of the energy would be dissipated along the glass interface.18
In the case of a structural resonance, the situation is much simpler: at the fluid side of the thin glass wall, vertical displacement and acoustic pressure show the same spatial distribution and this is replicated on the top surface. In order to establish the types of vibrations observed in the acoustofluidic system at the different input frequencies, the wavelength of the sinusoidal wave travelling in the glass directly above the main channel was measured (see Fig. 4) and multiplied by the driving frequency to obtain a surface wave velocity, V. The dispersion curve of this quantity was used to understand how the energy was transferred from the PZT to the channel.
In particular, Fig. 6 shows a comparison between the dispersion curve of the surface velocities V—non-dimensional, because reported relative to the shear speed —and the asymmetrical part of the first Lamb mode,54 calculated for a thickness of 3.0 mm (i.e., the total thickness of the glass chip). The trend in Fig. 6 shows that while for most of the frequencies the waves travelling on the top surface of the chip are asymmetrical Lamb waves, there are three regions where this is no longer true and a peak appears: 103 ± 3 kHz, 160 ± 5 kHz, 173 ± 3 kHz. For these peak frequencies, a standing wave pattern was observed on the top surface and a clear aggregation pattern was found in the microfluidic chip; energy reaches the channel through excitation of a resonance (i.e., a mode) of the whole glass microchip. Modes are more sensitive to temperature changes, but are also potentially stronger and can easily be identified by observing the motion of the top surface.
FIG. 6.
(Color online) Comparison of surface velocities along the direction of the main channel (diamonds) with the theoretical values for a Lamb asymmetrical mode (solid line). The vertical axis reports the ratio between the measured longitudinal speed V and the shear wave velocity .
Conversely, the frequency of 143 kHz, where aggregation was observed, follows Lamb's dispersion curve. A more thorough analysis of this frequency shows that acoustic manipulation at this frequency is only partially due to energy transferred to the channel via surface waves, like in other devices:55 this frequency corresponds in fact to a mode of the illumination window.
F. Pressure measurements in the channel by laser vibrometry
Having established that the observed modes are due to structural vibrations of the whole chip, it is possible to exploit the pairing between displacements on top of the channel (as measured by laser vibrometer) and FEM predictions to evaluate the acoustic pressure in the chip by laser vibrometry. The first step (Fig. 7) consists in comparing predicted displacements (e.g., at 164 kHz) and measured ones (e.g., at 164.33 kHz). Once a scaling factor on displacement is found, this is applied to the FEM-calculated pressure in the chip to get an estimated pressure based on measurements to get an overall calibration factor, , for vibrometer measurements. For chip K at 164.33 kHz, .
FIG. 7.
(Color online) Laser vibrometer measurements (164.33 kHz, 20 mVpp input voltage) vs predicted displacement (164 kHz, 130 Vpp on the transducer) at the upper surface of the device, over the main channel. The center of the K-shaped manifold is at X = 12.5 mm.
Assuming the FEM values are a fit to the experimental data and 2 degrees of freedom (i.e., the voltage and the frequency), a test on the data was performed to compare the measured displacements with their simulated “best fit” (i.e., the corresponding FE model).56 Typical results gave a confidence level of 90% for the fit. The overall uncertainty of this method was estimated at 15% (i.e., 1 standard deviation or 68% confidence level). This value takes into account the contribution from (∼9%) and a weight representing the 90% confidence with which the FE model predicts the measured displacements (i.e., the t-factor related to a 90% confidence, from the Student distribution with n–2 degrees of freedom, where n = 100 is the number of points in each laser vibrometer scan and t = 1.66).
This method allows a quick determination of the acoustic peak pressure in the channel. Its uncertainty, at least for the cases presented above, is potentially comparable to that of a calibrated hydrophone (±1 dB = ±12%). This method is non-invasive compared to hydrophone measurements, as nothing had to be inserted into the channel. Using a FE model calibrated by laser vibrometer to establish the pressure in the channel at different voltages has one major drawback: it assumes linearity between voltage, displacement and acoustic pressure in the channel. This hypothesis may fail as the driving voltage is increased and will be challenged in the next two sections of this work.
G. Force measurements by holographic optical tweezers
For the data in Fig. 8(a), the displacement of a 12.3 μm diameter Expancel bubble relative to its equilibrium position in the optical trap, due to the acoustic forces at 165 kHz was recorded at different positions along the main channel of chip C, in a region that included the center of the microfluidic chip. Displacements were transformed into force measurements using Hooke's law, and a value of the trap stiffness averaged between two measurements: one before and one after the acoustic field was on.17 With this method, the associated uncertainty on a single displacement measurement impacted largely on the uncertainty of the force measurements, which was estimated at ±0.1 pN.17
FIG. 8.
(Color online) Acoustic forces on a 12.3 μm Expancel bubble along the main channel as measured by optical tweezers: (a) force in the X direction (FX) and (b) force in the in the Y direction (FY). Input parameters: 5 mVpp and 7.5 mVpp input voltages at 165 kHz. The central part of the channel is between 12.1 and 12.9 mm. Laser parameters (Ref 46) were 74 ± 4 mW laser power at the trap, trap diameter at focus: 4.3 ± 0:1 μm, distance of the bubble from the coverslip = 30 μm. Uncertainties are reported at 68% confidence level.
Figure 8(a) shows the force in the X direction at 165 kHz (i.e., the force along the main channel, ) at both the tested voltages, and the expected negative gradient (which indicates a potential trapping position) near X = 12:5 mm, where the trap was visually observed. Data were fitted with the function using a least-squares method, where = 12:5 mm, k is the acoustic wave number and is the amplitude for each voltage. The fits in Fig. 8(a) correspond to values for the maximum force equal to and (R2 = 0:9): they describe trends compatible with a standing wave, a condition assumed in Eq. (2) and for pressure measurements based on particle tracking (Sec. III H). The force in the Y direction () showed no dependence on the voltage applied and negligible dependence on the spatial coordinate X [Fig. 8(b)]. Within the uncertainty of ±0.1 pN on each point, was compatible with a null value, thus confirming—for 165 kHz and the associated resonance—the plane-wave hypothesis in Eq. (2), at least in the 0.8 × 0.4 mm area in the center of the chip where simultaneous trapping can occur.
Unfortunately, due to limitations in the maximum force that can be measured, before the trapped bubble escapes the trapping potential or the QPD enters a non-linear regime for the force vs displacement relationship, it was not possible to record forces along the channel for values of the driving voltage higher than 10 mVpp. The obtained trends, however, were sufficient to provide in situ measurements of the acoustic force, and confirmed the sinusoidal aspect of the field predicted by the FEM model in the neighborhood of the chip center, thus allowing the use of the plane-wave approximation leading to Eq. (2) and particle/bubble tracking at 164.33 kHz.
In the following it will be assumed that this approximation is also valid at the other frequencies where aggregation was observed and in the proximity of other aggregation sites, thus allowing particle/bubble tracking also at the frequencies which show aggregation outside the central region (see Fig. 2). The latter assumption is justified by the FE model and by the laser vibrometer, which showed that the local acoustic field can always be approximated by a sinusoid, when standing waves are present.
It is worth noting that, equating the measured force with Eq. (2) and knowing the acoustophoretic contrast factor Φ, it is possible to obtain the local acoustic peak pressure using optical tweezers. If the presence of the polymeric shell is neglected and the bubble is assumed to maintain a spherical shape (a reasonable assumption at low acoustic pressures), the properties of iso-butane give and the peak pressures and .
H. Pressure measurements by particle tracking
Particle tracking is a well-established method to evaluate acoustical forces18,19,30 and, since the possibility of approximating the acoustic field near the central aggregation points with a sinusoidal plane wave has been demonstrated by optical tweezers (at least at 164.33 kHz), the expression in Eq. (2) can be used: peak pressures can be calculated straightforwardly knowing Φ and the particle radius.
For these experiments, a diluted suspension of CPC4000 polystyrene beads (speed of sound: ; density: ; Young Modulus: , Poisson's ratio: 0.34)32 was inserted in the microfluidic chip using a syringe, then the apertures at the end of the channels were sealed with Vaseline jelly to avoid spillage.
Finally, the microchip was positioned in a dedicated holder, which maintained the device parallel to the ground. A CCD camera was used to monitor particle motion toward the acoustic nodes, and to evaluate the pressure at 164.33 kHz for different driving voltages. These data were then compared with the values obtained by laser vibrometry (Fig. 9).
FIG. 9.
(Color online) Comparison of acoustic pressure amplitudes in the channel measured by FE-calibrated laser vibrometery, calibrated optical tweezers and particle tracking using CPC4000 particles at 164.33 kHz. The graph also reports the linear fit obtained from all the data between 5 mVpp and 80 mVpp (dashed line), with slope . Error bars represent 1 σ, for a 68% confidence level.
At least ten different particles were selected for each experimental condition (defined by frequency and trapping voltage) and their trajectories recorded using the MTrackJ plugin in ImageJ. The diameter of the selected particles was also measured in this process and the mode diameter was found to be (see also supplementary figure S3),28 in agreement with the one declared by the manufacturer (i.e., 3950 ± 50 nm). Selected particles met the following constraints:
-
•
They were isolated (i.e., at least 5 particle diameters from another particle) and far (i.e., at least 20 particle diameters) from the center of the aggregation area.
-
•
Tracking was interrupted when the presence of other particles altered the path.
-
•
As the voltage was increased, it was necessary to take more repeats due to the presence of acoustic streaming, in the form of vortices detaching from the junction between the two “legs” of the K-shaped manifold.
For each movie, the coordinate system was set at the center of the aggregation point, which was selected by the operator prior to tracking.
Trajectories were fitted using a least-squares method, imposing a balance between the radiation force [Eq. (2)] and Stokes drag. Using the single fitting parameter in Eq. (2) on the trajectories, a value of the peak acoustic pressure and an uncertainty could be assigned to each trajectory.30 A good agreement (i.e., R2 ∼ 0:9) was obtained in all cases. For each experimental condition (i.e., frequency and voltage of the driving signal), the final acoustic pressure amplitude was a weighted average of the calculated pressure over the analysed trajectories.
This method of determining acoustic pressure has potential for low uncertainties. When all the assumptions behind the model are verified (i.e., Stokes drag, constant shape of the particles during movement, planar wave), the major source of uncertainty on the pressure assigned to the ith trajectory (obtained with a driving voltage at frequency ) comes from the uncertainty of the associated particle diameter . As discussed above, the uncertainty related to the measured CPC4000 diameters was ∼5%. The second contribution to the total uncertainty on comes from the different values of and decreases with the number of trajectories considered, as a weighted average is performed to obtain . For the almost monodisperse CPC4000 particles considered in this study, a weighted average over ten particles leads to a final standard uncertainty lower than 5% for the value of pressure linked to each value (68% confidence level).
Figure 9 reports a comparison between the pressures measured by calibrated laser vibrometry and those obtained by particle tracking, for 164.33 kHz and voltages between 5 and 80 mVpp. Since a linear dependence between pressure and input voltage was expected, as this was found by other authors in other acoustofluidic geometries,18,30 a linear trend was used to fit the data (dashed line in Fig. 9) and the calibration coefficient was with R2 = 0.88.
A maximum calibration uncertainty of 5% (i.e., three times the uncertainty on the linear coefficient, for a 98% confidence level57) was assigned to the pressures calculated with this linear trend, relative to 164.33 kHz in the range 0–80 mVpp. The pressures measured by optical tweezers (Sec. III G) were also in good agreement with the calibration curve (see Fig. 9). This demonstrates that, at least for pressures up to 0.5 kPa, Expancel bubbles can be treated as uncoated gas particles. The validity of this assumption at higher voltages/pressures will be discussed in Sec. IV.
IV. INFORMATION DERIVED FROM BUBBLE TRAJECTORIES
A. Pressure measurements at 173.5 kHz
For these experiments, Expancel microbubbles were injected in the microfluidic chip (∼300 bubbles/mL) and the same procedure described above for particles was followed. At least ten different microbubbles were selected for each experimental condition and their trajectories recorded using the MTrackJ plugin in ImageJ (Fig. 10) (Mm. 6). A good agreement with the acoustophoretic model19,30 was obtained in all cases (i.e., R2 ∼ 0.9). A value of the pressure was calculated from each ith trajectory, treating Expancel as spherical, non-oscillating particles with negative acoustophoretic contrast factor (, calculated neglecting their polymeric shell).
FIG. 10.
(Color online) Example of Expancel bubble tracking in the microchannel (164.33 kHz, 20 mVpp). The lines represent the trajectories of isolated bubbles, as obtained by MTrackJ. An animation of the tracking process can be seen in Mm. 6.
Mm. 6.
Tracking of bubbles at 164.33 kHz. The movie shows an animation of the tracking process, joining the positions of the tracked bubbles in each frame with a continuous line. For each frame, positions were acquired by the operator clicking on the screen while using the MTrackJ macro of ImageJ. Also highlighted is the reference point (to measure velocities). This is a file of type “mov” (5 Mb).
As previously discussed, the uncertainty on , has two components: one associated to the diameter (3%–5% on each single diameter, for polydisperse Expancel) and another related to the fitting procedure (which was generally low, as typically R2 ∼ 0.9). For a given number of trajectories, however, the measurement of appeared noisier using bubbles than particles, probably reflecting the polydisperse nature of Expancel or their lower mass. The weighted average over 10 trajectories resulted in a conservative total uncertainty of 8% on each value of the acoustic pressure, , obtained by bubble tracking (68% confidence level).
An excellent agreement between the measured pressures (i.e., obtained either by bubble tracking or calibrated laser vibrometry) and the linear trend from Fig. 9 was observed at 173.5 kHz (Fig. 11): the pressure calibration within 5%, defined by particle tracking at 164.33 kHz is therefore also valid for this frequency, at least in the range 0–30 mVpp (i.e., for acoustic pressures below ∼1.5 kPa). This result extends the calibration of the acoustofluidic device for Expancel bubbles to a maximum pressure (∼1.5 kPa) three times higher than the limit previously obtained through optical tweezers measurements (∼0.5 kPa in Fig. 9).
FIG. 11.
(Color online) Comparison of acoustic pressure amplitudes in the channel measured by FE-calibrated laser vibrometery and bubble tracking at 173.5 kHz. The graphs also reports the linear fit obtained at 164.33 kHz (Fig. 9). Error bars represent 1σ, for a 68% confidence level.
In general, the hypothesis that microbubble shape remains constant during movement, thus neglecting deformations and inter-bubble interactions, need to be verified case by case. While this may be true for Expancel microbubbles far from resonance and at low applied pressures, this hypothesis may fail for lipid-coated microbubbles subject to the same acoustic field. In addition, the acoustic pressure obtained from the trajectories of coated bubbles may also be inaccurate due to the choice of neglecting the shell while calculating the acoustic contrast factor Φ. Finally, there might be an effect of the number concentration of microbubbles, as high number concentrations may give rise to bubble-bubble interactions (i.e., secondary Bjerknes forces27). Future works will look thoroughly at these issues as driving voltage is increased, but the rest of this study will focus on voltages below 30 mVpp.
B. Acoustic force spectroscopy
In the frequency range 160–175 kHz, with 20 mVpp input voltage at the frequency generator, it was always possible to identify a point toward which Expancel microbubbles converged, with a speed that depended on frequency. In practical terms, it was always possible to excite one of the resonances of the acoustouidic device (see Fig. 6).
A detailed analysis of the force spectrum for chip K, reported in Fig. 12(a) as the maximum force experienced by a 12 μm uncoated iso-butane bubble, was conducted using the Peak Analyzer in Origin 9.1 (OriginLab, 2014) and showed that four (Lorentzian) peaks were needed to fit the spectrum in the range 160–175 kHz (R2 = 0.89):
| (3) |
where is the frequency. is the baseline, is the area below each peak, its width, is the peak centre frequency. In chip K, the frequency of 164.33 kHz fell within the peak 1 (centered at , where uncertainties come from the fit) and was sufficiently far from the second peak (centered at ) not to be influenced by it. The frequency of 173.5 kHz fell in a region of the spectrum where the main contributions to the cumulative spectrum came from peak 1 and peak 4 (centered at ), but was similarly far from the third peak (centered at ), not to be influenced by it. A baseline of was also obtained from the fit.
FIG. 12.
(Color online) Maximum acoustic force on a 12 μm uncoated iso-butane bubble as a function of the driving frequency for two realisations of the microfluidic chip: (a) chip K and (b) chip C. Results were obtained by bubble tracking, at 30 mVpp input voltage (∼1430 Pa, according to calibration). Best fitting peaks (without the baseline) and cumulative fit also reported (see Table II for fitting parameters). According to this fit, the major contributions to the cumulative fit at 173.5 kHz come from the baseline, peak 4 and peak 1. Also reported in (a) are the frequencies relative of Figs. 9 and 11.
Four peaks were also observed in the spectrum of nominally-identical chip C, where the same experiment was repeated to test the robustness of this method and of the fabrication technique [Fig. 12(b)]. While the heights of the peaks and the baseline remained similar (see Table II), the central frequencies were found to be shifted – to for peak 1 (+0:4%), for peak 2 (−1%), for peak 3 (−0.7%) and for peak 4 (−0.4%) – but still within the regions where aggregation was observed (see Table I). The widths of peak 2 and 4 remained unaltered, while the ones of peak 1 and peak 3 changed when passing from the original realisation K to chip C.
TABLE II.
Main parameters of the fitting curves for two realisations of the acoustofluidic device, as calculated by Origin 9.1.
| Chip K | Chip C | Average central frequency | |
|---|---|---|---|
| Peak 1 | 163.1 ± 0.4 | ||
| Centre, (kHz) | 162.8 ± 0.1 | 163.5 ± 0.1 | |
| Amplitude, (pN) | 8.8 ± 1 | 8.5 ± 0.3 | |
| FWHM, (kHz) | 3.0 ± 0.7 | 1.5 ± 0.1 | |
| Peak 2 | 167 ± 1 | ||
| Centre, (kHz) | 167.9 ± 0.1 | 166.2 ± 0.1 | |
| Amplitude, (pN) | 5 ± 1 | 6 ± 1 | |
| FWHM, (kHz) | 1.0 ± 0.5 | 1.2 ± 0.3 | |
| Peak 3 | 171.8 ± 0.8 | ||
| Centre, (kHz) | 171.9 ± 0.3 | 170.4 ± 0.2 | |
| Amplitude, (pN) | 3 ± 1 | 2.0 ± 0.3 | |
| FWHM, (kHz) | 0.6 ± 1 | 1.5 ± 0.5 | |
| Peak 4 | 174.3 ± 0.6 | ||
| Centre, (kHz) | 174.7 ± 0.2 | 174.0 ± 0.5 | |
| Amplitude, (pN) | 6.1 ± 1 | 6.8 ± 0.2 | |
| FWHM, (kHz) | 0.7 ± 0.4 | 0.7 ± 0.5 | |
| Baseline, (pN) | 0.5 ± 0.2 | 0.5 ± 0.2 | |
| R2 | 0.89 | 0.90 |
The fitting procedure assigned a negligible baseline to both chips, but with a large uncertainty associated; a more relevant parameter to describe each peak becomes then its height above the baseline, (see Table II). The relatively large width of peak 1 may explain why motion toward an aggregation point was observed at all frequencies, even between peaks: in absence of a different resonance, this was the dominating field.
The changes observed in the spectrum were attributed to a combination of all the manufacturing differences between the two chips: each realisation of the chip will require a calibration prior to its use. Since 164.33 kHz is part of peak 1 [see Fig. 12(a)], it is reasonable to think that the plane wave approximation and the linear calibration of applies also to the whole peak. With a similar argument, based on the measurements at 173.5 kHz where the field comes from a contribution of peak 1 and peak 4, it can be expected that the linear calibration also applies to the whole of peak 4. The calibration for peak 2 and peak 3 will be tested in future studies. Finally, the presence of a baseline noise hints that bubble tracking may not be accurate for forces below 0.5 pN. Future studies will look into this potential limitation at different frequencies.
V. CONCLUSIONS
This work presented the pressure calibration of an acoustofluidic device designed for microbubble manipulation, featuring the simultaneous use of optical and acoustical tweezers. Pressure amplitudes in the device were estimated non-invasively by FE-calibrated laser vibrometry, confirmed by particle tracking and verified by direct acoustic force measurements on microbubbles using optical tweezers. Results showed a good agreement between the methods over the explored range of input voltages, so that final uncertainties not greater than 5% could be attributed to the pressure near an aggregation point in the frequency range of interest. It was also shown how laser vibrometry may give a more thorough understanding of how the energy is transferred to the microfluidic manifold, linking observed wave speeds with classical acoustic propagation theories. This part of the study will be beneficial for acoustofluidic applications where a precise and non-invasive determination of the acoustic pressure is needed.
The advantages and the limitations of the investigated methods were discussed and the benefits of a synergic use were highlighted, with particular focus on the possibility of using microbubbles as tracking particles. In particular, since both the laser vibrometer and the optical tweezers measurements confirmed that the field in the main channel of the chip could be described as a plane wave, it was possible to explore bubble dynamics and measure acoustic forces acting on bubbles beyond the limits of optical tweezers, with a 8% uncertainty.
Acoustic force spectroscopy20 in the device was achieved by bubble tracking, highlighting four acoustical modes in the frequency range of interest. At these frequencies, it was possible to observe simultaneously a peak in the acoustic spectrum, a standing wave on the chip surface and stable aggregation.
Future studies will exploit the presence of a linear calibration to investigate in more detail the conditions over which polymer-coated microbubbles can be treated as tracer particles without taking into account their number concentration (i.e., secondary Bjerknes forces) and their oscillations. The effect of the shell in particular, expressed in terms of a change in bubble compressibility, is expected to be extremely relevant at higher pressures,34 and will be investigated by measuring protocols used for cells.58 It is anticipated that similar considerations will apply to other deformable particles (e.g., organic micro-droplets, vesicles, liposomes), which include many systems of medical and industrial interest, and that studies in calibrated acoustic environments will lead to measuring material properties (e.g., shell stiffness) of micro- and nano- particles in dynamic conditions that are otherwise difficult to obtain by other methods (e.g., atomic force microscopy).
ACKNOWLEDGMENTS
The authors acknowledge funding from the National Physical Laboratory Strategic Research Fund (project: 114248). Thanks are also due to the NPL Apprentice scheme (which funded KOB) and the IMPACT scheme at University College London (which co-funded CRF). Thanks are finally due to C. Tran, who has helped with the measurements during a Nuffield Foundation Research Placement.
References
- 1. Stride E. and Saffari N., “ Microbubble ultrasound contrast agents: A review,” Proc. Inst. Mech. Eng. H 217, 429–447 (2003). 10.1243/09544110360729072 [DOI] [PubMed] [Google Scholar]
- 2. Azmin M., Harfield C., Ahmad Z., Edirisinghe M., and Stride E., “ How do microbubbles and ultrasound interact? Basic physical, dynamic and engineering principles,” Curr. Pharmaceut. Des. 18, 2118–2134 (2012). 10.2174/138161212800099955 [DOI] [PubMed] [Google Scholar]
- 3. Albrecht T., Blomley M., Bolondi L., Claudon M., Correas J.-M., Cosgrove D., Greiner L., Jäger K., de Jong N., Leen E., Lencioni R., Lindsell D., Martegani A., Solbiati L., Thorelius L., Tranquart F., Weskott H. P., and Whittingham T., “ Guidelines for the use of contrast agents in ultrasound–January 2004,” Ultraschall. Med. 25(4), 249–256 (2004). 10.1055/s-2004-813245 [DOI] [PubMed] [Google Scholar]
- 4. Hosnya N. A., Mohamedi G., Rademeyer P., Owen J., Wu Y., Tang M., Eckersley R. J., Stride E., and Kuimova M. K., “ Mapping microbubble viscosity using fluorescence lifetime imaging of molecular rotors,” Proc. Natl. Acad. Sci. 110, 9225–9230 (2013). 10.1073/pnas.1301479110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Tatstui J. M., Xie F., and Porter R. T., “ The use of microbubbles to target drug delivery,” Cardiovasc. Ultrasound 2(23), 1–7 (2004). 10.1186/1476-7120-2-23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Chen H. and Hwang J. H., “ Ultrasound-targeted microbubble destruction for chemotherapeutic drug delivery to solid tumors,” J. Therapeut. Ultrasound 1, 10 (2013). 10.1186/2050-5736-1-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Dijkmans P. A., Juffermans L. J. M., Musters R. J. P., van Wamel A., ten Cate F. J., van Gilst W., Visser C. A., de Jong N., and Kamp O., “ Microbubbles and ultrasound: From diagnosis to therapy,” Eur. J. Cardiogr. 5(4), 245–256 (2004). 10.1016/j.euje.2004.02.001 [DOI] [PubMed] [Google Scholar]
- 8. Harfield C., Fury C. R., Memoli G., Jones P., Ovenden N., and Stride E., “ Analysis of the uncertainty in microbubble characterization,” Ultrasound Med. Biol. 42(6), 1412–1418 (2016). 10.1016/j.ultrasmedbio.2016.01.005 [DOI] [PubMed] [Google Scholar]
- 9. Prentice P. A., MacDonald M. P., Frank T. G., Cuschieri A., Spalding G. C., Sibbett W., Campbell P. A., and Dholakia K., “ Manipulation and filtration of low index particles with holographic laguerre-gaussian optical trap arrays,” Opt. Exp. 12, 593–600 (2004). 10.1364/OPEX.12.000593 [DOI] [PubMed] [Google Scholar]
- 10. Jones P. H., Stride E., and Saffari N., “ Trapping and manipulation of microscopic bubbles with a scanning optical tweezer,” Appl. Phys. Lett. 89, 081113 (2006). 10.1063/1.2338512 [DOI] [Google Scholar]
- 11. Kokhuis T. J. A., Garbin V., Kooiman K., Naaijkens B. A., Juffermans L. M. J., Kamp O., Van der Steen A. F. W., Versluis M., and De Jong N., “ Secondary Bjerknes forces deform targeted microbubbles,” Ultrasound Med. Biol. 39(3), 490–506 (2007). 10.1016/j.ultrasmedbio.2012.09.025 [DOI] [PubMed] [Google Scholar]
- 12. Overvelde M., Garbin V., Sijl J., Dollet B., de Jong N., and Lohse D., “ Nonlinear shell behaviour of phospholipid-coated microbubbles,” Ultrasound Med. Biol. 36, 2080–2092 (2010). 10.1016/j.ultrasmedbio.2010.08.015 [DOI] [PubMed] [Google Scholar]
- 13. Helfield B. L. and Goertz D. E., “ Nonlinear resonance behaviour and linear shell estimates for definity and micromarker assessed with acoustic microbubble spectroscopy,” J. Acoust. Soc. Am. 133, 1158–1168 (2013). 10.1121/1.4774379 [DOI] [PubMed] [Google Scholar]
- 14. Helfield B. L., Leung B. Y. C., and Goertz D. E., “ The effect of boundary proximity on the response of individual ultrasound contrast agent microbubbles,” Phys. Med. Biol. 59, 1721–1745 (2015). 10.1088/0031-9155/59/7/1721 [DOI] [PubMed] [Google Scholar]
- 15. Garbin V., Dollet B., Overvelde M., Cojoc D., Di Fabrizio E., van Wijngaarden L., Prosperetti A., de Jong N., Lohse D., and Versluis M., “ History force on coated microbubbles propelled by ultrasound,” Phys. Fluids 21, 092003 (2009). 10.1063/1.3227903 [DOI] [Google Scholar]
- 16. Jones P. H., Maragó O. M., and Stride E. P. J., “ Parametrization of trapping forces on microbubbles in scanning optical tweezers,” J. Opt. A 9(8), S278 (2007). 10.1088/1464-4258/9/8/S23 [DOI] [Google Scholar]
- 17. Fury C., Jones P. H., and Memoli G., “ Multiscale manipulation of microbubbles employing simultaneous optical and acoustical trapping,” Proc. SPIE 9164, 91642Z (2014). 10.1117/12.2061622 [DOI] [Google Scholar]
- 18. Laurell T. and Lenshof A., eds., Microscale Acoustofluidics ( The Royal Society of Chemistry, London, UK, 2015), 574 pp. [Google Scholar]
- 19. Barnkob R., Augustsson P., Laurell T., and Bruus H., “ Measuring the local pressure amplitude in microchannel acoustophoresis,” Lab Chip 10, 563–570 (2010). 10.1039/b920376a [DOI] [PubMed] [Google Scholar]
- 20. Sitters G., Kamsma D., Thalhammer G., Ritsch-Marte M., Peterman E. J., and Wuite G. J. L., “ Acoustic force spectroscopy,” Nat. Meth. 12, 47–50 (2015). 10.1038/nmeth.3183 [DOI] [PubMed] [Google Scholar]
- 21. Rabaud D., Thibault P., Mathieu M., and Marmottant P., “ Acoustically bound microfluidic bubble crystals,” Phys. Rev. Lett. 106, 134501 (2011). 10.1103/PhysRevLett.106.134501 [DOI] [PubMed] [Google Scholar]
- 22. Rabaud D., Thibault P., Raven J., Hugon O., Lacot E., and Marmottant P., “ Manipulation of confined bubbles in a thin microchannel: Drag and acoustic Bjerknes forces,” Phys. Fluids 23, 042003 (2011). 10.1063/1.3579263 [DOI] [Google Scholar]
- 23. Thalhammer G., Steiger R., Meinschad M., Hill M., Bernet S., and Ritsch-Marte M., “ Combined acoustic and optical trapping,” Biomed. Opt. Exp. 2(10), 2859–2870 (2011). 10.1364/BOE.2.002859 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Bassindale P. G., Phillips D. B., Barnes A. C., and Drinkwater B. W., “ Measurements of force fields within an acoustic standing wave using holographic optical tweezers,” Appl. Phys. Lett. 104, 163504 (2014). 10.1063/1.4872462 [DOI] [Google Scholar]
- 25. Lakamper S., Lamprecht A., Schaap I. A. T., and Dual J., “ Direct 2D measurement of time-averaged forces and pressure amplitudes in acoustophoretic devices using optical trapping,” Lab Chip 15, 290–300 (2015). 10.1039/C4LC01144A [DOI] [PubMed] [Google Scholar]
- 26. Bjerknes. V., Vorlesungen uber hydrodynamischew Fernkrafte, nach C. A. Bjerknes Theorie (Lectures on Hydrodynamic Methods, According to C. A. Bjerknes Theory) ( Johann Ambrosius Barth, Leipzig, Germany, 1900). [Google Scholar]
- 27. Leighton T. G., The Acoustic Bubble ( Academic Press, Cambridge, MA, 1994), pp. 287–438. [Google Scholar]
- 28.See supplementary material at http://dx.doi.org/10.1121/1.4979933 E-JASMAN-141-036704 which gives a schematic of the experimental set-up and of the measurement techniques used, a technical drawing of the microfluidic chip, the size distributions for the particles/bubbles used in this study, a discussion on the viscous drag used and on temperature effects, an example of impedance scan, a mesh convergence analysis for the finite elements results.
- 29. van der Meer S. M., Dollet B., Voormolen M. M., Chin C. T., Bouakaz A., de Jong N., Versluis M., and Lohse D., “ Microbubble spectroscopy of ultrasound contrast agents,” J. Acoust. Soc. Am. 121(1), 648–656 (2007). 10.1121/1.2390673 [DOI] [PubMed] [Google Scholar]
- 30. Bruus H., “ Acoustofluidics 7: The acoustic radiation force on small particles,” Lab Chip 12, 1014–1021 (2012). 10.1039/c2lc21068a [DOI] [PubMed] [Google Scholar]
- 31. Gor'kov L. P., “ On the forces acting on a small particle in an acoustical field in an ideal fluid,” Sov. Phys. Dokl. 6, 773775 (1962). [Google Scholar]
- 32.National Physical Laboratory, Kaye and Laby, http://www.kayelaby.npl.co.uk/ (Last viewed June 2015).
- 33. Karlsen J. T. and Bruus H., “ Forces acting on a small particle in an acoustical field in a thermoviscous fluid,” Phys. Rev. E 92, 043010 (2015). 10.1103/PhysRevE.92.043010 [DOI] [PubMed] [Google Scholar]
- 34. Hoff L., Sontum P. C., and Hovem J. M., “ Oscillations of polymeric microbubbles: Effect of the encapsulating shell,” J. Acoust. Soc. Am. 107(4), 2272–2280 (2000). 10.1121/1.428557 [DOI] [PubMed] [Google Scholar]
- 35. Shorter R., Smith J. D., Coveney V. A., and Busfield J. J. C., “ Axial compression of hollow elastic spheres,” J. Mech. Mater. Struct. 5, 693–705 (2010). 10.2140/jomms.2010.5.693 [DOI] [Google Scholar]
- 36. Barsoukov E. and Macdonald J. R., eds., Impedance Spectroscopy: Theory, Experiment, and Applications ( Wiley, Hoboken, NJ, 2005). [Google Scholar]
- 37.PACSYS, PAFEC-VibroAcoustics, http://www.vibroacoustics.co.uk/ (Last viewed June 2015).
- 38. Glynne-Jones P., Boltryk R. J., and Hill M., “ Acoustofluidics 9: Modelling and applications of planar resonant devices for acoustic particle manipulation,” Lab Chip 12, 1417–1426 (2012). 10.1039/c2lc21257a [DOI] [PubMed] [Google Scholar]
- 39. Fury C., Gélat P. N., Jones P. H., and Memoli G., “ Laser vibrometry characterisation of a lab-on-a-chip device: A preliminary investigation,” J. Phys. Conf. Ser. 498, 012002 (2014). 10.1088/1742-6596/498/1/012002 [DOI] [Google Scholar]
- 40. Schindelin J., Arganda-Carreras I., Frise E., Kaynig V., Longair M., Pietzsch T., Preibisch S., Rueden C., Saalfeld S., Schmid B., Tinevez J.-Y., White D. J., Hartenstein K., Eliceiri V., Pavel T., and Cardona A., “ Fiji: An open-source platform for biological-image analysis,” Nat. Meth. 9(7), 676–682 (2012). 10.1038/nmeth.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Clift R., Grace J. R., and Weber M. E., Bubbles, Drops, and Particles ( Academic Press, Cambridge, MA, 1978), pp. 169–202 and 231–241. [Google Scholar]
- 42. Celata G. P., D'Annibale F., Di Marco P., Memoli G., and Tomiyama A., “ Measurements of rising velocity of a small bubble in a stagnant fluid in one- and two-component systems,” Exp. Therm. Fluid Sci. 31(6), 609–623 (2007). 10.1016/j.expthermflusci.2006.06.006 [DOI] [Google Scholar]
- 43. Leighton T. G., “ The inertial terms in equations of motion for bubbles in tubular vessels or between plates,” J. Acoust. Soc. Am. 130(5), 3333–3338 (2011). 10.1121/1.3638132 [DOI] [PubMed] [Google Scholar]
- 44. Barnkob R., Augustsson P., Laurell T., and Bruus H., “ Acoustic radiation- and streaming-induced microparticle velocities determined by microparticle image velocimetry in an ultrasound symmetry plane,” Phys. Rev. E 86, 056307 (2012). 10.1103/PhysRevE.86.056307 [DOI] [PubMed] [Google Scholar]
- 45. Silva G. T. and Bruus H., “ Acoustic interaction forces between small particles in an ideal fluid,” Phys. Rev. E 90, 063007 (2014). 10.1103/PhysRevE.90.063007 [DOI] [PubMed] [Google Scholar]
- 46. Fury C., Harfield C., Jones P. H., Stride E., and Memoli G., “ Experimental characterisation of holographic optical traps for microbubbles,” Proc. SPIE (Nanophotonics V) 9126, 91263L (2014). 10.1117/12.2055889 [DOI] [Google Scholar]
- 47. Gittes F. and Schmidt C. F., “ Interference model for back-focal-plane displacement detection in optical tweezers,” Opt. Lett. 23, 7–9 (1998). 10.1364/OL.23.000007 [DOI] [PubMed] [Google Scholar]
- 48. Verdeny I., Farr A., Mas J., López-Quesada C., Martn-Badosa E., and Montes-Usategui M., “ Optical trapping: A review of essential concepts,” Opt. Pura Aplicada 44, 527–551 (2011), available at http://www.sedoptica.ed/Menu_Volumenes/Pdfs/OPA44-3-527.pdf. [Google Scholar]
- 49. Pesce G., Volpe G., Maragó O. M., Jones P. H., Gigan S., Sasso A., and Volpe G., “ Step-by-step guide to the realization of advanced optical tweezers,” J. Opt. Soc. Am. B 32(5), B84–B98 (2015). 10.1364/JOSAB.32.000B84 [DOI] [Google Scholar]
- 50.As previously reported (Ref. 46), this type of trap leaves a degree of freedom for the bubbles in the downward z direction, so that in principle a movement in z could occur when the acoustic field is applied. A posteriori, no significant movement of this type was observed and the stiffness of the trap remained unchanged after applying the acoustic field.
- 51. Dual J. and Moller D., “ Acoustofluidics 4: Piezoelectricity and application in the excitation of acoustic fields for ultrasonic particle manipulation,” Lab Chip 12, 506–514 (2012). 10.1039/c1lc20913b [DOI] [PubMed] [Google Scholar]
- 52. Dual J., Hahn P., Leibacher I., Moeller D., and Schwarz T., “ Acoustofluidics 6: Experimental characterization of ultrasonic particle manipulation devices,” Lab Chip 12, 852–862 (2012). 10.1039/c2lc21067c [DOI] [PubMed] [Google Scholar]
- 53. Sadhal S. S., “ Acoustofluidics 16: Acoustics streaming near liquid-gas interfaces: Drops and bubbles,” Lab Chip 12, 2771–2781 (2012). 10.1039/c2lc40283a [DOI] [PubMed] [Google Scholar]
- 54. Gedge M. and Hill M., “ Acoustofluidics 17: Theory and applications of surface acoustic wave devices for particle manipulation,” Lab Chip 12, 2998–3007 (2012). 10.1039/c2lc40565b [DOI] [PubMed] [Google Scholar]
- 55. Silva G. T. and Baggio A. L., “ Designing single-beam multitrapping acoustical tweezers,” Ultrasonics 56, 449–455 (2015). 10.1016/j.ultras.2014.09.010 [DOI] [PubMed] [Google Scholar]
- 56. Taylor J. R., An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements ( University Science Books, Sausalito, CA, 1996), 488 pp. [Google Scholar]
- 57.Bureau International des Poids et Mesures, “ Evaluation of measurement data-Guide to the expression of uncertainty in measurement,” (2008), available at http://www.bipm.org/en/publications/guides/gum.html (Last viewed April 2017).
- 58. Hartono D., Liu Y., Tan P. L., Then X. Y. S., Yung L.-Y. L., and Lim K.-M., “ On-chip measurements of cell compressibility via acoustic radiation,” Lab Chip 11, 4072–4080 (2011). 10.1039/c1lc20687g [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1121/1.4979933 E-JASMAN-141-036704 which gives a schematic of the experimental set-up and of the measurement techniques used, a technical drawing of the microfluidic chip, the size distributions for the particles/bubbles used in this study, a discussion on the viscous drag used and on temperature effects, an example of impedance scan, a mesh convergence analysis for the finite elements results.