An Approach in Radiation Therapy Treatment Planning: A Fast, GPU-Based Monte Carlo Method

Abstract

An accurate and fast radiation dose calculation is essential for successful radiation radiotherapy. The aim of this study was to implement a new graphic processing unit (GPU) based radiation therapy treatment planning for accurate and fast dose calculation in radiotherapy centers. A program was written for parallel running based on GPU. The code validation was performed by EGSnrc/DOSXYZnrc. Moreover, a semi-automatic, rotary, asymmetric phantom was designed and produced using a bone, the lung, and the soft tissue equivalent materials. All measurements were performed using a Mapcheck dosimeter. The accuracy of the code was validated using the experimental data, which was obtained from the anthropomorphic phantom as the gold standard. The findings showed that, compared with those of DOSXYZnrc in the virtual phantom and for most of the voxels (>95%), <3% dose-difference or 3 mm distance-to-agreement (DTA) was found. Moreover, considering the anthropomorphic phantom, compared to the Mapcheck dose measurements, <5% dose-difference or 5 mm DTA was observed. Fast calculation speed and high accuracy of GPU-based Monte Carlo method in dose calculation may be useful in routine radiation therapy centers as the core and main component of a treatment planning verification system.

Introduction

Radiation dose calculation in radiation therapy is the main part of treatment planning for cancer treatment centers.[1,2] The accurateness of the dose calculation engine is one of the aspects in the quality of the RT treatment planning.[3,4] Moreover, the efficiency of the treatment planning can be significantly improved by using state-of-the-art techniques such as fast Monte Carlo (MC) and may be optimized by employing new methods such as artificial neural network modeling. In addition, widespread applications of MC method in both radiation therapy and radioiodine therapy aspects made it a very useful method for dose calculation even under in-vivo conditions.[5]

In treatment planning, existing dose was calculated using the following three models: pencil-beam convolution, point kernel convolution/superposition, and MC.[6,7,8,9] All of these algorithms can be commissioned to gain precise and accurate results in the water phantom.[10,11,12,13] Their accuracies differ in the presence of heterogeneities.[14,15,16,17] In complex heterogeneous geometries where enough computation time was not met, up to 10% discrepancy between the MC-derived results and the experimental measurements has been observed. To solve the computation time limitation, fast MC platforms such as voxel-based MC and dose planning method are used for dose calculation in radiation therapy. Using these methods may lead to decrease in the number of errors; in addition, the time of dose calculation was reported to reduce up to 50 times.[1]

The recent shift of computer architecture away from high-speed parallel processors toward graphic processing units (GPUs) has significantly led scientific researchers to begin restructuring key computational codes to exploit the performance of modern hardware. Recently, GPUs have been widely used to accelerate computational tasks in radiation therapy.[4]

The emergence of GPUs as a novel technological option mainly due to its low cost and high computation capability[18,19,20] has been revolutionary. In recent years, numerous publications have reported the use of GPUs in the field of health care, especially in the field of radiation oncology.[21] In addition, the GPUs have the capability to use CT imaging data as input data. In any radiation therapy center, fast GPU codes are not available, in spite of it being essential for fast dose calculation, particularly for inhomogeneous regions. The aim of this study was to implement a new, GPU-based radiation therapy treatment planning for accurate and fast dose calculation in radiation therapy centers.

Materials and Methods

Monte Carlo photon dose code

In this study, the hardware of GTX 970 (GeForce GTX 970, NVIDIA Corporation GM204) was used as a GPU with a sufficient performance. The card was installed on a computer with Linux CentOS version 6.6 Operating System (OS). CUDA (Release 6.5, Version 6.5.16, CUDA Compilation Tools, NVIDIA Corporation) was installed on the OS as the programming framework.

The Monte Carlo photon dose code (MCPDC) was written in C programming language based on the CUDA context. The code validation was performed by EGSnrc (Version 3, National Research Council Canada, Ottawa, Canada), DOSXYZnrc.[22] DOSXYZnrc is an EGSnrc-based MC simulation code for calculating dose distributions in a rectilinear voxel anthropomorphic phantom.[23]

DOSXYZnrc was run on a PC server, as a part of cluster server, with 32 AMD Opteron™ Processor 6274 cores and 128 giga bytes of random access memory (RAM) that was installed in the Isfahan University of Medical Sciences. It must be noted that, natively, “the DOSXYZnrc does not support multicore architectures” and, therefore, has not been modified.[23,24]

Phantom

An anthropomorphic phantom was designed and produced using a bone, the lung, and the soft tissue equivalent materials including polyurethane (ρ = 0.2 g/cm³), acrylic (ρ = 1.19 g/cm³), and Teflon (ρ = 1.8 g/cm³), respectively. Figure 1 shows the designed and fabricated anthropomorphic phantoms.

Figure 1.

Designed and fabricated anthropomorphic phantoms

The external and internal geometries of the produced phantom were designed based on the measured dimensions of CT phantom data at the Department of Radiology, Isfahan University of Medical Sciences, Iran. These data were converted to a digital phantom using CT-create program, which is specific for DOSXYZnrc.

Indeed, to investigate the MCPDC results with DOSXYZnrc in an inhomogeneous media, a virtual phantom was designed. This phantom contained Lung700ICRU, H2O700ICRU, and Bone700ICRU.

Dose measurement

All measurements were performed using a Mapcheck dosimeter (SunNuclear, Melbourne, Florida, United States). To compare the results of the digital phantom with the Mapcheck results, a 6 cm equivalent soft tissue material was established at a distance of 45 cm from the center of the mentioned phantom. The dose of the first 1.5 cm of this 6 cm was compared with the Mapcheck dose. The schematic setup of these phantoms is shown in Figure 2.

Figure 2.

The schematic setup of the Mapcheck (virtual) and the anthropomorphic phantoms (field size=5×5)

Dose calculation

Photon transport algorithm

Photon transport in MC has an analog behavior. The photon is followed until it leaves the medium in the simulated geometry or its energy becomes less than the predefined photon cutoff energy.

The MCPDC consists of all main photon interactions such as Compton scattering, photoelectric effects, and pair production effects. In a homogenous media, the distance between two collisions for each photon is expressed as[25] follows:

where the ξ is a random number between 0 and 1, μ(E, M) is the value of the total attenuation coefficient, σ’s are the total cross-section values for the corresponding interactions, N_A is the Avogadro’s number, A is the molecular weight, and ρ is the density. The values of μ(E, M) and σ’s are extracted from the EGSnrc code system in the interested energies and media. S is the distance between two collisions for each photon. The flowchart of the mentioned code is illustrated in Figure 3.

Figure 3.

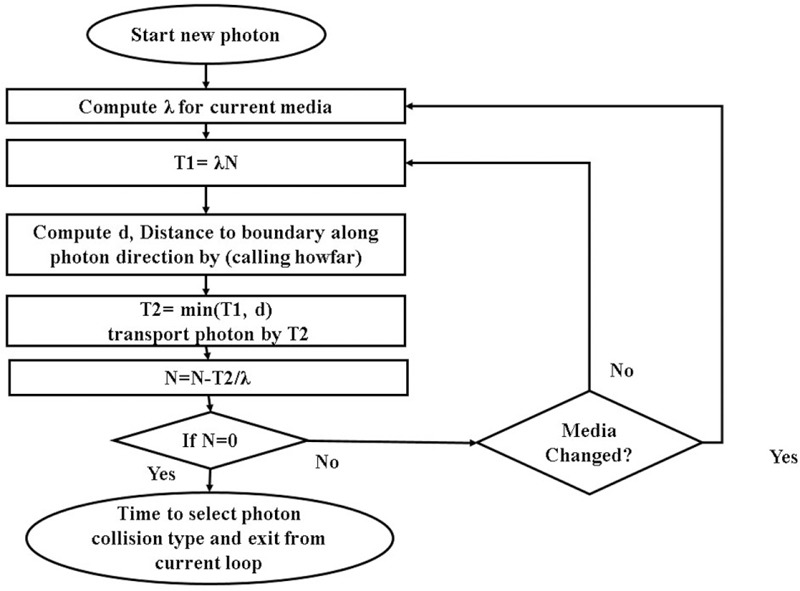
Flowchart of MCPDC for photon transport

In this code, to save the computation time, a simple semiempirical formula based on the Compton scattering interaction was excreted. In this method, the chances of photon deflection for all possible photon bending angles in any entrance photon energy (0.2–20 MeV with 0.01 MeV step) are scored. To perform this step, a subroutine code was written in the EGS5 code system, and then the Compton scattering in the interested energies was simulated to derive the photon bending angle (θ). Thereafter, θ was recorded in a text file for 10e6 photons in any energy step. To calculate probability of θ in the energy steps, a C++ interface program was constructed in a ROOT framework, which is an open source framework (An Object-Oriented Physics Analysis Infrastructure, CERN, Geneva).[26] The interface is used to make a probability of photons bending chance (bending is expressed as cos(θ)). The data are converted and stored as inverse cumulative distribution function (CDF⁻¹).[26] First-order spline linear function is used to fit the data as functions. Because only free electron Compton scattering is applied, the media change has no effect on the obtained data.

Because physical theory of the photoelectric interaction in the MC codes is a significantly complex process,[27] in this study, the photon’s energy was converted into an electron with the same kinetic energy. This approximation is excited, because the binding energy of the electrons is significantly lower than the photoelectrons.

Indeed, the photon’s energy is randomly distributed between the electron and the positron; thereafter, the electron is transported by its subroutine, and the positron is passed through the continuous slowing down approximation model using pair production interaction.

A condensed-history algorithm for electron transport needs to conflict with complex physics of electron interactions with matter. As an alternative, MCPDC used an inspiration from fast electron macro MC for electron transport algorithm. This method avoids the use of complex electron transport algorithms.[28]

In the first step, spherical geometry with fixed 0.05 cm radius was defined and simulated in EGSnrc. The electrons with fixed energy were entered into the defined sphere. Output was defined based on any exited particle from sphere. Position, transport vector, and energy of the exited particles were scored in a text file. Next, the text file was analyzed, and the needed parameters were derived for application in the electron subroutine.

Statistical data analysis

This part of the study was conducted based on the routine protocol in our radiotherapy center. A detailed explanation of this method is presented as below.

Gamma evaluation factor or index was used to compare the virtual phantom and the experimental measurement data.[20] It is a factor that accounts for both distance-to-agreement (DTA) and dose difference[20] as follows:

where Δd and ΔD are the DTA and the dose difference, respectively. r_r is the reference position and r_c is the position of the comparison point. D_r and D_c are the doses at reference and comparing points, respectively.

To determine Γ_r, any point of reference dose distribution was compared with all other comparison points, and the minimum value of Γ_r was selected for further processing. It should be noted that, in the case of Γ_r, the test is passed, otherwise it is failed. Finally, the results of the ratio number of passed points to the total points were reported.

Results

Figure 4 shows the results of the MCPDC simulation with fully tuned energy spectrum compared to DOSXYZnrc and experimental measurements in the water phantom. Less than 2% dose difference or 2 mm DTA between the MCPDC and DOSXYZnrc results was obtained [Figure 4]. Less than 1% point-to-point differences were obtained for depths above 19 mm. Similar results were seen for the MCPDC-derived results compared to the experimental measurements.

Figure 4.

The results of the MCPDC simulation with fully tuned energy spectrum compared to DOSXYZnrc and the experimental measurements in the water phantom

Figure 5 demonstrates the written code and the experimental measurement results for the designed and fabricated phantoms.

Figure 5.

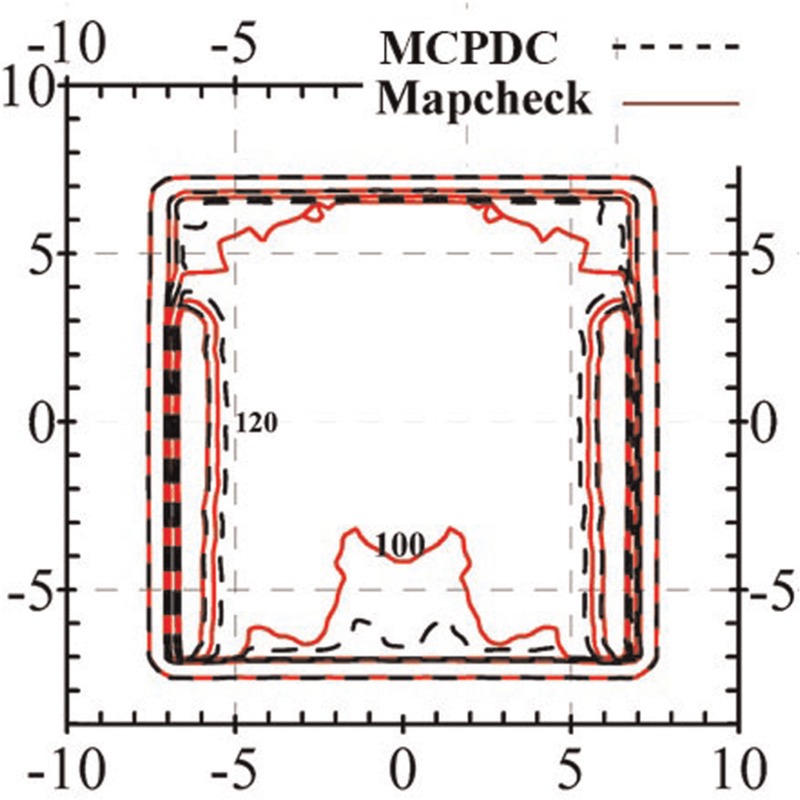
Comparison of dose distribution for both the written code and the experimental measurements for the designed and fabricated phantoms

Figure 6a and b illustrates the comparison of the dose distribution of the written code and DOSXYZnrc.

Figure 6.

Comparison of dose distribution of the written code and DOSXYZnrc. (a) Coronal view at x=0 and (b) sagittal view at z=10cm

Table 1 demonstrates the results of statistical analysis for dose discrepancies between the written code results and the DOSXYZnrc dose measurements.

Table 1.

The results of statistical analysis of dose discrepancies between the written code results and the DOSXYZnrc dose measurements

Discussion

In this study, a novel MCPDC is presented for fast and accurate dose calculation in radiation therapy centers. The MCPDC can perform radiation therapy planning dose calculation faster than usual with good accuracy.

To achieve this goal, a polyenergetic point source with specific spectrum and rectilinear collimation was used. For the anthropomorphic digital phantom, a field size of 10 cm ×10 cm and source-axis distance (SAD) of 100 cm were used. A field size of 10 cm ×10 cm and source to surface distance (SSD) of 100 cm were also applied for the virtual phantom. The percentage depth dose and the lateral profiles of the Siemens linac were measured using a photon diode detector (PFD^3G Model, Sweden).

As illustrated in Figure 6, the dose difference between the results of the written code and those derived from the DOSXYZnrc was 3% dose difference or 3 mm DTA for more than 95% of the voxels.

The results of statistical analysis for dose discrepancies between the written code results and the Mapcheck dose measurements are shown in Table 1. As indicated from the results of this table, the initial evaluation showed that, compared with those of DOSXYZnrc in the virtual phantom and for most of the voxels (>95%), <3% dose difference or 3 mm DTA was found. The results here were confirmed using both a virtual inhomogeneous phantom and also an anthropomorphic rotary asymmetric one.

Moreover, considering the anthropomorphic phantom, compared to the Mapcheck dose measurements, <5% dose difference or 5 mm DTA was observed. The very fast calculation speed and high accuracy in dose calculation may allow the code to be used in routine radiation therapy clinics as the central component of a treatment plan verification system and also as the dose calculation engine for MC-based planning. It should be noted that, in typical clinical use, the fraction of points that exceed 3% dose difference and 3 mm DTA can be extensive;[29] hence, compared to the other published reports, this criterion is acceptable for clinical evaluations. Low and Dempsey[29] evaluated the gamma dose distribution comparison method for clinical applications. They showed that the usage of 5% dose difference and 2–3 mm DTA was suitable for clinical radiation therapy plan evaluations.[29] In Task Group 120, it has been stated that, to create the pass or fail acceptance criteria of the results of an array detector such as the Mapcheck used in this study, careful consideration should be given.[22,30]

In this study, a novel GPU-based MC code is presented for fast and accurate dose calculation in clinical radiation therapy. This code was written using the premeasurement data of EGSnrc for different energies applied in radiation therapy. In addition, the probability density data were used to determine the Compton angle scattering, which is dominant in photon energy interactions in radiation therapy.

Conclusion

An accurate and fast radiation dose calculation is essential for successful radiation radiotherapy. To validate the results of the MCPDC, in addition to the virtual inhomogeneous phantoms, an anthropomorphic rotary asymmetric phantom was designed and fabricated. The accuracy of the code was validated using the experimental data, which were obtained from the anthropomorphic phantom as the gold standard. Fast calculation speed and high accuracy of GPU-based MC (MCPDC) method in dose calculation may be useful in routine radiation therapy centers as the core and main component of a treatment planning verification system.

Financial support and sponsorship

This work is a part of PhD thesis which financially supported by Isfahan University of Medical Sciences (Grant No. 393820).

Conflicts of interest

There are no conflicts of interest.