Speckle Noise Reduction in Optical Coherence Tomography Using Two-dimensional Curvelet-based Dictionary Learning

Abstract

The process of interpretation of high-speed optical coherence tomography (OCT) images is restricted due to the large speckle noise. To address this problem, this paper proposes a new method using two-dimensional (2D) curvelet-based K-SVD algorithm for speckle noise reduction and contrast enhancement of intra-retinal layers of 2D spectral-domain OCT images. For this purpose, we take curvelet transform of the noisy image. In the next step, noisy sub-bands of different scales and rotations are separately thresholded with an adaptive data-driven thresholding method, then, each thresholded sub-band is denoised based on K-SVD dictionary learning with a variable size initial dictionary dependent on the size of curvelet coefficients’ matrix in each sub-band. We also modify each coefficient matrix to enhance intra-retinal layers, with noise suppression at the same time. We demonstrate the ability of the proposed algorithm in speckle noise reduction of 100 publically available OCT B-scans with and without non-neovascular age-related macular degeneration (AMD), and improvement of contrast-to-noise ratio from 1.27 to 5.12 and mean-to-standard deviation ratio from 3.20 to 14.41 are obtained.

Introduction

Spectral domain optical coherence tomography (SD-OCT) is a high-resolution, noninvasive imaging technique in the identification and assessment of internal structures of retinal abnormalities and to image various aspects of biological tissues with high resolving power (5 μm resolution in depth).[1,2] The main problem regarding these images is in their inherent corruption by speckle noise due to its coherent detection nature. Traditional digital filtering methods including median and Lee filtering,[3] adaptive median and Wiener filtering,[4,5] and iterative maximum a posteriori-based algorithm[6] were employed for reducing speckle noise. These methods provide inadequate noise reduction under the high speckle noise contamination, as well as result in the meaningful loss of faint features. In recent years, some other approaches have been explored for speckle noise reduction such as anisotropic diffusion-based methods,[7,8,9,10] wavelet-based methods,[11,12] curvelet shrinkage technique,[13] dictionary learning-based denoising,[14,15] and robust principal component analysis-based method.[16] However, the necessity of the development of more advanced methods to provide minimum detail loss under suppression high speckle noise makes the speckle noise reduction as an important part of the OCT image processing.

Here, a novel speckle noise reduction algorithm is developed, which is optimized OCT image despeckling while preserving strong edge sharpness. For this purpose, we introduce K-SVD dictionary learning in curvelet transform (CUT) domain for speckle noise reduction of two-dimensional (2D) OCT images. As the low scale of curvelet coefficients are more affected by the noise and to take advantage of this sparse multiscale directional transform, we introduce a new scheme in dictionary learning and take CUT of noisy image, then a nearly optimal threshold for thresholding of curvelet coefficients for each scale and rotation is found based on the standard deviation of each coefficient matrix. Thresholded coefficients are employed, and a curvelet-based K-SVD with varying size dictionary dependent on the scale and rotation of coefficient matrix is introduced. This method does not need any high signal-to-noise ratio (SNR) scans (a fraction of repeated B scans from a unique position are captured slowly, then these images are registered and averaged to create a less noisy image with a sufficiently high SNR) for dictionary learning, which is used in other works.[14,15]

The paper is organized as follows. Section 2 provides an introduction to 2D digital CUT (DCUT). In Section 3, we describe the principles of conventional dictionary learning. Our proposed method is described in Section 4, and the results and performance evaluation are presented in Section 5. Finally, this paper is concluded in Section 6.

Two-Dimensional Digital Curvelet Transform

The CUT is a high-dimensional time–frequency analysis of images that gives a sparse representation of objects, and it has been developed to overcome the inherent limitations of conventional multiscale representations such as wavelets (e.g., poor directional selectivity). The directional selectivity of curvelets and localized spatial property of each curvelet can be utilized to preserve the image features along certain directions in each sub-band. The good directional selectivity, tightness, and sparse representation properties of this multiscale transform give new opportunities to analyze and study large datasets in medical image processing.[17]

This transform can be implemented by employing two simpler, faster, and less redundant methods, i.e., the unequally-spaced fast Fourier transform (USFFT) and the wrapping transform.[17,18] The main difference of these implementations is related to their choice of spatial grid to construct the curvelet atoms in each subband. Both algorithms have the same output, but the wrapping-based transform has faster computational time and is easier to implement than USFFT method.[18] The architecture of CUT via wrapping is roughly presented in the following form:

1. Take the 2D FFT of the image f and obtain Fourier samples 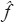(n₁, (n₂),...−n/2 ≤ n₁, n₂,...< n,...< n/2 (f is the original image with the size of n × n)

2. For each scale/angle pair (j, l), form the product d (n₁, n₂) = 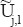(n₁, n₂) 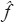(n₁, n₂), here, 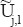(n₁, n₂) is the discrete localizing window[18]

3. Wrap this product around the origin and obtain 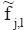(n₁, n₂) = W(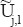 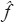) (n₁, n₂). If the corresponding periodization of the windowed data, i.e., d (n₁, n₂) is defined as Wd (n₁, n₂) = 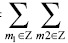d (n₁ + m₁ L_{1, j}, n₂ + m₂ L_2,j), then at each scale j, Wd (n₁, n₂) is restricted to indices (n₁, n₂) inside a rectangle with sides of length L₁,_j × L_2,j near the origin (L_1,j ~ 2_j and L_2,j ~ 2^j/2) to construct the wrapped windowed data

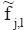4. Take the inverse 2D FFT of each for collecting the discrete coefficients, i.e., c^D (j, l, k).

K-SVD Dictionary Learning For Image Denoising

Image denoising problem can be viewed as an inverse problem. One of the most recent methods to solve an inverse problem is a sparse decomposition over over-complete dictionaries.[19,20] For a given set of signals delineated by Y, suitable dictionary D can be found such that y_i ≈ Dx_i, where x_i is a vector which involves the coefficients for the linear combination and y_i ∈ Y. The problem of sparse representation can thus be defined as an optimization problem of finding D and x_i, which satisfies:

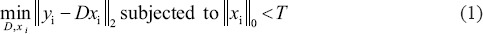
where T is a predefined threshold which restraints the sparseness of the representation and || · ||₀ indicates the l₀ norm which counts the number of nonzero elements of the vector. This problem is thus involved in a selection of the dictionary and a sparse linear combination of the atoms in the dictionary to illustrate each desired signal. For image denoising, the noisy image is broken up into patches and the vectorized version of each patch is considered as a signal. For a given image, which can be considered as a set of signals Y, the denoising problem can be done by finding a set of patches Z which are related by:

Y = Z + η (2)

where η is noise, which corrupts the patches.

To find the denoised patches 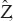, the following optimization problem should be solved:[19,20]

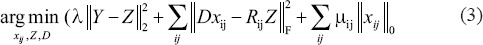
where λ and μ are Lagrange multipliers and Rij is defined as the matrix which selects the ijth patch from Z, i.e., Z_ij = R_ijZ.

The first term in (3) makes sure that the measured image Y is similar to its denoised version Z and the second and third parts are sparsity-inducing regulation terms.

For solving the above equation:

1. Initialization is done by setting

2. Z=Y, D = initial dictionary

3. Repeat K times

   • For each patch, R_ijZ computes the representation vector x_ij by using orthogonal matching pursuit (OMP) algorithm.[21,22] The OMP is easy in implementation and provides a satisfactory stable result. The algorithm attempts to find the best basis vectors (atoms) iteratively such that the representation error is reduced in each iteration
     
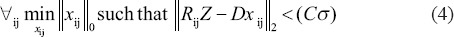     where C is the noise gain and σ is the standard deviation of noise
   • Once this sparse coding stage is done, the algorithm proceeds to update the atoms l = 1, 2,…, k of the dictionary one by one to reduce the error term. For this purpose the set of patches that use this atom D₁ = ([i, j]|x_ij (l) ≠ 0) are calculated and l-th atom from dictionary is deselected, then the coding error matrix (E_l) of these signals is calculated whose columns are:
     
   • Minimize this error matrix with rank-1 approximately from SVD that E_l= UΔV^T. Replace coefficient values of atom D_l with entries of V₁Δ₁ and updated dictionary column to be .

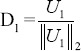4. Set

   

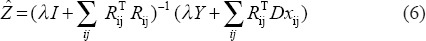
Proposed Denoising Method

Our curvelet-based approach consists of first taking the 2D forward DCUT of noisy image to produce the curvelet coefficients, then for each sub-band in the transform domain, the coefficients’ matrix is independently denoised based on K-SVD dictionary learning with the initial dictionary of discrete cosine transform (DCT), in which its size is specific for each scale.

In the proposed method for efficient representation of different structures in image, we select initial dictionary to be variable in size (depends on the size of curvelet coefficients’ matrix in each sub-band) instead of traditional fixed form. By increasing the scale of curvelet coefficients’ matrix (or reducing in resolution), the block size (indicates the size of the blocks to operate on) is also increased, while in high resolutions, the block size is reduced which results in better representation of particular structure in image.

The proposed method for image denoising is as follows.

Forward Digital Curvelet Transform

Take the 2D CUT of the data to produce the curvelet coefficients C (j, l) (j is the scale and l is the orientation).

According to our image size (512 × 1000), each image is decomposed into six scales (it is recommended to take the number of scales to be equal or less than the default value, ⌈(log₂ [min(M, N)] − 3)⌉ here M, N is the image size and x denotes the smallest integer being greater than or equal to x) then each scale is further partitioned into a number of orientations. The number of orientations is l=1, n, 2n, 2n, 4n, 4n… from finer to coarser scales, where n is the number of orientation at the second scale.

Initial denoising

For each scale, apply hard thresholding based on the standard deviation of each scale. The hard threshold T_{j, l} to each curvelet coefficient is selected such that:

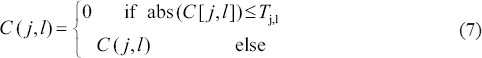
The threshold T_{j, l} is selected based on the standard deviation of selected coefficient matrix (C) in that scale and rotation (T_{j, l}= 0.5 standard deviation [C]).

Initial dictionary selection and K-SVD dictionary learning denoising

For each 2D-coefficient matrix in each scale and rotation, the varying size initial dictionary for each scale is chosen by employing DCT on each sub-band.

We let the block size in dictionary learning to be dependent on the size of each coefficient matrix, so the dictionary size also varies with block size. After finding the appropriate 2D initial dictionary, D, for each sub-band, the noisy curvelet coefficient matrices of noisy image in the same scale and rotation are despeckled based on K-SVD dictionary learning as described in Section 3.

According to the size of curvelet coefficient matrix C, the dictionary size and block size are set empirically to be:

Dictionary size = Block size.^3 (9)

where m, n are respectively the number of rows and columns of coefficient matrix C and [x] indicates the largest integer smaller than or equal to x.

Contrast enhancement

Since the CUT is successful in dealing with edge discontinuities, it is a good candidate for edge enhancement. Hence, to enhance the contrast of intra-retinal layer boundaries, denoised curvelet coefficients can be modified to enhance edges in a B-scan image,[23,24] before taking 2D inverse discrete CUT (2D-IDCUT). For OCT images, a function k_c (C_j,l) defines empirically that is similar to function defined by Starck for gray and color image enhancement,[25] which modifies the values of the curvelet coefficients as follows:

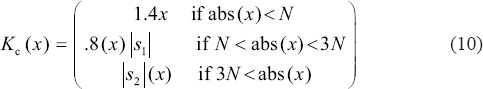
In this equation, N = 0.1M, where M is the maximum curvelet coefficient of the relative band, and s₁ and s₂ are defined as follows:

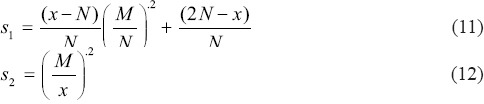
Converting to image domain

Then, we reconstruct the enhanced image from the denoised and modified curvelet coefficients by applying IDCUT. The outline of the whole denoising process is shown in Figure 1.

Figure 1.

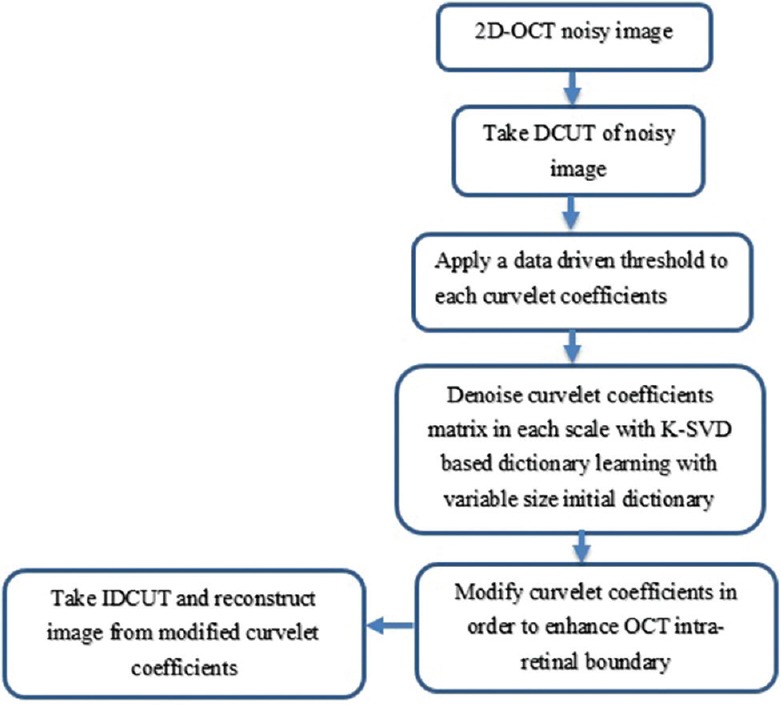
The outline of the proposed method

Results

We tested our algorithm on 100 selected 2D OCT B-scans of size 512 × 1000 from publically available datasets[15,26] that were acquired using SD-OCT, Bioptigen imaging systems, with and without non-neovascular AMD. For the better representation of image details in low scale, high-frequency components, the block size is selected to be dependent on the scale of coefficient matrix. On the other hand, for low scales, the coefficient matrix is small in size and the size of this matrix will be increased in high scale, low-frequency components of the image. Figure 2 demonstrates the samples of the variable size initial dictionaries in curvelet domain used for K-SVD-based denoising of each curvelet sub-band.

Figure 2.

Samples of the trained two-dimensional initial dictionaries in K-SVD-based denoising of each curvelet coefficient matrix. The block size in (a) is 3 × 3 and in (b) is 4 × 4

Figure 3 shows the reconstructed OCT images from curvelet-based K-SVD enhancement method.

Figure 3.

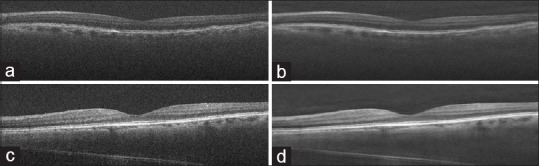
The implementation of proposed method (a and c) initial images and (b and d) obtained images by proposed method

For K-SVD denoising in each scale and rotation of curvelet coefficients, 1000 patches with equal distance between the samples in each dimension are selected. To obtain a compromise between having enough iterations to obtain a good result and having a correct processing time, we set K empirically to be 15 for our dataset. According to Eqs. 3 and 4, we also set C = 1.15 and λ = 30/σ, where σ is selected to be 25 for our dataset.

To compare the performance of different denoising algorithms quantitatively, we compute the averaged mean SNR[27] and contrast-to-noise ratio[28] obtained from ten regions of interest (ROIs) from B-scan OCT images [similar to the foreground ellipse boxes in Figure 4].

Figure 4.

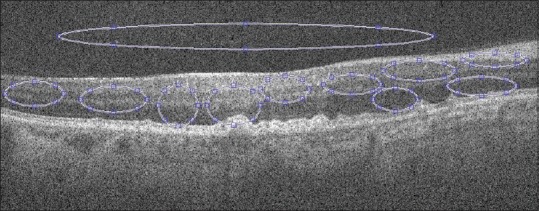
Selected background and foreground regions of interest for evaluation. Bigger ellipse outside the retinal region is used as background region of interest and other circles represent foreground regions of interest

The algorithm that has been implemented in MATLAB requires around 2 min of computation time for denoising each 512 × 1000 B-scan on an Intel (R) Core i7 CPU with 4 GB of RAM. The drawback of the proposed method[15] is its time complexity so that it takes more than 31 min for denoising each B-scan on the same Intel (R) Core i7 system.

Table 1 compares the quantitative performance measure values of our method with those from the available well-known denoising approaches[15] such as: Tikonov,[6] K-SVD[14] and multiscale sparsity-based tomographic denoising approach[15] (the reported results[15] are on 17 images of this dataset). To show the ability of proposed method in edge preserving, the average of the edge preservation (EP)[29] measure over the selected ROIs is obtained, that is, 0.83 ± 0.01. This EP measure ranges between 0 and 1, having smaller values when the edges inside the ROI are more blurred.

Table 1.

Mean and standard deviation of the mean signal-to-noise ratio and contrast-to-noise ratio results for 17 spectral domain optical coherence tomography retinal images using the Tikonov, K-SVD, multiscale sparsity-based tomographic denoising, and proposed methods

Figure 5 also shows the visual performance of our proposed method in comparison with some traditional state-of-theart denoising methodssuch as: Bernardes method[10] Tikonov,[6] and multiscale sparsity-based tomographic denoising algorithm.[15]

Figure 5.

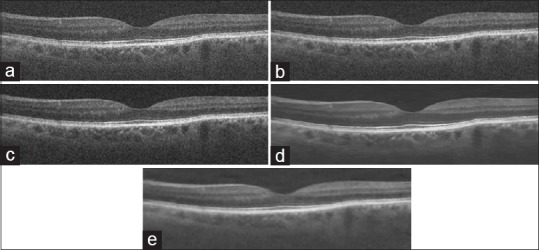
Visual performance for spectral domain optical coherence tomography retinal image using Bernardes, Tikhonov, multiscale sparsity-based tomographic denoising, and the proposed method. (a) Original noisy image (b) denoising results using the Bernardes method. (c) Denoising results using the Tikhonov method. (d) Denoising results using the multiscale sparsity-based tomographic denoising. (e) Proposed method

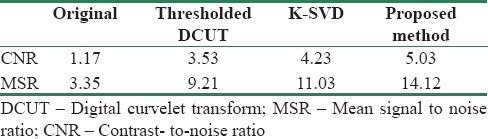
To show the ability of our proposed method (DCUT + K-SVD), we have demonstrated the reconstructed image with thresholded curvelet coefficients and the ability of K-SVD in image domain (block size = 8, dictionary size = 256) for noise suppression in Figure 6. Table 2 also compares the quantitative performance measure values of our method with thresholded curvelet coefficients (without dictionary learning) and the K-SVD-based denoising (without CUT) method.

Figure 6.

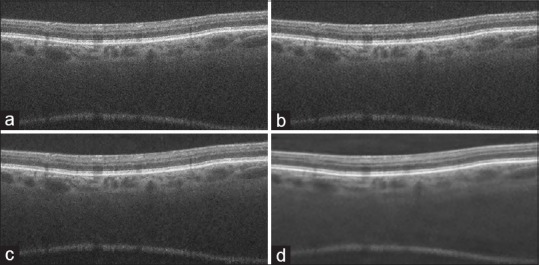
Visual comparison of our proposed method with thresholded digital curvelet transform coefficients and K-SVD (a) initial images, (b) reconstructed image with thresholded digital curvelet transform coefficients, (c) obtained images by using K-SVD on image domain (d) proposed method

Table 2.

Mean signal-to-noise ratio and contrast-to-noise ratio results of our proposed method in comparison with reconstructed image from thresholded digital curvelet transform coefficients and K-SVD-based denoising method in an image of Figure 6

Conclusion

Speckle noise in OCT images causes difficulty in the actual recognition of morphological characteristics which can be viewed and quantified using OCT tomograms, such as the thickness of intra-retinal layers and the shape of structural features (e.g., drusens, macular holes, macular edema, and nerve fiber atrophy and cysts, which can be used as markers in clinical investigation and diagnostics of retinal diseases). Hence, to suppress noise while preserving and enhancing the edges and to consider the geometric properties of structures and exploit the regularity of edges, we introduced a new curvelet-based K-SVD despeckling and contrast enhancement method for OCT datasets. We discussed the application of dictionary learning along with CUT for denoising of SD-OCT of normal and AMD retinal images. Our proposed method also does not need any high-SNR scans or any repeated scans (or averaged versions of scans) for dictionary learning (since in some cases, there is no access to the averaged frames). Moreover, since the proposed method decomposes the image into lower dimension sub-components, we achieved a significant reduction of computational time by reducing the size of initial dictionary to be dependent with the size of each scale. The EP value also shows that the proposed method can preserve edges very well while removing speckle noise. As OCT is a medical imaging technique that captures three-dimensional (3D) images from within optical scattering media, it seems that the direct analyzing of 3D images with 3D sparse transforms and also considering the 3D geometrical nature of the data outperform analyzing

2D slice-by-slice, which is our ongoing research to extend this work to 3D domain.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.