Adsorptive Water Removal from Dichloromethane and Vapor-Phase Regeneration of a Molecular Sieve 3A Packed Bed

Abstract

The drying of dichloromethane with a molecular sieve 3A packed bed process is modeled and experimentally verified. In the process, the dichloromethane is dried in the liquid phase and the adsorbent is regenerated by water desorption with dried dichloromethane product in the vapor phase. Adsorption equilibrium experiments show that dichloromethane does not compete with water adsorption, because of size exclusion; the pure water vapor isotherm from literature provides an accurate representation of the experiments. The breakthrough curves are adequately described by a mathematical model that includes external mass transfer, pore diffusion, and surface diffusion. During the desorption step, the main heat transfer mechanism is the condensation of the superheated dichloromethane vapor. The regeneration time is shortened significantly by external bed heating. Cyclic steady-state experiments demonstrate the feasibility of this novel, zero-emission drying process.

Introduction

Removal of impurities from chemicals and solvents is often crucial for selective production of pharmaceuticals. Dichloromethane (or methylene chloride (DCM)) is one of the most widely used chlorinated solvents, because of its ability to dissolve many organic compounds and its low boiling temperature.¹ For specialty pharmaceuticals and optoelectronics, DCM should be exceedingly pure and have low water content. The annual world production of dichloromethane is more than 500 000 tons, predominantly produced by the Hoechst and Stauffer processes,¹ which contains water as an impurity. Adsorption is one of the possible methods for obtaining ultrapure solvents.² Because of their high hygroscopicity, molecular sieves have already demonstrated their adsorption capability for the drying of ethanol,^3,4 higher alcohols^5,6 and esters,^7,8 toluene,⁹ and other hydrocarbons¹⁰ and solvents.¹¹ The general conclusion is that hydrophobic solvents are easier to dry.^2,11 For water removal from solvents that cannot penetrate the micropores of the zeolite, the adsorption equilibrium is the same as the pure water vapor isotherm.² In that case, the water vapor isotherm gives liquid-phase concentrations using different activity coefficient models. For a partially miscible system, such as water–DCM, the so-called NRTL model gives good predictions.¹²

Packed beds of various sizes have been widely used in the industry for adsorptive drying.¹³ Mathematical models are used to predict the size and operating times for a molecular sieve packed bed. In addition to adequate thermodynamic models that describe the equilibrium, external and intraparticle mass transfers are important for the accurate prediction of breakthrough curves. External mass transfer can play a significant role in the total mass-transfer resistance in the liquid phase.² However, information on the packed-bed liquid-phase adsorption is scarce, in comparison to the literature on gas drying.

Regeneration of the bed is an essential and energy-intensive step of adsorption processes. Regeneration of the adsorbent capacity is achieved by shifting the equilibrium to initiate desorption. The adsorption equilibrium can be affected by decreasing the pressure (pressure swing adsorption), increasing the temperature (temperature swing adsorption), purging (usually with inert gas), changing the solvent (solvent swing adsorption), or a combination of these.¹³ The pressure swing and purging method rely on a decrease of the partial pressure as the driving force for desorption. Although a few studies are present in the literature, most commonly, a temperature swing adsorption with inert gas purge is applied.¹⁴⁻¹⁶ The purge gas is then supplied counter-currently to the direction of the adsorption cycle, in order to adequately regenerate the end of the bed that determines the final product purity. Purge gas regeneration of a DCM adsorptive dryer would lead to the emission of DCM that would be present in the bed (macropores and static holdup) after the adsorption cycle. Emissions of DCM are strictly regulated, because of its toxicity, as well as health and greenhouse effects.¹⁷ However, emissions can be minimized to zero if the dried DCM is used as vapor in the regeneration cycle. Superheated DCM vapor heats up the bed and desorbs water. After cooling, condensed water and liquid DCM are separated based on the density difference. DCM used in desorption is dried again, minimizing emissions to zero in that way.¹⁸

This paper investigates the efficiency of the bed regeneration with a superheated DCM stream. First, the adsorption equilibrium of water in DCM on molecular sieves 3A at different temperatures are determined and compared to pure water vapor isotherms from the literature.^19,20 The liquid-phase packed-bed adsorption breakthrough curves are measured at different mass flows of DCM. The experiments are compared to a mathematical adsorption–desorption model. The model is used to assess the effect of the different mass- and heat-transfer resistances. Consecutively, the saturated-bed regeneration experiments with superheated DCM vapor are compared to the adsorption–desorption model. Cyclic steady-state experiments are performed to estimate the efficiency of the process.

Model

Mass and Energy Balances

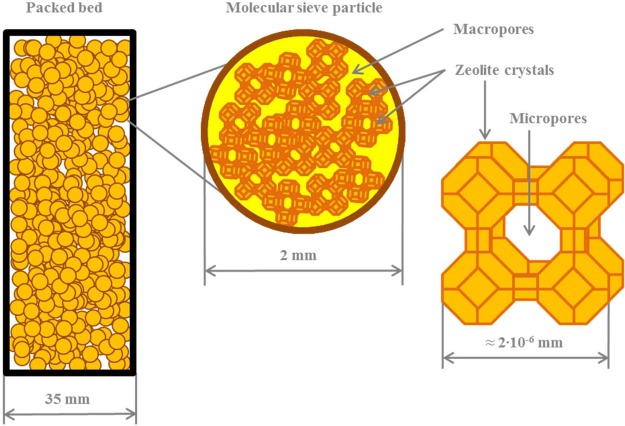
A mathematical model is developed to analyze and simulate mass- and heat-transfer resistances in a packed bed during various adsorption and desorption cycles. Figure 1 depicts the schematic representation of the model. The model is based on nonequilibrium, nonisothermal, and nonadiabatic conditions. The following assumptions were made to simplify the system of equations:

• fluid plug flow with axial dispersion;

• constant pressure (i.e., negligible pressure drop);

• constant fluid velocity (during adsorption);

• single adsorbate system;

• negligible radial temperature, concentration, and velocity profiles;

• negligible axial conduction by the column wall;

• ideal gas law applies for vapor phase;

• temperature-dependent general statistical thermodynamic approach (GSTA) model^20,21 representation of the equilibrium isotherm;

• uniform spherical particles, 2 mm in diameter;

• heat transfer to and through the column wall and to the environment was estimated using an overall heat-transfer coefficient; and

• external and internal (macropore and surface diffusion) mass-transfer resistances were considered.

Figure 1.

Schematic depiction of the molecular-sieve packed-bed adsorption system. Different length scales are presented accounting for external mass transfer, macropore diffusion, and surface diffusion in micropores.

With these considerations, the following model equations were derived. The plug flow with axial dispersion model^15,16,22,23 was adopted to represent the concentration profile for the fluid flowing through the packed bed:

1

The Danckwerts boundary conditions are described by the following:

2

3

The initial conditions are

4

5

Conduction and convection are the major means of heat transport, with a heat loss to the surroundings through the column wall.

The differential equation representing all these factors is described by the following expression:

6

with the Danckwerts boundary conditions:

7

8

and the initial conditions:

9

where U_w is the overall heat-transfer coefficient. T_amb is 22 °C, as reported in the Experimental Section, and h_air is a fitting parameter.

For the solid phase, a pseudo-first-order equation²⁴ was used to describe the adsorption kinetics, where the equilibrium loading was determined using the GSTA model. Together with macropore and surface diffusion (of the adsorbed water) resistances, the particle mass balance differential equation can be given as

10

with the Danckwerts boundary conditions:

11

12

and the initial conditions:

13

14

Heat generated or supplied during the process is transferred across the particle by conduction and is represented by the enthalpy balance for the particle:

15

with the boundary conditions:

16

17

and the initial conditions:

18

The loading in the adsorbed phase is represented by the following equation:

19

with the initial conditions:

20

21

where f(C_p) is the equilibrium loading calculated according to the GSTA model²⁰ for a fluid phase concentration C_p. Initial loading value for the particle was taken for saturated conditions from the GSTA model.

Modeling of the Vapor–Liquid Flow

Experimental observations show that dichloromethane condensation occurred during the regeneration step resulting in two-phase flow. The energy supplied by the superheated vapor phase heats up the particles and triggers desorption. In order to account for the vapor–liquid mixture in the bed, a no-slip condition between the two phases was assumed. Also, at the start of the desorption cycle, the macropores contained liquid DCM. The residual volume fraction of the bed occupied by the static holdup (ε_L⁰) was determined to be 0.046, by the correlation of Saez and Carbonell,²⁵ using the Eötvös number (eqs 23 and 24).

22

23

Thus, the liquid properties were used to define the initial conditions and the liquid film is assumed to be limiting the desorption when the bed was at boiling temperature.

In the model, the temperature is calculated from the enthalpy of the total flow. The advantage of this is the fact that, taking the latent heat of evaporation of dichloromethane into account, the fraction of vapor phase can be calculated.

The phase change is incorporated in the model based on the enthalpy and vapor fraction of the flow as described below:

24

where v_f is the vapor fraction of the fluid, described as

25

where H_L^bp is the enthalpy of pure liquid at the boiling point. The axial dispersion and the mass-transfer coefficient are defined in a similar manner.

The effective heat transfer coefficient for nodes which contain a vapor–liquid mixture is described taking into account the gas–liquid film heat-transfer coefficient and the liquid–solid heat-transfer coefficient.

Estimation of Model Parameters

The parameters in eqs 1–25 were all estimated using the following correlations, except for the surface diffusion coefficient. The latter is fitted to the experimental data, since there appears to be no appropriate predictive correlation in the literature.

The axial dispersion coefficient is estimated with the help of Wakao’s correlation:²⁶

26

The fluid phase axial thermal conductivity is estimated by the correlation given by Dixon:²⁷

27

External heat- and mass-transfer coefficients are determined for both liquid and vapor flow using the correlations of Wakao,^28,29 which are valid for the Re numbers used in this study:

28

29

The fluid and solid properties are summarized in Table 1.

Table 1. Packed Bed and Fluid Properties^a.

	DCM
physical property	liquid, 22 °C	vapor, 40 °C	vapor, 100 °C	molecular sieves
density (kg/m3)	1325	3.41	2.93	1100
viscosity (Pa s)	4.37 × 10–4	1.0 × 10–5	1.3 × 10–5
heat capacity (kJ/(kg K))	1.156	0.678	0.616	0.925
thermal conductivity (W/(m K))	0.1392	9.40 × 10–3	1.15 × 10–2	0.355

^aData taken from refs (1, 11, 13, and 17).

The value of the wall heat transfer coefficient is estimated using the correlation of Dixon:²⁷

30

Discretization Scheme

The partial differential equations are transformed into a set of ordinary differential equations (ODEs), using the central differencing scheme. The packed bed is discretized into 25 nodes in the axial direction. The molecular sieve particles are discretized into 5 nodes in the radial direction and are modeled for every node in the axial direction. Increasing the discretization scheme in the radial direction did not influence the modeling results. The set of ODEs is then solved using the ode15s solver in MATLAB.

Fitting Procedure

The adsorption breakthrough curve model was fitted to the experimental results using the surface diffusion coefficient (D_s) as a fitting parameter. All other parameters were estimated from the equations above. For each flow rate (experimental run), the surface diffusion coefficient was fitted to obtain the lowest error between experimental and model values resulting in a best-fit D_s value per flow rate. Since all experiments were performed at the same temperature, the same D_s value should be obtained. Taking an arithmetic mean of the best-fit D_s values per flow rate yields an average D_s value (for all flow rates). Each experimental run was performed at least 2 times. At least 11 experimental points per flow rate were used to obtain surface diffusion coefficient values.

Varying the value of the surface diffusion coefficient in the model to fit desorption breakthrough curves could not yield an accurate fit, especially of the temperature profiles. The only heat-transfer parameter not estimated via correlations was the heat transfer from the column wall to the environment (h_air). An average value of 1.4 kW/(m² K) for h_air provided an accurate description of the temperature profiles for all flow rates. This value is too high, meaning that the inaccuracy in the desorption model parameter is summarized in this parameter. The average surface diffusion coefficient fitted to the adsorption breakthrough experiments was corrected for the temperature influence and used in the desorption model.

Experimental Section

Adsorption Isotherm Measurements

Isotherms for water adsorption from saturated dichloromethane (VWR, The Netherlands) onto molecular sieve 3A beads, 2 mm diameter (Sigma–Aldrich), were measured at 25 and 40 °C. Molecular sieves were dried in an oven at 200 °C for 48 h. Adsorbent was then cooled to room temperature in a glovebox (MBraun MB 200B) kept in a dry nitrogen atmosphere (<0.3 ppm of water). Between 0.02 and 0.50 g of dry adsorbent was weighed and transferred into 60 mL vials capped with PTFE septum caps. 60 g of DCM saturated with demineralized water (Veolia Water Elga Purelab S7, 0.1 μS cm^–1) was injected into the same vials through the septum. A dry DCM sample was prepared in the same manner to detect potential contamination of the samples with water. The prepared samples were then placed inside a shaker (IKA) at 100 rpm at a preset temperature. Samples were taken at fixed time intervals with 2 mL syringes through the septum, to avoid water adsorption from air. The water content was measured with a coulometric Karl Fischer titrator (Metrohm Applikon Coulometer KFT 899). The equilibrium between the adsorbent and the liquid was reached within 2 days. The average mass loss of DCM was <1% (w/w).

Adsorption and Desorption Breakthrough Curve Measurements

A borosilicate glass column with a diameter (D_c) of 31 mm and a height (H_c) of 800 mm was designed according to the criteria provided in the literature,³⁰ so that the wall effects (eq 31) and axial dispersion (eq 32) are minimized.

31

32

At the top and bottom of the column, 50 mm was filled with glass beads of 8 mm diameter to act as a uniform flow distributor, while the midsection was packed with 385 g of dry molecular sieve 3A. The column was completely insulated. Temperature (Metatemp Pt100 class A) and pressure sensors (Huba Control, type 520) were installed on the top and the bottom of the column.

During adsorption breakthrough experiments, the bed was operated upward, while the desorption of the bed was performed from the top to the bottom (Figure 2). DCM saturated with water (approximately 1700 weight ppm) was pumped using a gear pump (Tuthill d-series) regulated with a Coriflow mass flow controller (Bronkhorst M50). The bed and fluid properties are summarized in Table 1. For adsorption breakthrough experiments, samples were collected at the top of the column and analyzed by Karl Fischer titration. Dried DCM exiting the column was resaturated in the feed vessel by passing through a stirred water layer on top of the saturated DCM bottom layer. Measurement of the water concentration in the feed vessels proved that saturation was always more than 91% at all mass flows. The volume of the vessels was 12.5 L. All adsorption experiments were performed at 22 ± 2 °C.

Figure 2.

Schematic representation of the experimental apparatus. Adsorption breakthrough experiments were performed upward through the column, while desorption was from top to bottom. DCM was fed from the “Wet DCM” vessel during the adsorption cycles, while regeneration was performed by pumping and evaporating dry DCM. Both desorbed water and DCM were condensed after the bed and collected in the “Wet DCM” vessel during the desorption cycle. The amount of water desorbed was quantified with the through flow graduated cylinder, in which water accumulated while DCM passed through, due to density difference. Water content of DCM exiting the graduated cylinder was measured by Karl Fischer titration to close the water mass balance. Legend: LI, level indicator; FC, mass flow controller; PI, pressure indicator; TI, temperature indicator; and TC, temperature controller.

When the bed was completely saturated with water, the flow direction was changed from the dry DCM vessel (200 ppm water content) through the evaporator (aDrop DV1c). The evaporated DCM was superheated to 100 °C by a heating cable (Thermocoax Isopad) around an insulated tubing. The vapor entered the column from the top, replacing the liquid present after the adsorption step. In this manner, heated DCM vapor triggered desorption and water evaporation. Simultaneously, because of the low initial bed temperature (22 °C), the vapor would partially condense and trickle down the bed. The bed was drained of liquid within 3 min, which is negligible, in comparison to the total duration of the desorption experiments (up to 5 h). To improve the desorption step, also experiments were performed using heating cables for external heating of the bed. The outlet of the column was connected to a glass heat exchanger cooled with an ethylene glycol/water mixture using a cooling unit (Huber Ministat, 230 cc). The water content of the condensate was determined by two methods.

The condensate exiting the heat exchanger was collected for analysis. Because of the low solubility of DCM in water, two liquid phases were observed: water and DCM. Ethanol (VWR, The Netherlands) was added to the samples to dissolve both phases so that the water content could be measured by the Karl Fischer titrator. By measuring the water content of ethanol and of the dissolved sample, the water content in the samples was calculated using a simple mass balance.

The second method of measuring the amount of desorbed water considers is using a “closed” graduated cylinder installed after the condenser. The rise in water liquid level was noted in certain time intervals. At the cylinder outlet, the DCM water content was measured. Both methods provided similar results with the second method having a better reproducibility due to averaging over a longer time period. Because of the inherent discreteness of the two-phase flow of the liquids, the variation of the water fraction was quite high for small sampling volumes.

After desorption, the bed was purged with nitrogen overnight before the following adsorption experiment.

Results and Discussion

Adsorption Isotherm Results

Experimental adsorption equilibrium data are presented in Figure 3 at 25 and 40 °C, along with pure water vapor isotherms from the literature.¹⁹⁻²¹ Measured values are slightly lower than the literature data for a pure 3A zeolite, in particular, at water concentrations of <400 ppm. A possible explanation is the presence of a binder in the molecular sieve particles. The binding material, usually clay, has larger pores and a negligible water capacity.³¹ The relatively large scatter in the data may be because of crushed molecular sieve inhomogeneities that become noticeable at low amounts of crushed molecular sieve. By repeating the experiments, we aimed to minimize this variation. Difference between gas (literature) and liquid (measured) adsorption isotherm data can result from potential errors in the estimation of the activity coefficients in the liquid. A modified NRTL model¹² is used to recalculate the liquid-phase concentrations into water partial pressures. The calculated activity coefficients predict the mutual solubility concentrations of 1.7% (w/w) (DCM in water) and 0.18% (w/w) (water in DCM), within 14% error.

Figure 3.

Water adsorption isotherms from DCM on zeolite 3A at (a) 25 °C and (b) 40 °C. Experimental data are in agreement with literature values.^19,20

From the agreement of the experimental and literature adsorption isotherm data, it can be concluded that DCM does not affect the adsorption of water on the 3A molecular sieve. The DCM molecule (kinetic diameter = 3.3 Å;³³ Lennard-Jones molecular diameter = 4.7 ų⁴) is too large to enter the 3 Å micropores of the zeolite. These results are in accordance with the findings of adsorptive drying of higher alcohols (>C4) and esters.^7,8 According to Basmadjian,² if solvent molecules cannot penetrate the pores of the molecular sieves, the water adsorption isotherm is independent of the solvent and is the same as a pure water vapor isotherm.

An increase in temperature from 25 °C to 40 °C (Figure 3) results in a decrease of 4% in the molecular sieve maximum capacity, while the curve maintains the same shape. Generally, the temperature influence on the molecular sieve capacity is small, which is the reason why manufacturers recommend regeneration temperatures of ∼300 °C.¹⁹

Simple adsorption isotherm models (e.g., Langmuir, Sips, Toth, Dubinin–Astakhov) cannot accurately predict the measured adsorption isotherms of water vapor in the 3A molecular sieve, because of the complex crystal structure of zeolites. Zeolite crystals consist of beta-cages and supercages. The beta-cages are first occupied with water molecules, the supercages subsequently. Water adsorbs to a variety of locations in both beta-cages and supercages and in different energy levels.^35,36 The General Statistical Thermodynamic Approach model (GSTA model)²⁰ analyzes the binding sequence in the zeolite and gives the best representation of water vapor isotherms at different temperatures; therefore, it is used in the packed-bed model presented here.

Adsorption Breakthrough Curves

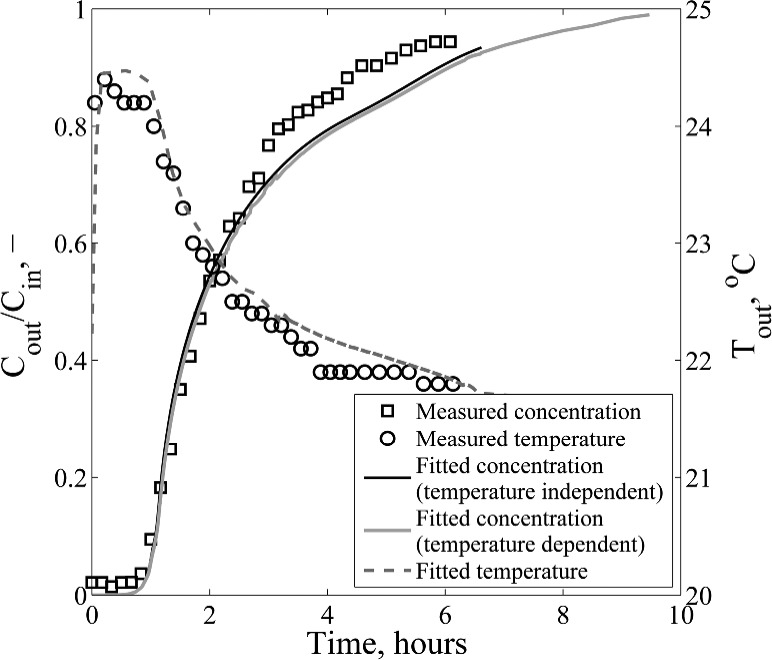
Adsorption breakthrough curves were measured at five different mass flows, with all experimental conditions summarized in Table 2. A characteristic breakthrough result is presented in Figure 4 for a mass flow of 4 g/s. Since adsorption is an exothermic process, the fluid temperature increases across the bed. After the initial increase, the temperature difference reaches a plateau at 2.5 °C. At this point, all of the water is adsorbed and the bed material has heated up to this adiabatic temperature rise. After 56 min, the bed becomes saturated, the exit concentration rises and the temperature decreases.

Table 2. Experimental Conditions for Adsorption, Desorption, and Cyclic Steady-State Runs.

run	ṁ (g/s)	V̇ (mL/s)	uf (m/s)	Re	kLS (m3/(m2 s))	Dporee (m2/s)	Dsf (m2/s)	Cin (ppm)	Tinlet (°C)
1a	2	1.52	0.002	13.5	0.91 × 10–4	1.4 × 10–9	4.5 × 10–12	1550	20.8
2a	3	2.27	0.003	20.2	1.09 × 10–4	1.4 × 10–9	4.8 × 10–12	1680	21.4
3a	4	3.03	0.004	27.0	1.24 × 10–4	1.4 × 10–9	4.9 × 10–12	1640	21.8
4a	5	3.79	0.005	33.7	1.38 × 10–4	1.4 × 10–9	7.1 × 10–12	1700	21.5
5a	7	5.30	0.007	47.2	1.62 × 10–4	1.4 × 10–9	2.2 × 10–12	1750	22.0
6b	0.55	196.43	0.260	138	0.1129	2.0 × 10–5	5.0 × 10–7	200	100
7b	0.65	232.14	0.307	164	0.1233	2.0 × 10–5	5.0 × 10–7	200	100
8b	0.75	267.86	0.355	214	0.1331	2.0 × 10–5	5.0 × 10–7	200	100
9b	0.85	303.57	0.402	239	0.1424	2.0 × 10–5	5.0 × 10–7	200	100
10b	0.95	339.29	0.449	265	0.1512	2.0 × 10–5	5.0 × 10–7	200	100
11c	0.95	339.29	0.449	265	0.1512	2.0 × 10–5	5.0 × 10–7	200	100
12d	3–0.95	2.27–339.29	0.003–0.449	20.2–265	1.24 × 10–4–0.1512	1.4 × 10–9–2.0 × 10–5	4.8 × 10–12–5.0 × 10–7	1700–200	22–100

^aAdsorption.

^bDesorption.

^cDesorption with external heating.

^dCyclic steady state with external heating.

^eData taken from Basmadjian et al.²

^fBest fit.

Figure 4.

Plot showing a typical adsorption breakthrough experimental run (run 3, 4 g/s). The mathematical model accurately describes the concentration profile and temperature rise in liquid DCM due to adsorption.

The model is able to describe the temperature rise across the bed within 2% error (Figure 4). The calculated enthalpy of adsorption is 2 times lower than the maximum value of 4188 kJ/kg, reported by the manufacturer of the molecular sieves.¹⁹ The adsorption enthalpy changes with surface loading, but it is a constant value in the model.²⁰ The temperature increase in the liquid phase is too small to have any influence on the concentration breakthrough curve, especially on the adsorption equilibrium. Comparing the two models (with and without energy balance), the temperature influence on the concentration profile is <1% (Figure 4). The simulation time of the model with temperature dependence was 10 times longer than that of the isothermal model (∼1.5 min), because of the addition and coupling of the energy balance with the mass balance. Numerous runs have been performed to obtain the best fit, as described previously. Therefore, the temperature influence is neglected in fitting the other mass flow data (Figure 5) by solving only the mass balance and decoupling the energy balance from the model.

Figure 5.

Influence of mass flow on the adsorption breakthrough curve. Different values of the surface diffusion coefficient give the best fit of the experimental data (solid lines), while the average value provides satisfactory results (dashed lines).

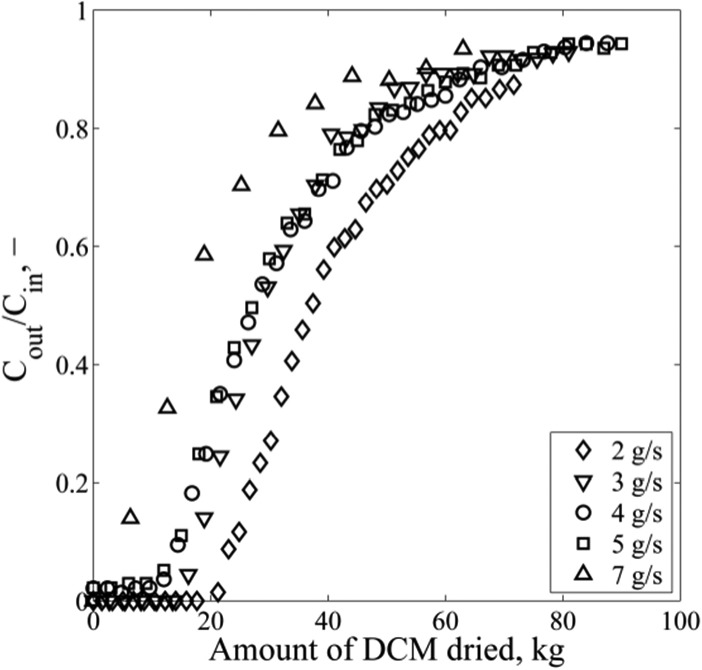
An increase in the mass flow results in a rapid decrease in the breakthrough time, because of a faster saturation of the bed (Figure 5). Higher mass flows improve the external mass transfer, which influences the initial part of the curve. Complete saturation of the bed takes a relatively long time (more than 10 h for a mass flow of 2 g/s), since the breakthrough curves have a low slope at a higher loading. The packed-bed water content is high at this point so the internal mass transfer dictates the overall process. The model underpredicts this part of the curve. The surface diffusion is a function of the water concentration and increases with water loading. The surface diffusion coefficient is used to fit the adsorption breakthrough curves to the temperature independent model, in the absence of predictive correlations in the literature (Figure 5). Individual values of the surface diffusion coefficient provide the best fit for the investigated mass flows, possibly because errors in other estimated parameters are lump-summed in the surface diffusion coefficient as the only fitting parameter. In addition, the surface diffusion is likely to be a function of the surface concentration,^9,10,37 which is not considered here. This can be the reason for the overestimation of the adsorption at high loading conditions. At high surface loadings, the adsorption enthalpy decreases, which increases the mobility of the adsorbed molecules.⁶ The value of the surface diffusion coefficient lies in the range of 10^–12–10^–11 m²/s, which corresponds well to values reported in the literature for water molecules.^6,13,38 The mathematical model describes the breakthrough time (when C_out/C_in = 0.10) for all mass flows, within 7% accuracy. All calculated data are within 15% of the measured concentration values (see Figure 6). Figure 7 shows that the bed is utilized more at low mass flow as more DCM is processed before the breakthrough occurs (20 kg at 2 g/s, in comparison to 11 kg at 5 g/s). Carton et al.⁴ also found that a decrease in the flow rate of liquid ethanol steeply increases the utilization of their 3A molecular sieve packed bed.

Figure 6.

Model accuracy for the best-fit values of the surface diffusion coefficient. Calculated values are within 15% of the measured breakthrough curves.

Figure 7.

Influence of mass flow on the amount of DCM processed. Increase in contact time dries more liquid until the breakthrough, indicating that most of the mass-transfer resistance is in the particle.

Sensitivity analysis of the model demonstrates that the surface diffusion has the largest impact on the shape of the breakthrough curve. The effects can be seen in Figure 5—even a small change in D_s from the best fit to the average fitted value decreases the model accuracy. For adsorptive drying of toluene with 4A molecular sieves, surface diffusion was also found to be the rate-limiting step.⁹ The surface diffusion coefficient is the most dominant at higher surface loadings, so the influence is larger at a higher bed loading. Macropore diffusion also significantly contributes to the shape of the breakthrough curve (Figure 8). The value for the macropore diffusion coefficient (1.4 × 10^–9 m²/s) is taken from Basmadjian² and agrees with values obtained by other authors for water macropore diffusion in molecular sieves.^9,10,23 The liquid film mass-transfer resistance and the axial dispersion coefficient do not influence the breakthrough curve, as expected, because of proper design of the column (eqs 31 and 32).

Figure 8.

Influence of the mean pore diffusion coefficient value on the adsorption breakthrough curve at 4 g/s. A one-order-of-magnitude change in value significantly affects the model predictions, especially in the lower loading region.

Desorption Breakthrough Curves

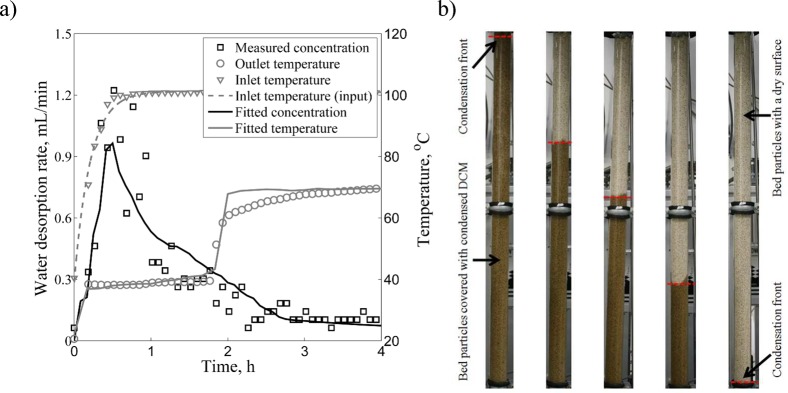
Typical concentration and temperature breakthrough curves for the desorption step are presented in Figure 9 for a DCM vapor mass flow of 0.95 g/s. Results are obtained for an initially completely saturated bed. The dry DCM vapor inlet temperature has a lag of 24 min, because of the heating up of the traced tubing and the equipment. This heating profile is identical for all desorption experiments. The transient inlet temperature is used as input for the model. At the beginning of the desorption step, the temperature of the bed outlet quickly rises from ambient to 39–40 °C, which is the boiling temperature of DCM. The energy needed for desorption is supplied by the cooling and condensation of the DCM vapor. The condensed DCM covers the particles, penetrates into the macropores, and trickles down between particles and exits the bed, together with saturated DCM/water vapor. The temperature rise decreases the zeolite capacity which triggers water desorption. Thus, the outlet water concentration follows the increase of the inlet temperature. After the initial desorption peak, the condensation front travels down the column resulting in an exponential decline in the outlet water concentration, because of the decreased bed water content (Figure 9b). After 1.8 h, the heat front reaches the column exit, increasing the outlet temperature. The amount of water desorbed is still significant since the lower parts of the bed are being desorbed more efficiently with DCM vapor of 70 °C. The outlet vapor temperature does not reach the inlet temperature, because of the heat loss to the environment.

Figure 9.

Representation of a typical desorption breakthrough experimental run (run 10, 0.95 g/s): (a) concentration and temperature breakthrough curves, and (b) condensation front moving through the bed.

The mathematical model of the desorption vapor condensation in the desorbing packed bed accurately describes the bed outlet temperature (Figure 9). The model underestimates the peak in the water desorption rate, possibly due to a heat-transfer coefficient that is too high in the vapor phase. A lower heat-transfer coefficient for the vapor in the model would give a larger condensation zone, with a higher outlet water content.

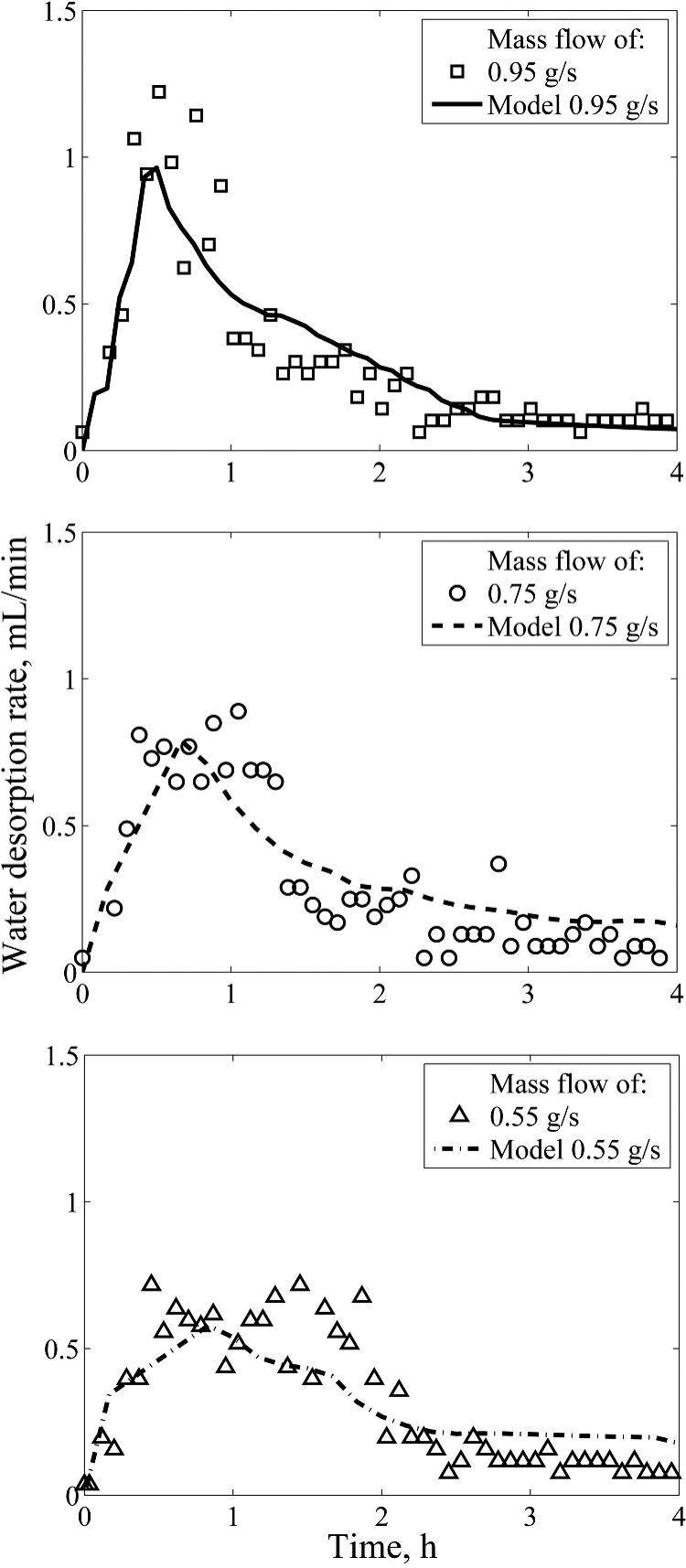
An increase of the vapor mass flow increases the amount of DCM condensed per unit of time and, therefore, increases the energy provided for desorption. This results in a peak of the desorbed water for 0.95 g/s mass flow (Figure 10). For lower mass flows (0.55 and 0.75 g/s), a plateau is present in the amount of the water desorbed. The duration and height of this plateau are also defined by the mass flow and, thus, by the heat transferred. The results of Schork et al.¹⁵ have already demonstrated that the outlet concentration curve consists of two transfer zones separated by a concentration plateau: one transfer zone where external mass transfer dominates, and one where intraparticle mass transfer dominates. The concentration plateau is lost for high mass flows, in which case the transfer zones overlap.^15,39 The second (latter) mass-transfer front forms a tail as the concentration difference between the solid phase and the fluid phase decreases with time.

Figure 10.

Influence of mass flow of DCM on the water desorption breakthrough curve. Higher mass flows emphasize the desorption due to more DCM condensed per unit of time.

Acceleration of the desorption with the increase of mass flow of DCM from 0.55 g/s to 0.95 g/s is obvious in the outlet temperature profile (Figure 11). Higher mass flows provide more energy per unit time, resulting in the faster regeneration of the bed. After the increase of the outlet temperature of the fluid, a different steady state is obtained, depending on the mass flow. Lower mass flows lead to more heat loss to the environment in a noninsulated bed, as in the work of Schork et al.¹⁵

Figure 11.

Influence of the mass flow of DCM on the outlet fluid temperatures. Arrows represent the moment when the condensation front reaches the bed outlet.

Experimental and model parameters are given in Table 2. The model describes a similar trend of the desorption rate (Figure 10) with slight deviations in the beginning due to an overestimated liquid phase desorption (Figure 11). More-efficient desorption at the start of the cycle decreases the concentration in the particle, decreasing the driving force, resulting in more tailing for the calculated values than for the experimental results. The model accurately describes the point at which the condensation front traveling down the bed reaches the bottom of the bed, the point at which the temperature at the outlet increases above the boiling point of DCM (Figure 11). The pore and surface diffusion coefficients in the model are increased due to the increased temperature, compared to the adsorption process.

The efficiency of the regeneration step can be evaluated using two parameters: the purge vapor consumption and the energy requirement.^14,15 The purge vapor consumption is usually presented as a function of contact time. This dependence should yield a minimum at which the heat losses to the environment and mass and heat transfer are optimal. Considering that, for the experimental system, the main energy supply to the bed is via DCM condensation, the amount of purge vapor needed is constant (see Figure 12). This also implies that the energy needed for the regeneration is the same for all of the mass flows, and is 2200 kJ. The mass flow dictates the regeneration time and heat losses, which is important for achieving lower bed loading. The second parameter, the energy requirement dependency of regeneration temperature, should have a minimum close to the characteristic temperature of the system.^2,14,15 However, only a temperature of 100 °C is investigated here, because of the safety precautions, preventing the thermal decomposition of DCM at temperatures >140 °C (120 °C in the presence of oxygen).¹ A higher regeneration temperature would result in a higher concentration peak and a shorter depletion time.¹⁶

Figure 12.

Influence of the mass flow of DCM on the amount of DCM consumed for bed regeneration. At all mass flows, 6 kg were consumed until the increase in outlet fluid temperature was observed, meaning that condensation is the main heat-transfer mechanism.

Desorption with External Bed Heating

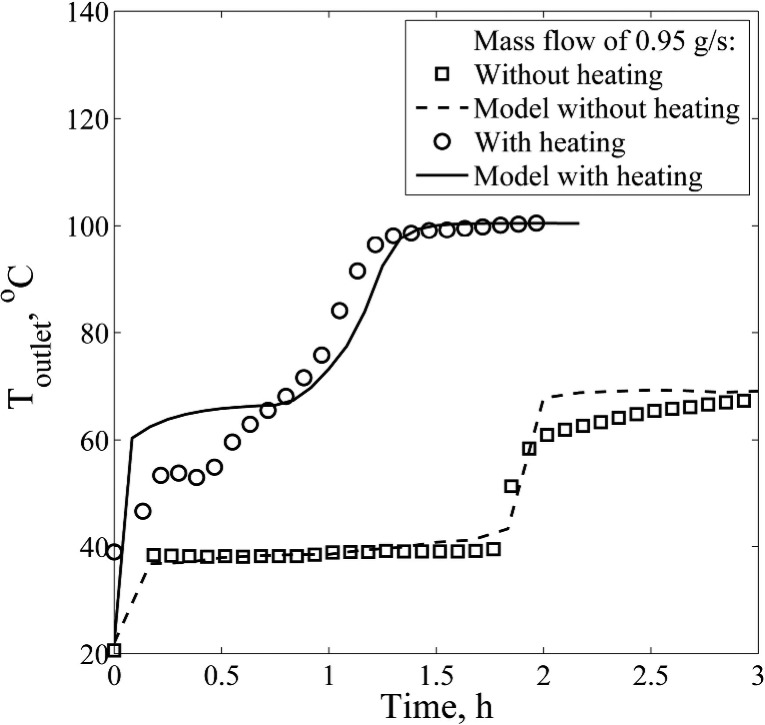
One of the options to overcome the condensed-liquid-film mass-transfer zone during desorption is to heat the bed externally. The experiments were conducted where the column was traced with the temperature maintained at 100 °C, while other conditions remained the same, as for the other desorption runs. The desorption concentration peak is now 2.5 times higher than in the experiment without external heating, for a mass flow of 0.95 g/s (see Figure 13). The outlet fluid temperature quickly rises above 40 °C (see Figure 14), meaning that a vapor DCM phase is present at the column outlet from the start of the experiment. After the initial temperature rise, a plateau is then present at 53 °C. The start of the increase of the outlet temperature corresponds to the peak in the concentration profile. From the water saturation pressure at this temperature, the water desorption rate would be 1.7 mL/min. However, the measured water desorption rate peak is at 2.7 mL/min, meaning that there is also liquid water leaving the bed. Because of efficient desorption, liquid water covers the particles, trickles down, and exits the bed, together with water-saturated DCM vapor. The particle concentration at the bed inlet is significantly decreased after 0.5 h, so the amount of water desorbed starts to decrease over time as the heat wave moves through the bed. Also, the surface of the molecular sieves is dried and desorption occurs completely in the vapor phase. After 1.5 h, the outlet temperature reaches 100 °C with a water content of 0%: full regeneration has been achieved. This is 0.6 h faster and 2.1 kg less DCM is used in the case of regeneration without external heating. In addition, a low residual loading is achieved due to higher temperatures obtained in the bed, resulting in a shorter tailing in the desorbed water profile.

Figure 13.

Comparison of depletion curves without (run 10) and with external heating of the bed (run 11) at a 0.95 g/s mass flow of DCM. The water desorption peak is narrow due to a faster energy supply for desorption in the case of the externally heated bed.

Figure 14.

Comparison of fluid outlet temperature profiles without (run 10) and with external heating of the bed (run 11) at 0.95 g/s mass flow of DCM. Temperature rises quickly above the boiling point of DCM, resulting in faster water desorption for the externally heated bed.

The temperature plateau for the model result is 12 °C higher (65 °C) and 3 times longer than that for the experimental runs. The reason for this could be that the heat transfer from the external heating is overestimated, leading to higher temperatures in the bed. Also, the model does not account for a liquid water phase present on the surface of the particle. The calculated water desorption rate peaks at the DCM vapor saturation water concentration. Decreased particle loading reduces the driving force for the mass transfer. The result is a sharp decrease in the water desorption rate with the temperature rise. From the energy balance, the resulting amount of heat supplied by the DCM vapor is only 140 kJ during the 1.5 h, since the external heating represents the main heat source.

Cyclic Steady-State Experiment (with External Heating Regeneration)

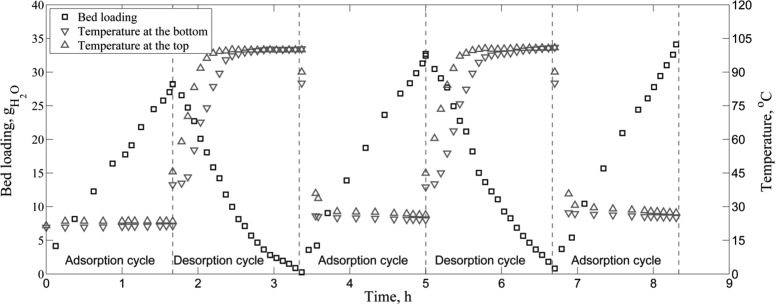
Cyclic operation was investigated by carrying out successive runs of adsorption and desorption. Experiments were conducted with DCM for an adsorption mass flow of 3 g/s and a desorption mass flow of 0.95 g/s (Table 2). The criterion for ending the adsorption cycle was chosen to be C_out/C_in = 0.15. The following desorption cycle with external heating was performed for the same duration as the preceding adsorption, representing one cycle of a two-packed bed configuration. Based on the measured inlet and outlet concentrations, the loading of the bed is calculated (see Figure 15). In all cycles, it is seen that the adsorption duration is the same, meaning that bed regeneration is complete in that period of time (1.67 h). The same is represented in the desorption loading profiles, during which the water content of the bed decreases to 0.67 and 0.81 g of water for the first and second cycles, respectively. This is expected, since the outlet temperature quickly rises to the inlet value of 100 °C, resulting in a low bed loading. Since the bed is only partially saturated with water, a plateau in the outlet temperature profile is not present as depicted in Figure 15. After desorption, adsorption is started immediately, without an in-between cooling step. The second and third adsorption cycles show the same trend as the first cycle, because high heat capacity and mass flow of liquid DCM quickly cool the bed. A total of 18 kg DCM was dried per adsorption cycle, with an average water content of 60 ppm. Deducting the 5.7 kg used for desorption, the net amount of DCM dried per cycle is 12.3 kg. The amount of water adsorbed per cycle (34 g) represents 41% of the maximum bed capacity.

Figure 15.

Cyclic steady state results for experimental run 12 (3 g/s adsorption, 0.95 g/s desorption with external heating). The amount of water accumulated during the adsorption step is removed in the following desorption step. The outlet fluid temperature quickly increases to the inlet value, resulting in low residual bed loading.

Conclusions

In the current work, the drying of liquid DCM with 3A molecular sieves and bed regeneration with the dry DCM vapor is investigated. The nonequilibrium, nonisothermal, and nonadiabatic packed-bed model is fitted to both adsorption and regeneration breakthrough experiments.

The adsorption equilibrium results are slightly lower than the results predicted by pure water vapor isotherms from the literature for zeolite 3A. The reason is a binder that is present in molecular sieve beads or an error in the activity coefficient calculation. The NRTL model predicts mutual solubility within an error of 14%. DCM does not affect the adsorption equilibrium, since it is excluded from the zeolite micropores. The GSTA model is used in the packed bed model as a representation of the pure water vapor equilibrium. The high adsorption capacity of molecular sieve 3A at low water concentrations results in ppm-dry DCM.

The plug flow with the axial dispersion model provides an accurate description of the experimental adsorption breakthrough results, within an accuracy of 15%. The surface diffusion coefficient represents the main mass-transfer resistance, with fitted values in the range of (2.2–7.1) × 10^–12 m²/s. The surface diffusion coefficient is probably not constant but increases with loading in the zeolite pores, because of a decrease in the adsorption enthalpy energy. The dependence of the surface diffusion coefficient on the surface concentration can be the reason why different values were obtained. Sensitivity analysis demonstrates that pore diffusion significantly affects the shape of the breakthrough curve. External mass transfer and axial dispersion do not influence adsorption at the adopted experimental conditions. Since the intraparticle resistance is limiting, longer contact time and smaller particles would provide better utilization of the bed. The temperature influence is negligible during liquid-phase adsorption.

Desorption is limited by heat transfer. DCM vapor condensation provides the energy for water desorption from molecular sieves. However, the formed liquid film also diminishes mass transfer. An increase in the mass flow decreases the time needed to reach the end of the desorption cycle. The DCM consumption is 93 g per 1 g of adsorbed water for all the mass flows.

External heating significantly increases the regeneration efficiency, decreasing the needed time from 2.1 h to 1.5 h (for 0.95 g/s mass flow). It also reduces the amount of DCM consumed (66 g per 1 g of adsorbed water), and could be further decreased with future optimization. Since external heating is an energy source for desorption, DCM vapor acts mainly as a stripping gas for water. A lower bed loading is obtained due to higher regeneration temperature achieved in comparison to experiments without external heating. External heating is responsible for faster water desorption and evaporation, since only 6% of the total desorption energy (2200 kJ) is supplied by DCM vapor.

Cyclic steady-state experiments demonstrate the successful regeneration of a partially saturated externally heated bed using dry DCM using at 31.67% of the adsorption flow rate, proving the drying process concept. A cycle time of 1.67 h is sufficient to desorb the water that accumulates in the preceding adsorption step with a flow rate of 3 g/s. The processed 18 kg of DCM has an average water content of 60 ppm.

The authors declare no competing financial interest.