Topographical Information-Based High-Order Functional Connectivity and Its Application in Abnormality Detection for Mild Cognitive Impairment

Abstract

Temporal synchronization-based functional connectivity (FC) has long been used by the neuroscience community. However, topographical FC information may provide additional information to characterize the advanced relationship between two brain regions. Accordingly, we proposed a novel method, namely high-order functional connectivity (HOFC), to capture this second-level relationship using inter-regional resemblance of the FC topographical profiles. Specifically, HOFC first calculates an FC profile for each brain region, notably between the given brain region and other brain regions. Based on these FC profiles, a second layer of correlations is computed between all pairs of brain regions (i.e., correlation’s correlation). On this basis, we generated an HOFC network, where “high-order” network properties were computed. We found that HOFC was discordant with the traditional FC in several links, indicating additional information being revealed by the new metrics. We applied HOFC to identify biomarkers for early detection of Alzheimer’s disease by comparing 77 mild cognitive impairment patients with 89 healthy individuals (control group). Sensitivity in detection of group difference was consistently improved by ~25% using HOFC compared to using FC. An HOFC network analysis also provided complementary information to an FC network analysis. For example, HOFC between olfactory and orbitofrontal cortices was found significantly reduced in patients, besides extensive alterations in HOFC network properties. In conclusion, our results showed promise in using HOFC to comprehensively map the human brain connectome.

INTRODUCTION

Enormous progress has been made toward our understanding of human brain connectome in multiple scales [1–5]. Among them, considerable research has utilized functional connectivity (FC) analysis, e.g., seed-based correlation, independent component analysis (ICA), complex network analysis, principal component analysis, and clustering, to reveal rich information exchange among brain regions. While the relationship among distributed brain areas is found dynamic [6, 7], causal [8], hierarchical [9], multi-way [10], many-to-many [5], and behavioral context dependent [11], most of the FC studies focused on the temporal coupling of blood-oxygen-level dependent (BOLD) signals from functional magnetic resonance imaging (fMRI) [1, 4, 12–15]. Although significant progress has been made using such a simple type of analysis, information beyond the low-order, such as the simple BOLD signal synchronization, has not been fully explored yet [11].

Studies on more complex relationship among brain regions have been carried out recently with the flourishing brain connectome projects and their advanced methods. For example, researchers have 1) used information theory-based metrics such as mutual information to investigate the nonlinear relationship between brain regions [11]; 2) used multivariate modeling [16] and ICA [17, 18] to investigate the underlying structure of FC; 3) conducted data fusion from multimodal data to study FC across imaging modalities [19]; 4) utilized machine learning algorithms, such as deep learning [20], latent variable modeling [21], and sparse coding [22], to learn more accurate FC; 5) calculated instant FC to reveal brain dynamics [7, 23]; and 6) examined dynamic FC as an input to compute correlations among the FC fluctuations [24–26]. While comprehensive understanding of our brain has been improved with these studies, the complexity of these methods may inevitably lead to difficulties in interpreting their results. For example, latent variable modeling and ICA introduce new variables that are difficult to interpret biologically. In addition, how to compare the dynamic FCs across different subjects is still an open issue, since time information introduced by dynamic analysis makes a direct comparison infeasible.

We find that a more complex FC could be approached in a simple and straightforward way. We refer it as a high-order FC, or HOFC, which is fundamentally different from FC obtained from the conventional BOLD signal synchronization-based methods. Inspired by feature extraction and feature-based similarity measurement as popularly used in machine learning-based analysis methods, we proposed to measure the functional resemblance between any two brain regions based on their connectivity profiles, rather than their original BOLD time series. Of note, this connectivity profile-based functional similarity defines FC in a different manner. For example, some brain regions may be more similar to each other in a feature space than the raw BOLD signal space. To clearly differentiate such a connectivity profile-based FC from the conventional FC analysis methods using lower-level BOLD signals, we label our new method HOFC while refer to the traditional method as FC. In our method, the connectivity profile of each brain region can be defined as a vector consisting of multiple conventional FC values by calculating the temporal correlations between the BOLD signal of this region and those of all other regions (one-to-all FC). In this way, a topographical profile for this region can be generated. Then, a second level of correlations can be calculated between the topographical profile of one region and the topographical profile of another region, thus forming pair-wise HOFC. Of note, similar strategies can also be found in, 1) machine learning field, e.g., classification based on the feature vectors extracted from a local spatial patch rather than a single feature from the center voxel [27], 2) neuroscience field, e.g., FC profile-based parcellation of the whole brain or a specific brain region [28–30], as well as multivariate distance-based connectome-wide association analysis [31], and 3) graph theory analysis as an analogue of “rich club”, i.e., the nodes with dense connections tend to connect with each other [32]. However, to the best of our knowledge, there is no study that explicitly uses such a strategy to define pair-wise connectivity and further builds complex brain network.

Since HOFC focuses on the correlation of spatial or topographical FC properties rather than actual temporal correlations, new information could be potentially revealed by this new metric. In clinical neuroscience applications, although conventional FC was dominantly used in biomarker detection studies using resting-state fMRI (rs-fMRI), it is possible that the similarity/difference in the FC profile may provide additional or more effective biomarkers. To demonstrate this, we first explain the concept of HOFC by emphasizing its potential advantage and ability to provide new information compared with the conventional FC; then, we apply it to identify biomarkers for early detection of Alzheimer’s disease (AD) by comparing patients with mild cognitive impairment (MCI), the prodromal state of AD, with the cognitively normal subjects (control group). Our hypothesis is that HOFC might be able to capture new group differences compared with those detected by the conventional FC. Our secondary hypothesis is that, by constructing a complex network based on pair-wise HOFC, a graph theory analysis may reveal novel information of the “HOFC network” properties, which could be complementary to the information captured by the graph theory analysis of the traditional FC networks.

MATERIALS AND METHODS

Theoretical analysis

HOFC measures similarity of the FC topographical profiles, rather than similarity of BOLD time series. Therefore, HOFC reflects high-level organization of brain functionality, i.e., functionally closed brain regions tend to have similar FC profiles. Suppose that the functional relationship between brain regions i and j (i, j ∈ ℜ, i ≠ j) is of interest, and ℜ is the overall set of R brain regions. Conventional FC between regions i and j, FC_ij, can be defined by measuring the temporal synchronization between two respective T-length BOLD signals, X_i and X_j, using Pearson’s correlation (Eq. 1),

$$\begin{array}{l}F{C}_{ij}=\frac{\langle {\mathbf{X}}_i,{\mathbf{X}}_j\rangle }{\left|{\mathbf{X}}_i\right|\left|{\mathbf{X}}_j\right|}\\ =\frac{{\displaystyle \sum _{t=1}^T(x_i(t)-\overline{x_i})(x_j(t)-\overline{x_j}})}{\sqrt{{\displaystyle \sum _{t=1}^T{(x_i(t)-\overline{x_i})}^2}}\sqrt{{\displaystyle \sum _{t=1}^T{(x_j(t)-\overline{x_j})}^2}}}\end{array}$$ (1)

where $\overline{x_i}=\frac{1}{T}{\displaystyle \sum _{t=1}^T{x}_i}(t)$, and analogously for $\overline{x_j}$. It is reasonable that the brain region i is also more or less functionally connected with all other brain regions k (k ∈ ℜ, k ≠ i, j) according to Eq. 1. Thus, the (R − 2) × 1 FC topographical profile (or FC profile for simplicity) of the brain region i can be formed as below:

$${\mathbf{L}}_i\leftarrow {\left\{F{C}_{ik(k\in \Re ,k\ne i,j)}\right\}}_{(R-2)\times 1}=F{C}_i.$$ (2)

Similarly, the FC profile of the brain region j can be defined as below:

$${\mathbf{L}}_j\leftarrow {\left\{F{C}_{jk(k\in \Re ,k\ne i,j)}\right\}}_{(R-2)\times 1}=F{C}_j.$$ (3)

HOFC between brain regions i and j, HOFC_ij, can be defined as the Pearson’s correlation between their respective (R − 2)-length vectors L_i and L_j according to Eq. 4:

$$\begin{array}{l}HOF{C}_{ij}=\frac{\langle {\mathbf{L}}_i,{\mathbf{L}}_j\rangle }{\left|{\mathbf{L}}_i\right|\left|{\mathbf{L}}_j\right|}\\ =\frac{{\displaystyle \sum _k\left(F{C}_{ik}-\overline{F{C}_i}\right)\left(F{C}_{jk}-\overline{F{C}_j}\right)}}{\sqrt{{\displaystyle \sum _k{\left(F{C}_{ik}-\overline{F{C}_i}\right)}^2}}\sqrt{{\displaystyle \sum _k{\left(F{C}_{jk}-\overline{F{C}_j}\right)}^2}}}\end{array}$$ (4)

Note that both L_i and L_j are in the full length of R − 2; that is, neither of them is thresholded, but all the elements are used to calculate HOFC. This allows us to take advantage of both strong and weak FC values when calculating HOFC.

Eqs. 1 and 4 take the same form of Pearson’s correlation; however, HOFC_ij are not always consistent with FC_ij. For example, there could be a situation that two regions have high FC (i.e., high BOLD signal synchronization) but low HOFC (i.e., distinct FC topographical profiles) or vice versa. A simple illustration of such discordance will be described in the Results. Actually, there are many reasons causing such discordance. Biologically, two brain regions may act more similarly in a high-level manner. For example, for two regions belonging to different functional networks (i.e., with low FC between them), their FC profiles could still be similar (i.e., with high HOFC; see Results). Another exemplar case is that the rs-fMRI time series of a region i at the bottom brain may have lower signal-to-noise ratio (contaminated by physiological or imaging noise), while the time series of a cerebral region j (should be closely connected with the region i) may not. Therefore, their FC could be low due to the noise. When looking at the FC profiles of region i, the FC values to other regions could be generally small (caused by additional noise); while the FC values in FC profile of the region j could be generally large. When calculating HOFC, since the mean of each region’s FC profile is first subtracted (Eq. 4), the correlation between these two FC profiles can still be high.

In clinical setting, additional valuable biomarkers may be detectable using HOFC. For example, a patient may have intact FC_ij but deteriorated HOFC_ij, due to different ways of disease-related alterations in L_i and L_j, e.g., several elements in L_i (but not in L_j) was slightly altered by disease. In this case, changes in FC profile may result in a prominent alteration in correlation between two FC profiles. In other words, as defined in a high-order fashion (i.e., correlation’s correlation), HOFC could be more informative in measuring such changes by providing additional information beyond the FC-based biomarkers. Therefore, we proposed that, by abstracting from similarity of time courses to similarity of FC profiles, HOFC may provide substantial benefit in neuroimaging based biomarker detection for the study of neurological and psychiatric diseases.

Moreover, pair-wise HOFC computation (Eqs. 2–4) can be easily extended to all regional pairs, thus producing a new correlation matrix. Each element in this new symmetric correlation matrix represents the HOFC between two brain regions. Similar to the conventional FC-based brain network, we can call this an HOFC-based brain network, or simply “HOFC network”. Then, the conventional complex network analysis with graph theory can be directly applied to the HOFC networks, for potentially providing more information on biomarker detection.

Participants

A total of 80 patients with MCI and 90 normally aged healthy controls (CON) were enrolled in this study. Although converging evidences have shown that the FC in AD patients is reduced in the olfactory cortex and the default mode network (DMN) [13, 33–36], MCI, the prodromal stage of AD [37], is believed to bear with pathological and compensatory changes in brain functional networks before changes in local biomarkers become evident [38–48]. Therefore, we used MCI patients as subjects in order to provide further evidence to the current hypothesis on MCI with the proposed HOFC method.

One control subject was excluded due to excessive head motion (see “Data preprocessing” below). Three MCI patients were excluded because of bad normalization. Therefore, data from 89 CONs (29 males, 60 females, age 72.93 ± 4.24 years) and 77 MCIs (25 males, 52 females, age 72.82 ± 5.67 years) were used. All participants were right handed, normal or corrected-to-normal visual acuity, and none reported a history of neurological or psychiatric disorders, alcohol or drug abuse. Subjects with regular use of psychotropics, stimulants, and beta-blockers were excluded. This study was approved by the local ethical committee and performed in accordance with the ethical standards as laid down in the 1964 Declaration of Helsinki and its later amendments. Informed written consent was obtained from each participant prior to their inclusion in this study.

The education level was assessed according to the Swiss education system, where 1 denotes “less than 9 years (primary school)”, 2 for “9–12 years (high school)”, and 3 for “more than 12 years (university or higher)”. A series of neuropsychological scales and cognitive tests were used for assessment of clinical symptom and cognitive impairments. Specifically, the CON group underwent Mini-Mental State Examination (MMSE), the Hospital Anxiety and Depression Scale (HAD), the Lawton’s Instrumental Activities of Daily Living Scale (IADL), Clinical Dementia Rating scale (CDR), digital symbol coding, trail making test, digit span (forward/backward), visual memory span (forward/backward), RI-48 cued recall test, shape test, Wisconsin Card Sorting Test (WCST), phonemic verbal fluency test, Boston naming, Ghent overlapping figures, ideomotor, reflexive and constructional praxis tests. Only those with CDR score of 0 and scores within 1.5 standard deviations of the age-appropriate mean in all other tests were included in the CON group.

For MCI participants, similar tests were carried out with additionally included RL/RI-16 free and cued recall tests. In agreement with Petersen’s criteria [49]), participants with a CDR score of 0.5 (but no dementia) as well as a score of more than 1.5 standard deviation below the age-appropriate mean in any of the above tests confirmed their MCI status. In several tests, most of the MCI patients halted their tests before their completion or had difficulties to complete the tests so that the examiner decided to interrupt the tests; in other cases, the tests were not conducted due to time management or external reasons (i.e., data unavailable). Therefore, we only compared the scores from a part of the tests between the two groups and further used them in correlation analysis.

Data acquisition

Data acquisition was performed on a clinical routine whole-body 3.0 T MR scanner (Trio, Siemens medical systems, Erlangen, Germany). Scanning sequences and parameters for each type of MR imaging data are provided as follows. For each participant, T1-weighted structural image was acquired using a Magnetization Prepared RApid Gradient Echo (MPRAGE) sequence with the following fundamental parameters: acquisition matrix = 256 × 256, 176 slices, voxel size = 1 × 1 × 1 mm³, echo time (TE) = 2.3 ms, and repetition time (TR) = 2300 ms. FMRI images were acquired using a standard echo-planar imaging (EPI) sequence with an acquisition matrix = 74 × 74, 45 slices, voxel size = 2.97 × 2.97 × 3 mm³, TE = 30 ms, TR = 3000 ms, and 180 repetitions (9 min).

Experimental paradigm

A simple block designed CO₂ challenge task [50] was conducted during fMRI acquisition, consisting of 1 min OFF (breathe normally through the nose with air), 2 min ON (breathe normally through the nose with 7% CO₂ with synthetic air), 2 min OFF, 2 min ON, and 2 min OFF. The CO₂ stimulus was applied via a nasal cannula. The on and off of CO₂ application was controlled manually using a standard clinical flow meter at a rate of 8 l/min. For more details, please see Richiardi et al. [50]. The CO₂ challenge task was originally designed for better identification of MCI patient according to abnormal cerebrovascular reactivity in MCIs [50, 51]. However, after regressing out the task evoked BOLD responses, the data was suitable for FC analysis, where the patterns of FC were proven to be comparable to those in conventional rs-fMRI studies [52] (see Supplementary Material 2 for details).

Data preprocessing

The data was preprocessed using Matlab 2013a (the MathWorks, Inc., Natick, MA), Statistical Parametric Mapping toolbox (SPM8, www.fil.ion.ucl.ac.uk/spm), REST version 1.8 [53] and DPARSFA version 2.2 [54]. Specifically, the first four images were discarded to allow signal stabilization. The remaining data was corrected for both slice timing and head motion. Subjects with maximal absolute head motion larger than 1.5 mm or 1.5° were excluded from further analysis. The T1 image was first co-registered to the averaged motion corrected fMRI data, and then segmented using Diffeomorphic Anatomical Registration Through Exponentiated Lie Algebra (DARTEL) [55], which produced a deformation field projecting from each subject’s original individual space to the Montreal Neurological Institute (MNI) space. The deformation field was applied to head motion corrected fMRI data for normalization. The fMRI data were further re-sampled to a resolution of 3 × 3 × × 3 mm³, cand spatially smoothed using a 6-mm full-width half-maximum isotropic Gaussian kernel. It was then de-trended to remove linear trend due to drift, and band-pass filtered (0.01–0.08 Hz) to remove extremely low- and high-frequency artifacts. Finally, several nuisance signals were regressed out to reduce the effect caused by artifacts, including the task effect, i.e., task-related square wave convoluted with a canonical hemodynamic response function in SPM, as well as the averaged signals from cerebrospinal fluid, white matter, and whole brain, and the six head motion parameters. We found that the conventional preprocessing, such as filtering and covariate removal, significantly reduced the task-evoked response (with details in Supplementary Material 2), allowing the following FC calculation [56].

FC profile calculation

The preprocessed fMRI data was fed into a traditional pair-wise FC calculation to build FC profiles for HOFC calculation. To this end, averaged BOLD signals for each of the 90 cerebral regions were extracted according to Automated Anatomical Labeling (AAL) atlas [57] (note that other 26 cerebellar regions were not used because the bottom brain might not be included during the scan and also the cerebellum and brain stem tend to be inaccurately registered); pair-wise Pearson’s correlation was calculated between any pair of regionally averaged time courses, forming a correlation matrix with the size of 90 × 90. Each element in this correlation matrix represented the conventional FC, i.e., region-wise linear co-variation (Fig. 1a). The FC matrix was further transformed to z-scores by using Fisher’s r-to-z transformation for improving the normality for the subsequent correlation analysis in the HOFC calculation.

Fig. 1.

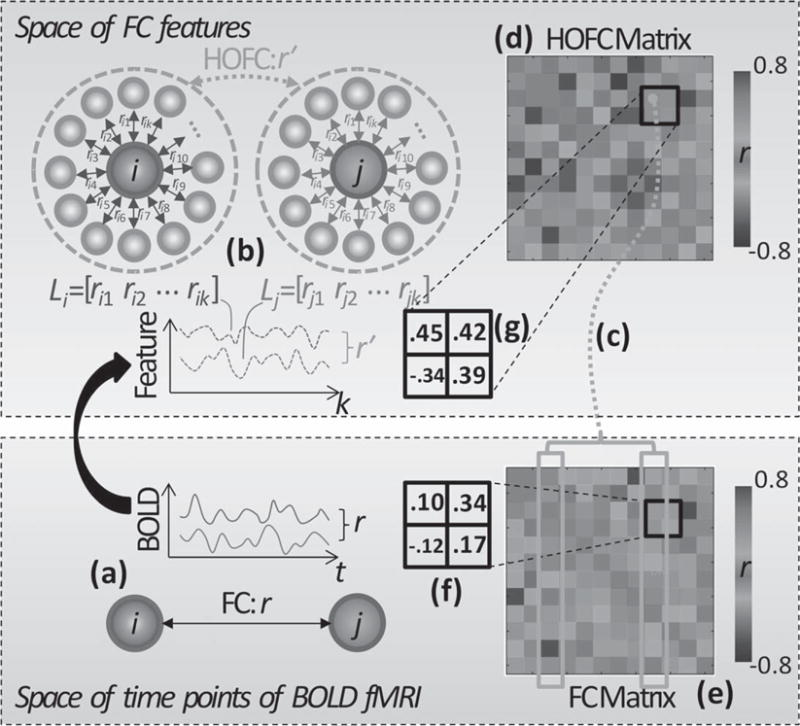
Flow chart of HOFC calculation. a) Previous FC computes correlation coefficient r based on a pair of BOLD time series from two brain regions i and j. b) Our proposed HOFC first calculates FC between the region i and all other regions, forming an FC feature vector, L_i; second, repeats FC calculation between another region j and all other regions, forming another FC feature vector, L_j; finally, calculates correlation r’ based on the two feature vectors to produce HOFC. The feature vectors are actually columns of the FC matrix (e); column-wise correlation (c) based on the FC matrix (e) produces one element in the HOFC matrix (d); looping over all column pairs in FC matrix generates the entire HOFC matrix (d). Four exemplar FC and HOFC values (the black squares in (f) and (g), respectively) were selected for a clear demonstration of their difference. From (f-g), we can see, although two regions have low FC strength (0.10), they can still have high HOFC strength (0.45). This is because the two regions have distinct BOLD fluctuations, but they still have similar FC features (see the two columns in FC matrix highlighted in yellow blocks in (e)). For illustration purpose, only 12 out of 90 brain regions were selected to show a simplified FC and HOFC matrices (d-e) in this example. For colored version of the figure, please see its online version.

HOFC calculation

Each column of the z-transformed FC matrix denotes the FC between a specific region and all other regions, thus forming an FC profile. For any two regions, a linear correlation was calculated based on their connectivity profiles (Fig. 1b). For 90 brain regions, we calculated Pearson’s correlation of the FC profiles between any two regions (i.e., column-wise correlation, see Fig. 1c), producing a new matrix with the same size of 90 × 90 (see a simple case of such a matrix in Fig. 1d), where each element represents “correlation’s correlation”, or HOFC. This HOFC matrix is different from the FC matrix (see a simple example in Fig. 1e). Of note, when performing column-wise FC profile-based correlation (Fig. 1c), self-connections in FC matrix (i.e., those in the diagonals of matrices) were not taken into consideration, i.e., only an FC-profile vector with the length of 88 (90 – 2, where “2” represents the two self-connections in the FC matrix) was used for correlation. This is because including self-connections will introduce a nuisance effect to HOFC calculations for several links.

Group difference in pair-wise HOFC

For each of the 4005 (90 × 89/2 = 4005) HOFC links, a multiple regression model-based two-sample t-test was used for group comparison (p < 0.0001, uncorrected for multiple comparisons) to detect if there was any HOFC change in MCI. Age, gender, and education level were used as covariates for the regression model to regress out potential nuisance group difference due to those covariates. This was done by fitting two regression models, i.e., one without covariates (reduced model), and the other with the covariates (full model). All the covariates and the “group” variable were centralized by removing the mean of each variable. F statistics was then obtained and converted to T statistics. Fisher’s r-to-z transformation was applied to HOFC values for transforming them into z scores before the statistical tests. To further compare the sensitivity in group difference detection between HOFC and FC, we also did the same group comparison analysis based on FC with the same threshold. To comprehensively compare the performance in-group difference detection, we also used multiple thresholds (e.g., p < 0.001 and 0.01, uncorrected). In case of potential false positive detections, we also applied multiple comparison correction to adjust statistical significance by using a false-positive adjustment [58, 59]. Specifically, we set p < 1/4005, where 4005 corresponds to the number of all possible pair-wise links among the 90 brain regions.

Group difference in HOFC-based complex network properties

Since HOFC was proposed to characterize region-wise functional relationship based on the FC profiles rather than BOLD signals, the configuration and organization (e.g., modularity, characterizing the community structure of a network) of the constructed HOFC network may also differ from that based on the conventional FC. Inspired by previous studies comparing complex network properties of FC networks, we also assessed the properties of HOFC networks and compared them between the two groups, i.e., CON and MCI. Notably, modularity characteristic is informative to understand the infrastructure of a network and is also sensitive to the subtle changes [14]. In addition, nodal centrality and edge centrality may help us better understand the main targeted nodes or links due to the pathological attack of MCI [60]. Therefore, we mainly focused on the above three metrics: modularity, nodal centrality, and edge centrality. Specifically, based on the binary HOFC matrix with network sparsity of 5% (i.e., totally 200 links out of all possible 4005 links, as suggested by Meunier et al. [14]), modularity index and the number of modules were calculated for each subject according to Newman’s method [61] and were normalized by the distribution of the equivalent properties of the comparable random networks simulated 500 times [14]. The modularity patterns from the group averaged HOFC networks for both groups were also calculated at a denser (compared with the 5% for individualized analysis) network with sparsity of 15% for visual demonstration purpose, as we empirically found that sparsity of 15% produced more interpretable group-level modularity analysis results [4, 5, 62, 63]. With network sparsity of 5%, the nodal centrality for all 90 AAL regions in the HOFC network for all subjects were calculated and standardized by the maximum nodal centrality for each subject; and the edge centrality for all 4005 possible links were also calculated and standardized in the same way. The relative nodal centrality and relative edge centrality were further compared between the two groups. Since not all possible links had nonzero edge centrality, we only compared the links with non-zero centrality for more than 80% subjects from both groups. Two sample t-tests with age, gender and education level as covariates were used for group comparison (p < 0.05, uncorrected). For comparison purpose, the properties of FC network were also calculated and compared with those of the HOFC network.

Correlation analysis

If group difference in pair-wise HOFC or HOFC network-based properties was found, Pearson’s correlation was then calculated between the z-transformed pair-wise HOFC and the scores of neuropsychological and cognitive tests. The correlations between the values of the HOFC network properties and the testing scores were also calculated. The tests used in correlation analysis included MMSE, IADL, RI-48, digit span, visual memory span, phonemic verbal fluency, and trail making. For the MCIs who failed in performing a digit span task (i.e., indicating a working memory function deficit), their scores were put to zero during the correlation analysis. For comparison, the same correlation analysis was also conducted using pair-wise FC.

RESULTS

Illustrations of HOFC calculation

Figure 1 shows how HOFC was calculated, along with the difference between FC and HOFC matrices. For better illustration, the small matrices (12 ×12) shown in Fig. 1d and e were evenly sampled from a full matrix (90 × 90) from a randomly chosen CON subject at every seven columns and rows. A 2 × 2 patch in the FC matrix (Fig. 1f) and a 2 × 2 patch in the same position of the HOFC matrix (Fig. 1g) were highlighted with black frames. Of note, the value of FC in the upper left of the patch was 0.1, indicating no significant connectivity between the two regions. In contrast, the corresponding HOFC was relatively high (0.45), indicating a strong positive connectivity between the same two nodes. This is because the two highlighted columns in FC matrix in Fig. 1e (i.e., the FC profiles of the two brain regions) were quite similar in their patterns (Fig. 1c).

Figure 2 shows an example from another subject, where the standardized averaged BOLD signals from the left anterior and the left posterior cingulate cortices (upper panel) as well as the FC profiles from the same regions (lower panel) were plotted. The correlation of the BOLD signals indicated a low FC (r = 0.24), because the posterior cingulate cortex is within the DMN and the anterior cingulate cortex is distributed to multiple networks (including the executive control network, the salience network, and the DMN). However, the highly similar FC profiles suggested a high HOFC (r = 0.71), indicating a close relationship among these higher cognitive function-related networks. These examples demonstrated that HOFC is not the same as, or linearly proportional to, FC, but has fundamental difference from FC in several links.

Fig. 2.

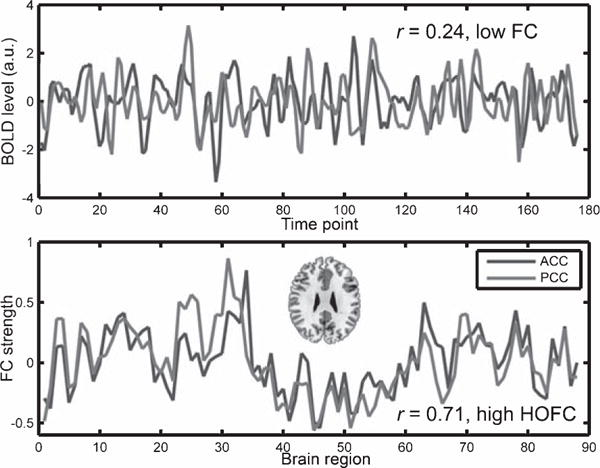
Example of discordant FC and HOFC values. The averaged BOLD signals in the anterior cingulate cortex and the posterior cingulate cortex of the AAL atlas from a randomly selected subject were plotted in the upper panel. For better illustration, both time courses were standardized by subtracting their own mean values and dividing by their own standard deviations. The Pearson’s correlation between them was 0.24, indicating a low FC. The FC profiles (i.e., the FC values between the ROI and other 88 regions of the AAL template) for the two regions were plotted in the lower panel, where prominent similarity, or high HOFC, was found (Pearson’s correlation coefficient between the two FC profiles was 0.71). Red color in an axial brain slice indicates the locations of the two brain regions. For colored version of the figure, please see its online version.

Demographic, clinical, and behavioral data

There is no significant group difference in gender (p = 0.99) or age (p = 0.52), except education level, which shows a trend in difference (p = 0.06). There were group differences in MMSE (p = 0.0005), IADL (p < 0.0001), phonemic verbal fluency (p = 0.0017), and RI-48 (p < 0.0001, computed based on 64 available MCIs’ data and all CONs’ data). Twenty-eight CONs failed in completion of backward digit and visual memory span tasks; 29/18/47 MCIs failed in completion of the backward digit span task, the forward and backward visual memory span tasks, respectively. See Table 1 for detailed information on group comparison results on these variables.

Table 1.

Demographic, clinical, and behavioral information

Variables	MCI	CON	p value
Total number of subjects	77	89
Gender (male/female)	25/52	29/60	0.99
Age (y)
Range	58–87	60–87
Mean±SD	72.82 ± 5.67	72.93 ± 4.24	0.52
Education (P/H/U1)	6/37/34	18/41/30	0.06
MMSE
Range	23–30	24–30
Mean±SD	27.53 ± 1.59	28.4 ± 1.29	0.0005*
CDR2	0.5	0	—
IADL	13.22 ± 8.72	8.16 ± 0.66	<0.0001*
HAD
Depression score	1.88 ± 1.77	1.47 ± 1.71	0.09
Anxiety score	4.22 ± 2.51	4.06 ± 2.33	0.83
Total score	6.1 ± 3.66	5.53 ± 3.47	0.31
Trail making test (B/A)	2.89 ± 1.19	2.74 ± 1.22	0.32
Phonemic verbal fluency	18.4 ± 6.54	21.4 ± 5.58	0.002*
RI-48 cued recall
Immediate verbal	35.14 ± 5.09	38.84 ± 5.3	<0.0001*
cued recall
Total free recall	15.69 ± 4.19	26.85 ± 5.4	<0.0001*
Instrusions	4.33 ± 5.66	1.70 ± 1.68	<0.0001*
Digit span
Forward	7.95 ± 1.79	8.48 ± 1.73	0.08
Backward3	3.20 ± 2.88	3.94 ± 3.18	0.13
Visual memory span
Forward3	5.39 ± 3.28	6.94 ± 1.66	0.01*
Backward3	2.48 ± 3.25	4.82 ± 3.54	<0.0001*

MCI, mild cognitive impairment; CON, normal control; MMSE, Mini-Mental State Examination; CDR, Clinical Dementia Rating scale; IADL, Lawton’s Instrumental Activities of Daily Living scale; HAD, Hospital Anxiety and Depression scale;

^*Significant group difference (p < 0.05).

¹Primary (<9 y)/High school (9–12 y)/University (>12 y);

²All CONs had the same CDR scores of 0, and all MCIs had the same CDR scores of 0.5;

³Several MCIs and/or CONs did not complete the test due to impairment; their scores were set to 0.

Group difference in pair-wise HOFC

Compared with the group mean FC matrices (shown in Fig. 3a, c), the group mean HOFC matrices (shown in Fig. 3b, d) have much higher absolute correlation values (for CON, the absolute HOFC and FC strength were 0.25 ± 0.18 and 0.17 ± 0.14, respectively, with p = 4.78 × 10⁻⁹⁷; for MCI, those values were 0.24 ± 0.18 and 0.17 ± 0.14, with p = 1.76 × 10⁻⁸⁰). The individual variance of HOFC values was generally higher than that of FC in most of the links for both CON (0.36 ± 0.07 versus 0.21 ± 0.04) and MCI groups (0.37 ± 0.07 versus 0.22 ± 0.04), indicating that HOFC is sensitive to individual difference, thus possibly informative for distinguishing MCIs from CONs (see the standard deviation maps of HOFC and FC across subjects from both groups in Supplementary Material 3). Group comparisons revealed one HOFC link with significant group difference of MCI < CON with p < 0.0001. This link is between the left olfactory cortex (OLF.L) and the left superior orbitofrontal gyrus (SFGorb.L). There was no group difference in the conventional FC strength with the same threshold. In addition, we found 3 links with group difference in HOFC, while 2 links with group difference in FC with p < 1/4005 (corrected using false-positive adjustment), with only 1 link shared between the two results. With a looser threshold of p < 0.001, 6 HOFC links and 4 FC links with group difference were found, with only 2 links shared (Table 2). By continuously relaxing the threshold to p < 0.01, we found 83 HOFC links (Fig. 3f) and 55 FC links (Fig. 3e) with group difference, in which 36 links are shared between them (Fig. 3g). Of those 83 links with HOFC differences, 42 links were MCI < CON, and 41 links were MCI > CON; of those 55 links with difference, we found MCI < CON in 32 links and MCI > CON in 23 links.

Fig. 3.

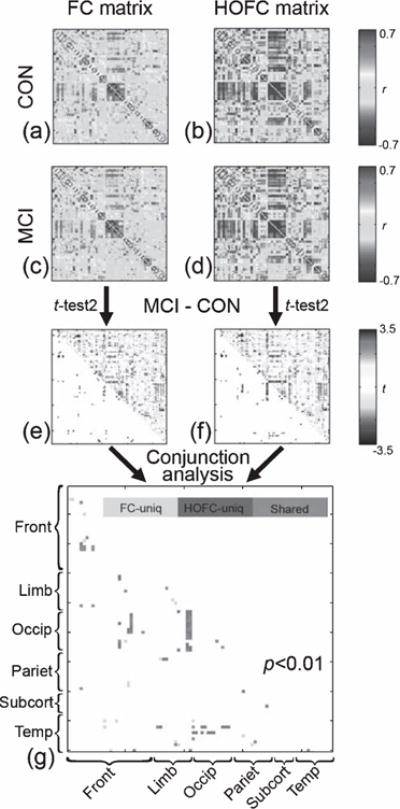
Group differences in pair-wise HOFC between CON and MCI. The matrices in (b) and (d) represent group averaged pairwise HOFC for all possible region pairs for CON and MCI groups (color range: correlation coefficients of −0.7 ~ 0.7), respectively. For comparison, the matrices of group averaged FC for both groups were shown in (a) and (c) with the same color range. The group comparison (MCI – CON) results in t maps for both HOFC and FC were shown in (f) and (e), where the upper triangular matrices are unthresholded t values, and the lower triangular matrices are thresholded results using a looser threshold (p < 0.01, uncorrected) to reveal more potential group differences in an exploratory manner. Comparison of the sensitivity to group difference detection between HOFC and FC was conducted using a conjunction analysis (g), where grey color indicates the group differences only found by HOFC with p < 0.001, green color indicates the group differences only found by FC using the same threshold, and purple color indicates the group difference found by both HOFC and FC. Of note, we use p < 0.001 to show the sensitivity difference between the two methods; the result with a more stringent p value can be found in the main text. In all matrices, the x-axis and y-axis consist of 90 AAL regions with the same order (please see [55] for more details). Basically, the 90 regions can be grouped into 6 sub-groups: frontal areas (Front), limbic system (Limb), occipital areas (Occip), parietal areas (Pariet), subcortical areas (Subcort) and temporal areas (Temp). For colored version of the figure, please see its online version.

Table 2.

Group difference in pair-wise HOFC/FC (p < 0.001)

	#	Region A	Region B	p	t	Direction*
HOFC	1	OLF.L	SFGorb.L	0.000044	−4.199	↓↓
	2	OLF.L	SFGorb.R	0.000752	−3.436	↓
	3	SFGorb.L	SFGorb.R	0.000106	−3.975	↓
	4	SFGorb.L	OLF.R	0.000149	−3.886	↓
	5	AMYG.R	SOG.L	0.000973	3.361	↑
	6	AMYG.L	MOG.L	0.000528	3.538	↑
FC	1	OLF.L	SFGorb.L	0.000209	−3.795	↓
	2	OLF.L	SFGorb.R	0.000780	−3.426	↓
	3	OLF.L	MFGorb.L	0.000162	−3.864	↓
	4	paraCL.L	SFGorb.L	0.000778	−3.426	↑

^*Direction of ↑ and ↓ indicates increased and decreased functional connectivity between regions A and B in MCIs compared with CONs with p < 0.001, uncorrected; ↓↓indicates decreased functional connectivity in MCIs compared with CONs with p < 0.0001, uncorrected. Note that the increase or decrease directions were based on absolute functional connectivity value. The shaded region pairs indicate the same findings from both HOFC and FC. For abbreviations of the brain regions listed above please see Supplementary Material 1.

Figure 4 shows a complete summary of the numbers of the links with group differences that were uniquely detected by HOFC and FC respectively, as well as the numbers of the links with group difference detected by both methods, under various thresholds (p < 0.0001, 0.0005, 0.001, 0.005, and 0.01). With each threshold, we calculated a metric named “sensitivity gain” to measure how much the usage of HOFC could increase the sensitivity in group difference detection compared with FC according to Eq. 5:

$$\begin{array}{c}\text{Sensitivity}\text{gain}={\text{(HOFC}}_{\text{uniq}}-\text{FCuniq})\\ /({\text{HOFC}}_{\text{uniq}}+{\text{FC}}_{\text{uniq}}+\text{Shared),}\end{array}$$ (5)

where HOFC_uniq indicates the number of the HOFC links that were uniquely identified to be statistically different between two groups; FC_uniq means the number of the FC links that were uniquely identified to be significantly different; and “Shared” means the number of links that were jointly identified with statistical difference between two groups by using HOFC and FC. As shown in Fig. 4, the sensitivity gain was around 25% (except the case of p < 0.0001, where no group difference in FC was found, thus HOFC leads to 100% sensitivity gain). That means, when HOFC is used, the sensitivity in-group difference detection may increase by about 25%.

Fig. 4.

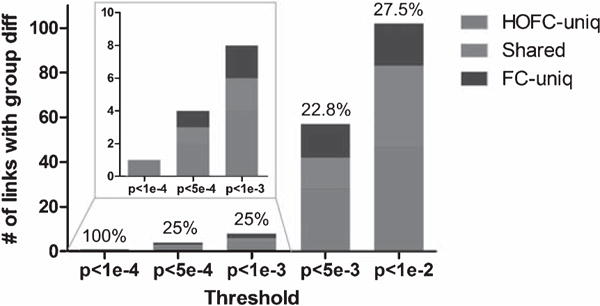
“Sensitivity gain” obtained by using HOFC compared with FC. Besides single threshold, multiple thresholds (from p < 0.0001 to p < 0.01) were applied to the group difference statistics matrices for both HOFC and FC. With each threshold, the number of pair-wise HOFC and FC with significant group differences were counted and compared. Specifically, the number of the group differences that were uniquely identified by either HOFC or FC, as well as the number of the group differences identified by both metrics was plotted with bar graph against different thresholds. Sensitivity gain, detailed in the main text, was also shown on top of each bar. Red (blue) color indicates the amount of HOFC (FC) differences uniquely detected by using a specific p value. Green color indicates the amount of shared group differences found by using both HOFC and FC. For colored version of the figure, please see its online version.

We also show those unthresholded group comparison results for complete comparisons between HOFC and FC in Fig. 3e and f. Non-parametric permutation test with the same corrected p value (i.e., p < 1/4005) revealed a similar result (see Supplementary Material 4).

Group differences in HOFC modularity

The modules detected from the group-averaged HOFC networks for both CON and MCI groups are shown in Fig. 5e and f. For better comparison, the modules for group averaged FC networks are also shown (Fig. 5c, d). The mean HOFC matrices show more prominent modular configuration than the mean FC matrices. The modularity pattern derived from the within-group mean HOFC network has more visible differences between the two groups than those from the within-group mean FC network. Especially, in MCIs, five HOFC modules (Fig. 5h) were found whereas in CONs, four HOFC modules were found (Fig. 5g). The group difference in modular infrastructure of the mean HOFC network was more prominent compared with the group difference in pair-wise HOFC, which was summarized as below. The modules from the conventional FC networks are shown in Fig. 5a and b, which resembles the report from the previous studies on the modules detected from FC networks [64]. Both CON and MCI have five modules, and they look quite similar.

Fig. 5.

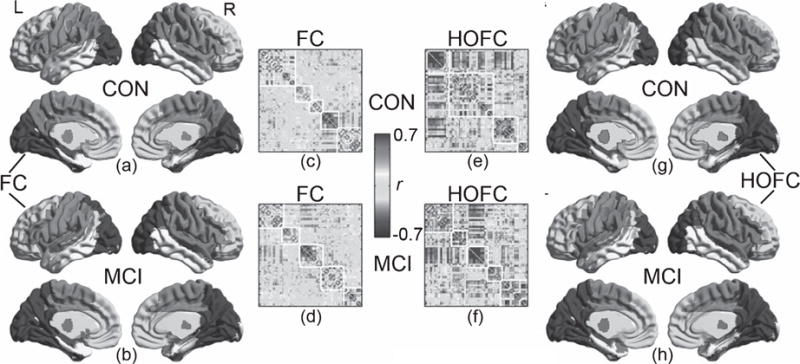
Modules detected by group-mean HOFC and FC matrices. The module detection was based on the Newman’s spectral optimization algorithm when the sparsity of both HOFC and FC-based networks was set to be 15%. A sparsity of 15% means that, for both groups’ mean HOFC and mean FC matrices, only the edges with the largest 15% connectivities were replaced with 1’s and those with lower connectivity strength were changed to 0’s. The modularity detections algorithm produced a modular label for each brain region (node). The matrices shown in (c – f) are the rearranged connectivity matrices according to the modular labels (i.e., the brain regions belonging to the same module were replaced to neighboring columns and rows). The border of the modules was delineated with white lines. The HOFC modules and the FC modules were visualized onto the brain surface, with different colors for different modules. For better comparison, modules at similar locations have the same color code. For FC network, both CON (a) and MCI (b) had five modules. However, for HOFC network, CON had four (g) and MCI (h) had five modules. See main text for the detailed description of these modules. For colored version of the figure, please see its online version.

As shown in the right panel of Fig. 5, there are 5 HOFC modules for MCI but 4 for CON group. For CONs, the HOFC modules are the visual areas (in blue), auditory, language, and motor areas (in purple), frontal and the DMN areas (in green), as well as the lateral and medial temporal areas (in yellow) (see Fig. 5g). For MCIs, the module consisting of auditory, language, and motor areas is split into two modules, with the motor area (in purple) separated out (from the auditory and language module shown in red). Other changes in modular architecture include: 1) bilateral middle temporal gyrus and the temporal pole switch from the module of the frontal area and DMN (the green part in Fig. 5g) to the temporal module (the yellow part in Fig. 5h); 2) bilateral superior parietal lobules switch from the visual module to the motor module; 3) bilateral caudate associate to the frontal and DMN module, instead of the module of auditory, language, and motor areas in CONs; and 4) the bilateral middle frontal gyrus, the left inferior frontal triangularis, and the right inferior orbitofrontal cortex move from the auditory, language, and motor module to the frontal and DMN module.

At individual level, however, the normalized modularity index and the normalized number of modules did not have significant group difference (p > 0.05). Specifically, for HOFC network, the normalized modularity indices for the MCIs and CONs were 25.18 ± 3.61 and 25.05 ± 3.60, respectively, and the normalized number of modules was 5.10 ± 1.58 and 5.08 ± 1.81, respectively. The group differences in modularity indices for FC networks were also not significant. In line with the findings from group-level networks, individual HOFC networks had significantly higher modularity index for both CON (paired t-test, p = 2.29 × 10⁻⁹) and MCI groups (p = 1.73 × 10⁻¹⁰) compared with individual FC networks. In addition, individual HOFC networks had significantly more modules for both CON (p = 9.24 × 10⁻⁵) and MCI groups (p = 7.13 × 10⁻⁶) than the individual FC networks.

Group differences in HOFC nodal and edge centrality

With network sparsity set to be 5%, 11 out of 90 brain regions show group difference in relative nodal centrality of HOFC network; and 8 regions have group difference in relative nodal centrality of FC network (Table 3). Interestingly, group comparison of HOFC networks revealed 10 unique nodes out of the 11 nodes with group difference, most of which have increased nodal centrality in MCIs compared with CONs. This indicates that HOFC network analysis can reveal highly complementary information to the FC network analysis. The edge centrality of HOFC network at 6 links was found to be significantly higher in MCIs than CONs, with 4 unique edges discovered compared with the FC network analysis result (Table 4). Similar to the nodal centrality, all the 6 edges in HOFC networks have increased edge centrality in MCIs compared with CONs.

Table 3.

Group differences in nodal centrality for HOFC/FC networks

#	HOFC			Direction*	#	FC			Direction*
	Regions	p	t			Regions	p	t
1	IFGoper.R	0.011	2.589	↑	1	IFGoper.R	0.004	2.926	↑↑
2	IFGtri.L	0.043	−2.042	↓	2	PreCG.R	0.023	2.303	↑
3	Calc.L	0.030	2.195	↑	3	ROLoper.R	0.038	2.091	↑
4	Calc.R	0.005	2.817	↑↑	4	SMA.L	0.036	2.117	↑
5	Ling.L	0.043	2.037	↑	5	PostCG.L	0.030	2.185	↑
6	Ling.R	0.038	2.096	↑	6	PostCG.R	0.034	2.135	↑
7	SOG.L	0.025	2.271	↑	7	MTG.L	0.040	−2.067	↓
8	SOG.R	0.031	2.177	↑	8	ITG.L	0.011	−2.563	↓
9	MOG.L	0.036	2.119	↑
10	MOG.R	0.008	2.671	↑↑
11	SPL.R	0.007	2.715	↑↑

^*↑ indicates increased nodal centrality in MCIs compared with CONs with p < 0.05; ↓indicates decreased nodal centrality in MCIs compared with CONs with p < 0.05; ↑↑ indicates changes with p < 0.01. The shaded results indicate the same finding from both HOFC and FC. For abbreviations of the brain regions listed above please see Supplementary Material 1.

Table 4.

Group differences in edge centrality for HOFC/FC networks

#	HOFC**		p	t	Direction*	#	FC***		p	t	Direction*
	Region A	Region B					Region A	Region B
1	PostCG.R	PreCG.R	0.046	2.010	↑	1	PostCG.R	PreCG.R	0.017	2.403	↑
2	Calc.L	Ling.L	0.039	2.081	↑	2	Calc.L	Ling.L	0.024	2.285	↑
3	SOG.L	Cun.R	0.012	2.545	↑	3	Calc.L	Calc.R	0.025	2.257	↑
4	SOG.L	SOG.R	0.043	2.042	↑	4	Calc.L	Ling.R	0.038	2.094	↑
5	SOG.R	MOG.R	0.041	2.064	↑	5	Put.L	Put.R	0.029	2.203	↑
6	STG.L	ROLoper.L	0.028	2.226	↑	6	STG.R	ROLoper.R	0.013	2.518	↑
						7	OLF.L	OLF.R	0.003	−3.077	↓↓
						8	MOG.L	MOG.R	0.018	2.391	↑

^*↑indicates increased edge centrality between regions A and B in MCIs compared with CONs with p < 0.05; ↓↓indicates decreased edge centrality in MCIs compared with CONs with p < 0.01;

^**Group differences were found for 20 HOFC edges that both group have > 80% subjects with non-zero edge centrality values;

^***Group differences were found for 42 FC edges that both group have > 80% subjects with non-zero edge centrality values. The shaded results indicate the same edges with group difference in both HOFC and FC. For abbreviations of the brain regions listed above please see Supplementary Material 1.

Correlation analysis

There was a close-to-significant correlation between MCIs’ HOFC at the link OLF.L – SFGorb.L and their performances in the backward visual memory span task (r = −0.21, p = 0.06) as well as in the phonemic verbal fluency task (r = −0.20, p = 0.07). The relative nodal centrality at the IFGtri.L correlated with the performance of the forward visual memory span task (r = −0.31, p = 0.006) and IADL score (r = 0.34, p = 0.003); the relative nodal centrality at the IFGoper.R correlated with the performance in the trail making task (r = 0.33, p = 0.003) and the MMSE score (r = −0.3, p = 0.007); and the relative nodal centrality at the SPL.R correlated with the backward visual memory span performance (r = −0.24, p = 0.033). The relative edge centrality for the links of both SOG.L – Cun.R and SOG.L – SOG.R correlated with the backward visual memory span performance (r = −0.25 and −0.28, p = 0.040 and 0.012, respectively). Although we found no group difference in the modularity index and the number of modules for individual HOFC network, we did find the number of modules correlated with trail making test scores (r = 0.30, p = 0.009) for MCIs, but the correlation was not significant for CONs (r = −0.15, p = 0.17). However, if using pair-wise FC and FC-based network properties to conduct correlation analysis, we found no significant correlation (p > 0.05).

DISCUSSION

General discussion

In this study, we proposed a novel concept of high-order functional connectivity (i.e., “correlation’s correlation”) to characterize high-level brain functional organizations. Of note, the BOLD-signal temporal synchronization-based FC, as widely used in the existing FC and graph theory studies, was a low-level metric and treated as a feature or input for HOFC calculation. One-to-many FC was calculated to form a topographical profile; HOFC was then calculated with a second level of correlation on the FC profiles of any two brain regions. To test the capability of our method in disease-related biomarkers detection, we have applied HOFC to detecting links with group difference between MCI and CON groups. The advantage of HOFC was proved by the experimental results, where more biologically meaningful group differences were detected, compared with the FC-based findings. For example, with the p value < 0.0001, the group difference was only detected by HOFC, but not by FC; and with varied significance levels, HOFC could consistently increase the sensitivity in group difference detection by ~25% (Fig. 4). The findings were still robust when the statistical significance was corrected to control false positives, and when a non-parametric permutation test was conducted.

The analysis was further extended from pair-wise HOFC to HOFC network analysis by accounting for all possible pair-wise HOFC links. We compared the properties of the HOFC-based complex network between MCI and CON groups. We particularly focused on modularity, an important network organization property, and also centrality (both nodal and edge centralities). HOFC-based network properties not only revealed greater group difference in overall modular structure (Fig. 5) but also provided supplementary information to the traditional FC-based network (Tables 3 and 4). Therefore, HOFC, as a new measurement of the brain functional organization, is able to reveal new potential neuroimaging markers for MCI. It is an important complement to our knowledge of brain connectome, which is mainly based on conventional FC network analysis. Of note, this new metric is by no means designed to replace the conventional FC, which has been found to be very successful for clinical neuroscience in searching for potential biomarkers [8, 47]. Our proposed HOFC can provide complementary information to FC findings for better understanding of our brain functional organization and its disturbance due to diseases.

Advantages of HOFC

This study identified five specific advantages of HOFC: 1) HOFC is more sensitive to group difference compared with conventional FC. For example, with p < 0.0001, group difference was detected if using pair-wise HOFC, while no group difference was detected if using the conventional FC. We also applied various thresholds to make sure that such increase of sensitivity is stable and consistent, and Fig. 4 shows that HOFC was consistently more sensitive to group difference detection than FC (i.e., when switching FC to HOFC, the number of unique pairwise connectivity differences increased by ~25%). 2) HOFC could better capture individual variability than FC. As shown in Supplementary Material 3, the standard deviation of HOFC matrix across subjects from each group was greater than that of FC matrix. This indicates that HOFC could capture highly individualized information that might be helpful for individual classification. 3) For both groups, HOFC network shows a more prominent modular structure than FC network (Fig. 5). The modular structure is an important property for a complex network [14]. With dense intra-modular connectivity and relatively sparse inter-modular connectivity, a network can spread information with relatively low cost [4]. By identifying modular organization from network topology, we can better analyze a network by attributing edge and node specific roles (e.g., connectors) [14]. By using HOFC, such an analysis could be easier. 4) The difference in modularity of the group-averaged HOFC network between MCI and CON groups was more prominent than that of FC network (i.e., Fig. 5e and f have greater differences, compared with the difference between Fig. 5c and d). This could be due to the merit of clearer modular architecture detected by HOFC. For example, at the group level, we can easily distinguish MCI from CON purely based on the module number (i.e., 4 versus 5, for MCIs and CONs) of HOFC networks. This indicates that, subtle low-level feature (co-activity, or FC) changes may cause prominent alterations in HOFC network configuration (but not so prominent for FC network). 5) The HOFC network properties were found to be correlated with behavior data, but no such correlations were found for FC network properties. For example, as we found more modules in MCI group than CON group at the group level, we further tested whether the number of modules detected from individual HOFC networks was correlated with the behavior testing scores. The results showed that, for MCIs, the more modules they have, the slower they completed the trail making task. But there was no such relationship for FC network. This indicates that HOFC may be more informative and biologically meaningful.

Fundamental differences between HOFC and FC

First, the performance augmentation using HOFC may come from its definition, which is a fundamental difference from that of FC. Although HOFC is the correlation of FC profiles, it will magnify the subtle variance that may be informative to distinguish different groups. Generally, compared with HOFC, FC tends to be smaller and more uniform across all links and individuals (Supplementary Material 3). The small value might be due to the fact that the correlation was conducted across the whole length of scanning time; and that the two regions may not be well synchronized for the whole time. Also, since the true variability of a BOLD signal is quite small, while noise can lead to larger variability, the observed FC between two actually well-connected regions could be reduced. Then, because of the low values of FC, its ability of catching informative individual variance (affected by illness) might be limited. In contrast, HOFC, by integrating the information from one-to-many connectivity profiles, can increase the connectivity strength in the “backbone links” or “skeleton” of the FC matrix. This is because, intuitively, that if two brain regions certainly have functional connectivity, they could be in the same community, or the same functional network; thus their FC profiles to other regions tend to be quite similar and the elements in the FC profiles are likely to be diverse. Take clustering of rs-fMRI data as an example, where two regions will be put into the same cluster if they have similar BOLD time series. If one-to-all similarities are calculated for a region, the similarities to all the within-cluster regions should be high, but the similarities to all the regions in different clusters should be low. All these similarities and differences create a greater variability in FC profiles, based on which a second-level correlation analysis should produce a higher correlation value. This is why FC profile-based correlation (HOFC) can lead to enhanced connectivity value when compared with the original FC (see Supplementary Material 5). Such enhancement will magnify group difference in pair-wise FC, and also sharpen the difference in network infrastructure and other properties.

Second, in addition to such an overall magnification effect, we also noticed that there exist specific differences between a few pair-wise HOFC and FC, as well as between network properties for HOFC and FC networks. That is, not only the magnification effect but also the complementary effect which brings the novel findings. Group comparison results for the pairwise HOFC and FC did not simply overlap (Fig. 3 and Table 2). Moreover, group differences in nodal and edge centralities were almost complementary between HOFC and FC findings, with just 1 node and 2 edges shared by both methods (Tables 3 and 4). Especially, from the view-point of complex networks, the substantially new information was revealed by HOFC-based graph theory analysis. For example, compared with Table 2 and Table 3, nodal centrality of HOFC network has less shared group difference with that of FC network, compared to the pair-wise connectivity group comparisons. We found two types of such discrepancies between HOFC and FC values. On one hand, low FC corresponded to high HOFC. One example has been provided, which shows two regions with low FC (r = 0.1, Fig. 1f) but high HOFC values (r = 0.45, Fig. 1g). Another example is the relationship between the anterior cingulate cortex and the posterior cingulate cortex (Fig. 2). As a major part of the anterior cingulate cortex belongs to the so-called task-positive network, which is quite independent of the DMN, where the posterior cingulate cortex is the key node, the direct pair-wise FC between the two ROIs is fairly low. From the raw BOLD signals, we can see that sometimes these two ROIs were correlated, while sometimes they were anti-correlated. However, from the high-order functional relationship viewpoint, these two regions are both related to higher cognitive functions, and they may have the same connectivity profiles to other higher cognitive function-related regions and to the primary sensory-related regions; therefore, a high HOFC was observed (Fig. 2). On the other hand, the discordance between HOFC and FC also manifested low HOFC but high FC (see Fig. S8 in Supplementary Material 5). Interestingly, Fig. S9 in Supplementary Material 5 shows that even the overall relationship between HOFC and FC values could vary across subjects. This non-linear relationship could be used for better characterizing brain functional organizations in the future.

Third, as previously reported, noise and artifacts may significantly alter FC by contaminating the “observed” BOLD time course. For localized noise, a small disturbance of the BOLD time series could lead to a significant change in FC but not in HOFC because it is calculated indirectly rather than directly using BOLD time series. In HOFC calculation, this noise contaminated FC could be only one element in the vector of FC profile, thus limiting the influence of noise to HOFC value. For systematic noise with spatially wide spreading effect, the pair-wise FC values in the entire FC matrix will be uniformly lifted or reduced by a certain “base” value. This will make nearly all connectivities significantly “strong” or “weak”, which are largely the artifacts. This will result in false positives and, if used in-group difference detection, false negatives since both groups have uniformly strong connectivities. It will also affect the following complex network analysis if a group-unified threshold is used for FC matrix binarization. In contrast, HOFC is based on the second round of Pearson’s correlation, which is irrespective to the matrix-wise lifted or reduced average. Therefore, HOFC is not only insensitive to the outlier-like FC, but also to the noise-induced overall increased FC. In future, the influence of signal-to-noise ratio in the raw rs-fMRI data to both FC and HOFC should be systematically investigated. We emphasize that HOFC is a more robust metric if the data has mild-to-high noise level.

HOFC-based biomarkers for early AD detection

With HOFC, we found interesting connectivity changes in MCI (Figs. 3–5). Because the main purpose of this paper was to propose a new method, here we only emphasize the high-order connection between the olfactory cortex and the frontal cortex. The SFGorb is involved in cognitive processing of decision-making and adaptive learning [65, 66]. It is also included in ventral medial prefrontal cortex, a key node of the DMN, for emotional, reward, and self-referential processing [67, 68]. The SFGorb represents the main neocortical target of primary olfactory cortex [69]. The reduced bonding between the OLF and the SFGorb in MCIs indicates neurodegeneration-related early pathology changes, which is consistent with the spatial location of amyloid-β deposition in early AD [70]. The deteriorated olfactory function before damaging higher cognitive functions in preclinical AD also strongly supports our findings [71]. It is also exciting that the modularity configuration of the averaged HOFC network indicated higher diversity in MCIs (i.e., a total of 5 modules in MCIs but 4 in CONs), indicating a more functionally segregated brain, or a disconnection syndrome, possibly caused by neurofibrillary tangles and amyloid-β neuritic plaques. Specifically, MCIs were found to have more regions assigned to the module of frontal and DMN regions, which we speculate to be caused by a compensatory effect, due to heavy pathology burden in the related areas.

Future studies

The calculation of HOFC relies on correlation’s correlation; therefore, as suggested by a previous study [72], such an analysis may be heavily affected by noise. This is because that the noise levels at different brain regions could be different, thus introducing “artificial” variability to one-to-all FC profiles; based on this, the second round of correlation could be incorrect. In addition, a second level of correlations was conducted based on the first level of correlations, so the noise effect may propagate and be magnified by the second round of correlations. Although nuisance signals, such as head motion, has been regressed out before first level of correlations, it would be better to conduct a second round of regression analysis to remove the “artifacts” contained in one-to-all FC profiles. In the future, this can be handled by explicitly estimating the noise level (i.e., by using temporal signal-to-noise ratio) for each brain region, and generating a covariate vector consisting of all regions’ temporal signal-to-noise ratio values. This covariate vector, or noise-level profile, can be used in linear regressions to calculate HOFC, instead of second level correlations. In addition, as suggested by Varoquaux et al. [73, 74], estimating individual FC matrix by using covariance matrix could lead to a biased result due to additive noise. Inversion covariance matrix by sparse learning could reduce individual variability caused by different noise levels for different subjects and increase sensitivity in-group difference detection; partial correlation could help reduce such a bias. These methods could be used both in the first and second levels of correlation calculation to improve HOFC estimation. Besides these new strategies to the HOFC estimation stage, more advanced statistical model for comparing the brain-wide HOFC matrices should also be implemented to better approximate the null hypothesis [75]. Also, as suggested by spatially-constraint clustering-based functional parcellation studies [76, 77], the diffusion tractography based structural connectivity information can also be integrated as a weighting term for FC profile generation, which could provide more realistic estimation of the topographical profiles for HOFC analysis.

Limitations

In its current state, our method has several limitations. First, the HOFC uses Pearson’s correlation, which has several inherent drawbacks, such as ignorance of time-domain information (e.g., phase synchrony and dynamic property) and incapability of measuring complex inter-regional interactions (e.g., modulation effect, partial correlation, and mutual information). Future extension of the HOFC may utilize these more complex metrics. Second, as stated above, we only used two-level correlation computation. More levels can be added within the same computational framework by integrating time-varying, multi-frequency, and even multimodal information for even higher-order FC. Third, in this study, only the FC information extracted from fMRI was used for HOFC analysis. By integrating more features into the profile vector, HOFC is naturally able to fuse multi-channel information from multimodal images. For example, diffusion tensor imaging-based structural connectivity can be fused into the regional profile, forming a longer vector for HOFC calculation. Fourth, we used a coarse brain parcellation atlas (AAL) in this study. A finer parcellation of the brain will estimate FC more accurately and prolong the FC profile, which definitely benefits HOFC calculation.

CONCLUSION

A new fMRI metric, namely HOFC, was proposed in this paper by calculating feature-based FC (i.e., correlation’s correlation) rather than the conventional direct temporal synchronization based on BOLD signals. The capability of using HOFC as an effective metric for detecting biomarkers of MCI has been demonstrated, especially with higher sensitivity in detecting group differences and the ability in providing the complementary information to the conventional FC. Both pair-wise and complex network analyses based on HOFC were conducted. As an important complement to the conventional FC studies, HOFC is promising for the future studies of neurological diseases and psychiatric disorders.