Skip to main content
NCBI home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2017 Mar 8;25(5):538–544. doi: 10.1038/ejhg.2017.12

Prediction of years of life after diagnosis of breast cancer using omics and omic-by-treatment interactions

Agustín González-Reymúndez 1,5, Gustavo de los Campos 1,2,5, Lucía Gutiérrez 3, Sophia Y Lunt 4, Ana I Vazquez 1,*,5
PMCID: PMC5437894  PMID: 28272536

Abstract

Breast cancer (BC) is the second most common type of cancer and a major cause of death for women. Commonly, BC patients are assigned to risk groups based on the combination of prognostic and prediction factors (eg, patient age, tumor size, tumor grade, hormone receptor status, etc). Although this approach is able to identify risk groups with different prognosis, patients are highly heterogeneous in their response to treatments. To improve the prediction of BC patients, we extended clinical models (including prognostic and prediction factors with whole-omic data) to integrate omics profiles for gene expression and copy number variants (CNVs). We describe a modeling framework that is able to incorporate clinical risk factors, high-dimensional omics profiles, and interactions between omics and non-omic factors (eg, treatment). We used the proposed modeling framework and data from METABRIC (Molecular Taxonomy of Breast Cancer Consortium) to assess the impact on the accuracy of BC patient survival predictions when omics and omic-by-treatment interactions are being considered. Our analysis shows that omics and omic-by-treatment interactions explain a sizable fraction of the variance on survival time that is not explained by commonly used clinical covariates. The sizable interaction effects observed, together with the increase in prediction accuracy, suggest that whole-omic profiles could be used to improve prognosis prediction among BC patients.

Introduction

Breast cancer (BC) is the second most common cancer worldwide and the main cause of cancer deaths in women.1, 2 Advances in adjuvant therapy have led to lower proportion of recurrence or metastasis in BC patients. However, adjuvant therapy can have serious negative side effects, including heart toxicity, infertility, cognitive impairment, and secondary cancers, which may increase the probability of death due to non-cancer causes.3, 4, 5, 6, 7 Indeed, a 5-year follow-up study of BC patients reported a larger number of non-cancer deaths, many attributable to the side effects of adjuvant therapy, compared with those attributed to BC itself.8 Therefore, deaths could be prevented and suffering reduced if we were able to predict, at the time of diagnosis, BC outcomes such as the likelihood of recurrence, the probability of developing distant metastasis, and the expected years of life after the diagnosis of BC.

The prognostic factors commonly used to assess the outcome of the disease and to guide the BC treatment include axillary lymph-node involvement, tumor size, patient age and ethnicity, lymphatic/vascular invasion, histological type and grade of the tumor, estrogen/progesterone, and Her2/neu receptor status.9 More recently, there has been an increased use of omic data to assess BC patients. For instance, Perou et al10 showed that gene expression (GE) data could be used to identify risk groups, which are both confirmatory of immunohistochemistry BC subtypes (eg, luminals) and predictive of prognosis.11 Other omics such as CNVs, methylation, and miRNA have also been considered for the assessment of prognosis.12, 13, 14, 15, 16

While clustering algorithms applied to GE data have succeeded in identifying groups with different prognosis, the proportion of interindividual differences in survival explained by these groups remains limited. A higher predictive power could be achieved using whole-omic profiles (WOPs),14, 16 integrating clinical and omics in a unified risk assessment method.16, 17 The integration of high-dimensional inputs, such as WOPs, presents important statistical and computational challenges. Recent advances in the fields of regularized and Bayesian regressions allow integrating high-dimensional inputs for prediction of disease risk. These methods have been successfully applied for the prediction of complex traits and disease using DNA information, the so-called whole-genome-regression (WGR) approach, in humans,18, 19, 20 plants,21 and animals.22 Methods similar to those used in WGR could be used to integrate GE and other omics for prediction of BC outcomes. For instance, VanRaden23 suggested the use of Omic Kriging, a method equivalent to the so-called genomic BLUP,24 to integrate omic data for prediction of complex traits. Additionally, Vazquez and co-workers25 described a Bayesian framework that allows integrating multiple omics platforms for prediction of cancer outcomes.

Although advances in adjuvant therapy have led to a significant improvement in the survival of BC patients, it is also clear that individuals are quite diverse in their responses to treatment.26, 27, 28, 29 For example, luminal A patients usually exhibit a poor response to chemotherapy (CT), while luminal B patients are considered viable candidates for the use of both anthracyclines and taxanes.30 Similarly, differential responses to treatment have been observed in other types of cancer, such as colon cancer, where the differential risk of recurrence strongly depends on the individual expression profiles and application of either surgery alone or in combination with adjuvant CT.31 From a statistical point of view, these differential responses to treatments can be modeled as interactions between omics, such as whole-genome GE and treatments.

None of the studies that have integrated whole omics for prediction of disease outcomes (eg, Vazquez et al16 and VanRaden23) considered treatments or interactions between omics and treatments. Therefore, in this study, we extended the framework described in Vazquez et al16 to accommodate interactions between omics and treatments, adapting at the same time, this framework for a survival model. We used the resulting Bayesian model and data from Molecular Taxonomy of Breast Cancer Consortium (METABRIC) to integrate clinical covariates (COVs) (including age at the moment of diagnosis, cancer subtype (CS), histological class, Nottingham Prognostic Index (NPI), and treatment), whole-genome GE profiles, CNVs, and interactions between these omics and treatments (CT, hormonal treatment (HT), and radiotherapy (RT)). Using these data, we evaluated the contribution of COVs, omics, and interactions to interindividual differences in years of life after a diagnosis of BC, using both variance components and a measure of prediction accuracy in cross-validation.

Materials and methods

Data

The METABRIC data set12 comprised information from 1977 white Caucasian women who were diagnosed with BC. Survival data consisted of patient state (dead or alive) and time to either death or last follow-up. Feature data consisted of COVs, along with GE and DNA CNV data. METABRIC CNV data (the gene-by-patient matrix log 2 values from Synapse) is a measure of somatic copy number alteration in the tumor. It identifies tumor CNV in reference to normal tissue,12 meaning that any CNV present in the tumor, and also in the normal tissue, was not considered as a tumor CNV. In addition to the original edition criteria, four observations corresponding to genomic data outliers for at least one omic were removed.

Our response variable was the time from diagnoses to death due to cancer. Other non-cancer deaths, as well as loss of follow-up data (cases in which the patients were alive at the last contact time), were treated as censored observations. There were a total 622 deaths due to cancer, 50% occurring at ~17 years. The same analysis was performed for overall survival (Supplementary Material). The total number of deaths was 887 cases, with 50% of survival at ~12 years. For both sets, the 50% survival occurred at ~7 years (Supplementary Figure S5). The average times to censor were 9.2 (4.8 SDs) and 9.5 (4.9) years, for each set, respectively. The resulting Bayesian model and data from METABRIC were used to integrate COVs (including age at the moment of diagnosis (AGE), CS, type of carcinoma (TC), the NPI,32 and treatment), whole-genome GE profiles, copy number variants (CNVs), and interactions between these omics and treatments. The NPI consists of a well-validated prognostic score that takes information from tumor size, grade, and nodal involvement, specifically NPI= (0.417 × size)+(0.76 × lymph-node stage)+(0–82 × tumor grade), typically ranging between 2 and 7;33 the higher the score the shorter the lifespan prognosis for the patient. Histological type was defined as a TC and was subdivided into two levels: one including in situ medullary, invasive medullary, mucinous or tubular ductal tumors; and the other including non-ductal carcinomas, such as lobular, phyllodes, and ‘grab bag' classified tumors. CS11 was binary coded, either as whether the patient has a triple negative BC (Her2− and ER− and PR−) or not ((Her2− and ER+ or PR+) and Her2+ subtypes). Treatment included whether or not the patient received CT, RT, and HT.

Normalization, quality control, and summarization for the GE and CNV intensity (at a gene level in the CNV) data are described elsewhere.34 Briefly, DNA genotypes and GE were performed on the Affymetrix SNP 6.0 (Affymetrix Inc., Santa Clara, CA, USA) and Illumina HT 12v.3 (Illumina Inc., San Diego, CA, USA) platforms, respectively. In the case of GE, the data were not summarized because the majority of the probes were designed to interrogate distinct mRNA transcripts. The edited omic data included the log 2 of the intensity of the CNV for 18 538 regions and 49 473 bead-level GE array probes.

Statistical models

We modeled the logarithm of survival time in a Bayesian setting, accounting for COVs, omics main effects, and their interactions. Inference was obtained from the posterior distribution of the unknowns given the data and the hyperparameters. The likelihood and prior distribution assumed to obtain the posterior distribution are described below.

The model for log time to death can be represented as t*i=ηi+ɛi, where t*i is the logarithm of the time to either the last follow-up or the time to death for the ith subject (i=1, …, n), ηi is a linear function of the COVs, omics, and their interactions, and ɛi is the residual error that follows a normal distribution centered on 0, with residual variance σ2ɛ. Alive subjects at the last follow-up time were considered right-censored (ie, observations where the beginning of the treatment was observed but not the occurrence of the event); therefore, the joint conditional distribution of the log-transformed survival time (t*=[t*1, …, t*n ]T) is then given by

graphic file with name ejhg201712e1.jpg

where η=[η1, …, ηn ]T and ci indicates whether the data are censored (ci=1, if the subject was alive at the last observation and ci=0, if the subject was dead at the time of last follow-up observation, that is, the data are not censored).

To include prior information about the linear predictor, we assumed multivariate normal distribution for the vector η, of the form N(Xβ, Σ), where X was the model matrix of the standardized COVs as columns and individuals as rows, β was the vector of COVs effects (assumed to have a flat prior distribution), and Σ was the variance–covariance matrix of the genomic effects, including the main effects of both omics and the interactions between GE and a given treatment. For ease of notation, hereafter we will use only CT to account for the interactions between GE and given treatment: the models including the terms corresponding to HT or RT are equivalents, changing GE|CT by GE|HT or GE|RT. So far, the full model linear predictor can be written as:

graphic file with name ejhg201712e2.jpg

where uCNV was the vector of genomic main effects due to the CNV, uGE was the vector of genomic effects due to GE, and uGE|yCT and uGE|nCT were the interaction effects between GE and both levels of CT, either when CT was applied (yCT) or not (nCT). Σ was obtained as described elsewhere,24 and corresponds with a weighted sum of kernels. 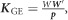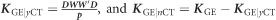For instance, the kernels for GE, GE|yCT, and GE|nCT, are respectively, computed as Inline graphic, and Inline graphic, where W is the matrix of standardized GE features, p is the number of features, and D is a diagonal matrix with ones for those patients with CT, and zero otherwise.

To obtain the relative contribution of each omic main effects and GExCT interactions, together with the model's prediction ability, we used the Gibbs sampler implemented in the BGLR.35 Basically, BGLR allows to handle an arbitrary number of linear predictors terms, each one with different distributional assumptions, while also allowing to fit numerical, categorical, or truncated response variables.

A sequence of nested models was adjusted to evaluate the predictive accuracy and to compare the impact of including COVs, omics, and the interaction between omics and covariates. The baseline model (COV) included only COVs and their effects. This model was further extended to include either copy number variation (COV+CNV), GE (COV+GE), or (COV+GE+CNV). In addition, COV+GE was also extended to include the interactions between each treatment and GE, adding the effects of the interaction with the CT (COV+GE+GExCT), RT (COV+GE+GExRT) and hormone therapy (COV+GE+GExHT).

Model prediction accuracy

We evaluated the models in terms of their ability in predicting survival. To do that, we performed a 10-fold cross-validation (CV), repeating 10 times the random assignation of subjects in folds. With the paired information of survival probability and patient's status at different time points (from 1 to 7 years), we calculated the area under the receiver-operating characteristic curve (AUC) in each CV. In addition, we performed a survival analysis, using the Kaplan–Meier model with the time of follow-up as response and patient status as ‘event', to compare the models in their ability to discriminate between low- and high-risk groups. These groups were defined based on the average predicted values across CVs: subjects with predicted survival below the first quartile were considered in the high-risk group, whereas those with values over the third quartile were considered in the low-risk group.

Results

The outcome analyzed was survival (years of life) after diagnosis of BC, with individuals who were alive at the last follow-up treated as censored (results for analysis based on years of life for all-cause deaths are given in the Supplementary Data). Years of life after diagnosis of BC was regressed on COVs (including age at the moment of diagnosis, NPI, hormone receptor status, histological type, and treatment) and on WOP (including GE and CNV) and interactions between WOP with treatments (RT, HT and CT all defined as Yes/No). COVs were treated as fixed effects, whereas WOP and the interactions between treatment and GE were treated as random (see Supplementary Table S1 for the fixed-effects estimation for the full model COV+CNV+GE). Models were fitted using the BGLR R-package.35 Further details about the models used are given in the Materials and methods section.

Proportion of variance explained by COVs, omics, and omic-by-treatment interactions

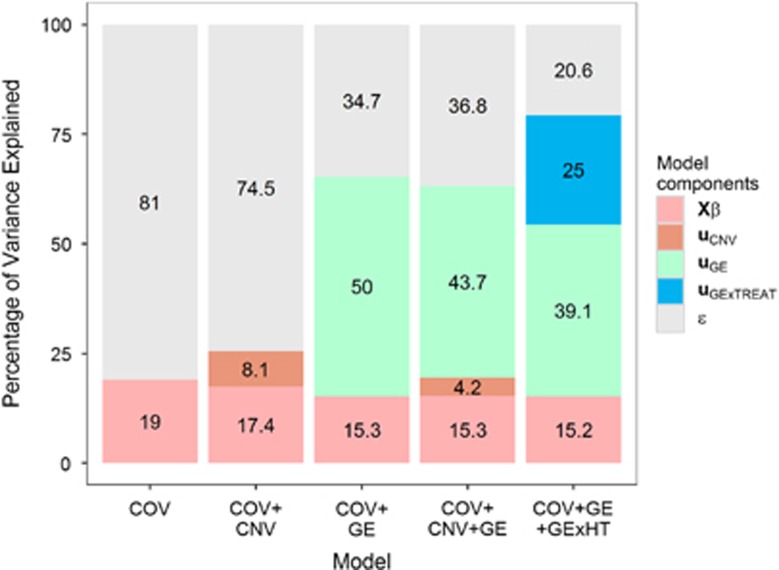
Figure 1 shows the (estimated) proportion of variance explained by inputs for each of the models fitted. The baseline model used only COV and explained ~19% of the interindividual differences in survival time. When CNV data were added to the model, the total proportion of variance explained increased by a small margin (about 6%). However, the addition of GE led to a substantial increase in the proportion of variance explained by the model from 19% (COV model) to 65.3% (COV+GE model). Combining CNV and GE (COV+GE+CNV model) did not lead to a substantial increase in the proportion of variance explained already reached by the model COV+GE. Similarly, adding interactions between GE and either CT or RT did not substantially increase the overall proportion of variance explained by the model relative to COV+GE. However, adding interactions between GE and HT lead to a substantial increase in the total proportion of variance explained by the model. In the model including COV+GE+GExHT, the proportion of variance explained by the interaction term was substantial (25%). The results obtained using survival defined based on all-cause mortality (see Supplementary Figures S1 and S2) were similar to those reported in Figure 1.

Figure 1.

Figure 1

Open in a new tab

The proportion of interindividual differences (variance scale) in survival explained by each of the input set considered by the model.

Assessment of prediction accuracy in CV

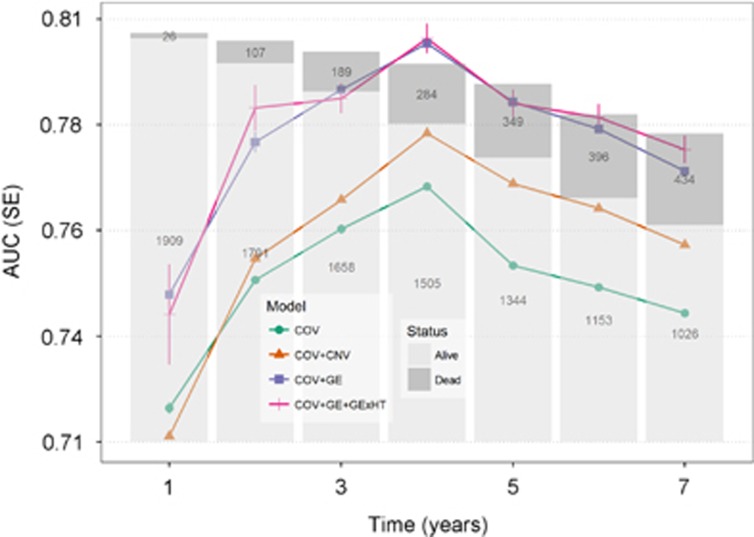
We evaluated the ability of each model to predict future outcomes using 10 replicates of a 10-fold CV. In each replicate, individuals were randomly assigned to 10-fold CVs. In each replicate, we evaluated the ability of each model to predict survival time (further details are given in the Materials and methods section). Prediction accuracy was measured using the CV AUC36) computed for dummy variables that indicate whether an individual lives longer than x years. Figure 2 shows the average CV AUC for models accounting for covariates, CNV, GE and the interaction between GE and HT. Supplementary Table S2 shows the AUC of models considering GE by CT and GE by HT interactions. Prediction accuracy improved from year 1 after diagnoses to the fourth year and lowered towards the next years in all models. Median survival time occurred at 7.4 years. Our results suggest that reasonably high prediction accuracy (AUC of ~0.8 in a testing subset of the data) can be achieved for prediction of whether a BC patient will live longer than 4 years after diagnosis.

Figure 2.

Figure 2

Open in a new tab

Prediction ability by model and time point in terms of AUC across CVs: the lines represent the average AUC across 10 repetitions of 10-fold CVs (the vertical segments represent standard error across CV). The number of dead and alive subjects at any time point is represented by the bars stacked. This figure includes the most relevant models: COV model, COV plus CNV (COV+CNV), COV plus GE (COV+GE), and covariates plus GE and interaction between GE and RT (COV+GE+GExHT).

The model with only COV had AUC values between 0.70 and 0.78, depending on how many years after treatment were being predicted. Combining COV and CNV have gains in CV AUC of the order of two points of AUC relative to the use of COV only for prediction of long-term survival. However, adding CNV to the model did not result in a substantial change in CV AUC for prediction of early mortality (eg, whether a patient lived longer than 1 or 2 years after diagnosis of BC). Combining GE with COV gave substantial gains (≥3.5) in CV AUC relative to the COV model. These gains in CV AUC were observed both for prediction of early, intermediate, and late mortality. The results for overall survival (see Supplementary Figure S3) were similar to those presented in Figure 2, which are based on deaths due to BC.

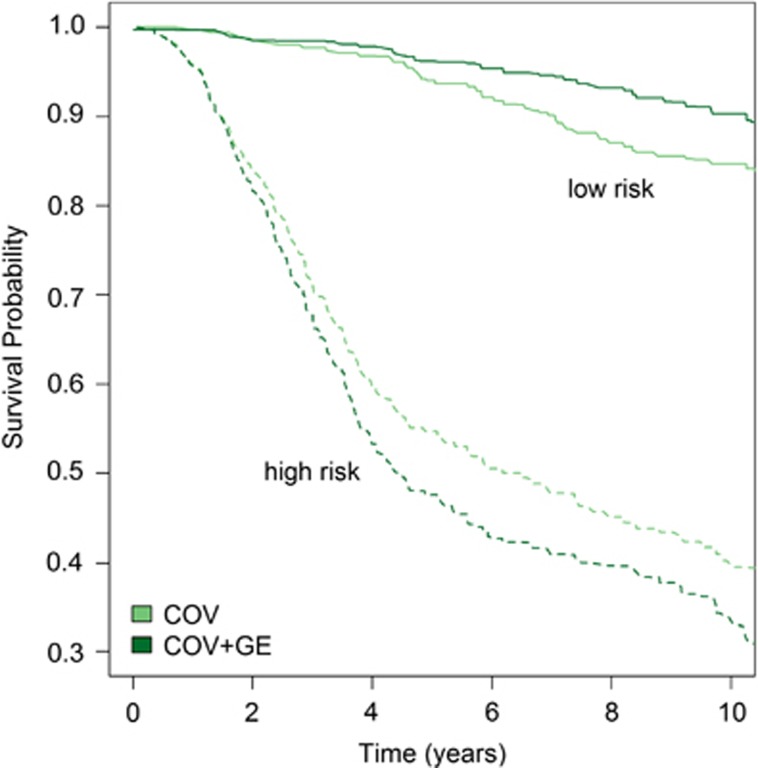
Using CV predictions of years of life, we classify individuals in high- and low-risk groups (corresponding to the individuals ranking in the lower and higher quartiles for predicted years of life) and subsequently computed (Kaplan and Meier) survival curves for each of these groups. Figure 3 displays these curves for the groups defined based on predicted years of life using COV and COV+GE. Both methods produce highly accurate classifications. For instance, at year 4, >95% of the individuals classified as being in the low-risk groups were still alive; on the other hand, <60% of the individuals classified as being at high risk were alive after 4 years of diagnosis. The model using COV+GE had greater discriminatory power than COV only; indeed; the survival curve for the low (high)-risk groups identified with this model run always above (below) the ones corresponding to the classification based on COV.

Figure 3.

Figure 3

Open in a new tab

Average Kaplan–Meier estimates by risk group for COV and COV+GE models across CVs: the curves show the average across CV and separating individuals as high or low risk. COV, model with COVs; COV+GE, model with COVs plus whole-genome GE.

None of the models that included interactions produced a clear improvement in prediction accuracy relative to the model using COV+GE (Supplementary Table S2).

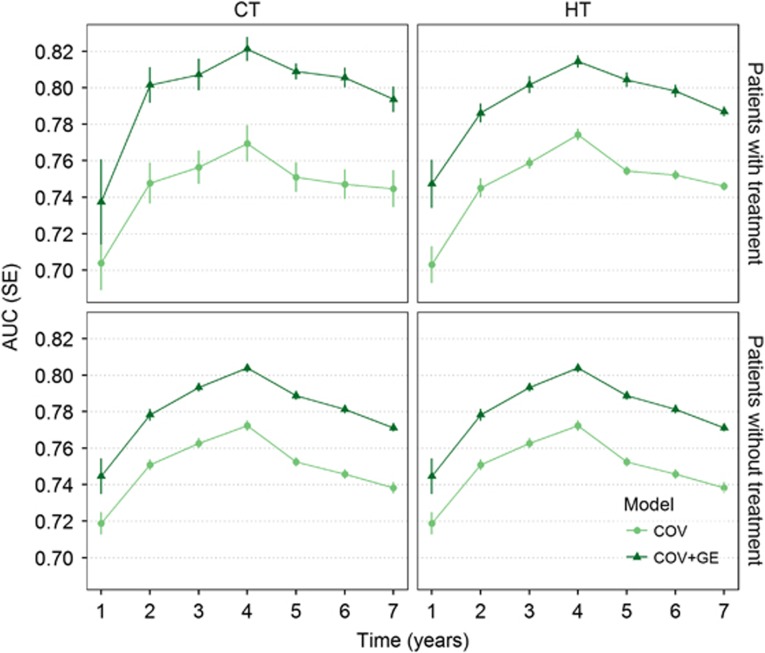
The results shown in Figure 4 are based on the prediction accuracy assessed using all patients. Using the predictions presented in Figures 2 and 3, we evaluated prediction accuracy for groups defined by the treatments received. The figure shows the prediction accuracy obtained by the COV and COV+GE models using sets of patients who did or did not receive hormone therapy or CT (results for RT are shown in Supplementary Figure S4). Again, prediction accuracy is expressed in AUC by thresholds of years of life after a diagnosis of BC for each subgroup of women. This analysis revealed that prediction accuracy increases for patients receiving treatment, and such increment seems not to depend on the specific treatment. Additionally, women receiving CT or HT showed better predictions for longer periods (until the seventh year BC-specific death). Lower predictive accuracy was obtained for overall survival. Nevertheless, the same AUC variation across time was obtained (Supplementary Figure S3).

Figure 4.

Figure 4

Open in a new tab

Prediction ability obtained with COV and COV+GE by sets of patients with and without treatment: the treatments are CT and HT. Prediction accuracy for patients who received treatment are in the top panels; the bottom panels correspond with those without treatment. Prediction accuracy was obtained as the average AUC for each treatment. Average AUC is presented for subjects with (upper panels) and without treatment (lower panels). The models compared contained COVs and COVs plus GE (COV+GE).

Discussion

In this study, we first determined the importance of genomic effects of CNVs and GE on survival. Additionally, we determined the prediction achieved when covariates, omics, and interactions between omics and treatments are being accounted. Accordingly, survival models were implemented for both BC-specific and overall deaths. In a primary analysis, we first studied the survival rates for each COV separately, preselecting the covariates associated with survival. Using the significant covariates with the integrative model (ie, COV+CNV+GE), younger (under 50 years) and older (above 70 years) age women have the worst prognosis. In older patients, factors such as chronic diseases and lower applications of CT can be associated with bad prognosis.37 Poor prognosis for younger patients, on the other hand, is attributed to more aggressive tumors.38 Additionally, the NPI showed an inverse relationship with prognosis: the prognosis decrease as the NPI values increase.39, 40

CNVs can modify GE by changing gene dosages or by breaking down regulatory sites.41 In BC, CNV has been reported as affecting genes associated with survival and tumor development (eg, PIK3CA, EGFR, FOXA1, and HER2).42 The addition of CNV to COVs allowed to explain an extra 6.5% more of the survival variance. Although this proportion of variance explained is smaller than that of GE, we note that adding CNV to a model based on COVs increased prediction accuracy. However, these results were moderated as compared with GE. Accordingly, Curtis et al12 also found a less relevant effect on survival of germline copy numbers (the CNV used here) than somatic copy numbers (CNA, the copy number originated by the tumoral process). Our results are also consistent with those from Vazquez et al,42 although they had a considerably smaller sample size and only explored survival at the third year. The inclusion of GE in the covariates model increased, even more, the prediction accuracy and explained even a bigger portion of the survival variance than the model COV+CNV. A possible reason for the moderated variance explained by CNV may be due to the fact that CNV was summarized at the gene level, leaving all non-coding regions not represented in the summary (see Supplementary Materials from Curtis et al12). Eventually, an underestimated effect of CNV could be related to missing CNVs in non-codifying regions distally affecting transcription.43

GE is an important disease risk indicator, which can relegate individuals into cancer subtypes.11, 12, 44, 45, 46, 47 Subgroups can also be derived by combining several platforms to define consensus groups by meta-analysis.48 We confirmed not only the primary role of the GE by explaining cancer subtype but also that GE explains a larger portion of the total survival variability than cancer subtype clusters. Models including GE explained the largest amount of survival variability and increased the prediction accuracy by many AUC units. Interestingly, overall survival showed a lower proportion of overall death survival variance, explained by the model containing both CNV and GE, further suggesting a more relevant role of both GE and CNV in the cancer process and less in unrelated deaths. The overall deaths included cancer-related deaths and other non-cancer-related ones. Although other causes of death are also related to more aggressive cancer (thus patients are exposed to more aggressive treatments), our results indicate that only predicting cancer-related deaths is more accurate (ie, omics are related to cancer deaths and not to overall survival). However, it is likely that deaths not due to BC could be actually induced or related to the cancer treatment. Other studies have indicated a higher rate of cancer unrelated deaths in BC patients than the expected mortality rate.8

BC patients can have a heterogeneous response to a given treatment, due to evolving subclonal architecture49 and stroma microenvironment conditions50 of the tumor. For instance, abnormal vasculature creates poorly oxygenated zones and can limit the supply of nutrients and drugs that affect the success of both radio and CTs.50 This variability was echoed in this work by the variance of BC survival explained by the GE × Treatment interactions (ie, variance magnitude dependent on whether a treatment was given or not), with different magnitudes by treatment perhaps due to how they were administrated in these data set. Most likely, all patients in our data received RT, while application CT was more restricted: almost all ER-negative patients (triple negative, Her2+, and some luminal patients) received CT, while ER positives (most of the luminal patients) did not.12 On the other hand, the administration of HT is provided to patients with positive hormone receptor status, markedly reducing the possibility of observing a sizable GExHT interaction.

The lack of improvement in AUC when interactions are included in the model may reflect poor sensitivity of AUC. To evaluate this, we also assessed prediction accuracy as the correlation between CV predictions of time to death and observed survival among patients with known time to death. This analysis showed a benefit of adding GE (the prediction correlation for COV was 0.22 and increase to 0.31 when GE was added to the model). However, the model including COV+GE+TRTxGE did not yield higher prediction correlation than the one using COV+GE. This was also true when all the interactions were included into the model (Supplementary Table S3).

To get an insight about which genes were contributing the most to survival variance, we also performed an ad hoc analysis using a spike-slab model to declare genes as up- or downregulated (ie, associated with either increasing or decreasing days of life, respectively) (Supplementary Figure S6). We found three genes with a probability of inclusion in the model >0.5: two upregulated on the sample of all patients (FGD3 and DNAJB9), and one downregulated on the subset of patients with hormone therapy (SERPINE3). FGD3 product is involved in signaling pathways regulating apoptosis.51, 52 On the other hand, DNAJB9 belongs to a group of genes related with the GIPC family that has an essential role in carcinogenesis and development.53 Finally, SERPINE3 is a member of the Serpin family, a very diverse group of proteins involved in many different biological processes, such as inflammation, immune function and tumorigenesis.54 Its product belongs to the clade E of human serpins (nexin/plasminogen activator inhibitor 1), although its function is not well understood.54 Additionally, our original method allows us to extract a very interesting biological interpretation of the results: the amount of interindividual differences in survival that can be explained by (1) well-known and widely used COVs (such as the state of the cancer, the cancer subtype, or a clinical treatment), (2) all the gene products (GE) present in the tumors, (3) CNV from the tumor, and (4) any possible interaction between treatments and GE.

This article focuses on the comparison of models based on COVs commonly used in clinical practice with others that incorporate WOPs as well as interactions of omics with treatments. Perou and co-workers55 demonstrated that clusters derived from GE profiles are confirmatory of the BC subtypes. Our COV model incorporates already the BC subtypes and therefore fully incorporates clustering. For these reasons the COV model is a high-quality benchmark for the model comparison. Nevertheless, the statistical learning literature offer a vast array of methods for incorporating high-dimensional inputs, including shrinkage and variable selection methods,56 support vector machines,57 and random forests.58 We considered the use of Bayesian regressions with Gaussian priors, which induce shrinkage of estimates. We also considered Bayesian models that combine variable selection and shrinkage simultaneously and did not find noticeable differences in neither proportion of variance explained nor in prediction accuracy. These results are in agreement with previous studies that have reported limited differences between various types of regularized regressions.59 In Breiman's words: ‘when it comes to prediction there are usually many equally good models'.58 However, our study is clearly not exhaustive, and Bayesian models are not necessarily granted to be universally superior methods. Further research involving comparison of these approaches with others such as support vector machines or random forest is granted.

Acknowledgments

AIV acknowledges financial support from NIH Grant 7-R01-DK-062148-10-S1. The authors also acknowledge support from the NIH Grants R01GM099992 and R01GM101219, NSF Grants IOS-1444543, subaward UFDSP00010707, AACR-Incyte Corporation NextGen Grant for Transformative Cancer Research, and Grant Number 16-20-46-LUNT, as well as the Office of the Assistant Secretary of Defense for Health Affairs W81XWH-15-1-0453. Opinions, interpretations, conclusions, and recommendations are those of the author and are not necessarily endorsed by the Department of Defense. Finally, we thank Kyle Grimes for his edition work on this manuscript. These data were accessed through Synapse (http://synapse.sagebase.org).

Footnotes

Supplementary Information accompanies this paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)

The authors declare no conflict of interest.

Supplementary Material

Supplementary Table S1
Click here for additional data file. (27.4KB, pdf)
Supplementary Table S2
Click here for additional data file. (81KB, pdf)
Supplementary Table S3
Click here for additional data file. (27.2KB, pdf)
Supplementary Figure S1
Click here for additional data file. (25.2KB, pdf)
Supplementary Figure S2
Click here for additional data file. (2MB, tif)
Supplementary Figure S3
Click here for additional data file. (3MB, tif)
Supplementary Figure S4
Click here for additional data file. (2.5MB, tif)
Supplementary Figure S5
Click here for additional data file. (2.4MB, tif)
Supplementary Figure S6
Click here for additional data file. (4.8MB, tif)

References

  1. Ferlay J, Soerjomataram I, Dikshit R et al: Cancer incidence and mortality worldwide: sources, methods and major patterns in GLOBOCAN 2012. Int J Cancer 2014; 136: E359–E386. [DOI] [PubMed] [Google Scholar]
  2. Bray F, McCarron P, Parkin DM: The changing global patterns of female breast cancer incidence and mortality. Breast Cancer Res 2004; 6: 229–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bradshaw PT, Stevens J, Khankari N et al: Cardiovascular disease mortality among breast cancer survivors. Epidemiology 2016; 27: 6–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Lawenda BD, Mondry TE, Johnstone PAS: Lymphedema: a primer on the identification and management of a chronic condition in oncologic treatment. CA Cancer J Clin 2009; 59: 8–24. [DOI] [PubMed] [Google Scholar]
  5. WHOCancer. WHO: Geneva, Switzerland, 2015; doi:/entity/mediacentre/factsheets/fs297/en/index.html.
  6. Baumgart J, Nilsson K, Evers AS, Kallak TK, Poromaa IS: Sexual dysfunction in women on adjuvant endocrine therapy after breast cancer. Menopause 2013; 20: 162–168. [DOI] [PubMed] [Google Scholar]
  7. Curigliano G, Cardinale D, Suter T et al: Cardiovascular toxicity induced by chemotherapy, targeted agents and radiotherapy: ESMO Clinical Practice Guidelines. Ann Oncol Off J Eur Soc Med Oncol 2012; 23 (Suppl 7): vii155–vii166. [DOI] [PubMed] [Google Scholar]
  8. Chapman J-AW, Meng D, Shepherd L et al: Competing causes of death from a randomized trial of extended adjuvant endocrine therapy for breast cancer. J Natl Cancer Inst 2008; 100: 252–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cianfrocca M, Goldstein LJ: Prognostic and predictive factors in early-stage breast cancer. Oncologist 2004; 9: 606–616. [DOI] [PubMed] [Google Scholar]
  10. Perou CM, Sørlie T, Eisen MB et al: Molecular portraits of human breast tumours. Nature 2000; 406: 747–752. [DOI] [PubMed] [Google Scholar]
  11. Sørlie T, Tibshirani R, Parker J et al: Repeated observation of breast tumor subtypes in independent gene expression data sets. Proc Natl Acad Sci USA 2003; 100: 8418–8423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Curtis C, Shah SP, Chin S-F et al: The genomic and transcriptomic architecture of 2000 breast tumours reveals novel subgroups. Nature 2012; 486: 346–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Jennings EM, Morris JS, Carroll RJ, Manyam GC, Baladandayuthapani V: Bayesian methods for expression-based integration of various types of genomics data. EURASIP J Bioinform Syst Biol 2013; 2013: 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Wang W, Baladandayuthapani V, Morris JS et al: iBAG: integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics 2013; 29: 149–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Shen R, Olshen AB, Ladanyi M: Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics 2009; 25: 2906–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Vazquez AI, Veturi Y, Behring M et al: Increased proportion of variance explained and prediction accuracy of survival of breast cancer patients with use of whole-genome multiomic profiles. Genetics 2016; 203: 1425–1438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Vazquez A, Wiener H, Shrestha S, Tiwari H, de los Campos G: Integration of multi-layer omic data for prediction of disease risk in humans; Proceedings of the 10th World Congress of Genetics Applied to Livestock Production, Vol 6, 2014.
  18. de los Campos G, Gianola D, Allison DB: Predicting genetic predisposition in humans: the promise of whole-genome markers. Nat Rev Genet 2010; 11: 880–886. [DOI] [PubMed] [Google Scholar]
  19. Vazquez AI, de los Campos G, Klimentidis YC et al: A comprehensive genetic approach for improving prediction of skin cancer risk in humans. Genetics 2012; 192: 1493–1502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. de los Campos G, Naya H, Gianola D et al: Predicting quantitative traits with regression models for dense molecular markers and pedigree. Genetics 2009; 182: 375–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Meuwissen THE, Hayes BJ, Goddard ME: Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001; 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Wheeler HE, Aquino-Michaels K, Gamazon ER et al: Poly-omic prediction of complex traits: OmicKriging. Genet Epidemiol 2014; 38: 402–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. VanRaden PM: Efficient methods to compute genomic predictions. J Dairy Sci 2008; 91: 4414–4423. [DOI] [PubMed] [Google Scholar]
  24. Shapiro CL, Recht A: Side effects of adjuvant treatment of breast cancer. N Engl J Med 2001; 344: 1997–2008. [DOI] [PubMed] [Google Scholar]
  25. de Los Campos G, Vazquez AI, Fernando R, Klimentidis YC, Sorensen D: Prediction of complex human traits using the genomic best linear unbiased predictor. PLoS Genet 2013; 9: e1003608. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Perez EA: Breast cancer management: opportunities and barriers to an individualized approach. Oncologist 2011; 16 (Suppl 1): 20–22. [DOI] [PubMed] [Google Scholar]
  27. Polyak K: Heterogeneity in breast cancer. J Clin Invest 2011; 121: 3786–3788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Børresen-Dale A-L, Sørlie T, Kristensen VN: On the molecular biology of breast cancer. Mol Oncol 2010; 4: 171–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Goldhirsch A, Wood WC, Coates AS et al: Strategies for subtypes – dealing with the diversity of breast cancer: highlights of the St. Gallen International Expert Consensus on the Primary Therapy of Early Breast Cancer 2011. Ann Oncol 2011; 22: 1736–1747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. O'Connell MJ, Lavery I, Yothers G et al: Relationship between tumor gene expression and recurrence in four independent studies of patients with stage II/III colon cancer treated with surgery alone or surgery plus adjuvant fluorouracil plus leucovorin. J Clin Oncol 2010; 28: 3937–3944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Haybittle JL, Blamey RW, Elston CW et al: A prognostic index in primary breast cancer. Br J Cancer 1982; 45: 361–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Rejali M, Tazhibi M, Mokarian F, Gharanjik N, Mokarian R: The performance of the Nottingham Prognosis Index and the adjuvant online decision making tool for prognosis in early-stage breast cancer patients. Int J Prev Med 2015; 6: 93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Margolin AA, Bilal E, Huang E et al: Systematic analysis of challenge-driven improvements in molecular prognostic models for breast cancer. Sci Transl Med 2013; 5: 181re1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pérez P, de Los Campos G: Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014; 198: 483–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Fawcett T: An introduction to ROC analysis. Pattern Recogn Lett 2006; 27: 861–874. [Google Scholar]
  36. Eaker S, Dickman PW, Bergkvist L, Holmberg L: Differences in management of older women influence breast cancer survival: results from a population-based database in Sweden. PLoS Med 2006; 3: e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Chung M, Chang HR, Bland KI, Wanebo HJ: Younger women with breast carcinoma have a poorer prognosis than older women. Cancer 1996; 77: 97–103. [DOI] [PubMed] [Google Scholar]
  38. Galea MH, Blamey RW, Elston CE, Ellis IO: The Nottingham prognostic index in primary breast cancer. Breast Cancer Res Treat 1992; 22: 207–219. [DOI] [PubMed] [Google Scholar]
  39. D'Eredita' G, Giardina C, Martellotta M, Natale T, Ferrarese F: Prognostic factors in breast cancer: the predictive value of the Nottingham Prognostic Index in patients with a long-term follow-up that were treated in a single institution. Eur J Cancer 2001; 37: 591–596. [DOI] [PubMed] [Google Scholar]
  40. Henrichsen CN, Chaignat E, Reymond A: Copy number variants, diseases and gene expression. Hum Mol Genet 2009; 18: R1–R8. [DOI] [PubMed] [Google Scholar]
  41. The Cancer Genome Atlas Network: Comprehensive molecular portraits of human breast tumours. Nature 2012; 490: 61–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Vazquez AI, Veturi Y, Behring M et al: Increased Proportion of Variance Explained and Prediction Accuracy of Survival of Breast Cancer Patients with Use of Whole-Genome Multiomic Profiles. Genetics 203: 1425–1438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Shlien A, Malkin D: Copy number variations and cancer. Genome Med 2009; 1: 62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Sørlie T, Perou CM, Tibshirani R et al: Gene expression patterns of breast carcinomas distinguish tumor subclasses with clinical implications. Proc Natl Acad Sci USA 2001; 98: 10869–10874. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Hu Z, Fan C, Oh DS et al: The molecular portraits of breast tumors are conserved across microarray platforms. BMC Genomics 2006; 7: 96. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Loi S, Haibe-Kains B, Desmedt C et al: Definition of clinically distinct molecular subtypes in estrogen receptor-positive breast carcinomas through genomic grade. J Clin Oncol 2007; 25: 1239–1246. [DOI] [PubMed] [Google Scholar]
  47. Daemen A, Griffith OL, Heiser LM et al: Modeling precision treatment of breast cancer. Genome Biol 2013; 14: R110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Mihály Z, Kormos M, Lánczky A et al: A meta-analysis of gene expression-based biomarkers predicting outcome after tamoxifen treatment in breast cancer. Breast Cancer Res Treat 2013; 140: 219–232. [DOI] [PubMed] [Google Scholar]
  49. Burrell RA, McGranahan N, Bartek J, Swanton C: The causes and consequences of genetic heterogeneity in cancer evolution. Nature 2013; 501: 338–345. [DOI] [PubMed] [Google Scholar]
  50. Junttila MR, de Sauvage FJ: Influence of tumour micro-environment heterogeneity on therapeutic response. Nature 2013; 501: 346–354. [DOI] [PubMed] [Google Scholar]
  51. Harrington AW, Kim JY, Yoon SO: Activation of Rac GTPase by p75 is necessary for c-jun N-terminal kinase-mediated apoptosis. J Neurosci 2002; 22: 156–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Salehi AH, Xanthoudakis S, Barker PA: NRAGE, a p75 neurotrophin receptor-interacting protein, induces caspase activation and cell death through a JNK-dependent mitochondrial pathway. J Biol Chem 2002; 277: 48043–48050. [DOI] [PubMed] [Google Scholar]
  53. Katoh M: GIPC gene family [review]. Int J Mol Med 2002; 9: 585–589. [PubMed] [Google Scholar]
  54. Heit C, Jackson BC, McAndrews M et al: Update of the human and mouse SERPIN gene superfamily. Hum Genomics 2013; 7: 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Sørlie T, Perou CM, Tibshirani R et al: Gene expression patterns of breast carcinomas distinguish tumor subclasses with clinical implications. Proc Natl Acad Sci USA 2001; 98: 10869–10874. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Hastie T, Tibshirani R, Friedman J: The Elements of Statistical Learning: Data Mining, Inference, and Prediction the Elements of Statistical Learning. Springer: New York, NY, USA, 2009. [Google Scholar]
  57. Cortes C, Vapnik V: Support-vector networks. Mach Learn 1995; 20: 273–297. [Google Scholar]
  58. Breiman L: Random forests. Mach Learn 2001; 45: 5–32. [Google Scholar]
  59. de Los Campos G, Hickey JM, Pong-Wong R, Daetwyler HD, Calus MPL: Whole-genome regression and prediction methods applied to plant and animal breeding. Genetics 2013; 193: 327–345. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Table S1
Click here for additional data file. (27.4KB, pdf)
Supplementary Table S2
Click here for additional data file. (81KB, pdf)
Supplementary Table S3
Click here for additional data file. (27.2KB, pdf)
Supplementary Figure S1
Click here for additional data file. (25.2KB, pdf)
Supplementary Figure S2
Click here for additional data file. (2MB, tif)
Supplementary Figure S3
Click here for additional data file. (3MB, tif)
Supplementary Figure S4
Click here for additional data file. (2.5MB, tif)
Supplementary Figure S5
Click here for additional data file. (2.4MB, tif)
Supplementary Figure S6
Click here for additional data file. (4.8MB, tif)

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES