A fast and accurate method for detection of IBD shared haplotypes in genome-wide SNP data

Abstract

Identical by descent (IBD) segments are used to understand a number of fundamental issues in genetics. IBD segments are typically detected using long stretches of identical alleles between haplotypes in phased, whole-genome SNP data. Phase or SNP call errors in genomic data can degrade accuracy of IBD detection and lead to false-positive/negative calls and to under/overextension of true IBD segments. Furthermore, the number of comparisons increases quadratically with sample size, requiring high computational efficiency. We developed a new IBD segment detection program, FISHR (Find IBD Shared Haplotypes Rapidly), in an attempt to accurately detect IBD segments and to better estimate their endpoints using an algorithm that is fast enough to be deployed on very large whole-genome SNP data sets. We compared the performance of FISHR to three leading IBD segment detection programs: GERMLINE, refined IBD, and HaploScore. Using simulated and real genomic sequence data, we show that FISHR is slightly more accurate than all programs at detecting long (>3 cm) IBD segments but slightly less accurate than refined IBD at detecting short (~1 cm) IBD segments. More centrally, FISHR outperforms all programs in determining the true endpoints of IBD segments, which is crucial for several applications of IBD information. FISHR takes two to three times longer than GERMLINE to run, whereas both GERMLINE and FISHR were orders of magnitude faster than refined IBD and HaploScore. Overall, FISHR provides accurate IBD detection in unrelated individuals and is computationally efficient enough to be utilized on large SNP data sets >60 000 individuals.

Introduction

Identical by descent (IBD) shared haplotypes – homologous chromosomal segments descended from the same common ancestor – have been used for genotype imputation,^{1, 2} IBD mapping,³ heritability estimation,⁴ phase inference,¹ and inference of population structure.^{5, 6} Under Haldane's⁷ model of recombination, the length of IBD haplotypes shared between two individuals is exponentially distributed with mean 100/2 g centiMorgans (cm) where g is the number of generations since the common ancestor. Although a pair of individuals sharing a common ancestor 15 generations ago is highly unlikely to share any IBD haplotypes from that ancestor, when they do, the expected length of the segment is ~3.3 cM. Such IBD shared haplotypes are typically inferred from long stretches of identical alleles in phased, whole-genome single nucleotide polymorphism (SNP) arrays, but accurate and efficient IBD detection from such data is difficult for several reasons. First, phase and SNP call errors can split long IBD segments into two or more shorter segments or lead to artificial truncation of IBD segments, inflating the false-negative (miss) rates of IBD detection. Second, the sheer number of comparisons that must be made at each site (~twice the squared sample size), combined with the low base rate of true IBD segments between pairs of unrelated individuals, means that a substantial fraction of called IBD segments can be false positives. Finally, because of the computational complexity of IBD detection, algorithms that sacrifice speed for accuracy can be unusable on the large sample sizes (eg, sample size >50 000 requires nearly 5 billion comparisons per genomic site) currently being accumulated. Thus, successful IBD detection programs must simultaneously meet a number of goals – computational efficiency, low false-positive rates, low false-negative rates, and accurate detection of IBD segment endpoints – that typically tradeoff with one another.

Many programs have been developed to discover IBD segments in SNP data sets when expected pedigree relatedness is low. GERMLINE,⁸ often considered the benchmark IBD discovery program, is computationally efficient and therefore usable on very large samples, but the literature has indicated that its accuracy is lower than more recently developed programs. Because GERMLINE is fast and can be run in a way that leads to few false-negative calls at the expense of many false-positive calls, two newer IBD detection programs that reportedly outperform GERMLINE in accuracy, refined IBD (rIBD)⁹ and HaploScore,¹⁰ use GERMLINE to detect candidate IBD segments that are then post-processed by extending, removing, or slicing the candidate segments in the hope of providing more accurate detection of IBD segments. rIBD uses a probabilistic hidden Markov model to give locations along candidate IBD segment obtained from GERMLINE a posterior LOD score as to whether they are truly IBD or not. rIBD has a lower false-positive rate than GERMLINE with only a modest increase in the false-negative rate, but it is computationally intensive and therefore has a very long run time for large data sets. HaploScore uses information on the switch error rate and the SNP error rate to give a posterior probability of whether each candidate segment from GERMLINE is truly IBD or not.

The current paper describes a new program, FISHR (Find IBD Shared Haplotypes Rapidly), which improves upon existing IBD detection programs. Most centrally, as we show below, existing programs tend to either overextend true IBD segments or split true IBD segments into multiple smaller ones. Because such systematic biases in IBD segment length lead to biased heritability estimates, incorrect inferences of demographic history, and inaccurate phase/imputation information near the ends of called segments, our main goal was to develop an algorithm that accurately estimates endpoints and true lengths of IBD segments while achieving a computational efficiency similar to GERMILNE and an accuracy similar to rIBD.

Materials and methods

Description of the FISHR algorithm

FISHR is written in C++ and is freely available for download at https://github.com/matthew-c-keller/FISHR.git, along with scripts to evaluate IBD detection. FISHR utilizes GERMLINE (described in detail by Gusev et al.⁸), as an initial screen to quickly detect candidate segments. By default, FISHR uses the –h_extend method in GERMLINE, which incorporates information on phased mismatches, to detect candidate segments between two individuals or within individuals (runs of homozygosity). FISHR then further refines the candidate segments as follows. First, because two long IBD calls separated by a short distance may actually be a single contiguous IBD segment that was artificially broken apart in GERMLINE due to phase or SNP call errors, FISHR stitches together segments separated by a user-defined number of SNPs (-gap). Next, FISHR finds the locations of ‘implied errors' (IEs) – likely SNP call or phase errors – for all called segments. To do this, FISHR finds the longest exact match between either of the two phased haplotypes of the first person and either of the two phased haplotypes of the second person (a total of four possible combinations), starting at the first SNP of the called segment. An IE occurs at the mismatching SNP after the exact haplotypic match ends. FISHR then finds the next longest exact match between any of the four possible combinations of phased haplotypes, starting from the SNP following the previous IE, and extends until the next mismatching SNP is encountered. This process continues until the end of the called segment (Supplementary Figure S1).

IEs represent locations along a candidate segment that are potentially inconsistent with IBD inheritance. Some IEs are expected by chance due to SNP and phase errors even in truly IBD segments. However, too many IEs within a particular region are a likely signal that the segment is not IBD in that area and that the segment should be truncated (if near an endpoint of the segment) or split into two (if in the middle of the segment). To determine such called segment endpoints, FISHR calculates a moving average (MA) of IEs centered at each SNP within a user-defined window (using the –window flag) of SNPs. FISHR then starts at the center of the called IBD segment and moves towards each endpoint until it reaches the first SNP with a MA value greater than the user-defined maximum (-emp-ma-threshold). These points signal the endpoints of a called segment. Supplementary Figures S1 and S2 illustrate the process of calculating MA from a possible IBD segments and determining the endpoints using MA, respectively. As has recently been investigated,¹¹ one source of error in IBD detection could be the erroneous merging of separate distinct IBD segments. Therefore, in addition to trimming the segment ends, this process can split a GERMLINE candidate segment into two or more shorter segments, depending on the distribution of the MA values. Moreover, if the flag –count-gap-errors is set to TRUE, as it is by default, segments that had been stitched together from the first step can be broken up again at this stage if enough IEs are clustered near the gap. Because segments that are too short, in terms of either number of SNPs or cM distance, are increasingly likely to be false positives, FISHR drops segments shorter than user-defined thresholds of both SNP and cM length (using the –min-snp and –min-cm flags, respectively). Finally, FISHR calculates the total proportion of SNPs that are IEs (PIE) within each remaining segment. Too many IEs scattered across the entire length of a segment are a signal that the whole segment is unlikely to be IBD. Thus, if the PIE of a segment is greater than the value supplied in the –emp-pie-threshold argument, the segment is dropped.

Because recombination patterns can differ across populations,¹⁴ it is important that the population used to create the genetic map input by FISHR corresponds as closely to the study sample as possible to avoid spurious false-positive and false-negative calls. Furthermore, threshold values for PIE and MA, as well as values for –bits, –err-hom, and –err-het, depend on the density of SNPs and the quality of SNP calls and phasing in the data at hand. Poorly called or poorly phased data would necessitate lower values for the –bits (eg 30) and higher values for the –err-hom and -err-het (eg 2) arguments to allow the GERMLINE subroutine to detect a sufficient number of potential IBD segments. A utility program, parameter_finder, (available for download at https://github.com/matthew-c-keller/GL.parameter.finder.git) is supplied alongside FISHR to help users choose values for –emp-pie-threshold and –emp-ma-threshold, which influence the tradeoff between false positives and false negatives the most strongly. To do this, parameter_finder provides distributions of PIE and MA from segments in the user's data that are truly IBD (defined as the middlemost 50% of all stretches of the genome>8 cM that contained no opposite homozygotes between pairs of individuals) and similar distributions of PIE and MA from non-IBD segments (defined as segments between random pairs of individuals with the same start and endpoints as the truly IBD segments). Users can then compare the IBD and non-IBD distributions of PIE and MA (displayed in Supplementary Figure S3) to choose PIE and MA thresholds that produce a desired sensitivity or specificity, depending on the users' priorities.

Simulated sequence and SNP data

We simulated genotypic data using the sequence simulator HAPGEN2,¹² which simulated haplotypes by conditioning on a reference set of population haplotypes (here, the 1000 Genomes Project¹³ European ancestry (CEU) haplotypes of chromosome 15) and created a new population by combining haplotypes according to a fine-scaled recombination rate map (from deCODE¹⁴). Here, we defined the effective population sizes as 11 418, the typical value used when simulating individuals of European descent,¹⁵ and the sample size (defined as ‘controls' in HAPGEN2) as 13 000. For computational efficiency, we created 13 independent data sets of 1000 individuals each and averaged all results across these 13 replicates. The data had LD, haplotype diversity, and allele frequency distributions that mimic those in the initial set of haplotypes.

We used the perfectly phased, simulated sequence data with no errors obtained from HAPGEN2 to obtain ‘true IBD segments.' To increase computational efficiency and ensure that rare mutations that arose on a haplotype since the common ancestor did not cause a true IBD segment to be missed, we pruned this sequence data to have MAF>0.05, resulting in a density of ~1 variant per 1000 base pairs. To create data that mimicked post–quality-control SNP data on existing platforms, we then extracted SNPs pseudo-randomly such that the MAF distribution was~uniform and the density of SNPs was one per 6750 base pairs (corresponding to~400 000 SNPs genome-wide). To simulate SNP call errors, we randomly changed one allele to its alternative allele at a rate of 0.2%, roughly the average error rate of what has been found empirically for SNP calls.^{16, 17, 18, 19} Finally, we unphased the SNP data and rephrased it using SHAPEIT2.²⁰

Positive predictive value (PPV) and sensitivity were the two main metrics used in determining accuracy of called IBD segments (illustrated in Supplementary Figure S4). PPV was calculated as the length of the overlap between called and true segments, divided by the length of the called segment. Values for each called segment were then averaged, weighted by the base pair length. Sensitivity was calculated as the length of the overlap, divided by the length of the true segment. Then, values for each true segment were averaged, weighted by length in base pairs.

Real sequence data

We also compared performance of the IBD detection algorithms using the UK10K ALSPAC sequence data on 1872 unrelated individuals.²¹ In this data, we utilized four subchromosomes (5q, 9q, 14q, and 20q) and removed markers with less than a 1% MAF, markers in violation of Hardy–Weinberg equilibrium with p-values of less than 0.0001, and markers that contained missing data for any individuals. We then extracted 58 024 SNPs from four subchromosomes (5q, 9q, 14q, and 20q) that were on the Illumina 650K SNP panel and phased this data using SHAPEIT2 for calling segments using each program. We retained the remaining markers (MAF>0.05) on these four chromosomes not in the SNP data (an average of one marker per 3000 base pairs) as a holdout sample to calculate the proportion of opposite-homozygote (OH) SNPs within called segments.

To determine the accuracy of IBD detection, we calculated the proportion of OH in and around regions where segments were called by each program. An OH (eg, an A–A genotype in one individual and a C–C genotype in the other) at masked markers within and around the called segments can be used to estimate the programs' rates of false-positive and false-negative calls and to infer where called segments over- or underextended true IBD segments.²² Even when the underlying haplotypes are truly IBD, sporadic mismatching alleles along these phased haplotypes within a called segment can occur due to SNP errors, and a string of such mismatches can occur due to one or more phase errors. However, phase errors cannot cause OH at true IBD locations; only the rare event of SNP call errors changing a heterozygous SNP to the opposite homozygous call can cause (very low levels of) sporadic false OH in the data. Therefore, locations where the rate of OH in holdout markers is high within the boundaries of called segments suggest regions of false-positive calls (typically overextended segments), whereas locations where the rate of OH is low outside the boundaries of called segments suggest regions of false-negative calls (typically underextended calls). See Supplementary Figure S5 for more details on how we used OHs to determine the accuracy of IBD detection.

Running the four IBD detection programs

We ran FISHR, GERMLINE, rIBD, and HaploScore on the simulated SNP data that was phased using SHAPEIT2, varying input parameters to determine the optimal parameters for discovering IBD segments with minimum lengths of both 1 and 3 cM for each program (see Table 1). For each program, we then plotted the PPV against sensitivity using the combination of parameters that led to results closest to a sensitivity and PPV of 1. As rIBD uses a hidden markov model for IBD detection, the program can be run multiple times with the results combined.⁴ However, multiple runs appear to increase the rate of both true and false IBD segment detection,⁴ so it is not clear that this strategy substantially improves its performance. Moreover, because run time is the primary limiting factor for using rIBD on large samples, multiple runs would only be feasible to perform in smaller data sets. We therefore used a single run of rIBD in these analyses.

Table 1. Parameters used for running FISHR, GERMLINE, rIBD, and HaploScore with values used to determine the optimal set of parameters in brackets.

Program	Command
FISHR
GERMLINE step	-bin_out -err_hom {0, 1, 2, 3} -err_het {0, 1, 2, 3} -reduced -bits {30, 45, 60, 75, 90} -min_m 1.5 -homoz -Method {-w_extend -h_extend}
FISHR step	-min-snp 30 –min-cm 3 -window {25, 50, 75} -gap {0, 1, 30, 60} –emp-ma-threshold {0.025, 0.045, 0.065, 0.085} –emp-pie-threshold {0.005, 0.015, 0.025} –count-gap-errors {TRUE, FALSE} –output-type finalOutput
GERMLINE	-bin_out -err_hom {0, 1, 2, 3} -err_het {0, 1, 2, 3} -bits {30, 45, 60, 90, 120, 150} -min_m 3 {-w_extend, -h_extend} -homoz
rIBD	java -Xmx4000m -jar b4.r1196.jar usephase=true ibd=true burnin-its=5 overlap={100, 157, 200} window={7500, 10 000, 12 500} ibdscale={2.5, 3, 3.16, 3.5} ibdtrim={11, 16, 21} ibdlod={1, 2, 3, 4, 5, 6}
HaploScore
GERMLINE step	-err_hom {0, 1, 2, 3} -err_het {0, 1, 2, 3} -homoz -bits {30, 45, 60, 90, 120} -min_m 1.5 {-w_extend, -h_extend}
HaploScore step	—genotype_error {6e-04, 1.25e-03, 2.5e-03, 1e-02} —switch_error {5e-04, 1e-03, 1.5e-03, 1e-02}

The optimal values for detecting 3+ cm segments in the simulated data are bolded.

Results

Comparison of run times

Table 2 presents the run times (in seconds) of the four programs as a function of five sample sizes (see also Supplementary Figure S6). We calculated run times based on the optimal parameters found for each of the programs as described above. Run times were averaged from three separate simulated subchromosomes that were on average 16 cM long and contained 1185 SNPs each. GERMLINE is used as a first step with user-defined parameters for FISHR and HaploScore, and internally for rIBD (such that run time for GERMLINE used as the first stage in rIBD could not be reported). We used three different sets of GERMLINE parameters specific to (and that optimized performance of) GERMLINE, FISHR, and HaploScore.

Table 2. Run time, in seconds, for GERMLINE, FISHR (including both GERMLINE and FISHR subroutines), HaploScore (including both GERMLINE and HaploScore subroutines), and rIBD in simulated chromosomes that averaged 16 cM in length with 1185 SNPs, for varying sample sizes.

	GERMLINE	FISHR			HaploScore			rIBD
Sample Size	Total	GERMLINE	FISHR	Total	GERMLINE	HaploScore	Total	Total
500	1.67	2.67	1.19	3.85	1.67	530.69	368.02	187.48
1000	6.13	10.67	3.81	14.48	21.00	1468.72	1475.39	1405.56
2000	23.78	42.67	15.55	58.22	25.67	5800.98	5826.65	17 258.32
4000	92.31	167.00	58.56	225.56	104.33	23 029.38	23 133.71	397 238.55
8000	379.75	677.00	235.82	912.82	1382.67	95 231.45	95 650.45	a

^aProgram ran for 1 month (~2 500 000 s) before the server went offline for routine maintenance.

GERMLINE was the fastest program at any sample size, with FISHR approximately doubling to tripling its run time at all sample sizes. Most of the increase in run time for FISHR compared to GERMLINE was caused by using a smaller minimum cM threshold for the initial GERMLINE segment discovery, which is necessary in order for FISHR to stitch together any segments that GERMLINE splits apart. Both HaploScore and rIBD had run times hundreds to thousands of times longer than FISHR, with this ratio increasing with larger sample sizes for rIBD. To gauge how the programs performed on a realistic, large SNP data set, we also calculated run time on a sample of 17 093 individuals aggregated from four data sets from the NIH Genotype and Phenotype database. Because IBD detection is typically done in parallel for each subchromosome arm, we analyzed the longest chromosome arm, 5q, which contained 19 772 SNPs on the Affy 6.0 SNP array. When the threshold for segment length was set to 1 cm, GERMLINE took about 1.5 days to run, FISHR took about 6.5 days (including 5 days, 16 h for GERMLINE initial candidate segment discovery), whereas both rIBD and HaploScore ran for nearly two months before the server required maintenance and the processes were stopped. From extrapolations of the run times on simulated data (Table 2), we predict that HaploScore would have finished running in just over two months and rIBD would have required over a year to finish.

Accuracy of called segments in simulated data

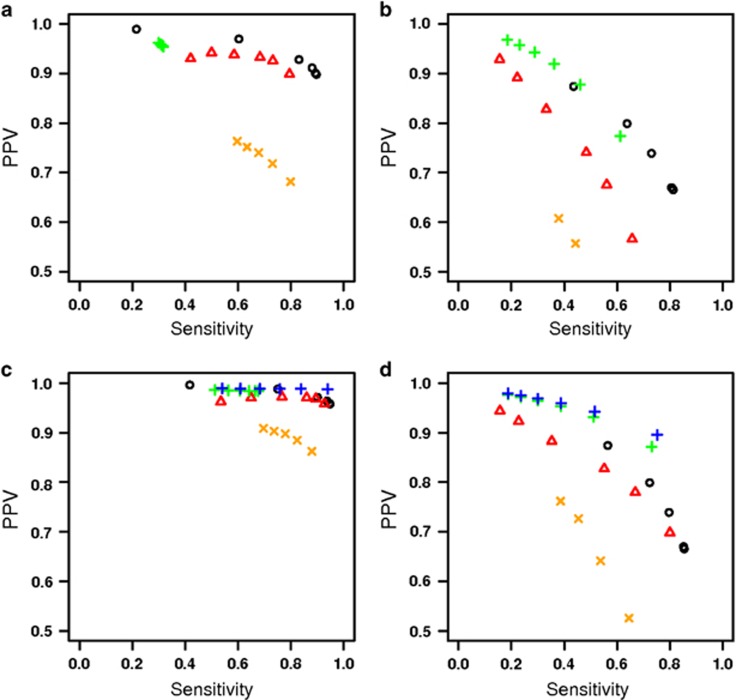
Figure 1a displays PPV and sensitivity where both called and true IBD segments had minimum lengths of 3 cm, while Figure 1b had IBD segments with a minimum length of 1 cm. For each program, we varied thresholds to produce a spectrum of conservative to liberal segment calling. In particular, we varied the moving average threshold for FISHR, the minimum LOD score for rIBD, and the bits argument for GERMLINE and HaploScore. At 3 cm minimum segment lengths, FISHR outperformed every other program with a higher PPV for any given sensitivity or, alternatively, a higher sensitivity for any given PPV. At 1 cm minimum, FISHR and rIBD performed similarly and outperformed both GERMLINE and HaploScore.

Figure 1.

PPV-Sensitivity plots for FISHR (o), GERMLINE (), rIBD (), and HaploScore () when (a) calculated using a minimum of 3 cm for called IBD and a minimum of 3 cm for true IBD, (b) when using a minimum of 1 cm for called IBD and a minimum of 1 cm for true IBD, (c) when calculated using a minimum of 3 cm for called IBD and a minimum of 1.5 cm for true IBD for calculating PPV and using a minimum of 1.5 cM for called IBD and a minimum of 3 cm for true IBD for calculating sensitivity, and (d) when using a minimum of 1 cM for called IBD and a minimum of 0.5 cm for true IBD for calculating PPV and using a minimum of 0.5 for called IBD and a minimum of 1 cM for true IBD for calculating sensitivity. Additional measures are present for rIBD () when using a minimum true IBD length of 0.5 cM for PPV and no minimum called cm length for sensitivity (c) and a minimum true IBD length of 0.25 cm for PPV and no minimum called cM length for sensitivity (d).

By using the same minimum length thresholds (eg, 3 cm) for both the called and true IBD segments, the results displayed in Figure 1a and b are highly sensitive to the accuracy of the endpoints of the called segments, as well as to truncation and splitting errors. For example, all sensitivity estimates of rIBD in Figure 1a are less than 0.3, below those of other programs and below those reported in the manuscript introducing rIBD.⁹ As demonstrated below, this is because rIBD tends to split true IBD segments into multiple, smaller called segments; when these called segments are shorter than the threshold (eg, 3 cm), they appear as false negatives. Because the endpoints of segments called by GERMLINE and especially FISHR are more accurate, the performances of these programs are not degraded to the same extent.

An alternative definition of sensitivity that is less affected by such truncation/split errors is to compare all true IBD segments greater than a length threshold (3 or 1 cm) to all called segments that are at least half that length (1.5 or 0.5 cm, respectively). Similarly, for PPV, we compared all called segments greater than 3 or 1 cm to all true IBD segments greater than 1.5 or 0.5 cm, respectively. Figure 1c and d show PPV and sensitivity calculated in this way. The performance of all programs improved but the improvement was greater for programs that were inaccurate at endpoint estimation than for programs that were more accurate at endpoint estimation. At 3 cm minimum called (PPV) and true IBD (sensitivity) segment lengths, FISHR performed slightly better than GERMLINE or rIBD, whereas at 1 cm minimum thresholds, rIBD outperformed all programs. Because rIBD uses a posterior probability instead of a minimum cm length threshold to call segments, Figure c and d also show rIBD results when no minimum length was used in calculating sensitivity and when much smaller true IBD lengths (0.5 cm for Figure 1c and 0.25 cm for Figure 1d) were used for calculating PPV. The sensitivity values for these instances of rIBD were improved and show rIBD to be superior to all other programs with respect to IBD detection accuracy. As demonstrated below, the improved sensitivity of rIBD when there was no minimum length of called segments occurred because rIBD often splits long, true IBD segments into multiple, short called segments.

Accuracy of called segment endpoints in simulated data

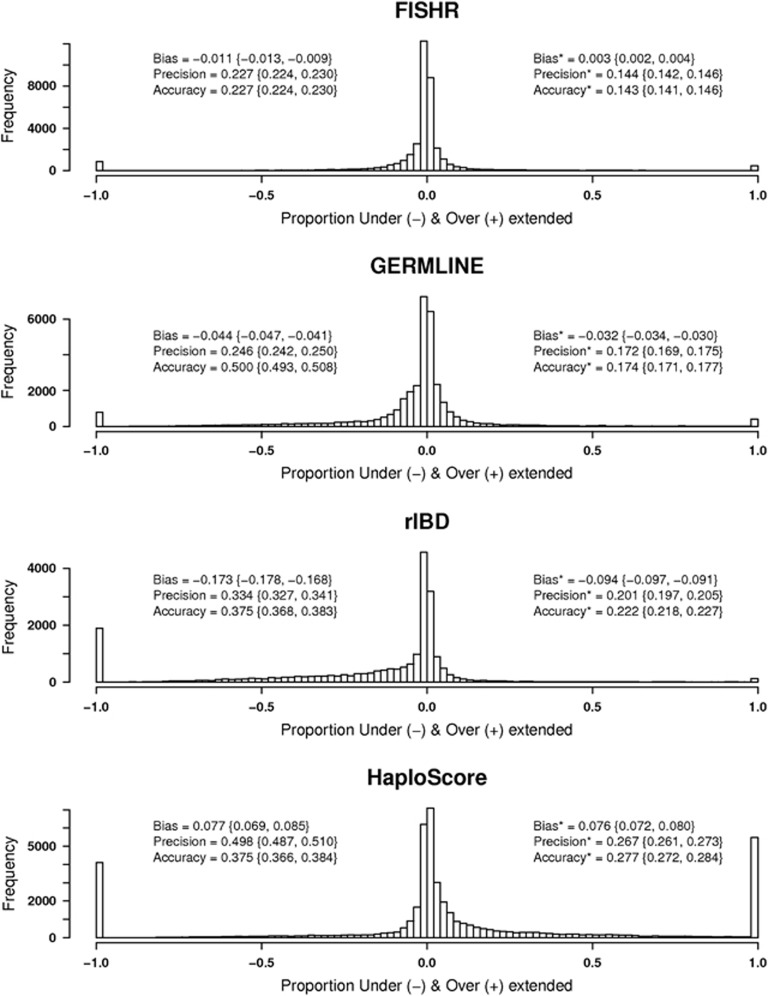
As noted above, there is no single best way to define PPV and sensitivity, as these values depend upon the degree to which the accuracy of endpoints is defined to affect these metrics (compare Figures1a and b vs Figure 1c and d). To further quantify accuracy of endpoint estimation, we divided the length of over- or underextension of each called segment endpoint by the length of the corresponding true IBD segment. Figure 2 shows the distribution of these proportions – the degree to which each endpoint was over- or underextended – when called segments had minimum length of 3 cm and true IBD segments had minimum length of 1.5 cm (results for 1 cm called and 0.5 cm true thresholds were similar; see Supplementary Figure S7). It should be noted that using a 3 cm threshold for called and 1.5 cm for true IBD segments resulted in more accurate and precise IBD calls for all programs (Supplementary Figure S8 compared to Figure 2). Any called segment that had no corresponding true IBD segment (false positive) was given an arbitrary value of 1 and any truly IBD segment with no corresponding called segment (false negative) was given a value of −1. The text to the left of each histogram shows the bias (defined as the mean proportion), precision (defined as the standard deviation of the proportion), and accuracy (defined as the standard deviation from 0 rather than from the mean proportion) when the false-positive and false-negative calls were included. As these values measure variation between true and estimated endpoints, values closest to zero are more desirable.²³ Accuracy provides an estimate of how accurate the called segments are compared to perfect calls with no under- or overextension, and incorporates information on both bias and precision (accuracy²=bias²+precision²). FISHR had the most accurate (0.227 vs 0.250, 0.375, and 0.504) endpoints and was the most precise (0.227) of all algorithms. FISHR also showed very little bias (−0.011) with respect to under- or overextending calls. HaploScore (bias=0.077) tended to overextend segments, whereas GERMLINE (bias=−0.044) and to a greater extent rIBD (bias=−0.177) tended to call segments that were shorter than the true IBD segments. These conclusions remained unchanged when we excluded false-positive and false-negative calls (reported on the right side of histograms in Figure 2).

Figure 2.

Distributions of the proportion of under- and overextension for each called IBD segment >3 cm for FISHR, GERMLINE, rIBD, and HaploScore. Called segments were compared to true IBD segments with a minimum length of 1.5 cm. Called segments with no corresponding true IBD segments (the entire segment was overextended) were given values of 1, and true IBD segments with no corresponding called segments (the entire ‘called' segment was underextended) were given values of −1. Bias was defined as the mean proportion, precision as the standard deviation of the proportion, and accuracy as the standard deviation from 0 rather than from the mean proportion, with optimal values of precision and accuracy being closest to 0. Results listed to the left of the histograms included false-positive and false-negative calls. Results to the right of histograms (denoted by *) only included the called segments which had a corresponding true IBD segment.

Accuracy of called segment endpoints in real data

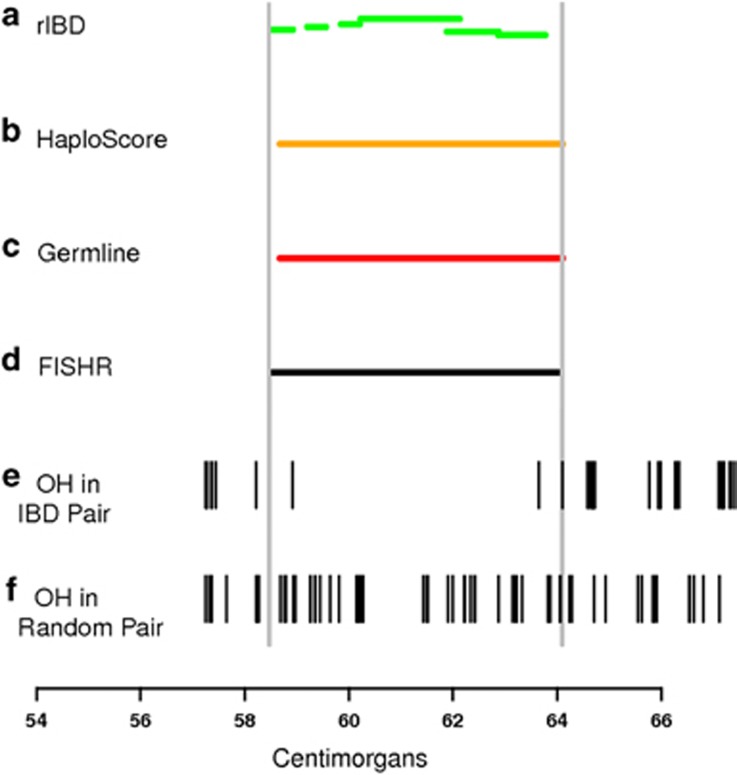
All previous results used simulated data where the true IBD segment endpoints were known within a small margin of error. We used the proportion of OH (POH) markers from a holdout sample in the UK10K data set to determine how well the programs detect IBD segment endpoints in real data. Figure 3 shows an example of a region where all four programs called a segment between two individuals and the locations where OH occurred in the holdout sequence data. Figure 3 also shows OHs at holdout markers between a pair of randomly selected individuals who are ostensibly non-IBD at this location. Given the highly discrepant rate of OH between the focal pair and the random pair, we conclude that a true IBD segment existed between the focal individuals at this region, and the endpoints of this true IBD segment can be inferred from where the OH rates between the focal individuals increase in the holdout sequence data. The results depict a fairly typical example in which rIBD apparently broke up a long true IBD segment into multiple short called segments. FISHR, GERMLINE, and HaploScore appear to have done better in this example at discovering one long true IBD segment, with the main differences between programs being where the endpoints were estimated. Multiple IBD segments that occur at the same location for rIBD are estimated to be IBD 2+ FISHR, GERMLINE (when using the –h_extend command as we have done here), and HaploScore are unable to detect IBD 2 segments. IBD 2+ segments can be found using the –haploid command in GERMLINE, but the overall accuracy (not shown) was much lower. Supplementary Figures S9–S16 display eight additional examples chosen at random from among two called segments for each program.

Figure 3.

An example of called IBD segments between two individuals in the UK10K data set, from (a) rIBD, (b) HaploScore, (c) GERMLINE, and (d) FISHR, with (e) opposite homozygous SNPs (OH) occurring for that pair of individuals in and surrounding the FISHR called IBD segment, and (f) OH occurring in a random pair of individuals at the same location of the called IBD segment. The horizontal offset seen in the rIBD segments represent multiple detected segments, with overlapping segments showing IBD 2.

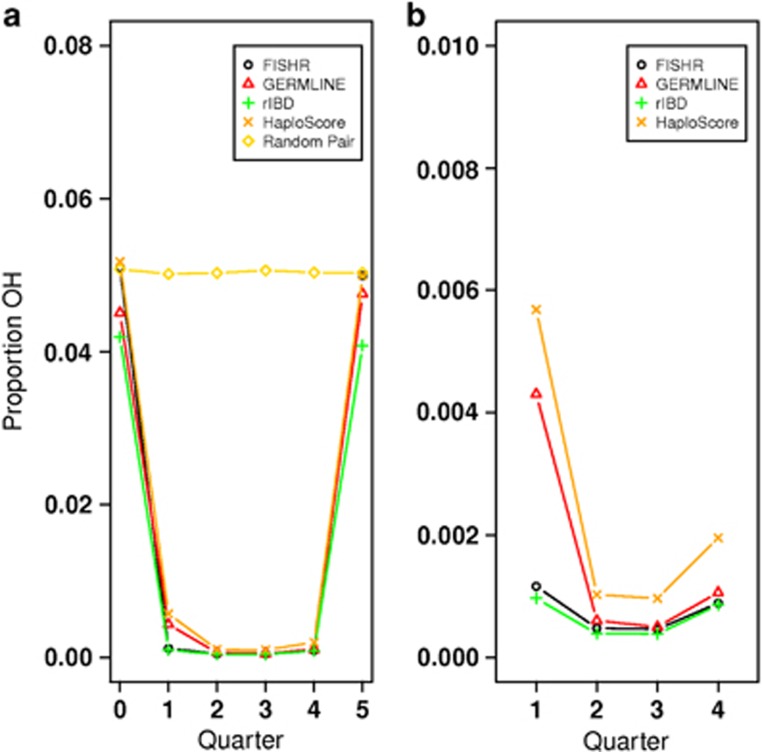
To quantify the accuracy of the called segment endpoints for each program in this real data set, we calculated the POH of holdout markers in 4 quarters of each called segment from the UK10K data, as well as two regions of the same base pair length upstream and downstream from the called segment (Figure 4). These results corroborate our earlier conclusions about endpoint accuracy of the four programs in the simulated data (Figure 2). Figure 4a displays the four quarters of the called segment and the flanking regions, whereas the Figure 4b displays only the first through fourth quarters within the called segments on an expanded scale. Supplementary Figure S5 illustrates how POH profiles should appear for programs that estimate endpoints perfectly or that under-/overextend them. Of the four programs, the POH profile of FISHR was the most similar to the profile expected when the estimated endpoints of the called segments are correct; FISHR had levels of POH in the two flanking regions (‘downstream' and ‘upstream') very close to that between pairs of random individuals, indicating very little underextension, and it had ~0 POH in quarters 1 through 4, indicating very little overextension. rIBD was very precise at finding segments that were truly IBD (~0 POH in quarters 1 through 4), but as predicted, it tended to underextend the IBD segments much more than any of the other programs (low POH in the flanking regions). On the other hand, HaploScore tended to overextend true IBD segments, as indicated by its higher POH in the first and fourth quarters. GERMLINE tended to both overextend called segments and underextend them.

Figure 4.

Results of the analysis of proportion of opposite homozygosity (OH) in (a) four quartiles of called IBD segment and the two flanking regions and in (b) just the four quartiles of the called IBD segments for FISHR (o), GERMLINE (), rIBD (), HaploScore (), and random individuals at the same location of called IBD () where called IBD segments were a minimum of 3 cM. FISHR's pattern of results are closest to that expected from perfect estimation of IBD endpoints.

Discussion

We developed FISHR as an alternative method to detect segments of the genome shared IBD between pairs of individuals in a sample measured on genome-wide SNP data. Our goal was to develop a program that would be fast enough to be utilized with very large SNP data sets and be more accurate than existing programs at detecting IBD segments and their true endpoints. As demonstrated using simulated data where true IBD status was known, FISHR performs as well or better than the presented competitor programs in terms of PPV and sensitivity for detecting long IBD segments, but slightly worse than rIBD but better than GERMLINE and HaploScore at detecting short IBD segments. Moreover, FISHR excelled at accurate estimation of segment endpoints. This is important for several reasons. First, the length of IBD segments is relevant to many parameters of interest in population genetics (time to recent common ancestor, effective population size, population bottlenecks, etc); systematic biases in estimating these lengths, which especially occurs when true IBD segments are broken into multiple small segments, can lead to incorrect conclusions regarding these and other parameters. Second, phasing and imputation¹ based on IBD segments can be affected by the accuracy of the endpoints, with under- and overextensions of IBD segments causing regions near called IBD segment endpoints to be incorrectly imputed or phased. Finally, in calculating genome-wide relatedness using IBD segments,⁴ programs that tend to overextend IBD calls lead to systematically inflated relatedness, and those that tend to underextend IBD calls to deflated relatedness. This leads to under- and overestimates of heritability, respectively, when using genome-wide relatedness from IBD haplotypes.

FISHR is fast enough to be used on very large SNP data sets (eg, >60 000 individuals), running two to three times slower than GERMLINE but running over a thousand times faster than rIBD and HaploScore at large sample sizes. One practical downside of FISHR is that it requires much more RAM than its competitors because all candidate segments need to be sorted in order to be (potentially) stitched together. We have developed a version of FISHR (using the –low-ram flag) that uses a negligible amount of RAM at the cost of failing to stitch together called segments that are erroneously split. The accuracy of this version of FISHR is only slightly degraded compared to the default version.

An additional limitation of FISHR vis-à-vis rIBD is that although FISHR can estimate runs of homozygosity, using the approach we presented here, FISHR cannot call regions that are greater than IBD 1 – that is, where more than one IBD segment exists at the same location between individuals. For example, ~25% of regions between siblings are expected to be IBD 2, meaning both haplotypes are IBD. FISHR (as well as GERMLINE when run without the –haploid flag and HaploScore) would call these regions as IBD 1, whereas rIBD can call these regions as IBD 2+. Because such IBD 2+ situations are extremely rare among unrelated individuals (occurring at a rate proportional to the square of relatedness, or ~0.0001 for IBD 2 vs 0.01 for IBD 1 in typical data sets of nominally unrelated individuals), the benefit of these additional called segments is probably negligible in data sets of unrelated individuals. Nevertheless, FISHR's limitation to detecting IBD 1 must be kept in mind when working with siblings, in which case the lack of IBD 2 calls can cause a substantial bias in estimations of relatedness.

A limitation of the simulation approach used here was that we inferred true IBD status from perfectly phased and highly dense simulated SNP data. Therefore, the true endpoints of IBD segments may have been slightly longer or shorter than we inferred. For example, it is possible that a short IBD segment near a longer one led to overestimation of the length of the long IBD segment. However, this type of conflation leads to only a small amount of overextension (~6%) in IBD segments>2 cM in typical SNP data,¹¹ and our simulated data was six times denser than typical SNP data, almost certainly lessening the impact such errors had on our inferred true IBD segments. Moreover, the results from our simulated data agreed very closely with the results obtained in real data, increasing confidence that any limitations to our simulation do not affect the conclusions of our manuscript.

Finally, it is evident that all programs discussed in this manuscript had difficulty accurately detecting short (eg, 1 cm) IBD segments. One goal for future IBD detection should be to increase the accuracy of detecting these small segments while maintaining computational efficiency.

Conclusion

With increasingly large whole-genome SNP data sets being accumulated, it is important to have a method for detecting IBD segments that is both accurate and efficient. We introduced a program, FISHR, that accomplishes both, and that is particularly accurate at estimating endpoints of IBD segments. We demonstrated these properties using simulations, and confirmed these conclusions using a novel approach on real sequence data from the UK10K project. Due to the number of pairwise comparisons that must be made in IBD detection, computationally intensive programs such as rIBD and HaploScore cannot be easily run on data sets of more than ~10 000 individuals. FISHR is a more accurate alternative to GERMLINE as an IBD detection program on large data sets, with only a modest increase in run time.