Inferring Rates and Length-Distributions of Indels Using Approximate Bayesian Computation

Abstract

The most common evolutionary events at the molecular level are single-base substitutions, as well as insertions and deletions (indels) of short DNA segments. A large body of research has been devoted to develop probabilistic substitution models and to infer their parameters using likelihood and Bayesian approaches. In contrast, relatively little has been done to model indel dynamics, probably due to the difficulty in writing explicit likelihood functions. Here, we contribute to the effort of modeling indel dynamics by presenting SpartaABC, an approximate Bayesian computation (ABC) approach to infer indel parameters from sequence data (either aligned or unaligned). SpartaABC circumvents the need to use an explicit likelihood function by extracting summary statistics from simulated sequences. First, summary statistics are extracted from the input sequence data. Second, SpartaABC samples indel parameters from a prior distribution and uses them to simulate sequences. Third, it computes summary statistics from the simulated sets of sequences. By computing a distance between the summary statistics extracted from the input and each simulation, SpartaABC can provide an approximation to the posterior distribution of indel parameters as well as point estimates. We study the performance of our methodology and show that it provides accurate estimates of indel parameters in simulations. We next demonstrate the utility of SpartaABC by studying the impact of alignment errors on the inference of positive selection. A C ++ program implementing SpartaABC is freely available in http://spartaabc.tau.ac.il.

Introduction

Comparative-genomic studies rely on a detailed description and understanding of the evolutionary forces that drive sequence variation among genes and genomes. Probabilistic evolutionary models are currently the main work-horse to study such sequence variation, and as such, they must account for base-pair substitutions as well as insertion and deletion (indel) events.

Inferring indel parameters within a likelihood framework is substantially more challenging compared with substitution parameters (Cartwright 2005; Fletcher and Yang 2009). Factors contributing to this challenge include the dependency among sites introduced by indel events and the existence of overlapping indels. Due to this challenge, indel data are often ignored or treated as missing data in downstream analyses. These include the reconstruction of phylogenetic trees (McTavish et al. 2015; Kalaghatgi et al. 2016), the inference of divergence dates (Lartillot et al. 2009) and the elucidation of selection regimes (Will et al. 2010). The difficulty of handling indel dynamics is also reflected in common programs to compute multiple-sequence alignments (MSAs), such as MAFFT (Katoh and Standley 2013) and PRANK (Löytynoja and Goldman 2005; Löytynoja and Goldman 2008). To date, such programs offer parameters to control gap dynamics (e.g., gap open and extension penalties); however, there is no rigorous methodology to learn what values these parameters should take from any specific set of unaligned sequences. Finally, studies that aimed to elucidate how indel dynamics vary among genes and taxa rely on ad hoc methodologies for indel rate inference (e.g., Chang and Benner 2004). Of note, Navarro Leija et al. (2016) recently explored variation in indel rate independent of the substitution rate across a given MSA. They account for this variation by presenting a stochastic model, where the gap character “-“ is added to the DNA alphabet as a fifth character. However, by doing so their model implicitly assumes complete site independence for indels. This is in contrast to the more realistic modeling of indel length distribution discussed below and studied in this work.

For sequence-evolution analyses, integrating indel data into the computation may involve three steps: 1) describing an adequate combined model for indel and substitution events; 2) inferring the indel and substitution model parameters; and 3) inferring all other model parameters (tree, MSA, divergence dates, etc.) accounting for the indel-substitution dynamics. For the first step, probabilistic models of sequence evolution along a tree that include both substitution and indel events were previously developed in the context of sequence simulators, which allow generating MSAs with various levels of indels (Rambaut and Grassly 1997; Stoye et al. 1998; Cartwright 2005; Gesell and von Haeseler 2006; Hall 2008; Shavit Grievink et al. 2008; Fletcher and Yang 2009; Sipos et al. 2011; Koestler et al. 2012). Although simulating with these models is relatively straightforward, those methodologies generally do not provide a means to reliably estimate the parameters of these models from a specific data set. In this work, we focus on addressing the second step, namely, developing ways to accurately infer indel parameters for such models. We hope that making progress in the second step will also accelerate the third step, that is, that these models will be progressively integrated into various downstream analyses.

Recently we developed SPARTA, a simulation-based algorithm to learn indel parameters from input MSAs (Levy Karin et al. 2015). SPARTA first extracts a vector of summary statistics from an input MSA. It then searches the indel parameter space and uses a sequence simulator to generate a set of N MSAs under each examined parameter combination. Next, a vector of summary statistics is computed for each of the N MSAs in the simulated set. Finally, the Mahalanobis distance between the vector of summary statistics of the input MSA and the collection of N vectors of summary statistics computed for each of the N MSAs is calculated. The indel parameter combination under which the Mahalanobis distance receives a minimal value is returned as the parameter combination that best fits the data.

In this study, we further develop a simulation-based approach to learn indel parameters by utilizing an Approximate Bayesian Computation (ABC) inference framework (Rubin 1984; Tavaré et al. 1997). An ABC methodology for parameter inference is especially useful in cases where the likelihood function cannot be termed or easily solved. Briefly, ABC relies on 1) sampling possible parameter values from a prior parameter distribution, 2) simulating data based on the sampled parameter values, and 3) comparing the simulated data to the input data for which parameters should be inferred. Repeating this procedure numerous times and keeping only parameter values under which the simulated data had a satisfactory level of resemblance to the input data allows for the approximation of the posterior parameter distribution (Tavaré et al. 1997; Pritchard et al. 1999; Beaumont et al. 2002; Beaumont 2010). Harnessing the ABC framework to infer parameters has proven to be a useful and efficient method, especially in cases where the stochastic models describing the process at hand are complex and parameter-rich (e.g., Cornuet et al. 2008; Nakagome et al. 2013; Buzbas and Rosenberg 2015).

Our new algorithm, SpartaABC, is an ABC rejection algorithm for inferring indel parameters. As such, it extracts a vector of summary statistics from its input; it then performs repeated simulations using an integrated sequence simulator (Fletcher and Yang 2009) under various indel parameters. From each such simulated data set it extracts a vector of summary statistics and computes its distance from the vector extracted for the input using a weighted Euclidean distance. SpartaABC retains a subset of the simulations for which the distance from the input was small enough. According to the type of input it can process, we develop SpartaABC to offer three modes of inference: one MSA-mode where the input to the algorithm is a multiple sequence alignment (MSA) and two variants of Pairwise-mode where the input is a set of unaligned sequences in which computations rely solely on pairwise alignments. These two latter modes of inference are motivated by the need to overcome alignment uncertainty. A similar approach was recently utilized by Bogusz and Whelan (2016) in the context of phylogeny inference. Next, we study the performance of each of these modes of inference in simulations.

Searching for sites within coding genes which are subject to positive Darwinian selection has been the goal of many studies (Enard et al. 2002; McCauley et al. 2007; Stern et al. 2007; Proux et al. 2009; Roux et al. 2014; Daub et al. 2017). Given an MSA, the detection of such sites often involves fitting models to estimate the rate of nonsynonymous to synonymous substitutions at each codon site (e.g., Yang et al. 2000; Swanson et al. 2003). Because MSAs are computed by alignment programs rather than observed, various studies focused on describing the effect of errors in the MSA on the detection of positive selection (e.g., Fletcher and Yang 2010; Jordan and Goldman 2012; Spielman et al. 2014). These studies relied on similar concepts; in each study, sequence sets were simulated either with positive selection or without it. Next, MSAs were computed from these sets and finally the presence of positive selection was determined, measuring the false positive rate and power of the detection of positive selection from computed MSAs. However, up until now, the indel parameters used for such simulations could not be inferred from biological data sets. Thus, previous studies resorted to scanning a wide range of parameter values (Jordan and Goldman 2012) or focusing on specific indel parameter values (Fletcher and Yang 2010; Spielman et al. 2014). Here, we use SpartaABC to first study the indel parameters from a biological data set of 189 mammalian coding genes. We then use these indel parameters to simulate sequence sets with and without positive selection, align each such set using PRANK (Löytynoja and Goldman 2005, 2008; Löytynoja 2014) and measure the false positive rate and power of the detection of positive selection.

Materials and Methods

Indel Parameters and Their Use in the Simulation Study

The indel parameters learned by the SpartaABC algorithm are the indel-to-substitution rate ratio (IR), which controls the proportion of events in the simulation in which an indel is created, the “a” parameter of the power law distribution, which controls the distribution of indel length, and the length of the sequence at the root of the tree (RL).

The following parameter configurations were used as part of the simulation study:

1. Basic configuration: “a” = 1.3, IR = 0.02, RL = 350

2. Alternative configuration 1: “a” = 1.3, IR = 0.02, RL = 100

3. Alternative configuration 2: “a” = 1.3, IR = 0.02, RL = 500

4. Alternative configuration 3: “a” = 1.1, IR = 0.02, RL = 350

5. Alternative configuration 4: “a” = 1.7, IR = 0.02, RL = 350

6. Alternative configuration 5: “a” = 1.3, IR = 0.01, RL = 350

7. Alternative configuration 6: “a” = 1.3, IR = 0.1, RL = 350

Each of the alternative configurations differs by one parameter from the basic one, allowing testing the effect of individual parameters on the accuracy of SpartaABC. The values were chosen to reflect the range of plausible parameters (See also Levy Karin et al. 2015). These parameters in each configuration were given as input to the sequence simulation program INDELible (Fletcher and Yang 2009). All other INDELible parameters were set to: “NUCLEOTIDE 1” model, substitution model: “JC,” maximum indel length: 50. For all simulations, the Azurin tree with 29 species was used (Levy Karin et al. 2015). The tree is provided as supplementary information, Supplementary Material online.

SpartaABC Algorithm

Prior Parameter Distributions and Search Space

SpartaABC proposes indel parameter combinations by sampling values from the joint prior distribution. In this work, we assumed that all parameters are mutually independent and that the marginal prior of each parameter is uniformly distributed. Specifically, the “a”parameter value is sampled from a wide range: (1,2], the IR parameter value is sampled from a wide range: [0,0.15], and the RL parameter range was determined empirically according to the input by measuring a characteristic l. In the SpartaABC MSA-mode, l denotes the length of the input MSA, whereas in SpartaABC Pairwise-mode, l denotes the length of the longest sequence in the input set of unaligned sequences. The range of the RL was set to [50,1.25*l].

Computed Summary Statistics

The following summary statistics are computed as part of the SpartaABC algorithm:

1. Total number of gap blocks in the alignment: gap blocks are one or more consecutive gap characters. Each alignment row is analyzed independently and the summary statistics is the sum of all alignment rows.

2. Total number of unique gap blocks in the alignment: cases in which two or more rows have a gap block that starts and ends at the same positions are coded as a single unique gap.

3. Average gap block length: the total number of gap characters divided by the total number of gap blocks.

4. Average unique gap block length: the total number of gap characters divided by the total number of unique gap blocks.

5. Number of gap blocks of length one.

6. Number of gap blocks of length two.

7. Number of gap blocks of length three.

8. Number of gap blocks of length four or more.

9. Alignment length: the number of columns in the alignment.

10. Minimal length of sequence in the input.

11. Maximal length of sequence in the input.

Summary Statistics Weight Computation

The SpartaABC algorithm computes a weighted Euclidean distance between the vector of summary statistics, $\underset{\_}{s}$, extracted from the input alignment and the vector of summary statistics computed for each set of examined indel parameters, ${\underset{\_}{s}}^{*}$. The weighted Euclidean distance between $\underset{\_}{s}$ and ${\underset{\_}{s}}^{*}$ based on m summary statistics is defined as: $d^{*}=D\left(\underset{\_}{s},{\underset{\_}{s}}^{*}\right)=\sqrt{{\sum }_{i=1}^m{\left[w_i\left(s_i-s_i^{*}\right)\right]}^2}$ where $s_i$ and $s_i^{*}$ are the i^th summary statistic computed for the input alignment and for the simulated alignment, respectively, and $w_i$ is the weight assigned to the i^th summary statistic. Prior to using SpartaABC for data analysis, we computed the weight for each summary statistic i as: ${\mathrm{w}}_{\mathrm{i}}=1/\widehat{{\mathrm{\sigma }}_{\mathrm{i}}}$ where $\widehat{{\mathrm{\sigma }}_{\mathrm{i}}}$ is the empirical standard deviation of the i^th summary statistic across 100,000 simulations with indel parameter combinations drawn at random from the prior. These weight sets were determined separately for each of the SpartaABC run modes examined in this study: MSA-nucleotide, Pairwise-nucleotide, MSA-codon. We provide the files with these computed weights as supplementary material, Supplementary Material online.

The Distance Threshold for Rejecting

In this study, we follow the practice suggested by Beaumont et al. (2002) to set the distance cutoff, ɛ, empirically so that the percentage of accepted parameter combinations (simulations) is p% of the total simulations. Throughout this study, unless stated otherwise, we set p to be 0.05% (50/100,000) of the simulations.

Pairwise Alignment Computation

In its pairwise mode, SpartaABC implements the Gotoh (1982) algorithm of an affine gap penalty score. Throughout this study, in its pairwise mode, SpartaABC was run with the following pairwise alignment parameters: gap-open = 5, gap-extend = 1.

Error Estimation

To evaluate the performance of SpartaABC on a given parameter configuration with K = 50 instances (data sets simulated from the configuration), we compute the average percent absolute error for each of the indel parameters as follows:

$$average\mathrm{ }percent\mathrm{ }estimation\mathrm{ }error=100\mathrm{ }\times \frac{1}{K}\sum _{i=1}^K\frac{\left|{\widehat{\mu }}_i-\mu \right|}{\mu }$$

where $\mu$ is the real parameter value and ${\widehat{\mu }}_i$ is the inferred parameter value in instance i.

Study of Positive Selection

Mammalian Orthologous Genes Data Set

A Perl script to collect all human gene IDs was used to query the Ensembl database (Yates et al. 2016) (version 84, accessed on 21/06/2016). An additional Perl script was then used to query the Ensembl database and search for 1:1 orthologs for each of these human genes, across 41 mammalian species (the full mammalian species list is available as supplementary material, Supplementary Material online). When querying the Ensembl database, only genes with transcripts whose status is “known” and “coding” were retained. In cases for which more than one transcript was available per human gene, the longest one was retained. For each of the 41 mammalian orthologs, if more than one transcript was available, the transcript with the highest Needlemen and Wunsch (1970) score against the retained human transcript was chosen. This procedure resulted in 961 genes (sequence sets) for which transcripts for 42 mammalian species (human + 41 orthologs) were collected. Of these, 189 sequence sets were randomly selected for further analyses. We provide these sets online in http://spartaabc.tau.ac.il. Codon MSAs for each of these sets were computed using a Perl script, by first aligning the translated protein sequences using PRANK V140603 (Löytynoja 2014) with the “+F” argument and then back-translating this MSA to nucleotide-based alignment.

Mammalian Species Topology

A topology reflecting the evolutionary relationships between the 42 mammalian species in our data set was based on current literature (Blanga-Kanfi et al. 2009; Perelman et al. 2011; Nyakatura et al. 2012; Song et al. 2012). This topology is provided as supplementary material, Supplementary Material online.

Inference of Positive Selection

The mammalian species topology together with each codon MSA were provided as input to the PAML 4 program (Yang 2007). The program was run in two modes; fitting either the M8a model that does not allow for positive selection (Swanson et al. 2003), or the M8 model that allows for positive selection (Yang et al. 2000). For either model, the PAML program provides the following output: 1) the log-likelihood (LL) score, 2) the ML codon tree—optimized branch lengths for the input topology (in terms of codon substitutions per site), 3) nine dN/dS (omega) categories with the proportion of alignment positions predicted to belong to each category. For each gene in our data set, selection between the M8a and M8 models was done according to a Likelihood Ratio Test (LRT) for comparing nested models. The LRT test statistic $D=2\left({LL}_{M8}-{LL}_{M8a}\right)$ was compared with the critical value for 0.95 statistical confidence, with 1 degrees of freedom. A gene was considered positively selected if D >3.84.

Inferring Indel Parameters

The indel parameters for each mammalian MSA were inferred using SpartaABC (in MSA-mode). To this end, the maximum-likelihood codon tree from the PAML output for the selected model for that gene together with the mammalian MSA and the MSA-codon weights set were provided as input to SpartaABC. The search range for the IR parameter was [0,0.15], the search range for the “a” parameter was [1,2], and the search range for the RL parameter was determined according to the shortest and longest sequences (measured in nucleotides) in the MSA; setting the lower bound to be 10% shorter than the shortest sequence and the upper bound to be 10% longer than the longest sequence, divided by three to obtain length boundaries in codons.

Simulated Data Sets

Codon sequence data sets were simulated using INDELible (Fletcher and Yang 2009) with a codon model either with or without positive selection. When simulating with (without) positive selection, the parameters for the INDELible control file were determined based on the parameters inferred from genes for which the M8 (M8a) model was selected. The indel parameters for the simulation were set by taking the posterior expectation of each of the indel parameters as inferred by SpartaABC. The phylogenetic tree, the transition-to-transversion rate ratio (i.e., the kappa parameter), and the omega category values and proportions were determined according to the PAML M8 (M8a) output for each gene.

Algorithm Implementation

The algorithm was implemented in C ++. We provide its source code, a precompiled version for UNIX systems, a short manual and a run example at http://spartaabc.tau.ac.il.

Results

The SpartaABC Algorithm

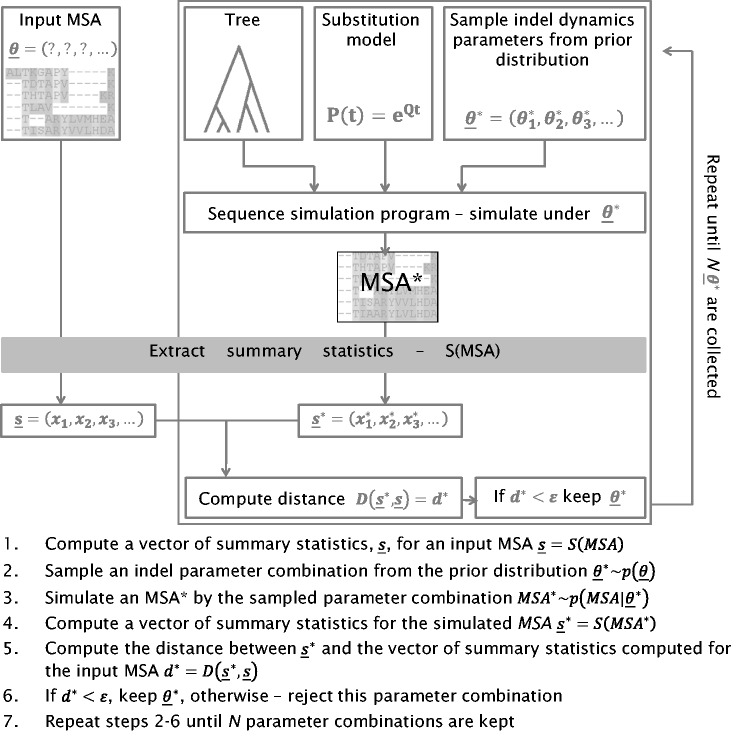
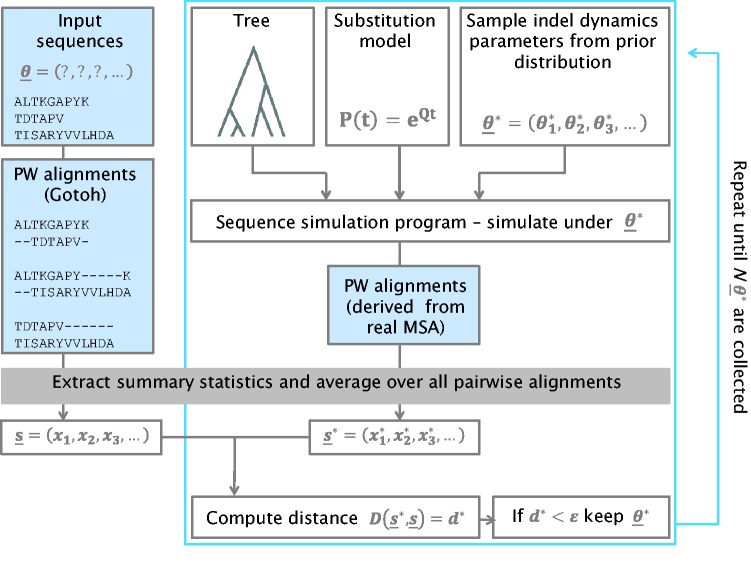
In this study, we propose a statistical framework to infer the parameters governing indel processes. Our algorithm, SpartaABC, uses an Approximate Bayesian Computation (ABC) reject procedure (Tavaré et al. 1997; Beaumont et al. 2002; Beaumont 2010). As input, SpartaABC takes T, a phylogenetic tree with branch lengths, and a set of sequences of the extant species in T. SpartaABC has three modes of computation; in the first, the input set of sequences is given as an MSA and in the other two modes, it is a set of unaligned sequences. We first present the MSA-mode of computation and in a later section the Pairwise-mode and the Pairwise-exhaustive-mode. Given the input MSA, SpartaABC computes a vector of summary statistics; these are numerical attributes that depict prominent features of the MSA. It then performs numerous iterations, considering various indel parameter combinations. In each such iteration, SpartaABC uses an integrated sequence simulator (Fletcher and Yang 2009) to simulate an MSA by T and the sampled indel parameter combination. It then computes a vector of summary statistics for the simulated data set. Next, it computes a weighted Euclidean distance, a commonly used metric in ABC algorithms (Beaumont et al. 2002; Prangle 2016), between the vectors of summary statistics obtained for the input MSA and the simulated MSA. The parameter sets from simulations with a small distance are used to infer the parameter values behind the input MSA. In this study we focus on three indel parameters: IR—the indel-to-substitution rate ratio, “a”—the shape parameter for the power law distribution controlling the indel length, and RL—the root length parameter (although the root length is not a pure indel parameter, it was included here as it strongly affects the resulting MSA). The SpartaABC procedure is presented schematically in figure 1 and its full details are provided in the Material and Methods section.

Fig. 1.

— SpartaABC algorithm scheme (MSA-mode).

Algorithm Calibration

Determining the Acceptance Cutoff

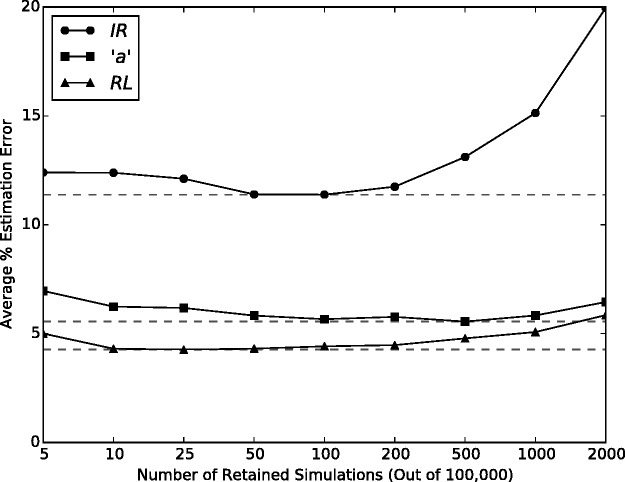
As a first step of calibrating the SpartaABC method, we determined the acceptance cutoff for keeping parameter combinations (simulations). As detailed above, indel parameter combinations are proposed by SpartaABC according to their prior distributions. An MSA is next simulated using this set, and a distance between the summary statistics of this MSA and the input MSA is computed. According to these distances, an acceptance cutoff should be determined. Setting a fixed value for the distance cutoff, ɛ, often poses problems in terms of 1) the specificity of distance values to individual inputs, that is, its tendency to vary from input to input in a noninformative way and 2) running times issues; a too small cutoff could mean a prolonged-to-infinite simulation process (Beaumont et al. 2002). Therefore, in this study we follow the practice suggested by Beaumont et al. (2002) to set the distance cutoff, ɛ, empirically so that the percentage of accepted parameter combinations is p% of the total simulations. Here, we implemented SpartaABC to propose a total of N = 100,000 indel parameter combinations, a number that offers a good sampling of the parameter space while assuring reasonable running times. Given N = 100,000, we set to determine the number of simulations to retain. To this end, we simulated 50 instances under known indel parameters of IR = 0.02, “a” = 1.3 and RL = 350 (“basic parameter configuration”, see Materials and Methods). We then provided each of these MSAs to SpartaABC as input and retained various numbers of simulations (ranging between 5 and 2,000) to approximate the posterior distribution. Next, we estimated the indel parameter values by computing the posterior expectation based on each of the different sized posterior sets. We found that retaining 50–100 parameter combinations offers the most accurate indel parameter estimations. Keeping fewer combinations seems to be too noisy whereas keeping many combinations risks distorting the posterior distribution towards the prior (fig. 2). We thus continued with keeping 50 parameter combinations throughout this study.

Fig. 2.

— Retaining the closest 0.05% of simulations minimizes the estimation error of indel parameters. Posterior distributions are approximated by retaining simulations with the smallest distances. Points represent average percent absolute estimation errors based on 50 simulations from the basic parameter configuration. In each instance a total of N = 100,000 parameter combinations were proposed according to the prior distributions.

Choice of Summary Statistics

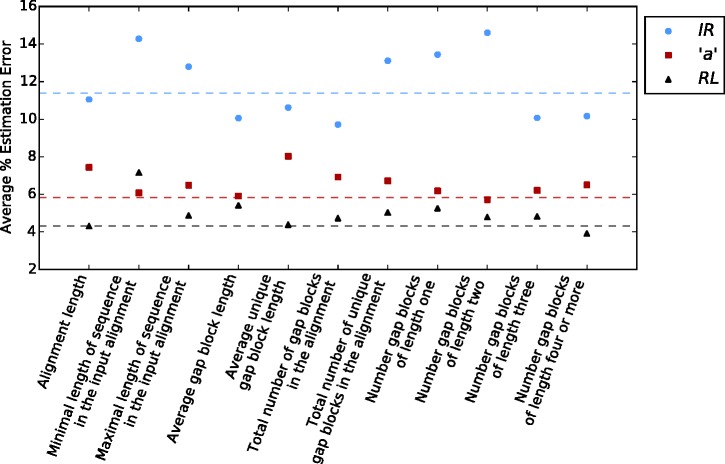
Next, we set to examine the impact of each individual summary statistic on the inference accuracy of SpartaABC. Eleven summary statistics are computed from the input and simulated data sets (for full details, see Materials and Methods). In order to determine which of these to include in the standard SpartaABC inference procedure, we performed a leave-one-out analysis. In this analysis, we provided SpartaABC with fifty simulated instances from the “basic parameter configuration” (see Materials and Methods) and compared the average percent estimation error obtained when all 11 summary statistics were included to that obtained when each summary statistic was excluded from the computation. This comparison was done with respect to each of the three indel parameters (IR, “a,” and RL). Generally, we found that exclusion of each summary statistic resulted in minor changes to the accuracy of parameter estimation (reducing or increasing the average percent estimation error by up to 2.5%, fig. 3). These differences were not found to be statistically significant (Mann–Whitney Test, see supplementary table 1, Supplementary Material online). When examined by their type, summary statistics relating to sequence length (alignment length, minimal length of sequence in the input alignment, maximal length of sequence in the input alignment) were generally found to contribute to the inference of all indel parameters, and mostly to the IR parameter. Summary statistics relating to the abundance of gap character blocks (total number of gap blocks in the alignment, total number of unique gap blocks in the alignment, number of gap block of length 1, length 2, length 3, or length 4 or higher) did not display a specific pattern in increasing or reducing inference accuracy (fig. 3). As all summary statistics were found to have minor individual effects and as each summary statistic was found to contribute to the accuracy of at least one indel parameter we decided to include all summary statistics in all inference procedures reported below.

Fig. 3.

— Excluding single summary statistics results in insignificant changes to the accuracy of parameter estimation. The figure depicts the accuracy of parameter estimation as a function of the summary statistic excluded from the analysis (a leave-one-out analysis). Points represent average percent absolute estimation errors based on 50 simulations from the basic parameter configuration when a specific summary statistic was excluded. The dashed horizontal lines indicate the average percent error obtained when all summary statistics were included.

Accuracy Evaluation

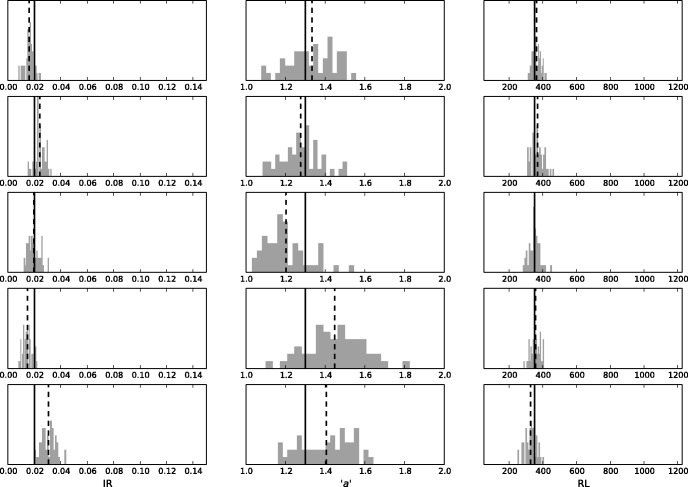
We set out to examine the ability of SpartaABC to reconstruct known indel parameters. To this end, we conducted a simulation study in which we produced data sets under seven indel parameter configurations. We used INDELible (Fletcher and Yang 2009) to simulate fifty instances from each such configuration (for full details concerning these configurations, see Materials and Methods). INDELible provides as output the real MSA as well as the simulated unaligned sequences. We next gave each real MSA to SpartaABC to infer its indel parameters. For each of these MSAs, SpartaABC outputs the indel parameter combinations of retained simulations; these approximate the posterior distribution of indel parameters. As part of its inference procedure, SpartaABC uses uniform priors to sample each of the indel parameters; it is thus interesting to compare the approximated posterior distribution with the uniform prior distribution. As can be seen in the visual examples for a few simulation instances performed on the basic parameter configuration (see Materials and Methods), the approximated posterior distribution of each of the indel parameters is not uniform but rather concentrated around the value of the real parameter behind the simulation (fig. 4). This serves as first indication that SpartaABC has inference ability.

Fig. 4.

— Approximated posterior distributions are consistent with real parameter values. Each row shows the approximated posterior distributions for a simulation from the basic parameter configuration. The real parameter value is marked as a solid line, and the inferred posterior expectation is marked as a dashed line. The gray histograms denote the parameter values in each of the retained simulations (approximated posterior distribution).

From the obtained approximate posterior distribution one could derive point estimates for each of the parameters. In this study, we focused on using the inferred posterior expectation of each of the parameters (hereafter, when we refer to “inferred parameter” we mean “inferred posterior expectation of the parameter”). Using the posterior expectation as a point estimate, we next examined the performance of SpartaABC over all indel parameter configurations. Overall, SpartaABC showed a good ability to reconstruct the indel parameters with <15% average estimation error for all parameters in six out of the seven parameter-configurations. Not surprisingly, when the RL parameter was set to 100, data are limiting and the performance of SpartaABC was less accurate, with an increased estimation error (table 1). When examining the ability of SpartaABC to reconstruct each of the parameter values across all configurations, we found that the RL and “a” parameter had a relatively small average percent estimation error (3–10%, table 1) whereas the average percent estimation error for the IR parameter was higher (7–25%, table 1). Finally, we compared the performance of SpartaABC to that of SPARTA (Levy Karin et al. 2015). We found that on average, with the same order of magnitude in run times, the two algorithms provided similar accuracy in parameter estimation, as measured by the percent estimation error. However, in most configurations, parameter estimations by SpartaABC varied less among simulation instances, suggesting its inference is less noisy (supplementary tables 2 and 3, Supplementary Material online).

Table 1.

SpartaABC Performs Well on Simulated Data

Config.	Value	Real		ClustalW		MAFFT		PRANK		Pairwise		Pairwise-exh.
		PE	Error (%)	PE	Error (%)	PE	Error (%)	PE	Error (%)	PE	Error (%)	PE	Error (%)
IR
basic	0.02	0.021	11	0.01	48	0.011	45	0.017	17	0.051	154	0.022	15
alt1	0.02	0.023	25	0.014	32	0.014	36	0.02	20	0.047	137	0.028	43
alt2	0.02	0.02	11	0.01	51	0.01	48	0.016	21	0.051	153	0.021	12
alt3	0.02	0.022	15	0.011	45	0.012	39	0.018	14	0.059	193	0.023	18
alt4	0.02	0.02	13	0.01	51	0.01	52	0.015	27	0.036	82	0.020	12
alt5	0.01	0.01	15	0.007	27	0.007	33	0.011	19	0.031	213	0.013	28
alt6	0.1	0.102	7	0.016	84	0.022	78	0.044	56	0.126	26	0.104	10
“a” Parameter
basic	1.3	1.311	6	1.36	8	1.218	8	1.213	7	1.928	48	1.346	8
alt1	1.3	1.401	10	1.388	10	1.331	7	1.325	7	1.894	46	1.445	12
alt2	1.3	1.315	6	1.394	9	1.22	8	1.214	8	1.93	48	1.317	6
alt3	1.1	1.148	5	1.287	17	1.126	4	1.133	4	1.921	75	1.251	14
alt4	1.7	1.702	4	1.608	6	1.511	12	1.431	16	1.939	14	1.66	6
alt5	1.3	1.321	8	1.412	10	1.255	6	1.248	8	1.927	48	1.421	10
alt6	1.3	1.311	5	1.203	9	1.116	14	1.12	14	1.936	49	1.289	5
RL
basic	350	346.5	4	350.1	5	347.3	5	346.2	4	346.5	2	349.4	1
alt1	100	96.3	8	100	7	97.8	7	94.9	9	99.3	3	98.8	2
alt2	500	498.7	4	499.4	3	497.5	4	497.7	4	496.1	1	499.1	1
alt3	350	347.2	5	352.8	6	345.7	6	345	6	347.1	2	348.7	1
alt4	350	347.3	3	350.1	3	349.5	3	347.6	3	348.1	1	349.8	1
alt5	350	348.7	3	351.5	3	350.4	3	348.8	3	348	1	349.5	1
alt6	350	354.6	8	350	8	340.5	10	325.5	12	366.1	5	351.0	3

Fifty MSAs were generated for each of the seven simulation configurations. Posterior expectations (PEs) for each of the indel parameters were inferred six times. First, each real MSA was given to SpartaABC in MSA-mode. Then, MSAs were computed by ClustalW, MAFFT, or PRANK and given as input to SpartaABC in MSA-mode. Next, SpartaABC was run in the Pairwise-mode. Finally, SpartaABC was run in Pairwise-exhaustive-mode. Highlighted in bold are cases in which the Pairwise-mode or Pairwise-exhaustive-mode were the most accurate among all cases in which the input was computed (i.e., excluding cases in which the real MSA was provided as input).

SpartaABC Is Generally Robust to Alignment Errors

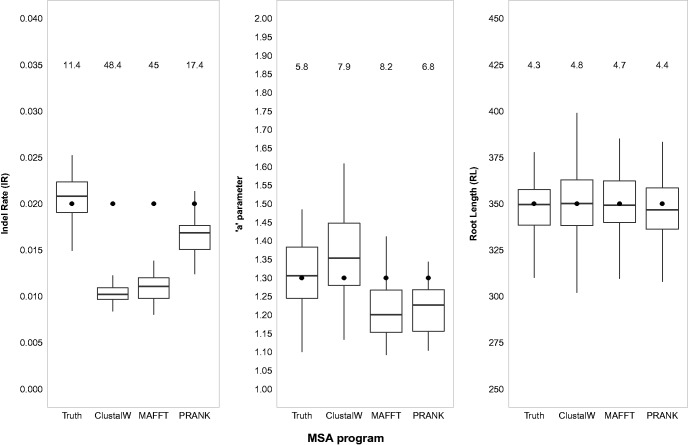
When studying biological data outside the realm of simulations, the real MSA, reflecting all homology relationships in a set of sequences is not known but rather, has to be computed using an alignment program. It has been previously reported that such alignment programs are prone to errors (Blackshields et al. 2006; Nuin et al. 2006; Thompson et al. 2011; Sela et al. 2015), over-alignment (Löytynoja and Goldman 2008; Katoh and Standley 2016) and often disagree with each other (Lassmann and Sonnhammer 2005; Blackburne and Whelan 2012). Hence, it is interesting to examine the performance of SpartaABC in cases where its input MSA is computed by alignment programs. We thus used three popular alignment programs: ClustalW V1.8 (Thompson et al. 1994), MAFFT V7 (Katoh and Standley 2013), and PRANK V140603 (Löytynoja 2014) to align each set of sequences obtained in the simulation configurations mentioned above. We next used SpartaABC to infer the indel parameters from each of these computed MSAs. We found that inferred indel parameter values were overall close to the real parameter values even when SpartaABC was run on MSAs computed by alignment programs (an overall average error of 18% across all configurations, parameters and alignment programs, table 1). However, the accuracy in parameter estimation was reduced, compared with that obtained when providing SpartaABC with the real INDELible MSAs (table 1). Moreover, we found that inference accuracy varied between the different alignment programs and between indel parameters. Specifically, the IR parameter was underestimated using all alignment programs (fig. 5, supplementary fig. 1A–F, Supplementary Material online); estimation error was most severe with ClustalW (an average error of 48% across all configurations, table 1), slightly less so with MAFFT (an average error of 47% across all configurations, table 1), and least severe with PRANK (an average error of 25% across all configurations, table 1). Notably, the estimation of the IR parameter suffered the greatest inaccuracies when the IR parameter was set to a high value (IR = 0.1, table 1). The estimation of the “a” parameter was overall rather accurate and similar between all alignment programs (an overall average error of 9% across all configurations and alignment programs, table 1). Finally, the inference of the RL parameter was accurate using any of the alignment programs (an overall average error of 5% across all configurations and alignment programs, table 1). For a full account of the statistical significance of the differences in parameter estimations through the three alignment programs see supplementary table 4, Supplementary Material online.

Fig. 5.

—SpartaABC is generally robust to different alignment algorithms. Fifty sequence data sets obtained using the basic parameter configuration were aligned by either ClustalW, MAFFT, or PRANK. The MSAs computed by each alignment program were given as input to SpartaABC. The real parameter values are marked as bold points. As reference, we also present the inferred values using the real MSAs generated by INDELible. Numbers above each boxplot indicate average percent estimation error.

Pairwise-Mode of Inference

High indel-to-substitution rate ratio values such as the one examined in this study (IR = 0.1) were shown to pose a more challenging task for alignment programs (Nuin et al. 2006; Jordan and Goldman 2012; Levy Karin et al. 2014). It is thus not surprising that alignment programs compute less accurate MSAs for input simulated by high indel-to-substitution rate ratio. Moreover, the process of computing an alignment for multiple sequences often relies on numerous steps in which pairwise alignments are joined together, thus possibly propagating errors during MSA construction (Gotoh 1996; Wallace et al. 2005). We suspected this error propagation process contributed to the inaccurate estimation of the IR parameter in the high-IR configuration when the input was an MSA computed by an alignment program (alt6 configuration, table 1). We thus, sought a way to infer indel parameters in a manner that is free of an MSA. To this end, we developed the SpartaABC “Pairwise-mode”. In this mode, the input to SpartaABC is a set of unaligned sequences. As a first stage, all pairwise global alignments are computed between each pair of sequences in the set, using the Gotoh algorithm (1982). The SpartaABC’s summary statistics are computed from each pairwise alignment and are then averaged to obtain a single representative summary statistics vector of the input. Next, the sequence simulation procedure takes place as detailed above, producing a simulated real MSA. A set of pairwise alignments is derived from the simulated real MSA by taking the projected alignment over each pair of sequences and removing columns that contain a gap character in both sequences. In a similar manner to the input, summary statistics are computed from each pairwise alignment and are averaged to obtain a single representative summary statistics vector of the simulation. The distance between the vector of summary statistics computed from the input and the vector computed from each simulation is calculated as before. This procedure is depicted schematically in figure 6, with stages unique to the “Pairwise-mode” highlighted with a blue background.

Fig. 6.

—SpartaABC algorithm scheme (Pairwise-mode). Highlighted in a blue background are the steps unique to the Pairwise-mode.

We next set to examine the performance of this Pairwise-mode of inference. To this end, we ran SpartaABC over unaligned sequence sets obtained in the seven parameter configurations of the above described simulation study. We found that inference of the RL parameter was more accurate in the Pairwise-mode compared with running SpartaABC in MSA-mode with any of the examined alignment programs. However, inference of the “a” parameter was poorer in the Pairwise-mode (table 1). Interestingly, inference of the IR parameter depended greatly on the IR value. In six out of the seven examined parameter configurations, the IR value was set to be 0.02 or lower. In all these configurations, more accurate results were obtained with SpartaABC in MSA-mode than those obtained in SpartaABC Pairwise-mode. However, when IR was high (0.1), the SpartaABC Pairwise-mode was superior to SpartaABC MSA-mode for all MSA programs (26% error in the pairwise-mode compared with 56%, 78%, and 84% based on PRANK, MAFFT, and ClustalW, respectively, table 1). We thus conclude that when a high indel rate is expected or when an MSA cannot be reliably computed, the RL and IR parameters can be better inferred in a pairwise manner.

Pairwise-Exhaustive Mode of Inference

A possible source of bias in the above-described pairwise mode is that the real data and the simulated data are processed differently. Specifically, the summary statistics from the pairwise sequences of the real data are inferred after applying the Gotoh algorithm (1982) for each pair, whereas in the simulated data, the pairwise alignments are derived from the simulated MSA, and summary statistics are derived from these pairwise alignments. In order to study the impact of this potential bias, we developed a variant of the SpartaABC Pairwise-mode, in which the pairwise alignments in each simulation stage were not derived from the simulated real MSA, but rather were computed using the Gotoh algorithm, similar to the sequence pairs of the real data. This variant, which we denote “Pairwise-exhaustive-mode”, thus performs the exact same computation on the input data and on the simulated data. However, as its name suggests, computing O(n^2) Gotoh pairwise alignments (where n is the number of sequences) in each simulation stage poses a heavier computation burden, compared with deriving the pairwise alignments from the real MSA. We next examined the performance of SpartaABC Pairwise-exhaustive-mode across all seven indel parameter configurations. We found that with an average of 10% estimation error across all indel parameters and all configurations, SpartaABC Pairwise-exhaustive-mode was the most accurate of all SpartaABC inference methods (table 1). For a full account of the statistical significance of the differences in parameter estimations between MSA-mode using PRANK and the two variants of the Pairwise-mode see supplementary table 5, Supplementary Material online.

The comparison of the running times of all SpartaABC modes is given in table 2. As can be seen, the SpartaABC MSA-mode and Pairwise-mode take an average of 43 min per computation instance. Although offering greater accuracy in parameter estimations, the Pairwise-exhaustive-mode has longer running times by a factor of 45, on average (an average of 32.25 h per computation instance).

Table 2.

SpartaABC’s Running Times

Config.	MSA-Mode	Pairwise-Mode	Pairwise-Exhaustive-Mode
basic	34 ± 5	30 ± 7	1,867 ± 496
alt1	16 ± 4	23 ± 2	252 ± 61
alt2	51 ± 10	63 ± 3	3,395 ± 991
alt3	42 ± 6	36 ± 7	2,359 ± 448
alt4	30 ± 7	37 ± 7	1,660 ± 384
alt5	29 ± 6	46 ± 3	1,762 ± 334
alt6	119 ± 23	54 ± 7	2,254 ± 1,142

Note.–The average running time for each of the SpartaABC computation modes over all seven parameter configurations in minutes (± standard error).

Alignment Errors and the Inference of Positive Selection

We next set to use SpartaABC to study the impact of alignment errors on positive selection inference. To this end we obtained a set of 189 mammalian coding genes. Each gene in this set had orthologous sequence information for 42 mammalian species and was aligned using PRANK V140603 (Löytynoja 2014) (for full details on how this data set was composed, see Materials and Methods). We first inferred positive selection for each gene by using the program PAML (Yang 2007). The program was run in two modes: fitting either the M8a model (Swanson et al. 2003), constraining no positive selection, or the M8 model (Yang et al. 2000) allowing for positive selection. Using the log-likelihood scores of each model, as computed by PAML, we conducted a likelihood ratio test (LRT) for each gene to select between the models (for full details concerning the LRT, see Materials and Methods). For 69 out of 189 (36.5%) genes in our data set the null model was rejected, indicating a signal for positive selection.

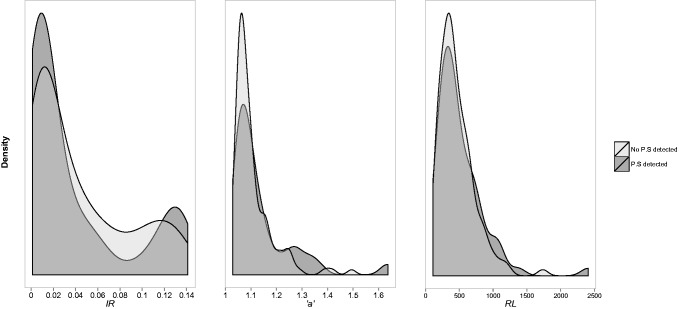
We then used SpartaABC to study the indel parameters from each of the 189 MSAs in the mammalian data set (in MSA-mode). We found no significant difference (Mann–Whitney test) between the distributions of indel parameters characterizing the set of genes detected to undergo positive selection and the set of genes where no positive selection was detected (fig. 7). The mean indel parameter values for the mammalian data set were: IR = 0.04, “a” = 1.118, and RL = 478 (codons).

Fig. 7.

—There are no significant differences between the indel processes of genes that have experienced positive selection and those that have not. The figure depicts the density of indel parameter values as inferred by SpartaABC based on 189 mammalian coding genes aligned with PRANK.

Next, the inferred substitution parameters for the selected codon model for each gene (for example, the transition/transversion ratio and the dN/dS categories, see Materials and Methods for full details), as inferred by PAML were used together with its indel parameters, as inferred by SpartaABC to simulate 120 data sets under no positive selection and 69 data sets with positive selection (Fletcher and Yang 2009). Each of the simulated data sets was then analyzed in the same way the original mammalian genes were analyzed: computing codon alignments using PRANK, using PAML to fit the M8 and M8a models, and selecting between the models with an LRT.

For the 120 null data sets, we found that the null model was rejected 12 times, suggesting a false positive rate of 10% and for the 69 alternative data sets, we found that the null model was rejected 66 times, suggesting power of 95.7%. For the 120 null data sets, we also computed the proportion of cases in which the null model was rejected when using the real INDELible MSAs. Using the real INDELible MSAs, the null model was rejected five times, yielding a false positive rate of 4.2%, which is close to the 5% false positive rate one would expect.

These results are in line with previous results showing over-estimation of the rate of positive selection (Wong et al. 2008; Fletcher and Yang 2010; Markova-Raina and Petrov 2011; Privman et al. 2012). The over-estimation of the false positive rate was abolished when the real MSA was given, lending further support for the cause of this inflated estimation rate. However, unlike these previous reports, the simulations conducted here were based on indel parameters that were estimated from the relevant data, and were not chosen arbitrary (see discussion).

Assuming that the false positive rate for the empirical mammalian data set is indeed 10% suggests that the number of genes evolving under positive selection is closer to 62 out of 189 (32.8%) rather than 69 out of 189 (36.5%). These results show more than 6-fold enrichment of positively selected genes compared with the null expectation.

Discussion

In this study, we have presented SpartaABC, an approximate Bayesian computation algorithm to infer indel parameters from sequence data. With three inference modes, the input to SpartaABC can be either a multiple sequence alignment (MSA-mode) or a set of unaligned sequences (Pairwise-mode and Pairwise-exhaustive-mode). SpartaABC relies on numerous sequence simulations, each of which under a sampled combination of proposed indel parameters. It then retains the indel parameters for which the simulated sequences resembled the input as measured by a vector of extracted summary statistics. Using the retained indel parameters, posterior distributions as well as point estimates for the indel parameters are computed. Our simulation study shows that SpartaABC results in reliable parameter estimations, even when the input MSA was computed using an alignment program and thus not guaranteed to be free of errors. However, when the indel-to-substitution rate ratio (IR) was very high, the ability of SpartaABC to infer this parameter through computed MSAs was reduced. We have shown that under these conditions, using either the Pairwise-mode or, even better, the Pairwise-exhaustive-mode allowed for more accurate estimations of this parameter. However, the Pairwise-exhaustive-mode is on average 45 times slower than the other two modes of inference. Therefore, if the indel-to-substitution rate ratio is expected to be high and computational resources are limiting, one could combine two fast strategies to infer indel parameters by using the MSA-mode to infer the “a” parameter and using the Pairwise-mode to infer the RL and IR parameters.

One possible reason for the increased accuracy of the Pairwise-exhaustive-mode could be that the exact same computational procedure is performed on the input to SpartaABC and on the simulated sequences in each simulation step. This is in contrast to the Pairwise-mode, in which in each simulation step, projected pairwise alignments are produced by using the real simulated MSA. That is, in each simulation step, there is an implicit use of information about the homology relationships between all pairs of sequences as coded in the full MSA; such information is of course, unavailable when computing the set of all pairwise alignments from the input. Differences in the computational procedure performed on the input and on the simulated data exist in the MSA-mode as well, as the input MSA is computed by an alignment program whereas the MSA examined in each simulation is the real MSA provided by the integrated sequence simulator. However, in this mode of computation, the set of sequences as a whole is available to the alignment program to consider at once. Thus, the difference between the available implicit information in each simulation step and in the computation performed on the input is probably smaller when compared with the difference in the Pairwise-mode. Nonetheless, a variant of SpartaABC in which an alignment program such as PRANK (Löytynoja and Goldman 2005; Löytynoja and Goldman 2008; Löytynoja 2014) is integrated into SpartaABC and used in each simulation step could be developed to minimize the difference in available information for this mode of computation. This option was not implemented because it requires realigning each of the N simulated MSAs, a task which is exceedingly computationally intensive.

As part of this study we compared the performance of SpartaABC in MSA-mode to that of SPARTA (Levy Karin et al. 2015). On average, the two algorithms provided similar accuracy in parameter estimation with similar running times. However, in most configurations, parameter estimations by SpartaABC in MSA-mode were less noisy (supplementary tables 2 and 3, Supplementary Material online). Generally, SpartaABC offers the following advantages over SPARTA: 1) unlike SPARTA, which is an ad-hoc procedure, SpartaABC is nested within a statistical framework of inference; 2) unlike SPARTA, SpartaABC is not a search algorithm—it approximates the posterior distribution of indel parameters. As such, it is not subject to problems of local minimum; 3) SpartaABC offers three modes of inference (as opposed to a single mode in SPARTA). Its two pairwise modes are of special use when the input MSA is highly unreliable. 4) SpartaABC offers more summary statistics than SPARTA and more flexibility in the inclusion/exclusion of each of them in its computation.

One interesting future direction to this research is to develop richer indel models and study their parameters using SpartaABC. For example, in the current implementation, a single free parameter (IR) controls the relative occurrence of indel versus substitution events. An indel model with one parameter controlling the rate of insertions and one for the rate of deletions is expected to fit biological data significantly better (Ajawatanawong and Baldauf 2013). Additional assumptions that are potentially oversimplified and can be relaxed include not considering spatial variation of indel parameters along the sequence and uniform indel rates along the phylogeny, to name a few.

Should SpartaABC be extended to deal with more complex models of sequence simulations, it would probably be useful to extract additional summary statistics from the input and from the simulated data. In this study, we used a leave-one-out approach to examine the individual contribution of each summary statistic. When dealing with larger numbers of summary statistics, more sophisticated approaches, such as partial least squares (PLS) can be used to select summary statistics and reduce their dimensionality (Boulesteix and Strimmer 2006; Wegmann et al. 2009).

Currently, SpartaABC provides the integrated sequence simulator with a single tree topology. By doing so, it implicitly makes the assumption that the provided tree is the correct description of the phylogenetic relationships between the sequences in the input set. SpartaABC can be further extended to deal with tree uncertainties by sampling the tree topology from a set of possible trees. Such a set could be generated in various ways; for example, by obtaining a credible set of trees, as computed, by MrBayes (Ronquist et al. 2012) from the posterior distribution of tree topologies. Furthermore, the tree topology itself can be a parameter for SpartaABC to infer, with retained simulations reflecting more probable tree topologies concerning indel dynamics.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.