A chiral pentagonal polyhedral framework for characterizing virus capsid structures

Abstract

Recent developments of rational strategies for the design of antiviral therapies, including monoclonal antibodies (mAbs), have naturally relied extensively on available viral structural information. As new strategies continue to be developed, it is equally important to continue to refine our understanding and interpretation of viral structural data. There are known limitations to the traditional (Caspar-Klug) theory for describing virus capsid structures that involves subdividing a capsid into triangular subunits. In this context, we describe a more general polyhedral framework for describing virus capsid structures that is able to account for many of these limitations, including a more thorough characterization of inter-subunit interfaces. Additionally, our use of pentagonal subunits instead of triangular ones accounts for the intrinsic chirality observed in all capsids. In conjunction with the existing theory, the framework presented here provides a more complete picture of a capsid's structure and therefore can help contribute to the development of more effective antiviral strategies.

Understanding Viral Capsid Structural Information

The widespread availability of viral capsid structural information has played a key role in the rational engineering of novel antiviral agents. For example, recent reports have successfully demonstrated the design of monoclonal antibodies (mAbs) that target linear and conformational viral epitopes in order to neutralize viruses such as dengue and influenza [1,2]. These structure-guided approaches to effective mAb design inherently rely on the accurate determination of the atomic coordinates of viral capsid epitope residues using techniques such as x-ray crystallography and three-dimensional electron cryo-microscopy (cryo-EM) [3-8]. As researchers continue to leverage this existing structural knowledge to further develop new antiviral strategies, it is equally important to continue to refine our understanding and interpretation of viral structural data. Our current understanding of this information is naturally based deeply in the history of past approaches for describing virus capsid structures. In 1956, Watson and Crick proposed that virus capsids are built from a number of identical coat proteins (or subunits) that arrange themselves according to cubic symmetry [9]. This hypothesis was based on the observation that it would require quite a large amount of genetic material to code for a complete viral capsid, so it would be much more efficient if the capsid were composed of many identical smaller subunits. Furthermore, of the three types of cubic symmetry, tetrahedral, octahedral, and icosahedral, it was thought that the latter would be most commonly observed in such capsid structures. This is because an icosahedron would enable a capsid containing individual viral subunits of a given size to enclose the largest possible volume [10]. As more viral capsid structures were solved, it became clear that icosahedral symmetry does indeed dominate [11,12]. Of course, the requirement of icosahedral symmetry is not a rule for all virus structures as there are several viruses that do not exhibit it [12].

A capsid structure possessing icosahedral symmetry requires six five-fold symmetry axes, ten three-fold axes, and fifteen two-fold axes. For example, in a regular icosahedron, a five-fold axis passes through each vertex, a three-fold axis through each face, and a two-fold axis through each edge. If a capsid were to be composed of strictly identical subunits, the maximum number of possible subunits would be sixty, where each icosahedron face is decorated with three subunits symmetrically about the three-fold axis. However, the evidence of structures containing more than sixty subunits that furthermore are not necessarily all identical led Caspar and Klug to formulate their theory of quasi-equivalence, which allowed overall icosahedral symmetry to be preserved while relaxing the constraint of strict equivalence [10]. This theory introduced the concept of the triangulation number T=H^2+HK+K^2, where (H, K) is any pair of nonnegative integers. This number refers to the number of smaller triangles (or subunits) that are present in the full assembly.

As more capsid structures were solved, it became clear that the Caspar-Klug rules and the notion of triangulation number alone do not account for all observed icosahedral capsids [12]. For example, icosahedral capsids consisting of 120 identical subunits in theory should correspond to a triangulation number of two (T=2). However, this value of T is not permitted since there are no two integers (H, K) that solve H^2+HK+K^2=2. This type of structure is commonly observed in dsRNA viruses, including the fungal L-A virus and others [13, 14]. Other notable exceptions to the triangulation number rules include viruses of the papilloma-polyoma type, whose capsids consist of 360 subunits, corresponding to the forbidden T=6 case [15]. High-resolution structural studies show that these 360 subunits are organized as 72 pentamers located on a T=7d icosahedral lattice [15, 16]. This is not true T=7 symmetry, as that would require 420 subunits organized as 60 hexamers and 12 pentamers [17]. Therefore, this observed structure of only pentameric capsomers cannot be explained in terms of triangulation numbers and traditional Caspar-Klug theory.

A few previous efforts have been made to provide explanations for these exceptions to the traditional Caspar-Klug theory. For example, a recent extension of the Caspar-Klug theory is able to approximately predict in general the locations of viral subunits on a spherical icosahedral lattice [18]. In contrast to a lattice-based approach, an alternative polyhedral approach would be valuable since the properties of a given polyhedron's faces, including the relative orientations of two adjacent faces, would have important implications for a capsid's overall surface structure. In this vein, some other approaches have applied viral tiling methods using multiple types of shapes [19]. However, a polyhedral framework that uses only one type of subunit shape possesses an appealing simplicity that increases its potential for future use in structure determination applications.

In an attempt to develop such an applicable yet simple polyhedral framework, we first revisit the specific exceptions to the Caspar-Klug theory discussed above and note that it is not adequate to describe these exceptional capsid structures using triangular units. However, triangular units are still commonly used to represent nearly all capsids, save for a few specific models that have used trapezoids, and even these use underlying triangular scaffolds [20-22]. We consider herein some specific aspects of capsid structure that are not sufficiently described by triangles alone, focusing particularly on the orientations of inter-subunit interfaces. Motivated by these observations and the limitations of the original Caspar-Klug theory, we first develop a broad method of investigating viral capsid structures in terms of their specific associated icosahedral polyhedra that can be applied both to structures that follow the triangulation number rules and those that do not. We apply this approach to propose specific, simple solutions that provide explanations for capsid structures that are “forbidden” in the view of or cannot be explained by the triangulation number theory, including those of the L-A virus and viruses of the papilloma-polyoma type. Based on these specific analyses, we propose a general framework for describing capsid structures using pentagonal units instead of triangles, which accounts for intrinsic capsid chirality and provides a more complete characterization of inter-subunit interfaces. We suggest that this general approach can be applied to offer new insight into the details of capsid geometry, regardless of whether they follow the Caspar-Klug triangulation rules.

Polyhedral Framework for Describing Virus Capsid Structure

Though the concept of triangulation numbers is undoubtedly useful in categorizing capsid structures, a triangulation number alone does not fully characterize the geometry of a given viral capsid. Namely, it alone does not define the orientation of inter-subunit interfaces of the capsid and the relationship between subunits in the complete assembly. These interface orientations are critically relevant in order to accurately understand mAb binding to conformational epitopes, which is important both for mAb design and effective vaccine design in the context of such epitopes [23-25]. In order to ensure a complete characterization of such interfaces and the structure as a whole, a given capsid structure's associated polyhedron must be taken into account.

Nearly all of the icosahedral polyhedra that correspond to viral capsids can be classified as hexecontahedra, meaning polyhedra with sixty faces (Supp. Figure 1). There are only a few such spherical shells, namely the four Catalan-type solids: the pentagonal and deltoidal hexecontahedra, the pentakis dodecahedron, and the triakis icosahedron [26]. In addition, the rhombic triacontahedron, which has thirty faces, can be thought of as a hexecontahedron if each of the rhombic faces is divided into two triangular faces. These hexecontahedra all possess icosahedral symmetry but differ in the shapes and orientations of their faces about the 5-3-2 symmetry axes.

Different viruses with the same triangulation number can still exhibit very different surface geometries depending on the hexecontahedron that they most closely resemble. The main distinction between these icosahedral polyhedra is the degree of curvature on the five-fold and three-fold axes. In the deltoidal hexecontahedron, the geometry on the three-fold axis is nearly planar. In this case, essentially all of the curvature is contained in the five-fold axes. However, in the triakis icosahedron, the triangular faces about the three-fold axes are not perpendicular to the three-fold axis, giving that axis some curvature, which is not present in the deltoidal hexecontahedron. An example of this would be the hepatitis A virus capsid structure, which has the appearance of a facetted triakis icosahedron [27].

The other two hexecontahedra, the pentakis dodecahedron and the rhombic triacontahedron, are also distinguished by differing degrees of curvature, this time on the two-fold axes. The rhombic triacontahedron is completely planar on the two-fold axes, while the pentakis dodecahedron is bent inwards. This difference at the two-fold axes does affect the curvatures about the three-fold and five-fold axes like in the previous case, but not to as great of a degree. For example, flaviviruses such as Zika and Dengue exhibit a “herringbone” pattern of dimers that requires a planar geometry on the two-fold axis [28]. The dimers would have to bend unnaturally to accommodate a pentakis dodecahedron, which is more appropriate for other viruses such as picornaviruses (Supp. Figure 2) [29].

All of the viruses discussed above are classified as T=3 or pseudo T=3 capsids, but it is clear that they are still very structurally distinct. In this way, the association of viral capsid structures with appropriate icosahedral polyhedra reveals important geometric information that is not accounted for by the triangulation number theory. This suggests the possibility that structures that do not follow the triangulation number rules might instead be better explained in terms of an icosahedral polyhedral framework. We show that in fact this approach does provide feasible solutions to the current structural puzzles of the L-A virus and papilloma-polyoma type virus capsids, where the triangulation number theory fails to provide rational explanations or a solution.

Polyhedral Framework Applied to the L-A Virus Capsid

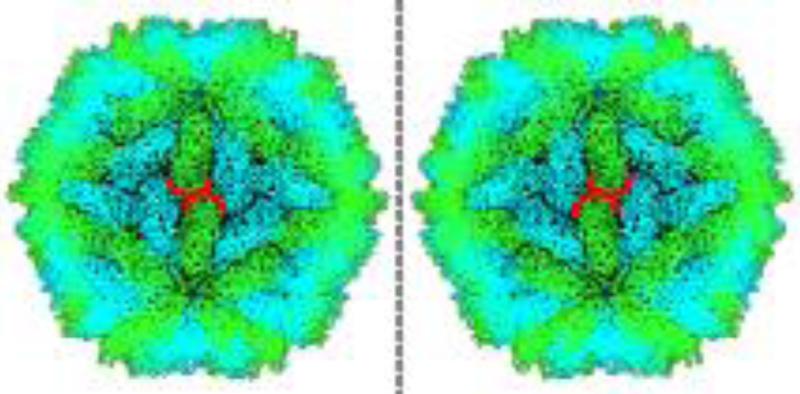
The L-A virus capsid consists of 120 subunits and therefore immediately cannot be explained by the triangulation number theory, since this corresponds to the forbidden T=2 case. However, there does exist an icosahedral polyhedron scaffold that is able to accurately describe this structure. As noted in the previous section, our search space of possible icosahedral polyhedron scaffolds for modeling virus capsids is restricted to the hexecontahedra. A particularly distinctive feature of the L-A virus capsid is its noticeably chiral assembly. This chirality is manifested in the relative “twist” between groups of subunits around adjacent five-fold symmetry axes (Figure 1). This “twist” and the resulting chirality require that any polyhedron that could potentially model this capsid must also possess intrinsic chirality. The pentagonal hexecontahedron is the only hexecontahedron that is chiral, making it the only suitable choice for the L-A virus structure.

Figure 1. The Chiral Nature of the L-A Virus Capsid.

A visualization of the actual crystal structure data is shown on the right (PDB ID: 1M1C). An artificial mirror image (“enantiomorph”) is shown on the left. The orientation of the two units outlined in red shows that the capsid assembly scaffold (indicated by the green colored subunits) possesses a definite handedness.

The pentagonal hexecontahedron has an asymmetric unit that is an irregular pentagon, defined by two lengths and two angles (Supp. Figure 3). Because of this irregularity, the full polyhedron exists in two forms, or “enantiomorphs” (Supp. Figure 4). From the location of the five-fold, three-fold, and two-fold symmetry axes in relation to the crystal structure data, the dimensions of an appropriate pentagonal asymmetric unit can be calculated (Supp. Figure 5).This pentagon shape closely fits the geometry of two adjacent subunits of the L-A virus capsid, since three of its edges align with inter-viral protein interfaces (Figure 2). This close fit in addition to appropriately describing the chirality further supports the suitability of the pentagonal hexecontahedron in describing the L-A virus capsid structure (Figure 3, Key Figure). In this way, the polyhedral approach is able to provide a rational model for a capsid structure that cannot be explained in terms of Caspar-Klug theory and triangulation numbers.

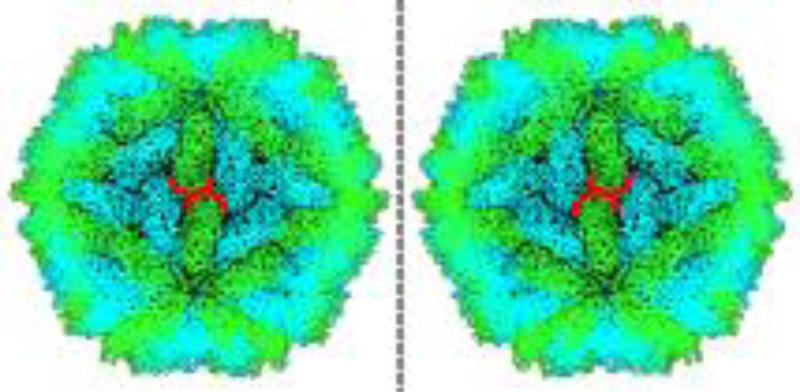
Figure 2. Pentagonal vs. Triangular Tilings.

Both images show projections of the L-A virus crystal structure viewed along a three-fold symmetry axis. The appropriate right-handed pentagonal tiling is shown on the left outlined in red, with the dashed line connecting the adjacent five-fold axes. A triangular tiling subdivided into deltoids is shown on the right, which does not capture the chiral twist of the viral subunits about the three-fold axis. The pentagonal tiling also places the two-fold axes along edges instead of at vertices, which affects the orientation of the interface at that position. The calculated dimensions of the appropriate pentagons are given in Supp. Figure 5.

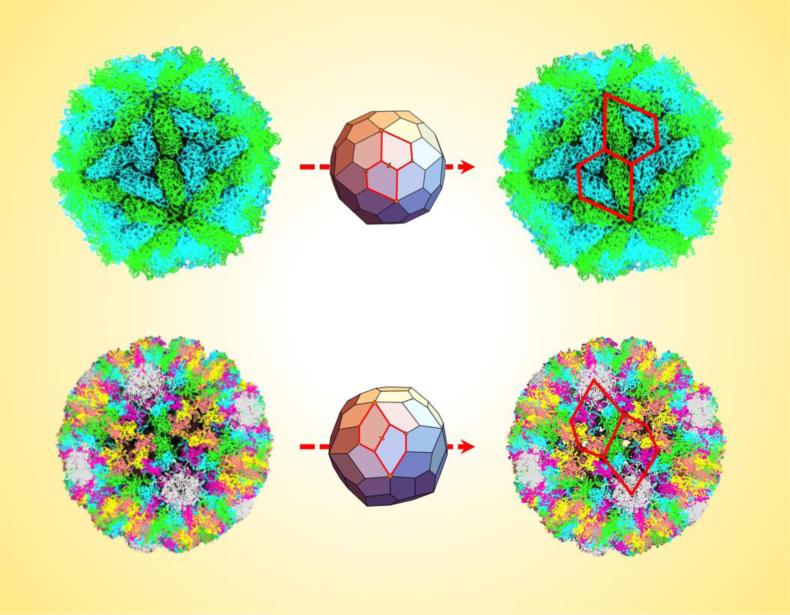
Key Figure, Figure 3. Chiral Pentagonal Frameworks Describe the L-A Virus and Polyomavirus Capsids.

The top images show how the pentagonal hexecontahedron is able to accurately capture the geometry of the L-A virus capsid (PDB ID: 1M1C) by superimposing two appropriate pentagons (outlined in red) around a two-fold axis of the assembly. Similarly, the bottom images show two units of the asymmetric pentagonal hexecontahedron superimposed on the polyomavirus capsid (PDB ID: 1SIE). In both cases, the pentagons capture the chirality and outline key viral protein subunit interfaces, thereby providing a more fitting description than triangles. The calculated dimensions of the appropriate pentagons are given in Supp. Figures 5 and 8.

Polyhedral Framework Applied to the Papilloma-Polyomavirus Capsid

The pentameric capsomers of the papilloma-polyoma type viruses are located at the vertices of a T=7 icosahedral lattice, with a total of seventy-two occupied locations. This lattice possesses an intrinsic handedness, so at a first glance it seems that the pentagonal hexecontahedron could also be suitable for describing a structure based on the T=7 lattice, again using the chirality argument. However, in the case of the polyomavirus structure, there are a few issues that make this particular pentagonal tiling unsuitable. In this case, to convert from the polyhedron model to the actual capsid, the vertices of the polyhedron would have to be “decorated” with the VP1 pentameric capsomers. A pentagonal hexecontahedron has 92 vertices so only 72 of these would be decorated with subunits or capsomers in order to reflect the polyomavirus structure. Therefore, each individual pentagon unit would need to be decorated at exactly four vertices. Due to the geometry of the pentagon unit of the pentagonal hexecontahedron, it is impossible to feasibly satisfy this decoration requirement. Let the vertices of the pentagon be labeled O, A, B, C & D (Supp. Figure 3). It would be possible to have a capsomer at O, A, and B, leaving C and D undecorated, but this would not add up to a total of 72 capsomers in the total assembly. Decorating either C or D (but not both) would give the correct total, but would not be feasible in terms of that one short inter-capsomer distance. This problem can be fixed by considering an alternate irregular pentagon unit, which can be derived from first going back to the dual of the pentagonal hexecontahedron, the Archimedean solid known as the snub dodecahedron (Supp. Figure 6).

From the snub dodecahedron, a solid or shell can be created that uses this geometry as a scaffold but ultimately consists of a spherical tiling of only one shape: an asymmetric irregular pentagon (Figure 3). Overall, the construction fixes the position of the true five-fold symmetry vertices and also adds a vertex on each three-fold axis. This vertex can remain undecorated because of its proximity to its two adjacent ones, since it would not be possible to decorate both C and D or B and D (Supp. Figure 7A). Therefore, if each vertex O, A, B, and C is decorated with a viral pentamer unit, the full assembly would include seventy-two as observed. In this way, the asymmetric pentagonal hexecontahedron would perfectly describe the geometry of the polyomavirus capsid.

Some lengths and angles can be varied, which generalizes to a family of such asymmetric irregular pentagons derived from the snub dodecahedron. In fact, these pentagons can be thought of as a combination of three triangles: two isosceles ones and the center triangle that can be of any type (Supp. Figure 7B). This results in a maximum of four different inter-capsomer distances. Any capsid arrangement of only pentamers can be described in terms of these four distances, and therefore any such arrangement can be described in terms of one of these asymmetric pentagons.

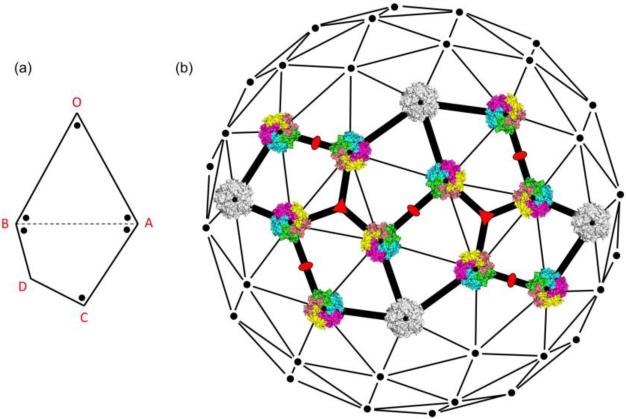
Regardless of the exact geometry of the asymmetric pentagon, the viral monomer vertex decoration will be the same in every case in order to ensure 72 pentameric capsomers (360 monomer viral protein units). In each pentagon, vertices O and C will be decorated with a single viral monomer since they are the smallest angles, vertices A and B will be decorated with two monomers since they have larger angles, and vertex D is undecorated for reasons described above, namely that the BD/CD distance is too short to support three capsomers at B, C, and D (Figure 4). If the decoration is done in this way, then there will always be five monomers at every point where three pentagons meet in the 3D assembly (at the vertices A, B & C), except at the three-fold axes (vertex D).

Figure 4. An Asymmetric Pentagon Describes the Polyomavirus Capsid.

(a) A pentagonal asymmetric unit with dots representing the locations of monomer viral protein units. Vertices are labeled O, A, B, C, and D to distinguish the different types of decorations observed (one, two, or zero monomer units). (b) The asymmetric pentagonal assembly superimposed on the 7d icosahedral lattice (adapted from Rayment et. al. [31]) along with polyomavirus capsomers (not to scale) in the appropriate orientations. The white pentamers fall on the true five-fold axes, while the colored ones fall on the pseudo five-fold axes. Other symmetry axes are denoted by orange symbols. The calculated dimensions of the appropriate pentagons are given in Supp. Figure 8.

From the available crystal structures of the polyomavirus, papillomavirus, and simian virus 40, the four relevant distances can be extracted and an asymmetric pentagon tiling can be constructed for each case. These capsids are very similar in structure, so it is not surprising that they yield very similar asymmetric pentagons. For the polyomavirus, using the crystal structure, we found that an asymmetric pentagon can be obtained by connecting the appropriate capsomers and raising the true five-fold vertex slightly (by about 10 Å) in order to put it in the same plane as the other three decorated vertices (Figure 3) [30]. A similar method can be applied to the crystal structures of the papillomavirus and simian virus 40 [32, 33]. Each pentagon has slightly different relative dimensions, but in every case the pentagon assembly is able to describe the observed geometry (Supp. Figure 8).

The Pentagonal Polyhedral Framework and Intrinsic Capsid Chirality

The two examples presented above are specific applications of the icosahedral polyhedral framework that result in solutions involving pentagonal subunits. An important facet of this pentagonal polyhedral framework is its ability to capture intrinsic capsid chirality. Chirality in virus capsids originates from the chirality of amino acids, as is the case with any protein complex. In the case of virus capsids, the overall chirality is additionally manifested by the orientations of viral subunits, as illustrated for example in Figure 1. We have shown that, in the particular case of the L-A virus, a tiling of triangles or deltoids is an inappropriate fit for the structure because it is impossible for such shapes to capture any sort of chiral assembly manifested by the subunit orientations (Figure 2). The only way to appropriately capture this chirality is to use variations of a pentagonal framework, which introduces the required asymmetries while preserving the overall icosahedral symmetry. The fact that all virus capsids are chiral in some way suggests that this approach can be readily applied to virtually any capsid. In other words, using chiral assembly scaffolds such as the pentagonal hexecontahedron and pentagonal units as structural references instead of achiral scaffolds and triangular units could lead to more accurate and complete structural information of any virus, since the latter approaches ignore this important feature of capsid structure.

Concluding Remarks

The chiral pentagonal polyhedral framework described here is able to address many of the gaps that remain in the current triangulation number theory. It can be applied to specific exceptions to the theory to offer new, simple solutions, and also has the potential for more general applications due to its ability to capture intrinsic capsid chirality. This framework, in conjunction with the existing theories, can be used to offer a more complete description of capsid substructure assemblies and inter-subunit interfaces, since many of the pentagonal unit edges fall along important such interfaces. Instead of solely relying on triangular subunits, pentagonal subunits along with the appropriate polyhedral scaffolds may be used as references to solve complete three-dimensional capsid structures and could therefore yield different relative atomic coordinates between subunits (see Outstanding Questions). A deeper understanding of viral structural information will be invaluable for the development of new antiviral approaches.

Outstanding Questions.

• Will structure-solving methods that rely on a pentagonal rather than triangular framework yield different solutions that will have biological relevance?

• How can this chiral pentagonal framework be implemented in order to solve viral capsid structures using electron cryo-microscopy?

• What are the implications of this chiral pentagonal framework when applied to all virus capsids, or even all caged proteins?

Trends Box.

• A detailed understanding of virus capsid structure, especially the relative orientations of viral subunits in the assembly, continues to be critical for effective antiviral and vaccine design.

• Though the traditional triangulation number theory used to characterize virus capsid structures is elegant and useful, notable exceptions to these rules still exist.

• The triangulation number alone does not account for all capsid features, such as interface and inter-subunit geometries, which motivates the development of additional frameworks for characterizing virus capsid structures.