Abstract
Objective
Evolution of resistance allows cancer cells to adapt and continue proliferating even when therapy is initially very effective. Most investigations of treatment resistance focus on the adaptive phenotypic properties of individual cells. We propose that the resistance of a single cell to therapy may extend beyond its own phenotypic and molecular properties and be influenced by the phenotypic properties of surrounding cells and variations in cell density. Similar variation exists in population densities of animals living in groups and can significantly affect the outcome of an external threat.
Methods
We investigate aggregation effects in cancer therapy using Darwinian models that integrate phenotypic properties of individual cells and common population effects found in nature to simulate the dynamics of resistance and sensitivity in the diverse cellular environments within cancers.
Results
We demonstrate that the density of cancer cell populations can profoundly influence response to chemotherapy independent of the properties of individual cells. Most commonly, these aggregation effects benefit the tumor allowing cells to survive even with phenotypic properties that would render them highly vulnerable to therapy in the absence of population effects.
Conclusion
We demonstrate aggregation effects likely play a significant role in conferring resistance to therapy on tumor cells that would otherwise be sensitive to treatment.
Significance
The potential rote of aggregation in outcomes from cancer therapy have not been previously investigated. Our results demonstrate these dynamics may play a key role in resistance to therapy and could be used to design evolutionarily-enlightened therapies that exploit aggregation effects to improve treatment outcomes.
Index Term: aggregation effects, cancer therapy, herd dynamics in cancer, evolution and ecology of cancer
I. INTRODUCTION
Most disseminated cancers remain fatal despite the availability of a large and growing number of potential treatments [1,2]. While first line therapy is frequently successful in reducing the tumor burden, the resulting cell death also generates intense Darwinian dynamics that select for resistant clones [3, 4]. Second, third, and fourth line therapies may be available but are typically less effective and tumor progression occurs more quickly as the cellular resistance strategies progressively broaden [5, 6]. Thus, the evolutionary dynamics that lead to therapy resistance are the proximate cause of death in most cancer patients and will likely remain so even as new agents are developed and deployed. Interestingly, Atkipis et al [7] recently found that despite this critical role of Darwinian Dynamics, evolutionary principles were cited in less than 1% of published cancer clinical trials and this has changed little in the past 3 decades.
Generally, investigations of sensitivity to therapy and evolution of resistance focus on the molecular mechanisms that produce resistant phenotypes in individual cells (e.g. P-glycoprotein, apoptosis disruption, and so-called tumor stem cells) [8–11]. Other investigations focus on molecular polymorphisms within patients as a source of variation [12]. More recently, studies have drawn attention to the spatial heterogeneity of tumors, though much of the research is focused on the subsequent genetic heterogeneity [13,14]. Here we propose the response of a cancer cell to therapy is governed both by these molecular properties, and by the properties of cells within its radius of interaction. We apply concepts from the ecology of “herd dynamics” [15,16] to the interactions of populations of tumor cells that may be phenotypically and environmentally diverse. In our model, individual cancer cells form a “herd,” or aggregation within a tumor. The number of neighbors within an aggregation is defined by the density of cells, a measure of compactness, and the interaction distance, the radius over which cancer cells influence each other.
The ecological concept of aggregation effects was initially described by Allee, who observed how increasing the size or density of a population could increase individual survival and fecundity rates [17]. While there has been virtually no formal experimental investigation of aggregation effects in cancer therapy, some observations are suggestive that these dynamics are significant. For example, size dependence in response to chemotherapy has been observed in multiple studies showing cytotoxic effects decreasing with increasing tumor cell density, often due to increased number of drug binding sites [18–21]. A recent meta-analysis demonstrated that tumor density based on diffusion-weighted MRI is a statistically significant predictor of breast cancer response to neo-adjuvant therapy [22].
Our model allows investigation of four aggregation effects: The “dilution” effect occurs when the absorption of chemotherapy drugs by one cell creates a reprieve for the others. Thus, a high density of cancer cells, each of which is absorbing multiple drug molecules, could create an intratumoral sink in which the chemotherapy drug concentration falls into the non-lethal range.
In contrast, the dense clustering of tumor cells may result in the “danger in numbers” effect as large numbers of cancer cells expressing antigenic mutant proteins may attract an increasing immune response causing inflammation that negatively affects neighboring cells even if they do not express the antigen.
The “group detoxification” effect allows the collective response of the group to an external threat to be greater than that of an individual. For example, tumor cells produce an acid environment that can confer a group benefit due to reduction in efficacy of immune response and multiple chemotherapy drugs [23–27].
Alternatively, while individual adaptations to therapy are beneficial to each cell, they may also initiate a detrimental “group sellout” effect. For example, an increased expression of membrane extrusion pumps – a common and well-studied resistance strategy in cancer [28, 29], is greatly beneficial to the individual cell, but the extrusion of drug back into the interstitial space will tend to increase the local concentration of drug for adjacent cells. In this way, large numbers of individuals essentially “sell out” their neighbors.
These four aggregation effects, dynamics that are well recognized in the evolution and ecology of herds of animals, could account for some of the complexity of tumor response and resistance to therapy. Acknowledging these aggregation effects may improve current efforts to explain evolution of resistance but more importantly could be used to design evolutionarily enlightened therapies exploiting the detrimental effects that neighboring cells may have on each other.
II. METHODS
Our model includes both the ecological dynamics of tumor cell numbers and the evolutionary dynamics of therapy resistance [30, 31]. To construct the model, we assume a population of tumor cells growing logistically and subjected to treatment-induced mortality:
where r is the cell’s growth rate in the absence of limitations, K is the carrying capacity or maximum sustainable tumor cell density, μ is cell mortality rate from the treatment, and x is the population density of tumor cells (individuals per unit tumor volume, or per area if measured from the histology of a two dimensional biopsy slice).
Cell death, μ, due to a chemotherapy regimen is a function of the drug dose, m, the lethality of the drug concentration in the absence of any resistance, 1/k, and the effectiveness of the tumor cells’ resistance strategy, b.
where v is a given tumor cell’s degree of resistance to the treatment, known as its resistance strategy or resistance phenotype. Under this expression, cell death declines as the cell’s resistance strategy value increases. The rate of decline is scaled by the effectiveness of resistance, b.
For consistency across all analyses, the initial population density is set to x = 100 corresponding to a maximum carrying capacity of Kmax = 100. The values of r, m, and k have been chosen to model a situation where treatment would be successful in the absence of the evolution of resistance; a moderate growth rate r = 0.1 and a very effective drug in the absence of resistance k = 0.1 given at a dosage m = 0.1.
The cost of increasing this resistance strategy value in our model comes as a penalty to the tumor population’s carrying capacity; K. Resources used for therapy resistance are diverted away from maintenance and proliferation, thus reducing the carrying capacity. This is perhaps best illustrated in the phenotypic cost of membrane extrusion pumps, such as P-glycoprotein described above. Prior investigations have demonstrated that up to 50% of the cell’s energy budget may be diverted to support the fixed (proteins synthesis and maintenance) and operational (pumping drugs) cost of P-glycoprotein [28,29]. For other mechanisms of resistance, the cost can be inferred by inverse reasoning. This is based on the evolutionary link between fitness and proliferation, which governs population size for each cell type. Thus, if the resistant phenotype is uncommon in the tumor population prior to therapy, we can assume that the cost of the resistance mechanism is correspondingly high and renders that population less fit than the non-resistant phenotype in the absence of therapy.
Under this formulation, carrying capacity is maximized at Kmax when the focal cell exhibits no resistance v = 0, and declines according to a Gaussian curve as the cell’s resistance strategy increases. The rate of decline is determined by . All models use to study a significant, but not severe cost of resistance.
We now incorporate the aggregation effects:
where N is the number of cells comprising the “neighborhood” that contributes to the aggregation effect experienced by a focal cancer cell. We explore two scenarios for considering neighborhood effects via the neighborhood size, N. First, we simply let N be a fixed number of neighboring cells that influence each other irrespective of total tumor size. This allows for an explicit exploration of the effects of N on population and evolutionary dynamics. As cells must presumably be in relatively close proximity for aggregation effects to occur, we chose N=5 to represent a neighborhood of only immediately adjacent cells and N=10 to study how the doubling of the interactions will affect dynamics. Second, we let N increase linearly with x. In this way N represents the tumor size and reflects the compression of cells resulting directly from overall tumor cell density, x. We also let N increase proportional to x where N = x/10 + 1. In this way a focal cell does not experience the full density of tumor’s cells, but only a percentage.
Two final parameters describe the aggregation effects fully; α and β. The term N∝ represents an “attraction” effect that renders the therapy more effective as the number of cells forming a neighborhood increases (α > 0), or less effective through collective blockage (α < 0). The term in the numerator describes a full dilution effect where one cell absorbing the treatment reduces the treatment threat to all of the neighboring cells.
In the denominator, the term Nβu represents the value of the resistance strategies of others, u, on a focal tumor cell. The term b scales the value of an individual tumor cell’s resistance strategy, v, to itself, while β scales the value of others’ resistance. Generally, it would be expected that the resistance strategy of others is less effective than the focal cell’s own resistance strategy so that b < β. In this way we have set a high effectiveness of the focal cell’s resistance strategy, b = 5, to allow for exploration of reasonable values of β. If the resistance strategy of a neighbor is in fact more valuable to a focal cell than its own this would indicate that β>b. Regardless of magnitude, β>0 models the group detoxification effect. We can model the group sell-out effect by setting β<0. With β<0, the resistance strategy of others is detrimental to the individual. Evolving resistance can make things worse for the tumor overall providing an attractive scenario for long-term therapy efficacy.
We used a total of eight combinations of α and β to explore the parameter space (Fig 1, Table 1).
Figure 1.
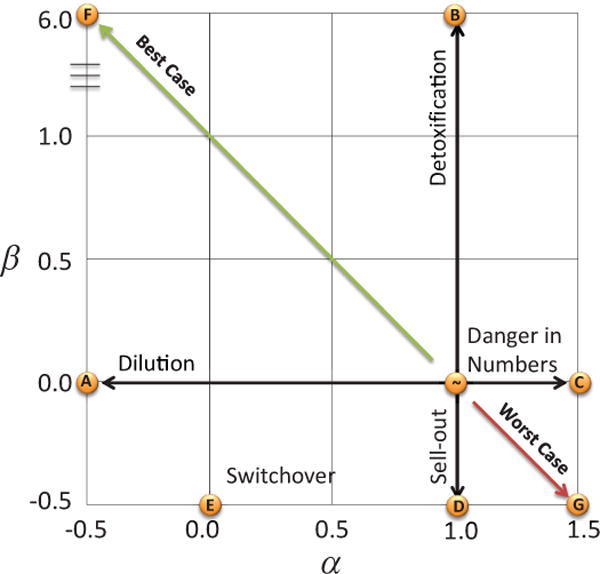
State space of Aggregation Effects. The parameters α (x-axis) and β (y-axis) define the aggregation effect state space. No cumulative aggregation effects occur at α =1 and β =0. The parameter α sweeps from beneficial dilution effects to detrimental danger in numbers while the parameter β sweeps from beneficial detoxification to detrimental group sell-out. Examples of these four pure aggregation effects are shown in models A, B, C, and D. Combinations of these aggregation effects are modeled in E, F, and G. Best and Worse Case is from the vantage point of the tumor cells, and opposite in terms of long-term treatment efficacy.
Table 1.
Model parameters. A full discussion of parameter selection is available in supplemental information.
| Parameter | Definition | Initial value | |
|---|---|---|---|
| u | Strategy (phenotype) | 0 | |
| x | Population density | 100 | |
| Kmax | Carrying capacity | 100 | |
| r | Growth rate | 0.1 | |
| m | Drug dosage | 0.1 | |
|
|
Cost of resistance | 1 | |
| b | Strategy effectiveness | 5 | |
| k | Naïve drug efficacy | 0.1 | |
| α | Aggregation parameter | [−0.5, 0, 1, 1.5] | |
| β | Aggregation parameter | [−0.5, 0, 6] | |
| N | Neighborhood size | [1, 5, x/10 + 1, 10, x] |
The fitness generating function (G-function), or combined eco-evolutionary model [32], gives the per capita growth rate of a focal tumor cell using strategy ν within a population of tumor cells described by strategy u and population density x. This yields an evolutionary game among the tumor cells as each cell’s fitness is determined by its own strategy and the strategies and population sizes of other cells. Our model of tumor growth and therapy produces the following G-function:
The Darwinian dynamics described by this G-function are utilized to build simulations that examine the short and long term efficacy of a therapy regimen. Initial conditions are set using values from Table 1, depending on the aggregation effect under study. All simulations were run in MATLAB. For each subsequent step of simulated time, the neighborhood size (if a function of population size) and the carrying capacity are first calculated using the current population size x, and current resistance strategy v, respectively. Then, the tumor cell population dynamics and resistance strategy dynamics are calculated where σ2g represents additive genetic variance and scales the speed of evolution. This process repeats until the ecological and evolutionary dynamics converge on an “evolutionarily stable strategy” (ESS). At this ESS, the system is both ecologically [(∂x/∂t) = 0] and evolutionarily stable [(∂G/∂v) = 0] at v=u* and x=x*. Comparing the values of u* and x* while varying the parameters N, α, and β allows us to investigate the consequences of different aggregation effects on therapy outcome.
III. RESULTS
We begin with a baseline model in which no aggregation effects occur by setting N = 1 for all values of α and β. Without aggregation effects, the therapy has an initial effectiveness of 99%, namely resulting in a maximal drop in tumor cell density to x′ < 1. Thereafter, individual cells evolve resistance to the drug reaching an ESS resistance strategy of u* = 0.62 and an ESS population density x* = 56.7. This represents the conventional clinical paradigm.
Figure 2 shows the values for u* (panel a) and x* (panel b) for all models. These two metrics describe the evolutionary and ecological consequences of therapy, respectively. Panel a shows the resistance strategy u* for each neighborhood size for all seven aggregation effects. The value of u* when N=1 is constant (u* = 0.62). Increases or decreases in u* from this baseline value shows whether the aggregation effect selected for more or less resistance in an individual cell, respectively. Panel b shows the population density x* for each neighborhood size for all seven aggregation effects. Again we see the value of x* when N=1 is constant (x* = 56.7). The increase or decrease of x* from the baseline shows whether the aggregation effect allowed the tumor population density to recover more or less from the treatment, respectively.
Figure 2.
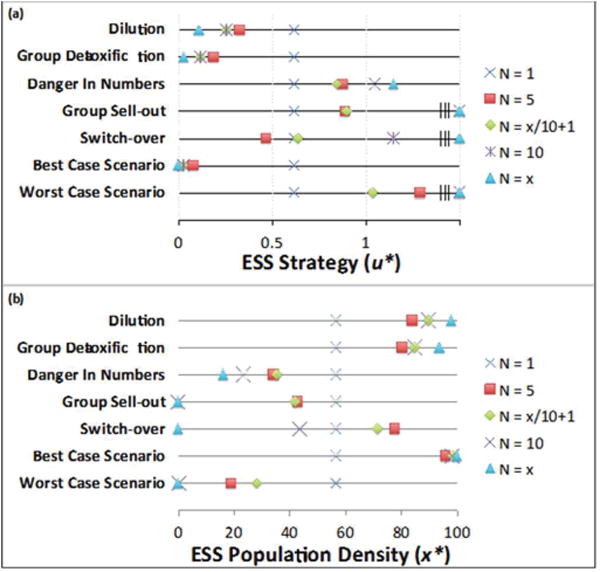
Post-therapy Evolutionary Stable Strategies and Population Densities.
Table 2 shows the exact values for u* and x* shown in figure 2 and include the minimum population density reached during therapy, x′, as an indicator of maximal therapy effectiveness.
Table 2.
Shows the exact values for u* and x* values in Figure 2 and the minimum population reached during therapy.
| FINAL | MINIMUM | ESS | |
|---|---|---|---|
| POPULATION DENSITY | POPULATION DENSITY | RESISTANCE STRATEGY | |
|
| |||
|
Dilution
| |||
| N=1 | 56.7 | <1 | 0.62 |
| N=5 | 83.9 | 41.4 | 0.33 |
| N=x/10+1 | 89.8 | 48.7 | 0.26 |
| N=10 | 89.8 | 61.5 | 0.26 |
| N=x | 97.8 | 92.5 | 0.11 |
|
| |||
|
Group Detoxification
| |||
| N=1 | 56.7 | <1 | 0.62 |
| N=5 | 80.4 | 36.6 | 0.19 |
| N=x/10+1 | 84.7 | 34.2 | 0.12 |
| N=10 | 84.9 | 36.8 | 0.12 |
| N=x | 93.7 | 36.8 | 0.03 |
|
| |||
|
Danger in Numbers
| |||
| N=1 | 56.7 | <1 | 0.62 |
| N=5 | 34.2 | <1 | 0.88 |
| N=x/10+1 | 35.5 | 1.8 | 0.85 |
| N=10 | 23.6 | <1 | 1.05 |
| N=x | 16.2 | <1 | 1.15 |
|
| |||
|
Group Sellout
| |||
| N=1 | 56.7 | <1 | 0.62 |
| N=5 | 43.0 | <1 | 0.89 |
| N=x/10+1 | 42.0 | <1 | 0.90 |
| N=10 | 0 | 0 | – |
| N=x | 0 | 0 | – |
|
| |||
|
Switchover
| |||
| N=1 | 56.7 | <1 | 0.62 |
| N=5 | 77.7 | 33.6 | 0.47 |
| N=x/10+1 | 71.5 | 35.1 | 0.64 |
| N=10 | 43.8 | 36.6 | 1.15 |
| N=x | 0 | 0 | – |
|
| |||
|
Best Case Scenario for tumor cells (worst case for treatment efficacy)
| |||
| N=1 | 56.7 | <1 | 0.62 |
| N=5 | 95.9 | 78.8 | 0.08 |
| N=x/10+1 | 98.6 | 91.6 | 0.03 |
| N=10 | 98.4 | 91.4 | 0.03 |
| N=x | 99.9 | 99.6 | 0.002 |
|
| |||
|
Worst Case Scenario for tumor cells (best case for treatment efficacy)
| |||
| N=1 | 56.7 | <1 | 0.62 |
| N=5 | 19.0 | <1 | 1.29 |
| N=x/10+1 | 28.4 | <1 | 1.04 |
| N=10 | <1 | <1 | 5.55 |
| N=x | 0 | 0 | |
A. Dilution Effects
The dilution effect is modeled by setting α = 0 and β = 0
Here the effective per tumor cell dose m of chemotherapy is divided by the neighborhood size, N. A possible example is seen in pancreatic cancer cells where gemcitabine is metabolized by deoxcytidine kinase [33] resulting in the local removal of the drug by individual cell resistance mechanisms. In this way, each cancer cell absorbs and eliminates some of the therapy treatment while still experiencing toxic effects.
As the neighborhood size increases through the four formulations for N, the required resistance strategy of the cells, u*, declines and the tumor population density, x*, recovers more completely. In other words, because of aggregation effects, each cell needs to invest fewer resources in drug resistance permitting greater substrate availability for proliferation and survival. The dilution effects seen in our model are consistent with measured inoculum effects that have been observed in cancer treatment (34–36).
Interestingly, as compared to a fixed neighborhood size N, when neighborhood size is related to population density, the model predicts a more precipitous drop in tumor cell density and a more rapid increase in cell densities as the ESS level of resistance evolves. This is because with initial population loss, the neighborhood size is smaller, and therefore the tumor cannot benefit from the dilution effects as readily during this time. These intermediate population size and resistance dynamics leading up to the ESS are shown in the supplemental information.
B. Group Detoxification
In nature, the “many eyes” aggregation effect occurs when group vigilance increases the protection of the individual to attacks by predators. In response to therapy, individual tumor cells can produce substances that diffuse into the tumor and benefit the entire group. We name this “group detoxification” as the beneficial “eyes” of neighboring tumor cells occur through their resistance strategy of neutralizing the therapy. For example, most cells in prostate cancer are dependent on exogenous testosterone for survival and growth. Thus, initial therapy removes testosterone from the circulation through “chemical castration.” However, a common adaptation is upregulation of CYP 17 hydroxylase, which allows the cell to produce testosterone [37, 38]. As a result of testosterone release into the tumor interstitium, the initial testosterone-dependent population can re-emerge and contribute to tumor progression. Similarly, the efflux of protons seen in many tumor cells to create an acidic microenvironment can globally benefit the tumor population by decreasing the immune response and/or decreasing the efficacy of some chemotherapy drugs [39–42].
This group detoxification effect to overcome the “predatory” effect of therapy can be modeled by setting α = 1 and β = 6 (model B) so that:
In this case where β > b (b = 5), the resistance strategies of other members of the population are more beneficial than that of the individual cell. Similar to the dilution effect, we find that as the neighborhood size increases, cells will survive even when they possess a level of resistance that would ordinarily (i.e. in the absence of group effects) not protect them against the lethal effects of therapy. As demonstrated in Fig 4, a resistance level u* = 0.62 evolves when each individual operates in isolation (N=1), but in the presence of a group cells with much lower levels of resistance (e.g. u* = 0.19 when N=5) will survive.
With group detoxification, as the neighborhood size increases, the initial effectiveness of the therapy declines (x′ increases) and the ESS level of resistance, u*, declines, while the new equilibrium population density, x*, increases. For a given neighborhood size of N ≥ 2, increasing the magnitude of group detoxification, β, will result in an increase in x′ and x*, and a decrease in u*.
C. Danger in Numbers
The above examples show how aggregation effects benefit the tumor cells, but of more importance, our model can also show when aggregation or group size effects actually enhance the effectiveness of therapy. For instance, if high cell density is associated with higher blood vascularity, then drug delivery will be positively associated with cell density, or neighborhood size. Similarly, death of a neighboring cancer cell within a tumor might enhance antigen presentation thus rendering tumor cells with larger numbers of neighbors more prone to attack by immune cells [43]. This aggregation effect results in “danger in numbers” to the tumor cells and enhances therapy effectiveness. To model a danger in numbers effect, we set α = 1.5 and β = 0 (model C) resulting in:
Here we see the opposite of the dilution effect. The effective per tumor cell dose m of chemotherapy becomes multiplied by the neighborhood size, N0.5. This requires each focal cell to evolve higher levels of resistance to the same dosage of drug m, as shown with increasing ESS values of u*. The ESS equilibrium population density, x*, decreases due to the cells diverting more resources from proliferation to cope with the therapy.
Interestingly, as compared to a fixed neighborhood size N, when neighborhood size is related to population density, the model predicts a less precipitous drop in tumor cell density in early treatment. This may seem paradoxical. But, because therapy efficacy declines with neighborhood size, as the population falls the tumor cells gain a reprieve from the detrimental aggregation effect. Low population sizes actually protects the tumor cells from danger in numbers. When N = x, this reprieve is not possible as the neighborhood size is always relatively large.
D. Group Sellout
Another example of when aggregation or group size effects actually enhance the effectiveness of therapy relative to no aggregation effects may occur when cancer cells evade therapy by extruding drugs through membrane pumps [44]. Individual cells with high levels of membrane pump activity return the drug into the interstitial space where it can “attack” neighboring cells. This leads to a game of “hot potato” in which energy must be expended by the tumor cells to constantly bat the drug molecule from its immediate vicinity into that of a neighbor. While this resistance strategy may ultimately be destructive to the whole population of tumor cells, it can be favored by natural selection. The eco-evolutionary dynamics will strongly favor maximal expression of membrane transporter and, counter-intuitively, rapid evolution of high levels of drug resistance within the population.
The group sellout effect can be modeled by setting α = 1 and β = −0.5 (model D) resulting in
In this case where β < 0, the evolution of resistance of other members of the population increases the cell death term μ. This effect is two-fold because this negative term only grows as population size increases, making μ even larger. With group sell-out, as the neighborhood size increases, the initial effectiveness of the therapy increases (x′ declines) and the ESS level of resistance, u*, increases, while the new equilibrium population density, x*, decreases.
Group sellout results in the first successful therapy outcome of this model when N ≥ 10 as seen with x* going to zero (complete elimination of the tumor). The decline in x with therapy provides the tumor cells minimal reprieve when . When the relationship between N and x is particularly strong (N = x) the tumor population is rapidly eradicated under a group sellout.
E. Mixed aggregation effects
The aggregation effects resulting directly from the neighborhood size (dilution and danger in number effects) or from spillover effects from the neighbors’ resistance strategy (group detoxification and group sellout) are not mutually exclusive and may operate simultaneously within a tumor or perhaps differently in different regions of the same tumor because of spatial heterogeneity in blood flow and cell density. Furthermore, cancer therapy increasingly combines different drugs and different treatment regimens to maximize tumor response. Our model can be used to examine combinations resulting from crossing the dilution or danger in number effects effect with the group detoxification or group sellout effects.
Consider a therapy in which both dilution and group sellout effects occur. This might consist of a mixed tumor population in which some phenotypes are highly vulnerable to therapy (producing a dilution effect) while other phenotypes are resistant because of membrane extrusion pumps that efflux the drug back into the environment so that it can adversely affect other cells (the group sell-out effect). This can be modeled by setting α = 0 and β = −0.5 (model E) resulting in
When the neighborhood is relatively small, increasing tumor cell density renders therapy less effective because the dilution effect predominates. This is seen when N = 5 and where the neighborhood effects are still sufficiently small that the beneficial dilution effect exceeds the detrimental (β = −0.5) group sell-out effects. However, as neighborhood size increases further, N ≥ 10, therapy is increasingly effective because group sell-out dynamics exceed the dilution effect. So with a dilution and group sellout effect, increasing neighborhood sizes results in an increase and then decrease in x′ and x*, and a decrease and then increase in u*.
Next we consider a combination of dilution effect and group detoxification effect by setting α = −0.5 and β = 6 (model F) resulting in
Clinically, this combination might be observed in, for example, pancreatic cancer cells that both metabolize gemcitabine [37] (the usual first line therapy) and excrete acid [45, 46] that can detoxify other chemotherapeutic drugs. This combination causes the interests of the group and the interests of individual tumor cells to align creating conditions ripe for a growing tumor and ultimate loss of therapy efficacy. Even with the small neighborhood size of N = 5 the drug results only in a 4% reduction in cell density and a remarkably low required resistance strategy. Further increase in neighborhood size only results in more drastic decreases in therapy efficacy.
Finally, consider a combination of danger in numbers and group sell-out by setting α = 1.5 and β = −0.5 (model G) resulting in
In this case, the interests of an individual run doubly against the interests of the group. This is the most favorable scenario for short-term and long-term therapy efficacy (worst-case for the tumor). Natural selection operating on individual tumor cells to evolve resistance can work towards the ruin of the tumor. As a kind of Prisoner’s Dilemma, the individual tumor cells at their ESS are primarily “defending” themselves against the resistance strategies of their neighbors (an indirect effect of therapy) rather than to the therapy directly. Once N reaches 10 the therapy eradicates the tumor.
Again we see that gives the most reprieve from the combination of detrimental aggregation effects because the population density can minimize the neighborhood size during early treatment. In this way, when , the tumor can survive even though the final population density is <1% and the required resistance is extremely high.
IV. CONCLUSION
It has long been recognized that the therapeutic response of mouse xenografts and human cancer (the former being much smaller than the latter) can differ significantly. Furthermore, clinical observations find that larger and acidic tumors respond less well than smaller ones [44–47]. While there are undoubtedly many factors that govern these dynamics, we propose that aggregation effects may be among them. Specifically, we hypothesize that the high density of individual cancer cells, may produce “herd effects” in which the interaction among the members of the group alter the outcomes of an applied perturbation. That is, the response of an individual cancer cell to an externally applied therapy may be altered by its interactions with neighboring cells. Because of this, the outcome of the perturbation may be substantially different than expected based on the phenotypic properties of the cell alone.
A number of potential aggregation effects may occur in a cancer population. The dilution and group detoxification effects permitted individual tumor cells to survive therapy with lower levels of resistance than would be necessary in the absence of group effects. The resulting decrease in phenotypic cost of resistance permitted more rapid proliferation and diminished both the amplitude and time of tumor response to treatment. This would manifest clinically as reduced response (based on change of tumor size) and faster time to progression. Danger in numbers and group sell-out aggregation effects were deleterious to the cancer cells. In this case group effects enhanced therapy efficacy and resulted in tumors that appear non-resistant, even though the actual resistance level of an individual cell will be remarkably high. Group-sellout effects resulted in the most successful therapy outcomes.
Mixes of the aggregation effects can result in group size effects where therapy is either most effective or least effective at intermediate neighborhood sizes. Finally, combinations of aggregation effects can result in the best-case scenario for a growing tumor where dilution and group detoxification protect the tumor from therapy but also can result in the worst-case scenario for growing tumors where danger in numbers and group-sellout effects cause the cells to defend themselves against the resistance strategies of their neighbors. Danger in numbers and group sell-out aggregation effects have the potential to enhance the efficacy of therapy and represent dynamics that could be exploited in cancer treatment strategies.
While the evolutionary unit of selection is the individual cancer cell, the interactions among the cells can affect the response of these individuals to a global external perturbation such as therapy. Such density-dependent dynamics, or aggregation effects, are well recognized in the evolution and ecology of groups of animals and we examined their potential effects in cancer.
The incorporation of aggregation effects into tumor response to therapy may improve current efforts to explain evolution of resistance and more importantly could be used, as outlined above, to design evolutionarily-enlightened treatment strategies exploiting the detrimental effects of large groups of cancer cells. We conclude that experimental investigation to test model predictions and develop more accurate parameter estimates is warranted.
Supplementary Material
Acknowledgments
This work is supported by NIH grants U54CA143970-1 and RO1CA170595, a grant from the James S. McDonnell Foundation, and European Commission, Marie Sklodowska-Curie Actions Research and Innovation Staff Exchange (RISE) SEP-210251279
Footnotes
DATA AND SOFTWARE
All software, data, and supplemental figures can be found at the following location:
https://github.com/cunninghamjj/Aggregation-Effects-in-Cancer
Contributor Information
Joel S. Brown, Cancer Biology and Evolution Program. Moffitt Cancer Center, Tampa, FLDepartment of Biological Sciences & Cancer Center, University of Illinois at Chicago, IL
Jessica J. Cunningham, Cancer Biology and Evolution Program. Moffitt Cancer Center, Tampa, FL
Robert A. Gatenby, Cancer Biology and Evolution Program at Moffitt Cancer Center, Tampa, FLDepartment of Integrated Mathematical Oncology, Moffitt Cancer Center, Tampa FL
References
- 1.Crawford S. Is it time for a new paradigm for systemic cancer treatment? Lessons from a century of cancer chemotherapy. Front Pharmocol. 2013;4:68. doi: 10.3389/fphar.2013.00068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gatenby RA. A change of strategy in the war on cancer. Nature. 2009;459:508–509. doi: 10.1038/459508a. [DOI] [PubMed] [Google Scholar]
- 3.Greaves M, Maley CC. Clonal evolution in cancer. Nature. 2012;481:306–313. doi: 10.1038/nature10762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Merlo LM, Pepper JW, Reid BJ, Maley CC. Cancer as an evolutionary and ecological process. Nat Rev Cancer. 2006;6:924–935. doi: 10.1038/nrc2013. [DOI] [PubMed] [Google Scholar]
- 5.Keats JJ, Chesi M, Egan JB, Garbitt VM, Palmer SE, et al. Clonal competition with alternating dominance in multiple myeloma. Blood. 2012;120:1067–1076. doi: 10.1182/blood-2012-01-405985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Silva AS, Gatenby RA. A theoretical quantitative model for evolution of cancer chemotherapy resistance. Biol Direct. 2010;5:1745–6150. doi: 10.1186/1745-6150-5-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aktipis CA, Kwan VS, Johnson KA, Neuberg SL, Maley CC. Overlooking evolution: a systematic analysis of cancer relapse and therapeutic resistance research. PLoS One. 2011;6:e26100. doi: 10.1371/journal.pone.0026100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Binkhathlan Z, Lavasanifar A. P-glycoprotein inhibition as a therapeutic approach for overcoming multidrug resistance in cancer: current status and future perspectives. Curr Cancer Drug Targets. 2013;13:326–346. doi: 10.2174/15680096113139990076. [DOI] [PubMed] [Google Scholar]
- 9.Abbaszadegan MR, Foley NE, Gleason-Guzman MC, Dalton WS. Resistance to the chemosensitizer verapamil in a multi-drug-resistant (MDR) human multiple myeloma cell line. Int J Cancer. 1996;66:506–514. doi: 10.1002/(SICI)1097-0215(19960516)66:4<506::AID-IJC14>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- 10.Futscher BW, Foley NE, Gleason-Guzman MC, Meltzer PS, Sullivan DM, et al. Verapamil suppresses the emergence of P-glycoprotein-mediated multi-drug resistance. Int J Cancer. 1996;66:520–525. doi: 10.1002/(SICI)1097-0215(19960516)66:4<520::AID-IJC16>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- 11.Karthikeyan S, Hoti SL. Development of Fourth Generation ABC Inhibitors from Natural Products: A Novel Approach to Overcome Cancer Multidrug Resistance. Anticancer Agents Med Chem. 2015 doi: 10.2174/1871520615666150113103439. [DOI] [PubMed] [Google Scholar]
- 12.Oliveira AL, Rodrigues FF, Santos RE, Aoki T, Rocha MN, et al. GSTT1, GSTM1, and GSTP1 polymorphisms and chemotherapy response in locally advanced breast cancer. Genet Mol Res. 2010;9:1045–1053. doi: 10.4238/vol9-2gmr726. [DOI] [PubMed] [Google Scholar]
- 13.Gerlinger M, Rowan AJ, Horswell S, Larkin J, Endesfelder D, et al. Intratumor heterogeneity and branched evolution revealed by multiregion sequencing. N Engl J Med. 2012;366:883–892. doi: 10.1056/NEJMoa1113205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sottoriva A, Spiteri I, Piccirillo SG, Touloumis A, Collins VP, et al. Intratumor heterogeneity in human glioblastoma reflects cancer evolutionary dynamics. Proc Natl Acad Sci U S A. 2013;110:4009–4014. doi: 10.1073/pnas.1219747110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Parrish JK, E-KL Complexity, pattern and evolutionary trade-offs in animal aggregation. Science. 1999;284:99–100. doi: 10.1126/science.284.5411.99. [DOI] [PubMed] [Google Scholar]
- 16.Eftime RdV G, Lewis MA. Complex spatial group patterns result from different animal communication mechanisms. Proceedings of the National Academy of Science, USA. 2006;104:6974–6979. doi: 10.1073/pnas.0611483104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Allee WCB E. Studies in animal aggregations: mass protection against colloidal silver among goldfishes. Journal of Experimental Zoology. 1932;61:185–207. [Google Scholar]
- 18.Steel GG, Adams K, Stanley J. Size dependence of the response of Lewis lung tumors to BCNU. Cancer Treat Rep. 1976;60:1743–1748. [PubMed] [Google Scholar]
- 19.Kobayashi H, Takemura Y, Ohnuma T. Relationship between tumor cell density and drug concentration and the cytotoxic effects of doxorubicin or vincristine: mechanism of inoculum effects. Cancer Chemother Pharmacol. 1992;31:6–10. doi: 10.1007/BF00695987. [DOI] [PubMed] [Google Scholar]
- 20.Ohnuma T, Arkin H, Holland JF. Effects of cell density on drug-induced cell kill kinetics in vitro (inoculum effect) Br J Cancer. 1986;54:415–421. doi: 10.1038/bjc.1986.192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kobayashi H, Takemura Y, Holland JF, Ohnuma T. Vincristine saturation of cellular binding sites and its cytotoxic activity in human lymphoblastic leukemia cells: mechanism of inoculum effect. Biochem Pharmacol. 1998;55:1229–1234. doi: 10.1016/s0006-2952(97)00615-1. [DOI] [PubMed] [Google Scholar]
- 22.Wu LM, Hu JN, Gu HY, Hua J, Chen J, et al. Can diffusion-weighted MR imaging and contrast-enhanced MR imaging precisely evaluate and predict pathological response to neoadjuvant chemotherapy in patients with breast cancer? Breast Cancer Res Treat. 2012;135:17–28. doi: 10.1007/s10549-012-2033-5. [DOI] [PubMed] [Google Scholar]
- 23.Warburg O, Wind F, Negelein E. THE METABOLISM OF TUMORS IN THE BODY. J Gen Physiol. 1927;8:519–530. doi: 10.1085/jgp.8.6.519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Warburg O. Origin of cancer cells. Oncologia. 1956;9:75–83. [PubMed] [Google Scholar]
- 25.DeClerck K, Elble RC. The role of hypoxia and acidosis in promoting metastasis and resistance to chemotherapy. Front Biosci (Landmark Ed) 2010;15:213–225. doi: 10.2741/3616. [DOI] [PubMed] [Google Scholar]
- 26.Gatenby RA, Gawlinski ET. The glycolytic phenotype in carcinogenesis and tumor invasion: insights through mathematical models. Cancer Res. 2003;63:3847–3854. [PubMed] [Google Scholar]
- 27.Gatenby RA, Gawlinski ET, Gmitro AF, Kaylor B, Gillies RJ. Acid-mediated tumor invasion: a multidisciplinary study. Cancer Res. 2006;66:5216–5223. doi: 10.1158/0008-5472.CAN-05-4193. [DOI] [PubMed] [Google Scholar]
- 28.Shen F, Chu S, Bence AK, Bailey B, Xue X, et al. Quantitation of doxorubicin uptake, efflux, and modulation of multidrug resistance (MDR) in MDR human cancer cells. J Pharmacol Exp Ther. 2008;324:95–102. doi: 10.1124/jpet.107.127704. [DOI] [PubMed] [Google Scholar]
- 29.Gottesman MM, Fojo T, Bates SE. Multidrug resistance in cancer: role of ATP-dependent transporters. Nat Rev Cancer. 2002;2:48–58. doi: 10.1038/nrc706. [DOI] [PubMed] [Google Scholar]
- 30.Ale SB, Brown JS. The contingencies of group size and vigilance. Evol Ecol Res. 2007;9:1263–1276. [Google Scholar]
- 31.Cunningham JJ, Gatenby RA, Brown JS. Evolutionary dynamics in cancer therapy. Mol Pharm. 2011;8:2094–2100. doi: 10.1021/mp2002279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vincent TL, BJS . Evolutionary game theory, natural selection, and Darwinian dynamics. Cambridge, UK: Cambridge University Press; 2005. [Google Scholar]
- 33.Sebastiani V, Ricci F, Rubio-Viqueira B, Kulesza P, Yeo CJ, Hidalgo M, et al. Immunohistochemical and genetic evaluation of deoxycytidine kinase in pancreatic cancer: relationship to molecular mechanisms of gemcitabine resistance and survival. Clin Cancer Res. 2006;12(8):2492–7. doi: 10.1158/1078-0432.CCR-05-2655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bulitta JB, Ly NS, Yang JC, Forrest A, Jusko WJ, et al. Development and qualification of a pharmacodynamic model for the pronounced inoculum effect of ceftazidime against Pseudomonas aeruginosa. Antimicrob Agents Chemother. 2009;53:46–56. doi: 10.1128/AAC.00489-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bhagunde P, Chang KT, Singh R, Singh V, Garey KW, et al. Mathematical modeling to characterize the inoculum effect. Antimicrob Agents Chemother. 2010;54:4739–4743. doi: 10.1128/AAC.01831-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fioramonti MC, Evans VJ, Earle WR. The effect of inoculum size on proliferation of NCTC strain 2071, the chemically defined medium strain of NCTC clone 929 (strain L) J Natl Cancer Inst. 1958;21:579–583. [PubMed] [Google Scholar]
- 37.Mostaghel EA, Marck BT, Plymate SR, Vessella RL, Balk S, Matsumoto AM, et al. Resistance to CYP17A1 inhibition with abiraterone in castration-resistant prostate cancer: induction of steroidogenesis and androgen receptor splice variants. Clin Cancer Res. 2011;17(18):5913–25. doi: 10.1158/1078-0432.ccr-11-0728. Epub 2011/08/03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.de Bono JS, Logothetis CJ, Molina A, Fizazi K, North S, Chu L, et al. Abiraterone and increased survival in metastatic prostate cancer. N Engl J Med. 2011;364(21):1995–2005. doi: 10.1056/NEJMoa1014618. Epub 2011/05/27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.DeClerck K, Elble RC. The role of hypoxia and acidosis in promoting metastasis and resistance to chemotherapy. Front Biosci (Landmark Ed) 2010;15:213–25. doi: 10.2741/3616. [DOI] [PubMed] [Google Scholar]
- 40.Sauvant C, Nowak M, Wirth C, Schneider B, Riemann A, Gekle M, et al. Acidosis induces multi-drug resistance in rat prostate cancer cells (AT1) in vitro and in vivo by increasing the activity of the p-glycoprotein via activation of p38. Int J Cancer. 2008;123(11):2532–42. doi: 10.1002/ijc.23818. [DOI] [PubMed] [Google Scholar]
- 41.Thews O, Gassner B, Kelleher DK, Gekle M. Activity of drug efflux transporters in tumor cells under hypoxic conditions. Adv Exp Med Biol. 2008;614:157–64. doi: 10.1007/978-0-387-74911-2_19. [DOI] [PubMed] [Google Scholar]
- 42.Wojtkowiak JW, Verduzco D, Schramm KJ, Gillies RJ. Drug resistance and cellular adaptation to tumor acidic pH microenvironment. Mol Pharm. 2011;8(6):2032–8. doi: 10.1021/mp200292c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Scheffer SR, Nave H, Korangy F, Schlote K, Pabst R, et al. Apoptotic, but not necrotic, tumor cell vaccines induce a potent immune response in vivo. Int J Cancer. 2003;103:205–211. doi: 10.1002/ijc.10777. [DOI] [PubMed] [Google Scholar]
- 44.Correnti M, Cavazza ME, Guedez N, Herrera O, Suarez-Chacon NR. Expression of the multidrug-resistance (MDR) gene in breast cancer. J Chemother. 1995;7(5):449–51. doi: 10.1179/joc.1995.7.5.449. [DOI] [PubMed] [Google Scholar]
- 45.Shannon AM, Bouchier-Hayes DJ, Condron CM, Toomey D. Tumour hypoxia, chemotherapeutic resistance and hypoxia-related therapies. Cancer Treat Rev. 2003;29(4):297–307. doi: 10.1016/s0305-7372(03)00003-3. [DOI] [PubMed] [Google Scholar]
- 46.Wojtkowiak JW, Verduzco D, Schramm KJ, Gillies RJ. Drug resistance and cellular adaptation to tumor acidic pH microenvironment. Mol Pharm. 2011;8(6):2032–8. doi: 10.1021/mp200292c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Suzuki C, Bloomquivs L, Sundin A, Jacobsson H, Bystrom P, Berglund A, Nygren P, Climelius The initial change in tumor size predicts response and survival in patients with metastatic colorectal cancer treated with combination chemotherapy. Annals of Oncology. 2011 doi: 10.1093/annonc/mdr350. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


