Sparse multidimensional iterative lineshape-enhanced (SMILE) reconstruction of both non-uniformly sampled and conventional NMR data

Abstract

Implementation of a new algorithm, SMILE, is described for reconstruction of non-uniformly sampled two-, three- and four-dimensional NMR data, which takes advantage of the known phases of the NMR spectrum and the exponential decay of underlying time domain signals. The method is very robust with respect to the chosen sampling protocol and, in its default mode, also extends the truncated time domain signals by a modest amount of non-sampled zeros. SMILE can likewise be used to extend conventional uniformly sampled data, as an effective multidimensional alternative to linear prediction. The program is provided as a plug-in to the widely used NMRPipe software suite, and can be used with default parameters for mainstream application, or with user control over the iterative process to possibly further improve reconstruction quality and to lower the demand on computational resources. For large data sets, the method is robust and demonstrated for sparsities down to ca 1%, and final all-real spectral sizes as large as 300 Gb. Comparison between fully sampled, conventionally processed spectra and randomly selected NUS subsets of this data shows that the reconstruction quality approaches the theoretical limit in terms of peak position fidelity and intensity. SMILE essentially removes the noise-like appearance associated with the point-spread function of signals that are a default of five-fold above the noise level, but impacts the actual thermal noise in the NMR spectra only minimally. Therefore, the appearance and interpretation of SMILE-reconstructed spectra is very similar to that of fully sampled spectra generated by Fourier transformation.

Introduction

With the introduction of ever stronger magnetic fields and high sensitivity cryogenic probes, the minimum time needed for recording multi-dimensional NMR data is often dictated by the number of time increments in the indirect dimensions required for reaching adequate spectral resolution. In fact, with increased field strengths it becomes more demanding, in terms of the number of time steps needed, to take full advantage of the higher spectral resolution intrinsically available. Although this problem can be mitigated by replacing the many phase cycling steps commonly used to reduce spectral artifacts by pulsed field gradients (Bax and Pochapsky 1992), even at a single scan per increment the total measurement time required for recording three- and four-dimensional NMR spectra at the highest possible resolution, limited only by transverse relaxation rates, often is unreasonably long.

A widely used solution to this problem takes advantage of the fact that NMR spectra consist of discrete resonances and are often quite sparse, i.e., the number of spectral components is many orders of magnitude smaller than the total number of data points in the final multi-dimensional spectrum. In this case, instead of relying on simple discrete Fourier transformation (FT), the frequency domain spectrum can be reconstructed from a much smaller number of time domain data points by using iterative or other nonlinear methods that include a regularizing term, as the relation between time and frequency domain data is no longer unique. A large variety of reconstruction algorithms and protocols, largely adapted from different scientific disciplines, have become widely used in the NMR community. The most popular and broadly used procedures are those that record a randomly or pseudo-randomly chosen subset of the very large number of increments required for a complete, on-grid, fully sampled multi-dimensional NMR spectrum. This approach is an extension of the proposal to use exponential sampling in the indirect dimension, first introduced in the NMR community some 30 years ago (Barna et al. 1987) to obtain enhanced resolution in the indirect frequency dimension.

The main problem with generating a full frequency domain spectrum from an incomplete set of time domain data is that it simply is not possible to uniquely generate N* frequency domain points from fewer than N* time domain data. Moreover, a simple discrete Fourier transformation (FT) requires a discrete equi-spaced time domain signal as input. However, a range of sensible regularizers can be used to find the “most reasonable” solution for transforming the time domain data into a frequency domain spectrum. These include the use of maximum entropy algorithms (Barna et al. 1987; Delsuc and Tramesel 2006; Mobli et al. 2007; Balsgart and Vosegaard 2012; Hoch et al. 2014), compressed sensing techniques such as iterative soft thresholding methods (Hyberts et al. 2012, 2013) and others (Holland et al. 2011; Kazimierczuk and Orekhov 2011; Bostock et al. 2012). The aim of these, and a host of other algorithms that have been demonstrated for NMR applications, is to minimize either the l1, l2 or Gaussian l0 norm of the frequency domain (Stern et al. 2007; Stern and Hoch 2015; Sun et al. 2015). Other intuitively appealing methods are based on an iterative algorithm to stepwise remove the point-spread function (PSF) artifacts caused when a regular FT is applied to a matrix where the not-sampled, on-grid data points have simply been replaced by zeros, one effective example being the Signal Separation Algorithm (SSA) (Stanek and Kozminski 2010). Alternatively, removal of PSF artifacts in the frequency domain can be accomplished by iterative algorithms such as FFT-CLEAN (Coggins and Zhou 2008; Werner-Allen et al. 2010) and SCRUB (Coggins et al. 2012), the latter being particularly effective for highly sparse data. The above methods and a range6 of ingenious related methods have been extensively discussed in a host of recent reviews (Coggins et al. 2010; Kazimierczuk et al. 2010; Orekhov and Jaravine 2011; Hoch et al. 2014; Mobli and Hoch 2014). We note that, from a practical perspective, these methods are rather different from ideas such as projection methods (Eghbalnia et al. 2005), GFT (Kim and Szyperski 2003), or the powerful multi-dimensional decomposition method (Orekhov et al. 2003), which aim to extract the information most relevant to the spectroscopist from cleverly chosen combinations of time domain data, thereby providing practical access to higher-dimensional (>4) NMR spectroscopy methods (Bermel et al. 2013; Piai et al. 2014) such as 6D APSY (Fiorito et al. 2006).

The non-linear aspect of processing NUS NMR data has given rise to much confusion regarding the intrinsic signal-to-noise (S/N) merits of non-uniform sampling (NUS), and despite clear warnings to the contrary (Yoon et al. 2006), the improved visual display of non-linearly processed data is often interpreted as improved sensitivity. Without lack of generality, when assuming a single signal to be on resonance, its intensity can simply be calculated from the sum of its exponentially decaying time domain signal. Data points closest to the origin have the highest time domain S/N; however, the signal frequency is encoded in the phase of the free induction decay (FID), which increases linearly with t while its amplitude decays with exp(−t/T₂). The derivative of this function with respect to t is zero for t = T₂, meaning that the phase (i.e., frequency) information is optimally sampled at t = T₂. Another important consideration is that, in the presence of noise, resolving two signals that differ in frequency by less than ca 1/(2T_acq), where T_acq is the duration of the acquisition time, is generally not feasible by any of the above analysis methods. In practice it even can be challenging to separate components separated by as much as 1/T_acq. Therefore, the discussion of sensitivity and resolution attainable with different sampling protocols and different reconstruction methods is quite complex (Rovnyak et al. 2004; Hyberts et al. 2010; Bostock et al. 2012). One common misconception, that NUS allows more transients per increment and thereby improves the S/N of the reconstructed spectrum, is analogous to the idea that narrowing the spectral window in an indirect dimension allows more averaging per increment, which was clearly refuted over 30 years ago (Levitt et al. 1984). Although, at least in principle, it is possible to gain a modest amount in S/N by sampling the decaying signal in the indirect time dimensions more densely at earlier time points, results shown below indicate that such sampling protocols may result in decreased accuracy of peak positions and widths.

The present study describes implementation of SMILE, a NUS reconstruction method that can be used directly as a plug-in to the popular NMRPipe program. One aim is to provide a simple and robust method for processing NUS data, while allowing the user flexibility to deviate from default settings for less common applications, such as resolution enhancement (Stern et al. 2007), extreme dynamic range data, limited computational resources, etc. A second aim is to provide output data that remain visually as close as possible to the appearance of regular fully sampled FT data, without non-linear treatment of noise. In spirit, SMILE is closest to the SSA algorithm (Stanek and Kozminski 2010), but the actual implementation is rather different in terms of peak detection and reconstruction, and takes advantage of the fact that NMR spectra can be phased to become purely absorptive. Taking advantage of this phase information has been used previously to enhance the results of linear prediction algorithms (Zhu and Bax 1990), and for constructing a “virtual echo” which was shown to benefit a range of sparse data reconstruction methods (Mayzel et al. 2014). A noteworthy feature of SMILE, which simultaneously benefits spectral resolution and sensitivity, is the automatic extension of the time domain by non-sampled data, which are treated just like the randomly non-sampled data during SMILE reconstruction. This mode of processing removes truncation artifacts without requiring undue apodization of actual experimental data at the end of the sampled time domain, an idea first introduced in spectral processing by Stern et al. (2007). Note that this mode of processing is equally beneficial to both conventional fully sampled data and NUS data.

Description of the computational approach

Expansion, conversion, and processing prior to the reconstruction

The SMILE algorithm has been implemented as a new processing function of the widely used NMRPipe program (Delaglio et al. 1995). In the usual workflow, non-uniformly sampled multidimensional time-domain data is first sorted and subsequently expanded to fill the not-sampled points with zeros using utilities in NMRPipe. This is a particular convenience, because the sorted and expanded NUS data can then first be treated by ordinary Fourier processing schemes. These generally yield results which are sufficient to establish and confirm processing details such as phase correction prior to performing a more time-consuming NUS reconstruction. In the case of SMILE, knowledge of the phase correction values for the indirect dimensions is used during the reconstruction.

The input for SMILE processing is the sorted and expanded NUS data, with the directly detected dimension processed in the usual way, with apodization, zero fill, and phase correction, and with the imaginary part then discarded. A subset range of the directly detected dimension may be extracted, as is commonly done for amide-detected data. The NMRPipe pipeline data format is sequential, and multidimensional processing proceeds by way of matrix transpositions. Prior to processing with SMILE, data are transposed so that the directly detected dimension becomes the final (slowest varying) dimension. The output of SMILE is a new fully sampled interferogram. This output can then be processed and analyzed by the same schemes used for conventional uniformly sampled data.

It is important to note that, unlike many other NUS reconstruction programs, SMILE reconstructs the data as one single spectrum rather than by treating each cross section orthogonal to the detected axis separately and independently. While the whole-spectrum approach increases the computational burden and memory space requirements, it critically helps to preserve the line shape in the directly detected dimension, particularly for weak resonances. In the faster, commonly used slice-wise approaches, reconstruction of the weaker signals in slices taken adjacent to the center of the peak in the detected dimension is suboptimal and can cause line shape distortion. Note that in a chunk-wise approach, described below in more detail, we can reduce memory demand for 4D reconstructions by reducing the chunk size to as little as three adjacent cubes in the F₄ dimension, and still perform a whole-spectrum reconstruction.

Initiation of SMILE processing

A SMILE reconstruction uses data sorted and expanded as described above, with zeros inserted for the not-sampled points. As with other NMRPipe processing functions, SMILE extracts its parameters from command line arguments, prepares its workspace, and then reads one complex vector at a time from the sequential pipeline stream of input data. In the case of SMILE, the entire spectral data matrix is initially read this way prior to further reconstruction.

The various steps of the SMILE reconstruction procedure are schematically illustrated in Fig. 1. Each iteration starts with an interferogram already transformed in the direct dimension, and with all the not-sampled points set to zero. During each iteration, the data are fully Fourier transformed, the strongest peaks are identified, and the peak information is filtered according to selection criteria. The parameters of the peaks selected are used to simulate corresponding time-domain signals, which are then subtracted from the interferogram used as input for the start of the iteration. The process is repeated, and iteration stops when the highest point in the Fourier transformed residual falls below a target value. The accumulated synthetic time-domain signal and final time domain residual are used to generate a fully sampled interferogram as output.

Fig. 1.

Flow chart of the SMILE NUS reconstruction procedure. The input data read by SMILE must be already sorted and expanded by tools in NMRPipe (e.g. nusExpand.tcl, and vdExpand.tcl) and the direct dimension must be processed first in the usual way. Prior to reconstruction iterations, SMILE performs once-only time domain operations as needed to the indirect dimensions, such apodization, negation of imaginaries, sign alternation, and zero order phase correction. Details regarding the other steps are provided in the main text

Before iteration begins, SMILE performs any time domain manipulations for the indirect dimensions which only need to be performed once, rather than repeated during each iteration. This includes apodization, zero order phase correction (which can be applied in the time domain), and sign manipulations such as negation of an imaginary component of the data, which is sometimes required to reverse the direction of a dimension in the frequency domain. If first order phase correction of a given dimension is required, this is instead performed in the frequency domain during each iteration, rather than as part of this once-only time domain processing, since it is difficult to perform the equivalent of a frequency domain linear phase correction in the time domain. The special exception to this case is for first order phase correction that is an exact integral multiple of 360°, i.e., a shift by an integral number of time points. In these special cases, we can optionally shift the sampling schedule in the corresponding dimension by one or more points during the NUS data expansion and the SMILE reconstruction, as an alternative to applying the corresponding first order phase correction. Once all preliminary data manipulation has been completed, SMILE internally retains only the experimentally sampled points in order to reduce memory space requirements, removing the points filled with zeros during the NUS expansion.

Converting observed line widths to time domain decay factors

A key aspect of SMILE is the interpretation of observed frequency domain line widths from a Fourier-processed spectrum in terms that allow generation of corresponding synthetic time domain signals that are a good match for the measured data. SMILE assumes that the underlying time domain signals are exponentially decaying sinusoids that after FT can be phased to be uniformly absorptive, whereas glitches, noise spikes and the like generally do not have these features, partially suppressing their reconstruction. Apparent peak width depends on the apodization functions used as well as on the sampling schedule, particularly when the sampling is not random but exponentially weighted. The various factors affecting observed line width in the frequency domain make it challenging to use the apparent line width to extract an accurate estimate of the transverse relaxation rate, R₂, for the corresponding time domain exponential decay, exp(−R₂ t). Even if good estimates for the transverse relaxation rates in each dimension are available, in practice, residuals remaining after a given SMILE iteration may appear as sharp or broad lines, requiring a range of different R₂ rates to closely match the overall signals.

To address the issue of relating apparent frequency domain signal parameters to the time domain, SMILE establishes a calibration between observed peak width in the apodized Fourier spectrum and the exponential decay of a corresponding synthetic signal in the time domain. To accomplish this, SMILE simulates a series of time-domain data sets by using a range of input R₂ values, with default values of R₂ stepping from 1/(4T_acq) to 3/T_acq, where T_acq is the acquisition time in that dimension. For example, in the case of the three indirect dimensions of a 4D data set using default settings, SMILE creates 30 3D cubes with each cube containing one peak, and with the R₂ for the peak in all 3 dimensions increasing linearly from the first to the last cube. As a result, for each of the three indirect dimensions, there are 30 apparent line widths corresponding to the 30 different input R₂ values. In addition, to calibrate line widths in the direct dimension, 30 1D spectra are generated, with each spectrum containing one peak of increasing width, yielding 30 R₂-linewidth pairs. The acquisition times and spectral widths in the simulated cubes and the 1D spectra are identical to the experimental values in each dimension, and the data are apodized using the same set of window functions used on the measured data. To include the potential effect of the sampling pattern on the peak shape, SMILE applies the same NUS sampling schedule to each simulated indirect cube prior to FT. In the end, a relation table between the R₂ values used in the simulation and the apparent peak widths is established. This R₂-linewidth relation table is used to correct the apparent peak width before each signal is reconstructed, thereby significantly improving the accuracy of the reconstruction at each iteration.

Processing and analysis of the indirect dimensions

After the preliminary processing and analysis of the input NUS data as described above has been completed, a SMILE iteration begins by resetting the not-sampled points of the NUS interferogram to zero, performing requisite zero filling, FT, and any first order phase correction in each indirect dimension, with imaginary components discarded after phasing. The FT of the indirect dimensions is generally the slowest step of a SMILE iteration. Optimization of this step is therefore important. In SMILE, Fourier processing is parallelized using the openMP multithreading library (OpenMP Architecture Review Board 2011), providing strong performance enhancement on multi-core CPUs, which are now ubiquitous, as well as on multi-CPU clusters.

Although only the all-real spectrum is eventually used for signal analysis, during the processing the intermediate frequency domain data remains hypercomplex. In the case of 4D data, this requires eight times (not 16, because the direct dimension is real only) more space than the final all-real spectrum, which can be prohibitively large. To address this issue, we implement the above mentioned chunk-wise strategy, which allows SMILE to run with a minimal array space sufficient for only one chunk, consisting of N ≥ 3 hypercomplex indirect cubes. These cubes correspond to adjacent cross sections orthogonal to the Fourier transformed F₄ axis of the 4D data set, and N is chosen by the program to be as large as possible for the user-specified memory size. The 4D data are then analyzed in overlapping groups of N sequential cubes, where each group overlaps by one cube with the previous group. Local maxima within each cube are tallied, and the results from each overlapping group of adjacent cubes are collated to identify points which are greater than all of their immediate neighbors in all dimensions. If these points meet the selection criteria, they are classified as peaks. This overlapping chunk-wise approach allows SMILE to run with no significant adverse impact on speed or performance when memory space is limited, since only N cubes need to be held in memory at any one time. More importantly, the entire 4D data set is still reconstructed seamlessly as one single spectrum rather than as individual planes or cubes, resulting in an improved lineshape in the direct dimension.

Peak detection and selection

Peak detection and filtering is a key step during the iterative NUS reconstruction process. Criteria used will impact not only the speed of the reconstruction, but also the quality of the final reconstructed spectrum. Failure to identify strong to moderate peaks will result in incomplete reconstruction and lead to larger residual NUS artifacts, while picking false peaks or noise slows down the reconstruction and can artificially lower the apparent noise level. Accepting too few peaks for reconstruction at each iteration increases the total number of iterations and therefore the time of the reconstruction, while accepting too many peaks for each iteration decreases the overall accuracy of the reconstruction. Ideally, only the most intense peaks remaining above a certain threshold should be reconstructed in each iteration. However, recognizing that peaks of comparable height that are separated by more than one line width in the direct dimension do not interfere substantially with one another, SMILE selects for reconstruction a set of peaks that are the strongest locally, i.e., within a small number of adjacent indirect cubes whose frequency span is at least equal to the direct dimension line width. This approach maximizes the number of peaks that can be reliably reconstructed in each iteration.

The process by which SMILE selects the peaks used for full time domain reconstruction is now described. Although the discussion below focuses on the case of a 4D spectrum, treatment of lower dimensional spectra is fully analogous, and simply requires substitution of “cube” by “two- or one-dimensional cross section orthogonal to the detected axis” for 3D and 2D spectra, respectively, unless otherwise noted.

First, the maximum number of peaks that can be simultaneously reconstructed in each cube is estimated using the following empirical equation:

$$\mathrm{M}=1+\text{sqrt}(\mathrm{K}/10),$$

where M is the maximum number of peaks allowed for each cube, and K the total number of experimentally sampled 1D FIDs (i.e., 8 and 4 times the number of selected points on the indirect sampling grid for 4D and 3D, respectively). For 2D data, M is always set to 1.

At each iteration, peaks are identified and selected according to these criteria:

1. A point can only be classified as a peak if it is a local maximum, i.e., it is greater than all immediately neighboring points in all dimensions.

2. Peaks weaker than intensity threshold f * I_max are excluded for the current iteration. Here, f is a user adjustable parameter with the default value of 0.80, and I_max is the largest intensity in the cube.

3. The intensity of the highest point and all its immediately neighboring points in all dimensions for a peak also must be higher than at least s times the thermal noise level of the spectrum. Here, s is a user adjustable parameter with a default value of 5, and an automated noise estimate is used unless a value is supplied by the user.

4. Selected peaks must be separated from each other by at least 2/T_acq in at least one dimension. For pairs of peaks separated by less than 2/T_acq, the stronger one is selected.

Peak analysis

Although conceptually the SMILE algorithm is analogous to the SSA method (Stanek and Kozminski 2010; Stanek et al. 2012), the actual implementation is quite different and represents a compromise between processing speed and optimal reconstruction. For example, SSA defines a sophisticated multidimensional peak boundary and then performs a least squares nonlinear fitting or, for overlapping peaks, a Hilbert Transform followed by an inverse FT to obtain the corresponding time-domain signal. In contrast, SMILE simply estimates the peak’s position, width, and height from the highest data point and its immediate neighbors in all dimensions. When the SMILE calibration scheme for relating observed frequency domain parameters to time-domain parameters is employed, the observed peak height, position, and width provide a good approximation of the amplitude, frequency, and R₂ of the corresponding time domain signal. We find that this approach is fast and generally quite robust. Importantly, as our analytical method only uses the three highest data points in each dimension for each peak, these most intense points are fractionally least impacted by the point spread function of other, not yet reconstructed signals in the spectrum. If reconstruction of a given peak is incomplete because height, position, or R₂ contain small errors, the effect of this “imperfection” is corrected in later iterations, where the difference between the true time domain signal and the reconstructed signal is treated as a new, independent time domain signal. In practice, a very intense peak may be reconstructed as several overlapping peaks, spaced very closely in the frequency domain, but typically with amplitudes that differ by about an order of magnitude from one another.

Signal reconstruction

To reconstruct the hypercomplex time/frequency domain signals for the selected peaks, SMILE generates a complex 1D FID for each dimension corresponding to an exponentially decaying sinusoid function with the extracted frequency, signal amplitude, and R₂. If a particular indirect dimension was recorded using constant- or mixed-time (Ying et al. 2007), the exponential function exp(−R₂ t) is either not applied to its FID, or only after the point where non-constant-time incrementation starts. These FIDs are subsequently apodized and their first points are scaled, depending on the linear phase in the corresponding dimension (Otting et al. 1986; Zhu et al. 1993). The complex vector for the directly detected dimension is then zero-filled and Fourier transformed to match the details of the measured data, and its imaginary component is discarded. For computational efficiency, the 4D time domain signal for any signal component is generated by first calculating 2D hypercomplex planes, consisting of vector outer products between the synthetic 1D FIDs for the first two dimensions, and between the FID for the third dimension and the 1D spectrum for the direct dimension. The 4D hypercomplex matrix is then reconstructed from the matrix outer product between each pair of the above 2D planes. The 4D signal for each peak is finally added to the matrix already constructed for the other peaks in the current and previous iterations. This step is highly parallelized, and the matrix reconstruction time for up to hundreds of peaks per iteration is generally small compared to the time needed for FT.

Calculation of the residuals and iteration of steps 4–8

For the data points selected on the NUS sampling schedule, the reconstructed value for each peak is subtracted from the experimentally sampled data, while the not-sampled points remain set to zero prior to the FT of the next iteration. The resulting difference matrix then represents the residuals obtained after the strongest peaks are removed. As a result, the artifacts associated with the point spread functions of these strong peaks are also suppressed, which allows the weaker peaks or residuals to be reconstructed in the new iteration starting from step 4 above. SMILE iterations continue until there are no peaks remaining above the threshold (the default threshold being five times the noise) or the maximum number of iterations defined by the user is reached.

Downscaling of the reconstructed signals

After completion of the above iterative process, SMILE down-scales the sum of the reconstructed signals by a value that is close to the sparsity of the sampled data before adding the reconstructed signals to the residual experimental data. The actual scaling factor used depends on the sampling protocol and the decay rate of the time domain signals, and is calculated from an on-resonance simulated time-domain signal of unit amplitude, having an R₂ estimated from the average line width of the peaks selected in the first iteration, with each dimension apodized using the same window function that was applied to the experimental data. The scaling factor is then determined as the sum of the intensities for only the sampled data points divided by the corresponding sum of all the points. This factor is very close to the sampling sparsity, if the sampling is random. For an exponentially weighted sampling list, with more data points sampled at the beginning of the time domain signal, the scaling factor can be noticeably higher than the sparsity. Conversely, the default extension of the reconstructed signals in each indirect dimension can significantly decrease the scaling factor, because the sum of all points becomes larger while the sum of the sampled points remains unchanged. Note that the choice of the apodization functions also impacts this scaling factor somewhat. For this reason, the reconstructed data SMILE outputs remain apodized. Note that an error in the scaling factor only changes the amplitude of all reconstructed signals relative to those of the below-threshold signals and the thermal noise. In practice, such errors are well below 10%.

The residual experimental data, again with its not-sampled points set to zeros, is added to the downscaled reconstructed time-domain signal. Downscaling of the reconstructed signals maintains the linearity of peak intensities in the reconstructed NUS spectrum. As a result, even if weak peaks are not included in the SMILE reconstruction, their heights remain perfectly valid when compared to those of the reconstructed peaks. Moreover, the noise in the final reconstructed spectrum is simply that of the originally Fourier transformed time domain matrix (with zeros for the not-sampled data points), but with the “noise-like” point-spread functions of the intense signals removed. Unless the user explicitly instructs SMILE not to make extensions, the output data is of larger size than the expanded input NUS data, but with its not-sampled points including the extended ones replenished by the scaled reconstructed values and the sampled points replaced by the sum of the residual and the scaled reconstructed time domain signal. This approach insures continuity of the time domain signals used to replace the not-sampled points, and also captures all of the signal originally present in the measured data. After SMILE is applied, the indirect dimensions can be finally processed by the same schemes used for conventional data, but no longer require apodization which is already included in the SMILE step.

Results and discussion

Illustration of a 1D reconstruction

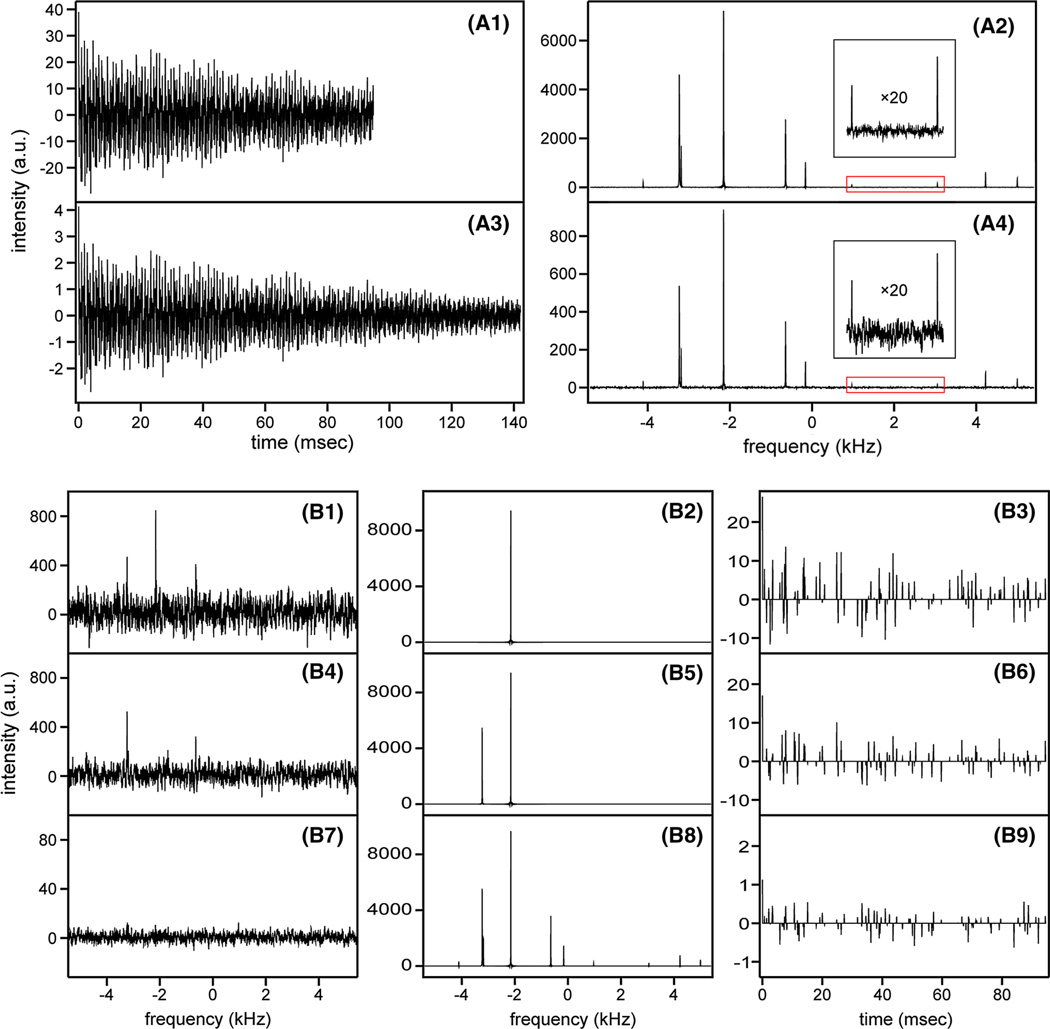
Although SMILE can only be applied to multi-dimensional data, we demonstrate its operation by selecting a one-dimensional cross section through a synthetic 2D data set, generated to approximately mimic an F₁ cross section through a 2D NOESY spectrum. Figure 2A1, A2 show the fully sampled time domain cross section and its FT, and similarly, A3 and A4 show its reconstructed 10% sampled time domain and FT, displayed on a vertical scale that is expanded by a factor of 10 to yield intensities comparable to the fully sampled FID.

Fig. 2.

An illustration of SMILE reconstruction. A 94.8-ms FID with ten signal components at randomly selected frequencies (within the spectral window of 10,803 Hz) was generated using the simTimeND program in the NMRPipe software suite, with random T₂ values (ranging from 67 to 172 ms). Amplitudes of the signals differed stepwise by factors of 1.63, yielding a ratio of 80:1 between the intensities of the strongest and weakest signals. The fully sampled time domain consists of 1024 complex data points and Gaussian noise was added such that the weakest peak in the fully sampled spectrum has a signal-to-noise ratio of 25:1. The fully sampled data were processed conventionally in NMRPipe and a randomly selected 10% fraction of the time domain data was reconstructed using SMILE. A1 The original fully sampled simulated FID. A2 The regular FT spectrum, obtained by processing the data of A1. A3 The final reconstructed FID generated by SMILE, including the default 50% extension of the time domain. A4 The reconstructed spectrum obtained by processing the FID of A3. B1 Fourier transform of the sparse FID. B2 FT of the reconstructed time domain after the first iteration (using the default 50% extension of the time domain); B3 the residual FID after the reconstructed time domain signal (FT shown in B2) is subtracted from the original sparse FID (sampled points only, and the 50% extension is therefore not shown). B4 Fourier transform of the sparse FID of B3. B5 FT of the reconstructed time domain after the second iteration and B6 residual FID after the reconstructed time domain (FT shown in B5) is subtracted from the original sparse FID. B7–B9 Analogous to B4–B6, but after the 13th iteration, where no signal above the noise threshold is detected. Note that data from different iterations are shown on expanded Y scales. The Fourier transform of B9, summed with the scaled synthetic spectrum of B8, yields the final NUS spectrum of A4. The NMRPipe processing script is included as Supplementary Material, and the entire simulated and processed data set can be downloaded at http://spin.niddk.nih.gov/bax/software/SMILE/

Clearly, the not-sampled points, set to zero before applying the FT, give rise to noise-like characteristics in the frequency domain (Fig. 2B1). In the first iteration, SMILE detects the strongest peak after FT, parametrically estimates its height, frequency and width from the spectral data point of largest amplitude and its two immediate neighbors. It then calculates for an on-resonance signal what amplitude of the time domain signal, with known decay constant, is needed to yield the amplitude observed in panel B1, and generates the (fully sampled) time domain data, for which the corresponding synthetic resonance is shown in Fig. 2B2. Note that only the time domain data is calculated by SMILE, and its FT is shown here only to illustrate the successive steps in the program. SMILE then subtracts the synthetic time domain data from the original sampled time domain data (Fig. 2B3). FT of this residual time domain data, from which the most intense spectral component has been removed, yields a spectrum with reduced PSF “noise”, which allows reliable parameterization of the second strongest resonance (Fig. 2B4). After removal of the time domain component of this second resonance, the procedure is applied to the next strongest resonance, and then repeated until no resonance stronger than five (default) times the root-mean-square noise remains (Fig. 2B9). The final reconstructed time domain then is generated by co-adding all the synthetic time domain data generated during the various iterative steps to the residual of the last iteration, where no peak above the noise threshold was detected. Note that the synthetic time domain signals need to be downscaled prior to co-adding them, to account for the sparsity of the time domain and the distribution of the time domain points (see step 9 in the above description of the computational approach for how this scaling factor is generated; 0.0898 for the example of Fig. 2).

As can be seen from the vertical scale in Fig. 2A4, the signal intensity in the 10% sampled spectrum is approximately 10-fold lower than in the fully sampled spectrum (A2), and the noise is lower by about a factor of 3 (note the difference in vertical scale axis), meaning that the apparent S/N of the NUS-processed spectrum is more than threefold lower compared to the fully sampled spectrum. Although some studies have suggested dramatically improved S/N for NUS data, this is largely a result of non-linear processing. As an example, for the case of random sampling, points in a fully sampled FID could be separated into 10 independent NUS FIDs, so that each one is sampled at 10% density and contains independent thermal noise. This allows reconstruction of 10 NUS-spectra with uncorrelated thermal noise, and their co-addition cannot improve the S/N over that of the regular FT spectrum. This means that each of the NUS spectra must have a S/N that is at least √10 lower than in the fully sampled spectrum. Modest gains can be made by using non-random selection of the sampling points, e.g. exponential sampling (Barna et al. 1987), but any intrinsic gain from such a choice is competing with residual “noise” from imperfect NUS reconstruction, i.e., imperfect removal of the PSF noise. Moreover, non-random sampling schedules that enhance S/N can have an adverse impact on the accuracy at which frequencies can be extracted, alter the peak line shapes in the sparsely sampled indirect dimensions prior to the reconstruction, and introduce a level of coherence in the PSF noise distribution. The SMILE line shape simulation routine largely accounts for these effects, allowing reasonably accurate reconstruction regardless of the sampling schedule.

Amplitude, line width and frequency fidelity of simulated data

We demonstrate the fidelity of amplitudes, line widths and frequencies of SMILE-reconstructed NUS data for both simulated and experimental data.

For the simulations, we generated ten separate 2D data sets that each contain 100 well separated columns with ten cross peaks whose intensities varied exponentially by factors of 1.63, to yield a dynamic range of 80:1 between the most intense and weakest signal at any given F₂ frequency. Essentially, the reconstruction of each spectrum corresponds to the reconstruction of 100 of the spectra used for the example of Fig. 2. For the 10 simulated data sets, the full t₁ time domain had a 94.8 ms duration and a spectral width of 10,803 Hz corresponding to 1024 complex data points, from which 10% were chosen following different variations on the random sampling protocols. T₂ values of the F₁ frequency components ranged from 60 to 127 ms and frequencies in the F₁ dimension were chosen randomly, but with separations of at least 200 Hz, except for the most intense and third weakest peaks, whose separation was fixed at 23 Hz in order to evaluate how well the algorithm can reconstruct a weak peak in the immediate vicinity of a much more intense peak. The noise level of the fully sampled spectrum is adjusted to yield a S/N of 21 for the weakest peak after cosine bell (0°–86°) apodization and zero filling to 8192 data points. Different 10% random NUS sampling schedules are generated for each of the ten 2D data sets, using five different schemes, including fully random sampling, T₂ weighted sampling (generated using the exponential sampling scheme in MddNMR (Orekhov and Jaravine 2011)), three different Poisson gap sampling schemes described by Hyberts et al. (2010) with no weight or with a weight of sin(θ), where the angle θ ranges from 0 to π/2 and from 0 to π. The intrinsic S/N of these 10% sampled spectra is √10 lower than for the fully sampled data set, but to allow quantitative comparison we also generated a fully sampled data set with all signals attenuated by √10, i.e., a S/N of ~7 for the weakest peaks. Both reconstructions by SMILE and istHMS extend the indirect time domain from 94.8 to 142.2 ms, and the reference peak position, line width and peak height are extracted from the noise-free fully sampled simulated data with the t₁ time domain matching the extended NUS data, which is critical particularly for the calculation of the NUS line width RMS deviations.

It is important to note that in all non-linearly processed NMR data sets, including SMILE, the definition of S/N becomes invalid, even if the noise retains its regular noise-like appearance. Rather than reporting the apparent S/N, we therefore evaluate the quality of spectral reconstructions in a manner that corresponds to what a user typically may wish to do: peak picking each of the 2D spectra at an intensity threshold level where 20–25% of the detected signals are spurious. For the detected true signals, comparison to the frequency, line width, and intensity parameters from the noise-free spectra shows the quality of the reconstructed data, while the number of missing signals shows the fraction that was not recognized at the intensity cutoff used during peak picking. Results obtained with SMILE are summarized in Table 1, and can be compared to results of the unextended fully sampled data set, simulated with the √10 weaker signals. All errors in heights, frequencies, and widths are reported relative to those of the noise free, fully sampled data set.

Table 1.

RMSD in SMILE peak position, width, and height, as well as the average height deviation relative to the noise-free, fully sampled reference data^a

Peak	Relative height	Fully sampledb	Randomc	T2 weightedc	Sine-weigthed poisson gapc
					θ: 0–π/2	θ: 0–π	no wt
RMSD in peak position (Hz)
1	1.0	0.720	0.753	0.984	2.236	1.051	0.809
2	1.6	0.418	0.488	0.615	1.798	0.613	0.542
3d	2.7	2.491	0.535	1.059	2.083	1.233	0.891
4	4.3	0.163	0.203	0.306	0.868	0.263	0.252
5	7.0	0.109	0.140	0.200	0.558	0.171	0.166
6	11.4	0.074	0.095	0.128	0.325	0.117	0.112
7	18.6	0.052	0.067	0.090	0.223	0.069	0.084
8	30.2	0.048	0.054	0.072	0.166	0.053	0.058
9	49.2	0.043	0.049	0.065	0.134	0.040	0.051
10	80.0	0.008	0.032	0.061	0.102	0.029	0.037
RMSD in peak width (Hz)
1	1.0	0.915	1.024	1.096	1.162	0.940	1.091
2	1.6	0.534	0.742	0.876	1.129	0.664	0.801
3d	2.7	1.378	0.737	1.856	2.519	2.110	1.125
4	4.3	0.197	0.418	0.531	0.879	0.310	0.468
5	7.0	0.128	0.311	0.420	0.717	0.209	0.341
6	11.4	0.075	0.227	0.313	0.506	0.140	0.253
7	18.6	0.046	0.159	0.235	0.409	0.093	0.178
8	30.2	0.029	0.123	0.165	0.300	0.074	0.126
9	49.2	0.018	0.100	0.145	0.216	0.052	0.118
10	80.0	0.011	0.089	0.159	0.176	0.048	0.109
RMSD in peak height relative to reference height (%)
1	1.0	14.0	16.9	18.7	33.1	18.2	17.5
2	1.6	9.1	13.6	14.2	26.1	14.3	14.0
3d	2.7	5.3	7.2	7.5	12.3	11.4	6.8
4	4.3	3.5	5.8	7.0	15.4	7.4	6.3
5	7.0	2.1	3.8	5.1	11.7	4.9	4.0
6	11.4	1.3	2.5	3.5	8.2	3.1	2.9
7	18.6	0.8	1.6	2.5	6.3	2.2	1.7
8	30.2	0.5	1.2	1.9	4.6	1.5	1.2
9	49.2	0.5	0.9	1.6	3.2	1.1	1.1
10	80.0	0.2	0.6	1.1	2.0	0.6	0.7
Average deviation in peak height relative to reference height (%)
1	1.0	2.5	−3.3	−1.1	17.0	−1.3	−4.0
2	1.6	0.3	−4.5	−3.7	6.8	−3.9	−4.8
3d	2.7	−0.3	−1.1	−1.9	−3.9	−6.1	−1.7
4	4.3	−0.2	−2.0	−2.1	−2.4	−3.0	−2.1
5	7.0	0.1	−1.5	−1.7	−3.8	−2.4	−1.1
6	11.4	0.1	−1.0	−1.1	−3.7	−1.5	−0.8
7	18.6	−0.2	−0.6	−0.7	−3.0	−1.1	−0.3
8	30.2	0.0	−0.2	−0.3	−1.7	−0.8	−0.1
9	49.2	−0.4	−0.0	0.0	−0.8	−0.5	0.1
10	80.0	0.0	−0.0	0.0	−0.0	−0.0	0.0
Missing peaks		0.1%	0.7%	0.5%	1.4%	0.9%	1.0%

^aThe time domain input data can be downloaded from http://spin.niddk.nih.gov/bax/software/SMILE, and all the scripts used for the simulation and reconstructions are included as Supplementary Material

^bSimulated fully sampled data set (t₁ = 94.8 ms) with the peak intensity scaled down by √10 and the deviations calculated from the data sets with and without the RMS noise added

^cCompared to the 142.2 ms (50% longer t₁) fully sampled noise-free data to match the 50% extended acquisition time in the F₁ dimension of the final SMILE spectra. Poisson gap sampling schemes as defined by (Hyberts et al. 2010). T₂-weighted exponential sampling scheme using the NUS sampler provided in MddNMR (Orekhov and Jaravine 2011)

^dThis peak was always placed 23 Hz away from the strongest peak (#10)

As can be seen in Table 1, even though an exponentially weighted random sampling scheme yields a slightly lower fraction of missing peaks (0.5 vs 0.7%), exponential sampling yields about 20% larger errors in peak position and line width compared to random sampling. It is particularly noteworthy that random sampling significantly outperforms the other sampling methods in more accurately determining the peak position and line width of the partially overlapping peak (i.e., the third weakest peak placed only 23 Hz away from the most intense peak). None of the Poisson gap sampling schemes are found beneficial for SMILE reconstruction, with all of them yielding a larger fraction of missing peaks, and larger errors in peak position and peak height than fully randomized sampling schemes (Table 1). In this respect, SMILE reconstruction differs from istHMS reconstruction, for which the previously reported benefits of Poisson gap sampling over random sampling are reproduced when the above test is applied to the same test data sets, with the best performance obtained for the 0 to π/2 sinusoidally weighted Poisson gap sampling (Table S1). However, even with this sampling scheme that strongly favors the earlier data points, the fraction of missing peaks does not improve significantly over the SMILE reconstruction of fully randomly sampled data, and comes at the expense of increased uncertainty in peak position and line width (Table S1).

Although random sampling with SMILE reconstruction performs well in the above described test, it does not quite reach the theoretical limit: comparison with the fully sampled data set, using the same noise level but √10 weaker signals shows that only 13 out of totally 1000 weakest peaks are missed when peak picking the 10 fully sampled data sets (Table 1). Only when further lowering the signals by an additional factor of 1.14 does the peak picking performance become comparable to those of the random NUS SMILE data set, suggesting that SMILE is able to reduce the PSF noise to add not more than about 14% over the thermal noise. It should be noted, however, that the magnitude of this residual PSF noise depends strongly on the sampling density and the complexity and dynamic range of the spectral components, i.e., it will vary for different spectra.

When comparing the fractional peak height errors obtained with SMILE for the 10 peaks, they scale approximately inversely with the intensity of the resonances, analogous to what is seen for fully sampled data. The root mean square error is found to be much larger than the average error (Table 1), indicating that the systematic underestimate seen in nearly all NUS reconstruction methods is very small (compare, for example, Table S1).

SMILE uses the assumption that the NMR resonances decay exponentially during its iterative approach. Even though this assumption often applies for solution NMR data, unresolved multiplets can have a more Gaussian decay profile, making the fitting procedure used by SMILE suboptimal. In principle, an option to fit the data to signals with a Gaussian decay profile could be used to optimize SMILE performance for such cases, but this option has not been implemented because its benefit is small and its need is relatively rare. Note that SMILE, and most other NUS reconstruction programs, perform poorly when applied to signals of very complex shapes, such as solid state NMR chemical shift anisotropy powder patterns, or time domain data collected for magnetic resonance imaging purposes.

Evaluation of SMILE reconstruction on experimental data

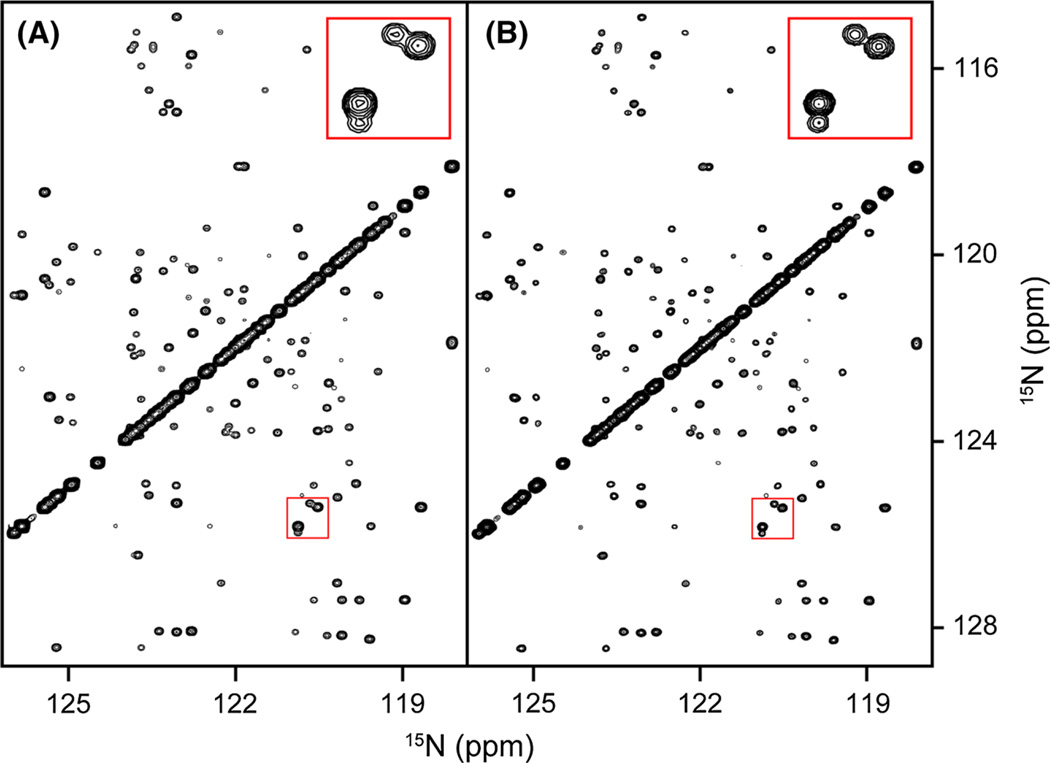
Next, we test the performance of SMILE on experimental data by comparing the results obtained for a quite large, fully sampled 3D (H)N(COCO)NH spectrum of α-synuclein with those of a randomly chosen 2.6% subset of that time domain matrix. The (H)N(COCO)NH spectrum links sequential amides by transfer through the ³J_C′C′ coupling between their adjacent carbonyl resonances (Hu and Bax 1996; Li et al. 2015). The intensity of the weak cross peaks relative to the intense diagonal resonances provides a direct measure for the absolute value of ³J_C′C′. This type of spectrum therefore provides a sensitive test for the accuracy at which cross peak intensities can be detected in the NUS data sets. Figure 3 shows a small region of the projection of the 3D spectrum on the ¹⁵N–¹⁵N plane, illustrating the high quality of both the fully sampled and NUS SMILE-reconstructed data set. With ³J_C′C′ values of ca 0.8 Hz (Lee et al. 2015), and ³J_C′C′ de- and re-phasing delays of 125 ms, the typical ratio between diagonal and cross peaks is ca 10:1. As can be seen by comparing the fully sampled and SMILE-reconstructed spectra, in particular when viewing the expanded insets, spectral resolution obtained by the SMILE reconstruction is somewhat higher than for the fully sampled spectrum. This enhanced resolution results from the default 50% extension of the truncated ¹⁵N time domains with zeros, which are treated just like other non-sampled data points during SMILE reconstruction (see also Fig. 2A1, A3). In principle, a much longer extension, e.g. three-fold, could be used. However, we note that even though this would result in further narrowing of resolved resonances, it will not resolve resonances for which the actual time domain length is shorter than about (1.5δ)⁻¹, where δ is their frequency difference. Extending much beyond 1.5-fold gradually will also adversely impact the accuracy of the resonance intensities, and extensions by a factor larger than two is not recommended for quantitative analysis.

Fig. 3.

Comparison of spectra obtained from a fully sampled matrix with that of a NUS-processed, randomly chosen 2.6% subset of that matrix. Shown are sections of the projection of a 600-MHz 3D (H)N(COCO)NH spectrum of α-synuclein on the 2D ¹⁵N–¹⁵N plane for A the fully sampled data set and B the SMILE-reconstructed data set. The indirect ¹⁵N dimensions in the fully sampled and SMILE reconstructed spectra were apodized using a cosine window ending at 86.4°. The default 50% extension in the indirect time domains, by adding zeros for the non-sampled time domain, makes the effective sparsity 1.15%, and improves spectral resolution as highlighted for the peaks in the insets shown at the top right of each panel. Final matrix size for the absorptive, real component of the spectrum is 928 × 928 × 464 points, i.e., 1.5 Gb; reconstruction time 14.6 min, using 4 Intel Xeon E5-2650 CPU cores, 1 Gb total memory, 300 SMILE iterations. The NMRPipe processing script is included as Supplementary Material

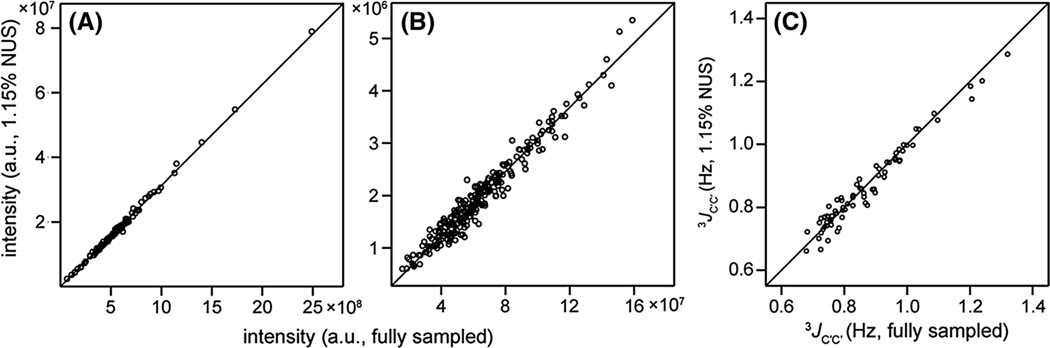
Comparison of the diagonal intensities of the fully sampled and SMILE-reconstructed spectra (Fig. 4A) shows excellent fidelity, with a Pearson’s correlation coefficient R_P = 0.997, as expected for these high S/N resonances. However, even intensities of the much weaker cross peaks correlate closely between the two spectra (R_P = 0.967; Fig. 4B), and the extracted ³J_C′C′ couplings correspondingly are very similar (R_P = 0.976; Fig. 4C) for the two data sets. Relative to a number of other powerful NUS reconstruction programs, we note that only SCRUB yielded intensity, and thereby ³J_C′C′ coupling fidelity, as high as SMILE for this very sparse, moderate S/N data set (Supporting Information Fig. S1). Parenthetically we note that the RMSD between ³J_C′C′ couplings derived from the SMILE-reconstructed and fully sampled spectra is about 25% lower when using NMRPipe for peak picking than Sparky, as the latter tends to underestimate the intensity of very weak resonances in our hands. For intense resonances, results of the two programs are essentially indistinguishable. The accuracy of the ³J_C′C′ couplings obtained from the 2.6% randomly sampled NUS-reconstructed spectrum is limited by the thermal S/N, which is intrinsically about six-fold lower for the NUS data set, owing to the 38-fold smaller number of input data. The RMSD in ³J_C′C′ derived from the NUS and the fully sampled data is 0.029 Hz for both SMILE and SCRUB, indicating excellent agreement between the small couplings derived from the reconstructed and fully sampled spectra.

Fig. 4.

Comparison of parameters extracted from the 2.6%-sampled (1.15% after time domain extension) NUS-reconstructed 3D (H)N(COCO)NH spectrum with those of the fully sampled spectrum. A Correlations between the strong diagonal peak intensities of the NUS-reconstructed and fully sampled spectra (R_P = 0.997). B Same as A but for the weaker crosspeaks (R_P = 0.967). C The ³J_C′C′ couplings of the NUS spectrum versus those extracted from the fully sampled spectrum (R_P = 0.976; RMSD = 0.029 Hz). ³J_C′C′ couplings were calculated from the cross peak to diagonal peak intensity ratios

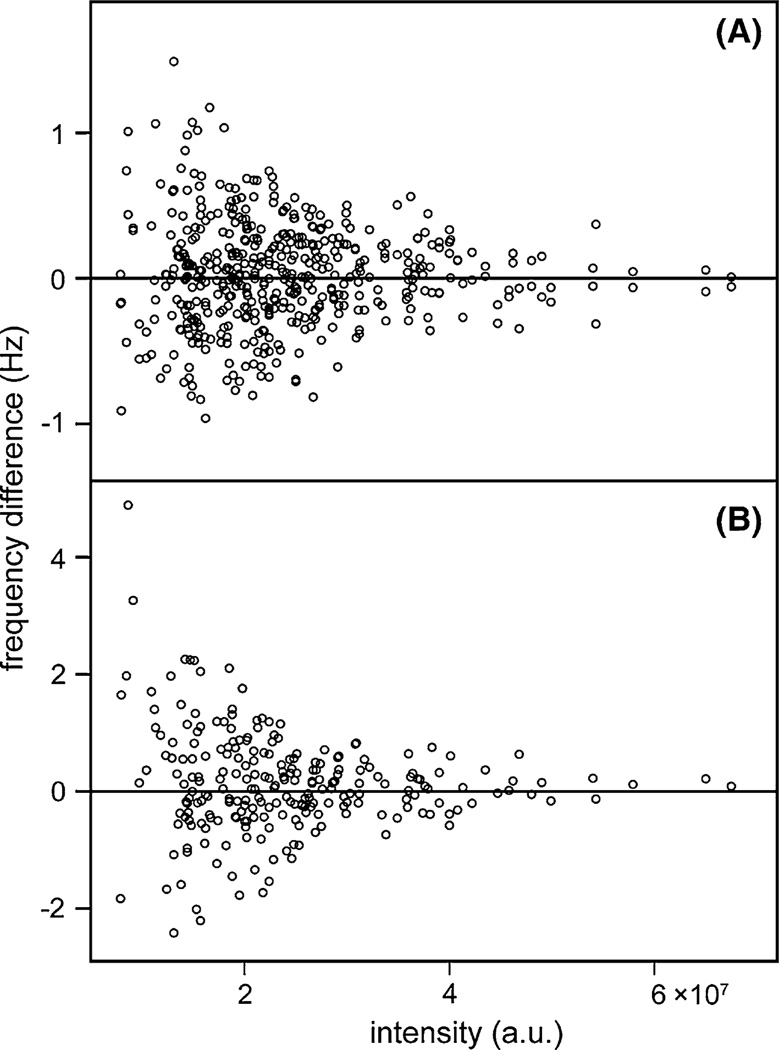
At moderate S/N levels, typically below 100:1, the uncertainty of peak positions is approximately given by 0.5 × LW/(S/N) (Kontaxis et al. 2000), where LW is the line width. This prediction is consistent with the reproducibility of the peak pick results when plotting the difference in frequencies observed between the fully sampled and NUS-reconstructed spectra against the intensity of the resonances (Fig. 5; Fig. S2). Indeed, the reproducibility of the peak positions scales with the inverse of its intensity. On average, the line width in the ¹H dimension is about 19 Hz, versus ca 11 Hz for ¹⁵N, and the accuracy (in Hz) at which the peak positions are reproduced correspondingly is about two-fold better for ¹⁵N than for ¹H. Interestingly, whereas the amplitude fidelity for weak resonances obtained by SMILE and SCRUB was somewhat better than for other methods (Supporting Information Fig. S1), the crosspeak frequency reproducibility was more comparable (RMSDs of 0.32/0.75, 0.44/1.10, 0.46/0.96, and 0.66/1.05 Hz for the ¹⁵N/¹H position by SMILE, SCRUB, istHMS, and SSA, respectively).

Fig. 5.

Reproducibility of cross peak positions between NUS and fully sampled spectra. A Differences between ¹⁵N frequencies measured in the SMILE-reconstructed spectrum of Fig. 3B and the reference spectrum (Fig. 3A), recorded with full sampling. The difference is plotted against the intensity of the resonance in the SMILE-reconstructed spectrum. B Differences between ¹H frequencies in the fully sampled and SMILE-reconstructed spectrum. The average line widths in the SMILE-reconstructed spectrum are ca 11 Hz (¹⁵N), and 19 Hz (¹H). See Fig. S2 for analogous comparison obtained with SCRUB

Application to fully sampled constant-time data

It has previously been shown that the same principles used for reconstructing non-sampled data points during an FID can also be used to extend the duration of a partially or fully sampled time domain, providing an alternative to extending data via linear prediction (Zhu and Bax 1990; Led and Gesmar 1991; Stern et al. 2002). In particular, when using the minimum l1 norm as a regularizer during iterative soft thresholding, impressive enhancements in resolution can be obtained relative to a simple FT (Stern et al. 2007). Here we demonstrate the use of SMILE for the same purpose. As already discussed above for default SMILE processing, the length of the time domain is by default extended by 50% with non-sampled data as part of the reconstruction. The reason we do not recommend further extension of the data is that, even though resolved resonances will appear narrower, their peak positions do not improve, and resonances that remain unresolved after a 1.5-fold extension typically will not reliably resolve upon further extension of the time domain data. Nevertheless, for fully sampled time domain data, particularly when the data is recorded in a constant-time manner, useful spectral resolution enhancement can be obtained when extending the time domain somewhat further, up to about two-fold.

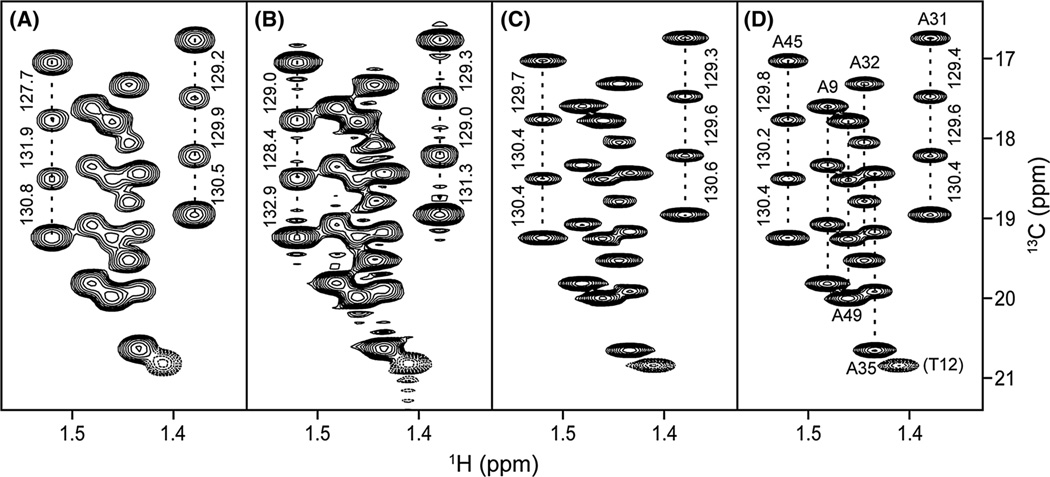
Figure 6 shows an example, where SMILE reconstruction was used to double the length of the ¹³C 28-ms constant- time domain of a standard CT-HSQC spectrum without ¹H decoupling during ¹³C evolution. The spectrum, recorded at 700 MHz for uniformly ¹³C-labeled toxin TA1A, shows the correlations for its six Ala residues. For the regularly processed spectrum (Fig. 6A), cosine-bell apodization was used to minimize truncation artifacts. Applying a cosine-bell that runs from 0 to 45°, i.e., an apodization that attenuates the last acquired t₁ data point by √2/2, leaves large truncation artifacts in the frequency domain (Fig. 6B). However, extending the time domain two-fold, using SMILE NUS reconstruction followed by cosine-bell apodization, yields a much improved spectrum (Fig. 6C) that is comparable in quality to a separate CT-HSQC spectrum, recorded with a double constant-time duration of 2/¹J_CC (Fig. 6D). The accuracy of peak positions can be judged by comparing the separations between the multiplet components of an individual methyl quartets, as indicated for Ala-45 and Ala-31, which should all be identical [ignoring small dynamic frequency shift effects (Tjandra et al. 1996)]. As can be seen from the values shown in Fig. 6, the peak position accuracy of the SMILE-enhanced spectrum is far better than that obtained with conventional processing (Fig. 6A), and nearly as good as that seen for the spectrum recorded with the double constant-time duration.

Fig. 6.

Example of spectral enhancement by SMILE time domain extension. Small sections of the methyl region of a 700-MHz 2D ¹H–¹³C CT–HSQC spectrum of insecticidal toxin Ta1a (Undheim et al. 2015) are shown, recorded without ¹H decoupling in the ¹³C dimension, and displaying correlations for its six Ala residues. All spectra were recorded with full, uniform sampling. A Spectrum recorded with a ¹³C constant-time duration of 1/¹J_CC, apodized in the ¹³C dimension with a cosine-bell window, extending from 0° to 90°, prior to four-fold zero-filling and FT. B Same data, processed using apodization with a cosine-bell window, extending from 0° to 45°, C Same data, using SMILE to double the length of the time domain data in concert with cosine bell (0°–90°) apodization, followed by zero filling, and FT. D Data recorded with a double CT ¹³C evolution period of 2/¹J_CC and the same total time domain length as the SMILE extended data, apodized and zero-filled as for (C). ¹J_CH splittings, as measured from the frequency differences between adjacent multiplet components of each quartet by NMRDraw peak picking, are marked for Ala-31 and Ala-45. Dashed contours (bottom right) correspond to the upfield quartet component of Thr-12. The NMRPipe processing script is included as Supplementary Material

Application to 4D NOESY

Non-uniform sampling is particularly useful for collecting 4D NMR spectra, where for practical reasons it is rarely feasible to collect fully sampled data at a resolution that is allowed by the transverse relaxation times. In particular the full resolution potential of high-field NMR spectrometers cannot typically be realized because data acquisition must be truncated long before the signal has decayed. Of the many 4D pulse schemes in use, 4D NOESY measurements are arguably the most critical to structural studies, as they can dramatically reduce the spectral crowding of 2D and 3D NOESY spectra (Kay et al. 1990; Clore et al. 1991; Zuiderweg et al. 1991). 4D NOESY of methyl–methyl interactions is particularly useful for deriving distance restraints in larger proteins, which often require perdeuteration with ILV-protonation of methyl groups (Tugarinov et al. 2005; Hiller et al. 2009; Sheppard et al. 2009; Coggins et al. 2012; Linser et al. 2014; Xiao et al. 2015). Here, we therefore include an example of the use of SMILE for processing of such a spectrum.

Even for smaller proteins, collection of 4D NOESY spectra on ILV-labeled proteins can be quite useful, and we previously applied this method to the structural study of the 196-residue extracellular domain of the cytomegalovirus m04 protein (Sgourakis et al. 2014), which had proven recalcitrant to conventional structural analysis due to its limited stability and tendency to dimerize. The CH₃-CH₃ region of the projection of the fully sampled spectrum onto the ¹³C–¹³C plane (Fig. 7A) illustrates the presence of numerous cross peaks between the 64 ¹³CH₃ groups, many of which can be resolved when inspecting individual planes, even while considerable resonance overlap also remains (Fig. 7C). Much higher spectral resolution is obtained when using fourfold longer acquisition times in all three indirect dimensions, corresponding to a sparsity of 1.56%, or 0.46% after the default 50% extension of the time domain data.

Fig. 7.

Example of SMILE reconstruction of a 1.56%-sampled 4D methyl HMQC-NOESY-HMQC spectrum collected at 600 MHz ¹H frequency, 200 ms NOE mixing time, for a 0.5 mM sample of the ILV methyl-labeled m04 protein of cytomegalovirus (Sgourakis et al. 2014). The acquisition time in the direct dimension is 128 ms, and default extension of the acquisition times by 50% in all three indirect dimensions, to 70 ms (¹H, t₂) and 60 ms (¹³C, both t₁ and t₃), during SMILE reconstruction makes the effective sampling sparsity 0.46%. Approximately quadrupling the time domain durations by zero filling, followed by FT, yielded a final all-real matrix size of 512 (F₁, ¹³C) × 512 (F₂, ¹H) × 512 (F₃, ¹³C) × 646 (F₄, ¹H), i.e., 323 GB for the processed 4D spectrum. The processing completed in ca 11 h using 16 Intel Xeon E5-2650 CPUs using 40 Gb memory (minimum required size 36 Gb). A ¹³CH₃ containing region of the projection on the ¹³C–¹³C plane of a separately recorded and processed conventional, fully sampled 4D spectrum with four-fold shorter acquisition times (relative to the NUS acquisition times prior to the 50% extension by SMILE) in all dimensions. B The corresponding projection of the SMILE-reconstructed spectrum. C, D Comparison of (¹H/¹³C) cross sections taken through C the fully sampled and D the NUS 4D NOESY spectrum, taken orthogonal to the location of the I31-Cδ/Hδ (F₃, F₄), labeled on the diagonal in B. The NMRPipe processing script is included as Supplementary Material

The SMILE-reconstructed NOESY spectrum is free of spectral artifacts but of lower S/N than the fully sampled spectrum, acquired in approximately the same amount of time. The reason for the lower S/N lies in the long acquisition times (40 ms for ¹³C, 47 ms for the indirect ¹H dimension) which were longer than the actual transverse relaxation times. Because a fully random sampling schedule was used to record these data, many of the time domain data points carried considerably lower signal strength than the data in the fully sampled spectrum, resulting in decreased sensitivity of the final spectrum. As is well known, this S/N loss can be mitigated by weighting the random sampling scheme to include more time domain data for shorter evolution times (Barna et al. 1987; Mobli and Hoch 2014). We note that modest extension of the truncated time domains by SMILE can actually enhance the S/N in the final spectrum, both for fully and sparsely sampled data sets, because this procedure prevents the scaling of valuable acquired data at the end of the time domain to near-zero values, normally needed to avoid truncation artifacts after FT.

Concluding remarks

Over the past three decades, a large number of valuable programs have been introduced that are capable of reconstructing sparsely sampled data, and many of these have been reviewed in recent years (Hoch et al. 2014; Mobli and Hoch 2014; Nowakowski et al. 2015). However, use of most of these programs has remained restricted to laboratories in which they were originally developed, a logical consequence of the complexity in optimal parameterization of the procedure and preparing input and output formats. The goal of developing SMILE was to create a routine that seamlessly interfaces with the widely used NMRPipe program, while minimizing the requirement for user expertise of its operation and optimization while delivering robust reconstruction. SMILE differs from most other NUS reconstruction procedures in that it does not include a non-linear procedure to remove the noise from the spectrum, and as a result the final spectra have an appearance very familiar to the spectroscopist, and give a realistic feeling for the reliability and accuracy of extracted spectral features.

Even though the SMILE program includes many user-adjustable parameters that can be used to optimize performance of the program, such as the length of time domain extension, signal fraction to be removed each iteration, or noise-cutoff level, the program generally works perfectly fine without specifying any of these, in which case the program resorts to its default parameters. As described in the SMILE manual, fine tuning of the performance by using non-default parameters can increase the speed of the program or treat more optimally special types of data sets, such as mixed-time or constant-time input data, but is generally not needed.

Conceptually, SMILE is closest to the SSA method of Kozminski and co-workers (Stanek and Kozminski 2010; Stanek et al. 2012). However, many of the details of the computational procedure differ substantially. Importantly, for optimal operation, SMILE requires that the spectrum has been recorded with absorptive phases for all signals, or that these phase parameters are provided by the user as regular NMRPipe phase parameters. Although this can be considered a drawback, in practice it enhances the quality of the reconstruction considerably in terms of accuracy of both peak position and intensity as well as lowering of PSF noise. The reason for the better performance of the algorithm using phased data relates to the fact that each resonance attains its maximum amplitude when phased absorptive, optimizing its detection against a noisy background. Moreover, one degree of freedom is removed for each dimension when describing the signal, allowing a more robust and rapid analytic parameterization in terms of intensity, frequency and peak width. Furthermore, this can be achieved using just the three most intense points of the observed line shapes in each dimension. Note that even though SMILE makes use of a very basic peak picking algorithm during its iterative signal reconstruction procedure, it is distinctly different from sophisticated peak analysis programs such as CRAFT, which relies on a Bayesian engine to analyze one-dimensional line shapes in an optimal manner (Krishnamurthy 2013).

SMILE is computationally rather demanding because it reconstructs each resonance as a multi-dimensional line shape, rather than treating cross sections through it in lower dimensional space. Nevertheless, by taking advantage of more efficient very fast FT algorithms, in conjunction with fast methods for generating time domain data for a collection of resonances that are parameterized in the frequency domain, SMILE reconstruction times remain comparable to or faster than other programs currently available, making it applicable to even the largest 4D reconstructions performed to date.