Efficient ³¹P Band Inversion Transfer Approach for Measuring Creatine Kinase Activity, ATP Synthesis and Molecular Dynamics in the Human Brain at 7T

Abstract

Purpose

To develop an efficient ³¹P MRS method for measuring creatine kinase (CK) activity, ATP synthesis and motion dynamics in the human brain at 7T.

Methods

Three band inversion modules differing in center frequency were used to induce magnetization transfer (MT) effect in three exchange pathways 1) CK-mediated reaction PCr → γ-ATP; 2) de novo ATP synthesis Pi → γ-ATP; and 3) ATP intramolecular ³¹P-³¹P cross-relaxation γ-(α-) ↔ β-ATP. The resultant MT data were analyzed using a five-pool model in the format of magnetization matrix according to Bloch-McConnell-Solomon formalism.

Results

With repetition time TR 4 sec, the scan time for each module was ~8 min. The rate constants were k_{PCr→ γATP} 0.38 ± 0.02 sec⁻¹, k_{Pi → γATP} 0.19 ± 0.02 sec⁻¹, and σ_{γ(α) ↔ βATP} − 0.19 ± 0.04 sec⁻¹, correspond to ATP rotation correlation time τ_c (0.8 ± 0.2) ·10⁻⁷ sec. The T₁ relaxation times were Pi 7.26 ± 1.76 sec, PCr 5.99 ± 0.58 sec, γ-ATP 0.98 ± 0.07 sec, α-ATP 0.95 ± 0.04 sec, and β-ATP 0.68 ± 0.03 sec.

Conclusion

Short-TR band inversion modules provide a time-efficient way of measuring brain ATP metabolism and could be useful in studying metabolic disorders in brain diseases.

INTRODUCTION

Adequate ATP energy supply is critical for the normal brain functions. Deficits in cerebral ATP production may cause mitochondrial dysfunction, further leading to brain aging and neurodegenerative diseases (1-6). There has been a great interest in measuring ATP metabolism using ³¹P magnetization transfer (MT), a non-invasive technique that offers measurements of de novo ATP synthesis, creatine kinase (CK) reaction, and ATP molecular motion dynamics in vivo (7-12).

However, quantitative measurement of ATP metabolism by ³¹P MT is challenging due to the co-existence of multiple competing pathways that tends to attenuate the targeted MT effect. To produce sizable MT effect suitable for quantitative analysis, conventional saturation transfer (ST) technique often relies on prolonged irradiation, but this may induce undesirable side effects such as high SAR exposure, off-resonance contamination and activation of small hidden pools (13-15). To overcome these side effects, alternative inversion transfer (IT) methods have been proposed (16-20), including EBIT (Exchange Kinetics by Band Inversion Transfer), by which the MT effect in a selected pathway can be amplified through band inversion of the spins that are involved in competitive pathways (18-20).

While EBIT has been applied to measuring ATP metabolism in the human brain and skeletal muscle (18-20), these studies were conducted under the condition of a long sequence repetition time (TR = 25 for brain or 30 sec for skeletal muscle). Long TR provide the needed recovery time for a perturbed magnetization to return to thermal equilibrium state (Mz°), making it easy to analyze MT data. However, experimentally it is time-consuming. The present study aims to provide a short TR formula for EBIT, with improved spectral SNR and acquisition speed. We plan to test three different band inversion modules with short TR of 4 sec. Each is intended to amplify the MT effect in a particular pathway, including CK-catalyzed reactions PCr → γ-ATP (Module I), de novo ATP synthesis through ATPase Pi → γ-ATP (Module II), and ATP intramolecular ³¹P-³¹P cross-relaxation γ- (α-) ↔ β-ATP. Given the short scan time of ~ 8 min, these modules can be easily integrated to provide a comprehensive view of cerebral ATP metabolism.

THEORY

For a given spin system comprised of n spins, the time dependence of the system’s magnetization after a B₁ perturbation can be described by

$$m\left(t\right)=I-e^{A\cdot t}\left(I-m\left(0\right)\right)$$ [1]

in which m represents the system’s normalized Z-magnetizations, which is a vector of n-dimension with m_i = M_z,i /M_z,i° (Mz° is the magnetization at thermal equilibrium, i = 1, …, n); m(0) is the initial magnetization immediately after the B₁ perturbation at t = 0; I is unity vector of n – dimension (I = 1 for n = 1); and A is an n × n matrix, describing the relaxation and exchange kinetics of the given spin system; it is therfore referred to as RE matrix. A special case is n = 1, in which the RE matrix A is reduced to a scalar −1/T₁.

In the brain, ATP is involved in chemical exchanges with both PCr and Pi. Together these three metabolites constitute a five-spin exchange system, responsible for the inter-molecular magnetic transfer effects observed in ³¹P MRS in vivo. MT effects also occur between neighboring dipolar-coupled ³¹P spins within ATP molecules, and the signal change from this intramolecular ³¹P-³¹P cross-relaxation is an example of the nuclear Overhauser effect (NOE). For such a five-spin exchange system, its normalized magnetization m, and exchange-relaxation (ER) parameter matrix A, can be written as

$$m=\left[\begin{array}{c}\hfill m_{\mathit{Pi}}\hfill \\ \hfill m_{\mathit{PCr}}\hfill \\ \hfill m_{\gamma }\hfill \\ \hfill m_{\alpha }\hfill \\ \hfill m_{\beta }\hfill \end{array}\right]$$ [2]

and

$$A=\left[\begin{array}{ccccc}\hfill -1∕T_{1,\mathit{Pi}}-k_{\mathit{Pi}\to \gamma }\hfill & \hfill 0\hfill & \hfill k_{\mathit{Pi}\to \gamma }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1∕T_{1,\mathit{PCr}}-k_{\mathit{PCr}\to \gamma }\hfill & \hfill k_{\mathit{PCr}\to \gamma }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill k_{\gamma \to \mathit{Pi}}\hfill & \hfill k_{\gamma \to \mathit{PCr}}\hfill & \hfill -1∕T_{1,\gamma }-k_{\gamma \to \mathit{Pi}}-k_{\gamma \to \mathit{PCr}}\hfill & \hfill 0\hfill & \hfill -{\sigma }_{\beta \gamma }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1∕T_{1,\alpha }\hfill & \hfill -{\sigma }_{\beta \alpha }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -{\sigma }_{\gamma \beta }\hfill & \hfill -{\sigma }_{\alpha \beta }\hfill & \hfill -1∕T_{1,\beta }\hfill \end{array}\right]$$ [3]

where the subscripts α,β,γ denote for α-, β- and γ-ATP, respectively, k denotes the first-order rate constant for the chemical exchanges with the forward and reverse reaction related by $k_{\mathit{ji}}=k_{\mathit{ij}}\frac{M_i^o}{M_j^o}$ (i,j = Pi, γ-ATP or PCr, γ-ATP), and σ denotes the rate constant of ³¹P-³¹P cross-relaxation within the ATP molecule, which is assumed to be a constant within any two neighboring ATP spins (σ_γβ = σ_βγ = σ_αβ = σ_βα). The ER parameter matrix A is based on the Bloch-McConnell-Solomon magnetization formalism, as described previously (18,20).

With ER matrix A, it becomes straightforward to derive the magnetization m(t) at any time point t, once the initial magnetization of the system m(0) is known (Eq. [1]). Now, let us consider the situation that the above-described five-spin system is repetitively pulsed by an inversion-recovery sequence (180° - t_d - 90° - τ)_n (Figure 1a). At steady state, the system’s magnetization prior-to the 180° pulse can be written as (from Eq. [1]):

$$m\left(0^{-}\right)=I-e^{A\tau }\left(I\right)$$ [4]

Following the inversion 180° pulse, the system’s magnetization is described by:

$$m\left(0^{+}\right)=f\cdot m\left(0^{-}\right)$$ [5]

where f represents the inversion fraction (f = −1 for a signal fully inverted, and f = 0 for a signal unaffected by the inversion).

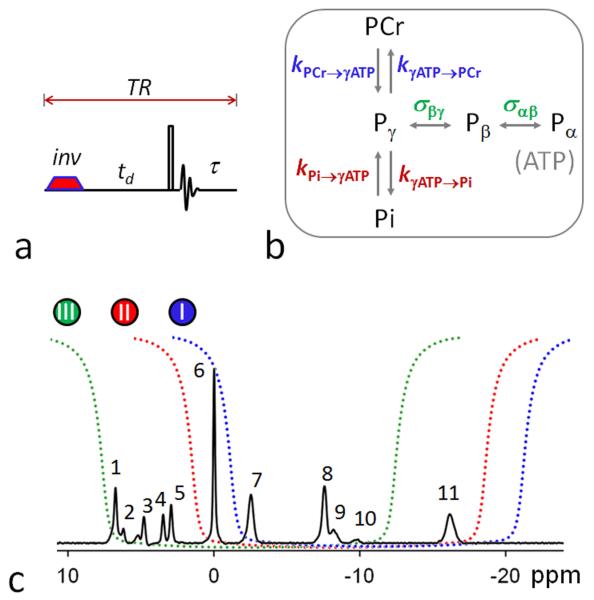
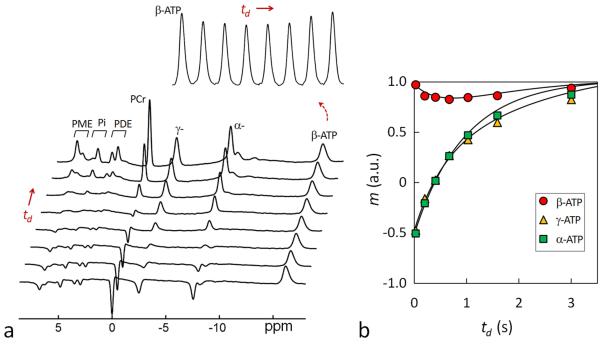
FIG. 1.

(a) The band inversion sequence consists of an adiabatic inversion pulse, followed by a varying delay t_d, a hard readout pulse and FID sampling and magnetization recovery period τ (≈ TR – t_d); (b) ³¹P magnetization exchange system in the human brain, showing various pathways that contribute to the magnetization transfer effects, including kinetic chemical exchange Pi → γ-ATP responsible for de novo ATP synthesis, kinetic chemical exchange PCr → γ-ATP catalyzed by creatine kinase (CK), and ATP intramolecular ³¹P-³¹P cross-relaxation γ-(α-) ↔ β-ATP, responsible for the nuclear Overhauser effect; and (c) the inversion profile of the three band inversion modules over a baseline-corrected brain ³¹P spectrum collected from the occipital lobe using pulse-acquire sequence with TR = 25 sec, NA = 6 and other common NMR parameters defined in Methods section (n = 6 subjects). Peak assignment: 1. Phosphoethanolamine (PE); 2. Phosphocholine (PC); 3. Intra- and extracellular inorganic phosphate (Pi); 4. Glycerolphophoethanolamine (GPE); 5. Glycerophosphocholine (GPC); 6. Phosphocreatine (PCr); 7, 8, 11. γ-, α-, and β-adenosine triphosphate (ATP); and 9. Nicotine adenine dinucleotide (NAD).

In the delay period t_d following inversion, the system’s magnetization evolves by (from Eq. [1]):

$$m\left(t_d\right)=I-e^{A\cdot t_d}\left(I-f\cdot m\left(0^{-}\right)\right)$$ [6]

This is the magnetization to be detected after the 90° readout pulse. Thus by measuring the m (t_d) value at a series of different t_d points, the relaxation and kinetic parameters encoded in ER matrix A can be determined.

Reference for z-magnetization normalization So far we have been using the notation m to represent the normalized z-magnetization Mz/Mz°, in which Mz° is the z-magnetization at the thermal equilibrium state, and used as a scaling reference for magnetization normalization. For fast MT experiments with short recovery time τ ≈ TR - t_d (ignoring the pulse width, Figure 1a), it is more convenient to use Mz*, as a reference in normalization, where Mz* denotes the steady-state z-magnetization acquired with pulse-acquire sequence at repetition time TR. The relationship between Mz° and Mz* is given by:

$$\frac{{M_z}^{\ast }}{{M_z}^o}=m_{\mathit{ref}}=I-e^{A\cdot \mathit{TR}}$$ [7]

This means that, to convert between references Mz* and Mz°, only a scaling factor is needed, as denoted by m_ref in Equation [7]. With this scaling factor, the m(t_d) ~ t_d plot for a given un-inverted resonance always starts with m(t_d = 0) = 1 under ideal conditions (no partial saturation), no matter how long the TR is. As TR increases, m_ref approaches unity. In fact, when TR reaches to ~ 4-5 T₁, Mz* is approximately equal to Mz°.

METHODS

Human Subjects

The protocol was approved by the Institutional Review Board of the University of Texas Southwestern Medical Center. Prior to the MRS study, informed written consent was obtained from all participants. Six subjects (4 male and 2 female), aged 50 ± 8 yr, BMI 27 ± 2, resting heart rate 71 ± 13, and peripheral capillary oxygen saturation (SpO₂) 98 ± 1%, participated in the study. All subjects were in normal health with no history of psychiatric or neurodegenerative diseases. Heart rate and blood oxygen saturation levels were monitored during the scan. The study was well tolerated by all subjects.

MRS Protocol

All subjects were positioned head-first and supine in the MRI scanner (7T Achieva, Philips Healthcare, Cleveland, OH), with the back of the head positioned in the center of the detection RF coil (Philips Healthcare, Cleveland, OH). The coil was a partial volume, double-tuned ¹H/³¹P quadrature TR coil consisting of two tilted, partially overlapping 10 cm loops. Axial, coronal, and sagittal T2-weighted turbo spin echo images were acquired for shimming voxel planning. Typical imaging parameters included field-of-view 180 × 180 mm (FOV), repetition time (TR) 2.5 s, echo time (TE) 80 ms, turbo factor 15, in-plane spatial resolution 0.6 × 0.7 mm², slice thickness 6 mm, gap 1 mm, bandwidth 517 Hz, number of acquisitions (NA) one, and acquisition time 2.1 min. Second order ¹H-based automatic volume shimming, located in the brain occipital lobes, was applied prior to ³¹P spectral acquisitions.

The EBIT pulse sequence consisted of an adiabatic inversion pulse, followed by a variable post-inversion delay time t_d, a hard 90° readout pulse, and a recovery period with TR = 4 sec (Figure 1a). A total of 7 delay times (t_d = 25, 197, 405, 668, 1026, 1589, and 3000 msec) and 16 scan averages were used. The inversion pulse was a short trapezoid-shaped adiabatic pulse (pulse width pw = 38 msec, including 7 msec of pre- and post-ramp time), maximal B₁ 13 μT, inversion bandwidth of 2700 Hz. To amplify the MT effect in a particular pathway, the center frequency of the adiabatic pulse was set to invert multiple ³¹P spins in a selected spectral region according to Figure 1b:

• Module I: α-, β- and γ-ATP in the upfield region (−2 – −20 ppm) are inverted, while PCr (0 ppm) and Pi (4.9 ppm) are observed for the MT effect in PCr → γ-ATP and Pi → γ-ATP pathways;

• Module II: PCr, α-, β- and γ-ATP are inverted, while Pi is observed for the MT effect through Pi → γ-ATP pathway.

• Module III: Pi, PCr, α- and γ-ATP are inverted, while β-ATP (−16.2 ppm) is observed for the MT effect through γ- ↔ β-ATP and α- ↔ β-ATP cross-relaxation, whose rate constant is denoted as σ_{γ(α) ↔ βATP}.

The data acquisition time for each module was ~ 8 min (NA 16, plus 1 dummy scan). A reference scan was recorded under the same condition (TR 4 sec, NA 16) but without inversion. An additional fully relaxed ³¹P spectrum was also acquired at TR = 25 sec and NA = 6 to derive equilibrium magnetization ratios for Pi/ATP and PCr/ATP, and the data acquisition time was 2.5 min. The execution of all three modules, one reference scan without inversion, and one scan for a fully relaxed spectrum was within 30 min. To test the reproducibility, the measurements were repeated once under the same sequence conditions without repositioning the subject and re-shimming the field, and the results were compared as “test” versus “retest”, with an interval of 30 min between them.

Other common ³¹P NMR parameters include sampling points 4 K, zero-filled to 8 K prior to FT, readout pulse dead-time (the delay prior to FID sampling for suppression of the broad background ³¹P peak) 0.5 ms, transmitter carrier frequency offset 50 Hz upfield from α-ATP signal, and one dummy scan prior to data acquisition. Although t_d is generally referred to as “post-inversion delay” in the text, it includes half of the width of inversion pulse (0.02 sec) as defined by the MRI instrument. The chemical shifts of all ³¹P metabolites were referenced to PCr at 0 ppm. Gaussian apodization (6 Hz) was applied to each FID prior to Fourier transformation using the scanner software (SpectroView, Philips Healthcare).

³¹P MRS Data Analysis

The frequency-domain ³¹P spectra were baseline corrected, and the intensity of each of the ³¹P peaks was fitted by a Voigt lineshape (a combination of Gaussian and Lorentzian lineshape) using ACD software (Advanced Chemistry Development, Inc., Toronto, Canada). The intensity measurements from the full relaxed ³¹P spectra were used to derive the metabolite ratios PCr/ATP and Pi/ATP, while those obtained at TR = 4 sec were used as magnetization reference Mz^* to derive the normalized z-magnetization m(t_d) for the t_d spectral series. The inversion fraction f, as defined by Eq.[5], was approximated by the m(t_d) value at t_d = 0.025 sec. The experimental f values varied in the range −0.4 – −0.6 depending on the inversion module and the inverted ³¹P signal, and was included in the fit model input. The m(t_d) ~ t_d datasets were fit according to Eqs. [1-7] to derive the parameters k_Pi→γATP, k_PCr→γATP, σ_{γ(α) ↔ βATP}, T_1,Pi, T_1,PCr, T_1,γ). T_1,α and T_1,β, The fitting was based on least-square function lsqcurvefit in Matlab (The MathWorks, Inc. Natick, MA). For comparison of the outcomes from different EBIT modules, the fitting was done either separately module-by-module using simplified models with pre-determined assumptions or together using the full five-pool exchange mode (Figure 1b). For Module I fitting, σ_{γ(α) ↔ β} = 0 was assumed; For Module II, σ_{γ(α) ↔ βATP} = 0 and k_PCr→γATP = 0 were assumed; and for Module III, k_Pi→γATP = 0 and k_PCr→γATP = 0 were assumed. For Module I and II combination, σ_{γ(α) ↔ β} = 0 was assumed, but no assumption was made for all other module combinations (I & III, II & III, and I & II & III). The ATP rotation correlation time τ_c was derived from σ as described previously (20).

³¹P MRS Data Simulation

To examine TR effect on the normalized z-magnetization, steady state magnetizations were simulated for the five-spin system assuming recovering from null Z-magnetization after a 90° readout pulse. The m-datasets were generated according to Eq. [1] for recovery time τ in the range 0 – 25 sec using the following parameters: Pi/ATP = 0.28, PCr/ATP = 1.46, k_Pi→γATP = 0.19 sec⁻¹, k_PCr→γATP = 0.38 sec⁻¹, σ = −0.19 sec⁻¹, T₁ = 7.26, 5.99, 0.98, 0.95, and 0.68 sec for Pi, PCr, γ-, α- and β-ATP, respectively (which are the fitted results from module combination I & II & III, Table 1). The outcomes were compared to those from a “no-exchange” model simulated with conditions k_Pi→γATP = k_PCr→γATP = σ = 0.

Table 1.

The ³¹P relaxation time (T₁), and rate constants of kinetic exchanges (k) and cross-relaxation (σ) obtained for the human brain at 7T by 5-pool model fitting using data combined from different band inversion modules (n = 6 subjects)

	Band Inversion Modules
	I & II	I & III	II & III	I,II & III	Refs
K or σ, (s−1)
Pi → γ-ATP	0.23 ± 0.07	0.17 ± 0.06	0.20 ± 0.06	0.19 ± 0.04	0.21a, 0.18d
PCr → γ-ATP	0.37 ± 0.02	0.39 ± 0.03	0.42 ± 0.10	0.38 ± 0.02	0.29c, 0.30d
α(γ)- ↔ β-ATP	[−0.19]e	−0.20 ± 0.03	−0.19 ± 0.04	−0.19 ± 0.04	−0.21b
T1, (s)
Pi	6.64 ± 2.25	7.50 ± 1.89	7.61 ± 1.71	7.26 ± 1.76	6.71a,6.02b, 3.77d
PCr	6.02 ± 0.84	5.74 ± 0.58	6.65 ± 1.10	5.99 ± 0.58	5.03b,4.89d
γ-ATP	0.97 ± 0.05	1.00 ± 0.08	0.96 ± 0.06	0.98 ± 0.07	1.08b,1.35d, 0.94d
α-ATP	0.93 ± 0.03	0.95 ± 0.04	0.96 ± 0.04	0.95 ± 0.04
β-ATP	0.68 ± 0.02	0.66 ± 0.03	0.69 ± 0.06	0.68 ± 0.03

^a: From Ren et al (19) by band inversion Module-II with long TR 30 sec;

^b: From Ren et al (20) by wide-band inversion Module-III with long TR 25 sec;

^c: From Du et al 2013 (9) by ST;

^d: From Du et al 2007 by long TR (>= 16 sec) ST and 3-pool exchange model (23); and

^e: value is square bracket indicates a fixed constant in data fitting.

Statistical Analysis

All data are reported as mean ± standard deviation, calculated using Matlab.

RESULTS

Simulated Data

To illustrate the effect of MT on the recovery of Z-magnetization, Figure 2 plots the datasets m(τ) ~ τ for Pi, PCr, α-, β- and γ-ATP simulated according to Eq. [1] using k, T₁, and σ values found in vivo. All m(τ) ~ τ curves appear to be exponential, but the shape of the recovery varies significantly among different ³¹P spins. The simulated curve shape also differs greatly between the “no-exchange” (k = σ = 0) and in vivo models (Figure 2a vs. 2b). In the presence of the MT effect, the long-T₁ Pi and PCr magnetizations recover more rapidly (blue and red traces, Figure 2a vs. 2b), while the shot–T₁ γ-ATP magnetization recovers much more slowly (black trace, Figure 2a vs. 2b).

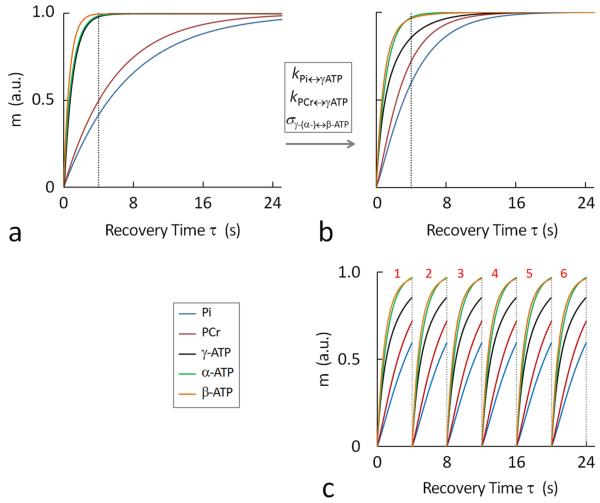
FIG. 2.

Simulated ³¹P magnetizations at varying recovery time τ, showing the recovery features of Pi, PCr, α-, β- and γ-ATP in the absence (a) and presence (b and c) of chemical exchanges and cross-relaxation, as defined in Figure 1b; (c) illustrating the principle of the short-TR band inversion approach in improving time efficiency in magnetization accumulation. A partial magnetization recovery in combination with increased number of sequence repetition leads to an accumulated magnetization larger than the thermal equilibrium state Mz° acquired with a single scan with long sequence recovery time. The magnetization curves were simulated according to 5-spin exchange model (Figure 1b) using k, σ and T₁ values given in Table 1. Abbreviation: Pi, inorganic phosphate; PCr, phosphocreatine; ATP, adenosine triphosphate.

Despite these differences, all ³¹P Z-magnetizations reach a nearly thermal equilibrium state (> 0.9999 $M_z^o$ for in vivo and > 0.965 $M_z^o$ for the “no exchange” model) after a long recovery period τ = 24 sec (Figure 2a and 2b). In terms of the magnetization change, the recovery is much more efficient in the early period of τ than in the late period. A major portion of magnetization is already recovered at short τ = 4 sec (Pi: 75%, PCr: 80%, α-ATP: 85%, β-ATP: 90% and γ-ATP: 95%). This means that shortening sequence repetition time (TR) is an effective strategy to improve SNR and time-efficiency in data acquisition. For example, instead of spending a long recovery period of τ = 24 sec to achieve $M_z^o$, fast sampling with τ = 4 sec allows more accumulations (NA = 6). Though each sampling leads to a reduced Z-magnetization ($M_z^{\ast }$), the accumulated magnetization 6 $M_z^{\ast }$ is multiple-fold greater than $M_z^o$ ($6M_z^{\ast }∕M_z^o$ ratio: Pi, 3; PCr, 4.8; α-ATP, 5.1; β-ATP, 5.4 and γ-ATP, 5.7).

Band Inversion Module-I

The intent of band inversion Module-I is to measure CK-catalyzed kinetic reaction PCr → γ-ATP by detecting the MT effect at PCr through co-inverting γ-ATP with α- and β-ATP. As shown in Figure 3, following band inversion of α-, β- and γ-ATP, the un-inverted PCr signal falls for a short period (~ 0.8 sec); then it gradually rises back, as anticipated for a typical inversion transfer phenomenon. With TR = 4 sec, the depth of the fall is measured 36%, in reference to the Z-magnetization at steady state without inversion. Half of this fall (18%) is counted as partial saturation effect, as evident from the magnitude of PCr signal at t_d ~ 0 (Figure 3b).

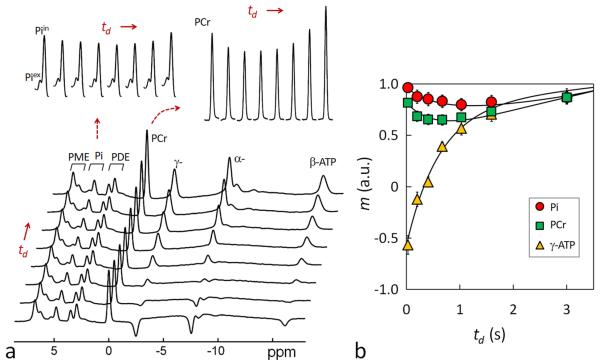
FIG. 3.

(a) A group-averaged ³¹P MR spectral series acquired from the resting human brain at 7T using band inversion module-I at constant TR 4 sec and varying inversion delay time t_d = 25, 197, 405, 668, 1026, 1589, and 3000 msec (n = 6 subjects). For comparison, the last trace of the spectral series represents a brain ³¹P MR reference spectrum acquired at TR 4 sec without applying the inversion pre-pulse. The magnetizations measured in the reference spectrum were used for normalizing the magnetizations of the t_d series. The inset displays the time course of Pi and PCr signals with respect to inversion delay t_d. Note the MT effects at PCr and Pi manifested as a “fall-rise” biphasic change. (b) Plots of normalized ³¹P magnetizations at different inversion delay t_d and the fitted curves according to the 5-spin exchange model illustrated in Figure 1b. For clarity, only Pi, PCr and γ-ATP datasets are shown.

Similar to PCr, the Pi signal also shows a “fall-rise” biphasic trend with t_d. This is induced by the MT effect between Pi and γ-ATP, reflecting kinetic reaction Pi → γ-ATP catalyzed mainly by ATPase. Compared to PCr, Pi’s maximal MT effect is smaller (15% vs 18%), and it occurs at a later time (t_d ~ 1.2 vs 0.8 sec).

Band Inversion Module-II

Module-II aims to measure ATPase-catalyzed kinetic reaction Pi → γ-ATP by detecting the MT effect at Pi through co-inverting γ-ATP with PCr, α- and β-ATP. Unlike in Module I, PCr is also inverted in Module II (Figure 4) in order to use it as a magnetization buffer to amplify the MT effect between Pi and γ-ATP. Indeed, with Module II, the MT effect at Pi is increased by 1/3, as compared to Module I (20% vs. 15%, Figures 3 and 4). Accompanied by this increase, γ-ATP signal recovers at a slower rate following co-inversion with PCr (Figures 3b vs 4b).

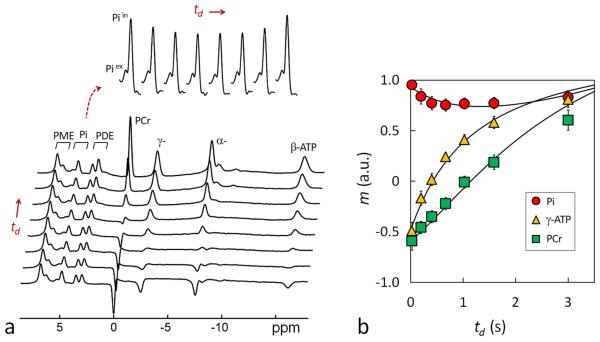
FIG. 4.

(a) A group-averaged ³¹P MR spectral series acquired from the resting human brain at 7T using band inversion module-II at constant TR 4 sec and varying inversion delay time t_d = 25, 197, 405, 668, 1026, 1589, and 3000 msec (n = 6 subjects). For comparison, the last trace of the spectral series represents a brain ³¹P MR reference spectrum acquired at TR 4 sec without applying the inversion pre-pulse. The magnetizations measured in the reference spectrum were used for normalizing the magnetizations of the t_d series. The inset displays the time course of Pi signals with respect to inversion delay t_d. Note the MT effect at Pi manifested as a “fall-rise” biphasic change. (b) Plots of normalized ³¹P magnetizations at different inversion delay t_d and the fitted curves according to the 5-spin exchange model illustrated in Figure 1b. For clarity, only Pi, PCr and γ-ATP datasets are shown.

Band Inversion Module-III

Module-III measures ATP ³¹P-³¹P cross-relaxation between two neighboring spin pairs α- ↔ β-ATP and γ- ↔ β-ATP. For this purpose, both α- and γ-ATP are inverted together with Pi, PCr, while the MT effect at β-ATP is observed. The large inversion band also covers PCr and Pi signals to further enhance the transfer effect between γ- and β-ATP. As anticipated, following co-inversion of Pi, PCr, α- and γ-ATP, a clear “fall-rise” biphasic pattern was observed for β-ATP (Figure 5). The maximal β-ATP reduction was 16%, occurred at inversion delay t_d ~ 0.84 sec (Figure 5).

FIG. 5.

(a) A group-averaged ³¹P MR spectral series acquired from the resting human brain at 7T using band inversion module-III at constant TR 4 sec and varying inversion delay time t_d = 25, 197, 405, 668, 1026, 1589, and 3000 msec (n = 6 subjects). For comparison, the last trace of the spectral series represents a brain ³¹P MR reference spectrum acquired at TR 4 sec without applying the inversion pre-pulse. The magnetizations measured in the reference spectrum were used for normalizing the magnetizations of the t_d series. The inset displays the time course of β-ATP signal with respect to inversion delay t_d. Note the MT effect at β-ATP manifested as a “fall-rise” biphasic change. (b) Plots of normalized ³¹P magnetizations at different inversion delay t_d and the fitted curves according to the 5-spin exchange model illustrated in Figure 1b. For clarity, only α-, β- and γ-ATP datasets are shown.

Data Fitting

To evaluate T₁, k and σ parameters, the m(t_d) ~ t_d datasets were fitted according to the Bloch-McConnell-Solomon magnetization formalism described in Equations [1-7] based on the 5-pool exchange model (Figure 1b). The m(t_d) ~ t_d datasets contain a total of 35 data points (= 7 t_d data points × 5 spins) for individual module fitting, or 70 data points (35 × 2) for paired module fitting (a combination of two different modules), or 105 data points (=35 × 3) for integrated module fitting (a combination of all 3 modules). On average, consistent T₁, k and σ results were obtained from all these fitting approaches, especially the integrated and paired module fittings (k_{Pi → γ-ATP}: 0.17 – 0.23 sec⁻¹, k_{Pi → γ-ATP} : 0.37 – 0.42 sec⁻¹, σ. −0.19 – 0.20 sec⁻¹, T_1,Pi: 6.64 – 7.61 sec, T_1,PCr: 5.74 – 6.65 sec, T_1,γATP: 0.97 – 1.00 sec, T_1,αATP: 0.93 – 0.96 sec, and T_1,βATP: 0.66-0.69 sec, Table 1). The T₁ values are in the order of Pi > PCr > γ-ATP ~ α-ATP > β-ATP (Table 1), with one order of magnitude difference between Pi (~ 7 sec) and β-ATP (~ 0.7 sec).

Using the cross-relaxation rate constant σ, ATP rotation correlation time τ_c was estimated to be (0.8 ± 0.2) ·10⁻⁷ sec in human brain.

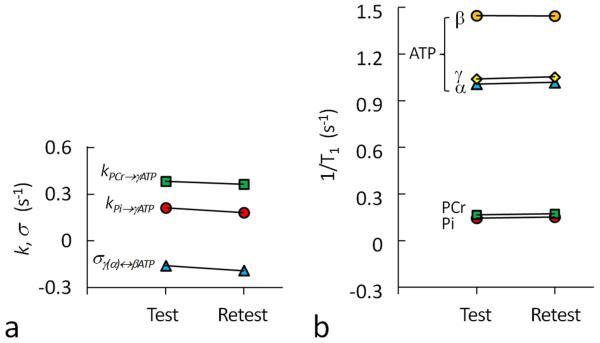
Reproducibility

To examine the reproducibility of the short-TR measurements, each of the three band inversion modules was repeated once after 30 min. This yielded two sets of measurements referred to as test and re-test. As plotted in Figure 6, the T₁, k and σ results are comparable between test and re-test, as measured by parameter coefficients of variation (k_{Pi → γ-ATP}, 10%; k_{PCr→ γ-ATP}, 4%; σ, 13%; T_1,Pi, 4%; T_1,PCr, 3%; T_1,γATP, 1%; T_1,αATP, 2%; and T_1,βATP, 1%). The k and σ values are found to be slightly reduced in re-test as compared to test (k_{Pi → γ-ATP}: 0.21 vs. 0.18 sec⁻¹, k_{PCr→ γ-ATP} : 0.38 vs. 0.36 sec⁻¹, and σ: −0.16 vs. −0.19 sec⁻¹).

FIG. 6.

(a) Comparison of rate constants k_Pi→γATP, k_PCr→γATP, σ_γ↔βATP (σ_α↔βATP) and 1/T₁ for Pi, PCr, α-, β- and γ-ATP between “test” and “retest” experiments, showing the reproducibility of short-TR band inversion performance at 7T. The results are from integrated fitting using ³¹P magnetization data acquired from all three modules as illustrated in Figure 1c.

DISCUSSION

Time-efficiency with Short-TR Sequence

The presence of multiple co-existent MT pathways among high-energy phosphates in vivo poses a hurdle to accurate and efficient measurement of ATP metabolism and basic NMR parameters by ³¹P MRS methods. The present work addressed this issue by using short-TR multiple band inversion modules.

We demonstrated that shortening TR to 4 sec from 25-30 sec leads to significant improvement in scan efficiency with a ~ 3-4-fold reduction in data acquisition time for an equivalent band inversion experiment (8 min vs 20 min (20) and 30 min (19)). This occurs without compromising the typical “fall-rise” biphasic feature that characterizes the observed spin in an inversion transfer experiment (Figures 3a-5a). The maximal MT effects measured by short-TR approach are comparable to those by the long-TR counterparts (19, 20).

Evaluation of Kinetic and Relaxation Parameters

Brain high-energy phosphates form a 5-spin exchange system composed of Pi, PCr, α-, β- and γ-ATP (Figure 1b). For such a complex system, a complete description of the evolution of all its Z-magnetizations under the entire IR sequence can be overwhelming by the classical Bloch-McConnell-Solomon equations which are generally presented in derivative form in literature (16). This work presented a more concise formula using normalized Z-magnetization in matrix format, by which the evolution of magnetization in each step of the IR sequence can be described mathematically (Eqs. [1-7]). An attractive feature of this format is that all the unknowns – the kinetic and relaxation parameters of the spin system – are included in the so-called ER matrix A (Eq. [3]), clearly separated from the vector of measurable magnetizations (Eq. [2]). This makes it convenient to evaluate the unknown parameters using a Matlab program.

Importantly, the magnetization equations (Eqs. [1-7]) derived for the 5-spin exchange model (Figure 1b) fit reasonably well with the ³¹P experimental data acquired under all three band inversion modules (Figures 3b-5b). The resultant T₁, k and σ parameters are consistent with the findings in human brains by long-TR band inversion approaches (19, 20) and by ST (9), as compared in Table 1. It should be noted that, except the ER matrix A (Eq. [3]) and the magnetization vector (Eq. [2]), which are specific to the 5-spin system illustrated in Figure 1b, the remaining equations can be extended, in principle, to other spin systems, regardless of the exchange pattern.

In this work, the equilibrium magnetization ratios for PCr/ATP and Pi/ATP were determined independently from the fully relaxed spectrum acquired at TR = 25 sec and NA = 6. The data acquisition time for recording this spectrum (2.5 min) can be saved if one chooses to include the magnetization ratios (PCr/ATP and Pi/ATP) in the fitting of experimental datasets m_ref, but at a cost of increased uncertainty in fitting parameters k, σ and T₁. Another option to consider in cutting scan time is to solve the matrix A for the additional free parameters Pi/ATP and PCr/ATP with input of an extra spectrum at a shorter TR, for instance TR 15 s. This could save 1 minute of scan time.

Band Inversion Modules

Three different band inversion modules were investigated, each targeting a particular MT pathway in the exchange system: CK-catalyzed kinetic pathway PCr → γ-ATP by Module-I, ATPase-catalyzed kinetic pathway Pi → γ-ATP by Module-II, and ATP intramolecular cross-relaxation pathway γ-(α-) ↔ β-ATP by Module-III. These three modules differ only in the center frequency of the inversion band. Through co-inversion of multiple spins, each of these modules aims to amplify the MT effect in a selected pathway by taking advantage of the “magnetization buffer” effect created by other MT pathways in the system.

Together, these three modules provide an array of m(t_d) ~ t_d datasets that contain both inverted and un-inverted magnetizations for the observed ³¹P spins (Pi, PCr and β-ATP). Such balanced data structure contributes to reducing potential confounding factors in curve fittings of the 5-spin exchange system which is governed by multiple parameters (a total of 8 parameters were evaluated here: 5 T₁’s, plus 2 k’s, plus 1 σ). However, it is possible to further improve fitting reliability by adding more inversion models that are not studied in this work. For example, one can co-invert Pi and PCr while observing MT effects at un-inverted ATP spins. The inclusion of this later module in the band inversion repertoire could contribute to γ- and α-ATP dataset balance and hence might further reducing fitting uncertainty for the whole system. However, with more modules added, data redundancy may arise and this may compromise the original intent of time-efficiency.

Data Fitting

In this study, a total of 15 m(t_d) ~ t_d datasets were generated for the 5-spin system by three band inversion modules. Fitting these data together yielded an integrated solution for the 8 unknown parameters as listed Table 1. To address the practical question of utilizing minimal datasets to achieve similar results, i.e, to balance between efficiency in data acquisition and accuracy in data analysis, we also performed data fitting using just two of the modules, referred to as paired fitting. This leads to three different combinations: Module I & II, Module I & III, and Module II & III. As compared in Table 1, Module I & III overall is superior to Module I & II and Module II & III, yielding very similar results in T₁, k, and σ values as the integrated fitting. This is not surprising, given that a combination of Modules I and II, like a combination of all three modules, provides a set of m(t_d) ~ t_d dataset balanced with inverted and un-inverted magnetizations for Pi, PCr and β-ATP.

Attempts were made to fit the data from the single modules. We noticed that fitting with Module I alone led to a relatively higher k_PCr→γATP value and shorter T_1,PCr value. Similarly, fitting with Module II alone led to a relatively higher k_Pi→γATP value and shorter T_1,Pi value (data not shown). The conclusion is that, for a multi-parameter fitting with limited data points, it is necessary to have a balanced data structure in order to reduce fitting uncertainty. Specifically, for an accurate evaluation of k_Pi→γATP (or k_PCr→γATP), the fitting should include not only the dataset with Pi (or PCr) as the observed spin (un-inverted) but also the dataset with Pi (or PCr) as the inverted spin.

For this cohort of subjects (n = 6), with integrated fitting, the kinetic rate constant k_Pi→γATP for the resting human brain was found to be 0.19 ± 0.04 sec⁻¹. This is comparable to the 0.21 sec⁻¹ reported by us previously using long-TR band inversion module II (19) and 0.18 sec⁻¹ by Du et al using ST method (23), both for human brain. The integrated fitting also yielded a rate constant of 0.38 ± 0.02 sec⁻¹ for k_PCr→γATP, as compared to 0.29 sec⁻¹ accessed by using γ-ATP selective saturation approach and 3-pool fitting model (23).

It should be pointed out that there is a large partial saturation effect of 18% at PCr with module I immediately following the band inversion, presumably due to the direct off-resonance effect from the adiabatic inversion pulse (Figure 1). This partial saturation effect was taken into account as approximate initial magnetization m(0) during data fitting. The MT effects observed in the t_d period do not contain any contamination from the off-resonance effect since there is no further pulsing (B₁ = 0) during the entire inversion recovery period. This is different from the ST mechanism by which off-resonance-induced magnetization reduction keeps growing with an increase in pulsing duration; such contamination should be appropriately corrected at each time point if present.

In addition to kinetic rate constants, the integrated fitting also provides quantitative measurements for ATP ³¹P T₁ and cross-relaxation in the resting human brain. The cross-relaxation rate constant σ value was found to be −0.19 ± 0.04 sec⁻¹, which is consistent with our previous results (−0.21 sec⁻¹) obtained by long-TR band inversion module-III (20). The σ-derived ATP rotation correlation time τ_c was measured (0.8 ± 0.2) ·10⁻⁷ sec. ATP T₁ relaxation time was 0.7 – 1.0 sec, significantly shorter than that found for Pi (7.3 sec) and PCr (6.0 sec). A similar trend has been noticed previously in the human brain (19) and skeletal muscle (16). The relative shorter T₁ relaxation time in ATP ³¹P spins was mainly attributed to the presence of the chemical shift anisotropy effect in ATP (20).

The good performance of the short-TR band inversion modules is further supported by the highly reproducible T₁ relaxation rate measurements between “test” and “retest” (Figure 6b). In contrast, both kinetic rate constants and cross-relaxation rate constants were slightly reduced in “retest”, as compared to in “test” (k_{Pi → γ-ATP}: 0.21 vs. 0.18 sec⁻¹, k_{PCr→ γ-ATP} : 0.38 vs. 0.36 sec⁻¹, and σ: −0.16 vs. −0.19 sec⁻¹). This might reflect decreased de novo ATP synthesis and CK activity together with a slowdown of ATP rotation movement in cellular space while at rest in the scanner.

Interestingly, while the T₁ relaxation values for both Pi and PCr were very similar between the human brain (Table 1) and human skeletal muscle (16), this is not the case for ATP T₁ relaxation. It is noticed that ATP T₁ values in the brain (0.7 – 1.0 sec) are significantly shorter than in skeletal muscle (1.1-1.7 sec, ref (16)). The reason for this difference is unclear at present, and it would be worthwhile to explore it further in the future using the same technique.

Like in the brain, the framework of the short-TR band inversion approach can also be applied to measure kinetic and relaxation parameters in other organs such as skeletal muscle. For a human skeletal muscle application, some fine-tuning on sequence parameters may be required, given the difference in metabolism between these two organs. For instance, in skeletal muscle, the rate constant for de novo ATP synthesis is about 3-4 fold smaller than that found in the human brain (k_Pi→γATP: 0.05 – 0.07 sec⁻¹ vs 0.18 – 0.21 sec), while the phosphocreatine magnetization buffer size, as measured by ratio [PCr]/[Pi], is about 2-fold larger in human skeletal muscle than in the human brain ([PCr]/[Pi]: 9.4 vs 4.8 refs.(16,20)). This leads to a much delayed transition point for the biphasic change of the MT effect at Pi in human skeletal muscle than in the human brain (~ 3.5 sec vs 1.2 sec). Therefore, for module II band inversion, the TR and t_d parameters should be increased substantially in order to capture a well-defined “fall-rise” biphasic MT effect at Pi in human skeletal muscle.

As we demonstrated previously (19), the brain ³¹P spectrum is characterized by the presence of two pools of inorganic phosphates, with well separated resonance signals (5.2 ppm vs 4.8 ppm). These two pools of Pi have distinctly different metabolic features due to being located in different cellular spaces (19). The major one at relatively upfield, assigned to intracellular Pi, is sensitive to γ-ATP inversion and hence metabolically active, while the minor one at relatively downfield, assigned to extracellular Pi, is insensitive to γ-ATP inversion and therefore metabolically inactive. The findings in the current study, as shown in Figures 3 and 4, are consistent with our previous observation at long TR (19). Our assignments are also supported by a recent ST study at 11.7 T using animal model (24).

With short TR 4 sec, the data acquisition time for each module is shortened to 8 min, as opposed to 30 min with long TR (19). Admittedly, this is still too long for routine clinical applications. In addition to reducing the number of scan average, several existing strategies can be used to further speed up the data acquisition, such as compressed sensing with random sparse t_d/τ data sampling (25), and multiple receiver acquisition (26). More recently, the feasibility has been demonstrated to combine short-TR band inversion with localized ³¹P MRS techniques such as single-voxel and 2D ISIS (27). More technical advances are expected to further improve the efficiency and accuracy of band inversion for measuring ATP metabolism.

In summary, we have demonstrated that band inversion can provide an integrated solution for evaluating multiple parameters related to ATP metabolism and basic NMR relaxation properties in the high-energy phosphate exchange system in the human brain. With the short-TR approach, the data acquisition efficiency are multiple-fold improved, while the common MT features can still be preserved. With further improvement, we expect that this MT technique could become clinically practical for the studies of patients with neurodegenerative diseases in which currently there is a lack of non-invasive imaging modality in evaluating the ATP energy metabolism.