Modeling protein–DNA binding via high-throughput in vitro technologies

Abstract

Protein–DNA binding plays a central role in gene regulation and by that in all processes in the living cell. Novel experimental and computational approaches facilitate better understanding of protein–DNA binding preferences via high-throughput measurement of protein binding to a large number of DNA sequences and inference of binding models from them. Here we review the state of the art in measuring protein–DNA binding in vitro, emphasizing the advantages and limitations of different technologies. In addition, we describe models for representing protein–DNA binding preferences and key computational approaches to learn those from high-throughput data. Using large experimental data sets, we test the performance of different models based on different measuring techniques. We conclude with pertinent open problems.

Introduction

The cell is equipped with several tools for regulating the amount of proteins it produces from each gene in a given condition—chromatin state, RNA interference, RNA editing and alternative splicing, to name a few. Perhaps the main regulatory mechanism is the transcriptional program, which describes when and to what extent each gene is transcribed to mRNA. Transcription is controlled primarily via regulatory sequence elements, located in the proximity of each gene's coding sequence. These are recognized and bound by specialized proteins, called transcription factors (TFs). Most TFs interact with DNA in a sequence-specific manner and this binding enhances (or prevents) the recruiting of polymerase for transcription initiation. As a consequence, the set of TFs that bind to the DNA and the intensity, or affinity, of these bindings affect the rate of transcription of the corresponding gene. Thus, different combinations of TFs and binding affinities can produce a huge variety of transcription profiles.

The DNA sequences bound by a TF are called its binding sites (BSs), or cis-regulatory elements. They are typically very short (6–15 bases) and degenerate [1]—a TF can bind, with varying affinities, to many different sequences that reflect a common pattern, called ‘motif’, which is characteristic of the factor. BSs may be found in the promoter, which is the region upstream of the gene's transcription start site (TSS), as well as downstream of the TSS and at large distance from the gene, in locations termed enhancers [2]. Some TFs are organized in cis-regulatory modules (CRM), a DNA segment bound by multiple TFs that cooperatively regulate specific genes, resulting in more complex and specific transcription profiles [3]. Reverse-engineering the transcriptional program of an organism requires identifying its TFs, the locations and affinities of their BSs, and the various CRMs they form and the target genes they regulate.

Deciphering protein–DNA binding in vivo is arguably the holy grail in understanding gene regulation, but it is a difficult task [4]. While TF binding is sequence specific, it is affected by many factors (an overview of these can be found in [5]): (1) the DNA has to be accessible for binding by the TF [6, 7]; (2) other TFs may compete for the same BSs, making it harder for the TF to bind to its potential BSs [8]; (3) in some instances, the TFs may only bind cooperatively, but current high-throughput technologies cannot distinguish between direct and indirect binding [9]; (4) many TFs are expressed or active in only specific cells or conditions; (5) DNA may be modified or shaped in a way that influences binding. On top of that, the set of BS sequences present in a genome is limited and does not cover all possible binding sequences. As a result, one cannot derive the full range of TF binding affinities from in vivo binding data. Learning the DNA binding preferences of a TF from in vivo data is hence hampered by assay complexity.

In contrast, in vitro data may enable a cleaner high-resolution measurement of TF-DNA binding preferences, as there are fewer confounding factors [10]. First, one can guarantee that no BSs are inaccessible owing to compressed chromatin. Second, there are no competing TFs and no co-factors are involved, as the experiment is performed using a single TF in a synthetic environment. Third, in some cases, the set of sequences tested for binding can be combinatorially designed to cover all words of the desired length k. In other cases, they are randomly generated such that together they are guaranteed to cover nearly all k-mers (DNA words of length k). So, if technological biases can be handled, the TF–DNA binding signal is expected to be much clearer.

Thanks to advancements in microarrays and sequencing technologies, high-throughput measurement of protein–DNA binding in vitro has been possible for several years now. The high-quality experimental data are later dissected using computational approaches that try to model protein–DNA binding and use these models for in vivo prediction. This review aims to cover the most prominent technologies for measuring protein–DNA binding, computational approaches for learning binding models from them and open problems in the field.

While the review focuses on the most prominent technologies, protein–DNA binding models and algorithms to infer them, many other technologies, models and algorithms exist and are not covered here owing to space constraints (see [11]). Moreover, we only sketch experimental details of in vivo and in vitro technologies.

Technologies that measure TF–DNA binding in vitro

Identifying the sites bound in vivo by a specific TF and their affinity was initially applied to few short, hand-chosen genomic loci by methods like DNA footprinting or chromatin immunoprecipitation (ChIP). The combined strategy of ChIP and promoter microarrays, also termed ChIP-chip, enables genome-wide identification of promoter segments that are bound by a specific TF, in a single experimental assay [12]. Replacing the microarray-based readout with high-throughput sequencing technologies, an approach called ChIP-seq, allows the detection of BSs throughout the entire genome [13].

Measuring protein–DNA binding in vitro gives a cleaner view of the TF binding preferences, but lacks the genomic context and does not depend on specific cell types and conditions. Because in vitro experiments are cheaper and easier, it is highly appealing to combine in vitro models with genomic information to predict in vivo binding (as discussed in detail below). In vitro technologies can measure several thousand binding events simultaneously, and report the binding intensity to each possible DNA k-mer. Using this information, the effects of mutations in the BSs can be predicted and ultimately help understand individual differences, cross-species divergence and the involvement of mutations in genetic disorders [14, 15]. Popular techniques that measure in vitro TF–DNA binding in high throughput include protein-binding microarrays (PBMs) and high-throughput SELEX (HT-SELEX).

Protein-binding microarrays

Universal protein-binding microarrays (uPBMs) are designed to measure protein–DNA binding intensity in a high-throughput and unbiased manner [16]. An array contains >41000 double-stranded DNA (dsDNA) probes, each containing a unique sequence of length 36 bp. These are designed to collectively cover all DNA 10-mers [17]. The tested protein binds some of the probes, and its binding intensity is measured using fluorescent tags (see [Figure 1A]). The final output of the experiment is the set of probe sequences and the binding intensity of the protein to each one. uPBMs can be used to test different proteins, without the need to redesign the probe set, as their content is universal. They provide accurate measurements for studying TF specificity, and in particular robust 8-mer binding scores, as each 8-mer appears multiple times in different 10-mers. uPBMs have been successfully applied to thousands of proteins [19].

Figure 1.

High-throughput in vitro technologies for measuring protein–DNA binding. (A) Overview of universal PBMs. These arrays are designed to include all possible DNA 10-mers in 36 bp long probe sequences. Protein binding intensity is measured using a fluorescent antibody. The experimental output is a list of > 41000 probe sequences and the binding intensity of the protein to each. [Adapted by permission from Macmillan Publishers Ltd: Nature Biotechnology [16], copyright (2006)]. (B) Overview of HT-SELEX. Each experiment starts from a random set of fixed-length oligonucleotides (lengths vary from 10 to 40 bp). The protein binds its BSs in the pool and the bound oligonucleotides are extracted and amplified. Some of these oligonucleotides are sequenced, and the rest are used in reiteration of the process. The experimental output is several sequence files, one per iteration. [Adapted by permission from CSHL Press: Genome Research [18], copyright (2010).]

An alternative to uPBMs are custom PBMs [20], which contain probes designed to study in detail variations of a particular BS. Several studies used them recently to test DNA binding of certain proteins [20–23]. A different technology, mechanically induced trapping of molecular interactions (MITOMI), based on microfluidics, measures protein–DNA binding to >1400 probe sequences covering together all 8-mers, each containing a unique subsequence of length 52 bp [24]. While MITOMI has lower throughput than uPBMs, it has the advantage of measuring absolute binding affinities as opposed to specificities, which are measured by PBM technologies. Additional approaches to measure protein–DNA binding, such as HiTS-FLIP [25] and B1H [26], are reviewed in [5, 10, 11].

High-throughput SELEX

HT-SELEX measures the binding of a single protein to millions of oligonucleotides over several enrichment cycles [18, 27]. Initially, a pool of pseudo-random fixed-length oligonucleotides is used. Oligonucleotide lengths in current implementations range from 10 to 40 bp. The protein binds to a subset of oligonucleotides in the pool. The set of bound oligonucleotides is retrieved, the protein is detached from them, they are amplified to form a new pool and a sample from that pool is sequenced. The new pool is then used as the initial sequence set for the next cycle. As the specificity of the oligonucleotides in the pool increases from one cycle to the next, so does the proportion of the bound oligonucleotides. The output is several sets of sequences, each corresponding to a different cycle. Each set contains from hundreds of thousands to tens of millions in current implementations. Figure 1B shows a schematic of the process. Recent studies have used HT-SELEX to measure the binding preference of hundreds of human, mouse and fruit-fly TFs [28, 29]. A similar technology to HT-SELEX that was developed in parallel is SELEX-seq, albeit the latter has been applied to much fewer proteins to date [30].

Comparison of PBM and HT-SELEX

Because both PBM and HT-SELEX aim to measure in high-throughput protein–DNA binding in vitro, it is important to evaluate the techniques in terms of accuracy, robustness and experimental noise. A recent comparison found that, on the whole, models derived from these technologies mostly agree [31]. The disagreements are limited to several TF families, such as Sox proteins and zinc fingers. One advantage of PBM technology is that its data allow better ranking of k-mers according to their binding intensities, compared with HT-SELEX data [31]. Moreover, while PBMs measure binding to both high- and low-affinity k-mers in the same way, results of advanced cycles in HT-SELEX may suffer from over-specification: they typically cover high-affinity k-mers well, but these may be over-represented at the expense of low-affinity k-mers. On the other hand, HT-SELEX-derived models were found to be more accurate in predicting in vivo binding [31], mostly owing to their ability to measure binding to longer k-mers (uPBMs are limited to scoring with good confidence k-mers with k ≤ 8, owing to space constraints of the microarray [16]).

PBM and HT-SELEX data repositories

High-throughput in vitro protein–DNA binding data can be found in several databases. Here we mention the most comprehensive and useful resources.

1. UniPROBE contains >400 PBM experiments covering different protein families and model organisms, mostly generated by Martha Bulyk's lab [32]. Each experiment includes the raw experimental data, probe sequences and binding intensities, 8-mer scores, binding models in position weight matrix (PWM) format learned by the Seed-and-Wobble and BEEML-PBM algorithms, and motif logos. The data can be downloaded in bulk, by study or by TF.

2. HT-SELEX data cannot be found in one inclusive database, but in the different studies. The most comprehensive studies cover >500 human and mouse TFs [28] and >240 fruit-fly TFs [29], both from Jussi Taipale's lab. The sequencing data can be downloaded from GEO database [33], while the inferred models can be found in the supplements of the papers.

3. CIS-BP is the most comprehensive database. The database includes >1000 PBM experiments from Tim Hughes's lab and other sources [14]. For each protein, probe sequences and binding intensities, 8-mer scores, binding models in PWM format learned by PWM-Align-Z, PWM-Align, FeatureREDUCE and BEEML-PBM, and motif logos, are available. It also includes models inferred by protein sequence similarity (as opposed to direct experimental data) for >40% of eukaryotic TFs in >300 species, and models based on other experimental sources (e.g. PBMs from other labs, HT-SELEX, ChIP-seq experiments and JASPAR and TRANSFAC databases [34, 35]).

Models for BS motifs

Several computational models have been developed for describing BS motifs. The models differ in complexity and interpretability. We review here the two most common models at the two extremes of the complexity spectrum.

Position weight matrix

The most popular model is the position weight matrix (PWM) [36]. This model represents a motif of k bases by a 4 × k weight matrix P, where p_b,i is the weight of base b in position i (see Figure 2A). The binding score assigned to a given k-mer w  =  w₁w₂…w_k is simply the sum of the corresponding matrix elements, i.e. ${\displaystyle \sum _{i=1}^k{p}_{w_i,i}}$. Thus, an inherent property of this model is position-independence: weights at different positions are assumed to be independent. The weight may be, for example, a log-probability or the free energy contribution of that nucleotide in that position. Equivalently, the model can be presented by a 4 × k position frequency matrix F, where f_b,i is the probability of observing nucleotide b at position i in the motif, and the probability of k-mer w is the product ${\displaystyle \prod _{i=1}^k{f}_{w_i,i}}$. F can be easily converted to P by taking the logarithms of its elements. Among the advantages of the PWM model are its simplicity, small number of parameters and an intuitive visualization [38]. The logo format (Figure 2A) visualizes the matrix by drawing the different nucleotides in each position in size according to their weights and ordered by their weights. The total height of each position is proportional to its information content (IC), which is an entropy-based score that measures the specificity of positions in a PWM model [39]. The score ranges from 0 to 2; positions with only one possible nucleotide have an IC of 2, while positions wherein all four nucleotides are equi-probable have an IC of 0. Generally, more specific positions are higher than less specific ones.

Figure 2.

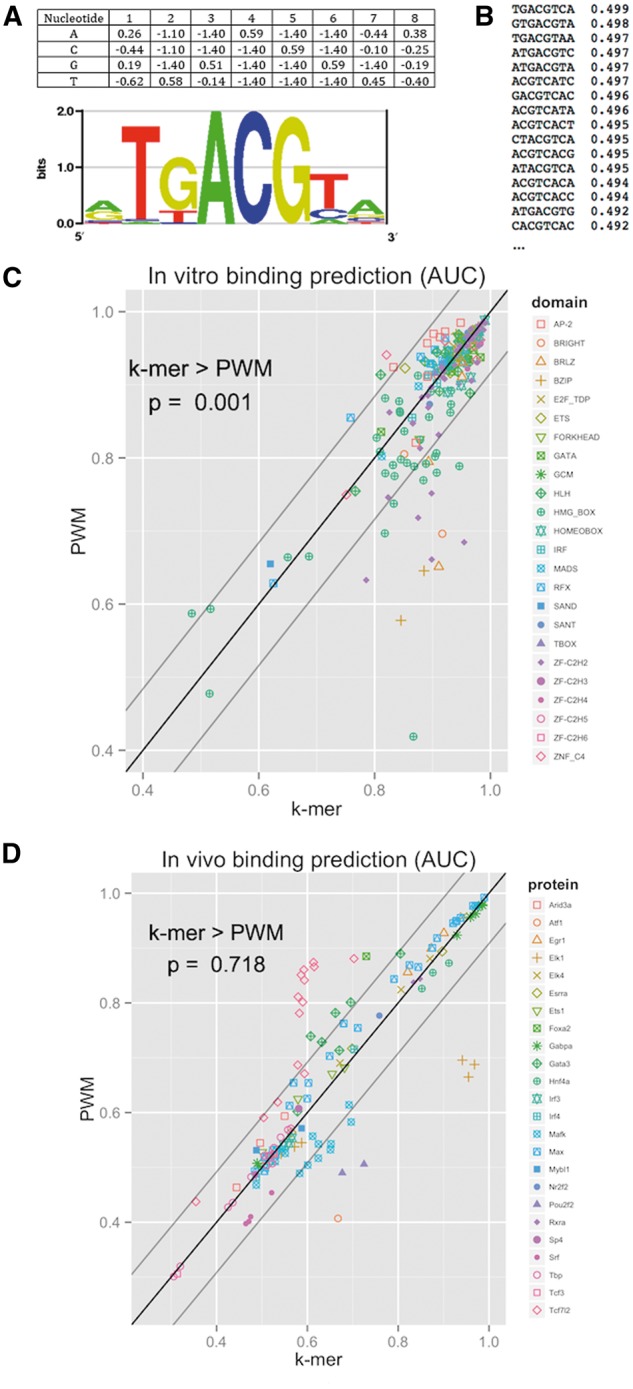
Models for protein–DNA binding preferences. (A) Position weight matrix. The matrix represents scores for each nucleotide position (eight in the example). The PWM logo plots the nucleotides by their weights and position entropy. The PWM and logo are of protein ATF1 (downloaded from CIS-BP [14], motif id M0295_1.02, generated by PWM-Align-Z). (B) K-mer model. Each k-mer is assigned a binding score. The example shows the top 16 8-mers and their E-scores for protein ATF1 (downloaded from CIS-BP, M0295_1.02). Note that multiple 8-mers correspond to different windows with respect to ATF1 ‘core’ motif (TGACGT). (C) Performance of PWM and k-mer models in in vitro prediction. For each paired PBM experiment (two experiments performed with the same TF using two arrays, each with a different probe design), a model was trained on data of one array and tested on the other. The AUC score reflects the accuracy in ranking positive probes at the top (see [37] for definitions). Two hundred fourteen experiments (covering 98 proteins) were included in the comparison. (D) Performance of PWM and k-mer models in in vivo prediction. For each ChIP-seq experiment, a model was trained on PBM data of the same TF and tested in ranking the top 500 peaks higher than a set of 500 control sequences from nearby genomic regions (see [37] for details). One hundred thirty-seven ChIP-seq experiments, covering 20 TFs, were used in the comparison. In C and D, gray lines stand for ±1 standard deviation (std) of AUC difference. P-values were calculated using Wilcoxon rank-sum paired test.

K-mer model

While the PWM model is popular and useful, it might be too simplistic for some TFs. The assumption of position independence made by that model has been shown to be untrue for some TFs [40, 41]. The most comprehensive model, assuming that k positions affect the binding, is the complete k-mer model [30]. In this model, every possible DNA k-mer has a binding score representing the affinity of the TF to it (Figure 2B). One way for visualizing the k-mer model is by its ‘specificity landscape’ in which k-mer scores are plotted in cycles corresponding to Hamming distances (the number of mismatches between two k-mers), allowing an assessment of the effect of single mismatches on the binding intensity [42]. One disadvantage of this model is the huge number of parameters, which may lead to over-fitting the model to experimental noise and technological artifacts [43].

Other models of intermediate complexity between PWM and all k-mers model are often extensions of the PWM by additional features. The most prominent features are di-nucleotide dependencies. To avoid the complexity of having too many features, usually only adjacent positions are considered, as dependence between neighboring positions was observed more often than between non-neighboring ones [44, 45].

Comparison of PWM and k-mer models

The PWM model has been the most popular model for years. However, high-throughput data in recent years have clearly demonstrated that the model is sometimes inaccurate, and more complex models are needed to allow position dependencies and understand the biological mechanism underlying protein–DNA binding. We performed a comparison of the models based on the most up-to-date data. In Figure 2C, we compared the accuracy achieved in prediction of both in vitro (PBM) and in vivo (ChIP-seq) binding by the PWM and k-mer models, inferred from PBM data using BEEML-PBM and average binding intensities, respectively. Sequence binding scores are the sum of their k-mer scores. (Note that the results of the comparison depend on the algorithm used. While BEEML-PBM is currently one of the two best known algorithm for PBM data [43], a future algorithm may fare better.) While the k-mer model is more accurate in predicting binding both in vivo and in vitro, its advantage is significant only in vitro, and it shows a profound improvement in accuracy (i.e. difference ≥2 SDs) for few proteins in vitro. The simplicity of the PWM and its interpretable visualization make it still the model of choice in the majority of the studies, while being only slightly less accurate than more complex binding models [43]. Note also that prediction of in vivo binding is much harder for both models, as reflected in much lower area under the curve (AUC) scores (the area under the receiving-operating curve, which evaluates binding predictions in terms of how well they rank positive sequences higher than negative ones [46]) (Figure 2D).

Motif finding methods and tools

Over the past several years, a variety of computational methods were developed for analyzing PBM and HT-SELEX experimental data. These methods suggest novel biological hypotheses in the shape of protein–DNA binding models, which can then be tested in vivo by further experiments, such as ChIP-seq. The challenge for such methods is that BSs are short and degenerate, and DNA probes are longer than typical BSs and thus may contain many putative sites, so it is difficult to distinguish between specific and nonspecific (background) binding. Moreover, each technology suffers from biases, which produce artifacts that may distort the measured intensities. Algorithms aim to extract the signal, i.e. the binding preferences of the TF, and distinguish it from the noise (background binding and technological biases). In genomic sequences, this challenge is known as the ‘motif discovery problem’: the computational challenge of constructing a TF motif or binding model based on experimental data on TF-DNA binding, and/or identifying the BSs in sequences. When the model parameters are unknown, the problem is termed the de novo motif discovery problem. De novo motif discovery has been tackled using a myriad of algorithmic techniques, such as Expectation Maximization (MEME [47]), Gibbs sampling (AlignACE [48]), efficient enumeration (Amadeus [49]) and neural networks (ANN-Spec [50]). Methods that use weights or a ranked list of genes include DRIM [51] and MatrixREDUCE [52]. A survey of motif finding tools can be found in [53, 54].

The problem of inferring a motif from high-throughput in vitro data can be naively solved by methods developed for motif finding in genomic sequences (as those listed above). For example, the set of DNA probes or sequences can be divided into a positive and a negative set, according to their binding intensity, and provided as input to a motif finding tool [55]. A more informative way is to designate the measured binding intensities as sequence weights, and use a tool that analyzes weighted sequences [56]. Unfortunately, such approaches have proved less accurate compared with technology-specific methods [43]. Thus, the problem requires algorithms that are tailored to these specific data.

Motif finding using PBM data

Several approaches have been proposed for inferring accurate binding models from PBM data. The most popular practice is to first derive scores for all possible k-mers (using often k = 8). These scores depend on the binding intensities of the probes that contain the k-mer. Some methods use average or median binding intensity, while others use enrichment scores (e.g. Wilcoxon–Mann–Whitney test [57]). The top scoring k-mer is identified as the consensus or seed in model construction. The list of k-mer scores can be directly used to predict binding, or collapsed into a more compact model, such as a PWM. Another option is to construct a model that has the best fit to the ranking of the probes, or to their binding intensities, without deriving k-mer scores from them. Then, an optimization procedure learns the model parameters (e.g. maximum likelihood using gradient descent [58] or Levenberg-Marquardt algorithm [59]). Methods for inferring BS models from PBM data include Seed-and-Wobble [16], RankMotif ++  [60], BEEML-PBM [61] and FeatureREDUCE [62]. Two recent studies evaluated the performance of different methods for inferring protein–DNA binding models from PBM data [43, 55].

BEEML-PBM infers PWM models from PBM data [61]. The inference is based on a biochemical model, which we review here. At equilibrium, given that the log of the ratio between free TF concentration and K_d of the reference sequence is μ, the binding probability to k-mer S is:

$$P\left(S\right)=\frac{1}{1+{\text{e}}^{\text{E}-\mu }}$$

where E, the free energy difference between S and the reference sequence, depends additively on positions based on a PWM model:

$$E={\displaystyle \sum }_{j=1}^k{f}_{w_j,j}$$

where $f_{w_j,j}$ is the energy contribution of nucleotide w_j in position j of k-mer S relative to the reference sequence.

Because TFs may bind both strands of dsDNA, the probability of binding to dsDNA sequence U, whose reverse complement is U', is:

$$F\left(U\right)=P\left(U\right)+\left(1-P\left(U\right)\right)P(U\text{'})$$

Binding probability to probe T is then:

$$F\left(T\right)={\displaystyle \sum }_{j=1}^{L-k+1}F(T_{j:j+k-1})$$

where T_{j:j + k-1} is the k-mer starting at position j of probe T. To account for positional bias in the probe, the probabilities can be summed in a weighted manner. The PWM and μ are then estimated from the experimental data (see [61] for details).

Motif finding using HT-SELEX data

Binding model inference from HT-SELEX data is different than from PBM data. As opposed to PBM technology, in theory, each DNA oligonucleotide in every cycle represents a BS. Binding intensity is not reported, but it can be computationally derived for k-mers of length smaller than the oligonucleotide (for k ≤ 12 many k-mers appear in thousands of oligonucleotides). K-mer scores are derived based on their frequency in the different cycles of the experiment. The ‘ratio statistic’ of a k-mer in HT-SELEX cycle i is defined as the ratio of the k-mer's frequency in cycle i and its frequency in cycle i-1. This statistic represents the k-mer's preference, which affects the changes in its frequencies between the cycles, and thus is an estimate of the binding preference of the TF to this DNA word. The first reported method for inferring binding models from HT-SELEX data was BEEML [27]. It uses the frequencies from two consecutive cycles to learn the binding preferences based on a free energy model. A method of Toivonen et al. uses k-mer frequencies from one of the last cycles as scores and constructs a model based on k-mers at Hamming distance ≤1 from the consensus [18, 29]. Another method, developed as part of the SELEX-seq protocol uses k-mer ratios (after correction for biases and artifacts) to derive a complete k-mer list as the binding model [63]. A comparison of the two SELEX methods in inference of binding models is still needed.

SELEX-seq

The following method infers k-mer binding scores from HT-SELEX data [63]. It estimates the preference of each k-mer S by comparing its count in the later cycles to its count in the initial cycle (most experiments have at least three cycles). The model assumes that at each cycle the frequency of S is multiplied by the same factor. Therefore, the r-th root of the ratio of S’s frequency in the r-th cycle $F_S^{(r)}$and in the initial cycle $F_S^{(0)}$is used as its binding score:

$$Binding\_score\left(S\right)=\sqrt[r]{F_S^{(r)}/F_S^{(0)}}$$

k, the width of the BS, is selected using KL-divergence [63]. The value of k that has the highest information gain in cycle r compared with the initial random pool is chosen, i.e. k maximizing:

$$D\left(r,k\right)={\displaystyle \sum }_{S\in S_{100}\left(r,k\right)}{F}_S^{\left(r\right)}\text{log}(F_S^{\left(r\right)}/F_S^{\left(0\right)}) + P_{-100}^{(r)}\log \left(\frac{P_{-100}^{\left(r\right)}}{P_{-100}^{\left(0\right)}}\right)$$

Here S₁₀₀(r,k) is the set of k-mers that appear at least 100 times in cycle r, and all other k-mers are pooled together, so that ${\text{P}}_{\text{-100}}^{\text{(r)}}$ is the sum of frequencies of all the k-mers that appear <100 times in cycle r.

A 5th-order Markov model is used to estimate k-mer frequencies in the initial cycle, as these have low counts, making their observed frequencies an inaccurate estimate. In the current implementation, cycle r = 1 is used, and LOESS-regression is used to incorporate information from multiple rounds of selection (see [63] for details).

Predicting in vivo binding from in vitro models

In vitro models predicting in vivo binding

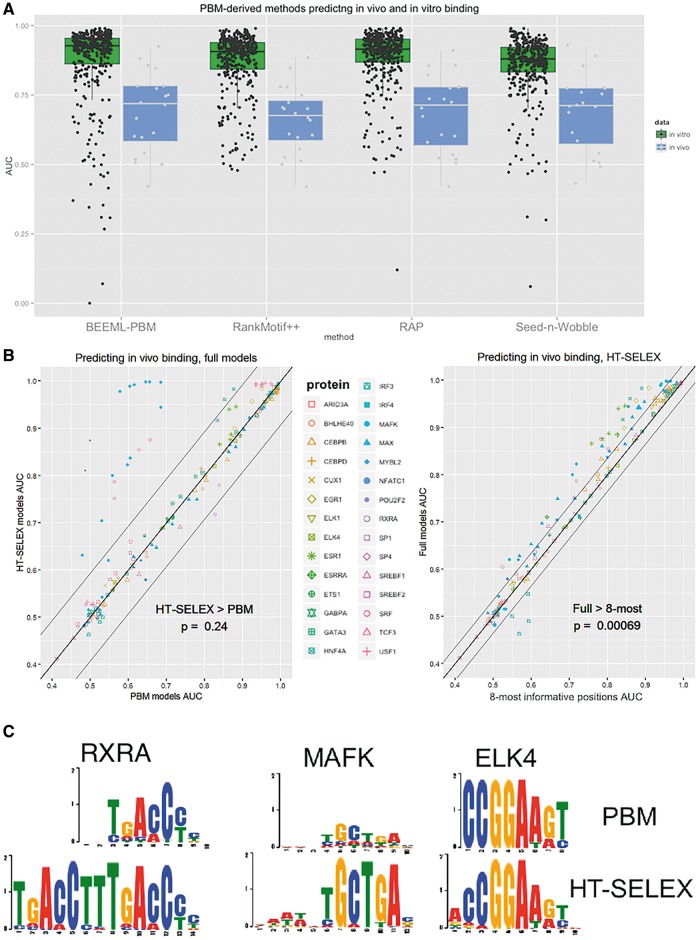
State-of-the-art methods for learning DNA-binding preferences of proteins from PBM data produce models that predict in vitro binding accurately. In contrast, constructing accurate models for in vivo binding is a harder challenge. In all studies, while predicting in vitro binding was accurate (average AUC reaching almost 0.9), predicting in vivo binding was much worse (average AUC ∼0.7) [43, 55] (compare also Figure 2C and D). We tested PBM-derived models on ChIP-seq experiments available on ENCODE (considered more accurate than the ChIP-chip experiments [64]), and the results were effectively the same as for ChIP-chip and ChIP-seq from other sources [43, 55]. For 20 TFs that had both a PBM model and a ChIP-seq experiment, the average AUC was 0.69. A comparison of the performance of different methods for deriving PWM models from PBM data revealed that no method had a significant advantage over all the rest (RAP and BEEML-PBM did show an advantage over RankMotif ++, P-value = 0.008 and 0.026, respectively, Wilcoxon rank-sum paired test) (see Figure 3A). The low accuracy may be owing to the complexity of the cellular environment and also owing to the simplicity of the produced models. Other factors that affect in vivo binding in addition to sequence-specific features include nucleosome positioning, competing TFs and cooperating TFs [4].

Figure 3.

In vitro models predict in vivo binding. (A) Performance of PBM-derived models in predicting in vivo and in vitro binding. Boxplots of AUC for the models inferred by different methods show that in vivo binding prediction using in vitro models is less accurate than in vitro binding prediction by the same models (P-value < 10 ^− 7 for each of the four methods, Wilcoxon rank-sum unpaired test). AUC values for in vitro were calculated for 355 paired PBM experiments (results taken from [37]), and for in vivo for 20 TFs tested by ChIP-seq experiments (downloaded from ENCODE). (B) Comparison of PBM- and HT-SELEX-derived models in predicting in vivo binding. Left: HT-SELEX models are more accurate on some proteins in predicting in vivo binding. In computing the significance, for each protein, the values for different experiments of that protein were averaged to avoid dependencies. (Without such collapsing of the data, the HT-SELEX advantage is significant, giving P  =  0.006.) Right: When only the eight most informative positions are used for modeling each TF, models are less accurate than full models. One hundred sixty-seven ENCODE ChIP-seq experiments covering 28 different TFs were used to gauge the accuracy of in vitro binding models. In vitro models were downloaded from CIS-BP. (C) Logos of some PBM- and HT-SELEX-derived models. RXRA (for which PBM is more accurate in in vivo prediction), MAFK (for which HT-SELEX is more accurate) and ELK4 (where the methods perform similarly).

The effect of motif flanks in predicting in vivo binding

In contrast to the high accuracy of PBM-derived models in predicting binding intensities of another PBM experiment, they do much worse in predicating in vivo binding (as measured in ChIP experiments). A recent study tested hundreds of human TFs in HT-SELEX experiments [28], 162 of which had a PBM experiment. We used ChIP-seq to determine from which technology, PBM or HT-SELEX, we can derive models that are more accurate in predicting in vivo binding. Here, we show an update of the comparison reported in [31]. When comparing the accuracy of in vivo peak binding prediction based on PBM (derived by BEEML-PBM) and HT-SELEX models (published in [28]) for the same TFs, using ENCODE ChIP-seq peaks, HT-SELEX is superior (see Figure 3B). The longer models produced by HT-SELEX are more accurate in in vivo binding prediction for a few proteins, achieving an average AUC of 0.761 compared with 0.728 for PBM-derived models (P-value  =  0.24, Wilcoxon rank-sum paired test). The comparison encompassed 167 ChIP-seq experiments covering 28 different TFs. This suggests that some of the signal directing protein–DNA binding lies in the flanking regions of the core motif (see Figure 3C for examples). (A set of positions with high IC, usually consecutive, are called ‘core positions’, while positions adjoining the core, of lower IC, are called its ‘flanks’.) Indeed, when we removed the side positions, leaving only the eight most informative positions (those with the lowest entropy [38]), HT-SELEX model performance decreased significantly (average AUC 0.761 compared with 0.739 on the same set, P-value  =  0.00069) (see Figure 3B).

Conclusions and open problems

Technological advancements of recent years provide several opportunities to further study the mechanisms behind TF-DNA binding. For example, the effect of sequences flanking the BS was observed through both PBM and HT-SELEX [20, 37]. With the new HT-SELEX technology, which measures the binding to longer motifs than those measured by PBM, additional features may be derived from sequences flanking the core. These may be added to the PWM as side positions or as local DNA shape features (used to describe 3D properties of each DNA base pair), as was proved useful in recent studies [20, 23, 65]. Similarly, accurate biomechanical models based on free energy contributions can be learned from high-quality data (using algorithms such as BEEML) and provide more direct link to the binding mechanism [27, 44, 61]. With technology improvements and broader data sets, more can be learned on the binding mechanisms of different protein families, and the mechanisms that differentiate between proteins in the same family can be better understood.

Techniques for measuring protein–DNA binding will continue to improve, thanks to plummeting costs of microarrays and high-throughput sequencing. The HT-SELEX technique demonstrates the benefit of high-throughput sequencing in measuring protein–DNA binding [27, 18, 30]. One of its main advantages over previous techniques is the ability to measure motifs of length >20 bp [31]. Its accuracy is expected to continue to get better with greater read coverage. Universal PBMs were recently extended by custom PBMs, which measure the binding of a TF to a predefined set of sequences, either wild-type genomic sequences [20, 21] or mutated and synthetic sequences designed for the TF in question (e.g. longer motifs for NFkB proteins [66] and cooperativity between two TFs [22]). As production of microarrays and oligonucleotide printing becomes cheaper, it is now possible to design arrays to test the binding preference of specific TFs to selected genomic or synthetic sequences in vitro.

On the computational side, we see more complex binding models emerging to replace the ‘good old PWM', and development of more advanced optimization methods for all models. Exceptions to the position-independence assumption have been observed since 1986 [67], and the accuracy of the PWM model has been repeatedly challenged [43, 44]. Studies that criticize this assumption suggest more complex models, mostly adding position-dependent features, such as di-nucleotide and 3-mers [44], or combining alternate or cooperative PWM models together [62]. The benefit of these additional features may be explained by their effect on local DNA shape features [68]. While these models have been shown to be more accurate, and it is possible to infer them from the new high-throughput data, they are not broadly used. There are three main challenges. The first is the interpretability. Models gain popularity when accompanied by a user-friendly and intuitive visualization, which is still missing for the more complex models. Second, the number of parameters is exponential in the BS width, which may lead to over-fitting, depending on the size of the training data and the chosen width. Third, it is difficult for a new model to reach broad impact, when most bioinformatics tools and pipelines accept as input a PWM. Further evidence on the advantage of complex models is needed to sway the community to adopt them. On the optimization side, application of new machine learning approaches may further improve models accuracy. A new approach termed ‘deep learning’ was recently applied to both PBM and HT-SELEX data and was shown to outperform the current state of the art, especially at predicting in vivo binding [69].

A key challenge is how to transfer the accuracy of the in vitro models into the in vivo domain. Measuring effects of flanking sequences and adding epigenetic information such as nucleosome occupancy was shown to improve prediction accuracy [5]. However, there is still a wide gap between the quality of in vitro and in vivo binding prediction. Key factors that should be addressed to narrow the gap are co-factors and competing proteins, whose effect is still unknown. Many TFs bind only as a complex, thus measuring the independent binding affinities of their components does not reflect their true regulatory role. A breakthrough in measuring DNA-binding preferences of pairs of TFs was recently achieved by an extension of HT-SELEX [70]. Similarly, distinct proteins with similar binding preferences compete for the same BSs. Comparing between them requires affinity measurements, which have lower throughput compared with binding specificity measurements. Only recently, measuring affinities to >100 preselected genomic sequences (as opposed to pseudo-random sequences as in [24]) in one experiment became possible [71]. Clearly, competition has to be modeled to improve in vivo binding prediction, taking into account both protein concentrations, localization and absolute affinities to putative BSs.

In conclusion, the field of gene regulation has seen a tremendous leap in recent years in throughput and accuracy of protein–DNA binding measurements. These have been used in numerous studies, producing better prediction models and improving the understanding of evolution of TFs. We expect these technologies and computational models to improve in coming years, advancing our ability to predict in vivo binding and to understand gene regulation.

Key Points

• Protein-binding microarrays (PBMs) and high-throughput SELEX (HT-SELEX) measure the binding of a single protein to many thousands of DNA sequences and report accurate binding intensities in vitro. Public databases contain hundreds of PBM and HT-SELEX experiments and models covering proteins from diverse model organisms.

• Protein–DNA binding models range from simpler position weight matrices (PWMs) to all k-mer models. The latter is more accurate, but hard to interpret and visualize and may over-fit the training data. Algorithms for inference of both models must be tailored to the specific experimental technique.

• HT-SELEX- and PBM-derived models mostly agree, but HT-SELEX models are more accurate in prediction of in vivo binding for a few proteins, mostly owing to coverage of longer sequences.

• The performance of in vitro binding models in predicting in vivo binding is rather poor; bridging this gap will require incorporation of the genomic context into the models.

Biographies

Yaron Orenstein, PhD, is a postdoctoral scholar at CSAIL, MIT. His research focuses on developing methods to learn protein–DNA and protein–RNA binding models from high-throughput data.

Ron Shamir, PhD, is a Sackler professor of Bioinformatics at the Blavatnik School of Computer Science and head of the Edmond J. Safra Center for Bioinformatics, Tel-Aviv University. He develops algorithms and tools for genomic and medical analyses.