Quantifying Adventitious Error in a Covariance Structure as a Random Effect

Abstract

We present an approach to quantifying errors in covariance structures in which adventitious error, identified as the process underlying the discrepancy between the population and the structured model, is explicitly modeled as a random effect with a distribution, and the dispersion parameter of this distribution to be estimated gives a measure of misspecification. Analytical properties of the resultant procedure are investigated and the measure of misspecification is found to be related to the RMSEA. An algorithm is developed for numerical implementation of the procedure. The consistency and asymptotic sampling distributions of the estimators are established under a new asymptotic paradigm and an assumption weaker than the standard Pitman drift assumption. Simulations validate the asymptotic sampling distributions and demonstrate the importance of accounting for the variations in the parameter estimates due to adventitious error. Two examples are also given as illustrations.

1. Introduction

Covariance Structure Models (CSMs) have been widely used in psychometrics. In a CSM, a structured covariance matrix Ω = Ω(ξ) is specified by hypothesizing relationships among latent and manifest variables and the parameters in vector ξ are estimated by fitting the covariance structure to data, usually in the form of a sample covariance matrix S. When evaluating the dispersion of the estimate ξ̂ or the fit of the model, the simplest assumption is that the covariance structure is correctly specified in the population, or the population covariance matrix Σ = Ω(ξ). Under this assumption, the estimation procedure takes into account only the error due to sampling uncertainty.

However, this assumption usually leads to the rejection of the model in most practical situations, especially with large sample size. This is not surprising, because CSMs, like all statistical models, are only approximations to reality and are never exactly correct in the statistical population (MacCallum, 2003; MacCallum and Tucker, 1991). This implies that the data are contaminated not only by sampling error but also by additional errors.

1.1. Adventitious Error and its Stochastic Nature

In most cases, a psychometric theory is established for a general group of people under a general measurement condition, but observations are only made on a specific group of people under some concrete condition. This deviation between the population from which observations are collected and the population for which the theory is hypothesized is defined as adventitious error, where the word “adventitious” refers to the fact that this error is random and arises in an unpredicable manner from unknown sources external to the design of a study. For example, suppose that the structure of a depression scale is hypothesized for adults in the U.S. measured under a general measurement condition. To validate this structure, data are collected from randomly selected adults in Chicago on a day of summer. In this case, the statistical population from which the observations can be viewed as a random sample is no longer the ratings by adults in the U.S. under a general condition. Instead, the observations are better viewed as a random sample from the ratings by adults from Chicago in summer. The difference between these two populations is adventitious error. It is very rare that a study uses a truly random sample from adults in the U.S.. Even if such a sample of people is obtained, the measurement of the sampled adults usually takes place in a specific span of time, which may not be representative of a general measurement condition. It should be noted that in most research, the “general population under a general measurement condition” of interest is an ideal construct that exists only in theory. In practice a sample is necessarily drawn from an operational and concrete population that differs from the theoretical population. In this sense, adventitious error is unavoidable.

The presence of adventitious error is the result of different and usually unknown sources of error that make the two populations different. Error unique to one study may result in systematic deviation of all observations obtained in this study from the pattern hypothesized by theory. In the example above, the particular location and time at which the measurement takes place, the way the measurement is administered and the conductors of the study may all be sources of error, and there are likely even more sources of error that are unknown to the researcher. It should be noted that all such errors of known or unknown sources are not of theoretical interest and cannot be distinguished from each other using observations from a single study. As a result, similar to the modeling of sampling error, their joint effect is combined into a single error and modeled with a distribution.

An important feature of adventitious error is its randomness. To better understand its stochastic nature, we need to consider hypothetical replications of a measurement. Still taking the example above, if the study in Chicago is to be replicated, it is more likely to be conducted by another investigator in another city at another time of year, because the theory to be validated concerns adults in the U.S. under a general measurement condition. In general, because a psychometric theory concerns a theoretical population, instead of assuming that replications of a study are taken repeatedly from the same operational population, it is more meaningful to assume that different replications are taken from this theoretical population operationalized in slightly different ways, and those different replications as a whole are representative of the general population of interest. In terms of adventitious error, it is more meaningful to assume that its different sources are realized differently across these different replications. The fact that adventitious error differs across different realizations of the same study highlights its randomness.

1.2. The Traditional Approach to Model Misspecification

The traditional approach to misspecification assumes an unknown but fixed covariance matrix Σ for the population from which the observations are a random sample. This covariance matrix deviates from the covariance structure Ω(ξ) and this deviation is referred to as discrepancy of approximation (Cudeck and Henly, 1991). Despite this discrepancy, the procedure of parameter estimation stays the same as for correctly specified models. Only the asymptotic distribution of the test statistic is adjusted to account for misspecification and the root mean square error of approximation (RMSEA, Steiger and Lind, 1980; Browne and Cudeck, 1992) can be estimated as a measure of the extent of misspecification.

Unfortunately, this traditional approach, though fairly successful, is still imperfect. The primary reason is that it was developed as minimal modification to the routine for correctly-specified models through post-hoc adjustments. Especially, misspecification is not actively modeled but is treated as the fixed discrepancy of approximation in the operational population. Neglecting the randomness of the operational population changes the replication framework discussed earlier and shifts the focus of the study from the general population of theoretical interest to the specific population of which the sample in the current replication of study is representative. This effectively limits the generalizability of the model. In addition, it also renders the parameter estimates less meaningful, because the model does not hold in the specific population and the parameters are better interpreted in terms of the general population where the model is correctly specified. The present paper will maintain the point of view that the operational population should be modeled formally as a stochastic quantity due to the presence of adventitious error and its randomness should be accounted for when estimating the parameters and evaluating the model.

1.3. Stochastic Approaches to Adventitious Error

The origination and role of a random adventitious error were first systematically studied by Tucker, Koopman and Linn (1969), in which the difference between a formal model (i.e. a covariance structure) and a simulation model (i.e. a population covariance matrix) was identified as an error due to the presence of minor factors. Especially, loadings on these minor factors “are taken as random variables somewhat out of the control of the designer of the variable and the experimenter collecting the data”, and the simulation model “conceives of each measure involving a sampling of influences on the behavior of the individual”. A more recent study by Briggs and MacCallum (2003) used the same stochastic approach to simulate population correlation matrices and considered conditions with either or both adventitious error and sampling error.

As both adventitious error and sampling error are present in the data and contribute to its randomness, the estimation procedure should include both of these two particular sources of error. Estimation under multiple sources of error has been an active subject of applied statistics and engineering (Kennedy and O’Hagan, 2001; Trucano et al., 2006). For example, for a nonlinear regression model, the standard practice is to obtain the least square estimates of its parameters. To account for misspecification, the traditional approach would assume a fixed model discrepancy and adjust the confidence intervals accordingly, and the test statistics would have a non-central χ² distribution (White, 1981; Wardorp, Grasman and Huizenga, 2006). To account for randomness in the actual physical process, Trucano et al. (2006, section 3) employ a Gaussian process to model the discrepancy between the true process and the nonlinear regression model, and parameters are estimated in a Bayesian framework. The issue of quantifying uncertainties has recently been introduced to psychology by MacCallum (2011a,b).

In this work, we quantify both the adventitious error and sampling error with distributions in line with the above discussion. In particular, the misspecified population covariance matrix Σ follows a distribution centered at the structure Ω(ξ), implying a stochastic adventitious error Σ – Ω(ξ) as a random effect. Although one could account for adventitious error with unaccounted minor factors as discussed in Tucker, Koopman and Linn (1969), we choose to use a simple conjugate distribution as a first attempt at this issue.

2. The Traditional Approach

2.1. Correctly-Specified Covariance Structures

Traditionally, a covariance structure Ω(ξ) is fitted to a sample covariance matrix S by minimizing a discrepancy function F(S, Ω(ξ)) (see, e.g., Browne, 1984, p.64). General classes of discrepancy functions include the generalized least squares (GLS, Browne, 1974) and the Swain (1975) family. As a member of both families, the maximum Wishart likelihood (MWL) discrepancy function (see, e.g., Lawley and Maxwell, 1971) is given by

$$F^{\mathrm{W}}=-ln\mid {\mathbf{\Omega }}^{-1}\mathbf{S}\mid +\text{tr}({\mathbf{\Omega }}^{-1}\mathbf{S})-p.$$ (1)

Minimizing this function is equivalent to maximizing the likelihood function of the Wishart distribution W_p(Ω(ξ)/n, n), the sampling distribution of S under the assumptions of Σ = Ω and normality. Under these assumptions, parameter estimate ξ̂^W has the asymptotic distribution (Shapiro, 2007, Theorem 5.5), $\sqrt{n}({\widehat{\mathit{\xi }}}^{\mathrm{W}}-{\mathit{\xi }}_0)\stackrel{\mathcal{L}}{\to }\mathrm{N}(\mathbf{0},2{({\mathbf{\Delta }}^{\prime }\mathbf{V}\mathbf{\Delta })}^{-1\ast })$, where $\mathbf{\Delta }=\frac{\partial \mathit{\omega }}{\partial {\mathit{\xi }}^{\prime }}$ and V = (Ω⊗Ω)⁻¹. Throughout the paper we use the notation ω = vecΩ, with σ and s defined similarly. The superscript * indicates evaluation at the true value ξ = ξ₀. Note that $\frac{1}{2}{({\mathbf{\Delta }}^{\prime }\mathbf{V}\mathbf{\Delta })}^{\ast }$ is the Fisher information matrix. The fit of a model is evaluated with the likelihood ratio test (LRT). The observed discrepancy function value n F̂ has an asymptotic distribution of ${\chi }_{df}^2$, where df is the difference in dimensions between the tested model and saturated model. As has been discussed in the Introduction, the LRT always rejects the structured model in practice when sample size is large enough due to misspecification.

2.2. Misspecified Covariance Structures

When the model is misspecified, there is no longer a true value ξ₀ in the parameter space Ξ such that Σ = Ω(ξ₀). However, under mild regularity conditions, the parameter estimate ξ̂^W is still consistent towards ξ^#, the minimizer of F(Σ,Ω(ξ)). White (1981, Theorem 3.3; 1982, Theorem 2.2) and Shapiro (1983, Theorem 5.4(a); 2007, Section 5.3) investigated the asymptotic distribution of ξ̂^W under a misspecification assumption and obtained equivalent results. Their results have rarely been used, partially because higher order derivatives of Ω(ξ) are involved when the model is misspecified.

Shapiro (1983, Theorem 5.4(c)) also derived the asymptotic distribution of the test statistic through a Taylor expansion of the discrepancy function and found that $\sqrt{n}(\widehat{F}-F^{\#})\stackrel{\mathcal{L}}{\to }\mathrm{N}(0,2{{\mathit{a}}^{\#}}^{\prime }(\mathbf{\sum }\otimes \mathbf{\sum }){\mathit{a}}^{\#})$, where F^# = F^W(Σ,Ω(ξ^#)) is the minimum discrepancy function value in the population, and $\mathit{a}=\frac{\partial F}{\partial \mathit{s}}$. The superscript ^# is used to denote the value evaluated at the fixed and possibly misspecified population s = σ and ξ = ξ^#. When misspecification is not present, F^# = 0, a^# = 0 and the normal distribution becomes degenerate. In this case, the quadratic term in the Taylor expansion gives a χ² approximation for n F̂.

Because F̂^W is bounded by 0 from below and has a skewed distribution in most cases, the normal approximation is not appropriate. To amend this situation, one introduces the Pitman drift assumption that the population Σ becomes closer and closer to the model Ω as sample size n increases, with $\sqrt{n}(\mathit{\sigma }-\mathit{\omega }({\mathit{\xi }}^{\#}))\to \mathit{\mu }$. Under this assumption, $n{\widehat{F}}^{\mathrm{W}}\stackrel{\mathcal{L}}{\to }{\chi }_{df,\delta }^2$, where δ = lim nF^#. This assumption also implies that ξ̂^W has the same asymptotic distribution as in a correctly specified model.

The RMSEA (Browne and Cudeck, 1992) given by $\epsilon =\sqrt{F^{\#}/df}$ measures the discrepancy per degree of freedom. Its bias adjusted point estimate is given by ${\widehat{\epsilon }}_0=\sqrt{{\left({\widehat{F}}^{\mathrm{W}}/df-1/n\right)}^{+}}$, where a⁺ = max{a, 0}, and its confidence interval (CI) can be obtained from the non-central χ² distribution of n F̂ discussed above (see also MacCallum, Browne and Sugawara, 1996). In practice, with the issue of model misspecification borne in mind, one does not discard the model immediately when exact fit is rejected. Instead, the RMSEA is estimated and tested against some criterion (e.g. ε < 0.05) through the use of a lower confidence bound (CB). If the RMSEA is regarded as below the tolerance value, the model is retained.

2.3. Problems of the Traditional Approach

As a post hoc amendment, the traditional approach only addresses the question of what would happen to the results from the procedure for a correctly specified model when misspecification is present. Consequently, it only acknowledges model misspecification, but does not model how it has occurred. For parameter estimates and CIs, the traditional approach uses the same procedure as for correctly-specified models. Especially, the traditional approach defines a “true value” ξ^# for the replication-specific population as the minimizer of F(Σ,Ω(ξ)). This may be misleading for two reasons: First, the discrepancy between Σ and Ω(ξ^#) is measured by a function used to measure a deviation due to sampling error, though clearly it is due to adventitious error in this case; Second, the “true value” is a property of the replication-specific population, which is only a noisy realization of the general population and is therefore not of theoretical interest. As mentioned in the Introduction, inference on ξ^# narrows the generalizability of the study.

A second problem of the traditional approach above concerns the stochastic nature of adventitious error. The traditional approach assumes only a fixed misspecification in the population and does not account for adventitious error as a source of variation. This assumption neglects the variation of the potential realizations across different replications of the same study, and would result in underestimation of the randomness in the sample, parameter estimates and test statistics.

In addition to issues mentioned above, a technical drawback is also present in the traditional approach, which invokes the Pitman drift assumption (see Section 2.2) as a mathematical convenience to justify the asymptotic noncentral χ² distribution of n F̂. Nevertheless, this assumption, which states that the population becomes gradually close to the model as sample size increases, is implausible in practice because the population should not be affected by sample size. Its use has been heavily debated (see, e.g., Yuan, Hayashi and Bentler, 2007; Yuan, 2008; Chun and Shapiro, 2009).

In the light of these problems, we present an alternative approach to misspecified covariance structures. This approach models not only the sampling error, but also the adventitious error.

3. A Model for Adventitious Error

Three quantities are particularly important in our model: the sample covariance matrix S, the covariance matrix Σ of the replication-specific population, and the structured covariance matrix Ω(ξ) of the general population given by theory. Between the three quantities, two sources of error are of primary concern: sampling error and adventitious error. Sampling error is the deviation of the observed sample from the replication-specific population due to the sampling process from this population. It is the main concern of most statistical procedures. In most situations, the effects of sampling error can be made small by increasing sample size. In contrast, adventitious error exists in the replication-specific population and is not related to the sampling process. Because of this error, the population from which we obtain a random sample fails to satisfy the structure implied by theory. Especially, if the same study is to be replicated multiple times, variations would be present among those populations from which we obtain observations. The effect of adventitious error can not be minimized by increasing sample size. As we can see from the above analysis, the discrepancy between sample and the model arises from both sources of error. Now we give a statistical formulation of our discussion of the two types of error above.

Under the normality assumption, the sample covariance matrix has a Wishart distribution:

$$(\mathbf{S}\mid \mathbf{\sum })~{\mathrm{W}}_p(\mathbf{\sum }/n,n)$$ (2)

where we assume S is the usual unbiased estimator of the unstructured population covariance matrix, and n is the degrees of freedom, usually sample size less 1. This gives the distribution of sampling error S–Σ. In addition, the population covariance matrix Σ is assumed to follow an inverted Wishart distribution, the conjugate distribution to the Wishart distribution¹:

$$(\mathbf{\sum }\mid \mathbf{\Omega },m)~{\text{IW}}_p(m\mathbf{\Omega },m)$$ (3)

where m > p–1 is a continuous precision parameter. The inclusion of the distribution of Σ follows from the rationale of a random adventitious error as discussed in the Introduction. It posits that the adventitious error Σ – Ω(ξ) be a random effect, so that Σ differs from the structure Ω and would have different realizations if the same study is to be replicated multiple times. An extra parameter m is introduced by the random effect and its inverse v = 1/m ∈ [0, (p – 1)⁻¹) denotes the dispersion of adventitious error and gives a measure of the extent of misspecification². Especially, as v → 0, from the weak law of large numbers (WLLN), we have $\mathbf{\sum }\stackrel{\mathbf{p}}{\to }\mathbf{\Omega }$ and no adventitious error is present.

Equations 2 and 3 were previously employed as an empirical Bayesian model in shrinkage estimation of an unstructured population covariance matrix Σ (Chen, 1979). Because the sample covariance matrix S is unstable when sample size is small, Chen (1979) proposed the shrinkage estimator Σ̂ = (m̂Ω(ξ̂)+nS)/(m̂+n), which is the posterior mode of Σ implied by Equations (2) and (3). This estimator stabilizes S by shrinking it towards some prespecified structure Ω(ξ), and the amount of shrinkage is governed by parameter m. Both ξ and m are estimated by maximizing the marginal likelihood.

Although we are using a similar model to Chen (1979), the following distinctions should be noted. First, the main purpose of the current research is the estimation of the structured covariance matrix Ω and the parameter v = 1/m in the presence of adventitious error, whereas Chen aimed at a better estimation of the unstructured population covariance matrix Σ. Second, in our research Σ is a random effect that is considered real in practice and its distribution is used to model the adventitious error. All asymptotic results will be derived under this two-level replication framework. In contrast, in Chen’s model Σ is considered fixed and its prior distribution is used to induce shrinkage to stabilize its estimator. The consistency of Σ̂ was derived assuming a fixed Σ. Third, to obtain parameter estimates, we maximize a modified marginal likelihood directly by means of the Newton-Raphson algorithm, while Chen maximized the true marginal likelihood through an EM algorithm, treating Σ as missing data. In summary, our model is similar to that of Chen (1979) only mathematically. The purpose, motivation, computation, replication framework and interpretation are all different.

4. Analytical Properties

4.1. The Marginal Distribution

The hierarchical model as presented by Equations (2) and (3), involves two unknown quantities in the upper level, the structured covariance matrix Ω(ξ) and the dispersion parameter v (or, equivalently, m = 1/v), to be estimated from the data. Estimates of these parameters can be obtained by maximizing the likelihood function given by the marginal distribution of the sample covariance matrix (S|Ω, m) with the unknown population covariance matrix Σ integrated out. Because of our choice of a conjugate distribution for Σ, this marginal distribution (S|Ω, m), derived by Roux and Becker (1984), is of a known type

$$(\mathbf{S}\mid \mathbf{\Omega },m)~{\mathrm{B}}_p^{\text{II}}(\frac{n}{2},\frac{m}{2},\frac{m}{n}\mathbf{\Omega }),$$ (4)

the second type of matrix variate beta distribution (see Gupta and Nagar, 1999, Chapter 5). This marginal distribution has pdf:

$$p(\mathbf{S}\mid \mathbf{\Omega },m)=\frac{1}{{\mathrm{B}}_p(\frac{n}{2},\frac{m}{2})}\times \frac{{\mid \mathbf{S}\mid }^{\frac{n-p-1}{2}}{\mid \mathbf{\Omega }\mid }^{\frac{m}{2}}}{{\mid m\mathbf{\Omega }+n\mathbf{S}\mid }^{\frac{n+m}{2}}}\times n^{\frac{np}{2}}{m}^{\frac{mp}{2}}$$

where B_p(a, b) = Γ_p(a)Γ_p(b)/Γ_p(a + b) is the multivariate beta function and Γ_p(a) is the multivariate gamma function (see Gupta and Nagar, 1999, Section 1.4). The negative twice beta log-likelihood is given by

$$\stackrel{\sim }{F}=-2lnp(\mathbf{\Omega },m)={\stackrel{\sim }{F}}_1+{\stackrel{\sim }{F}}_2$$

where

$${\stackrel{\sim }{F}}_1(m,n)=f(m)+f(n)-f(m+n)$$ (5)

$${\stackrel{\sim }{F}}_2(\mathrm{\Omega },m,\mathbf{S},n)=-(n-p-1)ln\mid \mathbf{S}\mid -mln\mid \mathbf{\Omega }\mid +(m+n)ln\mid \overline{\mathbf{\sum }}\mid$$ (6)

$$f(x)=2ln{\mathrm{\Gamma }}_p(\frac{x}{2})-\mathit{xp}ln\frac{x}{2}+xp$$ (7)

$$\overline{\mathbf{\sum }}=\frac{m\mathbf{\Omega }+n\mathbf{S}}{m+n}$$ (8)

Note that Σ̄ denotes a function of m, n, Ω and S but not of Σ.

The parameter estimate (estimator) obtained from maximizing the beta marginal likelihood will be referred to as the maximum beta likelihood (MBL) estimate (estimator), or MBLE.

4.2. Asymptotic Behavior

The marginal distribution of S involves sample size n in the sampling error’s Wishart distribution and the precision parameter m in the adventitious error’s inverted Wishart distribution. Intuitively, as the sample size n → ∞, sampling error is diminished and the marginal distribution should become the inverted Wishart distribution assumed for the population covariance matrix; as precision parameter m → ∞, or dispersion parameter v → 0, we expect the model to become the Wishart model for correctly specified covariance structures. These results are summarized in the proposition below.

Proposition 1

The marginal density function of (S|Ω, m) converges to that of (S|Σ = Ω) as v → 0 (m→∞) and to that of (Σ|Ω, m) as n→∞.

Proof

This follows from Lemma 7 in Appendix A.

In addition to the intuitive results above, we also have

Proposition 2

Assuming the model given by Equations 2 and 3, as n→∞ and m→∞ (i.e., v → 0),

$$\sqrt{\frac{mn}{n+m}}(\mathit{s}-\mathit{\omega })\to \mathrm{N}(\mathbf{0},2{\mathbf{M}}_p[\mathbf{\Omega }\otimes \mathbf{\Omega }])$$

where s = vecS, ω = vecΩ, and M_p is a p² × p² matrix of rank p(p + 1)/2 with typical element m_ij,rs = (δ_irδ_js + δ_isδ_jr)/2. The rows and columns of M_p are doubly indexed as 11, 12, · · ·, 1p, 21, 22, · · ·, 2p,· · ·, pp. (see, e.g. Gupta and Nagar, 1999, Section 1.2).

The proof of Proposition 2 is given in Appendix A. This result suggests that when both n and m are large enough, the marginal distribution of s can be approximated by N(ω, 2(v+ε)M_p(Ω⊗Ω)), where for symmetry in presentation, we use the notation ε = 1/n, which should not be confused with RMSEA ε. This fact will be exploited later to derive the sampling distribution of the estimators.

The normal approximation to the marginal distribution is not surprising given that both the Wishart (likelihood) and the inverted Wishart (prior) distributions can be approximated by normal distributions when their precision parameters are large. In fact, as n → ∞ and m → ∞, the sampling error s – σ has an approximate distribution N(0, 2εM_p(Ω ⊗ Ω)) and the adventitious error σ –ω has an approximate distribution N(0, 2vM_p(Ω⊗Ω)). The normal approximation of the marginal distribution combines the effects of both sources of error because its covariance matrix is the sum of the two covariance matrices for the two approximations above.

4.3. The Inverted Wishart Distribution

Among the limiting distributions discussed above, the inverted Wishart distribution is the least investigated in the psychometrics literature and has never been used to fit a CSM. Given its special role in our approach, we briefly investigate the inverted Wishart model for the population covariance matrix Σ. Through this investigation we will correct a potential bias in the MIWL estimation of v by modifying the inverted Wishart log-likelihood function and also obtain an asymptotic relationship between the dispersion parameter v and the RMSEA ε.

4.3.1. Model for a Known Population

The distribution of Σ as specified by Equation 3 has the inverted Wishart density (Gupta and Nagar, 1999, Section 3.4)

$$p^{\text{IW}}(\mathbf{\sum }\mid \mathbf{\Omega },m)=\frac{1}{2^{\frac{mp}{2}}{\mathrm{\Gamma }}_p(\frac{m}{2})}\times {\mid m\mathbf{\Omega }\mid }^{\frac{m}{2}}{\mid \mathbf{\sum }\mid }^{-\frac{m+p+1}{2}}{\mathbf{e}}^{-\frac{m}{2}\text{tr}(\mathbf{\Omega }{\mathbf{\sum }}^{-1})}$$

and we define

$${\stackrel{\sim }{F}}^{\text{IW}}=-2ln{p}^{\text{IW}}(\mathbf{\sum }\mid \mathbf{\Omega },m)={\stackrel{\sim }{F}}_1^{\text{IW}}+{\stackrel{\sim }{F}}_2^{\text{IW}},$$ (9)

where

$${\stackrel{\sim }{F}}_1^{\text{IW}}=f(m)=2ln{\mathrm{\Gamma }}_p(\frac{m}{2})-\mathit{mp}ln\frac{m}{2}+mp$$ (10)

$${\stackrel{\sim }{F}}_2^{\text{IW}}=(p+1)ln\mid \mathbf{\sum }\mid +m(-ln\mid \mathbf{\Omega }{\mathbf{\sum }}^{-1}\mid +\text{tr}(\mathbf{\Omega }{\mathbf{\sum }}^{-1})-p)$$ (11)

are the limits of F̃₁ and F̃₂ (see Equations (5) and (6)) as n→∞, respectively (see Lemma 7 in Appendix A).

Given a known Σ, it is possible to estimate ξ and v by minimizing F̃^IW. Since Ω is present only in the second term of ${\stackrel{\sim }{F}}_2^{\text{IW}}$, ξ can be estimated by minimizing

$$F^{\text{IW}}(\mathbf{\sum },\mathbf{\Omega })=-ln\mid \mathbf{\Omega }{\mathbf{\sum }}^{-1}\mid +\text{tr}(\mathbf{\Omega }{\mathbf{\sum }}^{-1})-p$$ (12)

which is a discrepancy function³ and a member of the Swain (1975) family⁴. However, it was not considered in Swain (1975) and has never been used before for the analysis of covariance structures. Shapiro (1985, p.80) very briefly mentioned it as a discrepancy function asymptotically equivalent to the MWL discrepancy function defined by Equation (1). The two discrepancy functions are related to each other through F^IW(Σ,Ω) = F^W(Ω,Σ) = F^W(Σ⁻¹,Ω⁻¹). The EM algorithm of Chen (1979) minimizes Equation 12 to obtain an update of ξ in the M step.

Equation 12 can be minimized using a scoring algorithm with gradient and Fisher information matrix given by

$$\frac{\partial F^{\text{IW}}}{\partial {\xi }_i}=\text{tr}\{({\mathbf{\sum }}^{-1}-{\mathbf{\Omega }}^{-1}){\mathbf{\Delta }}_i\}\text{and}\frac{{\partial }^2{F}^{\text{IW}}}{\partial {\xi }_i\partial {\xi }_j}\approx \text{tr}({\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_i{\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_j)$$

where Δ_i = ∂Ω/∂ξ_i is a p × p matrix.

Once ξ has been estimated, the minimum MIWL discrepancy function value F̂^IW = F^IW(Σ,Ω( ξ̂)) can be determined, and the estimate of v can be obtained by minimizing F̃^IW = f(m) + m F̂^IW + c, or by solving

$${\widehat{F}}^{\text{IW}}+f^{\prime }(m)=0$$ (13)

for m, where $f^{\prime }(m)={\sum }_{i=1}^p\psi (\frac{m-i+1}{2})-pln\frac{m}{2}$. Chen (1979) showed that for a given Σ, m̂^IW exists and is unique on (p−1,+∞], with m̂^IW = ∞ iff F̂^IW = 0, or the dispersion parameter v is estimated at 0 iff Σ satisfies the model.

4.3.2. Bias Correction

Because f′(m) as in equation 13 has the expansion $f^{\prime }(m)=-\frac{p(p+1)}{2}{m}^{-1}+o(m^{-1})$ (see Lemma 5 in Appendix A), Equation (13) implies ${\widehat{v}}^{\text{IW}}\approx {\widehat{F}}^{\text{IW}}{(\frac{p(p+1)}{2})}^{-1}$ when Σ is close to Ω. Further because $m{F}^{\text{IW}}(\mathbf{\sum },\mathbf{\Omega })=m{F}^{\mathrm{W}}({\mathbf{\sum }}^{-1},{\mathbf{\Omega }}^{-1})\stackrel{\mathcal{L}}{\to }{\chi }_{df}^2$ as m → ∞, $\mathrm{E}{\widehat{v}}^{\text{IW}}\approx \mathit{vdf}{(\frac{p(p+1)}{2})}^{-1}<v$, which means v̂^IW tends to underestimate v.

To correct this bias, we consider the following modified version of F̃^IW defined in equation 9

$${\stackrel{\sim }{F}}_{(\alpha )}^{\text{IW}}=\alpha {\stackrel{\sim }{F}}_1^{\text{IW}}+{\stackrel{\sim }{F}}_2^{\text{IW}}$$ (14)

in which α ≥ 0 is a constant serving as a tuning parameter. This family includes F̃^IW as a special case (α = 1). Equation (13) now becomes

$${\widehat{F}}^{\text{IW}}+\alpha f^{\prime }({\widehat{m}}^{\text{IW}})=0.$$ (15)

If $\alpha =df/\frac{p(p+1)}{2}$, we have v̂^IW = F̂^IW/df + o( F̂^IW) and is asymptotically unbiased.

Because the MIWL and MWL discrepancy functions are asymptotically equivalent, we further have

$${\widehat{v}}^{\text{IW}}=\frac{F^{\text{IW}}(\mathbf{\sum },\widehat{\mathbf{\Omega }})}{df}+o({\widehat{F}}^{\text{IW}})=\frac{F^{\mathrm{W}}(\mathbf{\sum },\widehat{\mathbf{\Omega }})}{df}+o_{\mathrm{p}}({\widehat{F}}^{\mathrm{W}})={\epsilon }^2+o_{\mathrm{p}}({\epsilon }^2)$$ (16)

which gives the relationship between the dispersion parameter and the RMSEA.

The same modification can also be applied to the MBL procedure by defining the following family of functions

$${\stackrel{\sim }{F}}_{(\alpha )}=\alpha {\stackrel{\sim }{F}}_1+{\stackrel{\sim }{F}}_2$$ (17)

As will be shown later (see Equation 35), in a similar manner to the case of MIWL, the MBLE obtained by minimizing the original function F̃ = F̃_(α=1) underestimates v, while the choice of $\alpha =df/\frac{p(p+1)}{2}$ corrects this bias.

5. The Maximum Beta Likelihood Estimate

5.1. The Saturated Covariance Structure

For a given sample covariance matrix S and a covariance structure Ω(ξ), the MBLE of the parameters can be obtained by maximizing the marginal likelihood of S. Before presenting the numerical algorithm for parameter estimation, we first examine the case of the saturated model.

To obtain the MBLE, F̃_(α) = αF̃₁ + F̃₂ needs to be minimized, where the two terms are defined in equations (5) and (6) and α is a pre-specified tuning parameter. For any fixed value of m, F̃₂ can first be minimized to obtain a conditional minimizer of F̃. For m < ∞, from the concavity of ln |A| on {A ≻ 0}, F̃₂ ≥ −(n−p−1) ln |S|−mln |Ω|+mln |Ω|+n ln |S| = (p + 1) ln|S|. The equality is achieved iff Ω = S. So for any finite m, F̃₂ (and therefore −2 lnL) is minimized at Ω̂ = S for saturated Ω. The case of m = ∞ can be shown easily by noting that the likelihood function becomes that of a Wishart distribution. Note the minimizer does not depend on m.

Because the minimum of F̃₂ at Ω̂ = S does not involve m, for α > 0, we only need to minimize F̃₁ = f(n) + f(m) − f(m + n) to obtain m̂. From Lemma 5 in Appendix A, we have f(m) − f(m + n) → 0 as m → ∞. To prove m̂ = ∞, we only need to show that f is monotonically decreasing, which follows from the fact that f′(x) < 0 as proved by Chen (1979, Appendix).

If α = 0, for any given m, the minimum of F̃_(α) over ξ ∈ Ξ is a constant. As a result, parameter m cannot be estimated. This is the case with the choice $\alpha =df/\frac{p(p+1)}{2}$ since df = 0 for a saturated model. This apparently undesired property is not unreasonable: if the covariance structure is saturated, the amount of deviation between Σ and Ω cannot be determined as the covariance structure is not falsifiable. Note the RMSEA cannot be calculated either in this case.

Above we have proved that for the saturated model, Ω̂ = S and v̂ = 0 (if α > 0). In this case, F_(α) achieves its minimum of αf(n)+(p+1) ln|S|. Because this minimum is finite, we can subtract this value from the function and obtain a discrepancy function

$$F_{(\alpha )}(\mathbf{\Omega },m,\mathbf{S},n)=\alpha F_1(m)+F_2(\mathbf{\Omega },m,\mathbf{S},n)$$ (18)

where

$$F_1(m,n)=f(m)-f(m+n)$$ (19)

$$F_2(\mathbf{\Omega },m,\mathbf{S},n)=-nln\mid \mathbf{S}\mid -mln\mid \mathbf{\Omega }\mid +(n+m)ln\mid \overline{\mathbf{\sum }}\mid$$ (20)

The two parts F₁ and F₂ correspond to F̃₁ and F̃₂ respectively. For α > 0, the function F_(α) satisfies F_(α) ≥ 0 and F_(α) = 0 iff S =Ω and v = 0. Note F_(α) is not a discrepancy function in the traditional sense as it involves sample size n and the non-structural parameter v.

5.2. Covariance Structures in General

For the general case where Ω = Ω(ξ) is structured with parameter vector ξ, a numerical procedure is needed for the estimation of both ξ and v. A Newton-Raphson algorithm with approximate Hessian matrix is adopted to minimize the modified discrepancy function F_(α). The gradient of F_(α) is given below. The Hessian matrix and its approximation are provided in Appendix B.

For the structural parameter ξ, we remember that F₁ does not involve Ω so its derivatives w.r.t the ξ_i’s are 0. Those of F₂ are given by

$$\frac{\partial F_2}{\partial \mathbf{\Omega }}=-m({\mathbf{\Omega }}^{-1}-{\overline{\mathbf{\sum }}}^{-1})=\frac{nm}{m+n}{\mathbf{\Omega }}^{-1}(\mathbf{\Omega }-\mathbf{S}){\overline{\mathbf{\sum }}}^{-1}$$ (21)

$$\frac{\partial F_2}{\partial \mathit{\xi }}={\mathbf{\Delta }}^{\prime }\text{vec}(\frac{\partial F_2}{\partial \mathbf{\Omega }})=\frac{nm}{m+n}{\mathbf{\Delta }}^{\prime }({\overline{\mathbf{\sum }}}^{-1}\otimes {\mathbf{\Omega }}^{-1})(\mathit{\omega }-\mathit{s})$$ (22)

where ${\mathbf{\Delta }}_i=\frac{\partial \mathbf{\Omega }}{\partial {\xi }_i}$ is a p × p matrix and $\mathbf{\Delta }=\frac{\partial \mathit{\omega }}{\partial {\mathit{\xi }}^{\prime }}$ is a p² × q matrix. The derivative w.r.t v is given by $\frac{\partial F_{(\alpha )}}{\partial v}=-m^2(\alpha \frac{\partial F_1}{\partial m}+\frac{\partial F_2}{\partial m})$, where

$$\frac{\partial F_1}{\partial m}=f^{\prime }(m)-f^{\prime }(m+n)$$ (23)

$$\frac{\partial F_2}{\partial m}=-ln\mid \mathbf{\Omega }{\overline{\mathbf{\sum }}}^{-1}\mid +\text{tr}(\mathrm{\Omega }\overline{\mathrm{\sum }})-p$$ (24)

To better understand a property of v̂, we consider the value of $\frac{\partial F_{(\alpha )}}{\partial v}$ at v = 0. Lemma 5 in Appendix A gives $f^{\prime }(x)=-\frac{p(p+1)}{2x}+O(x^{-2})$ and therefore

$$\frac{\partial F_1}{\partial m}=-\frac{p(p+1)}{2}(\frac{1}{m}-\frac{1}{m+n})+O(\frac{1}{m^3})=-\frac{p(p+1)}{2}\frac{n}{m^2}+O(\frac{1}{m^3}).$$ (25)

For Equation (24), we first note $\mathbf{\Omega }{\overline{\mathbf{\sum }}}^{-1}-\mathbf{I}=\frac{n}{m}(\mathbf{\Omega }-\mathbf{S}){\mathbf{\Omega }}^{-1}+O(\frac{1}{m^2})$. Applying Lemma 6 in Appendix A, we have

$$\frac{\partial F_2}{\partial m}=\frac{1}{2}\frac{n^2}{m^2}\text{tr}{\{(\mathbf{\Omega }-\mathbf{S}){\mathbf{\Omega }}^{-1}\}}^2+O(\frac{1}{m^3})$$

and

$$\frac{\partial F_{(\alpha )}}{\partial v}=-m^2\frac{\partial F_{(\alpha )}}{\partial m}=\alpha \frac{np(p+1)}{2}-\frac{n^2}{2}\text{tr}{({\mathbf{\Omega }}^{-1}\mathbf{S}-\mathbf{I})}^2+O(v)$$ (26)

When α > 0 and S satisfies the structure Ω(ξ), $\partial F_{(\alpha )}/\partial v=\alpha \frac{np(p+1)}{2}>0$, so a search performed by the Newton optimization algorithm will “hit” the boundary of v = 0 and we get v̂ = 0. However, if the overall deviation Ω – S is present, but is small in terms of tr(Ω⁻¹S – I)², the limit of the derivative may still be positive and we still have v̂ = 0. This shows a different picture from the MIWL procedure in section 4.3, where v̂^IW = 0 iff Σ satisfies the model. The reason is that the sample covariance matrix S used here involves sampling error. A sample that does not satisfy the model may still be regarded as coming from a population that satisfies the model.

5.3. Some Notes on Computation

It is interesting to note that the derivatives of F_(α) are functions of the observed sample covariance matrix S only through $\overline{\mathbf{\sum }}=\frac{m\mathbf{\Omega }+n\mathbf{S}}{m+n}$, which is the posterior mode of Σ and the inverse of the posterior mean of Σ⁻¹. This points to a relationship between our algorithm and the EM algorithm in Chen (1979), where the unobserved Σ was treated as missing data. For each iteration of his EM algorithm, Σ̄ is first calculated in the E-step and then the M-step essentially sets the derivatives of F_(α=1) to 0 to obtain temporary estimates of the parameters. Since the EM algorithm is iterative with iterative procedures nested in each iteration, it is expected to be slower than the direct minimization of F proposed here. In addition, because the unmodified marginal likelihood function was used, the estimate of v = 1/m is expected to be biased downwards.

A technical issue in this algorithm is to take care of the computation for large m. Because the program is intended to search around values of v close to 0, the discrepancy function and its derivatives need to be evaluated for very large m or for m = ∞. Both cases require special treatment. We can see that the quantity $f(m)=2ln{\mathrm{\Gamma }}_p(\frac{m}{2})-\mathit{mp}ln\frac{m}{2}+mp$ is present in F₁. When m is very large, f(m) = O(1) but the first term increases with m superlinearly. This implies that cancellation errors will be present and become more serious as m increases. Similarly, F₁ = f(m) − f(m+ n) = O(1/m) while f(m) = f(m+ n) = O(1), giving another source of such errors. The same problem is also present in the calculation of the derivatives of F₁. To avoid this problem, Taylor expansions in Lemma 5 were used to construct formulae that minimize the aforementioned issues.

6. Consistency and Sampling Distribution

In frequentist statistics, consistency and sampling distribution are major issues in evaluating estimators and both are related to how the estimator varies from one realization to another as sample size increases. Because both issues concern the imaginary process of multiple realizations beyond the current observation, they both depend on the replication framework assumed.

6.1. Replication Framework and Consistency

As has been stated in the Introduction, the motivation behind the current approach is the recognition of adventitious error as a distinct stochastic process. This assumption implies a replication framework in which both sampling error and adventitious error are random and vary across different realizations. In each realization, a Σ is first realized from the inverted Wishart distribution and an S is then sampled according to the Wishart distribution. Under this replication framework, the entire model can be regarded as a standard frequentist model in which the marginal type II matrix-variate beta distribution is the likelihood function, ξ and v are parameters in the model, and Σ is a random effect that has been integrated out.

Unsurprisingly, the estimators are not consistent as n→∞ alone under this replication framework. Note that both adventitious error and sampling error contribute to the variations among different realizations of S and the estimators. An infinite sample size only removes the variations due to sampling error, but those due to adventitious error are still present. In this case, S = Σ has an inverted Wishart distribution. As a result, the estimators as functions of S are still random quantities, and their randomness results from the uncertainty of the population covariance matrix due to adventitious error.

Alternatively, if we assume m→∞ in addition to n→∞, both types of error disappear and variations among realizations should also vanish. In fact, Proposition 2 implies that $\mathbf{S}\stackrel{\mathbf{p}}{\to }\mathbf{\Omega }({\mathit{\xi }}_0)$. The assumption of both large n and large m is similar to the Pitman drift assumption usually assumed in the traditional approach of CSMs. Both assumptions assume small misspecification. The differences between these two assumptions are: 1. The Pitman drift assumption handles a non-random misspecification, while in our model stochastic adventitious error is assumed; 2. The Pitman drift assumption assumes a particular rate of convergence, namely $\sqrt{n}(\mathit{\sigma }-{\mathit{\omega }}^{\#})\to \mathit{\mu }$, which would correspond to m/n = O(1) as n→∞ and m→∞ for stochastic adventitious error, but this is not assumed in our approach.

To establish consistency⁵, we first note that the function F_(α)(Ω(ξ), m, S, n) involves sample size n explicitly, so classical results for covariance structure analysis (e.g. Shapiro, 1984) where the discrepancy function does not involve sample size no longer apply. In addition, F_(α) does not have a 4-variate limit at point (Ω, m = ∞, S = Ω, n = ∞), and consequently results that assume such limit (e.g. White, 1981, Lemma 3.1) do not apply. The following proposition establishes the consistency of the parameter estimates using Lemma 2.2 of White (1980). Note this Lemma concerns almost sure convergence, but a version for convergence in probability can similarly be proved.

Proposition 3

Suppose that the covariance structure Ω(ξ) is defined and identified on a compact set Ξ and is continuous, and its smallest eigenvalue is bounded away from 0. Then we have

1. F₂(Ω(ξ), m, S, n) → F₂(Ω(ξ), m,Ω*, n) uniformly in ξ and m as S → Ω*.

2. F₂(Ω = Ω(ξ), m, S = Ω(ξ₀), n) → mF^IW(Ω = Ω(ξ),Σ = Ω(ξ₀)) uniformly for ξ ∈ Ξ and m < m₀ given any m₀ as n→∞.

3. $\widehat{\mathit{\xi }}\stackrel{\mathbf{p}}{\to }{\mathit{\xi }}_0$ and $\widehat{v}\stackrel{\mathbf{p}}{\to }0$ as n→∞ and m→∞.

Proof

1. Because

   $$F_2(\mathbf{\Omega }(\mathit{\xi }),m,\mathbf{S},n)-F_2(\mathbf{\Omega }(\mathit{\xi }),m,{\mathbf{\Omega }}^{\ast },n)=-nln\mid \mathbf{S}{\mathbf{\Omega }}^{\ast -1}\mid +(n+m)ln\mid (\frac{m}{n}\mathbf{\Omega }(\mathit{\xi })+\mathbf{S}){(\frac{m}{n}\mathbf{\Omega }(\mathit{\xi })+{\mathbf{\Omega }}^{\ast })}^{-1}\mid ,$$
   it is only necessary to prove that the second term converges to 0 uniformly. When this term is non-negative, following from the fact that ln(1 + x) < x,

   $$\begin{array}{l}\text{second}\text{term}\text{above}=(n+m)ln\mid \mathbf{I}+(\mathbf{S}{\mathbf{\Omega }}^{\ast -1}-\mathbf{I}){(\frac{m}{n}\mathbf{\Omega }(\mathit{\xi }){\mathbf{\Omega }}^{\ast -1}+\mathbf{I})}^{-1}\mid \\ \le n\text{tr}\{(\mathbf{S}{\mathbf{\Omega }}^{\ast -1}-\mathbf{I}){(\frac{m\mathbf{\Omega }(\mathit{\xi }){\mathbf{\Omega }}^{\ast -1}+n\mathbf{I}}{m+n})}^{-1}\}\end{array}$$

   Because the smallest eigenvalue of Ω(ξ) is bounded away from 0, convergence to 0 is uniform. The situation when the term is non-positive can be similarly proved.

2. We define Ω(ξ)Ω(ξ₀)⁻¹ = R and its eigenvalues λ_i, i = 1, ···, p, for convenience.

   $$\begin{array}{l}{F}_2(\mathbf{\Omega }(\mathit{\xi }),m,\mathbf{\Omega }({\mathit{\xi }}_0),n)-m{F}^{\text{IW}}(\mathbf{\Omega }(\mathit{\xi }),\mathbf{\Omega }({\mathit{\xi }}_0))\\ =-mln\mid \mathbf{R}\mid +(m+n)ln\left|\frac{n\mathbf{I}+m\mathbf{R}}{m+n}\right|-m(-ln\mid \mathbf{R}\mid +\text{tr}(\mathbf{R})-p)\\ =mp-p(m+n)ln(1+m/n)+(m+n)\sum _{i}ln(1+m{\lambda }_i/n)-m\sum _i{\lambda }_i\end{array}$$
   Because

   $$\mid (m+n)ln(1+m\lambda /n)-m\lambda \mid \le mln(1+m\lambda /n)+n\mid ln(1+m\lambda /n)-m\lambda /n\mid \le m_{0}ln(1+m_0\lambda /n)+m_0^2{\lambda }^2/2n$$

   and the λ_i’s are bounded on the compact set of Ξ, uniform convergence is established.
3. The above result 1 implies $F_{(\alpha )}(\mathbf{\Omega }(\mathit{\xi }),m,\mathbf{S},n)\stackrel{\mathbf{p}}{\to }{F}_{(\alpha )}(\mathbf{\Omega }(\mathit{\xi }),m,{\mathbf{\Omega }}^{\ast },n)$ uniformly in Ξ as $\mathbf{S}\stackrel{\mathbf{p}}{\to }{\mathbf{\Omega }}^{\ast }$. Result 2, along with identifiability of Ω(ξ), implies

   $$\underset{n>n_0}{inf}\underset{\mid \mathit{\xi }-{\mathit{\xi }}_0\mid >\epsilon ,m<m_0}{min}{F}_{(\alpha )}(\mathbf{\Omega }(\mathit{\xi }),m,\mathbf{\Omega }({\mathit{\xi }}_0),n)>0,$$

   or that the minimum of the limiting loss function is identifiably unique. Now the conditions of White (1980, Lemma 2.2) are satisfied and the conclusion follows.

6.2. Sampling Distribution and Confidence Interval

In traditional CSMs, sampling distributions are derived for a large sample size, n, which reduces parameter estimates to a neighborhood of their corresponding true values, where the parametric model can be locally linearized. In our approach, both assumptions of large n and large m are needed to employ the same technique.

Proposition 4

Suppose the covariance structure Ω(ξ) is continuously differentiable and nonsingular in a neighborhood of ξ₀, its derivative Δ has full rank at ξ₀, the “true value” ξ₀ is not on a boundary, and conditions required for consistency of the MBLEs are satisfied. The MBLEs ξ̂ and v̂ are asymptotically independent and have asymptotic sampling distributions

$$\frac{\widehat{\mathit{\xi }}-{\mathit{\xi }}_0}{\sqrt{v_0+\epsilon }}\stackrel{\mathcal{L}}{\to }\mathrm{N}(\mathbf{0},2{({\mathbf{\Delta }}^{\prime }\mathbf{V}\mathbf{\Delta })}^{\ast -1})$$ (27)

and

$$\frac{\widehat{v}+\epsilon }{v_0+\epsilon }\stackrel{\mathcal{L}}{\to }{\{{(\alpha \frac{p(p+1)}{2})}^{-1}{\chi }_{df}^2-\frac{\epsilon }{v_0+\epsilon }\}}^{+}+\frac{\epsilon }{v_0+\epsilon }$$ (28)

as n → ∞ and v₀ → 0, where V = Ω⁻¹ ⊗ Σ̄⁻¹ and the superscript * denotes evaluating the quantity at n = ∞, v₀ = 0, ξ = ξ₀ and s = ω*.

Proof

When no parameter is estimated on a boundary, we have $\frac{\partial F_{(\alpha )}}{\partial \mathit{\xi }}=0$. From Equation (22), we have (ω̂ − s)′V̂ Δ̂ = 0, which is equivalent to Δ̂′V̂(ω̂ − ω*) = Δ̂′V̂(s − ω*). As Δ is continuous in a neighborhood of ξ₀, we have ω̂ −ω* = Δ̄(ξ−ξ₀), where Δ̄ = Δ(ξ̄) with ξ̄ = ξ₀ + t(ξ̂ − ξ₀) and t ∈ (0, 1). So we have

$${\widehat{\mathbf{\Delta }}}^{\prime }\widehat{\mathbf{V}}\overline{\mathbf{\Delta }}(\widehat{\mathit{\xi }}-{\mathit{\xi }}_0)={\widehat{\mathbf{\Delta }}}^{\prime }\widehat{\mathbf{V}}(\mathit{s}-{\mathit{\omega }}^{\ast })$$

Because ${\widehat{\mathbf{\Delta }}}^{\prime }\widehat{\mathbf{V}}\overline{\mathbf{\Delta }}\stackrel{\mathbf{p}}{\to }{({\mathbf{\Delta }}^{\prime }\mathbf{V}\mathbf{\Delta })}^{\ast }\succ \mathbf{0}$, it must be nonsingular for large enough n and m, so

$$\widehat{\mathit{\xi }}-{\mathit{\xi }}_0={({\widehat{\mathbf{\Delta }}}^{\prime }\widehat{\mathbf{V}}\overline{\mathbf{\Delta }})}^{-1}{\widehat{\mathbf{\Delta }}}^{\prime }\widehat{\mathbf{V}}(\mathit{s}-{\mathit{\omega }}^{\ast })={({\mathbf{\Delta }}^{\prime }\mathbf{V}\mathbf{\Delta })}^{\ast -1}{({\mathbf{\Delta }}^{\prime }\mathbf{V})}^{\ast }(\mathit{s}-{\mathit{\omega }}^{\ast })+o_{\mathrm{p}}(\Vert \mathit{s}-{\mathit{\omega }}^{\ast }\Vert )$$ (30)

whose asymptotic distribution follows from Proposition 2.

Equation (27) implies $\widehat{\mathit{\xi }}-{\mathit{\xi }}_0=O(\sqrt{v_0+\epsilon })$, so

$$\widehat{\mathit{\omega }}-{\mathit{\omega }}^{\ast }={\mathbf{\Delta }}^{\ast }(\widehat{\mathit{\xi }}-{\mathit{\xi }}_0)+o_{\mathrm{p}}(\sqrt{v_0+\epsilon })={\mathbf{V}}^{\Vert \ast }(\mathit{s}-{\mathit{\omega }}^{\ast })+o_{\mathrm{p}}(\sqrt{v_0+\epsilon })$$

where V^|| = Δ(Δ′VΔ)⁻¹(Δ′V) is idempotent, and

$$\frac{1}{2}\frac{1}{v_0+\epsilon }{(\mathit{s}-\widehat{\mathit{\omega }})}^{\prime }{\mathbf{V}}^{\ast }(\mathit{s}-\widehat{\mathit{\omega }})=\frac{1}{2}\frac{1}{v_0+\epsilon }{(\mathit{s}-{\mathit{\omega }}^{\ast })}^{\prime }{\mathbf{V}}^{\perp \ast }(\mathit{s}-{\mathit{\omega }}^{\ast })+o_{\mathrm{p}}(1)\stackrel{\mathcal{L}}{\to }{\chi }_{df}^2$$ (31)

where V^⊥ = I − V^|| is also idempotent, and df is the degrees of freedom of the covariance structure and also the rank of V^⊥*.

For parameter v, if v̂ > 0, we have $\frac{\partial F_{(\alpha )}}{\partial m}=0$. From Equations (23) and (24), we have

$$\alpha \{-f^{\prime }(\widehat{m})+f^{\prime }(\widehat{m}+n)\}=-ln\mid \widehat{\mathbf{\Omega }}{\widehat{\overline{\mathbf{\sum }}}}^{-1}\mid +\text{tr}(\widehat{\mathbf{\Omega }}{\widehat{\overline{\mathbf{\sum }}}}^{-1})-p$$ (32)

Multiplying both sides by ${(\frac{\widehat{m}+n}{n})}^2\frac{m_{0}n}{m_0+n}$ and applying Lemma 6 to the right hand side give

$$\begin{array}{l}\alpha \{f^{\prime }(\widehat{m}+n)-f^{\prime }(\widehat{m})\}\frac{(\widehat{m}+n)\widehat{m}}{n}\frac{\widehat{v}+\epsilon }{v_0+\epsilon }=\frac{{(\widehat{m}+n)}^2}{n^2(v_0+\epsilon )}\left\{\frac{1}{2}\text{tr}{(\widehat{\mathbf{\Omega }}{\widehat{\overline{\mathbf{\sum }}}}^{-1}-\mathbf{I})}^2+o({\Vert \widehat{\mathit{\omega }}-\widehat{\overline{\mathit{\sigma }}}\Vert }^2)\right\}\\ =\frac{1}{v_0+\epsilon }\frac{1}{2}\text{tr}{\left\{(\widehat{\mathbf{\Omega }}-\mathbf{S}){\mathbf{\Omega }}^{\ast -1}\right\}}^2+o(\frac{{\Vert \widehat{\mathit{\omega }}-\mathit{s}\Vert }^2}{v_0+\epsilon })\end{array}$$ (33)

From Equation (31), the right hand side converges to ${\chi }_{df}^2$; from Lemma 5, the factor on the left hand side converges to $\alpha \frac{p(p+1)}{2}$, so the asymptotic distribution of v̂ follows. The asymptotic independence of ξ̂ and v̂ follows from that of (Δ′VΔ)*⁻¹(Δ′V)*(s − ω*) and (s − ω*)′V^⊥*(s − ω*).

It should be noted that the χ² distribution of v̂ is derived for v̂ > 0. The actual asymptotic distribution has a point mass of size $P({\chi }_{df}^2<\alpha \frac{p(p+1)}{2}\frac{\epsilon }{v_0+\epsilon })$. To remove this problem, we may modify v̂ and define

$${\widehat{v}}_0=\{\begin{array}{cc}\widehat{v}& \widehat{v}>0\\ {(\alpha \frac{p(p+1)}{2})}^{-1}\frac{1}{2}\text{tr}{\left\{(\widehat{\mathbf{\Omega }}-\mathbf{S}){\widehat{\mathbf{\Omega }}}^{-1}\right\}}^2-\frac{1}{n}& \widehat{v}=0\end{array}$$ (34)

so that

$$\frac{{\widehat{v}}_0+\epsilon }{v_0+\epsilon }\stackrel{\mathcal{L}}{\to }{(\alpha \frac{p(p+1)}{2})}^{-1}{\chi }_{df}^2$$ (35)

Note the estimator v̂₀ is asymptotically unbiased when $\alpha =df/\frac{p(p+1)}{2}$.

Once the sampling distributions are obtained, CIs and CBs can be obtained by inverting the sampling distribution. This is straightforward for the parameter v, whose 90% upper and lower CBs are given by $\alpha \frac{p(p+1)}{2}({\widehat{v}}_0+\epsilon )/{\chi }_{df}^2(10\%)-\epsilon$ and $\alpha \frac{P(p+1)}{2}({\widehat{v}}_0+\epsilon )/{\chi }_{df}^2(90\%)-\epsilon$.

For the covariance structure parameter ξ, its sampling distribution involves unknown parameters. Replacing those unknown parameters with their estimates, we have

$$\frac{{\widehat{\xi }}_i-{\xi }_{i0}}{\sqrt{2({\widehat{v}}_0+\epsilon ){[{\widehat{\mathbf{\Delta }}}^{\prime }\widehat{\mathbf{V}}\widehat{\mathbf{\Delta }}]}^{ii}}}\stackrel{\mathcal{L}}{\to }{\mathrm{t}}_{df}$$

as n → ∞ and m → ∞. Note that the distribution is a t distribution and its degrees of freedom df is that of the covariance structure and is not related to sample size. The 95% CI of a parameter ξ_i is given by ${\widehat{\xi }}_i\pm {\mathrm{t}}_{df}(97.5\%)\sqrt{2({\widehat{v}}_0+\epsilon ){[{\widehat{\mathbf{\Delta }}}^{\prime }\widehat{\mathbf{V}}\widehat{\mathbf{\Delta }}]}^{ii}}$. For bounded parameters such as correlations, a likelihood based CI (Neale and Miller, 1997; Cheung, 2012; Wu and Neale, 2012) can be used.

To apply the asymptotic distributions derived above under the assumption of v → 0 and n → ∞, one should note that it requires only a small v and a large n, in the same sense that only a large sample size n is required to use classic asymptotic results that assume n → ∞. Remember that weak convergence of distributions to a continuous asymptotic distribution is defined as the convergence of their cumulative distribution functions (cdf). In the case of v̂₀, this implies that at any given x, the cdf of (v̂₀ +ε)/(v₀ +ε) can be made arbitrarily close to that of the scaled χ² distribution by increasing n and decreasing v₀. The criteria on the sizes of v and n for the asymptotic results to work well may depend on the specific model and its parametrization.

7. The Evaluation of Covariance Structures

In the sections above we discussed parameter estimation procedure and the properties of the MBLE. A remaining issue is the evaluation of the covariance structure Ω(ξ). The model is rejected if the adventitious error in the operational population is large. When the adventitious error is large, the single operational population is not representative of the theoretical population of interest and as a result any inference on the population of interest is doubtful. Because our procedure lies on the assumption that the covariance structure Ω(ξ) holds in the theoretical population, it is also possible that the operational population is a valid representation of the theoretical population but the covariance structure does not hold. Under either possibility the model must be rejected as a suitable description of the population of interest.

A criterion must be chosen as the largest admissible amount of adventitious error to retain the model. Because we have established the relationship v ≈ ε² between parameter v and population RMSEA ε, the cut off values of RMSEA can be used as a guideline for the size of $\sqrt{v}$. Because v has an upper bound of 1/(p−1), a better choice is ṽ = 1/(m−p+1). A value of $\sqrt{\stackrel{\sim }{v}}$ smaller than 0.05 can be interpreted as indicating a small amount of adventitious error, a value between 0.05 and 0.08 indicates an acceptable amount of adventitious error, and a value beyond 0.08 indicates an unacceptable amount. A 90% CI on $\sqrt{\stackrel{\sim }{v}}$ can be used for this purpose.

8. Simulation Studies

In this section, results from three simulation studies are presented. The first study demonstrates the relationship between ${\widehat{\stackrel{\sim }{v}}}^{\text{IW}}$ and RMSEA ε given a population covariance matrix Σ. The second study validates the asymptotic sampling distributions and the coverage probabilities of the CIs. The third study contrasts the performance of the MWL of the traditional approach and that of the MBL.

8.1. Study I: The Relationship between ${\widehat{\stackrel{\sim }{v}}}^{\text{IW}}$ and ε

As has been shown in Section 4.3, given a population covariance matrix Σ, the relationship v̂^IW ≈ ε² holds when both measures are small, which also implies $\sqrt{{\widehat{\stackrel{\sim }{v}}}^{\text{IW}}}\approx \epsilon$. To demonstrate this relationship, 1000 population covariance matrices Σ were drawn from a structured covariance matrix Ω with dispersion parameter v uniformly chosen between 0 and 0.01, which corresponds to the range between 0 and 0.1 for RMSEA. The sampled Σ’s were then fitted to the covariance structure using both MIWL and MWL, and both $\sqrt{{\widehat{\stackrel{\sim }{v}}}^{\text{IW}}}$ and the population RMSEA ε were obtained.

Two covariance structures were used for this study. The first structure was a factor analysis model with 2 factors and 8 manifest variables. The factor loading matrix was chosen to be

$$\mathbf{\Lambda }={\left(\begin{array}{cccccccc}0.5& 0.5& 0.6& 0.6& 0& 0& 0& 0\\ 0& 0& 0& 0& 0.7& 0.7& 0.8& 0.8\end{array}\right)}^{\prime },$$ (36)

and the factor correlation was chosen to be ρ = 0.5. Unique variances were chosen as

$$\mathit{\psi }={[0.75,0.75,0.64,0.64,0.51,0.51,0.36,0.36]}^{\prime }$$ (37)

such that the model implied covariance matrix is a correlation matrix. This structure has 19 degrees of freedom. The second covariance structure was simply a 8×8 diagonal matrix, with 28 degrees of freedom.

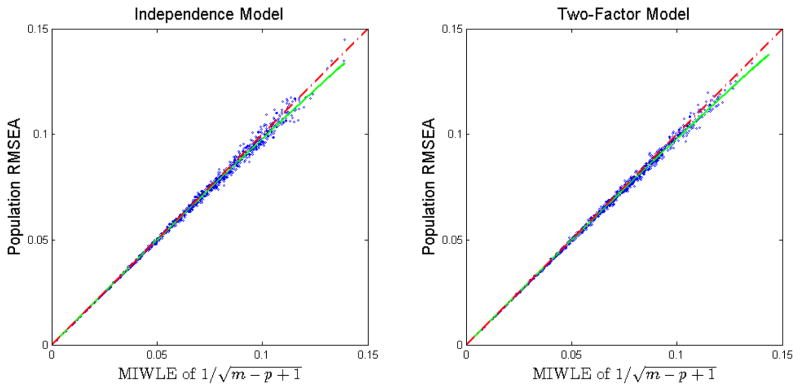
The results of the simulation are displayed in Figure 1, in which the RMSEA is plotted against $\sqrt{{\widehat{\stackrel{\sim }{v}}}^{\text{IW}}}$ for the two covariance structures respectively. The solid line shows the deterministic relationship between $\sqrt{{\widehat{F}}^{\text{IW}}/df}$ and $\sqrt{{\widehat{\stackrel{\sim }{v}}}^{\text{IW}}}$ implied by Equation (15). It is closely approximated by the dashed line of equality when RMSEA ≤ 0.1, validating the relationship ${\widehat{F}}^{\text{IW}}/df\approx {\widehat{v}}^{\text{IW}}\approx {\widehat{\stackrel{\sim }{v}}}^{\text{IW}}$ implied by the Taylor expansion of function f. For both covariance structures, points lie closely around the solid line as implied by the asymptotic equivalence of F^W and F^IW and are also very close to the dashed line, demonstrating $\sqrt{{\widehat{\stackrel{\sim }{v}}}^{\text{IW}}}\approx \epsilon$. Note the range ε ≤ 0.1 covers a wide range of misspecification. No difference can be detected between the two plots for different covariance structures because of the use of α = 2df/p(p + 1).

Figure 1.

Plot of population RMSEA and MIWLE of $\sqrt{\stackrel{\sim }{v}}=1/\sqrt{m-p+1}$.

8.2. Study II: The Sampling Distributions of Estimates

This study validates the asymptotic sampling distributions and CIs as derived in section 6.2. Samples were drawn from the marginal beta distribution and then fitted using the modified beta discrepancy function F_α. The empirical sampling distributions and coverage probabilities of CIs were then obtained and compared to their theoretical counterpart. The true model is the two factor model with true values specified in Study I. When fitting the sample, the factor structure was assumed for the correlation matrix instead of for the covariance matrix, and the covariance structure was given by Ω = D(ΛΦΛ′ + Ψ)D, where D is a diagonal matrix of standard deviations and the diagonal elements of the expression in parentheses were constrained to be 1. Because parameters λ₁₁ and λ₂₁ are in symmetric positions, the sampling distributions of their estimates must be the same. Simulated parameter estimates for both parameters were combined for graphical and tabular summaries concerning the two parameters. Other pairs of parameters are treated in the same way. Four levels of 200, 500, 1000 and ∞ were chosen for both m and n, yielding 15 conditions (excluding the invalid n = m = ∞ condition). Conditions with infinite sample size were included for comparison purposes. N = 50, 000 replications were used.

8.2.1. The Two Extreme Cases

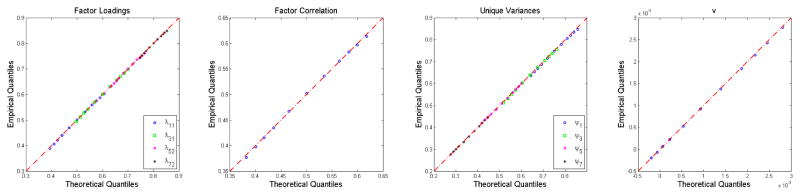
For the condition where n = m = 1000, Figure 2 displays QQplots of the empirical sampling distribution against the theoretical asymptotic distribution derived in section 6.2 for each covariance structure parameter and v. The plots show that the analytical asymptotic distributions give very good approximations when both n = m = 1000.

Figure 2.

QQplots of the simulated and asymptotic distributions of ξ̂ for n = m = 1000. Only the 1st, 2.5th, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97.5th and 99th percentiles are plotted.

Table 1 summarizes the missing rate (i.e. the complement of coverage rate) of CIs of covariance structure parameters (ξ) constructed using three methods: Type I CIs were constructed using the theoretical asymptotic normal distribution with true parameter values ξ₀ and v₀; Type II CIs were constructed using the asymptotic t distribution with true covariance structure parameter ξ₀ and estimated dispersion parameter v̂₀; Type III CIs were constructed using the asymptotic t distribution with parameter estimates ξ̂ and v̂₀. Only the type III CI is possible in practical applications. The first two types CIs are shown here only for comparison purposes.

Table 1.

The missing rates (%) of 95% CIs of ξ. Types of CI: I. Normal approximation with ξ₀ and v₀; II. t approximation with ξ₀ and v̂₀; III. t approximation with ξ̂ and v̂₀.

	n = m = 1000			n = m = 200
	I	II	III	I	II	III
λ11	5.09	5.16	5.49	5.73	5.57	7.14
λ31	5.09	5.06	5.30	5.97	5.74	6.96
λ52	4.97	4.96	5.34	5.27	5.26	6.99
λ72	5.02	5.07	5.39	5.20	5.24	6.89
ρ	5.14	5.14	5.59	5.83	5.63	7.68
ψ1	5.08	5.12	5.63	5.40	5.38	8.45
ψ3	5.07	5.06	5.43	5.58	5.52	7.67
ψ5	4.94	4.92	5.31	5.12	5.08	7.09
ψ7	5.04	5.03	5.37	5.08	5.13	6.84

For n = m = 1000, the missing rates of the type I and type II CIs are very close to 5%, reaffirming the accuracy of the analytical derivations as demonstrated in the QQplots. The missing rates of type III CIs, ranging from 5.3% to 5.6%, are slightly larger than the former two types of CIs, though they are still close to the nominal level. The poorer coverage rates of the type III CIs results from replacing the unknown ξ₀ by its estimate ξ̂. For the dispersion parameter v, the missing rates of the CBs of v are 4.80% and 4.85%.

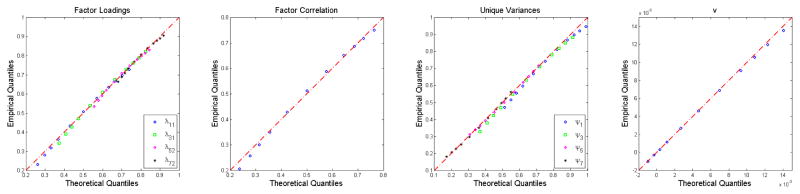
For m = n = 200, Figure 3 shows differences between the empirical and analytical distributions for parameters. For most covariance structure parameters, due to their natural boundaries, the empirical sampling distributions of their estimators have slightly shorter upper tails and longer lower tails than expected.⁶ This results in slightly larger missing rates of the type I CIs for the factor correlation, the first two factor loadings and the first two unique variances (Table 1). The missing rates of type III CIs are larger due to the use of parameter estimates ξ̂. For parameter v, the last panel of Figure 3 shows that its empirical sampling distribution has slightly shorter upper tail than its asymptotic distribution, leading to a missing rate of 4.33%, slightly smaller than 5% for the LCB. The missing rate for the UCB of v is 4.99%.

Figure 3.

QQplots of the simulated and asymptotic distributions of ξ̂ for n = m = 200. Only the 1st, 2.5th, 5th, 10th, 25th, 50th, 75th, 90th, 95th, 97.5th and 99th percentiles are plotted.

8.2.2. When n and m Vary

The Kolmogorov-Smirnov (KS) distance is used as a summary statistic to measure the discrepancy between two distributions. Table 3 gives the average KS distance between the simulated and asymptotic distributions across the 17 covariance structure parameters for each sample size combination. We can see that the KS distance decreases as m increases. However, this trend cannot be generally observed for n. One possible explanation is that the bias of the asymptotic distribution only decreases when m becomes larger.

Table 3.

The average 100×KS distances between the simulated and asymptotic sampling distributions of ξ̂.

	m = 200	m = 500	m = 1000	m = ∞
n = 200	4.14	2.53	1.99	1.54
n = 500	4.26	2.60	1.84	0.98
n = 1000	4.33	2.69	1.71	0.79
n = ∞	4.53	2.94	2.07	—

The missing rates for CIs of three parameters are tabled in Table 2. These are type III CIs computed using the parameter estimates. The first factor loading and the first unique variance are chosen as they generally have the largest missing rates. We can see the missing rates tend to be closer to the nominal value as both n and m increases. Although the missing rates of the type I and type II CIs (not shown here) assuming known ξ₀ are close to 5%, those of the type III CIs are generally greater than their nominal level, with the largest missing rate being 8.45%. Again, such distortion of missing rates are generally due to the use of parameter estimates, which deviate from the unknown true values for finite sample sizes.

Table 2.

The missing rates (%) of 95% CIs of selected covariance structure parameters.

		m = 200	m = 500	m = 1000	m = ∞
λ11	n = 200	7.14	6.38	6.06	5.99
	n = 500	6.72	5.93	5.56	5.35
	n = 1000	6.58	5.71	5.49	5.13
	n = ∞	6.34	5.53	5.30	—
ρ	n = 200	7.68	6.55	6.25	6.17
	n = 500	7.21	5.91	5.85	5.24
	n = 1000	7.03	5.88	5.59	5.09
	n = ∞	6.67	5.80	5.41	—
ψ1	n = 200	8.45	7.26	6.88	6.71
	n = 500	7.47	6.40	5.93	5.60
	n = 1000	7.23	6.05	5.63	5.28
	n = ∞	6.74	5.72	5.34	—

For the dispersion parameter v, The KS distances in Table 4 shows the χ² based approximation works very well under all conditions. Table 5 gives the missing rates of upper and lower CBs for different values of m and n. Missing rates are in general close to though slightly below the nominal level of 5%.

Table 4.

The 100×KS distances between the simulated and asymptotic unconditional sampling distributions for v̂₀.

	m = 200	m = 500	m = 1000	m = ∞
n = 200	0.96	0.61	0.42	0.60
n = 500	0.76	0.56	0.48	0.35
n = 1000	0.67	0.38	0.56	0.41
n = ∞	0.82	0.32	0.54	—

Table 5.

The missing rates (%) of 95% CBs of v.

	m = 200		m = 500		m = 1000		m = ∞
	LCB	UCB	LCB	UCB	LCB	UCB	LCB	UCB
n = 200	4.33	4.99	4.68	4.82	4.89	4.79	5.09	4.86
n = 500	4.43	4.92	4.54	4.99	4.86	4.89	5.06	5.00
n = 1000	4.46	4.88	4.80	5.01	4.80	4.85	5.03	5.01
n = ∞	4.69	4.85	5.01	4.94	4.81	5.12	—	—

8.2.3. Brief Summary

The simulation study confirms the asymptotic distributions derived in section 6.2. For large n and m, the missing rates of the CIs of structural parameters are close to their nominal value of 5%; with either small n or small m, the missing rates can be inflated mainly due to the use of parameter estimates in calculation of the CIs and the bounded range of the parameters. These issues are not specific to our new model or our new asymptotic paradigm. In fact, they are the problems of Wald type CI in general. The use of likelihood based CIs (Neale and Miller, 1997; Cheung, 2012; Wu and Neale, 2012) can avoid them. The CBs of the dispersion parameter v perform well under all conditions.

8.3. Study III: Comparison with the Traditional Approach

In the third study we compare the new approach with the traditional MWL approach. The 50,000 random samples obtained in the second simulation study for n = m = 1000 were used again and each of the samples was fitted to a MWL model to obtain point estimates and CIs.

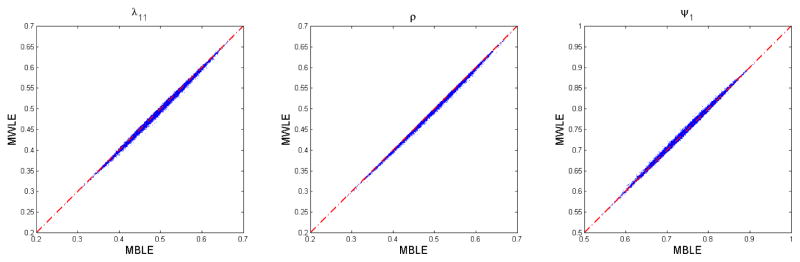
The point estimates of the covariance structure parameters are compared in Figure 4. MBLE and MWLE are very close to each other, which is not surprising given the asymptotic normality of the two distributions. A real difference between the two procedures can be found when comparing the performance of the CIs. As can be observed from the first two columns of Table 6, the missing rates of the MBL CIs are only slightly greater than nominal value of 5%, while those of the MWL CIs are far beyond 5%, ranging around 32%. This failure of MWL CIs originates from the fact that they only take into account the randomness in the parameter estimates due to the sampling error, while that due to adventitious error is neglected. Because only a part of the randomness is addressed in the CIs, the CIs are shorter than they are supposed to be and therefore failed to cover the true parameter values with the designated probability.

Figure 4.

Comparison of ξ̂ and ξ̂^W. n = m = 1000.

Table 6.

The missing rates (%) of the MBL and MWL 95% CIs with n = m = 1000.

	MBL	MWL
λ11	5.49	32.09
λ31	5.30	32.05
λ52	5.34	31.79
λ72	5.39	31.83
ρ	5.59	32.22
ψ1	5.63	32.24
ψ3	5.43	32.15
ψ5	5.31	31.86
ψ7	5.37	31.87

9. Examples

We use two data sets to illustrate the MBL procedure. Both data sets are available in the R package psych. The first data set comes from the manual of Revised NEO Personality Inventory (NEO-PI-R, Costa and McCrae, 1992). It is a correlation matrix of the six facets of the Neuroticism factor from a sample of size 1,000. A single-factor model was fitted to the data using both the traditional MWL and the MBL methods. The parameter estimates and CIs are shown in Table 7. The point estimates of the loadings from the two procedures are very close to each other, but the CIs are very different. The CIs given by MBL are about 2.7 times as wide as those given by MWL. This difference in variability comes from adventitious error. The amount of adventitious error is estimated at v̂ = 0.0044, more than four times the sampling error as measured by 1/999 = 0.0010. $\sqrt{\widehat{\stackrel{\sim }{v}}}=0.0673$ is very close to the estimated RMSEA ε̂ = 0.0672 in the MWL procedure, which is not surprising given their asymptotic relationship as discussed in section 4.3. The CI of $\sqrt{\stackrel{\sim }{v}}$ is wider than that of RMSEA due to the randomness of the adventitious error. A small amount of adventitious error is cannot be rejected, so the one factor model is retained.

Table 7.

Parameter estimates and CIs from both MWL and MBL procedures for the loadings of six facets on the Neuroticism factor of NEO-PI-R. The six facets are Anxiety, Angry-Hostility, Depression, Self-Consciousness, Impulsiveness and Vulnerability. The sample size is 1,000. The confidence level is 95% for the structural parameters and 90% for others.

	λ1	λ2	λ3	λ4	λ5	λ6	ε	v	$\sqrt{\stackrel{\sim }{v}}$
MWLE	0.770	0.602	0.837	0.705	0.468	0.763	0.0672
MWLCI	0.739	0.558	0.811	0.669	0.415	0.731	0.0496
	0.802	0.646	0.863	0.742	0.521	0.795	0.0861
MBLE	0.770	0.612	0.837	0.707	0.475	0.764		0.00442	0.0673
MBLCI	0.687	0.495	0.767	0.610	0.334	0.679		0.00188	0.0436
	0.854	0.729	0.906	0.805	0.616	0.849		0.01368	0.1212

The second data set comes from Tucker (1958) and was used as an example by Tucker and Lewis (1973). It is a correlation matrix of nine selected tests from two batteries studied by Thurstone and Thurstone (1941). Among the tests, five load on a word fluency factor and the remaining four on a verbal factor. For illustrative purpose, we fit a model in which factor loadings on the same factor are constrained to be the same. The parameter estimates and CIs are shown in Table 8. The relationship between estimates from the two procedures follows the same pattern as in the first example. The amount of adventitious error (v̂ = 0.0043) is about three times the sampling error (1/709 = 0.0014) and the CIs from MBL are twice as wide as those from MWL. A small amount of adventitious error is rejected.

Table 8.

Parameter estimates and CIs from both MWL and MBL procedures for the data set from Tucker (1958). The nine variables are Prefixes, Suffixes, First and Last Letters, First Letters, Four Letter Words, Vocabulary, Sentences, Completion and Same or Opposite. The first five tests load on a word fluency factor, while the remaining four on a verbal factor. The sample size is 710. The confidence level is 95% for the structural parameters and 90% for others.

	λ1	λ2	ρ	ε	v	$\sqrt{\stackrel{\sim }{v}}$
MWLE	0.698	0.840	0.466	0.0667
MWLCI	0.673	0.824	0.396	0.0553
	0.723	0.856	0.535	0.0785
MBLE	0.699	0.844	0.480		0.00430	0.0668
MBLCI	0.646	0.810	0.338		0.00257	0.0512
	0.751	0.877	0.623		0.00762	0.0901

10. Summary and Conclusions

Adventitious error is defined as the difference between the population from which observations are collected and the population for which the theory is hypothesized. The traditional approach to the analysis of CSMs does not account for uncertainty introduced by the adventitious error in both parameter estimates and the test statistic. It also shifts the focus of the theory behind the model, narrows its generalizability and affects the meaningfulness of the parameters. The technical assumption of Pitman drift employed in the traditional approach is implausible in practice.

To address these issues, we assume the deviation between the sample and the covariance structure are due to both sampling and adventitious error, and both are random quantities. This new replication framework allows us to account for the variations in parameter estimates due to adventitious error. In this approach, this error is modeled with an inverted Wishart distribution with a precision parameter m, whose inverse v measures the size of this error. In addition, the assumption of n → ∞ and v → 0 is assumed for derivations of consistency, sampling distributions and other properties of the model. This assumption is more plausible than the traditional Pitman drift assumption in that adventitious error is only assumed small, but not assumed to get smaller when the sample size increases.

Analytical derivations yielded several important results. First, the dispersion parameter v of Σ is related to RMSEA ε by v ≈ ε² when both are small. Under the assumption of large sample size and small adventitious error, the estimators for covariance structure parameters are consistent and asymptotically normally distributed, and both adventitious error and sampling error contribute to their variances. The estimator v̂₀ has an asymptotic distribution related to the χ² distribution.

A Newton-Raphson algorithm is also provided for the MBL procedure. Simulation experiments confirmed the validity of the analytical asymptotic sampling distributions and the CIs were also found adequate for large n and m. They also demonstrated that the effect of a random adventitious error cannot be neglected as it contributes to the dispersion of the estimators and that a procedure neglecting this effect produces CIs that are too short and give poor coverage rates.

The current research has opened a new framework for the analysis of uncertainty quantification in covariance structures. Because it is a first attempt to quantifying the stochastic adventitious error in covariance structures, it is not perfect. For example, the current procedure assumes a single group (i.e. one realization of the adventitious error) with no missing data or covariates. In addition, a Wishart distribution is assumed for the sampling error and its conjugate distribution is used for the adventitious error. Multi-group analysis with missing data and covariates and robust modeling methods can be subjects of future research.

Because models used in psychology are usually subject to adventitious error, the issue addressed in this research is more general than CSMs. The current research only considers this general issue in terms of a specific context. Quantifying adventitious error as well as other uncertainties in psychological models in general is a new area that deserves further research.

Computer Programs

The MATLAB programs for obtaining MBLE, MWLE and MIWLE are included in the attachment to this paper along with a description file.

A. Lemmas and Proofs

Lemma 5

Taylor expansions of function f as defined in Equation 7 and its derivatives are listed below.

$$\begin{array}{rr}\hfill f(x)=& \hfill -c_0(lnx)+c+c_1{x}^{-1}+c_2{x}^{-2}+2c_3{x}^{-3}+O(x^{-4})\\ \hfill f^{\prime }(x)=& \hfill -c_0{x}^{-1}-c_1{x}^{-2}-2c_2{x}^{-3}-6c_3{x}^{-4}+O(x^{-5})\\ \hfill f^{″}(x)=& \hfill c_0{x}^{-2}+2c_1{x}^{-3}+6c_2{x}^{-4}+24c_3{x}^{-5}+O(x^{-6})\end{array}$$

where

$$\begin{array}{l}{c}_0=\frac{p(p+1)}{2}{c}_1=\frac{p(2p^2+3p-1)}{12}{c}_2=\frac{(p-1)p(p+1)(p+2)}{24}\\ c_3=\frac{p(6p^4+15p^3-10p^2-30p+3)}{720}c=\frac{p(p-1)}{2}ln(2\pi )+pln(4\pi )\end{array}$$

Proof

Reference covered for blind review.

The following fact is used in a number of places in the paper.

Lemma 6

for any matrix A = O(1/n),

$$ln\mid \mathbf{I}+\mathbf{A}\mid =\text{tr}(\mathbf{A})-\frac{1}{2}\text{tr}({\mathbf{A}}^2)+\frac{1}{3}\text{tr}({\mathbf{A}}^3)+O(1/n^4)$$ (38)

Proof

Write A in its spectral decomposition and the result follows from the Taylor expansion of ln(1 + x).

The next lemma is used to establish Proposition 1.

Lemma 7

${lim}_n{\stackrel{\sim }{F}}_1={\stackrel{\sim }{F}}_1^{\text{IW}}=f(m),{lim}_n{\stackrel{\sim }{F}}_2={\stackrel{\sim }{F}}_2^{\text{IW}}$, lim_m F̃₁ = f(n), and lim_m F̃₂ = nF^W + (p+1) ln|S|, where F̃₁, F̃₂, ${\stackrel{\sim }{F}}_1^{\text{IW}},{\stackrel{\sim }{F}}_2^{\text{IW}}$, f and F^W are defined respectively by Equations 5, 6, 10, 11, 7 and 1.

Proof

We only prove the first two limits. The first limit follows from lemma 5. For the second limit, Lemma 6 gives

$$\begin{array}{l}{\stackrel{\sim }{F}}_2=(p+1)ln\mid \mathbf{S}\mid +mln\mid {\mathbf{\Omega }}^{-1}\mathbf{S}\mid +(m+n)ln\left|\frac{m}{m+n}(\mathbf{\Omega }{\mathbf{S}}^{-1}-\mathbf{I})+\mathbf{I}\right|\\ =(p+1)ln\mid \mathbf{S}\mid +mln\mid {\mathbf{\Omega }}^{-1}\mathbf{S}\mid +m\text{tr}({\mathbf{S}}^{-1}\mathbf{\Omega }-\mathbf{I})+O(1/n)\end{array}$$

Proof to Proposition 2

Proof

As m → ∞, we have $\mathbf{\sum }\stackrel{\mathbf{p}}{\to }\mathbf{\Omega }$, and $\sqrt{m}\text{vec}({\mathbf{\sum }}^{-1}-{\mathbf{\Omega }}^{-1})\stackrel{\mathcal{L}}{\to }\mathrm{N}(0,2{\mathbf{M}}_p{(\mathbf{\Omega }\otimes \mathbf{\Omega })}^{-1})$. Consequently, $\sqrt{m}(\mathit{\sigma }-\mathit{\omega })=-\sqrt{m}\text{vec}\{\mathbf{\Omega }({\mathbf{\sum }}^{-1}-{\mathbf{\Omega }}^{-1})\mathbf{\sum }\}=-\sqrt{m}(\mathbf{\sum }\otimes \mathbf{\Omega })\text{vec}({\mathbf{\sum }}^{-1}-{\mathbf{\Omega }}^{-1})\stackrel{\mathcal{L}}{\to }\mathrm{N}(0,2{\mathbf{M}}_p(\mathbf{\Omega }\otimes \mathbf{\Omega }))$. On the other hand, conditional on Σ, as n → ∞,

$$\sqrt{n}{(\mathbf{\sum }\otimes \mathbf{\sum })}^{-\frac{1}{2}}(\mathit{s}-\mathit{\sigma })=\sqrt{n}\text{vec}({\mathbf{\sum }}^{-\frac{1}{2}}\mathbf{S}{\mathbf{\sum }}^{-\frac{1}{2}}-\mathbf{I})\stackrel{\mathcal{L}}{\to }\mathrm{N}(0,2{\mathbf{M}}_p)$$

Note the finite sample distribution on the left hand side does not depend on Σ, so this conditional distribution is also the unconditional distribution and the convergence in distribution is uniform w.r.t Σ. From the Skorokhod Representation Theorem (see, e.g., Billingsley, 1999, Theorem 6.7; Resnick, 2001, Section 8.3), there exist two sequences of random variables z_n, n = 0, 1, ···, and x_m, m = 0, 1, ···, defined on the same probability space, such that

$$\begin{array}{llll}\hfill {\mathit{z}}_n={\mathit{z}}_0+o_{\mathrm{p}}(1)& \hfill (n\to \infty ),& {\mathit{z}}_n\stackrel{d}{=}\sqrt{n}{(\mathbf{\sum }\otimes \mathbf{\sum })}^{-\frac{1}{2}}(\mathit{s}-\mathit{\sigma })\hfill & \text{for}n>0,\hfill \\ \hfill {\mathit{x}}_m={\mathit{x}}_0+o_{\mathrm{p}}(1)& \hfill (m\to \infty ),& {\mathit{x}}_m\stackrel{d}{=}\sqrt{m}{(\mathbf{\Omega }\otimes \mathbf{\Omega })}^{-\frac{1}{2}}(\mathit{\sigma }-\mathit{\omega })\hfill & \text{for}m>0\hfill \end{array}$$

and z₀, ${\mathit{x}}_0\stackrel{i.i.d.}{\sim }\mathrm{N}(0,2{\mathbf{M}}_p)$. Now we have

$$\begin{array}{l}\sqrt{\frac{mn}{m+n}}{(\mathbf{\Omega }\otimes \mathbf{\Omega })}^{-\frac{1}{2}}(\mathit{s}-\mathit{\omega })\\ =\sqrt{\frac{m}{m+n}}\sqrt{n}{(\mathbf{\Omega }\otimes \mathbf{\Omega })}^{-\frac{1}{2}}(\mathit{s}-\mathit{\sigma })+\sqrt{\frac{n}{m+n}}\sqrt{m}{(\mathbf{\Omega }\otimes \mathbf{\Omega })}^{-\frac{1}{2}}(\mathit{\sigma }-\mathit{\omega })\\ \stackrel{d}{=}\sqrt{\frac{m}{m+n}}{(\mathbf{\Omega }\otimes \mathbf{\Omega })}^{-\frac{1}{2}}{(\mathbf{\sum }\otimes \mathbf{\sum })}^{\frac{1}{2}}{\mathit{z}}_n+\sqrt{\frac{n}{m+n}}{\mathit{x}}_m\\ =\sqrt{\frac{m}{m+n}}{\mathit{z}}_0+\sqrt{\frac{n}{m+n}}{\mathit{x}}_0+o_{\mathrm{p}}(1)(n,m\to \infty )\\ \stackrel{\mathcal{L}}{\to }\mathrm{N}(0,2{\mathbf{M}}_p)(n,m\to \infty )\end{array}$$

As a remark to the proof, the Skorokhod Representation Theorem represents the limiting distributions in terms of random variables defined on the same probability space. As such, their linear combination can be defined and investigated.

B. The Approximate Hessian Matrix

B.1. The Hessian Matrix

The typical element in the Hessian matrix corresponding to ξ_i and ξ_j is given by

$$\frac{{\partial }^2{F}_2}{\partial {\xi }_i\partial {\xi }_j}=m\text{tr}\{{\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_i{\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_j\}-(m+n)\text{tr}\{{(\mathbf{\Omega }+\frac{n}{m}\mathbf{S})}^{-1}{\mathbf{\Delta }}_i{(\mathbf{\Omega }+\frac{n}{m}\mathbf{S})}^{-1}{\mathbf{\Delta }}_j\}+\text{tr}\{\frac{\partial F_2}{\partial \mathbf{\Omega }}{\mathbf{\Delta }}_{ij}\}$$

The element corresponding to v and ξ_i is $\frac{{\partial }^2{F}_2}{\partial v\partial {\xi }_i}=-m^2\text{tr}(\frac{{\partial }^2{F}_2}{\partial m\partial \mathbf{\Omega }}{\mathbf{\Delta }}_i)$, where

$$\frac{{\partial }^2{F}_2}{\partial m\partial \mathbf{\Omega }}=-{\mathbf{\Omega }}^{-1}+(2+\frac{n}{m}){(\mathbf{\Omega }+\frac{n}{m}\mathbf{S})}^{-1}-\frac{m+n}{m}{(\mathbf{\Omega }+\frac{n}{m}\mathbf{S})}^{-1}\mathbf{\Omega }{(\mathbf{\Omega }+\frac{n}{m}\mathbf{S})}^{-1}$$

The last element in the Hessian is $\frac{{\partial }^2{F}_{(\alpha )}}{\partial v^2}=m^4\left(\alpha \frac{{\partial }^2{F}_1}{\partial m^2}+\frac{{\partial }^2{F}_2}{\partial m^2}\right)+2m^3\left(\alpha \frac{\partial F_1}{\partial m}+\frac{\partial F_2}{\partial m}\right)$,

where $\frac{{\partial }^2{F}_1}{\partial m^2}=f^{″}(m)-f^{″}(m+n),\frac{\partial F_1}{\partial m}=f^{\prime }(m)-f^{\prime }(m+n),\frac{{\partial }^2{F}_2}{\partial m^2}=-\frac{1}{m+n}\text{tr}{\{\mathbf{\Omega }{\overline{\mathbf{\sum }}}^{-1}-\mathbf{I}\}}^2$, and $\frac{\partial F_2}{\partial m}=-ln\mid \mathbf{\Omega }{\overline{\mathbf{\sum }}}^{-1}\mid +\text{tr}(\mathbf{\Omega }{\overline{\mathbf{\sum }}}^{-1})-p$

B.2. Expected Values and Approximations

To approximate the Hessian matrix for positive definiteness and simplicity, we note that $(\mathbf{S}\mid \mathbf{\Omega },m)~{\mathrm{B}}_p^{\text{II}}(\frac{n}{2},\frac{m}{2},\frac{m}{n}\mathbf{\Omega })$ implies $({[\mathbf{\Omega }+\frac{n}{m}\mathbf{S}]}^{-1}\mid \mathbf{\Omega },m)~{\mathrm{B}}_p^{\mathrm{I}}(\frac{m}{2},\frac{n}{2},{\mathbf{\Omega }}^{-1})$, the type I matrix variate beta distribution, and (Gupta and Nagar, 1999, Chapter 6)

$$\begin{array}{ll}\hfill \mathrm{E}{(\mathbf{\Omega }+\frac{n}{m}\mathbf{S})}^{-1}& =\frac{m}{m+n}{\mathbf{\Omega }}^{-1}\hfill \\ \hfill \mathrm{E}\left\{{(\mathbf{\Omega }+\frac{n}{m}\mathbf{S})}^{-1}\mathbf{A}{(\mathbf{\Omega }+\frac{n}{m}\mathbf{S})}^{-1}\right\}& =\frac{m[(m+1)(m+n)-2]}{(m+n)(m+n-1)(m+n+2)}{\mathbf{\Omega }}^{-1}\mathbf{A}{\mathbf{\Omega }}^{-1}+\frac{mn}{(m+n)(m+n-1)(m+n+2)}\text{tr}({\mathbf{\Omega }}^{-1}\mathbf{A}){\mathbf{\Omega }}^{-1}\hfill \end{array}$$

Taking expected value of the second derivatives, we have

$$\begin{array}{ll}\mathrm{E}\frac{{\partial }^2{F}_2}{\partial {\xi }_i\partial {\xi }_j}\hfill & =\frac{mn}{(m+n-1)(m+n+2)}\{(m+n)\text{tr}\{{\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_i{\mathrm{\Omega }}^{-1}{\mathbf{\Delta }}_j\}-\text{tr}({\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_i)\text{tr}({\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_j)\}\hfill \\ \hfill & \approx \frac{mn}{m+n}\text{tr}\{{\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_i{\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_j\}\hfill \\ \mathrm{E}\frac{{\partial }^2{F}_2}{\partial {\xi }_i\partial v}\hfill & =\frac{n{m}^2}{(m+n-1)(m+n+2)}\left(1+p-\frac{2}{m+n}\right)\text{tr}({\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_i)\approx \frac{(1+p)n{m}^2}{{(m+n)}^2}\text{tr}({\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_i)\hfill \end{array}$$

For $\frac{{\partial }^2{F}_{(\alpha )}}{\partial v^2}$, we note that

$$\begin{array}{ll}\hfill \frac{{\partial }^2{F}_1}{\partial m^2}& =f^{″}(m)-f^{″}(m+n)\approx \frac{c_0(n^2+2mn)}{m^2{(m+n)}^2}+\frac{2c_1(n^3+3m{n}^2+3m^{2}n)}{m^3{(m+n)}^3}\hfill \\ \hfill \mathrm{E}\frac{{\partial }^2{F}_2}{\partial m^2}& =-\frac{np[(m+n)(1+p)-2]}{m(m+n)(m+n-1)(m+n+2)}\approx -\frac{np(p+1)}{m{(m+n)}^2}+\frac{np(p+3)}{m{(m+n)}^3}\hfill \\ \hfill -\mathrm{E}\frac{\partial F_2}{\partial m}=\mathrm{E}\frac{\partial F_1}{\partial m}& =f^{\prime }(m)-f^{\prime }(m+n)\approx -\frac{c_{0}n}{m(m+n)}-\frac{c_1(n^2+2mn)}{m^2{(m+n)}^2}\hfill \end{array}$$

where c₀ and c₁ are defined in Lemma 5. So

$$\mathrm{E}\frac{{\partial }^2{F}_{(\alpha )}}{\partial v^2}\approx \alpha \left(-\frac{c_0{m}^2{n}^2}{{(m+n)}^2}+\frac{2c_1{m}^{3}n}{{(m+n)}^3}\right)+\frac{2c_0{m}^2{n}^2}{{(m+n)}^2}+\frac{2c_1(2m+n)mn}{{(m+n)}^2}+\frac{m^{3}np(p+3)}{{(m+n)}^3}$$

In the approximate Hessian matrix, block H_ξξ′ takes its approximate expectation. The off-diagonal block h_vξ′ is set to 0 because $\mathrm{E}\frac{{\partial }^2{F}_2}{\partial {\xi }_i\partial v}$ is small compared to $\mathrm{E}\frac{{\partial }^2{F}_2}{\partial \mathit{\xi }\partial {\mathit{\xi }}^{\prime }}$ and $\mathrm{E}\frac{{\partial }^2{F}_{\alpha }}{\partial v^2}$. The diagonal element h_vv takes its exact value $\frac{{\partial }^2{F}_{(\alpha )}}{\partial v^2}$ unless it is not positive, in which case its approximate expectation is employed.

When v = 0, we have

$$\begin{array}{ll}\hfill \mathrm{E}\frac{{\partial }^2{F}_2}{\partial \mathit{\xi }\partial {\mathit{\xi }}^{\prime }}& =n\text{tr}\{{\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_i{\mathbf{\Omega }}^{-1}{\mathbf{\Delta }}_j\}\hfill \\ \hfill \frac{{\partial }^2{F}_{\alpha }}{\partial v^2}& =n^3\{\text{tr}{({\mathbf{\Omega }}^{-1}\mathbf{S}-\mathbf{I})}^2-\frac{2}{3}\text{tr}{({\mathbf{\Omega }}^{-1}\mathbf{S}-\mathbf{I})}^3\}+\alpha \{-c_0{n}^2+2c_{1}n\}\hfill \end{array}$$