Assessment of non-linear combination effect terms for drug–drug interactions

Abstract

Drugs interact with their targets in different ways. A diversity of modeling approaches exists to describe the combination effects of two drugs. We investigate several combination effect terms (CET) regarding their underlying mechanism based on drug-receptor binding kinetics, empirical and statistical summation principles and indirect response models. A list with properties is provided and the interrelationship of the CETs is analyzed. A method is presented to calculate the optimal drug concentration pair to produce the half-maximal combination effect. This work provides a comprehensive overview of typically applied CETs and should shed light into the question as to which CET is appropriate for application in pharmacokinetic/pharmacodynamic models to describe a specific drug–drug interaction mechanism.

Introduction

Drugs interact with their targets in many different ways, e.g. compete for the same receptor, aim on different targets or act as antagonists to name a few. Understanding interactions is crucial to develop beneficial combination therapies but also to decode undesired effects. A wide range of diverse methodologies were developed to describe different drug–drug interaction (DDI) mechanisms. This work investigates and summarizes typically applied DDI mechanisms in pharmacokinetic/pharmacodynamic (PKPD) modeling [1].

In PKPD modeling the effect of a single dose is usually described by the Hill equation [2–4], also called sigmoidal function or Emax model. The Hill equation can be derived from first principles of drug-receptor binding kinetics [5] and describes a non-linear profile with saturation behavior. The equation has simple characteristics such as a maximal effect parameter to denote the saturation, a parameter to describe the concentration producing the half-maximal effect, and a coefficient to alter the shape towards sigmoidal profiles.

The effects of two drugs administered in combination depend on the interaction mechanism of the drugs. Ariëns and colleagues [6–8] presented mathematical expressions related to the Hill equation to describe different DDI mechanisms where we will focus on competitive, uncompetitive and non-competitive interaction. Other commonly used combination effect terms (CETs) are based on statistical assumptions such as Bliss Independence [9, 10], Loewe Additivity as in Greco’s model [9], simple summation of Hill equations, indirect response models [10], generalized surface response models [11–13] and sometimes equipped with additional interaction parameters [14, 15].

Although many of these CETs are extensively presented in the literature, a clear derivation of the CETs is often missing and therefore the underlying interaction mechanism is not obvious.

In this manuscript, we focus on CETs derived from drug-receptor binding kinetics, empirical or statistical summation principles, and interactions received from an indirect response model. We reveal the underlying mechanisms, rigorously derive the CETs, and investigate their properties. Some CETs are compared regarding the intensity of their predicted effects. Finally, we provide for selected CETs the optimal minimal drug concentration pair necessary to achieve the half-maximal effect.

In general, CETs are subunits which can be incorporated at any level of the full model complexity, e.g. in semi-mechanism based PKPD models, in more mechanistic approaches such as cell cycle based models or even in quantitative systems pharmacology models. To build a realistic model, CETs have to be chosen accordingly to the underlying interaction mechanism and positioned in the right spot of the interaction. Altogether this work should shed light into the question as to which CET is appropriate for application to describe a specific drug–drug interaction mechanism.

Derivation and properties of combination effect terms for drug–drug interaction

Introduction to combination effect terms

Single effect terms

A single drug effect of concentration C based on the Hill function reads

$$e(C)=\frac{E_{\mathit{max}}{\left(\frac{C}{E{C}_{50}}\right)}^{\gamma }}{1+{\left(\frac{C}{E{C}_{50}}\right)}^{\gamma }}$$ (1)

$$=\frac{E_{\mathit{max}}{C}^{\gamma }}{E{C}_{50}^{\gamma }+C^{\gamma }}$$ (2)

where E_max is the maximal effect, EC₅₀ the concentration necessary to produce the half-maximal effect $\frac{E_{\mathit{max}}}{2}$, and γ the Hill-coefficient. Equation (1) is the classical dimensionless representation whereas Eq. (2) is more common in PKPD modeling. The inhibitory form is

$$i(C)={\frac{I_{\mathit{max}}\left(\frac{C}{I{C}_{50}}\right)}{1+{\left(\frac{C}{I{C}_{50}}\right)}^{\gamma }}}^{\gamma }=\frac{I_{\mathit{max}}{C}^{\gamma }}{I{C}_{50}^{\gamma }+C^{\gamma }}$$ (3)

with the restriction I_max≤1.

Pharmacokinetic/pharmacodynamic drug–drug interaction modeling situations

In PKPD modeling roughly two categories of models are applied to describe data from drug–drug interaction (DDI) experiments. Data measured at two time points, i.e. at start and end of the experiment, are typically modeled by an effect surface without a time dimension of the form

$$P=P_0(1-I(C_A,C_B))$$ (4)

where P₀ is the response, e.g. proliferating cells, if no drug is present, and P the response after drug administration; see [14] or [16] for more details. The inhibition mechanism of the two drugs is specified by the CET I(C_A, C_B). From Eq. (4) restriction I(C_A, C_B)≤1 is obvious. For models characterizing dynamic growth over time, first a growth function g [17, 18] needs to be specified. Then cytostatic DDI effects can be modeled by inhibition of growth

$$\frac{d}{dt}P=g(P)(1-I(C_A,C_B)),P(0)=P_0$$

and cytotoxic effects by a killing term

$$\frac{d}{dt}P=g(P)-E(C_A,C_B)P,P(0)=P_0$$

where the CET is E(C_A, C_B).

In the above models, C_A and C_B can be the drug concentration in plasma [15] or delayed concentration effects [19], e.g. due to signaling pathways. A general PKPD structure with cytotoxic drug effects is shown in Fig. 1, to visualize a typical spot of DDI. Modified or extended formulations of this structure are frequently applied in drug development, see e.g. [15, 19–26]. Moreover, also in more mechanism-based models, such as cell cycle models [27, 28], appropriate CETs are necessary to model DDI at specific interaction targets, e.g. on different cell phases or induction of apoptosis [26]. The major task when developing a DDI model of the above forms is to incorporate an appropriate CET at a specific spot in the PKPD model that describes the underlying DDI mechanism.

Fig. 1.

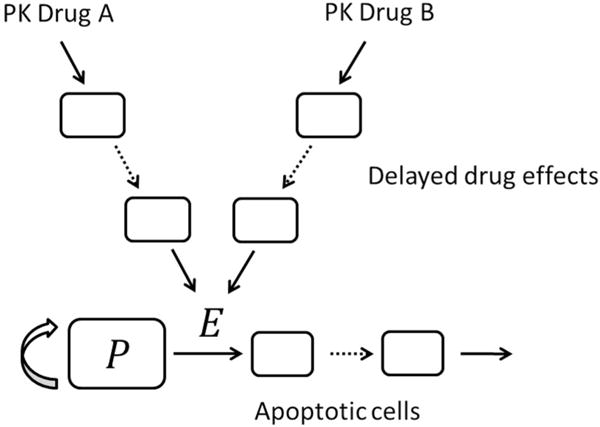
A schematic of a typical semi-mechanistic PKPD model with possible delayed drug effects and apoptotic cell population. The interaction of the two drugs is indicated by E denoting an appropriate combination effect term

Combination effect terms

In general, a CET is a mathematical function that combines the single drug concentrations C_A and C_B together with their individual parameters (E_maxA, EC_50A, γ_A) and (E_maxB, EC_50B, γ_B). More precisely, the parameters of a CET are those from the individual drugs and the maximal combination effect E_maxAB of the CET is then a result from the specific structure of the CET. We call a CET symmetric if interchanging the roles of drugs A and B leads to the same CET. Let us state and formalize the desirable properties of CETs that one somehow implicitly takes for granted:

Positivity

The effect of a CET should be bounded from above and below:

$$0\le E(C_A,C_B)\le E_{\mathit{maxAB},}{C}_A,C_B\ge 0.$$

Scaling

The CET should be linear in the maximal single effects, i.e. a doubling of E_max or E_maxA and E_maxB simultaneously should result in a doubling of the CET effect.

Diagonality

Symmetric CETs applied to drugs A and B with similar properties and γ_A = γ_B = 1, should be describable as a single effect term, i.e.

$$E\left(\frac{C_A}{2},\frac{C_A}{2}\right)=e(C_A+\sigma C_A^2),C_A\ge 0$$

where σ is a CET-specific constant. Hence, a symmetric CET acts like a single effect term with the double concentration plus perhaps some quadratic deviation.

In this work, CETs are derived from three structurally different underlying mechanism categories:

1. Drug-receptor binding kinetics

2. Empirical and statistical summation principles

3. Interactions from an indirect response model

CETs based on drug-receptor binding kinetics

Ariëns and colleagues [6] presented the competitive, uncompetitive and non-competitive CETs but, to our knowledge, omitted the derivations in their publications. In this section we deduce these three CETs from drug-receptor binding kinetics. The construction consists of two components: (i) establishing the underlying drug-receptor binding system, and (ii) defining the effect based on the drug-receptor complexes.

A general drug-receptor binding system is based on the following mechanisms. Molecules C_A of drug A bind to a receptor R and produce a drug-receptor complex RC_A. Drug molecules C_B of drug B also bind to this receptor R producing a drug-receptor complex RC_B and additionally bind to RC_A resulting in a third complex RC_AB: A necessary assumption for Ariëns CETs is that the binding and dissociation rates of drug B to produce RC_A or RC_AB are equal. The ordinary differential equations [29] are:

$$\frac{d}{\mathit{dt}}{C}_A=-k_{\mathit{onA}}{C}_{A}R+k_{\mathit{offA}}R{C}_A{C}_A(0)=C_A^0$$ (5)

$$\begin{array}{l}\frac{d}{\mathit{dt}}{C}_B=-k_{\mathit{onB}}{C}_{B}R+k_{\mathit{offB}}R{C}_B-k_{\mathit{onB}}{C}_{B}R{C}_A+k_{\mathit{offB}}R{C}_{\mathit{AB}}\\ C_B(0)=C_B^0\end{array}$$ (6)

$$\begin{array}{l}\frac{d}{\mathit{dt}}R=-k_{\mathit{onA}}{C}_{A}R+k_{\mathit{offA}}R{C}_A-k_{\mathit{onB}}{C}_{B}R+k_{\mathit{offB}}R{C}_B\\ R(0)=R^0\end{array}$$ (7)

$$\begin{array}{l}\frac{d}{\mathit{dt}}R{C}_A=k_{\mathit{onA}}{C}_{A}R-k_{\mathit{offA}}R{C}_A-k_{\mathit{onB}}{C}_{B}R{C}_A+k_{\mathit{offB}}R{C}_{\mathit{AB}}\\ R{C}_A(0)=R{C}_A^0\end{array}$$ (8)

$$\frac{d}{\mathit{dt}}R{C}_B=k_{\mathit{onB}}{C}_{B}R-k_{\mathit{offB}}R{C}_{B}R{C}_B(0)=R{C}_B^0$$ (9)

$$\frac{d}{\mathit{dt}}R{C}_{\mathit{AB}}=k_{\mathit{onB}}{C}_{B}R{C}_A-k_{\mathit{offB}}R{C}_{\mathit{AB}}R{C}_{\mathit{AB}}(0)=R{C}_{\mathit{AB}}^0$$ (10)

The binding rates are k_onA and k_onB, and the dissociation rates are k_offA and k_offB. The total amount of receptors R_tot = R + RC_A + RC_B + RC_AB implies

$$\frac{d}{\mathit{dt}}{R}_{\mathit{tot}}=\frac{d}{\mathit{dt}}R+\frac{d}{\mathit{dt}}R{C}_A+\frac{d}{\mathit{dt}}R{C}_B+\frac{d}{\mathit{dt}}R{C}_{\mathit{AB}}=0$$ (11)

and therefore a constant number of total receptors $R_{\mathit{tot}}^0$ exists. For drugs following target-mediated drug disposition the total receptor is additionally modulated. The resulting CETs due to Ariëns can be compared with TMDD models in baseline (see Eq. (21) in [30] for the competitive CET).

Typically, rapid binding of the drug with the receptor is assumed to produce the complex, see originally [5, 29]. From this assumption, k_onX and k_offX, where X stands for A or B, can be replaced by their dissociation constant $K_{\mathit{DX}}=\frac{k_{\mathit{offX}}}{k_{\mathit{onX}}}$. Under such steady state assumptions and observing that the total concentration of receptors $R_{\mathit{tot}}^0$ is constant, the equation system for the complexes RC_A, RC_B, and RC_AB is

$$\left(\begin{array}{ccc}1+\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}& 1+\frac{C_B}{K_{\mathit{DB}}}& \frac{C_B}{K_{\mathit{DB}}}\\ -\frac{C_B}{K_{\mathit{DB}}}& 0& 1\end{array}\right)\left(\begin{array}{c}R{C}_A\\ R{C}_B\\ R{C}_{\mathit{AB}}\end{array}\right)=R_{\mathit{tot}}^0\left(\begin{array}{c}\frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}\\ 0\end{array}\right).$$ (12)

This equation system (12) can be adjusted depending on which complexes are involved in the specific drug combination mechanism. The resulting equation system can then be solved with respect to the complexes. In the second step, the CETs are constructed by summation of the complexes driving the combination effects. For this purpose the intrinsic activity (the ability of a complex to produce maximum functional response) is applied. Let α and β denote the intrinsic activities of drugs A and B varying from 0 to 1 when acting as single drug. We define the functions

$$\begin{array}{l}a=\{\begin{array}{l}\alpha ,ifR{C}_A\mathit{drives}\mathit{the}\mathit{effect}\hfill \\ 0,\mathit{\text{else}}\hfill \end{array}\\ b=\{\begin{array}{l}\beta ,ifR{C}_B\mathit{drives}\mathit{the}\mathit{effect}\hfill \\ 0,\mathit{\text{else}}\hfill \end{array}\end{array}$$

and the general summation form becomes

$$E_{\mathit{AB}}=aR{C}_A+bR{C}_B+f(\alpha ,\beta )R{C}_{\mathit{AB}}.$$ (13)

Hence, the complexes RC_A and RC_B are either included or not depending on their contribution to the total effect. The function f(α, β) ≥ 0 combines the intrinsic activities α and β and describes how the interaction of the intrinsic activities of drug A and B drive the contribution of the complex RC_AB to the total effect. Ariëns presented the summation rules for the competitive, uncompetitive and non-competitive mechanisms. Using the solution of complexes RC_A, RC_B and RC_AB from Eq. (12), Eq. (13) can be reformulated to the general form of a CET

$$E_{\mathit{AB}}=\frac{R_{\mathit{tot}}^0\left(a\frac{C_A}{K_{\mathit{DA}}}+b\frac{C_B}{K_{\mathit{DB}}}+f(\alpha ,\beta )\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}\right)}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_B}{K_{\mathit{DB}}}+\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}}$$ (14)

See Appendix 1. From Eq. (14) it can be directly seen that any CET based on drug receptor binding kinetics can be written with dimensionless variables $\frac{C_A}{K_{\mathit{DA}}}$ and $\frac{C_B}{K_{\mathit{DB}}}$, i.e. in a fraction of the drug concentration and the dissociation constant.

Based on Eq. (14) we obtain the Emax-formulation E(C_A, C_B) for appropriate assignment of the total receptors $R_{\mathit{tot}}^0$ and the intrinsic activities. Further system (5)–(10) ensures that the effect E_AB is never negative and bounded by a maximal effect E_maxAB, i.e. E_maxAB≥E_AB≥0 for C_A, CB≥0. For the inhibitory formulation I(C_A, C_B) we have a; b; f(α, β)≤1 and, thus, I_maxAB≤1.

Competitive CET

For a competitive interaction, two drugs A and B exhibit an affinity for the same receptor system R [6]. More precisely, if a receptor is occupied by molecules of drug A, then molecules of drug B cannot bind to this receptor, see Fig. 2a for the binding schematic. The complex RC_AB is not present in this mechanism and equation system (12) reduces to

$$\left(\begin{array}{cc}1+\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}& 1+\frac{C_B}{K_{\mathit{DB}}}\end{array}\right)\left(\begin{array}{c}R{C}_A\\ R{C}_B\end{array}\right)=R_{\mathit{tot}}^0\left(\begin{array}{c}\frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}\end{array}\right).$$ (15)

Fig. 2.

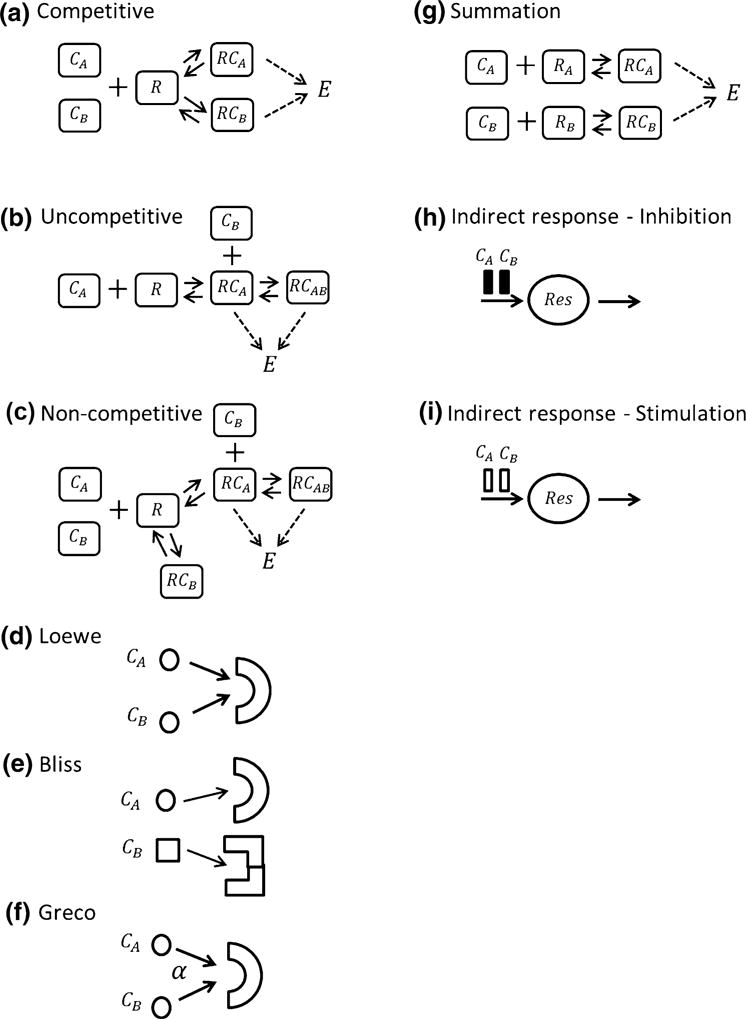
Mechanistic representation of presented CETs

The two complexes RC_A and RC_B are added together with their intrinsic activity α, β as weights by

$$E_{\mathit{AB}}^{\mathit{Com}}=\alpha R{C}_A+\beta R{C}_B$$ (16)

resulting in

$$E_{\mathit{AB}}^{\mathit{Com}}=\alpha \frac{R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_B}{K_{\mathit{DB}}}}+\beta \frac{R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_B}{K_{\mathit{DB}}}}$$ (17)

See Appendix 2. With the single maximal effects $E_{\mathit{maxA}}=\alpha R_{\mathit{tot}}^0$ and $E_{\mathit{maxB}}=\beta R_{\mathit{tot}}^0$, and the Hill coefficients γ_A, γ_B > 0 the Emax-formulation reads

$$\begin{array}{l}{E}^{\mathit{Com}}(C_A,C_B)=\frac{E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+E_{\mathit{maxB}}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}{1+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}\\ =\frac{E_{\mathit{maxA}}{C}_A^{{\gamma }_A}E{C}_{50B}^{{\gamma }_B}+E_{\mathit{maxB}}{C}_B^{{\gamma }_B}E{C}_{50A}^{{\gamma }_A}}{C_A^{{\gamma }_A}E{C}_{50B}^{{\gamma }_B}+C_B^{{\gamma }_B}E{C}_{50A}^{{\gamma }_A}+E{C}_{50A}^{{\gamma }_A}E{C}_{50B}^{{\gamma }_B}}\end{array}$$ (18)

where EC_50A = K_DA and EC_50B = K_DB are the single drug concentrations producing half-maximal single effects. The maximal combination effect is the maximal single effect

$$E_{\mathit{maxAB}}^{\mathit{Com}}=max\left\{E_{\mathit{maxA},}{E}_{\mathit{maxB},}\right\}.$$

The CET is symmetric and an inhibitory formulation exits. All properties are summarized in Table 1. The competitive term E^Com(C_A, C_B) with γ_A = γ_B = 1 was also presented in [31] and Eq. (18) was simplified to a single maximal effect $E_{\mathit{maxAB}}^{\mathit{Com}}=E_{\mathit{maxA}}=E_{\mathit{maxB}}$ in [32]. If drug B is an antagonist, i.e. binding of drug molecules only cause a blockage of the receptors and does not produce an effect, i.e. β = 0, E_maxB = 0 one obtains

$$\begin{array}{l}{E}^{\mathit{ComGad}}(C_A,C_B)=\frac{E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}}{1+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}\\ =\frac{E_{\mathit{maxA}}{C}_A^{{\gamma }_A}}{C_A^{{\gamma }_A}+E{C}_{50A}^{{\gamma }_A}+\frac{E{C}_{50A}^{{\gamma }_A}}{E{C}_{50A}^{{\gamma }_B}}{C}_B^{{\gamma }_B}}\end{array}$$

which is also called the Gaddum equation [33].

Table 1.

Properties of the presented CETs

CET	Equation	Construction principle	Symmetry	Positivity	Scaling	Diagonality	Maximal combination effect EmaxAB	Inhibitory form
Competitive	Equation (18)	DRBKa	Yes	Yes	Yes	Yes	max {EmaxA;EmaxB}	Yes
Uncompetitive	Equation (22)	DRBKa	No	Yes	Yes	–	(1+ β′)EmaxA	Yes for β′ ≤ 0
Non-competitive	Equation (24)	DRBKa	No	Yes	Yes	–	(1+ β′)EmaxA	Yes for β′ ≤ 0
Loewe	Equation (29)	ADDb	Yes	Yes	Yes	Yes	Emax	Yes
Bliss	Equation (33)	ADDb	Yes	Yes	Yes	Yes	Emax	Yes
Greco	Equation (37)	ADDb	Yes	No	Yes	Yes	Emax	Yes
Summation	Equation (39)	EmpSUMc	Yes	Yes	Yes	No	EmaxA + EmaxB	No
Inhibitory	Equation (42)	IDRd	Yes	Yes	No	No	ImaxA + ImaxB − ImaxAImaxB	–
Stimulation	Equation (43)	IDRd	Yes	Yes	No	No	EmaxA + EmaxB + EmaxAEmaxB	No

^aDrug-receptor binding kinetics

^bAdditive approaches

^cEmpirical summation approaches

^dIndirect response models

Uncompetitive CET

In uncompetitive interaction, drug B binds to the complex RC_A. Binding of drug B to R does not occur and therefore no complex RC_B exists; see Fig. 2b. Hence, drug B only produces an effect if drug A forms the complex RC_A. If drug B is administered alone no effect occurs, whereas if drug A is given alone, the effect corresponds to the single case. This is a non-symmetric behavior. The equation system for the complexes is

$$\left(\begin{array}{cc}1+\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ -\frac{C_B}{K_{\mathit{DB}}}& 1\end{array}\right)\left(\begin{array}{c}R{C}_A\\ R{C}_{\mathit{AB}}\end{array}\right)=R_{\mathit{tot}}^0\left(\begin{array}{c}\frac{C_A}{K_{\mathit{DA}}}\\ 0\end{array}\right)$$ (19)

and the summation of the complexes [6] becomes

$$E_{\mathit{AB}}^{Un}=\alpha R{C}_A+\alpha (1+{\beta }^{\prime })R{C}_{\mathit{AB}}$$ (20)

where −1≤β′ Depending on the sign of β′ the appearance of drug B increases or decreases the combination effect with drug B. With the complexes from Eq. (19), Eq. (20) is

$$E_{\mathit{AB}}^{Un}=\alpha \frac{R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}}+\alpha (1+{\beta }^{\prime })\frac{R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}}$$ (21)

See Appendix 3. We then obtain the E_max formulation

$$\begin{array}{l}{E}^{Un}(C_A,C_B)=\frac{E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+(1+{\beta }^{\prime })E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}{1+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}\\ =\frac{E_{\mathit{maxA}}\left(C_A^{{\gamma }_A}E{C}_{50B}^{{\gamma }_B}+C_A^{{\gamma }_A}{C}_B^{{\gamma }_B}\right)+{\beta }^{\prime }{E}_{\mathit{maxA}}{C}_A^{{\gamma }_A}{C}_B^{{\gamma }_B}}{C_A^{{\gamma }_A}E{C}_{50B}^{{\gamma }_B}+E{C}_{50A}^{{\gamma }_A}E{C}_{50B}^{{\gamma }_B}+C_A^{{\gamma }_A}{C}_B^{{\gamma }_B}}.\end{array}$$ (22)

Since β′ and not E_maxB is present in Eq. (22), the actual value of β′ has to be determined from the combination data and describes a synergistic or antagonistic influence on the combination effect. The maximal combination effect is

$$E_{\mathit{maxAB}}^{Un}=max\left\{1,1+{\beta }^{\prime }\right\}{E}_{\mathit{maxA}}.$$

For β′ ≤ 0 a reasonable inhibitory formulation exists.

Non-competitive CET

The non-competitive situation corresponds to the general scenario represented by Eqs. (5)–(10) where all complexes are involved see Fig. 2c for schematic. According to Ariëns [6] the complex RC_B does not contribute to the effect and the summation reads

$$E_{\mathit{AB}}^{\mathit{Non}}=\alpha R{C}_A+\alpha (1+{\beta }^{\prime })R{C}_{\mathit{AB}}$$

resulting in

$$E_{\mathit{AB}}^{\mathit{Non}}=\frac{R_{\mathit{tot}}^0\left(\alpha \frac{C_A}{K_{\mathit{DA}}}+\alpha \left(1+{\beta }^{\prime }\right)\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}\right)}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_B}{K_{\mathit{DB}}}+\frac{C_a}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}}.$$ (23)

Note the appearance of $\frac{C_B}{K_{\mathit{DB}}}$ in the denominator of Eq. (23) in contrast to Eq. (21). The Emax-formulation reads

$$\begin{array}{l}{E}^{\mathit{Non}}(C_A,C_B)=\frac{E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+(1+{\beta }^{\prime })E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}{1+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}\\ =\frac{E_{\mathit{maxA}}\left(C_A^{{\gamma }_A}E{C}_{50B}^{{\gamma }_B}+C_A^{{\gamma }_A}{C}_B^{{\gamma }_B}\right)+{\beta }^{\prime }{E}_{\mathit{maxA}}{C}_A^{{\gamma }_A}{C}_B^{{\gamma }_B}}{C_A^{{\gamma }_A}E{C}_{50B}^{{\gamma }_B}+C_B^{{\gamma }_B}E{C}_{50A}^{{\gamma }_A}+C_A^{{\gamma }_A}{C}_B^{{\gamma }_B}+E{C}_{50A}^{{\gamma }_A}E{C}_{50B}^{{\gamma }_B}}.\end{array}$$ (24)

In “Discussion” section we additionally discuss a non-competitive term from [14].

CETs from empirical and statistical summation principles

In this section, CETs are considered that are derived under an additivity or no-interaction assumption. However, we emphasize that the term “additivity” is used to describe different approaches [34–37], and therefore we cover all the different additivities as summation principles in the following.

Loewe Additivity CET

Loewe Additivity [34, 38] assumes that two drugs act additively through a similar mechanism on the same target [39, 40], see Fig. 2d. Given the single drug EC₅₀’s, the concentrations C_A and C_B necessary to produce the half-maximal combination effect have to fulfill

$$1=\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}.$$ (25)

Extending Eq. (25) for an arbitrary effect E ranging from 0 to E_maxAB gives

$$1=\frac{C_A}{D{C}_A}+\frac{C_B}{D{C}_B}$$ (26)

where DC_X is the concentration that produces for the single drug the given effect E and X either represents A or B. Greco and colleagues [9] applied the single drug Hill Eq. (1) of the form

$$E=\frac{E_{\mathit{max}}{\left(\frac{D{C}_X}{E{C}_{50X}}\right)}^{{\gamma }_X}}{1+{\left(\frac{D{C}_X}{E{C}_{50X}}\right)}^{{\gamma }_X}}$$ (27)

and rearranged Eq. (27) with respect to DC_X. Then substituting in Eq. (26) gives

$$1=\frac{C_A}{E{C}_{50A}{\left(\frac{E}{E_{\mathit{max}}-E}\right)}^{\frac{1}{{\gamma }_A}}}+\frac{C_B}{E{C}_{50B}{\left(\frac{E}{E_{\mathit{max}}-E}\right)}^{\frac{1}{{\gamma }_B}}}$$ (28)

See Appendix 4. For γ_A = γ_B = γ, Eq. (28) can be solved explicitly with respect to E and we obtain the Loewe CET

$$E^{\mathit{Loewe}}(C_A,C_B)=\frac{E_{\mathit{max}}{\left(\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}\right)}^{\gamma }}{1+{\left(\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}\right)}^{\gamma }}$$ (29)

See Appendix 4. In Eq. (29) both drugs have the same single maximal effect. Note that the Loewe CET Eq. (29) corresponds to the competitive CET for E_maxA = E_maxB = E_max and γ_A = γ_B = 1. Further if we insert the basic Loewe Eq. (25) into Eq. (29) we obtain the half-maximal effect $\frac{E_{\mathit{max}}}{2}$ again.

Bliss Independence CET

Bliss Independence [41] describes the additive effect of two drugs at different targets with independent mechanisms and no interaction between the drug action exists [39], see Fig. 2e. Bliss Independence is derived from probability theory. The probability for non-mutually exclusive events that either drug A or drug B acts is

$$\begin{array}{l}P(A\cup B)=P(A)+P(B)-P(A)P(B)\\ =P(A)+P(B)(1-P(A)).\end{array}$$ (30)

Following Jonker et al. [42] we set the probability of a single effect based on the single Hill function Eq. (1) with E_max = 1 and γ = 1 as

$$P(C_X)=\frac{\frac{C_X}{E{C}_{50X}}}{1+\frac{C_X}{E{C}_{50X}}}$$ (31)

where X represents either A or B. Equation (31) ranges from 0 to 1. Substituting Eq. (31) in Eq. (30) gives

$$P(A\cup B)=\frac{\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}+\frac{C_A}{E{C}_{50A}}\frac{C_B}{E{C}_{50B}}}{1+\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}+\frac{C_A}{E{C}_{50A}}\frac{C_B}{E{C}_{50B}}}.$$ (32)

We multiply Eq. (32) with E_max, introduce the Hill parameters, and obtain

$$\begin{array}{l}{E}^{\mathit{Bliss}}(C_A,C_B)=\frac{E_{\mathit{max}}\left({\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}\right)}{1+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}\\ =\frac{E_{\mathit{max}}{C}_A^{{\gamma }_A}}{E{C}_{50A}^{{\gamma }_A}+C_A^{{\gamma }_A}}+\frac{E_{\mathit{max}}{C}_B^{{\gamma }_B}}{E{C}_{50B}^{{\gamma }_B}+C_B^{{\gamma }_B}}\left(1-\frac{C_A^{{\gamma }_A}}{E{C}_{50A}^{{\gamma }_A}+C_A^{{\gamma }_A}}\right)\end{array}$$ (33)

$$=e(C_A)+e(C_B)\left(1-\frac{e(C_A)}{E_{\mathit{max}}}\right)$$ (34)

where a similar maximal effect of both drugs is assumed. Substituting

$$1=\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}+\frac{C_A}{E{C}_{50A}}\frac{C_B}{E{C}_{50B}}$$ (35)

with γ_A = γ_B = 1 in Eq. (33) provides the half-maximal effect $\frac{E_{\mathit{max}}}{2}$. Equation (35) corresponds to arguments from Chou and Talalay [40] for mutually nonexclusive drugs acting on different targets.

Greco’s model CET

Greco et al. [9] further extended Eq. (28) by adding an additional term resulting in

$$\begin{array}{l}1=\frac{C_A}{E{C}_{50A}{\left(\frac{E}{E_{\mathit{max}}-E}\right)}^{\frac{1}{{\gamma }_A}}}+\frac{C_B}{E{C}_{50B}{\left(\frac{E}{E_{\mathit{max}}-E}\right)}^{\frac{1}{{\gamma }_B}}}\\ +\alpha \frac{C_A{C}_B}{E{C}_{50A}E{C}_{50B}{\left(\frac{E}{E_{\mathit{max}}-E}\right)}^{\frac{1}{2{\gamma }_A}+\frac{1}{2{\gamma }_B}}}\end{array}$$ (36)

See Fig. 2f. In Eq. (36) an interaction parameter α is applied to indicate antagonism (α <0) and synergism (α > 0). For γ_A = γ_B = γ Eq. (36) could be solved explicitly with respect to E and Greco’s CET reads

$$E^{\mathit{Greco}}(C_A,C_B)=\frac{E_{\mathit{max}}{\left(\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}+\alpha \frac{C_A}{E{C}_{50A}}\frac{C_B}{E{C}_{50B}}\right)}^{\gamma }}{1+{\left(\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}+\alpha \frac{C_A}{E{C}_{50A}}\frac{C_B}{E{C}_{50B}}\right)}^{\gamma }}.$$ (37)

As shown before for α = 0, Eq. (37) is the Loewe CET as presented in Eq. (29). For α = 1 Eq. (37) formally results in the Bliss CET with γ_A = γ_B = 1. But keep in mind that the Bliss CET describes the effect when the two drugs act on different targets whereas the Greco CET is based on the Loewe Additivity assuming one target.

However, allowing negativity of the interaction parameter α could lead to a negative effect. As example we set γ = 1, C_A = EC_50A and C_B = EC_50B. Then we have

$$E^{\mathit{Greco}}(E{C}_A,E{C}_B)=E_{\mathit{max}}\frac{2+\alpha }{3+\alpha }$$

which is negative for α from −3 to −2.

Summation CET

An empirical approach to construct a CET with an increased maximal combination effect is to simply sum up the single drug effect terms, compare [15] for a linear CET and [19] for delayed effects of non-linear CETs, and see Fig. 2g. Assuming that the drugs act at different targets the summation CET reads

$$E^{\mathit{Sum}}(C_A,C_B)=\frac{E_{\mathit{maxA}}{C}_A^{{\gamma }_A}}{E{C}_{50A}^{{\gamma }_A}+C_A^{{\gamma }_A}}+\frac{E_{\mathit{maxB}}{C}_B^{{\gamma }_B}}{E{C}_{50B}^{{\gamma }_B}+C_B^{{\gamma }_B}}$$ (38)

$$=\frac{E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+E_{\mathit{max}B}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}+\left(E_{\mathit{maxA}}+E_{\mathit{max}B}\right){\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}{1+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}.$$ (39)

In contrast to all derived CETs before, the maximal combination effect is now the sum of the single maximal effects:

$$E_{\mathit{maxAB}}^{\mathit{Sum}}=E_{\mathit{maxA}}+E_{\mathit{maxB}}.$$

CETs from indirect response models

Indirect response models (IDR) [43] are probably the most frequently applied components in PKPD and are also important parts in complex systems pharmacology models. In this Section, we derive CETs from IDR models where the drugs either act on the inhibition or the stimulation of the production rate [10].

IDR inhibition CET

The first form is

$$\begin{array}{l}\frac{d}{\mathit{dt}}\mathit{Res}=k_{\mathit{in}}(1-i(C_A))(1-i(C_B))-K_{\mathit{out}}\mathit{Res}\\ \mathit{Res}(0)=\frac{k_{\mathit{in}}}{k_{\mathit{out}}}\end{array}$$ (40)

where Res denotes a response, k_in is the production rate, k_out the loss rate, and i(C) the single drug inhibition model Eq. (3), compare Fig. 2h for schematic. Rearranging Eq. (40) gives

$$\frac{d}{\mathit{dt}}\mathit{Res}=k_{\mathit{in}}(1-I^{\mathit{IDR}}(C_A,C_B))-k_{\mathit{out}}\mathit{Res}\mathit{Res}(0)=\frac{k_{\mathit{in}}}{k_{\mathit{out}}}$$ (41)

and the CET is obtained by calculating

$$\begin{array}{l}{I}^{\mathit{IDR}}(C_A,C_B)=i(C_A)+i(C_B)-i(C_A)i(C_B)\\ =\frac{I_{\mathit{maxA}}{\left(\frac{C_A}{I{C}_{50A}}\right)}^{{\gamma }_A}+I_{\mathit{maxB}}{\left(\frac{C_B}{I{C}_{50B}}\right)}^{{\gamma }_B}+\left(I_{\mathit{maxA}}+I_{\mathit{maxB}}-I_{\mathit{maxA}}{I}_{\mathit{maxB}}\right){\left(\frac{C_A}{I{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{I{C}_{50B}}\right)}^{{\gamma }_B}}{1+{\left(\frac{C_A}{I{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{I{C}_{50B}}\right)}^{{\gamma }_B}+{\left(\frac{C_A}{I{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{I{C}_{50B}}\right)}^{{\gamma }_B}}\end{array}$$ (42)

It is clear from Eq. (39), that an inhibitory formulation of the summation CET does not exist. The scaling condition is fulfilled but diagonality is violated, see Appendix 6.

See Appendix 7. In [14, 16], Eq. (42) was applied to non-dynamic models, compare Eq. (4). In the literature [10, 14, 16], Eq. (42) was thought to be the non-competitive CET from Ariën’s approach. Although Eq. (42) looks structurally similar to the CETs from Ariën’s theory, Eq. (42) does not match into the Ariëns formalism, since multiplication of the single maximal values

$$I_{\mathit{maxA}}{I}_{\mathit{maxB}}=\alpha \beta {\left(R_{\mathit{tot}}^0\right)}^2$$

produces a quadratic amount of total receptors whereas the Ariëns concept implicitly assumes a fixed number $R_{\mathit{tot}}^0$ of receptors, see Eq. (11). The scaling property is violated by Eq. (42) due to I_maxAI_maxB. However, for I_maxA and I_maxB close to identity, Eq. (42) reduces to the inhibitory form of the Bliss Independence CET Eq. (33). Hence, Eq. (42) can be interpreted to act on two different targets and colloquially considered as non-competitive.

In the Emax-formulation of Eq. (42) the effect could become negative which can simply be seen from

$$\frac{2E_{\mathit{maxA}}+2E_{\mathit{maxB}}-E_{\mathit{maxA}}{E}_{\mathit{maxB}}}{4}<0$$

if E_maxA, E_maxB>4. Hence, Eq. (42) is only useful in the inhibitory formulation Eq. (42).

IDR stimulation CET

If the production rate is stimulated in IDRs

$$\begin{array}{l}\frac{d}{\mathit{dt}}\mathit{Res}=k_{\mathit{in}}(1+e(C_A))(1+e(C_B))-K_{\mathit{out}}\mathit{Res}\\ =k_{\mathit{in}}(1+E^{\mathit{Stim}}(C_A,C_B))-k_{\mathit{out}}\mathit{Res}\mathit{Res}(0)=\frac{k_{\mathit{in}}}{k_{\mathit{out}}}\end{array}$$

compare Fig. 2i for schematic, then by similar calculations the corresponding CET reads

$$E^{\mathit{Stim}}(C_A,C_B)=\frac{E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+E_{\mathit{maxB}}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}+\left(E_{\mathit{maxA}}+E_{\mathit{maxB}}+E_{\mathit{maxA}}{E}_{\mathit{maxB}}\right){\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}{1+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}$$ (43)

Summary of CET properties

Properties of the presented CETs are summarized in Table 1. We indicate the construction principles and symmetry of CETs. Validity of the desired properties namely positivity, scaling and diagonality are stated. The maximal combination effect E_maxAB is listed and we indicate whether the CET can be written in an inhibitory form, i.e. can be applied as (1−I(C_A, C_B)), compare e.g. Equation (4). In Fig. 3, a comparison of the presented CETs with respect to the maximal effect and the number of targets is shown.

$$=e(C_A)+e(C_B)+e(C_A)e(C_B).$$ (44)

Fig. 3.

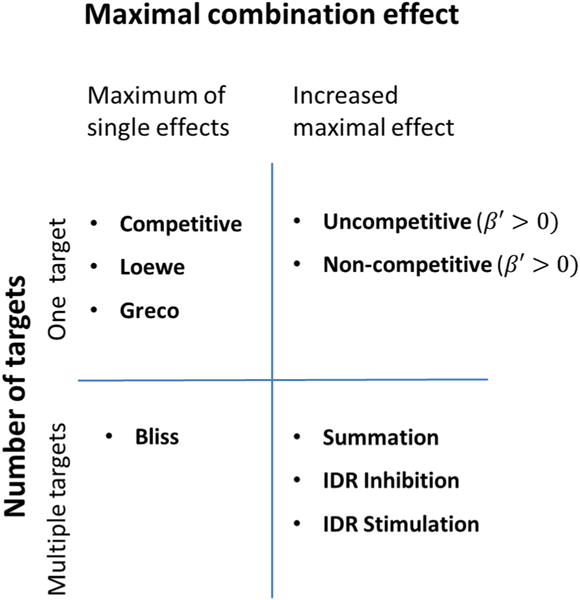
Comparison of presented CETs with respect to the maximal effect and the number of targets

In [44], Eq. (43) was applied in non-dynamic models describing stimulatory effects. Note that no negativity occurs because of the summation of the term E_maxAE_maxB in Eq. (43). Nevertheless, justification based on Ariën’s approach also does not hold, because of the quadratic amount of receptors and also the scaling property is violated. Equation (44) can be considered as an extension of the summation CET Eq. (38) with an additional build-in synergism term e(C_A)e(C_B) to produce a higher maximal combination effect. In [20] a structurally similar approach to Eq. (44) with linear CETs was applied.

Relationship of CETs and the optimal concentration pair for half-maximal effect

We investigated several DDI mechanisms and derived the corresponding CETs. Hence, if the underlying DDI mechanism is known in application, the appropriate CET can be applied directly at the specific interaction position in the PKPD model. For example, often the combination of endogenous substances with exogenous agents acts in a competitive manner on the same receptor [30]. However, if the underlying DDI mechanism is not known, e.g. in early drug development, different CETs have to be tested and selection criteria need to be formulated.

First, we present relationships of the symmetric CETs regarding their effect, if the same drug concentration is applied, which may help to identify the corresponding DDI mechanism. Second, we investigate selected CETs regarding the optimal drug concentration pair to achieve the half-maximal effect. In contrast to the single case, where a unique concentration, the EC₅₀, exists to produce the half-maximal effect, for CETs several concentration combinations are possible for the half-maximal combination effect $\frac{E_{\mathit{maxAB}}}{2}$. Based on a pharmacological reasonable objective function, we determine the optimal concentration pair for each CET and classify the interaction of the two drugs into synergistic, additive and antagonistic.

Relationship and ranking of the symmetric CETs

A ranking of the presented symmetric CETs is established with respect to their effect for the same drug concentrations. In the case of arbitrary E_maxA, E_maxB, γ_A, γ_B> 0 one can show (Appendix 8)

$$0<E^{\mathit{Com}}(C_A,C_B)<E^{\mathit{Sum}}(C_A,C_B)<E^{\mathit{Stim}}(C_A,C_B).$$ (45)

For E_maxA=E_maxB and γ_A, γ_B> 0 we obtain

$$\begin{array}{l}0<E^{\mathit{Com}}(C_A,C_B)<E^{\mathit{Bliss}}(C_A,C_B)\\ <E^{\mathit{Sum}}(C_A,C_B)<E^{\mathit{Stim}}(C_A,C_B).\end{array}$$ (46)

If E_maxA=E_maxB and γ_A=γ_B=1 the realtions

$$\begin{array}{l}0<E^{\mathit{Com}}(C_A,C_B)<E_{0<\alpha <1}^{\mathit{Greco}}(C_A,C_B)<E^{\mathit{Bliss}}(C_A,C_B)\\ <E^{\mathit{Sum}}(C_A,C_B)<E^{\mathit{Stim}}(C_A,C_B)\end{array}$$ (47)

hold where $E^{\mathit{Com}}(C_A,C_B)=E^{\mathit{Loewe}}(C_A,C_B)=E_{\alpha =0}^{\mathit{Greco}}(C_A,C_B)$ and $E_{\alpha =1}^{\mathit{Greco}}(C_A,C_B)=E^{\mathit{Bliss}}(C_A,C_B)$. Exemplarily we visualized the relations from Eq. (45) as heat map in Fig. 4.

Fig. 4.

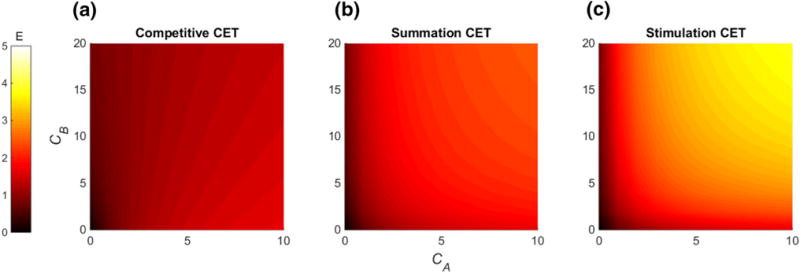
Heat maps visualizing the effect of the competitive (E_maxAB = 2) Eq. (18), summation (E_maxAB = 3) Eq. (39), and stimulation (E_maxAB = 5) Eq. (43) CET are shown. Brighter color denotes a higher combination effect. The single maximal effects were set to E_maxA = 2 and E_maxB = 1 (Color figure online)

Optimal concentration pair for the half-maximal effect of CETs

For CETs the discussion about the necessary concentrations to produce the half-maximal combination effect $\frac{E_{\mathit{maxAB}}}{2}$ is much more extensive than for single effect terms, since the concentration pair to produce $\frac{E_{\mathit{maxAB}}}{2}$ is no longer unique and, in addition, every CET has to be treated separately. This provides the opportunity to compute the optimal concentration pair $({\overline{C}}_A,{\overline{C}}_B)$ (denoted by bars) to produce $\frac{E_{\mathit{maxAB}}}{2}$ for every CET.

For single effect terms the equation defining the unique half-maximal effect reads

$$e(c)=\frac{E_{\mathit{max}}{\left(\frac{C}{E{C}_{50}}\right)}^{\gamma }}{1+{\left(\frac{C}{E{C}_{50}}\right)}^{\gamma }}=\frac{E_{\mathit{max}}}{2}$$

that is equivalent to

$$1={\left(\frac{C}{E{C}_{50}}\right)}^{\gamma }$$ (48)

and the necessary concentration C = EC₅₀ can be directly seen from Eq. (48). However, for CETs the drug concentration pairs (C_A, C_B) satisfying

$$E(C_A,C_B)=\frac{E_{\mathit{maxAB}}}{2}$$

form a curve in the 2-dimensional (C_A, CB)-space that we call the half-maximal effect curve.

To calculate the optimal concentration pair for a CET, two steps are necessary: (i) establish the half-maximal effect curve, and (ii) optimize the concentration pair with respect to an appropriate objective function.

Any presented CET in this work could be written with the dimensionless variables, i.e. as a fraction of actual concentration and the concentration necessary to produce half-maximal single effect:

$$\frac{C_A}{E{C}_{{50}_A}}\mathit{\text{and}}\frac{C_B}{E{C}_{50B}}$$

For example, compare Eqs. (18), (22), (24), (29), (33), (37), (39), (42) and (43). For simplicity we assume γ_A = γ_B = 1 in this Section. The half-maximal effect curve of all possible concentration pairs (C_A, C_B) for the given single EC_50A and EC_50B reads

$$\begin{array}{l}\left\{\left(\frac{C_A}{E{C}_{50A}},\frac{C_B}{E{C}_{50B}}\right);E(C_A,C_B)=\frac{E_{\mathit{maxAB}}}{2},C_A,C_B\ge 0\right\}\\ =\left\{\left(\frac{C_A}{E{C}_{50A}},\frac{C_B}{E{C}_{50B}}\right);\frac{C_B}{E{C}_{50B}}=\phi \left(\frac{C_A}{E{C}_{50A}}\right),C_A,C_B\ge 0\right\}\end{array}$$

where φ is a function being specific for the underlying CET.

To calculate the optimal concentration pair $\left(\frac{{\overline{C}}_A}{E{C}_{50A}},\frac{{\overline{C}}_B}{E{C}_{50B}}\right)$ to achieve $\frac{E_{\mathit{maxAB}}}{2}$ for given single EC₅₀’s, we utilize as objective function either the Loewe Additivity Eq. (25) or the Bliss Independence Eq. (35) depending on the underlying mechanism. If the drugs act at the same target, we apply as objective function in our optimization task an extended version of Eq. (25) with a combination index CI [45]

$$C{I}^{\mathit{Loewe}}=\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}.$$ (49)

If it is assumed that the two drugs do not share the same target, do not interfere with each other, and are mutually non-exclusive the resulting combination index is

$$C{I}^{\mathit{Bliss}}=\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}+\frac{C_A}{E{C}_{50A}}\frac{C_B}{E{C}_{50B}}$$ (50)

See [40]. However, both approaches Eqs. (49), (50) assume an equal maximal single effect and due to their own symmetry they are only applicable to symmetric CETs. In both scenarios, we are looking for a solution pair $\left(\frac{{\overline{C}}_A}{E{C}_{50A}},\frac{{\overline{C}}_B}{E{C}_{50B}}\right)$ on the half-maximal effect curve generating the minimal CI^Loewe or CI^Bliss. The CET specific functions φ are independent of the actual values of E_maxA and E_maxB. Additionally, based on Eqs. (49) or (50) the area of antagonistic (CI^Loewe or CI^Bliss> 1), additive (CI^Loewe or CI^Bliss= 1), or synergistic (CI^Loewe or CI^Bliss< 1) behavior of a CET can be classified.

For all necessary calculations of the following see Appendix 9. For the competitive CET Eq. (18) with E_maxB = E_maxA all pairs on the half-maximal effect curve are optimal, i.e.

$$\left(\frac{{\overline{C}}_A}{E{C}_{50A}},\frac{{\overline{C}}_B}{E{C}_{50B}}\right)=(\epsilon ,1-\epsilon ),\epsilon \text{ between}0\text{and}1,$$

compare Fig. 5a. For the Greco CET Eq. (37) with |α| ≤1 the optimal solution pair is

$$\begin{array}{l}\left(\frac{{\overline{C}}_A}{E{C}_{50A}},\frac{{\overline{C}}_B}{E{C}_{50B}}\right)\\ =\{\begin{array}{ll}(\epsilon ,1-\epsilon )\hfill & \epsilon \text{between }0\text{and }1,if\alpha =0\hfill \\ \left(\frac{\sqrt{1+\alpha }-1}{\alpha },\frac{\sqrt{1+\alpha }-1}{\alpha }\right),\hfill & if0<\left|\alpha \right|\le 1\hfill \end{array}\end{array}$$

Fig. 5.

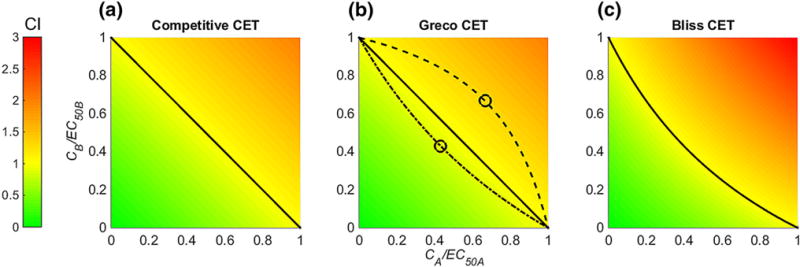
For the competitive (a) Eq. (18), Greco (b) Eq. (37) and Bliss Eq. (33) (c) CET optimal concentration pairs from Loewe Additivity (a, b) and Bliss Independence (c) are indicated (solid black line and yellow area). Green surface denotes area of synergism and red surface is area of antagonism. Additionally, for the Greco CET (b) half-maximal effect curves for α = 0.75 (dashed dotted line) and α = −0.75 (dashed line) are shown, and the corresponding unique optimal concentration pair is indicated (circles) (Color figure online)

See Fig. 5b. Hence, for 0<|α| ≤1 we have a unique optimal solution. For the Bliss CET Eq. (33) the optimal solution with respect to Eq. (50) is

$$\left(\frac{{\overline{C}}_A}{E{C}_{50A}},\frac{{\overline{C}}_B}{E{C}_{50B}}\right)=(\epsilon ,{\phi }_{\mathit{Bliss}}(\epsilon )),\epsilon \text{between }0\text{and }1$$

with

$${\phi }_{\mathit{Bliss}}\left(\frac{C_A}{E{C}_{50A}}\right)=\frac{1-\frac{C_A}{E{C}_{50A}}}{1+\frac{C_A}{E{C}_{50A}}}$$

and again all pairs on the half-maximal effect curve are optimal, see Fig. 5c.

Comparing Eq. (25) with Eq. (49) and Eq. (35) with Eq. (50) directly shows that the Loewe and Bliss-CET satisfy CI^Loewe = 1, CI^Bliss = 1 on their entire half-maximal effect curve. Hence, symmetric CETs whose drugs share the same (not the same) target behave synergistic, additive or antagonistic, if they perform better, equal or worse than the Loewe (Bliss) CET.

More care is necessary for CETs with higher maximal combination effects than the maximal effect from the single drug, since the objective functions Eqs. (49), (50) defining the classifications have to be scaled appropriately with E_maxA and E_maxB. For the summation CET Eq. (39) application of our minimization method leads to the optimal solution

$$\left(\frac{{\overline{C}}_A}{E{C}_{50A}},\frac{{\overline{C}}_B}{E{C}_{50B}}\right)=(1,1)$$

if E_maxA = E_maxB.

For more general assumptions, such as different maximal single effects and individual Hill coefficients, the presented method in the Appendix can be applied but more detailed investigations and calculations are necessary.

Discussion

CETs are important components to construct PKPD models with DDI effects. Therefore, it is essential to have a rigorous knowledge about their underlying pharmacological mechanism and mathematical properties.

We investigated CETs based on drug receptor binding kinetics, statistical and empirical summation principles, and indirect response models. The presented CETs could be categorized based on different criteria. First, for some CETs the maximal combination effect E_maxAB, is the maximal single effect, whereas for others it is a combination of the two single maximal effects. Second, most CETs are symmetric, i.e. interchanging the roles of A and B leads to the same CET. However, we also presented non-symmetric CETs where only an effect exists, if drug A is an agonist and drug B an antagonist. Third, some CETs describe the DDI on one target, whereas others assume action on two targets.

A general drug-receptor binding kinetic concept is presented according to Ariëns who derived the competitive, uncompetitive and non-competitive CETs from first principles. These three CETs fulfill positivity and scaling, and the symmetric competitive CET also diagonality.

Additive interaction is usually defined based on two different principles. The Loewe Additivity assumes that the two drugs act on one target whereas Bliss Independence assumes two independent mechanisms on two different targets. From these two fundamental principles we also derived CETs which describe two different types of additivity. The constructed Loewe CET becomes equal to the competitive CET, derived from drug-receptor binding kinetics, if the single maximal effects are equal and the Hill coefficients have the value 1. Further we investigated Greco’s model that is based on the Loewe Additivity. This model is equipped with an interaction parameter α to account for antagonistic or synergistic behavior but surprisingly can produce negative effects, if the interaction parameter indicates antagonism and the CET is used with sufficiently large concentrations. This is not an issue when fitting data only but may produce paradox results for simulations. However, the interaction parameter α in the Greco model connects the Loewe Additivity for α = 0 with the Bliss Independence for α = 1, which explains the flexibility of Greco’s model. All these CETs are symmetric and fulfill the diagonality condition but CETs with two targets have some deviation in contrast to CETs describing one target. The summation CET is structurally different since it realizes a maximal combination effect which is the sum of the single maximal effects and it does not fulfill the diagonality criteria.

Finally, we investigated CETs derived from indirect response models. These CETs are fundamentally different to the previous ones from Ariëns, Loewe and Bliss due to a multiplication term of the single maximal drug effects in the enumerator. They do not fulfill the scaling and diagonality conditions. However, interestingly the frequently applied CET Eq. (42) is structurally close to the Bliss CET if the two single maximal inhibition parameters are nearly unity.

For comparison of the different symmetric CETs, a ranking regarding their combination effect for the same drug concentrations was established. Depending on the relations of single maximal effect parameters among each other and the Hill coefficients, orderings of different CETs can be shown. Such relationships may open the route to identify an appropriate CET regarding its predicted effect.

The last part of this work was dedicated to the computation of an optimal concentration pair, which is essential in application. In general, optimization can be performed at different levels of the model. For example, Gabrielsson et al. [46] presented the optimal concentration pair for a cytotoxic and a cytostatic drug to achieve tumor stasis for a specific tumor growth PKPD model. Since we are interested in different CETs and do not consider a specific PKPD model, the optimal drug concentration pair to achieve the half-maximal effect $\frac{E_{\mathit{maxAB}}}{2}$ was investigated. In general, to apply optimization techniques, an objective function representing reasonable pharmacological evaluation criteria has to be chosen. Since one part of the CETs deal with one target and the others describe two targets, we either chose as objective function the Loewe Additivity or the Bliss Independence, both equipped with a combination index. Because every CET has to be treated separately, we selected the competitive, Bliss, Greco and the summation CET to introduce the optimization method and to present the optimal concentration pair for half-maximal effect. To simplify the calculations and to avoid distinction of cases, we investigated only Hill coefficients equal to one. Additionally, we focused our investigations to equal maximal single effects due to the properties of Eqs. (49)–(50). But we would like to emphasize that the objective functions based on Loewe or Bliss principles can be generalized for varying maximal single effects and Hill coefficients.

The Loewe, summation and IDRCETs can be straightforward extended for more than two drugs. An example of the Loewe CET for three drugs is shown in [47]. The competitive and Bliss CET have to be re-derived from their basic principles. In the non-symmetric uncompetitive and non-competitive situation more knowledge about the desired interaction mechanisms is necessary.

Obviously, several other CETs exist to describe DDI. To obtain more flexibility, additional parameters were introduced, e.g. based on polynomials [13], multi-parametric models with varying potencies [11] were developed, and approaches to cover wider ranges of combination behavior [12] were constructed. However, methods of such types were out of the scope of this manuscript.

In conclusion, the presented CETs are crucial components to describe a certain DDI mechanism in a PKPD model, and the presented and derived knowledge about CETs is essential to construct more mechanism-based PKPD models for DDI.

Appendix 1: Drug receptor binding kinetics

General derivation

From the conservation of receptors and complexes Eq. (11) we obtain the receptor representation

$$R=(R_{\mathit{tot}}^0-R{C}_A-R{C}_B-R{C}_{\mathit{AB}}).$$ (51)

Rewriting the complexes Eqs. (8)–(10) with Eq. (51)

$$\begin{array}{l}\frac{d}{\mathit{dt}}R{C}_A=k_{\mathit{onA}}{C}_A(R_{\mathit{tot}}^0-R{C}_A-R{C}_B-R{C}_{\mathit{AB}})\\ -k_{\mathit{offA}}R{C}_A-k_{\mathit{onB}}{C}_{B}R{C}_A\\ +k_{\mathit{offC}}R{C}_{\mathit{AB}}\end{array}$$ (52)

$$\frac{d}{\mathit{dt}}R{C}_B=k_{\mathit{onB}}{C}_B(R_{\mathit{tot}}^0-R{C}_A-R{C}_B-R{C}_{\mathit{AB}})-k_{\mathit{offB}}R{C}_B$$ (53)

$$\frac{d}{\mathit{dt}}R{C}_{\mathit{AB}}=k_{\mathit{onB}}{C}_{B}R{C}_A-k_{\mathit{offB}}R{C}_{\mathit{AB}}.$$ (54)

Pseudo steady-state analysis of Eqs. (52)–(54) for the complexes and substituting Eq. (54) into Eq. (52) then leads to

$$\begin{array}{l}0=k_{\mathit{onA}}{C}_A(R_{\mathit{tot}}^0-R{C}_A-R{C}_B-R{C}_{\mathit{AB}})-k_{\mathit{offA}}R{C}_A\hfill \\ 0=k_{\mathit{onB}}{C}_B(R_{\mathit{tot}}^0-R{C}_A-R{C}_B-R{C}_{\mathit{AB}})-k_{\mathit{offB}}R{C}_B\hfill \\ 0=k_{\mathit{onB}}{C}_{B}R{C}_A-k_{\mathit{offB}}R{C}_{\mathit{AB}}.\hfill \end{array}$$

With $K_{\mathit{DA}}=\frac{k_{\mathit{offA}}}{k_{\mathit{onA}}}$ and $K_{\mathit{DB}}=\frac{k_{\mathit{offB}}}{k_{\mathit{onB}}}$ we obtain

$$0=C_A(R_{\mathit{tot}}^0-R{C}_A-R{C}_B-R{C}_{\mathit{AB}})-K_{\mathit{DA}}R{C}_A$$ (55)

$$0=C_B(R_{\mathit{tot}}^0-R{C}_A-R{C}_B-R{C}_{\mathit{AB}})-K_{\mathit{DB}}R{C}_B$$ (56)

$$0=C_{B}R{C}_A-K_{\mathit{DB}}R{C}_{\mathit{AB}}.$$ (57)

Dividing Eq. (55) by K_DA and Eqs. (56)–(57) by K_DB we obtain the matrix notation Eq. (12)

$$\left(\begin{array}{ccc}1+\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}& 1+\frac{C_B}{K_{\mathit{DB}}}& \frac{C_B}{K_{\mathit{DB}}}\\ -\frac{C_B}{K_{\mathit{DB}}}& 0& 1\end{array}\right)\left(\begin{array}{c}R{C}_A\\ R{C}_B\\ R{C}_{\mathit{AB}}\end{array}\right)=R_{\mathit{tot}}^0\left(\begin{array}{c}\frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}\\ 0\end{array}\right).$$

We apply Cramer’s rule and obtain

$$\begin{array}{l}{M}_0=\det \left(\begin{array}{ccc}1+\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}& 1+\frac{C_B}{K_{\mathit{DB}}}& \frac{C_B}{K_{\mathit{DB}}}\\ -\frac{C_B}{K_{\mathit{DB}}}& 0& 1\end{array}\right)=1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_B}{K_{\mathit{DB}}}+\frac{C_A{C}_B}{K_{\mathit{DA}}{K}_{\mathit{DB}}}>0\\ M_1=\det \left(\begin{array}{ccc}{R}_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}& 1+\frac{C_B}{K_{\mathit{DB}}}& \frac{C_B}{K_{\mathit{DB}}}\\ 0& 0& 1\end{array}\right)=R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\ge 0\\ M_2=\det \left(\begin{array}{ccc}1+\frac{C_A}{K_{\mathit{DA}}}& R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}& R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}& \frac{C_B}{K_{\mathit{DB}}}\\ -\frac{C_B}{K_{\mathit{DB}}}& 0& 1\end{array}\right)=R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}\ge 0\\ M_3=\det \left(\begin{array}{ccc}1+\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}& R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}& 1+\frac{C_B}{K_{\mathit{DB}}}& R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}\\ -\frac{C_B}{K_{\mathit{DB}}}& 0& 0\end{array}\right)=R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}\ge 0.\end{array}$$

Note that M₀ is strictly positive and M_i, i = 1, 2, 3 are non-negative for C_A, C_B≥0. The complexes then read

$$R{C}_A=\frac{M_1}{M_0}=\frac{R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A{C}_B}{K_{\mathit{DA}}{K}_{\mathit{DB}}}}$$ (58)

$$R{C}_B=\frac{M_2}{M_0}=\frac{R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A{C}_B}{K_{\mathit{DA}}{K}_{\mathit{DB}}}}$$ (59)

$$R{C}_{\mathit{AB}}=\frac{M_3}{M_0}=\frac{R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A{C}_B}{K_{\mathit{DA}}{K}_{\mathit{DB}}}}.$$ (60)

Inserting Eqs. (58)–(60) in Eq. (13) then results in Eq. (14).

Appendix 2: Competitive CET

Derivation

Applying Cramer’s rule to Eq. (15) gives

$$\begin{array}{l}{M}_0=\det \left(\begin{array}{cc}1+\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}& 1+\frac{C_B}{K_{\mathit{DB}}}\end{array}\right)=1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_B}{K_{\mathit{DB}}}>0.\\ M_1=\det \left(\begin{array}{cc}{R}_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}& 1+\frac{C_B}{K_{\mathit{DB}}}\end{array}\right)=R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\ge 0\\ M_2=\det \left(\begin{array}{cc}1+\frac{C_A}{K_{\mathit{DA}}}& R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\\ \frac{C_B}{K_{\mathit{DB}}}& R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}\end{array}\right)=R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}\ge 0.\end{array}$$

The complexes then read

$$R{C}_A=\frac{M_1}{M_0}=\frac{R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A}{K_{\mathit{DA}}}}$$ (61)

$$R{C}_B=\frac{M_2}{M_0}=\frac{R_{\mathit{tot}}^0\frac{C_B}{K_{\mathit{DB}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A}{K_{\mathit{DA}}}}.$$ (62)

Inserting Eqs. (61)–(62) in Eq. (16) then results in Eq. (17).

Maximal effect

$$\begin{array}{l}{E}^{\mathit{Com}}(C_A,C_B)\le max\{E_{\mathit{maxA}},E_{\mathit{maxB}}\}\frac{{\left(\frac{C_A}{E{C}_{50,A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50,B}}\right)}^{{\gamma }_B}}{1+{\left(\frac{C_A}{E{C}_{50,A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50,B}}\right)}^{{\gamma }_B}}\\ <max\{E_{\mathit{maxA},}{E}_{\mathit{maxB}}\}.\end{array}$$

Diagonality

If drug A equals drug B, we have

$$\begin{array}{l}{E}^{\mathit{Com}}\left(\frac{C_A}{2},\frac{C_A}{2}\right)=E_{\mathit{maxA}}\frac{\frac{C_A}{2E{C}_{50A}}+\frac{C_A}{2E{C}_{50A}}}{1+\frac{C_A}{2E{C}_{50A}}+\frac{C_A}{2E{C}_{50A}}}=\frac{E_{\mathit{maxA}}\frac{C_A}{2E{C}_{50A}}}{1+\frac{C_A}{E{C}_{50A}}}\\ =e(C_A).\end{array}$$

Agonistic-antagonist

For an antagonistic drug B we have e(C_B)=0 for C_B≥0 and therefore E_maxB = 0. Hence, we obtain with Eq. (18)

$$\begin{array}{l}{E}^{\mathit{Com}}(C_A,C_B)=\frac{E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+E_{\mathit{maxB}}{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}{1+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}\\ >\frac{E_{\mathit{maxA}}{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}}{1+{\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}+{\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}}=E^{\mathit{ComGad}}(C_A,C_B).\end{array}$$

Appendix 3: Uncompetitive CET

Derivation

The determinants for Cramer’s rule applied to Eq. (19) are

$$\begin{array}{l}{M}_0=\det \left(\begin{array}{cc}1+\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ -\frac{C_B}{K_{\mathit{DB}}}& 1\end{array}\right)=1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_B}{K_{\mathit{DB}}}\frac{C_B}{K_{\mathit{DB}}}>0\\ M_1=\det \left(\begin{array}{cc}{R}_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}& \frac{C_A}{K_{\mathit{DA}}}\\ 0& 1\end{array}\right)=R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\ge 0\\ M_2=\det \left(\begin{array}{cc}1+\frac{C_A}{K_{\mathit{DA}}}& R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\\ -\frac{C_B}{K_{\mathit{DB}}}& 0\end{array}\right)=R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}\ge 0.\end{array}$$

The complexes then read

$$R{C}_A=\frac{M_1}{M_0}=\frac{R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}}$$ (63)

$$R{C}_B=\frac{M_2}{M_0}=\frac{R_{\mathit{tot}}^0\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}}{1+\frac{C_A}{K_{\mathit{DA}}}+\frac{C_A}{K_{\mathit{DA}}}\frac{C_B}{K_{\mathit{DB}}}}.$$ (64)

Inserting Eqs. (63)–(64) in Eq. (20) then results in Eq. (21).

Appendix 4: Loewe CET

Derivation

Rearranging Eq. (27) with respect to DC_X gives

$$D{C}_X=E{C}_{50X}{\left(\frac{E}{E_{\mathit{max}}-E}\right)}^{\frac{1}{{\gamma }_X}}.$$ (65)

Substituting Eq. (65) in Eq. (26) gives Eq. (28). Equation (28) can be written with γ_A = γ_B = γ as

$$E^{\frac{1}{\gamma }}={(E_{\mathit{max}}-E)}^{\frac{1}{\gamma }}\left(\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}\right)$$

resulting in

$$E=(E_{\mathit{max}}-E){\left(\frac{C_A}{E{C}_{50A}}+\frac{C_B}{E{C}_{50B}}\right)}^{\gamma }.$$ (66)

Rearranging of Eq. (66) gives the Loewe CET Eq. (29).

Appendix 5: Bliss CET

Diagonality

We have

$$\begin{array}{l}{E}^{\mathit{Bliss}}(\frac{C_A}{2},\frac{C_B}{2})=\frac{E_{\mathit{max}}\frac{C_A}{2E{C}_{50A}}+E_{\mathit{max}}\frac{C_A}{2E{C}_{50A}}+E_{\mathit{max}}\frac{C_A}{4E{C}_{50A}}\frac{C_A}{E{C}_{50A}}}{1+\frac{C_A}{2E{C}_{50A}}+\frac{C_A}{2E{C}_{50A}}+\frac{C_A^2}{2E{C}_{50A}^2}}\\ =\frac{E_{\mathit{max}}\left(\frac{C_A}{E{C}_{50A}}+\frac{C_A^2}{4E{C}_{50A}^2}\right)}{1+\frac{C_A}{E{C}_{50A}}+\frac{C_A^2}{4E{C}_{50A}^2}}=e\left(\frac{C_A}{E{C}_{50A}}+\frac{C_A^2}{4E{C}_{50A}^2}\right).\end{array}$$

Hence, the diagonality condition is satisfied with $\sigma =\frac{1}{4}$.

Appendix 6: Greco and Summation CET

Diagonality of the Greco CET

For γ_A = γ_B = 1 we obtain with Eq. (37)

$$\begin{array}{c}{E}^{\mathit{Greco}}\left(\frac{C_A}{2},\frac{C_A}{2}\right)=\frac{E_{\mathit{max}}\left(\frac{C_A}{2E{C}_{50A}}+\frac{C_A}{2E{C}_{50A}}+\alpha \frac{C_A}{4E{C}_{50A}}\frac{C_A}{E{C}_{50A}}\right)}{1+\frac{C_A}{2E{C}_{50A}}+\frac{C_A}{2E{C}_{50A}}+\alpha \frac{C_A^2}{4E{C}_{50A}^2}}\\ =e\left(\frac{C_A}{E{C}_{50A}}+\alpha \frac{C_A^2}{4E{C}_{50A}^2}\right)\end{array}$$

and the diagonality condition is fulfilled with $\sigma =\frac{\alpha }{4}$.

Diagonality of the summation CET

For equal drugs we can compute

$$E^{\mathit{Sum}}\left(\frac{C_A}{2},\frac{C_A}{2}\right)=2\frac{E_{\mathit{maxA}}\frac{C_A}{2E{C}_{50A}}}{1+\frac{C_A}{2E{C}_{50A}}}=2e\left(\frac{C_A}{2}\right)>e(C_A)$$

Thus, $E^{\mathit{Sum}}\left(\frac{C_A}{2},\frac{C_A}{2}\right)$ cannot be written in the form assumed in the diagonality condition. To see the last inequality please note that with

$$f_1(x)=2e(x),f_2(x)=e(2x)$$

we have

$$\begin{array}{l}{f}_1(0)=f_2(0),\\ f_1^{\prime }(x)=2e^{\prime }(x),f_2^{\prime }(x)=2e^{\prime }(2x).\end{array}$$

Since e′(x)> 0 and e′ monotone decreasing, f₁(x)> f₂(x), x > 0 follows and with $x=\frac{C_A}{2}$ the inequality.

Appendix 7: IDR CETs

Equivalent formulation for the inhibitory CET

To demonstrate the equivalence of Eq. (40) with Eqs. (41)–(42), we have to show

$$i(C_A)+i(C_B)-i(C_A)i(C_B)=I^{\mathit{IDR}}(C_A,C_B.)$$

The denominator from Eq. (42) can be written as

$$De=\frac{I{C}_{50A}^{{\gamma }_A}I{C}_{50B}^{{\gamma }_B}+C_A^{{\gamma }_A}I{C}_{50B}^{{\gamma }_B}+C_B^{{\gamma }_B}I{C}_{50A}^{{\gamma }_A}+C_A^{{\gamma }_A}{C}_B^{{\gamma }_B}}{I{C}_{50A}^{{\gamma }_A}I{C}_{50B}^{{\gamma }_B}}$$

and the numerator reads

$$Nu=\frac{I_{\mathit{maxA}}{C}_A^{{\gamma }_A}I{C}_{50B}^{{\gamma }_B}+I_{\mathit{maxA}}{C}_B^{{\gamma }_B}I{C}_{50A}^{{\gamma }_A}+(I_{\mathit{maxA}}+I_{\mathit{maxB}}-I_{\mathit{maxA}}{I}_{\mathit{maxB}})C_A^{{\gamma }_A}{C}_B^{{\gamma }_B}}{I{C}_{50A}^{{\gamma }_A}I{C}_{50B}^{{\gamma }_B}}.$$

Hence, we obtain

$$\begin{array}{c}\frac{Nu}{De}=\frac{I_{\mathit{maxA}}{C}_A^{{\gamma }_A}\left(I{C}_{50B}^{{\gamma }_B}+C_B^{{\gamma }_B}\right)+I_{\mathit{maxB}}\left(I{C}_{50A}^{{\gamma }_A}+C_A^{{\gamma }_A}\right)-(I_{\mathit{maxA}}{I}_{\mathit{maxB}})C_A^{{\gamma }_A}{C}_B^{{\gamma }_B}}{\left(I{C}_{50A}^{{\gamma }_A}+C_A^{{\gamma }_A}\right)\left(I{C}_{50B}^{{\gamma }_B}+C_B^{{\gamma }_B}\right)}\\ =\frac{I_{\mathit{maxA}}{C}_A^{{\gamma }_A}}{\left(I{C}_{50A}^{{\gamma }_A}+C_A^{{\gamma }_A}\right)}+\frac{I_{\mathit{maxA}}{C}_B^{{\gamma }_B}}{\left(I{C}_{50B}^{{\gamma }_B}+C_B^{{\gamma }_B}\right)}-\frac{I_{\mathit{maxA}}{C}_A^{{\gamma }_A}}{\left(I{C}_{50A}^{{\gamma }_A}+C_A^{{\gamma }_A}\right)}\frac{I_{\mathit{maxA}}{C}_B^{{\gamma }_B}}{\left(I{C}_{50B}^{{\gamma }_B}+C_B^{{\gamma }_B}\right)}.\end{array}$$

Diagonality of the stimulation CET

If drug A equals drug B, we have

$$\begin{array}{l}{E}^{\mathit{Stim}}\left(\frac{C_A}{2},\frac{C_A}{2}\right)=\frac{E_{\mathit{maxA}}\frac{C_A}{2E{C}_{50A}}+E_{\mathit{maxA}}\frac{C_A}{2E{C}_{50A}}+(2E_{\mathit{maxA}}+E_{\mathit{maxA}}^2)\frac{C_A}{4E{C}_{50A}}\frac{C_A}{E{C}_{50A}}}{1+\frac{C_A}{2E{C}_{50A}}+\frac{C_A}{2E{C}_{50A}}+\frac{C_A^2}{4E{C}_{50A}^2}}\\ =e\left(\frac{C_A}{E{C}_{50A}}+\frac{C_A^2}{4E{C}_{50A}^2}\right)+\frac{\frac{1}{4}(E_{\mathit{maxA}}+E_{\mathit{maxA}}^2)\frac{C_A^2}{E{C}_{50A}^2}}{1+\frac{C_A}{2E{C}_{50A}}+\frac{C_A}{2E{C}_{50A}}+\frac{C_A^2}{4E{C}_{50A}^2}}.\end{array}$$

Eq. (46). In the case of E_maxA = E_maxB = E_max and γ_A = γ_B = 1 we obtain Eq. (47) with evaluation of Eq. (67) at η ∈ (0,1), η = 1 in Eq. (68).

Hence, $E^{\mathit{Stim}}\left(\frac{C_A}{2},\frac{C_A}{2}\right)$ cannot be written in form of a single drug effect term. With similar calculations we obtain the same conclusion for I^IDR

Appendix 8: Relationships

To simplify the notation we set

$$x={\left(\frac{C_A}{E{C}_{50A}}\right)}^{{\gamma }_A}\mathit{\text{and}}y={\left(\frac{C_B}{E{C}_{50B}}\right)}^{{\gamma }_B}.$$

For E_maxA, E_maxB, γ_A, γ_B> 0, Eq. (45) follows from

$$\begin{array}{l}\frac{E_{\mathit{maxA}}x}{1+x+y}+\frac{E_{\mathit{maxB}}y}{1+x+y}<\frac{E_{\mathit{maxA}}x}{1+x}+\frac{E_{\mathit{maxB}}y}{1+y}<\frac{E_{\mathit{maxA}}x}{1+x}\\ +\frac{E_{\mathit{maxB}}y}{1+y}+\frac{E_{\mathit{maxA}}x}{1+x}\frac{E_{\mathit{maxB}}y}{1+y}.\end{array}$$

In the case of E_maxA = E_maxB = E_max> 0 and γ_A, γ_B> 0 we have

$$E_{\mathit{max}}\frac{x+y}{1+x+y}<E_{\mathit{max}}\frac{x+y+\eta xy}{1+x+y+\eta xy}$$ (67)

$$<E_{\mathit{max}}\frac{x+y+2\eta xy}{1+x+y+\eta xy}$$ (68)

where η > 0 indicates existence of the multiplicative term xy. In Eqs. (46)–(47) the last inequality is obvious. Evaluation of Eq. (67) at η = 1 and Eq. (68) at η = 1 yields

Appendix 9: Optimal concentration pair for half-maximal combination effect

In the following calculation we assume γ_A = γ_B = γ = 1 and set

$$x=\frac{C_A}{E{C}_{50A}},y=\frac{C_B}{E{C}_{50B}}.$$ (69)

Competitive CET

We assume E_maxB = E_maxA = E_max> 0. Using Eq. (18) by definition of the half maximal effect curve we have to solve

$$E^{\mathit{Com}}(C_A,C_B)=\frac{E_{\mathit{max}}x+E_{\mathit{max}}y}{1+x+y}=\frac{E_{\mathit{maxAB}}}{2}=\frac{E_{\mathit{max}}}{2}$$

which is equivalent to

$$2x+2y=1+x+y.$$

This leads to

$$y=1-x$$

and the CET specific function for the half-maximal effect curve reads

$${\phi }_{\mathit{Com}}(x)=1-x.$$ (70)

The next step is to investigate the CI values on the half-maximal effect curve which is due to Loewe Additivity Eq. (49) given by the objective function

$$h(x)=x+y=x+\phi (x)$$ (71)

with its specific φ under the constraints x≥0; φ(x) ≥0. In case of the competitive CET we obtain

$$h_{\mathit{Com}}(x)=x+(1-x)=1$$ (72)

which gives the solution CI^Loewe = 1 and optimal concentration pairs are given by

$$(\overline{x},y)=\left(\frac{{\overline{C}}_A}{E{C}_{50A}},\frac{{\overline{C}}_B}{E{C}_{50B}}\right)=(\epsilon ,1-\epsilon ),0\le \epsilon \le 1\mathit{arbitrary}.$$

Greco CET

With Eq. (69) we obtain from Eq. (37) with $E=\frac{E_{\mathit{max}}}{2}$

$$1=x+y+\alpha xy=x+(1+\alpha x)y$$

resulting in

$${\phi }_{\mathit{Greco}}(x)=\frac{1-x}{1+\alpha x},-1\le \alpha \le 1.$$

With Eq. (71) the objective function reads

$$h_{\mathit{Greco}}(x)=x+{\phi }_{\mathit{Greco}}(x)$$

and we calculate

$$h_{\mathit{Greco}}^{\prime }(x)=1+\frac{-(1+\alpha x)-(1-x)\alpha }{{(1+\alpha x)}^2}=1+\frac{-(1+\alpha )}{{(1+\alpha x)}^2}=0$$

if and only if

$${(1+\alpha x)}^2=1+\alpha .$$

This leads to

$$\overline{x}=\frac{{\overline{C}}_A}{E{C}_{50A}}=\frac{\sqrt{1+\alpha }-1}{\alpha },0<|\alpha |\le 1.$$

Using

$${\phi }_{\mathit{Greco}}\left(\frac{\sqrt{1+\alpha }-1}{\alpha }\right)=\frac{\sqrt{1+\alpha }-1}{\alpha }=\frac{{\overline{C}}_B}{E{C}_{50B}}$$

we obtain

$$C{I}^{\mathit{Loewe}}=2\overline{x}=\frac{2}{\alpha }\left(\sqrt{1+\alpha }-1\right),0<|\alpha |\le 1.$$

For α = 0 we have h_Greco(x) = x + φ_Greco(x)=1 which leads to CI^Loewe = 1.

Bliss CET

Using Eq. (33) we obtain

$$\frac{x+y+xy}{1+x+y+xy}=\frac{1}{2}$$

which is equivalent to

$$x+y+xy=1.$$ (73)

This leads to

$${\phi }_{\mathit{Bliss}}(x)=\frac{1-x}{1+x}.$$

According to Eq. (50) and Eq. (73) the objective function reads

$$h_{\mathit{Bliss}}(x)=x+y+xy=1.$$

We obtain the solution

$$(\overline{x},\overline{y})=(\epsilon ,{\phi }_{\mathit{Bliss}}(\epsilon )),0\le \epsilon \le 1$$

with CI^Bliss = 1.

Summation CET

With Eq. (69) and E_maxA = E_maxB = E_max we obtain from Eq. (38)

$$E_{\mathit{max}}\left(\frac{x}{1+x}+\frac{y}{1+y}\right)=\frac{E_{\mathit{maxAB}}}{2}=E_{\mathit{max}}.$$

Rearranging with respect to y

$$x+y+2xy=1+x+y+xy$$

results in

$$y=\frac{1}{x}={\phi }_{\mathit{Sum}}(x).$$

We set with Eq. (50)

$$\begin{array}{l}{h}_{\mathit{Sum}}(x)=x+y+xy=x+{\phi }_{\mathit{Sum}}(x)+x{\phi }_{\mathit{Sum}}(x)\\ =x+\frac{1}{x}+1\end{array}$$

and obtain

$$h_{\mathit{Sum}}^{\prime }(x)=1-\frac{1}{x^2}=0$$

and therefore

$$\overline{x}=1.$$

Hence, we obtain

$${\phi }_{\mathit{Sum}}(1)=1$$

and the optimal pair is

$$(\overline{x},\overline{y})=(1,1)$$

with CI^Bliss = x+y+1=3. Please note that a classification of the area of antagonistic, additive, or synergistic does not hold since the objective functions Eqs. (49), (50) defining the classifications have to be scaled appropriately, if E_maxAB > max{E_maxA, E_maxB}.