Abstract
Epithelia remove excess cells through extrusion, and prevent accumulation of unnecessary or pathological cells. The extrusion process can be triggered by apoptotic signaling1, oncogenic transformation2,3, and overcrowding of cells4–6. Despite the important links of cell extrusion to developmental7, homeostatic5 and pathological processes2,8,9 such as cancer metastasis, its underlying mechanism and connections to the intrinsic mechanics of the epithelium are largely unexplored. Here, we show that apoptotic cell extrusion is provoked by singularities in cell alignments9,10 in the form of comet-like topological defects. We find a universal correlation between the extrusion sites and positions of nematic defects in the cell orientation field in different epithelium types. We model the epithelium as an active nematic liquid crystal and compare numerical simulations to strain rate and stress measurements within cell monolayers. The results confirm the active nematic nature of epithelia for the first time, and demonstrate that defect-induced isotropic stresses are the primary precursor of mechanotransductive responses in cells such as YAP (Yes-associated protein) transcription factor activity11, caspase-3 mediated cell death, and extrusions. Importantly, the defect-driven extrusion mechanism depends on intercellular junctions, since the weakening of cell-cell interactions in α-catenin knockdown (α-catKD) monolayer reduces the defect size and increases both the number of defects and extrusion rates, as also predicted by our model. We further demonstrate the ability to control extrusion hotspots by geometrically inducing defects through microcontact-printing of patterned monolayers. Together we propose a novel mechanism for apoptotic cell extrusion: spontaneously formed topological defects in epithelia govern cell fate. This new finding has important implications in predicting extrusion hotspots and dynamics in vivo, with potential applications to tissue regeneration and metastasis suppression. Moreover, we anticipate that the analogy between the epithelium and active nematic liquid crystals will trigger further investigations of the link between cellular processes and the material properties of epithelia.
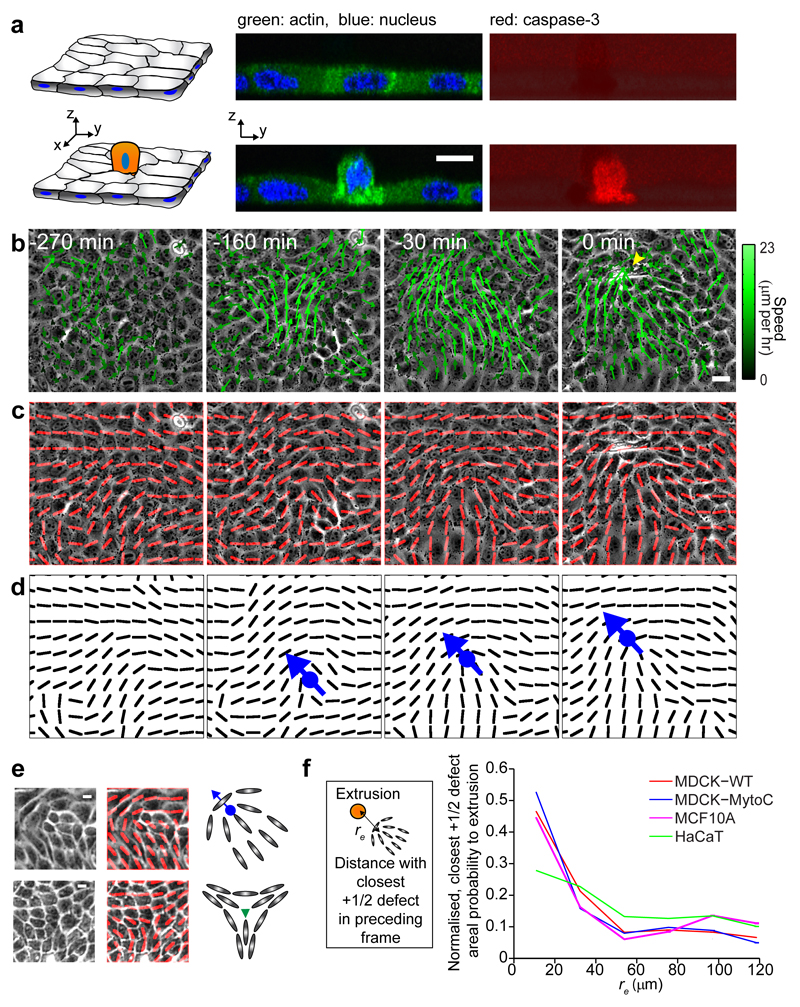
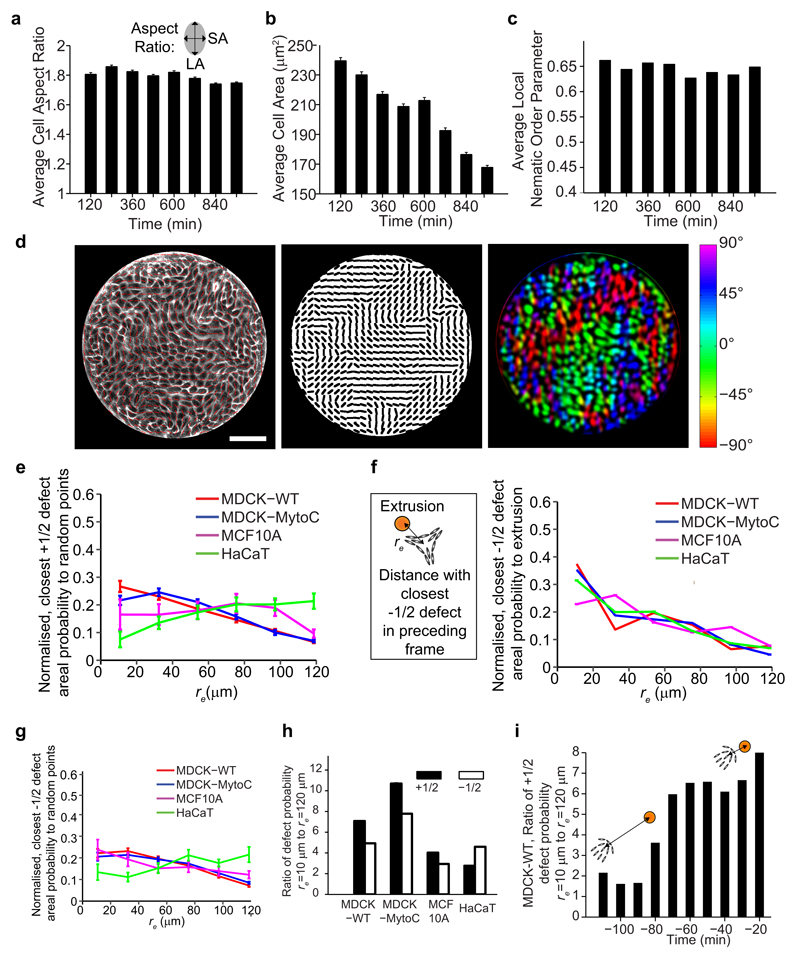
To understand the mechanisms that underlie apoptotic cell extrusion (Fig. 1a), we investigated the relationship between extrusion and epithelial monolayer remodeling. By culturing Madin Darby canine kidney (MDCK) epithelial cells at confluency on micropatterned substrates coated with extra-cellular matrix proteins (see Methods), we observed that extrusion events were preceded by a coordinated, long-range flow of cells toward the eventual location of the extrusion (Fig. 1b: -160 min, Supplementary Movie 1). The group of cells that constituted these flows consistently formed a comet-like shape, with the head portion of the comet pointing toward the cell destined for extrusion (Fig. 1c, d). Since the cells in the monolayer were anisotropic in shape over long periods of time (Extended Data Fig. 1a, b) and demonstrated supracellular orientational order in their alignment (Extended Data Fig. 1c, d), the comet shape can be identified as a singularity in the cellular alignment10,11. Interestingly, the singularity takes the form of a topological defect with +1/2 topological charge, where the orientational ordering is destroyed in a nematic liquid crystal. There are predominantly two types of defects in nematic liquid crystals, i.e. +1/2 and -1/2, and both were identified in the monolayer (Fig. 1e, see Methods)12. Such nematic topological defects have been identified in a wide variety of biological systems including lipid vesicles13, fibroblast cell colonies10,11, suspensions of microtubule bundles14, motility assays of driven filaments15, and growing E. coli colonies16.
Figure 1. Extrusion correlates with singularities in cell orientation (+1/2 defects) in the epithelia.
a, (left) Schematics of confluent monolayer and extruding cell (grey: cell body, blue: nucleus, orange: apoptotic extruding cell). (middle) Side view confocal image of confluent MDCK monolayer and extruding cell (green - actin, blue - nucleus). (right) Corresponding images of activation of caspase-3 signal (red). b, Phase-contrast images showing monolayer dynamics before extrusion (yellow arrowhead) at t = 0 min, overlaid with velocity field vectors. Length of vectors is proportional to their magnitude. c, d, Corresponding images overlaid with red lines (represented as black lines in panel below) showing average local orientation of cells. The group of cells moving toward the extrusion forms comet-like configuration (blue dot: comet core, arrow: comet tail-to-head direction). e, Experimental and schematic images of +1/2 defect (top – comet configuration) and -1/2 defect (bottom – triangle configuration). Red lines denote average cell orientations, blue dot and arrow represent defect core and tail-to-head direction of +1/2 defect. Green triangle represents -1/2 defect core. f, (left) Schematic: determination of correlation between +1/2 defects and extrusions: distance, re of each extrusion to its closest +1/2 defect in the preceding frame is measured, and the number of these defects per unit area as function of re is normalized (right). See Methods. n = 50 (MDCK, WT) extrusions from 4 independent movies in 3 independent experiments, n = 61 (MDCK, mytomycin-c treatment) extrusions from 3 independent movies in 2 independent experiments, n = 85 (MCF10A) extrusions in 2 independent movies, n = 79 (HaCaT) extrusions in 2 independent movies. Scale bars, 10 μm.
Intriguingly, we found that extrusion events were strongly correlated to the positions of a subset of +1/2 defects (and less so to -1/2 defects) (Fig. 1f and Extended Data Fig. 1e-h, see Methods). We further found similar extrusion-defect links in different types of epithelium (Fig. 1f and Extended Data Fig. 1e-h), including a cell-division-inhibited MDCK monolayer, a breast cell line (MCF10a) and a human epithelial skin (HaCaT). In the latter case, we found a correlation between extrusions and defects, but with stronger correlation with -1/2 defects, which may be attributed to the multi-stratified organization of HaCaT cells as well as the HaCaT cell layers being more elastic than the MDCK monolayer17. We then analyzed the temporal correlation between nematic defects and cell extrusions within MDCK epithelial monolayers. It turned out that defects occurred well before cell extrusion and caspase activation (at about 100 min) (Extended Data Fig. 1i) consistent with spatio-temporal cellular flows observed in these regions. It suggests that singularities in cellular alignment are spontaneously generated in the epithelial monolayer in the form of nematic topological defects, and the defects in turn trigger cell apoptosis and extrusion.
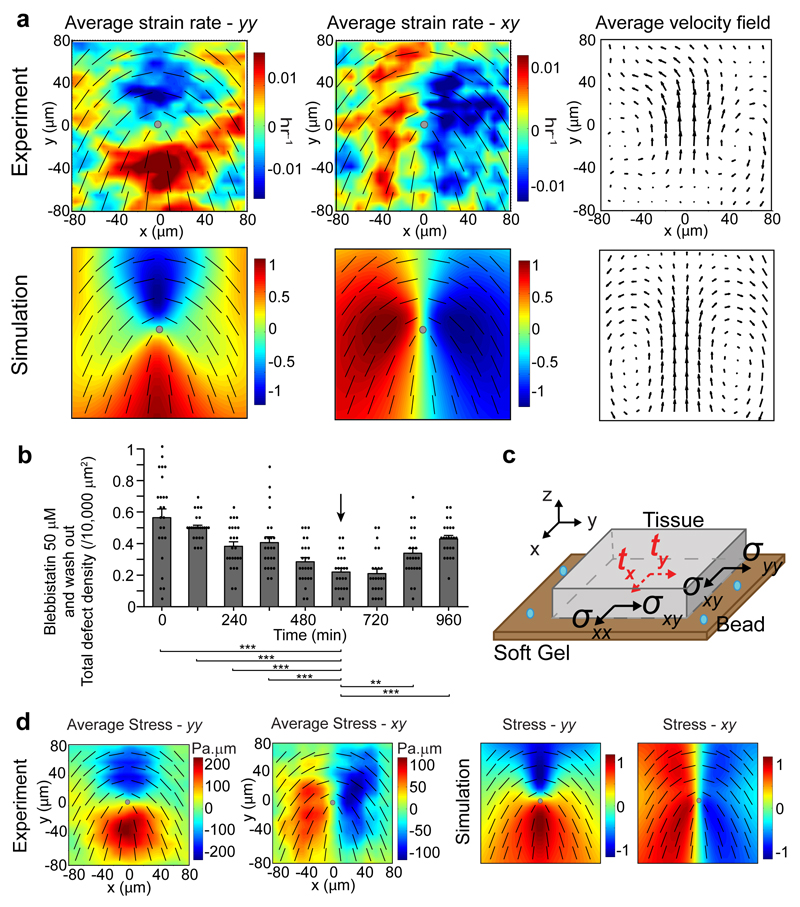
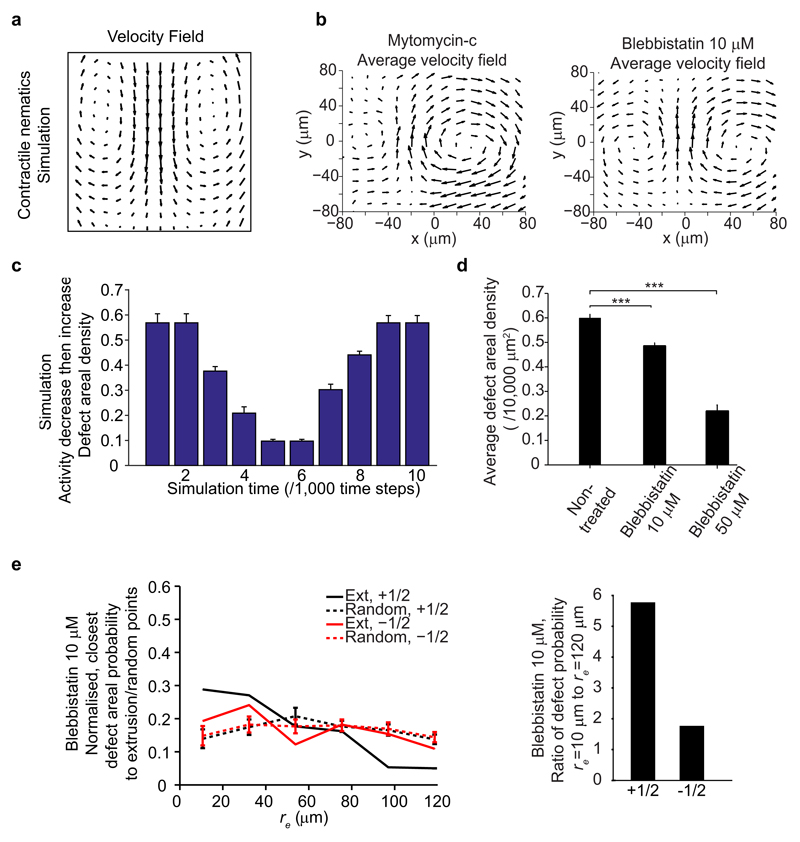
To probe the first part of the hypothesis, we studied the properties of singular points of cellular alignment in wild-type (WT) MDCK to confirm their identification with topological defects in active nematic liquid crystals. We used Particle Image Velocimetry18 (PIV - see Methods) to measure experimentally the velocity and strain rate fields around the singular points in cell alignment (Fig. 2a - Experiment), and compared them to numerical simulations (see Methods) of active nematic liquid crystals (Fig. 2a - Simulation)19. The close match between strain rate patterns and velocity fields around +1/2 topological defects in experiments and simulations (Fig. 2a) revealed that the epithelium monolayer of cells indeed behaves as an extensile, active nematic. The extensile nature is manifest as flow along the elongated axes of the cells that moves toward the head region of the defect (Fig. 2a - average velocity field), in contrast to contractile flow, which is directed toward the tail region (Extended Data Fig. 2a). Previous studies have shown that other active systems exhibited extensile behaviors including reconstituted microtubule bundles14, E. Coli bacteria20, sperm cells21, and cell division induced flow field in an epithelium19,22. We checked that cell division inhibition did not alter the extensile nature of MDCK (Extended Data Fig. 2b, Mytomycin-c). Moreover, active nematic theory predicts that the defect density scales proportionally with the activity of the cells25 (Extended Data Fig. 2c, Supplementary Movie 2). Since active stresses in the cell monolayer originate to a large extent from the acto-myosin activity23, we tested this by introducing blebbistatin treatment. When blebbistatin was added to reduce activity at various concentrations (10 and 50 μM), there was a steady and considerable drop in the defect density with respect to the concentration we used (Extended Data Fig. 2d), and this trend was reversed during the washout phase (Fig. 2b, Supplementary Movie 3). Both the rates of defect density decrease and increase were similar as the defect density dropped to ˜ 33% of its original value in ˜ 10 hrs of blebbistatin treatment, and increased back to ˜ 66% of the original density in ˜ 6 hrs of washout. The blebbistatin treated monolayer maintained an extensile flow field (Extended Data Fig. 2b, Blebbistatin 10 μM). In addition, the extrusion-defect spatial correlation was slightly reduced under blebbistatin treatment, suggesting a stress regulation around the defects through acto-myosin activity (Extended Data Fig. 2e). Altogether, these results confirm that the epithelium is behaving as an active nematic liquid crystal and topological defects are spontaneously formed by active stresses in the monolayer. This is in contrast to a recent finding that fibroblast cells in a packed environment behaved as a non-active, nematic liquid crystal10, where the number of topological defects relaxed to the equilibrium state.
Figure 2. MDCK WT epithelia behaves as a 2D, extensile, active nematic liquid crystal.
a, Average yy- and xy- component of strain rate map around +1/2 defect in experiments and corresponding average velocity flow field (n = 2142 defects from 4 independent movies in 3 independent experiments), compared with simulation of extensile, active nematic liquid crystal. Color code is positive for stretching and negative for shrinkage. b, Time evolution of (total) defect areal density under 50 μM blebbistatin treatment and washout (arrow). Data for each time point is binned over duration of 120 min (n = 6 different time frames), in n = 4 independent movies. t-test for each time point against time = 600 min. Data are represented as mean ± standard error of the mean (s.e.m.). **P < 0.01, ***P < 0.001. c, Schematic of TFM setup to measure traction (tx and ty) and to infer monolayer 2D stress (σxx, σyy and σxy). d, Average yy- and xy- component of stress map around a +1/2 defect in experiments (n = 1339 defects in 2 independent experiments), compared with simulation of extensile, active nematic liquid crystal. Color code is positive for tensile stress and negative for compressive stress. Overlaid black lines in panels show representative nematic directors, grey circle denotes defect core.
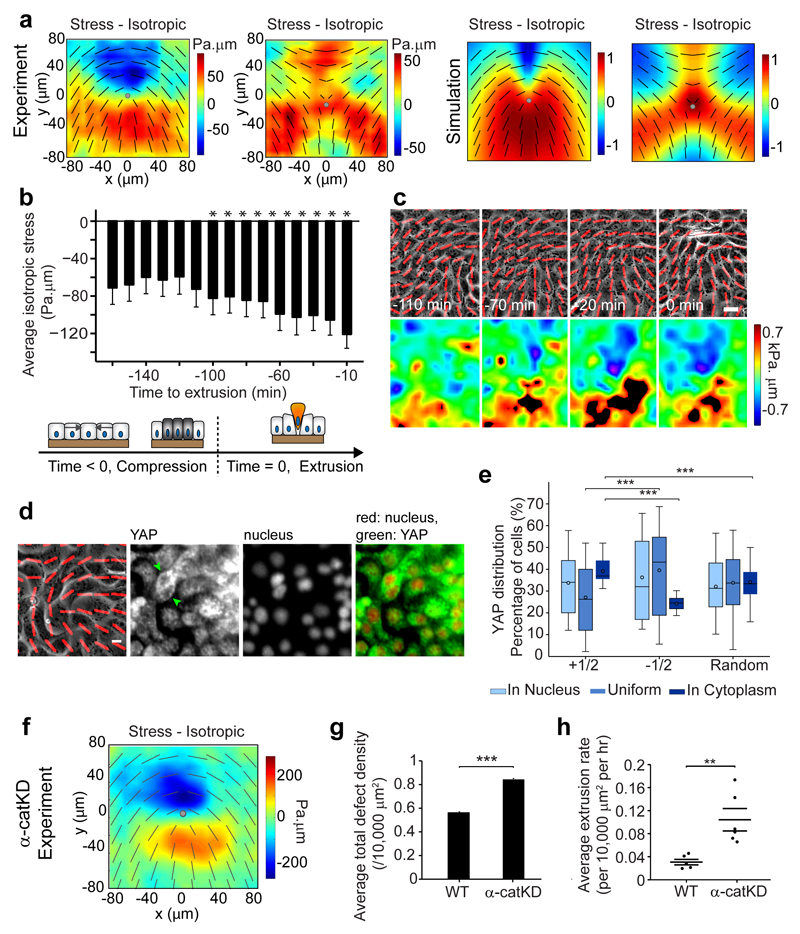
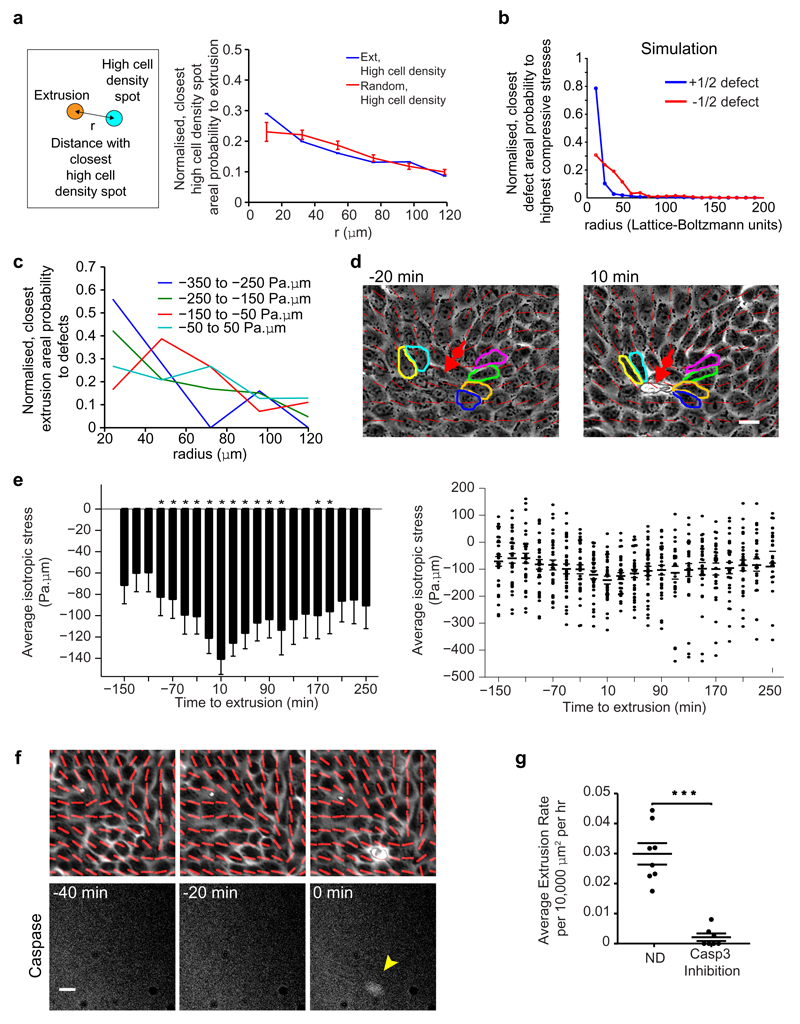
To understand why extrusions were related to defects, we first speculated that defects might generate high, local cell density regions that induced extrusions, as tissue crowding is known to play a role in cell extrusion4–6. However, we did not find a clear spatial correlation between extrusions and the highest local cell density regions (Extended Data Fig. 3a, see Methods). The next clue came from liquid crystal theory12, where the spontaneously formed topological defects are expected to generate mechanical stress in their vicinity, due to high distortions in the cell orientation. We thus hypothesized that +1/2 defects generated spatially localized, elevated compressive stress that is sufficient to provoke cell response, apoptosis and extrusion. This hypothesis is supported by simulations showing that the highest compressive isotropic stresses are strongly correlated with the locations of +1/2 defects and less so to -1/2 defects (Extended Data Fig. 3b), which is reminiscent of the stronger extrusion correlation to +1/2 defects than to -1/2 defects in experiments (Fig. 1f and Extended Data Fig. 1f). To investigate the impact of mechanical stress on cell extrusions, we measured mechanical traction exerted by cells on the underlying substrate with Traction Force Microscopy17 (TFM - see Methods), and converted the traction to two-dimensional stress in the monolayer (Fig. 2c) using Bayesian Inversion Stress Microscopy24 (BISM - see Methods). Consistent with the velocity field results, the stress pattern around +1/2 defects in the experimental measurements is again highly similar to that in extensile nematic simulations (Fig. 2d). To directly prove that cells are more compressed at +1/2 defects, we calculated the isotropic contribution to the monolayer stress measured experimentally around topological defects. The isotropic stress provides a clear distinction between +1/2 and -1/2 defects as it is only highly compressive (negative) at the head portion of a +1/2 defect, while being more tensile at a -1/2 defect (Fig. 3a - Experiment). These distinguishing isotropic stress distributions around the defects are again reflected in the simulations (Fig. 3a - Simulation). We then measured the time evolution of the average isotropic stress for cells that were going to extrude and found that such cells were increasingly being compressed (increasingly negative isotropic stress with time - Fig. 3b) in the time leading up to their extrusion. Notably, the time at which stress started to become more compressive (˜ -110 min) was consistent with the start of the long-range flow and with the rise in the defect-extrusion correlation (Fig. 1b and Extended Data Fig. 1i). These results matched the observation that a +1/2 defect is first created and propagated in the monolayer, and subsequently a cell is extruded at the head region of the defect where the compressive stress is concentrated (Fig. 3c). There was also a higher probability for a defect with higher compressive stress to induce an extrusion (Extended Data Fig. 3c, see Methods). Interestingly, we observed that the +1/2 defects tended to maintain their overall orientation as the neighbor cells elongated to compensate for the extruding cell (Extended Data Fig. 3d), leading to a slow relaxation (˜ 250 min) of the average compressive stress (Extended Data Fig. 3e).
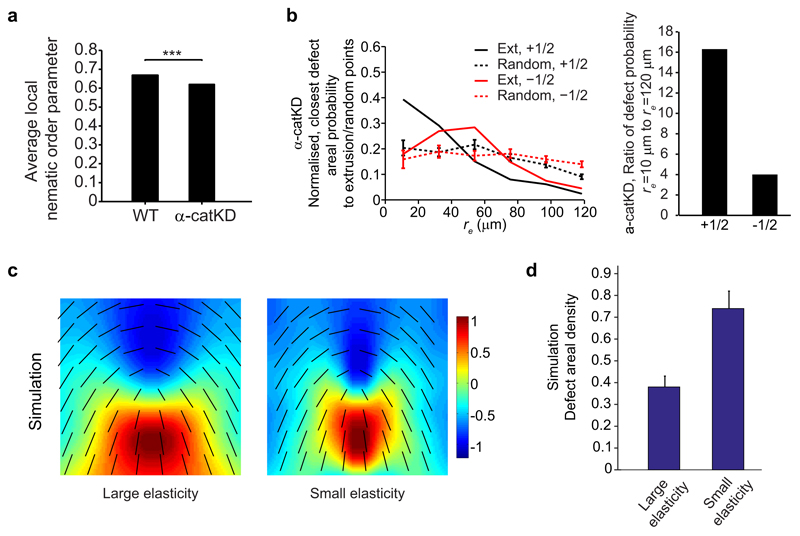
Figure 3. Compressive stresses at +1/2 defects trigger cell extrusion and YAP mechanosensitive response, and can be modulated by cell-cell junction strength.
a, Average isotropic stress around + and -1/2 defect in experiments (n = 1339 (+1/2) defects in 2 independent experiments, n = 2454 (-1/2) defects in 2 independent experiments), and simulations. Color code, positive for tensile state, negative for compression. b, Average isotropic stress around cells to extrude at t = 0 min with negative values (spatially averaged over 65*65 μm2; n = 32 extrusions in 2 independent experiments). t-test for each time point against normal distribution centered at zero. *P < 0.0001. c, Isotropic stress around a +1/2 defect flowing to top left corner of image, and extrusion. d, Nucleus and YAP distribution of cells at a +1/2 defect. Green arrowheads: cells with YAP in cytoplasm. e, Percentage of cells with YAP in nucleus, cytoplasm or uniformly distributed, at either+1/2 defects head, -1/2 defects core or random points. n = 78 (+1/2), n = 77 (-1/2), n = 78 (random) from 17 independent movies in 2 independent experiments. See Methods. Data represented as minimum, first and third quartiles, median, maximum (lines) and mean (circle). ks-test, ***P < 0.001. f, Average isotropic stress around +1/2 defect (α-catKD experiments). n = 1940 defects from 3 independent movies. Similar color code as (a). g, h, Average defect areal density and extrusion rate in WT and α-catKD MDCK. (g) n = 685 frames from 3 independent movies in 2 independent experiments (WT), n = 360 frames from 3 independent movies (α-catKD). Two sample t-test, ***P < 0.001. (h) n = 6 independent movies in 4 independent experiments (WT), n = 6 independent movies in 2 independent experiments (α-catKD). ks-test, **P < 0.01. All data, except (e), represented as mean ± s.e.m. Black lines show representative nematic directors, grey circle denotes defect core. Red lines show local cell orientation. Scale bars, 10 μm.
We then investigated potential mechanotransductive impacts of the stress localization observed at defects, on biochemical signals within the monolayer. To this end, we first checked the YAP transcription factor distribution in cells (see Methods) as YAP is known to respond to compressive mechanical signals25, act as potent inhibitor of apoptosis by translocating between the nucleus and cytoplasm26, and is also implicated in extrusion27. We observed that there were significantly more cells at the head region of +1/2 defects compared to -1/2 defect cores that had YAP sequestered in their cytoplasm (Fig. 3d, e). As YAP is known to translocate to the cytoplasm under compression25 this finding clearly indicates that certain cells at +1/2 defects are subjected to high compressive stress that may lead to YAP inactivation and as such, further confirm cell apoptosis in these regions. We then observed that caspase-3 activation (marker for cell death1) only occurred when there was an extrusion (Extended Data Fig. 3f). Along this line, we found that caspase-3 inhibition largely eliminated the occurrence of extrusions (Extended Data Fig. 3g), even though the defect density was maintained. These results showed that compressive stress localization at defects induced cell death signals which in turn triggered extrusion1.
To further test the contribution of intercellular junctions to this mechanism, we perturbed collective cell movements and intercellular forces by knocking down α-catenin17,18, which is known to be a core mechanosensor of force transmission at cell-cell junctions28. We observed that α-catKD MDCK cells maintained similar levels of orientational order and similar extrusion-defect correlation patterns as WT-MDCK at a similar cell density range (Extended Data Fig. 4a, b, Fig. 1f and Extended Data Fig. 1e-h). However, the defects were smaller in size and had more spatially focused stress patterns compared to WT (Fig. 3a, f, Supplementary Movie 4). From the nematic model the size of the defect core scales as R ˜ √K, where K is the orientational elasticity constant characterizing the resistance of nematic directors to a change in the orientation12 and thus the smaller defect size seen in α-catKD experiments can be interpreted as a reduction in K (Extended Data Fig. 4c). Collective cell bending may be favored in epithelial α-catKD cells where the alteration of the mechanical connection between cell–cell adhesion proteins and the contractile actomyosin cytoskeleton facilitates the relative movements of adjacent cells17,28. More importantly, the nematic theory predicts that the number of topological defects is inversely related to the orientational elasticity (Extended Data Fig. 4d), therefore a reduction in the orientational elasticity is expected to result in a larger number of topological defects. Indeed, experiments showed that there was ˜ 40% increase in the number of defects from WT to α-catKD cells (Fig. 3g), which can explain a marked increase in the extrusion rate in α-catKD cells (Fig. 3h). These results suggest that the weakening of cell-cell junctions in α-catKD cells facilitated collective in-plane bending of multiple cells that decreased K, thus increasing defect formation and extrusion.
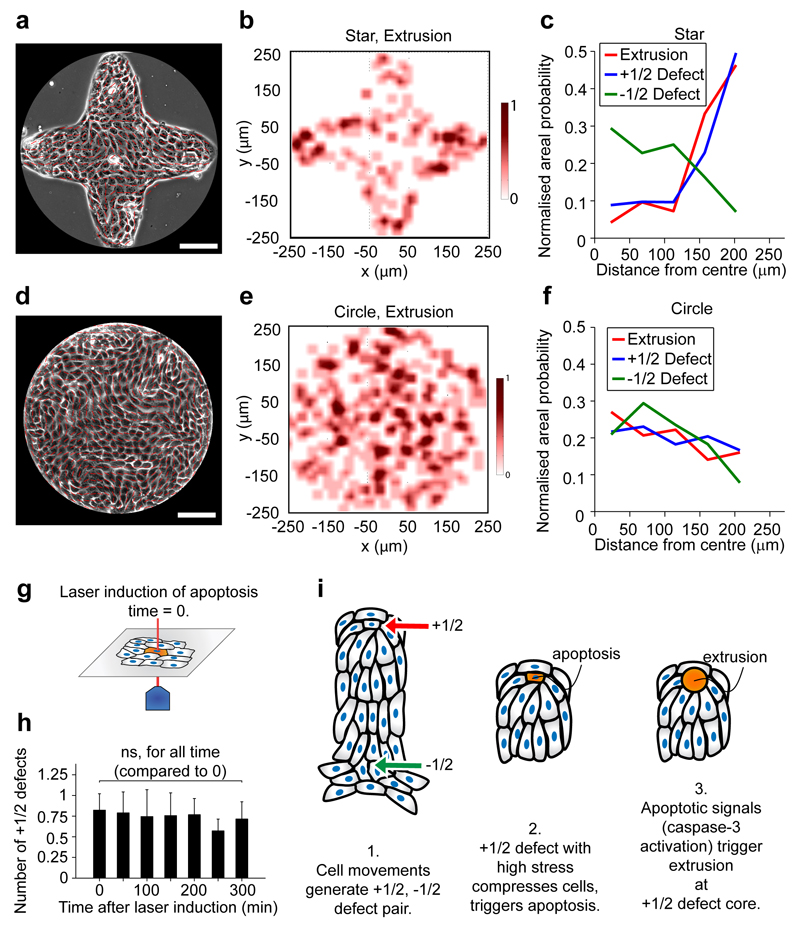
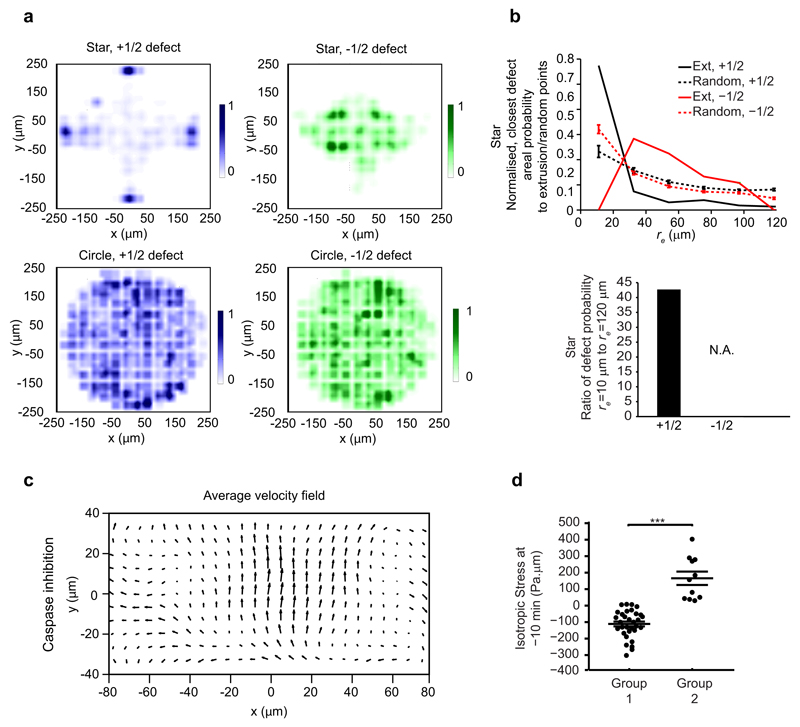
To further prove the causal role of defects for extrusions, we sought to control defect locations in the monolayer29, thus allowing the control of extrusion hotspots. Since MDCK cells preferentially align tangential to the boundary between monolayer-adherent and non-adherent substrates18, we microcontact-printed (see Methods) a star-shaped cell monolayer (Fig. 4a) to geometrically force comet-like defects to the four tips of the star. The length scale of the tip of the star (˜ 100 - 200 μm) was chosen to match the size of the defects. We indeed found that the defect density increased at the corners of the star and that extrusions predominantly happened close to the four tips (Fig. 4b, c and Extended Data Fig. 5a, Supplementary Movie 5). In contrast, the -1/2 defect density became larger near the center of the star, but there was no increase in extrusion events in this region. This biased distribution of extrusions was not found in a circular-shaped monolayer (Fig. 4d - f and Extended Data Fig. 5a). The extrusions were also more correlated with +1/2 defects (more decorrelated with -1/2 defects) in the star than for the circle shaped monolayer (Extended Data Fig. 5b, Fig. 1f and Extended Data Fig. 1e-h). Thus, we demonstrated that extrusions could be controlled by artificially controlling the positions of +1/2 defects in the monolayer.
Figure 4. Topologically induced +1/2 defects can control extrusion hotspots.
a, d, Confluent MDCK monolayer confined on star and circle shape. Scale bar, 100 μm. Red lines show local cell orientation. b, e, Heat map of normalized extrusion number per unit area. c, f, Normalized, average areal density of extrusions, +1/2 defects and -1/2 defects as function of distance from confinement center, rfc. Each point on the curve is averaged over full 360° for each specific range of rfc. n = 145 extrusions, n = 6738 (+1/2) defects and n = 5083 (-1/2) defects from 12 independent movies in 2 independent experiments (star). n = 361 extrusions, n = 5389 (+1/2) defects and n = 4858 (-1/2) defects from 8 independent movies in 3 independent experiments (circle). g, Schematic of laser induction of single cell apoptosis. h, Time evolution of average number of +1/2 defects within radius of 80 μm around laser induced cell apoptosis (laser induction at t = 0 min, n = 9 independent apoptotic induction experiments). ks-test for each time point against t = 0 min, p-values for t = 50 – 300 min are respectively P = 0.86, 0.74, 0.81, 0.75, 0.30, and 0.73. Data represented as mean ± s.e.m. i, Schematic of apoptotic cell extrusion induced by nematic defect.
These findings reinforce the idea that comet-like defects in epithelia can mechanically induce cell apoptosis and extrusions. However, one may ask the reverse question: can apoptotic cells destined for extrusion produce certain biochemical signals that can increase cell activity1,30 and hence generate new local defects to expedite their own extrusion? To challenge this possibility, we first checked defect-related properties in a caspase-3 inhibited monolayer, and found that the defect density was similar to a non-treated monolayer and the flow field patterns at +1/2 defects still showed an extensile flow field albeit having a reduced pattern size (Extended Data Fig. 5c). This suggested that cell death signals did not contribute significantly to the extensile nature and the activity of the epithelium. In another more direct experiment, we used a UV laser to induce a single cell apoptosis7 (see Methods) and followed the time evolution of the number of +1/2 defects immediately afterward (within a radius of 80 μm - Fig. 4g) and up to several hours, until the first extrusion occurred. We did not observe any increase in the average number of defects after the laser induction of cell apoptosis (Fig. 4h), which confirmed that there was minimal influence of the apoptotic signaling on triggering more defects.
Taken together, our results show that as cells collectively move in the epithelial monolayer, topological defects in cell alignments are formed spontaneously. The emergence of +1/2 defects provides hotspots of compressive stress, which lead to a higher probability of cell apoptosis and extrusion (Fig. 4i). This newly identified mechanism appears to be the main pathway that triggers apoptotic extrusion in epithelia, as around 70% of cell extrusion events occurred at compressive stress regions (Extended Data Fig. 5d) that increased in compression as a function of time leading to extrusion (Fig. 3b). Knowledge of this mechanism allows tuning of extrusion hotspots through the control of topological defects in the tissue32. Notably, the magnitude of the compressive stress needed for extrusion is modest (up to 350 Pa.μm or ˜ 35 - 70 Pa taking the typical cell height to be ˜ 5 - 10 μm, Extended Data Fig. 3e) compared to other measured stress values in 2D and 3D epithelium or cell aggregates31–33, suggesting that mechanical activation of apoptosis, extrusions and other mechanosensitive cell activities could be triggered not just in extreme physical environments or niches (e.g. extremely curved substrate surfaces, overcrowding4–6).
We conclude that the epithelial cell monolayer behaves as an active extensile nematic material and spontaneous formation of singularities in cellular alignment in the form of nematic topological defects is a previously unidentified cause of cell apoptosis, suggesting that such defects govern cell fate. Hence, it is anticipated that the defect-induced extrusion mechanism could be a common strategy for preserving homeostasis of a normal epithelium in vivo and for suppressing tumor invasion. It would be interesting to explore how differences in the intrinsic mechanical properties of different epithelia can influence the stress distributions around topological defects and thus alter the influence of defects on apoptosis and extrusion. Another interesting question is to probe the role of topological defects in pathological conditions including oncogenic cell extrusion.
Methods
Part I: Experimental Techniques
Cell culture and reagents
MDCK strain II WT (MDCK-WT) and HaCaT (Cell Lines Service) cells were maintained in a culture medium composed of high glucose DMEM 1X medium (Invitrogen), 100 μg/ml penicillin, 100 μg/ml streptomycin (Invitrogen), and 10% fetal bovine serum (Invitrogen). Culture medium for MDCK with stable GFP-actin and stable α-Catenin knockdown MDCK (α-catKD), kindly gifted by James W. Nelson, Stanford University, was additionally supplemented with 250 μg/ml geneticin (Invitrogen). MCF10a cells were maintained in MEGM (Lonza) medium supplemented with cholera toxin (100 ng/ml). All cells were grown at 37 °C and 5% CO2. For microscopy imaging, DMEM was replaced with low glucose Leibovitz (Sigma-Aldrich). MCF10A imaging was done in its culture medium. To reduce MDCK-WT acto-myosin activity, blebbistatin (Selleckchem) was added at 10 μM for 1 hr before imaging. To observe the defect density temporal evolution as a function of activity, 50 μM blebbistatin was added and then washout after certain amount of time. To inhibit MDCK proliferation, mytomycin-C (Sigma) was added at 10 μg/ml for 1 hr, and rinsed before imaging. For live imaging of fluorescent cell nuclei, the confluent monolayer was incubated with Hoechst at 1 µg/ml for 5 min and rinsed. To monitor cell viability in experiments, caspase-3 indicator NucView (Abcam) was added in the medium at 1:1000 dilution for ˜ 30 min before imaging. Cell apoptosis was inhibited by adding Z-VAD-FMK (Promega) to the medium at 50 μM.
Microscopy imaging
A mature and confluent monolayer was allowed to develop overnight before experiments started. Confluency is reached when all space presented to the epithelium is filled. Typical experiments were run for 1 - 2 days. Phase contrast and fluorescence time-lapse imaging for monolayer on a glass-bottom petri dish, PDMS spin-coated dish, and TFM soft gel were performed using a Biostation (Nikon) or Olympus 1X2-UCB inverted microscope. Confocal time-lapse images were obtained on a Nikon A1R MP laser scanning microscope or Zeiss upright Z2 microscope.
Microcontact printing
Silicon wafers with desired patterns were made using SU-8 photoresist for soft lithography34. To form stamps, PDMS (Sylgard 184, Dow Corning) at 1:10 mixture ratio (curing agent: silicone elastomer) was molded onto silanized wafers and cured at 80 °C for 2 hr. A mixture of 50 μg/ml pure fibronectin (Roche) and 25 μg/ml conjugated fibronectin (Cy5.5 or Atto dye, GE Healthcare and Sigma) was incubated on the stamps for 1 hr and dried before stamping. Patterns were stamped onto a UV-activated, PDMS spin-coated petri dish and the unstamped area was passivated by 1% Pluronics (F127, Sigma) for 1 hr. Samples were rinsed with PBS before cell seeding.
Traction Force Microscopy (TFM)
Soft silicone gel attached with fluorescent beads was used as substrate for TFM so that in-plane cell traction forces on the substrate could be measured35. To prepare the gel with a stiffness of 10 - 20 kPa, CyA and CyB components (Dow Corning) were mixed at 1:1 ratio and spin-coated on a petri-dish to achieve a flat substrate of height ˜ 60 - 100 μm. After curing at 80°C for 2hr, the substrate was silanized with 5% (3-Aminopropyl) trimethoxysilane (Sigma) in ethanol for 5 min. Carboxylated fluorescent beads (100 nm, Invitrogen) were functionalized on the substrate at 1:500 dilution in DI water. The beads were passivated with 1X Tris (Sigma) for 10 min and pure fibronectin (50 μg/ml) was incubated on the substrate for 1 hr prior to cell seeding. Between each step, the samples were rinsed 3 times with 1X PBS. After the experiment, the cells were completely removed by adding SDS, such that the resting state of the gel can be measured. Bead displacements (with respect to its resting state) acquired during experiments were measured and converted to cell traction forces with an ImageJ plugin36.
Cell apoptosis induction
Laser induction of cell apoptosis7 was done on a Nikon A1R MP laser scanning confocal microscope with Nikon Apo 60x/1.40 oil-immersion objective. An ultraviolet laser (355 nm, 300ps pulse duration, 1 kHz repetition rate, PowerChip PNV-0150-100, Teem Photonics) was focused on the nucleus of a target cell for 10 s at a laser power of 25 nW at the back aperture of the objective.
YAP antibody staining
Cells were seeded till confluency in circularly stamped regions and then imaged using 10X phase contrast, before being fixed and stained with YAP. The monolayer was fixed with 4% PFA in 1X PBS for 15 min, then incubated with blocking buffer i.e. 5% horse serum (GIBCO) and 0.3% Triton X-100 in 1X PBS for 1 hr. To stain for YAP localization, the sample was first incubated with a YAP antibody (1:500) kindly gifted by Marius Sudol (MBI, Singapore) for 1 hr then incubated with a secondary antibody (1:1000, Goat anti-Rabbit IgG (H+L), Alexa Fluor 568, Invitrogen) for 30 min, both diluted in the blocking buffer. Between each step, the samples were rinsed 3 times with 1X PBS.
Part II: Image Analysis
Cell extrusion and apoptosis determination
The typical geometry of an extruded cell as a protrusion out of the relatively flat epithelial monolayer allowed simple and clear detection of the extrusion under phase contrast or bright field imaging (the extrusion appears as a bright spot). In fluorescence microscopy, extrusion is marked by the disappearance of the nucleus. The first frame where the extruding cell started to adopt a distinct morphology from its neighbor cells was defined as the time of initiation of extrusion. All extruding cells checked for viability displayed clear caspase-3 activation simultaneously with the initiation of extrusion, showing that the extrusions were apoptotic extrusions (Fig. 1c).
Automated nematic characterization of experimental images
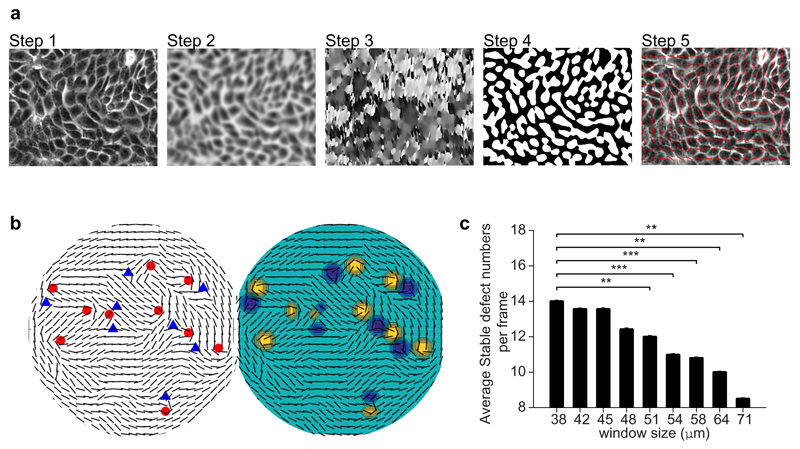
To obtain the nematic director field in an epithelium, a clear epithelial monolayer image (which can be phase contrast or fluorescence image) was obtained, with individual cell boundaries visible (Extended Data Fig. 6a, Step 1). The image was smoothed using Bandpass Filter in ImageJ to remove unnecessary details (Extended Data Fig. 6a, Step 2). The filter size of small structures was set to roughly one-third the size of a single cell. The ImageJ plugin, OrientationJ was used to detect the direction of largest eigenvector of the structure tensor of the image37 for each pixel (for window size of roughly one quarter of size of single cell), outputted as gray-values from -90° to +90° (Extended Data Fig. 6a, Step 3). The local nematic order parameter tensor, Q12 was calculated (the nematic window size averages over pixel directions in a fixed-size region that contained 3 - 5 cells) for each point on a grid that discretized the image, using an in-house Matlab code. The grid distance was 75% of the nematic window size. Only pixels that resided in the region of the cell body were taken into account for this calculation (white regions obtained by Auto Local Threshold function in ImageJ, Extended Data Fig. 6a, Step4) as cell boundary regions could have orientations that are perpendicular to the cell body. The largest eigenvector of Q was taken to be the local orientation of 3 - 5 cells, and plotted (red lines) over the original image for inspection (Extended Data Fig. 6a, Step 5). Once the nematic director field was established, automatic nematic defect detection was done based on calculation of winding number38. Only two types of defects (+1/2 and -1/2) were predominantly found. To reduce false positives, only stably detected defects (i.e. defects found in at least two consecutive frames at the same location) were considered for further analysis. See below for detailed discussion regarding the robustness and optimality of this method, with respect to small variations to the chosen algorithm parameters. To determine a measure for the global ordering of the epithelium, the order parameter, S12 (Extended Data Fig. 1c) for all local regions (which can incorporate ˜ 16 nematic directors each) throughout the epithelium was averaged.
Cell Aspect Ratio, area and density calculation
The outline of cells in typical phase contrast images was tracked in MATLAB using Fogbank software39. The cell outline for several images were manually traced to verify the results. These outlines were fitted with ellipses using ImageJ and the aspect ratio taken as the ratio of the long axis to the short axis. The area of these outlines and the number of cells were also calculated.
Particle Image Velocimetry (PIV)
The velocity field in 10X, phase contrast epithelium time-lapse images was obtained using an open source MATLAB code (PIVlab40), with three-passes (64*64, 32*32, and 16*16 pixel size interrogation window with 50% overlap each). The interrogation window sizes were scaled accordingly for higher magnification images.
YAP spatial localization in the cells at +1/2 and -1/2 defects
Using an in-house ImageJ script, the nucleus-to-cytoplasmic YAP intensity ratio (NCYap-ratio) of cells in the monolayer was measured, where cells were classified as having YAP in the nucleus (NCYap-ratio > Min_threshold), in the cytoplasm (NCYap-ratio < Max_threshold) or uniformly distributed across the whole cell (other cells not falling in the other two categories). Parameter values were varied with a combination of pairs of Min_threshold ∈ (1.02, 1.05, 1.1, 1.15, 1.2) and Max_threshold ∈ (0.95, 0.96, 0.97, 0.98, 0.99) and were all considered for the statistics. The corresponding phase contrast movie taken earlier for each circular shaped, fixed monolayer was used for identification of the defects. Cells falling in a circular ROI of radius, r ˜ 10 μm centred at the head region of +1/2 defects, ˜ 22 - 25 μm away from the +1/2 defect cores, were considered as cells at +1/2 defects, while cells falling in an ROI (r ˜ 10 μm) centred at the -1/2 defect cores were considered as cells at -1/2 defects. For comparison, cells at randomly generated points were considered. For each pair of Min_threshold and Max_threshold values, the percentage of cells having YAP in the nucleus, in the cytoplasm and uniformly distributed were calculated.
Part III: Calculation of physical quantities
Local cell density was calculated as the number of cells divided by area in a square area of side length ˜ 50 μm, centred on points on a grid that discretized the entire monolayer. High local cell density spots were defined as the grid points with the highest density value in each time frame.
Extrusion correlation to defects and temporal evolution
If extrusions correlated with defects spatially, there would be a high probability of finding a defect close to an extrusion. To quantify this, the distance, re for each extrusion with its closest defect in the preceding frame was determined. The number of closest defects (+1/2 or -1/2 done separately) within a given distance range to their corresponding extrusions was converted into the areal probability of the defects at the specific distance, and the areal probabilities were normalized such that they sum to 1 (to facilitate comparison between different experimental conditions). A similar closest defect areal probability as a function of distance was also obtained for random points for comparison. For each extrusion, a random point was generated in the same frame as the extrusion, but at a random location (uniformly spaced in the monolayer). For the closest defect probability curve with random points, n = 30 (different sets of random points). A defect probability curve which shows a higher spatial correlation between extrusion and defect has larger positive values at re close to 0 μm. The ratio of the defect probability at re = 10 μm (closest region to extrusions, between re = 0 - 20 μm) to re = 120 μm (furthest point, between re = 110 - 130 μm) is calculated as a measure of the strength of the extrusion-defect correlation. For example, since this ratio for the +1/2 MDCK-WT case is ˜ 7 (Extended Data Fig. 1h), this tells us that there is ˜ 7-fold higher probability to find the closest defect for an extrusion situated at ˜ 10 μm compared to ˜ 120 μm from it. To quantify when the corresponding defects start to spatially approach the extrusions, this defect probability ratio is calculated as a function of time (t < 0 min) leading to extrusion at t = 0 min, comparing at each time frame between the defects in this frame and the eventual extrusion spots at t = 0 min.
Strain rate and stress measurements
Strain rate was calculated using the formula , Eij = (∂iuj + ∂jui)/2, with i, j ∈ (x, y) and velocity field, ui obtained from PIV measurements. Stress was estimated from traction force data by inversing the force balance equation24. This underdetermined problem was solved by Bayesian inversion from the BISM method, independently of the epithelial rheology (see Methods for details). The stress estimate was defined as the mode of the posterior stress pdf (maximal a posteriori estimate, see below for details). Isotropic stress was taken as half the trace of the stress tensor, (σxx + σyy)/2 in the tissue. Average strain rate and stress maps for the defects were calculated by rotating and aligning the defects to the y-axis at the origin, and averaging the values of the rotated vectors and matrices (in their new basis) for the corresponding pixel locations in all defects. Smoothing was done by linear interpolation of maps.
+1/2 defect stress magnitude as indicator of the ability of defect to induce extrusion
For each +1/2 defect, the distance to the closest extrusion within the next 40 min after the time of the defect was determined. These distances were pooled into groups based on the values of the compressive isotropic stress at the head regions (area of 60*60 μm2) of their corresponding defect. The number of extrusions within a given distance range was converted into the areal density of the defects at the specific distance, and the areal densities were normalized such that they sum to 1. The peak in each areal density curve increases near r = 0 μm, as the compressive stress categorizing the group increases. This shows that as the defect compressive stress magnitude increases, the probability for the defect to induce an extrusion increases.
Part IV: Simulations, models and robustness studies of techniques
Robustness of the nematic director and defect detection method
To verify the effectiveness of the winding angle approach in detecting half-integer topological defects, a different algorithm based on diffusive topological charge16,41 to detect the defects was used and compared to the original approach. The results were found to be identical in both cases. Extended Data Fig. 6b shows an example of topological defects detected using the winding angle approach and diffusive charge approach.
In addition, errors could occur in the identification of the nematic director field from the pattern of cells in the images, rather than in identifying the defects from the director field. As a check, we have performed a systematic variation of the relevant parameters in the orientation analysis and confirmed the robustness of our approach against small variations in the parameter values. Extended Data Fig. 6c shows the effect of varying the coarse-graining window size (for each nematic director, we average over the orientation of the cells within the corresponding window) on the number of topological defects detected. To reduce the number of false defects detected:
Each nematic director represents the average orientation of 3-5 cells within the window (window size of ˜ 50 μm. This reduces the possible errors due to fluctuations in the orientation of each cell.
Only the stably detected defects were kept (defects that appear in at least 2 consecutive frames).
The final window size was chosen as ˜ 51 μm (80 pix) (after checking a range of 60 – 110 pix). The minimum window size checked was ˜ 38 μm (60 pix), corresponding to 2-4 cells, which clearly showed “noise defects” detected. The maximum window size checked was ˜ 71 μm (110 pix), which was too big so that the orientation field was too smooth and certain clear defects were clearly missed out. 51 μm was chosen as a compromise between these values (Extended Data Fig. 6c).
Active nematic model for epithelial monolayer
Individual cells in a confluent epithelial monolayer have an in-plane anisotropic shape, which can be approximated by an ellipse, and are constantly moving in the epithelium, corresponding to a non-zero velocity field. Cell alignments show local orientational order of the cells. The orientational order is destroyed at singular points called topological defects. The strength of a defect is determined by the change in the orientations of cells in a closed curve around the defect core. Integer (±1) and half integer (±1/2) topological defects correspond to ±2π and ±π rotation of the cell alignment along a closed curve around a singular point12. The strength of topological defects in cell alignment is an important determinant of the type of orientational order of cells with ±1 specific to polar and ±1/2 specific to nematic materials respectively. Therefore, the emergence of ±1/2 defects in the experiments indicates that despite their individual polarity, MDCK cells behave as nematic materials (the orientation vector is ‘head-tail’ symmetric) at the level of the epithelium.
In order to capture the dynamics of cell motion and orientation we use a continuum model of nemato-hydrodynamics for the monolayer42,43 to account for the combined effects of cell velocity and orientation. This nematohydrodynamic approach has proven successful in describing active systems19,44–47. The orientational order of cells is characterized by the nematic tensor Q = 3S(nn – I/3)/2, valid for a 3D or quasi-2D simulation used here, where n is the cell orientation, S is the magnitude of the order and I is the identity matrix. The nematic tensor is evolved according to the Beris-Edwards equation48:
| (S1) |
where (∂t + uk∂k) is the total derivative with u denoting the velocity field and
| (S2) |
is the co-rotation term accounting for the response of cell orientation to the velocity gradients. Here, velocity gradients are characterized by the strain rate tensor Eij = (∂iuj + ∂jui)/2 and the vorticity tensor, Ωij = (∂iuj - ∂jui)/2, corresponding to extensional and rotational flows, respectively. The relative strength of extensional and rotational flows is determined by the alignment parameter λ. Therefore, the alignment parameter accounts for the different responses of particles of different shapes to the symmetric and asymmetric parts of the velocity gradient tensor49. Mapping the alignment parameter to the Leslie-Ericksen equation for liquid crystal dynamics gives 48,50, where β = a/b is the ratio of the length of the cell along its axis of symmetry, a to its length perpendicular to this axis, b. Therefore, for prolate ellipsoids β > 1, while for oblate ellipsoids β < 1 and for spherical particles β = 1, which correspond to λ > 0, λ < 0, and λ = 0, respectively. The experiments show that MDCK cells exhibit an in-plane anisotropic shape in the form of prolate ellipses and therefore are characterized by λ > 0. The molecular field in Eq. (S1),
| (S3) |
describes the relaxation of the orientational order to the minimum of the free energy F = Fb + Fel. The bulk free energy Fb is calculated from the Landau-De Gennes expansion,
| (S4) |
where AQ, BQ and CQ are material constants. In addition, the free energy corresponding to spatial inhomogeneities in the orientation field is described by the Oseen-Frank expansion using a single elastic constant approximation12,
| (S5) |
where K is the elastic constant. There are in general two elastic constants corresponding to bend, Kb and splay, Ks in 2D systems. However, setting different values of Kb and Ks, gives only small qualitative changes in the flow fields around topological defects in the simulations as these are predominantly controlled by active stresses (introduced below).
The velocity field in the monolayer is evolved according to the incompressible Navier-Stokes equation:
| (S6) |
| (S7) |
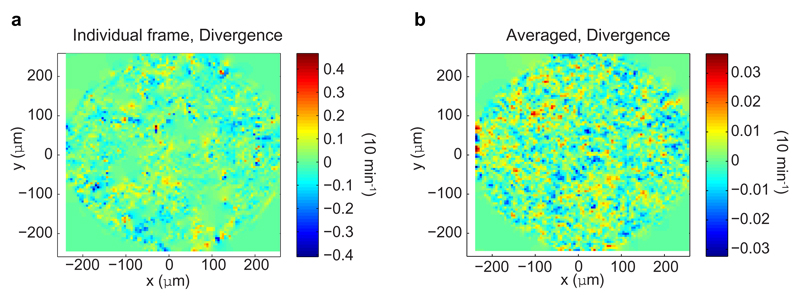
which reduces to the force balance equation ∂jσij = 0 in the low Reynolds number limit relevant to monolayer mechanics. The assumption of an incompressible monolayer in Eq. (S6) is supported by experimental measurements of the divergence of the flow field in the epithelium. Although, divergence hotspots (larger values) do arise at singular points in the epithelium, the temporal average of this divergence field shows only small deviations from zero (< 4% every 10 min, Extended Data Fig. 7a).
Equation (S7) describes how the rate of change of linear momentum is driven by stress gradients in the monolayer. The total stress, σ consists of four contributions: isotropic pressure, -Pδij, viscous stress, nematic elastic stress, and active stress, The elastic stress,
| (S8) |
corresponds to distortions in cell alignments. Finally, the active stress,
| (S9) |
accounts for the local stresses generated by active processes in the cells including acto-myosin polymerization and cell contractility22,46,51–53. The activity coefficient, ζ determines the strength of the activity with positive and negative values for extensile and contractile stresses. The extensile stress corresponds to the flow generated by the cell activity outwards along the elongated axis of the cell, while contractile stress characterizes the flow outwards along its shorter axis. The measurements of strain rates around defects in the experiments and comparison with the simulations show that the cells produce extensile stresses in the epithelium and that the epithelium behaves as an extensile active nematic.
Within this framework, the isotropic contribution to the total stress reduces to just the pressure and an isotropic contribution from the nematic elastic stress, as the trace of is zero because Qij is traceless and the trace of is also zero due to the incompressibility condition Eq. (S6). Thus, the specific spatial patterns of the isotropic part of the total stress in the simulations are determined only by the elastic stress.
The hybrid Lattice Boltzmann algorithm is used to solve the equations of motion (S1, S6 and S7). Details of the algorithm can be found in44,54,55. The simulation parameters used are Γ = 0.34, AQ = 0.0, BQ = -0.3, CQ = 0.3, K = 0.08, ζ = 0.006, λ = 0.7 and η = 2/3, in lattice units, unless otherwise is stated.
Bayesian Inversion Stress Microscopy (BISM)
According to Newton’s Laws, the stress in a cell monolayer is balanced by the traction forces the monolayer exerts on its substrate everywhere in space and time. In 2D and neglecting inertia, the force balance reads,
| (S10) |
where σ is the stress tensor field (units Pa.μm in 2D) and is the 2D in-plane cell-substrate traction force field. In Cartesian component form, the equations
| (S11a) |
| (S11b) |
can be discretized on a square grid of spatial resolution l and rewritten in a matrix format,
| (S12) |
where the vectors and respectively consist of all stress and traction components over the whole of space (see24 for the exact forms of A, and ). Since is readily measured by Traction Force Microscopy (TFM), the stress components could be determined by inverting the matrix A. However, the equation is underdetermined as σ has three components (σxx, σyy, σxy) at each space position, while has only two components (tx and ty), and thus cannot be solved for even if is fully known. Bayesian inference provides a statistical framework for the integration of current data, prior knowledge and reasonable assumptions about the system to extract information (in the form of a probabilistic distribution) from such ill-conditioned situations56,57. Two distributions i.e. the likelihood function, and prior density, need to be constructed to calculate the desired output distribution that describes σ. accounts for the physical relation between measured data, and through (S10) up to an additive noise. Assuming the noise has a Gaussian profile with zero mean, the likelihood can be written as,
| (S13) |
where s2, the variance of the noise, allows the definition of a diagonal covariance matrix S = s2I, with I the identity matrix. accounts for any additional constraints and assumptions on the stress components. Specifically, the off-diagonal components of the stress are enforced to be equal, i.e. (with an extra hyperparameter α) and stress is also assumed to be Gaussian with zero mean and covariance The prior is written as,
| (S14) |
with the covariance matrix of the prior, embedding the two quadratic terms in B.
Bayes’ theorem links the posterior distribution on (conditional probability of given data and assumptions), with and by a product rule,
| (S15) |
Since the likelihood and prior are both Gaussian, is also Gaussian with covariance matrix SΠ and mean written as,
| (S16) |
And
| (S17) |
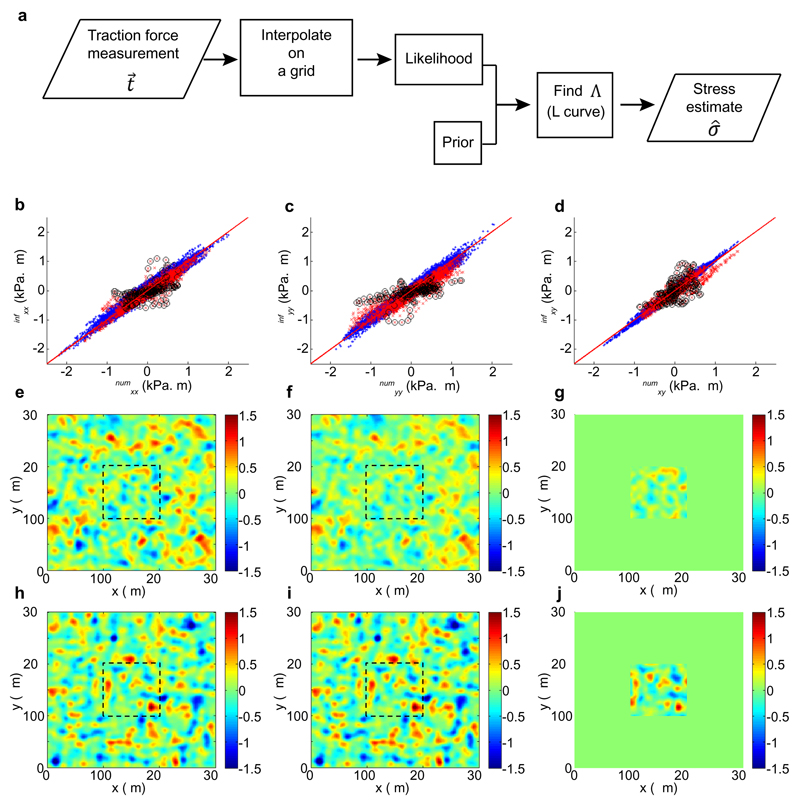
where At is transpose of is the inference of monolayer stress that we need. Recall that whereas actual stress, cannot be obtained (because the matrix A itself cannot be inverted), can be readily calculated since the inversion of is possible. The Maximum A-Posteriori (MAP) solution to the inference problem is the posterior mode, identical to the mean for a Gaussian: (see Extended Data Fig. 8a for a schematic of the BISM algorithm). The solution depends on the dimensionless parameter which is found using the L-curve method58. Note that error bars on the inferred stress are provided by the posterior covariance if needed.
In this paper, the hyperparameter α is fixed to a value (103) large enough to enforce the equality of off-diagonal components of the stress tensor. With a spatial resolution l = 5.12 μm, the L-curve method yields a value of Λ = 10-6 that we use for all stress inferences.
Robustness study: Validation of BISM with unknown boundary conditions
BISM has been validated primarily for confined systems where the boundary conditions are known (free boundary conditions where is the vector normal to the boundary)24, but not yet in the case of unknown boundary conditions (applicable for our current study as explained below). For the former case, the boundary conditions are incorporated in the prior, with a supplementary term (compare with S14):
| (S18) |
with a modified covariance matrix where the three quadratic terms are embedded in BBC. The inferred stress is then obtained from (S16-17) using SBC instead of S0. BISM has been validated using numerical simulations that yield stress and traction force data sets, as well as using experimental data in a quasi-1D geometry24. In particular, we showed that the absolute value of the stress could be inferred in confined systems. Further, the robustness of the method for different likelihood and prior distribution functions has also been tested. In particular, we checked that a non-Gaussian prior, a non-Gaussian likelihood, or a smoothness prior all lead to the same level of accuracy as the Gaussian model presented here.
Since the focus in this paper is on extrusions and defects occurring in the bulk of the monolayer, we needed to perform stress inference away from physical boundaries, without knowledge of the correct boundary conditions applying to the epithelium patch that surrounds the extrusion. We now present an additional numerical validation for this case. Briefly, we used BISM on a larger and confined area using free boundary conditions in the prior (S18), and compared the stress thus inferred in a smaller, central region to that obtained without imposing the boundary conditions in the prior (S14), see Extended Data Fig. 8b-j. Good agreement between the two inferences showed that, except in the vicinity of the boundaries, BISM infers the absolute value of the stress also in the case where the boundary conditions are unknown.
Following previous work, we used a simplified, viscous rheology, neglecting orientational degrees of freedom, with the constitutive equation
| (S19) |
and drove the fluid layer with active moving force dipoles. Including a dissipative interaction with the substrate through an effective fluid friction force, the traction force reads:
| (S20) |
The active force derives from the sum of nd force dipoles, with a density of 10-2 dipoles per μm2, such that for each dipole is defined as:
| (S21) |
with deviatoric angular matrices and amplitudes kPa.μm, kPa.μm for the trace and deviator (numerical values taken from experiments59). The dipole positions and orientations ϑn are random variables uniformly distributed over the spatial domain and [0, 2π] respectively. The delta functions are implemented as finite-size Gaussian distributions, with a spatial extension 2d = 10 μm of the order of a typical cell size. We chose material parameter values typical for cell monolayers60–62: friction coefficient ξu = 100 kPa.μm-1.s, shear viscosity η = 103 kPa.μm.s and compression viscosity η′ = η.
With the finite element software FreeFem++63, we solved the equations (S10–S19–S20) for on a 300×300 μm2 square with boundary conditions The stress σnum (Extended Data Fig. 8e, h) and traction force fields are derived from the velocity field and sampled over a regular cartesian grid of spatial resolution l = 2 μm, giving N = 50 points for 100 μm. To account for the measurement error, we add a white noise to the traction force field with an amplitude sexp equal to 5% of the maximum traction force amplitude. We apply our algorithm to these numerical traction forces in two cases:
-
-
whole monolayer of area 300×300 μm2 with zero stress boundary conditions and prior (S18). We obtain the stress σwhole with 3N×3N values for each component (Extended Data Fig. 8f, i).
-
-
central part of the monolayer of area 100×100 μm2: without boundary conditions and prior (S14). We obtain the stress σcentral with N×N values for each component (Extended Data Fig. 8g, j).
We compare the outcomes of two inferences with the exact stress field σnum, and find excellent agreement between σnum and both σwhole (blue dots) and σcentral (red dots – Extended Data Fig. 8b-d). Note that the inference is less accurate close to the border of the central part (black circles), yet allows obtaining the correct absolute values of the stress in the bulk of the central domain with an accuracy equivalent to that of the whole system inversion.
Statistical analysis
No statistical methods were used to predetermine sample size. The sample size was chosen to see a statistical difference between data sets. In case where no differences were observed, the sample size chosen was at least as big as those where differences were observed. Blinding was achieved when comparing results between experimental analysis, active nematic numerical simulations and Bayesian stress inference as these are done independently in three different institutes. All experimental data were tested with the Anderson-Darling test to check for normality of the distribution. In case when comparing data which were normally distributed and have similar variance, two-sided t-test was used. Otherwise, the non-parametric Kolmogorov-Smirnov test (ks-test) was used. Throughout, *P < 0.05, **P < 0.01, ***P < 0.001, apart for data in Fig. 3b and Extended Data Fig. 3e, where *P < 0.0001. All relevant statistics are reported in the corresponding legends.
Data and code availability
Source data and codes for cell orientation detection, active nematic simulations and bayesian inference of tissue stress are available upon request.
Extended Data
Extended Data Figure 1. Further characterization of cell, monolayer and extrusion-defect correlation properties.
a, b, Time evolution of cell aspect ratio and cell area in a confluent MDCK epithelium. Data for each time point is binned over a duration of 120 min. From lowest to highest time points, n = 5101, 5537, 5772, 6549, 6572, 6876, 6593 and 6831 cells. c, Time evolution of nematic measure (averaged local order parameter, S) of corresponding epithelium (see Methods), n = 294 data points for each bar. d, MDCK monolayer in circular confinement (left). Red lines (represented again as black lines in middle) show local cell orientation, colour coded in right. Scale bar, 100 μm. e, Normalized, number of closest +1/2 defects per unit area as function of re against random points in monolayer. n = 30 different random point sets. See Methods. f, Schematic: determination of correlation between -1/2 defects and extrusions: distance, re of each extrusion to its closest -1/2 defect in preceding frame is measured, and the number of these defects per unit area as function of re is normalized (right). See Methods. n = 50 (MDCK, WT) extrusions from 4 independent movies in 3 independent experiments, n = 61 (MDCK, mytomycin-c) extrusions from 3 independent movies in 2 independent experiments, n = 85 (MCF10A) extrusions in 2 independent movies, n = 79 (HaCaT) extrusions in 2 independent movies. g, Similar plot as (e), but between random points and -1/2 defects. h, Ratio of closest defect density against extrusion points at re = 10 μm to re = 120 μm (first and last points in respective density curves). i, Ratio of the closest +1/2 defect density against eventual extrusion points, at re = 10 μm to re = 120 μm, as function of +1/2 defect distributions at each time point (WT-MDCK). All data represented as mean ± s.e.m.
Extended Data Figure 2. Further examination of the active nematic properties and the extrusion correlation to defects in the epithelium under different conditions.
a, Velocity field around +1/2 defect in contractile, active nematic liquid crystal simulation. b, Average velocity field around +1/2 defect for mytomycin-c and blebbistatin treated MDCK. n = 2003 (mytomycin-c) defects from 3 independent movies in 2 independent experiments, n = 3061 (blebbistatin) defects from 3 independent movies. +1/2 defect has same orientation and position as in Fig. 2a. c, Total defect areal density evolution in simulation, activity parameter decreased at simulation time t = 0, then increased at t = 5. d, Average total defect density for WT-MDCK and blebbistatin (10 μM and 50 μM) treated MDCK. n = 314 frames from 4 independent movies in 3 independent experiments (WT), n = 155 frames from 3 independent movies (blebbistatin 10 μM), n = 26 frames from 4 independent movies (blebbistatin, 50 μM). t-test, ***P < 0.001. e, (left) Normalized, number of closest + and -1/2 defects per unit area as function of distance, re against extrusion and random points in 10 μM blebbistatin treated monolayer. n = 78 extrusions in 3 independent movies. n = 30 different random point sets. (right) Ratio of closest defect density against extrusion points at re = 10 μm to re = 120 μm. All data represented as mean ± s.e.m.
Extended Data Figure 3. Further investigation of the relation between local cell density, compressive stress, defects and extrusions, and the role of caspase-3 activation.
a, Normalized, number of closest high cell density spots per unit area as function of radius, r against extrusions or random points in monolayer. n = 50 (MDCK, WT) extrusions from 4 independent movies in 3 independent experiments. n = 30 different random point sets. b, Normalized, number of closest defects per unit area as function of distance, re against spots with top 5% of all compressive stresses in simulation domain. See Methods for calculation of simulation stress. c, Normalized, number of closest extrusions per unit area as a function of distance against +1/2 defects, grouped by magnitude of compressive stress at head regions of defects. Extrusions are within 40 min after the frame of defect. From lowest (least negative) to highest compressive isotropic stress (most negative), n = 331, 215, 180 and 72 defects in 2 independent experiments. d, Typical example of extrusion event, showing configuration of +1/2 defect before and after extrusion. The same neighbor cell before (t < 0 min) and after (t > 0 min) extrusion is outlined with same color. e, (left) Same data as Fig. 3b, evolution of average isotropic stress around cells to extrude at t = 0 min with negative values, before and after extrusion (n = 32 extrusions in 2 independent experiments). t-test for each time point against normal distribution centred at zero, *P < 0.0001. (right) Scatter plot of same data. f, Typical example of extrusion event with caspase-3 activation (yellow arrowhead) (t = 0 min). Red lines show local cell orientation. g, Average extrusion rate in non-drug-treated (ND) and caspase-3 inhibited MDCK. n = 8 (ND) independent movies in 3 independent experiments, n = 7 (caspase-3 inhibited) independent movies in 2 independent experiments. ks-test, ***P < 0.001. All data represented as mean ± s.e.m.
Extended Data Figure 4. Order parameter and extrusion-defect correlation for α-catKD MDCK, and simulations comparing small and large nematic bending elasiticity.
a, Average local order parameter, S for WT and α-catKD MDCK epithelium. n = 3 (WT) independent movies in 2 independent experiments, n = 3 (α-catKD) independent movies. t-test, ***P < 0.001. b, (left) Normalized, number of closest + and -1/2 defects per unit area as function of distance, re against extrusion and random pointsin α-catKD MDCK. n = 56 extrusions in 3 independent movies. n = 30 different random point sets. (right) Ratio of closest defect density against extrusion points at re = 10 μm to re = 120 μm. c, d, Simulations comparing size of defects (c) and total defect areal density (d) for small and large nematic bending elasticity, K. K is 0.02 and 0.08 for (c), and 0.04 and 0.08 for (d). All data represented as mean ± s.e.m.
Extended Data Figure 5. Further analysis on topologically induced defects and extrusions.
a, Normalized number of + and -1/2 defects per unit area maps in star and circle epithelium confinements. n = 6738 (+1/2) defects and n = 5083 (-1/2) defects from 12 independent movies in 2 independent experiments (star), n = 5389 (+1/2) defects and n = 4858 (-1/2) defects from 8 independent movies in 3 independent experiments (circle). b, (left) Normalized, number of closest + and -1/2 defects per unit area as function of distance, re against extrusion and random points in star-shaped monolayer. n = 145 extrusions from 12 independent movies in 2 independent experiments. n = 30 different random point sets. (right) Ratio of closest defect density against extrusion points at re = 10 μm to re = 120 μm. c, Average velocity field around +1/2 defect in caspase-3 inhibited monolayer. n = 2993 defects from 7 independent movies in 2 independent experiments. Defect has same orientation and position as in Fig. 2a. d, Isotropic stress measured around cells just before extrusion (t = 0 min is time of extrusion). >70% (<30%) of cells experienced negative (positive resp.) stress, denoted as Group 1 (Group 2 resp.). n =44 total number of extrusions in 2 independent movies. ks-test, ***P < 0.001. All data represented as mean ± s.e.m.
Extended Data Figure 6. Automated nematic director detection and robustness study.
a, 5 step process of automated nematic director detection. (Step 1) Phase contrast image of monolayer is obtained. (Step 2) Details of image is smoothened. (Step 3) Local orientation of cells are obtained using OrientationJ. (Step 4) Local contrast is applied to identify cell body regions. (Step 5) Nematic directors are obtained. b, Example of defect detection in a given nematic director field using winding number approach (left, red for +1/2 defect, blue for -1/2 defect) and diffusive charge approach (right, yellow for +1/2 defect, blue for -1/2 defect). c, Number of stable defects detected as function of window size to average over number of local cell orientations. Averaging is done over n = 50 frames of a monolayer movie, for each window size analysis. ks-test, **P < 0.01, ***P < 0.001. Data are represented as mean ± s.e.m.
Extended Data Figure 7. Epithelium can be modeled as a 2D, incompressible material.
a, (left) One snapshot of instantaneous (for every 10 min frame interval) velocity divergence field in circularly confined epithelium. (right) Temporal average of velocity divergence field in circularly confined epithelium (averaged over ˜ 20 hrs or 128 images consecutively).
Extended Data Figure 8. Bayesian Inference Stress Method (BISM) and robustness study.
a, Schematic of inference algorithm. b-d, Plots of inferred stress vs. simulated stress for each component, in kPa.μm. Red line is bisector y = x. Blue dots: 3N×3N stress, σwhole for the whole system, Red dots: N×N stress, σcentral for the central region, Black circles: stresses obtained less than 2 μm from the boundary of the central region. e-g, Pressure and h-j, shear stress fields in kPa.μm: from left to right exact values, σnum, inferred values obtained for whole monolayer, σwhole and inferred values obtained for central part, σcentral. Black dashed box represents the central region within the whole tissue.
Supplementary Material
Acknowledgements
The authors thank Grégoire Peyret, Shreyansh Jain, René-Marc Mège and group members from MBI for helpful discussions, as well as Ivan Yow, Anh Phuong Le, Simon Begnaud and Alexandre Kehren for experimental assistance, and Simon Begnaud for providing the YAP nucleus-to-cytoplasm ratio quantification algorithm. The authors would also like to thank MBI Microfabrication core, MBI Microscopy core and MBI Science Communication core for continuous support. The authors are grateful to W. James Nelson and Marius Sudol for their generous gift of MDCK cell lines and YAP antibody respectively. Financial supports from the European Research Council under the European Union's Seventh Framework Program (FP7/2007-2013)/ERC grant agreements n° 617233 (BL) and n° 291234 (JMY) and the Mechanobiology Institute are gratefully acknowledged. T.B.S. is supported by an NGS scholarship.
Footnotes
Author Contributions
T.B.S., A.D., J.M.Y. and B.L. designed research, T.B.S., L.K., Y.T. performed experiments, A.D., S.T. implemented the numerical method and did the in silico simulations, T.B.S., A.D., V.N., P.M. contributed new reagents, modeling and computational tools, T.B.S., A.D., J.M.Y. and B.L. wrote the paper, C.T.L, J.M.Y. and B.L. supervised the project. All authors read the manuscript and commented on it.
Authors do not have conflict of interests to declare.
References
- 1.Rosenblatt J, Raff MC, Cramer LP. An epithelial cell destined for apoptosis signals its neighbors to extrude it by an actin-and myosin-dependent mechanism. Curr Biol. 2001;11:1847–1857. doi: 10.1016/s0960-9822(01)00587-5. [DOI] [PubMed] [Google Scholar]
- 2.Hogan C, et al. Characterization of the interface between normal and transformed epithelial cells. Nat Cell Biol. 2009;11:460–467. doi: 10.1038/ncb1853. [DOI] [PubMed] [Google Scholar]
- 3.Wagstaff L, et al. Mechanical cell competition kills cells via induction of lethal p53 levels. Nat Commun. 2016;7 doi: 10.1038/ncomms11373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Marinari E, et al. Live-cell delamination counterbalances epithelial growth to limit tissue overcrowding. Nature. 2012;484:542–545. doi: 10.1038/nature10984. [DOI] [PubMed] [Google Scholar]
- 5.Eisenhoffer GT, et al. Crowding induces live cell extrusion to maintain homeostatic cell numbers in epithelia. Nature. 2012;484:546–549. doi: 10.1038/nature10999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Levayer R, Dupont C, Moreno E. Tissue Crowding Induces Caspase-Dependent Competition for Space. Curr Biol. 2016 doi: 10.1016/j.cub.2015.12.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Toyama Y, Peralta XG, Wells AR, Kiehart DP, Edwards GS. Apoptotic force and tissue dynamics during Drosophila embryogenesis. Science. 2008;321:1683–1686. doi: 10.1126/science.1157052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Slattum GM, Rosenblatt J. Tumour cell invasion: an emerging role for basal epithelial cell extrusion. Nat Rev Cancer. 2014;14:495–501. doi: 10.1038/nrc3767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kemkemer R, Teichgräber V, Schrank-Kaufmann S, Kaufmann D, Gruler H. Nematic order-disorder state transition in a liquid crystal analogue formed by oriented and migrating amoeboid cells. The European Physical Journal E. 2000;3:101–110. [Google Scholar]
- 10.Duclos G, Erlenkämper C, Joanny J-F, Silberzan P. Topological defects in confined populations of spindle-shaped cells. Nat Phys. 2016 [Google Scholar]
- 11.Dupont S, et al. Role of YAP/TAZ in mechanotransduction. Nature. 2011;474:179–183. doi: 10.1038/nature10137. [DOI] [PubMed] [Google Scholar]
- 12.de Gennes P-G, Prost J. The physics of liquid crystals. Oxford University Press; USA: 1995. 0.20. [Google Scholar]
- 13.Hirst LS, et al. Morphology transition in lipid vesicles due to in-plane order and topological defects. Proc Natl Acad Sci. 2013;110:3242–3247. doi: 10.1073/pnas.1213994110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sanchez T, Chen DT, DeCamp SJ, Heymann M, Dogic Z. Spontaneous motion in hierarchically assembled active matter. Nature. 2012;491:431–434. doi: 10.1038/nature11591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schaller V, Bausch AR. Topological defects and density fluctuations in collectively moving systems. Proc Natl Acad Sci. 2013;110:4488–4493. [Google Scholar]
- 16.Doostmohammadi A, Thampi SP, Yeomans JM. Defect-Mediated Morphologies in Growing Cell Colonies. Phys Rev Lett. 2016;117:048102. doi: 10.1103/PhysRevLett.117.048102. [DOI] [PubMed] [Google Scholar]
- 17.Vedula SRK, et al. Epithelial bridges maintain tissue integrity during collective cell migration. Nat Mater. 2014;13:87–96. doi: 10.1038/nmat3814. [DOI] [PubMed] [Google Scholar]
- 18.Vedula SRK, et al. Emerging modes of collective cell migration induced by geometrical constraints. Proc Natl Acad Sci. 2012;109:12974–12979. doi: 10.1073/pnas.1119313109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Doostmohammadi A, et al. Celebrating Soft Matter's 10th Anniversary: Cell division: a source of active stress in cellular monolayers. Soft Matter. 2015;11:7328–7336. doi: 10.1039/c5sm01382h. [DOI] [PubMed] [Google Scholar]
- 20.Drescher K, Dunkel J, Cisneros LH, Ganguly S, Goldstein RE. Fluid dynamics and noise in bacterial cell–cell and cell–surface scattering. Proc Natl Acad Sci. 2011;108:10940–10945. doi: 10.1073/pnas.1019079108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Guasto JS, Rusconi R, Stocker R. Fluid mechanics of planktonic microorganisms. Annual Review of Fluid Mechanics. 2012;44:373–400. [Google Scholar]
- 22.Rossen NS, Tarp JM, Mathiesen J, Jensen MH, Oddershede LB. Long-range ordered vorticity patterns in living tissue induced by cell division. Nat Commun. 2014;5 doi: 10.1038/ncomms6720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Prost J, Jülicher F, Joanny J. Active gel physics. Nat Phys. 2015;11:111–117. [Google Scholar]
- 24.Nier V, et al. Inference of internal stress in a cell monolayer. Biophys J. 2016;110:1625–1635. doi: 10.1016/j.bpj.2016.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Aragona M, et al. A mechanical checkpoint controls multicellular growth through YAP/TAZ regulation by actin-processing factors. Cell. 2013;154:1047–1059. doi: 10.1016/j.cell.2013.07.042. [DOI] [PubMed] [Google Scholar]
- 26.Dong J, et al. Elucidation of a universal size-control mechanism in Drosophila and mammals. Cell. 2007;130:1120–1133. doi: 10.1016/j.cell.2007.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chiba T, et al. MDCK cells expressing constitutively active Yes-associated protein (YAP) undergo apical extrusion depending on neighboring cell status. Scientific Reports. 2016;6 doi: 10.1038/srep28383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yonemura S, Wada Y, Watanabe T, Nagafuchi A, Shibata M. α-Catenin as a tension transducer that induces adherens junction development. Nat Cell Biol. 2010;12:533–542. doi: 10.1038/ncb2055. [DOI] [PubMed] [Google Scholar]
- 29.Doostmohammadi A, Adamer MF, Thampi SP, Yeomans JM. Stabilization of active matter by flow-vortex lattices and defect ordering. Nat Commun. 2016;7 doi: 10.1038/ncomms10557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kuipers D, et al. Epithelial repair is a two-stage process driven first by dying cells and then by their neighbours. J Cell Sci. 2014;127:1229–1241. doi: 10.1242/jcs.138289. [DOI] [PubMed] [Google Scholar]
- 31.Tambe DT, et al. Monolayer stress microscopy: limitations, artifacts, and accuracy of recovered intercellular stresses. PloS One. 2013;8:e55172. doi: 10.1371/journal.pone.0055172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Campàs O, et al. Quantifying cell-generated mechanical forces within living embryonic tissues. Nat Methods. 2014;11:183–189. doi: 10.1038/nmeth.2761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Moussus M, et al. Intracellular stresses in patterned cell assemblies. Soft Matter. 2014;10:2414–2423. doi: 10.1039/c3sm52318g. [DOI] [PubMed] [Google Scholar]
- 34.Vedula S, et al. Microfabricated environments to study collective cell behaviors. Method Cell Biol. 2013;120:235–252. doi: 10.1016/B978-0-12-417136-7.00016-1. [DOI] [PubMed] [Google Scholar]
- 35.Brugués A, et al. Forces driving epithelial wound healing. Nat Phys. 2014 doi: 10.1038/nphys3040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Martiel J-L, et al. Measurement of cell traction forces with ImageJ. Method Cell Biol. 2015;125:269–287. doi: 10.1016/bs.mcb.2014.10.008. [DOI] [PubMed] [Google Scholar]
- 37.Rezakhaniha R, et al. Experimental investigation of collagen waviness and orientation in the arterial adventitia using confocal laser scanning microscopy. Biomech Model Mechan. 2012;11:461–473. doi: 10.1007/s10237-011-0325-z. [DOI] [PubMed] [Google Scholar]
- 38.Huterer D, Vachaspati T. Distribution of singularities in the cosmic microwave background polarization. Phys Rev D. 2005;72:043004. [Google Scholar]
- 39.Chalfoun J, et al. FogBank: a single cell segmentation across multiple cell lines and image modalities. BMC Bioinformatics. 2014;15:1. doi: 10.1186/s12859-014-0431-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Thielicke W, Stamhuis EJ. PIVlab–Towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J Open Res Softw. 2014;2:e30. [Google Scholar]
- 41.Blow ML, Thampi SP, Yeomans JM. Biphasic, lyotropic, active nematics. Phys Rev Lett. 2014;113:248303. doi: 10.1103/PhysRevLett.113.248303. [DOI] [PubMed] [Google Scholar]
- 42.Giomi L, Mahadevan L, Chakraborty B, Hagan M. Excitable patterns in active nematics. Phys Rev Lett. 2011;106:218101. doi: 10.1103/PhysRevLett.106.218101. [DOI] [PubMed] [Google Scholar]
- 43.Thampi SP, Golestanian R, Yeomans JM. Instabilities and topological defects in active nematics. Europhys Lett. 2014;105:18001. [Google Scholar]
- 44.Marenduzzo D, Orlandini E, Cates ME, Yeomans JM. Steady-state hydrodynamic instabilities of active liquid crystals: Hybrid lattice Boltzmann simulations. Phys Rev E. 2007;76:031921. doi: 10.1103/PhysRevE.76.031921. [DOI] [PubMed] [Google Scholar]
- 45.Thampi SP, Golestanian R, Yeomans JM. Vorticity, defects and correlations in active turbulence. Philos T Roy Soc A. 2014;372:20130366. doi: 10.1098/rsta.2013.0366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bittig T, Wartlick O, Kicheva A, González-Gaitán M, Jülicher F. Dynamics of anisotropic tissue growth. New J Phys. 2008;10:063001. [Google Scholar]
- 47.Volfson D, Cookson S, Hasty J, Tsimring LS. Biomechanical ordering of dense cell populations. Proc Natl Acad Sci. 2008;105:15346–15351. doi: 10.1073/pnas.0706805105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Prost J. The physics of liquid crystals. Oxford University Press; 1995. [Google Scholar]
- 49.Larson RG. The structure and rheology of complex fluids. Vol. 33 Oxford University Press; New York: 1999. [Google Scholar]
- 50.Edwards SA, Yeomans JM. Spontaneous flow states in active nematics: a unified picture. Europhys Lett. 2009;85:18008. [Google Scholar]
- 51.Bittig T, Wartlick O, González-Gaitán M, Jülicher F. Quantification of growth asymmetries in developing epithelia. Eur Phys J E. 2009;30:93–99. doi: 10.1140/epje/i2009-10507-6. [DOI] [PubMed] [Google Scholar]
- 52.Basan M, Joanny J-F, Prost J, Risler T. Undulation instability of epithelial tissues. Phys Rev Lett. 2011;106:158101. doi: 10.1103/PhysRevLett.106.158101. [DOI] [PubMed] [Google Scholar]
- 53.Delarue M, et al. Mechanical control of cell flow in multicellular spheroids. Phys Rev Lett. 2013;110:138103. doi: 10.1103/PhysRevLett.110.138103. [DOI] [PubMed] [Google Scholar]
- 54.Denniston C, Marenduzzo D, Orlandini E, Yeomans JM. Lattice Boltzmann algorithm for three-dimensional liquid–crystal hydrodynamics. Philos T Roy Soc A. 2004;362:1745–1754. doi: 10.1098/rsta.2004.1416. [DOI] [PubMed] [Google Scholar]
- 55.Fielding S, Marenduzzo D, Cates ME. Nonlinear dynamics and rheology of active fluids: simulations in two dimensions. Phys Rev E. 2011;83:041910. doi: 10.1103/PhysRevE.83.041910. [DOI] [PubMed] [Google Scholar]
- 56.von Toussaint U. Bayesian inference in physics. Rev Mod Phys. 2011;83:943. [Google Scholar]
- 57.Kaipio J, Somersalo E. Statistical and computational inverse problems. Vol. 160 Springer Science & Business Media; 2006. [Google Scholar]
- 58.Hansen PC. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992;34:561–580. [Google Scholar]
- 59.Du Roure O, et al. Force mapping in epithelial cell migration. Proc Natl Acad Sci. 2005;102:2390–2395. doi: 10.1073/pnas.0408482102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Cochet-Escartin O, Ranft J, Silberzan P, Marcq P. Border forces and friction control epithelial closure dynamics. Biophys J. 2014;106:65–73. doi: 10.1016/j.bpj.2013.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Harris AR, et al. Characterizing the mechanics of cultured cell monolayers. Proc Natl Acad Sci. 2012;109:16449–16454. doi: 10.1073/pnas.1213301109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Jenkins AD, Dysthe KB. The effective film viscosity coefficients of a thin floating fluid layer. J Fluid Mech. 1997;344:335–337. [Google Scholar]
- 63.Hecht F. New development in FreeFem++ J Numer Math. 2012;20:251–266. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source data and codes for cell orientation detection, active nematic simulations and bayesian inference of tissue stress are available upon request.