Gender Differences in the Formation of a Field of Study Choice Set

Abstract

Women now surpass men in overall rates of college graduation in many industrialized countries, but sex segregation in fields of study persists. In a world where gender norms have changed but gender stereotypes remain strong, we argue that men’s and women’s attitudes and orientations toward fields of study in college are less constrained by gendered institutions than is the ranking of these fields. Accordingly, the sex segregation in the broader choice set of majors considered by college applicants may be lower than the sex segregation in their first preference field of study selection. With unique data on the broader set of fields considered by applicants to elite Israeli universities, we find support for this theory. The factors that drive the gender gap in the choice of field of study, in particular labor market earnings, risk aversion, and the sex composition of fields, are weaker in the broad set of choices than in the first choice. The result is less segregation in considered majors than in the first choice and, more broadly, different gender patterns in the decision process for the set of considered majors and for the first choice. We consider the theoretical implications of these results.

The spread of egalitarian norms had a huge role in the emergence of a female advantage in college academic achievement (Buchmann and DiPrete 2006; Goldin, Katz, and Kuziemko 2006). Women now surpass men in overall rates of college graduation in many industrialized countries, and women attain master’s, professional, and doctoral degrees at rates that approach, equal, and even sometimes exceed men’s in some Western countries (Buchmann and DiPrete 2006; Goldin et al. 2006; DiPrete and Buchmann 2013). In light of this spread in egalitarian norms and the attendant steady gains in relative educational attainment, it is paradoxical that the trends in gender sex segregation in fields of study have followed a very different trajectory. During the period from the 1960s through the early 1990s, the closing and then reversal of the gender gap in rates of college degree attainment was associated with a decline in sex segregation in fields of study. In recent years, however, the trend in sex segregation has stabilized even as the share of college degrees earned by women has continued to grow (Mann and DiPrete 2013). Women still pursue science, technology, engineering, and mathematics (STEM) degrees at much lower rates than their male peers do, but segregation exists even within STEM majors (Jacobs 1995; Charles and Bradley 2002; England and Li 2006; Mann and DiPrete 2013; Morgan, Gelbgiser, and Weeden 2013).

The persistence of horizontal sex segregation both in general and particularly within STEM fields has negative implications for the supply of qualified labor in science and engineering and for the closing of the gender gap in earnings (Dey and Hill 2007), because the STEM fields that women pursue generally pay less well than do the fields pursued by men (Casselman 2014). It is also an unsolved theoretical puzzle. The question of why this gap persists has become the subject of intense research by a large community of scholars. We argue that an important reason for the persisting puzzle is a failure of researchers to sufficiently appreciate the complexity of the decision process that causes women and men to end up in different fields despite the sociocultural changes that have ostensibly reduced the salience of gender in educational and career choices, especially as these choices involve elite professions.

Research on the gender gap in field of study has frequently taken a “pathways” approach (e.g., Xie and Shaumann 2003), which focuses attention on the determinants of intent to major in certain fields at various points in the educational life course. The choice model that underlies this approach assumes that students form preferences for majors based on perceptions of their own field-specific aptitudes and opportunities, along with personal taste, values, and expected gender roles and environmental support in alternative scenarios. Student performance, tastes, values, and perceptions are assumed to be shaped by the home environment, peers, and teachers as well as the broader environment. These environmental influences produce systematic differences between boys and girls in the values, perceptions of opportunity, and perceptions of self-competence via the production of stereotypes and other cultural forces (Eccles et al. 1983; Ridgeway and Bourg 2004; Ridgeway and Correll 2004; Steele 1997).

This model for gender differences is informative, but it is limited by its lack of attention to the choice process that is embedded within it. The standard choice model in economics and rational choice-based sociology assumes that decision makers rank the possible options and choose the one that maximizes utility. From this perspective all options are considered using the same set of criteria, and the “best” one wins. We argue that this model, which is implicitly or explicitly embedded in the study of gender differences in behaviors such as field of study in college, obscures important aspects of the process that produces gender differences in choice in our world where gender norms are becoming more egalitarian but where gender stereotypes remain salient (Ridgeway and Correll 2004; Ridgeway 2011; Steele 2010). It is important for more general theoretical reasons to develop decision models that more accurately reflect the processes that actually produce decisions about behavior. While much attention has been focused on how actual decisions deviate from rational choice models through the use of screening heuristics that lessen cognitive burden (Goldstein 2009), we argue that decision-making outcomes can deviate from standard models when the sociocultural environment contains ambiguities and tensions that complicate the decision process in gender-distinctive ways.

Choosing a field of study and a career is an example of an important behavior where cultural models are ambiguous and in conflict—one that pushes men and women toward traditional gender-differentiated behavior, the other toward the ideal of gender egalitarianism. A world of cultural change and conflict between alternative cultural models creates ambiguity over the salience of gender for educational and career decisions. This ambiguity and tension between different cultural models may produce inconsistent rankings of fields of study according to the various criteria that a student uses to make a decision. As a consequence of this tension, the weighting of factors that a student uses to generate a list of seriously considered options may give way to alternative weightings for settling on the option that a student ranks as a first choice. In particular, competing criteria may cause gender segregation in the considered options for such behavior, that is, the broader choice set of considered majors, to be lower than are the gender differences in the most preferred major selections (i.e., first choice).

This conjecture is difficult to test because data about the fields of study that are considered by students are almost never available to researchers. The student’s actual field of study is not necessarily the same as the first-choice major (even ignoring the issue of preference change) because entry into fields of study is often competitive. Moreover, neither “intent to major” or declared major questions in surveys nor administrative data about the college experience allow scholars to observe the student process of ranking and choosing from among candidate fields. In one recent study in economics, students were asked to provide their preference orderings across all majors including their actual major and then were asked for subjective assessments about their abilities or expected earnings in alternative majors (Arcidiacono, Hotz, and Kang 2012). This study did not focus on gender and used as data “low-stakes” rankings, where the named preferences were “subjective” and did not involve actual behavior with consequences. Zafar (2009) examined the reasons for gender differences in the choice of major at an American university, but he used similar “subjective” data on preference rankings for a sample of college sophomores to examine gender differences in pecuniary and nonpecuniary factors connected with alternative majors The problem, then, is that the typical study either employs subjective data that do not have behavioral consequences or uses actual major as the outcome even though actual major mixes the outcomes of two decision-making processes: the individual (choices) and the institution (admission) whenever the entry into a major is the result of a competitive process. Hällsten (2010), in contrast, recently used actual behavioral data on major rankings for Sweden (where one can apply to multiple majors but must rank them in the application process), but his focus was on class differences in rankings and the extent to which class effects differed by gender.

In sum, the accumulated evidence on sex segregation in field of study is arguably biased because it is largely based on the majors that enrolled students chose and were admitted to, and not on their larger set of preferences. With unusual data on the broader set of fields applied to (including the ranking of choices) in the actual application process by applicants to elite Israeli universities, the Technion and Tel Aviv University, we study the final stage of the consideration process behind the formation of major choice sets and the gender gap in making real educational choices. By using data that allow us to explore the major choice set, we examine whether the interplay of two powerful forces—one that pushes for traditional gender-differentiated behavior, the other for a widely accepted (and even more widely acknowledged) ideal of gender egalitarianism—results in greater gender segregation in the first choice than in the set of considered options.

According to our hypothesis, attitudes and orientations that form the set of considered majors may be less constrained by gendered institutions than the ranking of the first choice. We test the hypothesis with a formal choice model for the formation of the major choice set. Our results provide clear evidence that students are weighting gender-relevant criteria differently in constructing their strongly considered options and in making their top choice. We discuss the implications of our results regarding the decision-making process for selecting a college major for the future of sex segregation in higher education and in occupations.

The Gender Gap in College Major Preferences

Various theories for the persistence of the gender gap have been proposed, but they explain relatively little of the horizontal sex segregation in statistical terms (Xie and Shaumann 2003; Mann and DiPrete 2013). The inability to explain gender segregation satisfactorily in terms of academic skills or work and family values has caused scholars to invoke “gender-essentialism” as the explanation for the divergent pattern for women and men (Charles and Bradley 2009) and has refocused attention on the childhood experiences that may account for the persisting gender gap in fields of study.

Relatively little is known about the evolution of academic and occupational preferences over the childhood, adolescent, and early adult life course. Yet research shows that childhood aspirations and evaluations tend to become more realistic as children get older (Ginzberg et al. 1951; Csikszentmihalyi and Schneider 2001; Tracey et al. 2005). Moreover, gendered stereotypes and gendered preferences emerge early in childhood and continue to elaborate throughout childhood and adolescence (Legewie and DiPrete 2014). Research indicates that parents and educators tend to perceive girls as less qualified than boys in math-oriented fields, which are largely considered masculine, and to view these fields as less important for girls’ future career paths than boys’ (Correll 2001; Eccles and Jacobs 1986; Eccles, Jacobs, and Harold 1990). These stereotypes are internalized by children and adolescents and help shape gender identities, and they contribute to gender differentiation in academic interests and career choices (Eccles et al. 1983; Ridgeway and Correll 2004; Ridgeway 2011).

Several studies suggest that the relative importance given to intrinsic, altruistic, or social rewards of a job and for the extrinsic rewards of power, money, and prestige of a job vary by gender (Hakim 1991; Beutel and Marini 1995; Johnson 2001; Konrad et al. 2000). At least in part, these differences may be traceable to gender differences in work–family conflict, which many young women anticipate long before they experience it as a reality in their daily lives (Cinamon 2006). Indeed, it has been documented that while expected earnings are an essential component in the selection of a college major, women are less influenced by this factor than are men (Montmarquette, Cannings, and Mahseredjian 2002). Women value the nonpecuniary aspects of jobs—such as security, flexibility in hours, paid leave, and vacation provisions—more than they value wages (Currie 1997; Zafar 2009).

Women may further perceive the work environments of certain, otherwise desirable occupations as unsupportive for women (DiTomaso 1989; Heilman et al. 2004).¹ Moreover, studies have found evidence that women may also perceive the educational environments of predominantly male majors such as engineering as “chilly” and unpleasant for women (Ulku-Steiner, Kurtz-Costes, and Kinlaw 2000; Ecklund, Lincoln, and Tansey 2012). Alon and Gelbgiser (2011), for example, demonstrate that female students thrive in female-dominated learning and social environments. Moreover, groups are aware of stereotypes about them—this is the core idea in stereotype threat theory (Steele and Aronson 1995; Steele 1997)—and women, therefore, may avoid male-dominated fields where stereotype threat is more likely to be activated.

Perceived conflict between one’s gender identity and otherwise attractive academic and career options may affect the extent to which women value certain career options and their estimates of their probability of success in fields that lead to these options. These perceptions may in turn produce gender disparities in social and psychological attributes such as risk aversion, confidence, and attitudes toward competition. Laboratory experiments demonstrate that women may be more risk averse and less competitive than men (Bertrand 2010; Croson and Gneezy 2009; Eckel and Grossman 2008; Gneezy, Niederle, and Rustichini 2003; Niederle and Vesterlund 2007). For example, Eckel and Grossman (2002) found that men are more likely than women to choose riskier gambles with higher expected payoffs. Gneezy et al. (2003) report that although women perform as well as men in single-sex settings, men outperform women in more competitive circumstances.² But whether this difference in risk aversion/confidence is an “essentialist” characteristic of gender—even a personality trait that may be related to testosterone levels—or a behavioral preference shaped by cultural beliefs, socialization and environmental factors and thus a response to the gender differences in valuations of career options and estimates of the chances of success is unknown (Bertrand 2010). It could be, for example, that men’s inclination toward more competitive fields may stem from the fact that jobs with greater levels of risk and competition are paid higher wages (Hartog, Ferrer-i-Carbonell, and Jonker 2002).

Formation of a Field of Study Choice Set When Cultural Models Are Ambiguous and in Conflict

Clearly gender norms and cultural beliefs about gender roles shape the field of study preferences of both men and women. The standard choice model would see preferences and choices arise from a weighting of the advantages and disadvantages of each alternative. The foregoing review provides several insights as to what men and women may see as an advantage or a disadvantage of each field. Given that men are more predisposed to competition than women are, we expect that men would tend applying to exceptionally competitive majors relative to their female counterparts. Women, alternatively, will demonstrate greater tendency to choose female-dominated fields. We also expect that the labor market returns of a major may shape men’s choices more strongly than women’s.

However, we argue that the process of forming a list of preferences for fields of study is more nuanced than this simplistic representation. The decision-making process for selecting a college major begins with a list of options, which narrows to a few favorites until it is whittled down to a first and second choice. The standard choice model assumes that the ranking of any alternative is determined by the same set of criteria applied to each alternative’s specific attributes. Thus the probability of any particular alternative being chosen first, second, third, or in any other ranked position is similarly governed by a uniform set of criteria. This implies that women’s preference for female-dominated fields and men’s preference for lucrative and competitive fields is constant across all ranked options. Under this model we can expect that the level of sex segregation will be the same across all alternatives. We refer to this model, with its strong assumption about the uniformity of preference determination across the ranking of preference options, as the unidimensional preferences model. This is the model used by Hällsten (2010) to study class differences in preferences for field of study in Sweden. Zafar (2009) and Arcidiacono et al. (2012) also employ the unidimensional preferences model to study the effects of various attributes of majors and expected career outcomes on ranked major preferences; yet they did not have data on actual choices.

We argue, however, that this choice model is too crude because it does not take into account that the cultural models that shape field of study and career choices are ambiguous and in conflict—one pushes for traditional gender-differentiated behavior, the other for the ideal of gender egalitarianism. It is possible that the influence of egalitarian and traditional forces, both of which are interwoven into this decision-making process of both men and women, is differential and varies by stage. Egalitarian forces sway individuals’ orientation—what we define here as the considered options for behavior—toward social institutions more than they guide their actual behavior, defined here as the preferred option.

Accordingly, we posit that the unidimensional preference model may break down in situations where people use different criteria to decide whether an alternative is near the top of their preferences and whether it is their first choice. In particular, it may break down in distinguishing the criteria that applicants use to rank a field highly in their preference ordering from the criteria that applicants use to rank this field as their first choice. In other words, an applicant’s model for selecting a set of considered options may differ from the applicant’s model for selecting a first choice. Traditional gender norms may, for example, have a stronger impact on the first choice than on the considered options. Consequently the level of gender segregation in the considered options may be lower than the segregation revealed in the pattern of first choices.

We argue that a multinomial preference model may be more appropriate to describe the formation of the choice set and horizontal sex segregation. In a multinomial preference model, applicants may use different utility weights for the considered majors and for the top choice, conditional on the considered majors. This implies the possibility of a different set of weights in the rank-ordered logit model for the first choice and for the second choice, given the first. If women and men are influenced by egalitarian forces when making educational and career choices, it may be that the alternatives that women and men consider seriously are less colored by gender than are the choices they actually make. This may reflect a process in which a change in orientation precedes behavioral adaptations or, alternatively, a two-layered system in which egalitarianism shapes orientation (as operationalized by the considered choice set), while behavior (the selection of the first choice) remains more tightly controlled by traditional norms.

From this vantage point, we test the validity of the unidimensional preference model and its fit for capturing the process of ranking and choosing which majors to apply to. Specifically, we examine whether the gender gap in weighting these criteria varies for the process of choosing the set of majors to include at the top of their preference list and when they decide on their first choice. We also examine whether the level of gender segregation in the set of considered options is lower than in the first choice.

Setting

The application and admission processes for a bachelor’s degree at Israeli universities makes them attractive for the current investigation: both the application and admission processes are specific to each combination of major and institution, and departments within each institution vary in their selectivity levels; most professional degrees are offered at the undergraduate level; and applicants need to rank their preferences in the application form. The ranking process means that an applicant is considered by every department to which the applicant applies and is either accepted or rejected by each one. If the applicant is accepted to more than one department, the applicant is informed about the acceptance decision to the department to which was given the highest preference ranking.

Admission decisions at elite Israeli universities are formulaic, based entirely on a composite score that is calculated by taking the weighted mean of an individual’s matriculation diploma grades (weighted by type and level of courses) and psychometric test score (similar to an SAT score). The outcome of the application process depends almost entirely on three variables: the applicant’s composite score, the difficulty of gaining admission, and the preference ranking assigned to departments by the applicants. The difficulty of gaining admission depends, of course, on the level of competition, but other factors also matter: universities set constraints on the size of the major based on factors such as the resources needed to teach students in each particular major, absolute standards set by majors for applicant quality, labor market considerations, and the historically determined factors (such as the capacity of teaching laboratories) that affect each department’s ability to handle a class of any given size. Applicants may also apply to departments at other universities and thus may choose to decline the invitation to matriculate in a specific department at a specific university.³

Data and Sample

We focus this investigation on applicants seeking to pursue STEM and mathematically oriented college majors. This focus helps us circumvent one of the popular explanations for gender disparities in field of study selection, namely, the tendency of women to avoid STEM and mathematically oriented majors in college. At the same time, as others have found, and as we also show here, the choice of specific major is strongly gender segregated even for the subset of students who pursue STEM degrees (Mann and DiPrete 2013). The question we examine is whether, within this group of highly qualified applicants, there is a gender gap in the formation of the field of study choice set and how gender affects the distinction between strongly considering an alternative and ranking an alternative as one’s top choice.

To assess the gender differences in field of study choice set, we used administrative data obtained directly from Israeli universities for periods ranging from 10 to 12 consecutive years (circa 1997 to 2008; for more details, see Alon [2011]). Our investigation focuses on the Technion (TECH), a research university that offers degrees in STEM fields only.⁴ To substantiate the Technion results, we replicated the analyses with STEM-bound applicants to Tel Aviv University (TAU), another elite university in Israel.⁵ Appendix C provides additional information on the analyses for TAU and a set of tables and figures that parallel those presented for the TECH. It is reassuring that the results for TAU depict a similar picture to the one obtained from the TECH.

We analyzed data for applications to the Technion from 1998 to 2008. Because the specification of the choice model uses lagged variables, we excluded the applicants for the first year for each of these universities from the models. The analytical sample includes around 27,000 applicants to the Technion over a period of 10 years (1999 to 2008; we omitted the 1998 applicants), with entries for both first and second choices and complete data for all the relevant variables. The analyses are based on 1,414,822 person-major-choice observations.

The Technion is a highly selective institution. In addition to the typical admission requirements for elite Israeli universities, applicants to the Technion are required to have taken the highest level of math and physics offered in high school. Not surprisingly, as an institution limited to STEM fields, the TECH has a maledominated student body: only 34 percent of its students from 1998 to 2008 were women, compared to 55 percent in the other three leading universities in Israel. Yet there has been a steady rise in the share of women among TECH applicants, admits, and graduates. In the recent decade, for example, the share of women applicants rose from 34 to 39 percent (1998 and 2008, respectively).⁶

We focus on the major choice set of first-time applicants. When applying to the Technion, applicants can list only two ranked preferences for their major (hereinafter referred to as first choice and second choice, respectively), and they cannot choose a dual major.⁷ During the period of investigation, the Technion offered degrees in 28 fields of study, and these are the majors we used in our analysis.⁸ Table 1 lists and characterizes these majors by their student bodies. We describe briefly these and other variables used in our analysis in the following text.

Table 1.

Fields of Study and Selected Characteristics, TECH 1998–2008¹

Major # and Title		Share of Students	% Women Students	Academic Threshold (P25 Admits)	Expected Monthly Salary (NIS)2
3	Electrical Engineering	14.5	14	88	17,777
12	Computer Science	10.7	23	88	17,019
8	Industrial and Management Engineering	9.9	41	84	14,262
2	Mechanical Engineering	9.3	10	80	12,128
1	Civil and Environmental Engineering	7.2	23	77	8,223
7	Aerospace Engineering	4.1	17	82	8,745
5	Biotech and Food Engineering	3.7	70	84	8,745
15	Education in Tech and Science	3.6	47	74	6,113
4	Chemical Engineering	3.5	58	79	8,464
10	Physics	3.3	15	80	10199
19	Environmental Engineering	3.2	32	77	8,745
17	Biology	3.1	73	80	5,430
21	Materials Engineering	2.5	41	82	8,745
24	Electrical Engineering and Physics	2.5	15	92	17,777
25	Biomedical Engineering	2.3	57	90	8,745
26	Information System Engineering	2.0	35	86	8,745
18	Math and Computer Science	1.9	26	86	12,518
6	Agricultural Engineering	1.9	18	74	8,745
16	Chemistry	1.8	63	76	4,502
9	Math	1.7	35	81	1,141
11	Economics and Management	1.6	54	83	9,812
20	Molecular biochemistry	1.6	72	81	4,966
13	Landscape Architecture	1.0	68	77	6,782
14	Medical Laboratory Science	0.9	76	84	5,430
23	Math and Physics	0.8	24	82	10,199
27	Biochemistry Engineering	0.7	69	86	8,745
22	Quality Engineering	0.6	73	80	8,745
28	Physics and Computer Science	0.1	20	89	17,019

Note: Sorted by the share of students. Correlation between % Women Students and Academic Threshold is −0.247; between % Women Students and Expected Monthly Salary, −0.659; between Academic Threshold and Expected Monthly Salary, 0.691.

¹Biomedical Engineering started in 1999; Information System Engineering in 2001; Biochemistry Engineering in 2004; and Physics and Computer Science in 2005.

²Based on averages of graduates between 2000 and 2003.

Individual and Field of Study Characteristics

In this study we examine how the field of study’s characteristics shape the major choice set of applicants. We use three objective characteristics to assess how men and women with excellent quantitative skills both rank their alternatives: the expected wage from a job arising from any particular field of study, its sex composition, and the ease or difficulty in being admitted into any particular field of study.

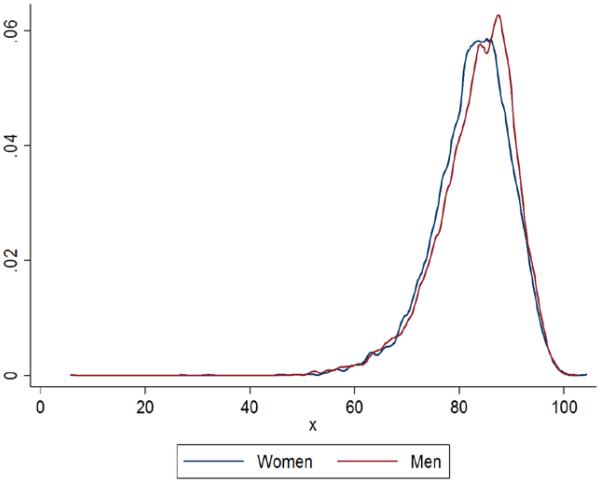
To estimate the ease or difficulty of gaining admission, we used the academic performance information used by the admissions committees of these two universities. An individual’s composite academic score is the only criterion for admission used by Israeli universities. It is calculated by taking the weighted mean of an individual’s matriculation diploma grades, which are similar to Advanced Placement (AP) grades, and a psychometric test score, which is similar to an SAT score. We use the score calculated by the Technion for all its applicants. The score emphasizes applicants’ achievements in math and physics courses taken in high school as well as quantitative skills. This variable ranges from 6 to 104 among applicants, but more than 75 percent of them scored above 80 (m = 83; SD = 7). Figure 1 shows the distribution of the composite academic scores of female and male applicants. As can be seen, male scores are slightly higher on average than female scores; the male mean is 83.2 with a standard deviation of 7.5, and the female mean is 82.6 with a standard deviation of 7.3. These gender differences are reversed from what is generally found in the population, but it is important to keep in mind that this sample is highly selected to favor academically talented applicants with an interest in science.

Figure 1.

Distribution of Academic Scores, by Gender, TECH

The difficulty of gaining admission to a major depends not only on one’s own academic score but also on the academic scores of the applicants one is competing against. To compute academic threshold scores, we gathered information on the academic scores of individual admits by major and by year. For each combination of major and year, we calculated the 25th percentile (Q1, bottom quartile) based on the academic scores of admitted students. This variable approximates each major’s admission threshold, information that is readily available to applicants. Every year before the application season, the universities in Israel publish these “thresholds” for admission, computed from the academic scores of the previous year’s admits. At the Technion, electrical engineering, computer science, and biomedical engineering are the majors with the highest academic threshold, on average (see Table 1), while chemistry, agricultural engineering, and a program for science teaching are the majors with the lowest.

During the application process, applicants typically compare their individual academic scores to the previous year’s admission thresholds.⁹ This way they can obtain a rough estimate of their likelihood of admission to major j. We created a variable that measures the risk involved in the application process to each of the possible majors for each student. This variable is calculated as the distance between an applicant’s academic score and the academic threshold for each major based on data from the previous year. A negative value for this variable indicates that the applicant’s academic score is below the 25th percentile for major j, while a positive value indicates the opposite.¹⁰ We allow this variable to have nonlinear effects by transforming this difference measure into a set of categorical variables based on the size of the difference. To obtain thresholds for the categorical variables, we used the cut points for the deciles of these difference scores across the distribution of applicants’ first and second choices, where the top decile consists of applicants who are least likely to be admitted to a major and the bottom decile consists of applicants who are most likely to be admitted. Table 2 presents the mean gaps for each decile.¹¹

Table 2.

Mean Scores for the Individual–Major Match by Deciles

Decile		Mean Score
1	Most risky	−15.87
2		−7.7
3		−4.06
4		−1.39
5		0.89
6		3.04
7		5.22
8		7.54
9		10.37
10	Least risky	15.33

Note: Deciles are calculated as the distance between the applicant’s academic score and the major’s academic threshold (P25) in the previous year. Category 1 indicates individuals below major’s threshold: most risky application choice. Category 10 indicates individuals above major’s threshold: least risky application choice. "Perfect match": category 5

On one side of the risk distribution (decile 1), we observe the largest negative individual-major gaps (−16 points on average at the Technion). This gap suggests that the individuals in this category are underqualified for major j, that their likelihood of admission to that major is low, and that applying to major j (as opposed to other majors at the Technion) is the most risky choice for them.¹² At the Technion, the 5th decile contains students with the closest match with the 25th percentile of admits in the previous year for major j and thus serves as the omitted category in the specification. On the other side of the distribution (decile 10), we have the largest positive gaps—15 points on average at the Technion—which implies overqualification, a high likelihood of admission to major j, and the least risky application choice. Applicants who apply to majors with more negative gaps are taking bigger risks with their application choice than are students who apply to majors with smaller gaps. Individual differences in risk do not necessarily indicate that one applicant is more risk averse than the other in the pattern of applications; it may instead be the case that one applicant’s preference for highly competitive majors is greater than that of another student. The same observation applies to gender differences in average risk taking. We return to this issue in the following section.

We also gathered information on the gender of individuals by major and by year and display the average annual share of females in each major’s student body. The results in Table 1 show that the share of women is lowest in mechanical engineering (10 percent), electrical engineering (14 percent; with or without physics), and physics (16 percent). Twelve percent of the student body studied computer science, another male-dominated and lucrative field (77 percent of computer science students are male). The share of women in industrial and management engineering, however, rises to 41 percent (9 percent of the student body), and in chemistry, molecular biochemistry, medical laboratory sciences, and biology exceeds 70 percent. These patterns are similar to what is reported in data for elite universities in the United States (e.g., Arcidiacono, Aucejo, and Spenner 2012).

To measure labor market expectations, we used a measure for earnings that captures the monthly salary that a graduate in a certain field can anticipate upon labor market entry. The earnings information was obtained from the published reports of the Israeli Central Bureau of Statistics, which are based on the tax authorities’ administrative records for salaried workers, by major and institution. The pay data, based on individual monthly salaries during a graduate’s first two years in the labor market, was collected for four cohorts of university graduates (2000 to 2003).¹³ Table 1 lists the expected salaries by field of study. The salaries range from 4,500 to 20,000 New Israeli Shekels (NIS), in 2004 prices. It is clearly the case that the majors which lead to the highest paying jobs tend to be male dominated. Electrical engineering, for example, is not only one of the largest majors at both institutions, but also the one with the lowest share of female student and the highest expected salary. The least lucrative majors are female-dominated fields. The share of females in a major turns out to be negatively correlated both with the expected salary (−0.66) and with the major academic score (−0.25).

The Choice Model: Unidimensional or Multinomial?

The typical rational choice model fit to choice data is a latent index model; individuals assign utilities to each of the possible outcomes, rank the utilities, and choose the highest ranked option. With the notation of Allison and Christakis (1994), individual i has utilities

$$U_{ij}={\mu }_{ij}+{\epsilon }_{ij}$$

where j indexes the options from 1, … , J The standard model presumes that μ_ij is a function of alternatives of chooser and of option, that is,

$${\mu }_{ij}={\beta }_j{x}_i+\gamma z_j+\theta w_{ij},$$ (1)

where x_i are characteristics of choosers, z_j are characteristics of the alternatives, and w_ij are relations between choosers and alternatives. A single set of coefficients determines the relative preference for any alternative relative to any other alternative. This same set of coefficients determines the probability that any particular option would be the first choice, second choice, or any other ordered choice, given the values of the covariates in Equation (1).

If data about the ranking of preferences are available, then this standard framework allows the estimation of a “rank-ordered logit model” (Allison and Christakis 1994), which in the marketing literature is referred to as the “exploded logit model.” Using this framework and letting Y_ij be the rank of alternative j for individual i, then the probability that any particular alternative (e.g., alternative j^′) is ranked first becomes

$$P(Y_{i{j}^{\prime }}=1)=\frac{\text{exp}\left({\mu }_{i{j}^{\prime }}\right)}{\left(\sum _{j=1}^J\text{exp}\left({\mu }_{ij}\right)\right)}.$$ (2)

The probability that another alternative (j^′) is the second choice becomes

$$P(Y_{i{j}^{\prime \prime }}=2)=\text{exp}\left({\mu }_{i{j}^{\prime \prime }}\right)∕\left(\sum _{j\ne j^{\prime }}\text{exp}\left({\mu }_{ij}\right)\right)$$

and so forth for ranks 3, … , J. In this model, the ranking of any alternative is determined by a vector of coefficients applied to each alternative’s specific attributes When the same coefficient vector is used to determine the ranking of all alternatives, the probability of any particular alternative being chosen first, second, third, or in any other ranked position is governed by a uniform set of criteria. We refer to a model with uniform preference weights as a unidimensional preferences model

The rank-ordered logit model has frequently been applied in marketing research and very occasionally in sociology. As mentioned, Hällsten (2010) recently used a unidimensional preferences rank-ordered logit model to study class differences in preferences for field of study in Sweden.¹⁴ We examine the validity of the unidimensional preference assumption by studying how gender affects the distinction between strongly considering an alternative and ranking an alternative as one’s top choice. We argue that a multinomial preference model, in which applicants use different utility weights for the considered majors and for the first choice—which implies a different set of utility weights for ranking the first choice and for ranking the second choice, conditional on the first choice—may be more appropriate to describe the formation of the choice set and horizontal sex segregation. Our analytical strategy assesses this hypothesis and tests for the validity of the unidimensional preferences model.

Formation of the Field of Study Choice Set

Horizontal Sex Segregation

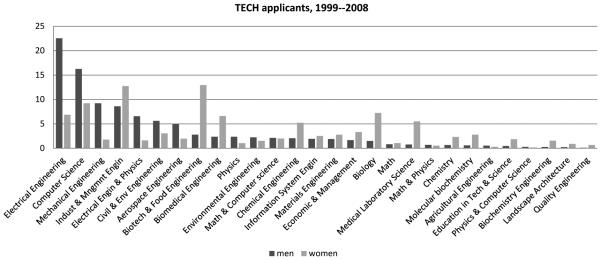
The first step in testing the hypothesis that egalitarian influences are stronger in shaping the first choice is to assess whether the level of horizontal sex segregation is greater in the broader set of candidate fields than in the first choice. Figure 2 presents the popularity of majors in each institution as revealed by male and female applicants’ first choices. About a third of male applicants to the Technion sought admission to electrical engineering (29 percent, including the track with a concentration in physics). The second most popular major among men was computer science (about 20 percent, including the variant tracks with concentrations in physics and math). Thus, about half of the men listed these two majors as their first choice. An additional 9 percent of male applicants to the Technion listed mechanical engineering as their first choice. Whereas men’s distribution of first choices is quite skewed by their strong preference for electrical engineering and computer science, women’s first-choice distribution is more dispersed. The two most in demand fields of study among the Technion women are the industrial and management engineering major and the biotech and food engineering major (each of these majors accounts for 13 percent of female applicants). Computer science and biology follow these majors in third and fourth place.¹⁵

Figure 2.

The Distribution of First-choice Majors, by Gender, TECH

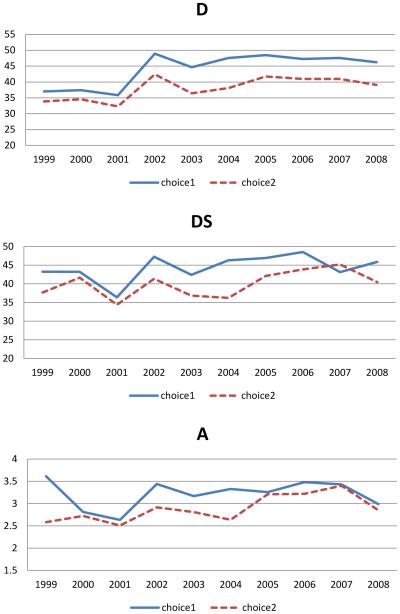
To formally measure the level of horizontal sex segregation in the first choice and to assess whether it is lower in the second choice, as we hypothesize based on the multinomial preferences model, we calculated indices of dissimilarity for each of the application cohorts between 1999 and 2008. Figure 3 presents results for three indices of dissimilarity: the D Index (Duncan and Duncan 1955),the DS Index (Gibbs 1965),and the A Index (Charles and Grusky 2004). We find a high and persistent level of horizontal sex segregation among the applicants to both institutions, even after accounting for majors’ size and the influx of women into the applicant pool. Pertinent to the distinction between the considered options and their ranking is the evidence that in almost all years of the investigation, the level of sex segregation in the first-choice majors is higher than in the second choice majors. This pattern challenges the assumptions of the unidimensional preferences model. Later in the article, we formally test the validity of this model with its strong assumption about the uniformity of preference determination across the ranking of preference options.

Figure 3.

Level of Horizontal Sex Segregation by Choice, TECH. The three indices of dissimilarity are the D Index (Duncan and Duncan 1955), the DS Index (Gibbs 1965), and the A Index (Charles and Grusky 2004).

Unidimensional Preferences Model

We begin the assessment of the formation of the field of study choice set with the unidimensional preference model as a baseline. In this analysis we assumed that both men and women rank their alternatives based on two characteristics: the expected wage from a job arising from any particular field of study and the ease or difficulty in being admitted into any particular field of study. We further assume that women and men use a single set of weights to rank alternatives, which implies that the same weights are used to rank the first choice and to rank the second choice among the remaining alternatives. Models 1 and 2 in Table 3 shows the estimated coefficients of the rank-ordered logit model (without controlling for major dummy variables) for men and women under this assumption. There is a big gender gap in the responsiveness of applicants to the economic potential of majors, and in the expected direction. For men, higher expected returns translates into a higher probability of applying to that major, net of the distance between that major’s threshold and one’s own composite academic score: every extra 1,000 NIS per month boosts the odds by 25 percent that a male applying to the Technion will apply to this major. In contrast, expected earnings have a small negative effect on a woman’s likelihood of applying to a major.¹⁶ This provides insights into the reasons why women who pursue STEM careers end up majoring in fields that—taken as a group—pay less well than the fields pursued by men.

Table 3.

Unidimensional Preferences Model: Effects of Expected Wage and Difficulty of Being Accepted, by Gender, on the Ranked Choice, TECH

	F (1)	M (2)	F (3)	M (4)
Decile 1: most risky	−1.287† (0.053)	−2.655† (0.038)	−1.654† (0.078)	−1.274† (0.053)
Decile 2	−0.806† (0.037)	−1.547† (0.026)	−1.018† (0.050)	−0.763† (0.034)
Decile 3	−0.382† (0.031)	−0.838† (0.021)	−0.495† (0.037)	−0.351† (0.025)
Decile 4	0.050* (0.027)	−0.159† (0.019)	0.002 (0.028)	0.084† (0.020)
Decile 6	−0.410† (0.029)	−0.188† (0.020)	−0.389† (0.030)	−0.423† (0.021)
Decile 7	−0.829† (0.032)	−0.531† (0.023)	−0.793† (0.037)	−1.001† (0.027)
Decile 8	−1.460† (0.039)	−0.894† (0.028)	−1.403† (0.047)	−1.586† (0.034)
Decile 9	−2.106† (0.047)	−1.294† (0.035)	−1.999† (0.061)	−2.243† (0.044)
Decile 10: least risky	−3.376† (0.069)	−2.029† (0.050)	−3.127† (0.090)	−3.376† (0.064)
Wage	−0.013† (0.003)	0.231† (0.002)
Controls for major dummy variables:	N	N	Y	Y
Observations	221,905	485,506	221,905	485,506

Note: Standard errors in parentheses.

^†p < 0.01;

^*p < 0.1.

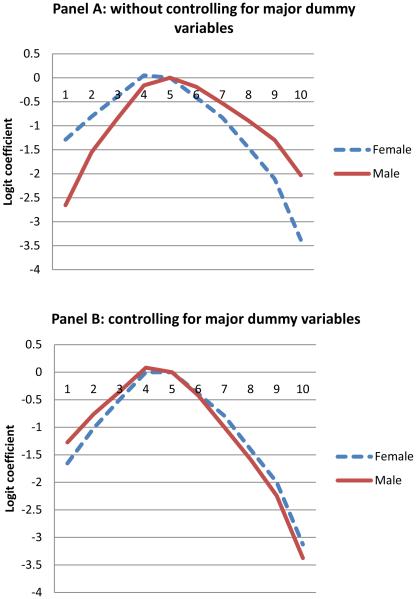
Next we turn to the gender profiles of risk behavior displayed by applicants at the Technion. Female applicants appear to be less risk averse than men in their application decisions (see Models 1 and 2 in Table 3). To ease the interpretation of the gender gap in the profiles of risk behavior, Figure 4 charts the coefficients from the first part of Table 3. As can be seen, the modal decile for the risk’s level preferred by female applicants when choosing a major is category 4, which is riskier than the modal category (category 5) for men.¹⁷ Moreover, female students are relatively more likely to apply to majors in high risk deciles than are men, and they are also less likely to apply to majors for which they are “overqualified” than are men.

Figure 4.

Unidimensional Preferences Model: Effects of Difficulty of Being Accepted on Choice, TECH. Based on the results of Table 3. (A) Without controlling for dummy variables. (B) Controlling for dummy variables.

However, these results are not necessarily informative about the true gender differences in risk aversion. An individual applicant may apply to highly competitive majors because she is risk loving, but she may instead simply prefer the majors that are highly competitive for other reasons. Similarly, men may appear more risk averse than women only because their average preferences for majors differ on other grounds than risk from those of women. We can better isolate the impact of risk on the pattern of applying to majors by including fixed effects for the different major possibilities in the models for each university. A fixed effects model will show whether year-to-year fluctuations in the difficulty of getting into specific majors affect the pattern of applications that year differently for men and women. This model, therefore, will provide a clearer measure of how male and female applicants respond to changes in risk, which, as we described earlier, the applicants are generally aware of. Table 3 and Figure 4 display the coefficients for risk in the fixed effects model (Models 3 and 4, controlling for major dummy variables).¹⁸ As expected, the results show that female applicants are apparently more risk averse than male applicants, once the underlying differences in the gender pattern of major preferences are controlled.¹⁹ Net of the baseline “essentialist” gender pattern of major preferences, female applicant odds of applying to a major in the highest risk category at the Technion were only 68 percent as high (relative to the middle category) as for men, and female odds of applying to the second highest risk category were only 77 percent those of men.²⁰

In sum, our findings show a gender gap in the criteria for choosing a college major. As expected, men apply to exceptionally competitive majors relative to their female counterparts. Women, alternatively, prefer female-dominated fields. Finally, men, more than women, seek fields of study that increase the prospects of a lucrative job. We discern three distinct, though not mutually exclusive, interpretations of the meaning of this gender pattern. It may be that men are more confident than women and more inclined to compete in the application process for the most competitive majors. It may instead be the case that men care predominantly about the expected size of their salaries. Because the most competitive majors are the ones that pay the highest average salaries, male applicants are therefore often in a position of being only marginally competitive or worse for their preferred major unless they have top academic scores. Women are less interested in competing for these majors because they are less interested in external rewards than are men. A third possibility, which we assess subsequently, is that female applicants are deterred from applying to the most competitive and lucrative majors because these majors are male dominated and uncomfortable for women. In this third interpretation, the male domination of these majors, rather than women’s lack of interest in external rewards, affects female preferences.

Multinomial Preferences Model

All the results discussed to this point make the strong assumption that the unidimensional preferences rank-ordered logit model is correct both as the basis for determining the set of considered options and for determining the final choice. As discussed, our theoretically preferred model is a multinomial preferences model in which applicants use different utility weights in their first choice than they do in their second choice, which implies in the two-choice context that two distinct coefficient vectors are needed in the rank-ordered logit model to accurately predict preference rankings. We test for the validity of the unidimensional preferences model by suppressing information about the second choice from the data and estimating a conditional logit model; this is equivalent to a rank-ordered logit model (Equation (1)) when only the top choice is ranked in the data. The important question for us is whether the unidimensional preferences model accurately captures the full process of considering and ranking the choice majors. We report statistical (Hausman) tests for the unidimensional preferences model in Appendix A and clearly reject the null hypothesis that the rankings of majors by Technion (and TAU) applicants follows the unidimensional preferences model for male applicants only, for women applicants only, and for the two genders combined. The process of deciding one’s first choice and one’s second-choice major cannot accurately be described as a simple matter of ranking majors on their characteristics using a single set of utility weights for either women or men.

The first part of Tables 4A and 4B shows the set of coefficients that correspond to Table 3 (without and with fixed effects), except that they pertain to the first choice only. The results reveal that women applicants are less responsive to the wage expectations of majors than men. Figure 5A charts the risk coefficients for the first choice by gender (from the fixed effect model). What is clear is that both men and women take more risks in their first choice than when deciding about all the considered options (compare Figure 5A to Figure 4B). Yet men take greater risks than women when picking a major as a top choice, once the underlying “essentialist” preference structure for majors is controlled. Moreover, the gender gap in risk behavior is larger for the first choice than it is for the considered options taken together.²¹ The evidence that the gender gap in risk orientation disappears in the second-choice selection of major sheds light on the nature versus nurture debate that surrounds the issue of gender gaps in psychological attributes (see Bertrand [2010] for a review of recent literature). Our findings suggest that in making educational choices, the gender gaps in risk aversion, competitiveness, and confidence are situational. Our results do not rule out the possibility of biological grounds for the gender gap in risk aversion, but they do suggest that innate differences, if they indeed exist, are moderated by environmental forces.

Table 4A.

Multinomial Preferences Model: Effects of Expected Wage and Difficulty of Being Accepted, by Gender, on the First Choice, TECH

	F (1)	M (2)	F (3)	M (4)
Decile 1: most risky	−0.804† (0.070)	−2.205† (0.051)	−1.417† (0.106)	−0.765† (0.073)
Decile 2	−0.470† (0.050)	−1.223† (0.035)	−0.810† (0.068)	−0.388† (0.047)
Decile 3	−0.143† (0.042)	−0.617† (0.029)	−0.325† (0.050)	−0.100† (0.035)
Decile 4	0.207† (0.036)	0.017 (0.026)	0.128† (0.039)	0.272† (0.028)
Decile 6	−0.565† (0.041)	−0.353† (0.030)	−0.517† (0.044)	−0.594† (0.031)
Decile 7	−1.201† (0.050)	−0.819† (0.036)	−1.115† (0.056)	−1.311† (0.040)
Decile 8	−1.887† (0.061)	−1.301† (0.046)	−1.766† (0.072)	−2.029† (0.054)
Decile 9	−2.829† (0.081)	−1.742† (0.059)	−2.625† (0.098)	−2.738† (0.070)
Decile 10: least risky	−4.141† (0.117)	−2.600† (0.088)	−3.673† (0.142)	−4.032† (0.105)
Wage	−0.014† (0.003)	0.239† (0.003)
Controls for major dummy variables:	N	N	Y	Y
Observations	221,905	485,506	221,905	485,506

Note: Standard errors in parentheses.

^†p < 0.01

Table 4B.

Multinomial Preferences Model: Effects of Expected Wage and Difficulty of Being Accepted, by Gender, on the Second Choice, TECH

	F (5)	M (6)	F (7)	M (8)
Decile 1: most risky	−1.834† (0.080)	−3.164† (0.056)	−2.011† (0.117)	−1.874† (0.079)
Decile 2	−1.187† (0.056)	−1.908† (0.038)	−1.296† (0.075)	−1.197† (0.051)
Decile 3	−0.649† (0.046)	−1.070† (0.031)	−0.700† (0.054)	−0.618† (0.037)
Decile 4	−0.127† (0.040)	−0.354† (0.027)	−0.144† (0.042)	−0.125† (0.029)
Decile 6	−0.262† (0.040)	−0.047* (0.027)	−0.269† (0.042)	−0.276† (0.029)
Decile 7	−0.511† (0.044)	−0.311† (0.031)	−0.532† (0.050)	−0.764† (0.036)
Decile 8	−1.097† (0.052)	−0.608† (0.036)	−1.120† (0.065)	−1.273† (0.045)
Decile 9	−1.575† (0.060)	−0.993† (0.045)	−1.588† (0.081)	−1.900† (0.058)
Decile 10: least risky	−2.795† (0.088)	−1.670† (0.063)	−2.753† (0.120)	−2.933† (0.085)
Wage	−0.015† (0.004)	0.221† (0.003)
Controls for major dummy variables:	N	N	Y	Y
Observations	213,576	467,262	213,576	467,262

Note: Standard errors in parentheses.

^†p < 0.01;

^*p < 0.1

Figure 5.

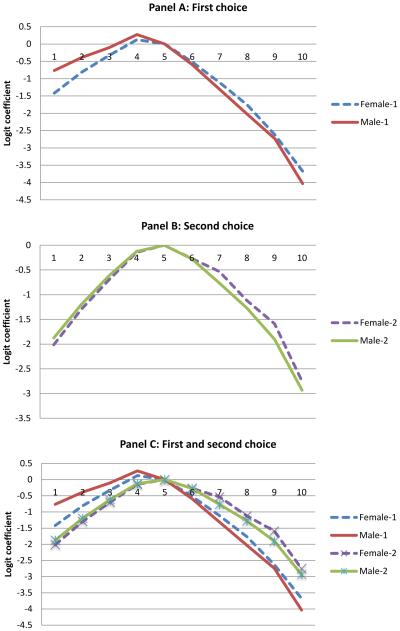
Multinomial Preferences Model: Effects of Difficulty of Being Accepted on First-choice and Second-choice TECH. Based on the results of Tables 4A and 4B (A) First choice, controlling for major dummy variables. (B) Second choice, controlling for major dummy variables. (C) First and second choices, controlling for major dummy variables.

We next fit a model for the second-choice major, given that the applicant had already made a first choice, which gives the second dimension of coefficients in the multinomial rank-ordered logit model. This step estimates the weights of factors that determine an applicant’s second choice and allow us to contrast the decision process separately for second choices and for first choices. The second part of Tables 4A and 4B show the set of coefficients in the second-choice model (without and with fixed effects). Two findings are evident from the comparison of the coefficients in Tables 4A and 4B for the first and second choices. The first finding is that women and men differ in the importance of expected wages when deciding on their second choice, just as was true for their first choice. Women applicants to the Technion pay no attention to expected wages for either their first or their second-choice major (the coefficients are negative but small in magnitude), whereas male applicants to the Technion put considerable weight on expected wages in deciding both choices. The second finding is that both women and men are more risk averse in their second-choice application than in their first, but the shift toward risk aversion is much larger for male than for female applicants. Figure 5B charts these coefficients for the second choice by gender, and Figure 5C shows the coefficients for both choices. Male applicants to the Technion are as risk averse in their second-choice major as are women. To put it another way, men are considerably more willing to apply to risky majors for their first choice than are women, whereas for the second choice, the men are as much focused on risk as are the women.

The strategy just described corresponds to a behavioral decision process in which applicants first determine their top choice, and then determine their second choice from the remaining options (a sequential multinomial preferences model). An alternative conceptualization, however, is that applicants first narrow their choices to a set of considered options, and then in a second step, they decide which of the considered options is their first choice (a considered options multinomial preferences model). We discuss these alternatives for the multinomial preferences model in Appendix B. With the data at hand, we cannot adjudicate between the sequential multinomial preference process and the considered options multinomial preference process, and it is even possible that students differ in which of these preference models more accurately corresponds to their decision-making process. The results from the two models, however, are very similar; applicants are more likely under either model to take a greater risk for their top choice than for the second choice, and both models show that men take more risks than women.

The Sex Composition of Fields

We next test the possibility that the sex composition of fields (and occupations) is an important criterion in shaping women’s choices, and we specifically test the hypothesis that sex composition is a weaker criterion for deciding on the second choice (or—equivalently—for deciding on the set of seriously considered options) than for deciding on the first choice. We perform this test in two ways. First, we use the predicted major choices for the applicants from a model with dummy variables for each major to compute the index of dissimilarity for the first choices and for the second choices as well as from the unidimensional preferences model, and we compare these values directly. Second, we include a one-year lagged value for each major’s sex composition of the majors, and we compare the coefficient of sex composition for the unidimensional preferences model and for the multinomial preference model. The results from these tests are displayed in Table 5.

Table 5.

Measures of the Impact of Gender Composition in the Major on the Pattern of Applications, TECH

	Index of Dissimilarity	% Female in Major
		Coef.	SE
Unidimensional preference model	0.414	0.020	(.001)
Multinomial preferences model:
First choice of all alternatives	0.434	0.026	(.001)
Second choice of remaining alternatives	0.367	0.016	(.001)

Note: The coefficient for percentage female in major is from the model estimated on female applicants only.

The first column of Table 5 shows the index of dissimilarity of the distribution of predicted majors under alternative models for the major choice process at both institutions. The level of segregation predicted by the unidimensional preferences model (D = .414) is lower than is predicted for the first choice under the multinomial preference model (D = .434). Moreover, the table clearly shows that first-choice majors at the Technion are more gender segregated than are second-choice majors (D = .367) and that this difference is statistically significant. A difference of 0.434 and 0.367 is large enough to be of substantive importance; it equals the change in the index of dissimilarity measure for gender segregation of occupations in the U.S. labor force between 1980 and 2000 (Blau et al. 2012) or the overall change in gender segregation in fields of study for BA recipients in the United States between the late 1980s and the present (Mann and DiPrete 2013).

One might argue that the lower level of segregation visible in predicted second-choice options relative to first-choice options is driven not by differences between female applicants’ orientation and behavior but rather by changes in male behavior that imply strategic behavior in the process of selecting the first- and second-choice major. According to this interpretation, men prefer male-dominated, high-paying, hard-to-get-into majors, and they use more gender-integrated majors as second-choice backups to their often more high risk first choices. Though there is certainly some truth to this interpretation, it is not the whole story. Partly this is because women’s risk preferences also differ significantly between their first and second choices, even if the difference in this regard for women is not as large as it is for men.²² Importantly for our theory, moreover, women’s first and second choices differ in their response to the gender composition of majors. To show this, we next focus only on the female applicants and analyze the implications of the percentage female in a major on a woman’s choice patterns. The second column in each panel of Table 5 shows that the impact of the percentage female of a major on a female applicant’s major choice is stronger on her first-choice major than on her second-choice major. At the Technion, every one percentage point increase in the sex composition of a major increases a woman’s odds of applying to that major as her first choice by 2.6 percent but only increases her odds of applying to the major as a second choice by 1.6 percent. This difference is statistically significant.²³

One might imagine that high-ranking choices for women would be more female dominated than low-ranking choices purely as a consequence of women preferring majors that have higher proportions that are female (in the same way that a person who likes chocolate will rank more chocolaty desserts higher than less chocolaty desserts). Our results, however, imply that women applicants have an accelerated preference for female-dominated majors for the first choice relative to the second choice (by analogy, the selected dessert is even more chocolaty than one would predict about a diner’s preference for chocolate based on knowing the two desserts that were in contention for the final choice out of the entire menu of desserts). The distribution of STEM majors would be less gender segregated than it is if women’s preference for a high percentage female major (or—perhaps more accurately from a theoretical perspective—for whatever characteristics they see in prospective majors that produce gender segregation) were the same for the first-choice major as for the second-choice major (or, equivalently, for the set of options they seriously consider before selecting a top choice).

Discussion

The results of this study contribute several key insights to the literature on gender inequality in higher education and in the labor market. The first pertains to the decision-making process for selecting a college major. After the list of options has been narrowed to a few favorites, university applicants use different criteria to decide whether an alternative is near the top of their preferences and whether it is their first choice. We show that the multinomial preference model, in which applicants use different utility weights for the considered majors and the top choice, is more appropriate for describing the formation of the choice set. In particular, women’s preference for female-dominated fields and men’s preference for lucrative and competitive fields are not constant across all ranked options. As a result, sex segregation in the broader choice set of considered majors is lower than in the first-choice selections.

The empirical support for the multinomial preference model in the formation of women’s and men’s choices points to the possibility of a process of social change. In a world where gender norms are becoming more egalitarian but where gender stereotypes remain salient, our findings demonstrate that attitudes and orientations toward fields of study in college are less constrained by gendered institutions and traditional forces than are attitudes toward an applicant’s top choice. The results suggest that egalitarian forces have a stronger influence on young women’s and men’s orientation toward sex roles than is visible in the gender segregation of STEM majors. However, their effect on the final choice of field of study is still weak as it is moderated by cultural perceptions about gender identity and gender differences in competence (Correll 2004). Our results confirm just how powerful these traditional forces are: they curb the aspirations and career choices of women with the highest levels of academic competence and quantitative skills and, over time, can outweigh the effect of egalitarian forces. This supports Charles and Grusky’s (2007) view that horizontal sex segregation is not a residual pattern that is destined to wither away as culture evolves. At the same time, our findings that orientations are less segregated than actual behaviors resist their notion that segregation is an organic feature of modern economies and that egalitarianism failed to alter the choices made by men and women. Our results, therefore, suggest that there is room for optimism.

Further research should systematically assess the pattern and pace of social change. It should examine whether change is occurring in the considered option sets of applicants, whether change is occurring in the top choice major, and whether the changes in the considered options set are more rapid than are the changes in the top choice major. The period of time covered by these data is one of relatively weak trends in the gendered character of major preferences. In this way, the Israeli data are similar to data for the United States (Mann and DiPrete 2013), where recent trends are also weak. Nonetheless, when change picks up again or when more years of data are available in the contemporary world of slow change, we predict that additional data will show that change comes more quickly to the considered options set than it does to the final choice itself. If true, such a finding would also imply that behavioral change is a multipart process in which people first take an option seriously and then more seriously before they finally begin to behave in ways that reveal their shifting orientations. This perspective, we argue, applies to other choice situations where the gender gap has narrowed. Occupational decisions, relocation decisions, and decisions about household division of labor are all examples where trends in considered options may lead trends in behavior.

Another interesting question is how social change is transmitted. Is there a group of early adopters of egalitarian views? It is possible that the STEM-bound applicants we study here are members of a group that is most strongly influenced by egalitarian forces and, as such, they signal the prospect of social change because their behavior will influence the orientations and behavior of others. If this is the case, then our findings are predictive of the process of social change that will spread to other groups in the population. More data are needed to establish the validity of our prediction as well as to understand how the barriers between attitudes and behavior erode over time.