Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Jul 1.
Published in final edited form as: Laryngoscope. 2016 Nov 22;127(7):E225–E230. doi: 10.1002/lary.26410

Dynamic nanomechanical analysis of the vocal fold structure in excised larynges

Gregory R Dion 1, Paulo G Coelho 2, Stephanie Teng 1, Malvin N Janal 3, Milan R Amin 1, Ryan C Branski 1
PMCID: PMC5440222  NIHMSID: NIHMS824841  PMID: 27873325

Abstract

Introduction

Quantification of clinical outcomes after vocal fold (VF) interventions is challenging with current technology. High speed digital imaging and optical coherence tomography (OCT) in excised larynges assess intact laryngeal function, but do not provide critical biomechanical information. We developed a protocol to quantify tissue properties in intact, excised VFs using dynamic nanomechanical analysis (nanoDMA) to obtain precise biomechanical properties in the micrometer scale.

Methods

Three pig larynges were bisected in the sagittal plane, maintaining an intact anterior commissure, and subjected to nanoDMA at nine locations with a 250μm flat-tip punch and frequency sweep load profile (10–105Hz,1000μN peak force) across the free edge of the VF and inferiorly along the conus elasticus.

Results

Storage, loss, and complex moduli increased inferiorly from the free edge. Storage moduli increased from (mean and range) 32.3kPa (6.5–55.38) at the free edge to 46.3kPa (7.4–71.6) 5mm below the free edge, and 71.4kPa (33.7–112) 1cm below the free edge. Comparable values were 11.6kPa (5.0–20.0), 16.7kPa (5.7–26.8), and 22.6kPa (9.7–38.0) for loss modulus, and 35.7kPa (14.4–56.4), 50.1kPa (18.7–72.8), and 75.4kPa (42.0–116.0) for complex modulus. Another larynx repeatedly frozen and thawed during technique development had similarly increased storage, loss, and complex modulus trends across locations.

Conclusions

NanoDMA of the intact hemilarynx provides a platform for quantification of biomechanical responses to a myriad of therapeutic interventions to complement data from high speed imaging and OCT.

Level of Evidence

N/A

Keywords: larynx, vocal fold, mechanical testing, storage moduli, loss moduli, complex moduli, Tan Delta, voice

INTRODUCTION

Physiologically relevant, pre-clinical models are crucial for the development and refinement of therapies across disease processes. The development of novel therapies for laryngeal abnormalities, however, is likely hindered by the lack of standardized means to fully ascertain the impact of interventions on vocal fold function given the profound and unique biophysical demands placed up this specialized tissue. Although significant resources have been dedicated to quantifying the precise biomechanical properties of these tissues, the specific techniques are neither standardized nor optimized.1,2 Furthermore, traditional histological outcomes do not adequately capture vocal fold dynamics; advanced biomechanical assessment of the vocal folds is critical.

Ideally, biomechanical properties of VFs could be easily obtained in vivo in both pre-clinical and clinical scenarios. In spite of innovative work dating back several decades, high speed digital imaging and four-dimensional optical coherence tomography do not provide quantifiable insight into the inherent mechanical properties of the vocal folds.3,4 Researchers continues to seek ideal techniques to clarify both the relevant dependent and independent variables germane to vocal fold tissue. Dynamic models in excised larynges using force-elongation measurement, torsional parallel-plate rheometry, simple-shear parallel plate rheometry, linear skin rheometry, and, more recently, indentation have all been employed to assess these properties in vocal folds.2,5 These techniques each have benefits and limitations. Our laboratory and others recently described indentation-based methods that hold significant promise for precise assessment of mechanical vocal fold tissue properties.6,7 As initially described by Chhetri et al, indentation was employed to obtain data regarding the elastic properties of the vocal folds.6,8,9 In one study, static measurements of bisected larynges in various forms were obtained, and in the other, the explanted cover layer of the true vocal fold was tested. These two studies were the first application of this technique to vocal fold tissue. The vocal fold cover elastic modulus varied from 4.7–5.4kPa on the superior medial surface to 6.0–7.3kPa on the inferior medial surface.6,9 These measures, however, only included a portion of the multilayer vocal fold normally held under tension at rest and during phonation. When the ligament and muscle were included, mid-membranous TVF Young’s modulus values were 5.3–13.1kPa in the intact hemilarynx.6

The goal of that preliminary study was to quantify Young’s modulus (elastic modulus), a static material property. As phonation is dynamic with airflow through the larynx producing a soft tissue mucosal wave originating in the conus elasticus extending to the free edge of the true vocal fold, measurement of viscoelastic dynamic properties are likely more clinically relevant. As compared to static measurements where stress and strain are assessed after application of a set force and elastic and/or plastic deformations measured, dynamic testing of viscoelastic materials is designed to quantify the elastic and viscous contributions that vary across a frequency spectrum of interest. Adapting viscoelastic measurements using the recent indentation measurement platform could provide clinically-relevant and precise mechanical property measurements not previously feasible.

The storage modulus, loss modulus, complex modulus, and Tan Delta reflect these viscoelastic properties. The storage modulus represents elastic stored energy within the material, is associated with the “stiffness” of a material, and is related to the static Young’s Modulus. The loss modulus represents the viscous portion of a material that, in practice, is lost as heat and allows for some resistance to flow and generation of a mucosal wave in a vocal fold. The complex modulus is the ratio of stress to strain during vibration and has both real and imaginary components that relate to stored potential energy released on deformation and energy lost as heat during this deformation. Finally, the Tan Delta reflects a material’s ability to absorb energy, essentially the damping in the system, and is the ration of the loss and storage moduli. Tan Delta reflects the viscous versus elastic properties of a tissue and is measured as the tangent of the phase angle between the storage and loss modulus. At the most fundamental biologic level, these properties quantify macroscopic reactions to external forces and have been thoroughly described in the material science of polymers. These dynamic properties are most relevant to studying biologic tissues under motion. Our laboratory recently described a novel technique to assess explanted vocal folds utilizing the dynamic mechanical analysis capabilities of a nano-indenter (nano-DMA).10

In nano-DMA, a small probe contacts the surface of a material and applies variable forces in a non-destructive manner. The resulting force and material displacement are recorded, yielding both static and viscoelastic dynamic material properties. Nano-DMA has been applied to a variety of soft tissues and viscoelastic materials.11–14 Biological tissues tend to be anisotropic with significant variation in tissue properties within the same tissue type due to changes in measurement orientation. This anisotropy makes testing biological tissues particularly challenging. In this regard, our previous technique involved embedding the larynx in poly-methyl-methacrylate (PMMA). These blocks were then sectioned, potentially altering the inherent tissue properties limiting the accuracy and utility of the technique. To address this limitation, we refined our technique to employ nano-DMA on whole larynges, as maintenance of the intact larynx is likely critical to the biomechanical properties.

METHODS

Tissue Preparation and Setup

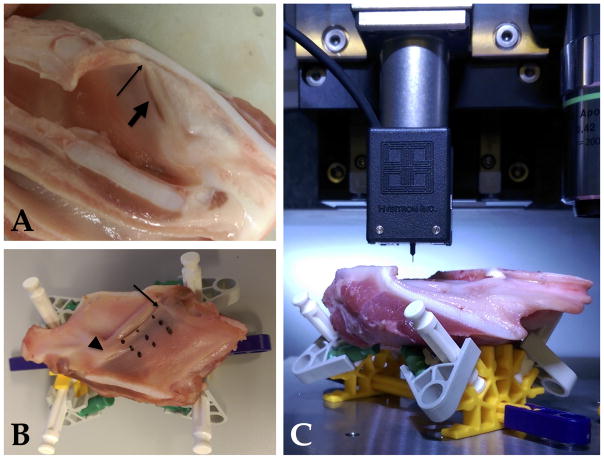
Fresh female pig larynges were flash frozen to −80°C. In preparation for testing, they were stored at −20°C for at least 24 hours. A tissue band saw with moisture applied to the sample was employed to prepare the tissue. Careful attention was paid to maintain an intact anterior commissure (Figure 1A). Prepared specimens were then thawed at 4C° for 2–4 hours and then maintained at room temperature. To avoid erroneous damping or movements during dynamic testing, a custom constructed apparatus was designed (Figure 1B and 1C). Testing was performed in a single setting on each of the three specimens. An additional specimen was tested and refrozen, thawed, and retested, to evaluate the influence of refreezing. During thawing, a marker was used to note three locations across the free edge of the true vocal fold; one near the anterior commissure, one mid-fold, and one near the vocal process. Using digital calipers to measure 5mm and 1cm inferior to the free edge of the true vocal folds, markings were made in similar locations (Figure 1B). Each specimen was marked in identical locations. Three specimens were employed for analysis and a fourth for testing setup.

Figure 1.

Figure 1

Open in a new tab

Nanomechanical testing setup (A). Sectioned hemilarynx with intact anterior commissure (thin arrow) and vocal fold (thick arrow). Testing locations on larynx marked with black ink between the anterior commissure (thin arrow) and vocal process (thick arrow; B). Intact hemilarynx in stabilizing apparatus within the namomechanical testing system (C).

Dynamic Nanomechanical Testing

Dynamic nanomechanical testing was conducted using a Hysitron TI950 TriboIndenter® (Minneapolis, MN). A 250μm, round, flat-tip punch was installed and calibrated per Hysitron protocols. In addition, prior to testing, the system was calibrated daily in both dry and wet environments using the Hysitron Triboscan™ software calibration procedure. A variety of load function values and profiles were assessed to ensure adequate tip-tissue contact and collection of data throughout a variety of frequencies. A 1000μN force was applied over a frequency sweep from 10 to 200Hz with a 220μN setpoint value. All data was recorded using the Hysitron Triboscan™ software.

Data Analysis

Nine locations on each specimen, as shown in Figure 1B, were tested at 15 different frequencies between 10 and 200Hz (10, 23.6, 37.1, 50.7, 64.3, 77.9, 91.4, 105, 118.6, 132.1, 145.7, 159.3, 172.9, 186.4, and 200Hz). Multiple test cycles were completed at each frequency, between 18 and 198 repetitions depending on the frequency, at an average indentation depth of 2,763nm for each cycle (804 data points per location). During testing, room temperature saline was applied to the hemilarynx every 20 minutes to maintain tissue hydration. Dynamic instability, indicated by negative estimates of elastic modulus, was observed above 105Hz and data from those trials were excluded. Intra- and inter-specimen data were compared. A second analysis was completed on specimens tested before and after freezing and thawing to assess the effects of dehydration. Moduli are described as a function of specimen, frequency, and inferior-superior-anterior-posterior position using scatter plots constructed using R and RStudio (v0.99.879).

RESULTS

Figure 2 shows the storage modulus for each specimen as a function of frequency, anterior to posterior (A-P) position, and superior to inferior (S-I) position. Similarly, Figure 3 shows loss modulus for each specimen based on frequency and position. Figures 4 and 5 illustrate complex and Tan Delta findings related to frequency and position, respectively. Uncertainty values were calculated for storage, loss, and complex moduli at each location(Figure 1B). At each location for a single dynamic nanoindentation, the indenter cycled through eight frequency bins of interest between 10–105Hz for each dynamic indentation test. Each of these frequency bins included many indenter cycles while in contact with the tissue (indentations), resulting in standard deviation values for each of the eight frequency bins in all nine sample locations in all three specimens. Given that minimal uncertainty was observed between frequency bins, specimens, and locations on a specimen, ranges of uncertainty measurements are reported. Standard deviations varied between 0.15 and 2.2kPa for storage moduli, 0.02 and 0.58 for loss moduli, and 0.04 and 2.08 for complex moduli. A clear pattern emerged of decreased storage and complex moduli and increased loss modulus with increased frequency. The Tan Delta shifted higher with increasing frequency reflecting more viscous properties at higher frequencies. Moduli were quite consistent across specimens at superior and middle locations (see Figures 2–4), but a generally stiffer response was observed at the inferior location in one specimen. Storage modulus averaged 49.71, 50.29, and 52.07kPa between the anterior, mid, and posterior portions of the vocal fold, respectively, when averaging the horizontal data from all three specimens. Similarly, loss modulus mean values were 16.80kPa, 17.43kPa, and 17.37kPa across the three horizontal positions combining horizontal position data from all specimens. Finally, complex modulus mean values were 53.25kPa, 54.24kPa, and 55.71kPa across the three horizontal positions combining data from all three specimens.

Figure 2.

Figure 2

Open in a new tab

Three-dimensional plot of Storage Modulus values at varying vertical distances in the larynx (from the free edge of the true vocal fold, to 5mm and 10mm inferiorly). Shapes represent the three possible horizontal positions. Circles represent measurements at the anterior true vocal fold, squares represent measurements at the mid portion of the true vocal fold, and plus signs represent measurements at the posterior portion of the true vocal fold. The grid is superimposed on the figure as a function of vertical height and frequency as a function of the changes in storage modulus. A. Specimen 1. B. Specimen 2. C. Specimen 3.

Figure 3.

Figure 3

Open in a new tab

Three-dimensional plot of Loss Modulus values at varying vertical distances in the larynx (from the free edge of the true vocal fold, to 5mm and 10mm inferiorly). Shapes represent the three possible horizontal positions. Circles represent measurements at the anterior true vocal fold, squares represent measurements at the mid portion of the true vocal fold, and plus signs represent measurements at the posterior portion of the true vocal fold. The grid is superimposed on the figure as a function of vertical height and frequency as a function of the changes in the loss modulus. A. Specimen 1. B. Specimen 2. C. Specimen 3.

Figure 4.

Figure 4

Open in a new tab

Three-dimensional plot of Complex Modulus values at varying vertical distances in the larynx (from the free edge of the true vocal fold, to 5mm and 10mm inferiorly). Shapes represent the three possible horizontal positions. Circles represent measurements at the anterior true vocal fold, squares represent measurements at the mid portion of the true vocal fold, and plus signs represent measurements at the posterior portion of the true vocal fold. The grid is superimposed on the figure as a function of vertical height and frequency as a function of the changes in the Complex Modulus. A. Specimen 1. B. Specimen 2. C. Specimen 3.

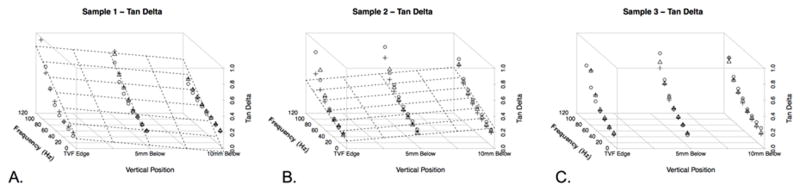
Figure 5.

Figure 5

Open in a new tab

Three-dimensional plot of the Tan Delta values at varying vertical distances in the larynx (from the free edge of the true vocal fold, to 5mm and 10mm inferiorly). Shapes represent the three possible horizontal positions. Circles represent measurements at the anterior true vocal fold, squares represent measurements at the mid portion of the true vocal fold, and plus signs represent measurements at the posterior portion of the true vocal fold. The grid is superimposed on the figure as a function of vertical height and frequency as a function of the changes in the Tan Delta. A. Specimen 1. B. Specimen 2. C. Specimen 3. In Specimen 3, the grid was excluded as the variability precluded a smooth surface plot.

Across the eight frequencies between 10 and 105Hz (10Hz, 23.6Hz, 37.1Hz, 50.7Hz, 64.3Hz, 77.9Hz, 91.4Hz, and 105Hz), a trend towards decreased storage modulus, increased loss modulus, and slightly decreased complex modulus was observed as shown along the frequency axis in Figures 2–5. Across frequency and S-I orientation, storage, loss, and complex moduli were similar at anterior, middle and posterior locations along the length of the vocal fold. With regard to frequency and A-P location, storage, loss, and complex moduli trended higher from superior (free margin of the true vocal fold) to inferior. Storage moduli mean (range) values were 32.3kPa (6.5–55.38) at the free edge, 46.3kPa (7.4–71.6) 5mm below the free edge, and 71.4kPa (33.7–112) 1cm below the free edge. Loss moduli values were 11.6kPa (5.0–20.0), 16.7kPa (5.7–26.8), and 22.6kPa (9.7–38.0) progressing inferiorly. Complex moduli values were 35.7kPa (14.4–56.4), 50.1kPa (18.7–72.8), and 75.4kPa (42.0–116.0) progressing inferiorly as well. In initial setup testing, higher storage, loss and complex modulus values were obtained in the specimen that underwent repeated freeze/thaw cycles. Although all locations were not sampled during this experimental setup, increases of nearly 20 percent or more were seen after repeat freeze-thaw cycles.

DISCUSSION

The development of clinically-relevant models to quantify the biomechanical properties of the vocal folds is critical to the advancement of novel therapeutics from the pre-clinical to the clinical milieus. This initial work using whole organ nanoindentation of the larynx yielded values similar to previous work using force elongation on intact vocal folds.15 As expected in a dynamically-tested composite larynx, the results were larger than isolated static testing of different vocal fold layers, which have static elastic moduli between 2.0 and 13.0kPa as measured in humans and canines.6,16 Although swine vocal folds likely vary compared to other species, the value differences were larger than expected, particularly given the relative anatomic homology between the human and swine vocal folds. Jiang, Raviv, and Hanson reported that the distance from the free margin of the TVF to the cricoid cartilage was the same in humans, swine, and canines.17 The swine TVF was slightly longer (up to 4mm) than human and canine larynges.17 The testing design specifically included an intact anterior commissure and the entire posterior hemilarynx to ensure that preload tissue characteristics from the suspension of the vocal fold between the anterior commissure and the vocal process remain intact. All testing was performed with the nanoindenter tip perpendicular to the tissue, with the setup rotated in between positions to ensure that that tip remained perpendicular to the point of contact.

Currently, no comparable nanomechanical testing data of vocal folds exists. Chhetri et al dissected the vocal fold cover and subjected it to isolated static indentation testing.6 Therefore, no existing preliminary data were available to construct mechanical loading profiles. In dynamic nanomechanical analysis, selection of an appropriate loading profile is crucial to determine mechanical properties of interest. To achieve the primary goal of assessing different locations across the vocal folds, a frequency sweep load profile at 1,000μN permitted frequency-specific analysis.

Storage moduli increased and loss moduli decreased from the free edge inferiorly. These changes reflect a “stiffer” material or general stiffening of the material towards the subglottis. This finding correlates to anatomical differences as the vocal fold cover is essentially draped over the thyroarytenoid muscle at the free margin and then has much less soft subcutaneous support inferiorly. Similarly, the values obtained at the three locations in the anterior to posterior dimension at each of the vertical positions were similar. These data likely suggest that vertical position relative to the free edge of the true vocal fold may have important mechanical property differences when evaluated as composite tissue (mucosal layer and underlying tissues combined). As noted in Chhetri et al’s static indentation study, a subtle increase in Young’s modulus was noted moving inferior from the superior surface of the vocal fold cover.

Nanomechanical testing using this technique is also time-dependent to avoid tissue dehydration. As demonstrated by Balooch and colleagues using dentin in an oral surgery study, tissue dehydration associated with prolonged testing or freeze-thaw cycling resulted in elevated storage modulus values even after rehydration.18 Our data concur; a single sample was tested multiple times to verify system setup. Continued testing with intermittent saline hydration is critical to obtain repeatable and accurate results.

No current soft tissue mechanical testing standards exist relating to nanoindentation or nanomechanical analysis. However, the use of a flat tip punch eliminates secondary uncertainty that would originate from the use of a conical, spherical, or Berkovich tip (three-sided pyramidal design for indentation of hard materials). Using a non-flat indentation tip creates the potential for sample contact area to change as the contact surface area is used to determine results. In this study, varying initial setpoint forces were assessed until values plateaued to ensure that tip contact was complete. By verifying the setpoint force was a value where complete tip-tissue contact occurred and using a frequency sweep load profile, accurate frequency-dependent effects were obtained. The minimal standard deviation ranges noted between each frequency bin, location, and specimen supported this measurement accuracy.

This initial study was not without limitations. As the current study sought to determine feasibility, only three samples were included. Larger sample size would permit comprehensive assessment of absolute values of mechanical properties across tissue position. Furthermore, repeated testing of sample locations would provide additional data for statistical analyses. However, in mechanical material analysis, the risk of local deformation would cause secondary testing results to be altered due to inherent tissue characteristic changes. In the case of composite soft tissues such as the vocal folds, localized changes may result in changes to tissue in the immediate vicinity of deformation. This change in local tissue properties was found in preliminary testing repeated adjacent to the prior indentation, even at indentation depths of only 2,763nm. Thus, measurements were made only once in each target location.

In addition, despite a number of tissue adjustments and testing refinements, dynamic instability persisted at frequencies above 105Hz. Based on manufacturer experience with soft tissue work during operational development, this instability is suspected to be secondary to buildup of moisture within the specimen or between the specimen and indentation tip. The inclusion of water between the tip and tissue would then result in nonsensical data, as the tip and tissue would no longer be in synchronous motion with the movement of water in the system. As vocal fold tissues are both moist and have liquid within the layers, overcoming this artifact was challenging. Testing techniques to increase initial tip-tissue contact setpoint parameters and allowing for additional lag within the system were not successful at addressing this issue. As typical phonation frequencies exceed this range, additional work is required to ensure the system mimics human phonatory frequencies. However, the tested frequencies do carefully match those used previously with other measurement techniques.

CONCLUSION

NanoDMA of the intact hemilarynx provides a platform for quantification of biomechanical responses to a myriad of therapeutic interventions to complement data from high speed imaging and OCT. This initial experiment demonstrated feasibility of whole-organ nanoindentation of the hemilarynx and yielded initial information regarding tissue properties relative to regions of the larynx. This model also serves as a basis to continue mechanical testing of the intact hemilarynx.

Acknowledgments

Funding for the work described in this manuscript was provided, in part, by the National Institutes of Health/National Institute on Deafness and Communication Disorders (RO1 DC013277; Principal Investigator-Branski)

Footnotes

Contents of this manuscript were accepted for presentation at the American Laryngological Association for consideration for presentation at the upcoming Combined Otolaryngology Spring Meetings.

The authors have no conflicts of interest or financial disclosures.

References

  • 1.Miri AK. Mechanical characterization of vocal fold tissue: a review study. J Voice. 2014;28:657–667. doi: 10.1016/j.jvoice.2014.03.001. [DOI] [PubMed] [Google Scholar]
  • 2.Dion GR, Jeswani S, Roof S, Fritz M, Coelho P, Sobieraj M, Amin MR, Branski RC. Functional Assessment of the ex vivo vocal folds through biomechanical testing: A review Materials science & engineering C. Materials for biological applications. 2016;64:444–453. doi: 10.1016/j.msec.2016.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Deliyski DD, Hillman RE. State of the art laryngeal imaging: research and clinical implications. Current opinion in otolaryngology & head and neck surgery. 2010;18:147–152. doi: 10.1097/MOO.0b013e3283395dd4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Chang EW, Kobler JB, Yun SH. Triggered optical coherence tomography for capturing rapid periodic motion. Sci Rep. 2011;1:48. doi: 10.1038/srep00048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Chhetri D, Berke G, Lotfizadeh A, Goodyer E. Control of vocal fold cover stiffness by laryngeal muscles: a preliminary study. Laryngoscope. 2009;119:222–227. doi: 10.1002/lary.20031. [DOI] [PubMed] [Google Scholar]
  • 6.Chhetri DK, Zhang Z, Neubauer J. Measurement of Young’s modulus of vocal folds by indentation. J Voice. 2011;25:1–7. doi: 10.1016/j.jvoice.2009.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Coelho PG, Sobieraj M, Tovar N, et al. Preliminary investigation of a novel technique for the quantification of the ex vivo biomechanical properties of the vocal folds. Materials science & engineering C, Materials for biological applications. 2014;45:333–336. doi: 10.1016/j.msec.2014.08.051. [DOI] [PubMed] [Google Scholar]
  • 8.Chhetri DK, Zhang Z, Neubauer J. Measurement of Young’s modulus of vocal folds by indentation. J Voice. 2011;25:1–7. doi: 10.1016/j.jvoice.2009.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Chhetri DK, Rafizadeh S. Young’s modulus of canine vocal fold cover layers. J Voice. 2014;28:406–410. doi: 10.1016/j.jvoice.2013.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Coelho PG, Sobieraj M, Tovar N, et al. Preliminary investigation of a novel technique for the quantification of the ex vivo biomechanical properties of the vocal folds. Mater Sci Eng C Mater Biol Appl. 2014;45:333–336. doi: 10.1016/j.msec.2014.08.051. [DOI] [PubMed] [Google Scholar]
  • 11.Nayar VT, Weiland JD, Hodge AM. Macrocompression and nanoindentation of soft viscoelastic biologic materials. Tissue Eng Part C Methods. 2012;18:968–975. doi: 10.1089/ten.TEC.2012.0034. [DOI] [PubMed] [Google Scholar]
  • 12.Nayar VT, Weiland JD, Hodge AM. Elastic and viscoelastic characterization of agar. Mech Behav Biomed Mater. 2012;7:60–68. doi: 10.1016/j.jmbbm.2011.05.027. [DOI] [PubMed] [Google Scholar]
  • 13.Akhtar R, Schwarzer N, Sherratt MJ, et al. Nanoindentation of histological specimens: Mapping the elastic properties of soft tissues. J Mater Res. 2009;24:638–646. doi: 10.1557/JMR.2009.0130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Ebenstein DM, Pruitt LA. Nanoindentation of soft hydrated materials for application to vascular tissues. J Biomed Mater Res. 2004;69:222–232. doi: 10.1002/jbm.a.20096. [DOI] [PubMed] [Google Scholar]
  • 15.Perlman A, Titze IR, Cooper D. Elasticity of canine vocal fold tissue. J Speech Hear Res. 1984;27:212–219. doi: 10.1044/jshr.2702.212. [DOI] [PubMed] [Google Scholar]
  • 16.Hess M, Mueller F, Kobler JB, Zeitels SM, Goodyer E. Measurements of Vocal Fold Elasticity Using the Linear Skin Rheometer. Folia Phoniatr Logop. 2006;58:207–213. doi: 10.1159/000091734. [DOI] [PubMed] [Google Scholar]
  • 17.Jiang JJ, Raviv JR, Hanson DG. Comparison of the phonation-related structures among pig, dog, white-tailed deer, and human larynges. Ann Otol Rhinol Laryngol. 2001;110:1120–1125. doi: 10.1177/000348940111001207. [DOI] [PubMed] [Google Scholar]
  • 18.Balooch M, Wu-Magidi IC, Balazs A, et al. Viscoelastic properties of demineralized human dentin measured in water with atomic force microscope (AFM)-based indentation. J Biomed Mater Res. 1998;40:539–544. doi: 10.1002/(sici)1097-4636(19980615)40:4<539::aid-jbm4>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]

RESOURCES