Asymmetric osmotic water permeation through a vesicle membrane

Abstract

Understanding the water permeation through a cell membrane is of primary importance for biological activities and a key step to capture its shape transformation in salt solution. In this work, we reveal the dynamical behaviors of osmotically driven transport of water molecules across a vesicle membrane by molecular dynamics simulations. Of particular interest is that the water transport in and out of vesicles is highly distinguishable given the osmotic force are the same, suggesting an asymmetric osmotic transportation. This asymmetric phenomenon exists in a broad range of parameter space such as the salt concentration, temperature, and vesicle size and can be ascribed to the similar asymmetric potential energy of lipid-ion, lipid-water, lipid-solution, lipid-lipid, and the lipid-lipid energy fluctuation. Specifically, the water flux has a linear increase with the salt concentration, similar to the prediction by Nernst-Planck equation or Fick’s first law. Furthermore, due to the Arrhenius relation between the membrane permeability and temperature, the water flux also exhibits excellent Arrhenius dependence on the temperature. Meanwhile, the water flux shows a linear increase with the vesicle surface area since the flux amount across a unit membrane area should be a constant. Finally, we also present the anonymous diffusion behaviors for the vesicle itself, where transitions from normal diffusion at short times to subdiffusion at long times are identified. Our results provide significant new physical insights for the osmotic water permeation through a vesicle membrane and are helpful for future experimental studies.

I. INTRODUCTION

A cell will change its shape in salt solution due to the osmotic permeation of water molecules through the cell membrane, which also regulates ionic concentrations inside the cell and affects biological activities. Unique dynamical behaviors have been observed when the water molecules permeate across the membrane protein channels, such as aquaporin-1 and Glpf.¹ However, it deserves to note that without any channel involved, water can also diffuse across bilayer membranes, which is energetically unfavorable and the free-energy barriers have been determined for different systems.^2–6 A recent simulation work ascribed the driving force for this process to the potential energy fluctuations of bilayer membranes.⁷ To some extent, this point of view is in agreement with a newest experimental work that shows the evidence of the formation of short-lived nanometer-scale lipid clusters and transient pores, facilitating the passive molecular transport across the bilayer membrane.⁸ Thus, conformation and energy fluctuations should play a key role in the membrane permeation.

Up to now, our knowledge on the transport properties of water molecules through nanometer channels has been dramatically enhanced due to the large number of previous work.^9–17 However, as far as we know, the dynamical behaviors of water across bilayer membranes are still poorly understood. It seems that the water permeation events happen rarely in the bilayer membranes,⁷ and thus it should be a little difficult for simulations to collect enough and reliable water flux. Coincidently, most of the previous atomistic molecular dynamics (MD) simulations focus on the thermodynamics of water permeation through bilayer membranes, summarized by a recent review.¹⁸ Hence, it is necessary and urgent for us to explore the dynamics of membrane permeation, which captures the fundamental features of biological activities and cell shape transformations.

It is well-known that vesicles are closed structures after the self-assembly of amphiphiles, such as lipids, block copolymers, or surfactants and can be thus regarded as “synthetic cells.” Vesicles are versatile since they are synthesized for various purposes. Vesicle shape transformation can greatly help us to recognize the complex shapes of cells¹⁹ triggered by the membrane permeation of water molecules. Meanwhile, recent experimental work inspires some biological and medical applications for vesicles by inserting protein channels such as Aquaporin Z (AQP) and Gramicidin A (GA), where the water permeability can be significantly enhanced by several hundreds of times.^20–24 Without these biological channels, the transient local perturbations, known as “lipid pores,” can also lead to the water flux across lipid bilayers, where the permeability is independent of the ion type in solution.²⁵

From the listing of pervious work above, it is convincible that water can permeate across vesicle membranes and the permeability can be remarkably increased when biological channels are embedded. Nonetheless, our knowledge on the detailed transport properties is still rather poor. This is because unlike computer simulations, it is still difficult for experiments to reveal the dynamics at molecular levels. Meanwhile, the vesicle involved systems are generally quite large, which makes atomistic simulations unaffordable, exemplified by flat bilayer membranes.¹⁸

Consequently, in this work we use large scale coarse-grained (CG) MD simulations to investigate the osmotic water transport through a vesicle membrane in salt solution. The coarse-grained method allows the construction of huge vesicle systems and longer simulation time, facilitating considerable water permeation events. An interesting phenomenon is that when the salt is placed outside vesicles, it can always induce a higher water flux than inside situations, implying an asymmetric transportation. This asymmetric phenomenon can be well deciphered by the bifurcation of the potential energy of lipid-ion, lipid-water, lipid-solution, lipid-lipid, and the lipid-lipid energy fluctuation existing in a wide-range parameter space such as the salt concentration, temperature, and vesicle size. A detailed relation between the water flux and these parameters is uncovered and discussed based on the Nernst-Planck equation or Fick’s first law, as well as the Arrhenius-type equation. These results for the first time reveal the unique osmotic water permeation through a vesicle membrane, enhancing our absent knowledge on the dynamics part and should be helpful to capture the subsequent shape transformations.

II. MODEL AND SIMULATION METHOD

Our previous simulation work demonstrated rich morphology evolutions of both fluid and crystalline vesicles composed of ionic amphiphiles, i.e., −1 palmitic acid (C₁₅–COOH) and +3 trilysine (C₁₆–K₃),¹⁹ where some faceted polyhedron shapes can be an analogy to experiments.²⁶ It deserves to note that in that work and other related simulations, the water volume inside vesicles is always removed partially in order to speed up the osmotic process that takes time beyond the simulation ability. However, in a natural process and experiments, vesicle shape transformation is clearly a result of osmotic water transport. Thus, knowing the osmotic behavior should be of paramount importance to predict the vesicle shape variation and related biological activities. The coarse-grained method should be an excellent tool for addressing this question since the simulation system and time can be enlarged tremendously.

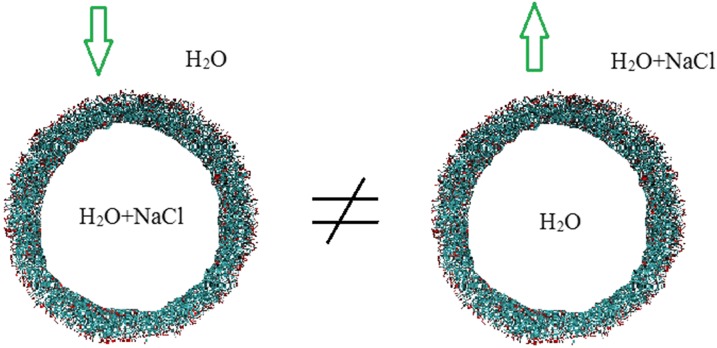
Similar to previous work,^19,26 we use −1 palmitic acid (C₁₅–COOH) and +3 trilysine (C₁₆–K₃) as the building blocks to construct electroneutral vesicles with an average ionization of 30% in the palmitic acid molecules, corresponding to a 4.0 pH value in experiments.²⁶ The elementary ionic amphiphiles can spontaneously form bilayer, spherical vesicles filled with water, where the melting temperature for such bilayer membrane is around 328 K, determined by experiments.²⁶ The numerically synthesized vesicles are several tens of nanometers in size, within the range in experiments.^20–24 The value for the outer diameter is ranging from 28 nm (containing 1000 +3 lipids, 3000 −1 lipids, and 7000 neutral lipids) to 47 nm (with the number of lipids tripled), and a large amount of water molecules and salts (NaCl) are included, corresponding to a system size of 0.6–1.7 × 10⁶ particles. In addition to the vesicle size, we also change the salt concentration and system temperature. Specifically, we consider two independent cases, namely, salt-in and salt-out, shown in Fig. 1. The salt-in implies that the salt solution is inside the vesicle while the outside environment is pure water, and vice versa for the salt-out. These two cases represent two opposite directions of the concentration gradient, similar to the regulation of the ionic balance of cells. Remarkably, the osmotic force will drive the water flow from pure water to the salt solution compartment.

FIG. 1.

Simulation snapshot. Water permeation through a vesicle membrane is induced by the salt concentration difference between the vesicle interior and outside solution. The salt is either inside (left) or outside (right) the vesicle and the arrow implies the water flux direction. The system contains 0.6–1.7 × 10⁶ particles, depending on the vesicle size.

All molecular dynamic simulations were performed using the Gromacs 5.0 software package²⁷ and the MARTINI coarse-grained force field (version 2.1) was used.^28,29 The pressure (1 bar) and temperature were controlled by the Berendsen method.³⁰ The periodic boundary conditions were applied in all directions. The MARTINI force field is generally based on the four-to-one mapping rule, where four heavy atoms are represented by one single interaction bead. According to the capability of hydrogen-bonding or the polarity degree, four main interaction types (polar, intermediate polar, apolar, and charged) and some subtypes are classified. The mapping methodology for the present lipids can be found in the previous work.²⁶ The water molecules are pure interacting beads through the Lennard-Jones (LJ) potential. Unlike channel involved membranes, the water permeation events happen rarely, requesting long simulation time to collect the reliable water flux. To this end, for each set of the system (salt concentration, temperature, vesicle size, salt-in, and salt-out), the simulation time was up to 1 μs and we have conducted two independent runs for each set with different initial states. Error bars were estimated by the two independent runs. It was still time consuming to run the largest system of 1.7 × 10⁶ particles. As we can see that there will be several thousands of water flux through the vesicle membrane after 1 μs MD simulations, and the error bars from the two independent runs are within 5%. Thus, it is believed that 1 μs should be long enough for the present work.

The MARTINI force field^28,29 has optimized especially the long-rage Coulomb interaction to a short-range one with cutoff 1.2 nm, which may cause a higher tendency of the colligative effect than the atomistic method. However, as the current simulation system is very large (0.6–1.7 × 106 particles), the colligative effect should be reduced significantly. Besides, using the MARTINI force field, we can run large systems for a long time, which is beyond the ability of typical atomistic MD simulations. Thus, the coarse-grained (CG) and atomistic methods both have two-sides, and due to the large size of vesicles and the slow osmotic process, we have to use the CG method without considering some atomistic details.

In the frame of MARTINI method,²⁹ water is only described by single CG beads (4-to-1 mapping) through the LJ potential. The partial charges in water are optimized by the LJ well depth and diameter. Although some very detailed properties such as the hydrogen bonds cannot be reflected, the bulk density, the isothermal compressibility, and the diffusion constant can be well reproduced. Thus, the water model should meet the requirement for a general study. We also note that in the MARTINI method, the CG particle can represent a hydrated ion, where the six hydration waters (around a sodium or chloride) are considered to be implicit in the CG ions. In the previous work,²⁹ we can see an excellent match of the pair distributions between the CG and atomistic simulations. The implicit hydration shell indicates strong hydrogen bonding. Although the electrostatic interaction is in short range, the CG ions are expected to model realistic ions from moderate to high ionic strength (above 0.1M). In a similar optimization method for sodium chloride, the CG ions could be used for other salts. As a whole, with regardless of some more detailed atomistic information, the MARTINI method should be successful in modeling the salt solutions.

III. RESULTS AND DISCUSSION

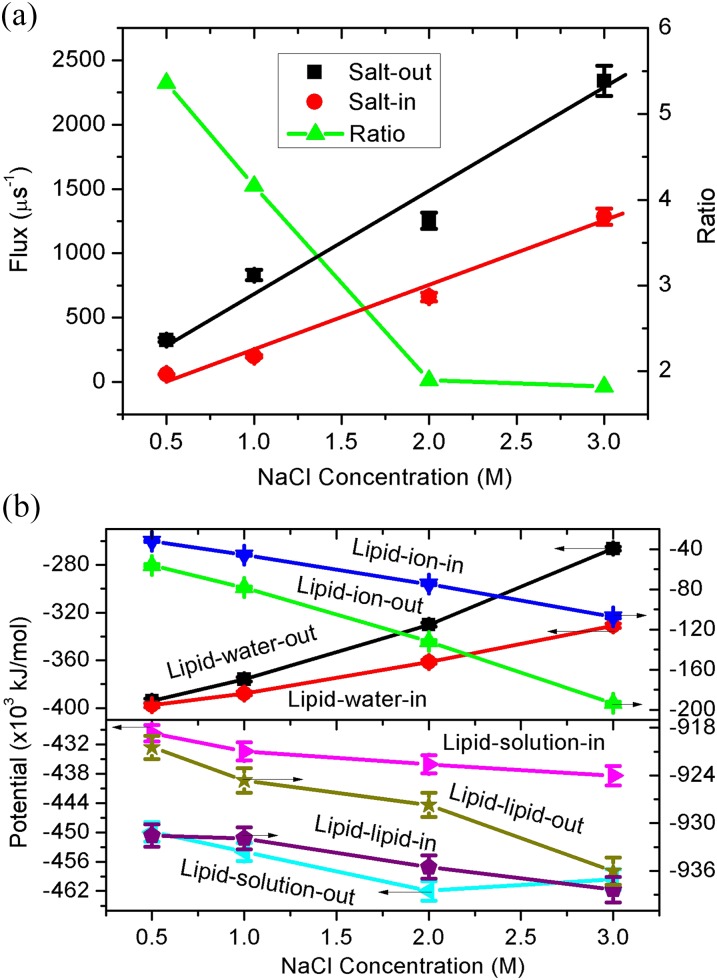
In nature, a cell will regulate its interior ionic balance through the exchange of solution inside and outside the cell membrane. Inevitably, the osmotic water transport happens and depends on the concentration difference between the cell interior and exterior. Herein, to mimic both the vesicle filling and emptying process, we consider the salt-in and salt-out cases, shown in Fig. 1. Clearly, due to the osmotic force, water molecules will transport from the vesicle exterior to interior for the salt-in and vice versa for the salt-out. First, we consider the dependence of water flux on the salt concentration and the results are presented in Fig. 2(a). Herein, the temperature and vesicle diameter are fixed as 350 K and 28 nm, respectively. The vesicle diameter is referred to its initial size. As the water flux amount after 1 μs is still very small compared to the total water volume inside the vesicle (see more details in Sec. IV), the sphere vesicle shape and diameter will be unchanged. The net water flux is determined by the water number difference between the initial and final states, where we count the water number inside the vesicle exactly using a local computer code.

FIG. 2.

(a) Water flux through the vesicle membrane and its ratio as a function of the salt concentration, with the temperature T = 350 K and vesicle diameter R = 28 nm. Lines are linear fittings for the same color data points. The salt-out and salt-in represent that the salt is outside and inside the vesicle, respectively. The flux ratio is salt-out/salt-in. (b) The corresponding potential energy of lipid-ion, lipid-water, lipid-solution, and lipid-lipid as a function of the salt concentration, where salt-out and salt-in also refer to the salt location. Error bars are shown for two independent MD runs.

Apparently, for both the salt-in and salt-out cases, the water flux exhibits linear increases with the salt concentration, similar to the experimental observations for flat membranes.³¹ To our surprise, given that the concentration difference is the same, the flux for salt-out is several times larger than that of salt-in, indicated in Fig. 2(a) by the ratio of salt-out/salt-in. We also note that the slopes for salt-out and salt-in are 730.9 ± 100.7 and 375.9 + 61.9, respectively. Thus, the salt-out case can not only induce higher osmotic water flux but also exhibits higher flux increase rate with the salt concentration. As a whole, the osmotic water transport in and out of a vesicle should be asymmetric and dependent on the direction of the salt concentration gradient. This finding should be insightful and deserves future experiments to pursue. It is believed that if cells also exist similar asymmetric phenomenon, some biological activities should be affected.

In an effort to uncover the reason behind this asymmetric transport, we calculated the potential energy of lipid-ion, lipid-water, lipid-solution (lipid-ion + lipid-water), and lipid-lipid, shown in Fig. 2(b). Overly, we can see clear bifurcations between the salt-in and salt-out cases for all the four interactions. Ions play a nontrivial role in the structures of ionic lipid membranes since the head groups of lipids are charged.³² The values of lipid-ion-out are obviously larger than those of lipid-ion-in. There should be two reasons for this result. First, the NaCl number of salt-out is more than an order (16–18 times) larger than that of salt-in; second, as the bilayer thickness is around 3 nm, the outer surface area is clearly larger than that of inner. Consequently, there should be more ions interacting with the vesicle outer surface, leading to the larger lipid-ion potential energy.

Oppositely, the values of lipid-water-out are smaller than those of lipid-water-in, caused by the similar reasons. For the salt-in case, the pure water outside the vesicle not only has larger number but also can have more interaction surface area with the vesicle. As a whole, there should be a clear competition between the lipid-ion and lipid-water interactions, where the lipid-ion interaction should be dominative because the total lipid-solution interaction exhibits the same behavior as it, e.g., the lipid-solution-out is the larger. Finally, we can see that the interaction of lipid-lipid-out is smaller, which should be caused by the larger lipid-solution-out interaction. This because the larger lipid-solution-out interaction means a higher exposure of lipids to the solution, and thus the likelihood of lipid-lipid contacting will be reduced, resulting in smaller lipid-lipid-out interaction. Up to know, we have found the reason for the asymmetric transport phenomenon above. The smaller lipid-lipid-out interaction implies a more loose structure for the vesicle, facilitating the water transport, while the stronger lipid-lipid-in interaction is corresponding to a more tighten or compact vesicle, leading to the smaller water flux.

For the present work, the osmotic force between the vesicle inner and outer compartments should be a direct driving force. However, for a bilayer membrane in a pure water system, previous atomistic simulations ascribe the permeation events to the potential energy fluctuations of the membrane,⁷ similar to some experimental views, namely, transient local perturbations and “lipid pores.”^8,25 Thus, not only the membrane conformation but also its potential fluctuation should play a key role in the water transport. We thus further compare the fluctuations of the lipid-lipid potential energy for the salt-in and salt-out cases, where the standard deviations are presented in Fig. S1(a) of the supplementary material. We can see that, the potential fluctuation of salt-out is larger than salt-in, meaning more intensive fluctuation of the membrane structures. Therefore, compared to the salt-in case, larger number of lipids will expose to the ions for the salt-out, which makes the higher energy of lipid-lipid and its fluctuation, facilitating the water permeation.

Actually, the flux J(z) of a neutral solute in an inhomogeneous medium through a unit area of the membrane at a depth z can be described by the one-dimensional Nernst-Planck equation¹⁸

$$J\left(z\right)=-D\left(z\right)\frac{dC\left(z\right)}{dz}-C\left(z\right)D\left(z\right)\frac{d\left[\mathit{w}\left(z\right)∕k_{B}T\right]}{dz},$$ (1)

where D(z), C(z), w(z), k_B, and T are the diffusion coefficient, concentration, potential of the mean force, Boltzmann constant, and absolute temperature, respectively. By several steps of mathematical handling,¹⁸ one can obtain the final total flux through the whole membrane

$$J=-\frac{1}{{\int }_{-\frac{L}{2}}^{\frac{L}{2}}\frac{e^{\mathit{w}\left(z\right)∕k_{B}T}}{D\left(z\right)}dz}\left[C\left(L∕2\right)-C\left(-L∕2\right)\right],$$ (2)

where L is the membrane thickness with the center of z = 0, and $\mathrm{\Delta }C=C\left(-L∕2\right)-C\left(L∕2\right)$ is the concentration difference across the membrane in the direction of the positive flux. The permeability coefficient can be

$$P_m=1/{\int }_{-L∕2}^{L∕2}\frac{e^{\mathit{w}\left(z\right)∕k_{B}T}}{D\left(z\right)}dz.$$ (3)

Thus, the flux can be simplified as

$$J=P_m\cdot \mathrm{\Delta }C.$$ (4)

In fact, the Nernst-Planck equation is an extension of Fick’s first law of diffusion that only considers the first term of Eq. (1), and in three dimensions, it has

$$J=-D\nabla \text{C}\text{.}$$ (5)

Both Eqs. (4) and (5) indicate a linear relation between the flux and concentration difference. It deserves to note that the flux and concentration difference should be referred to the same molecular species since molecules will diffuse from a high concentration region to low concentration region. For our current work, the osmotic water flux is clearly flowing from pure water to salt solution and, that is, from high “water concentration” to low “water concentration,” yielding to the linear relation of Eq. (4) or (5). Therefore, to some extent, the Nernst-Planck equation or Fick’s first law should be helpful for us to understand the simulation results.

Although the experimental value for the water permeability of the current ionic lipid bilayer membrane is still unavailable, a recent experimental work has measured the water permeability coefficient for similar lipid bilayers, where the permeability has an Arrhenius relation with the temperature.³³ A theoretical model also indicates Arrhenius relations between the permeability or diffusion coefficients and temperature.³⁴ Actually, the experimental diffusion coefficient for bulk water also has an Arrhenius relation with temperature.³⁵ Thus, according to the Arrhenius-type equation, we should have

$$P_m=P_0\text{exp}\left(\frac{-E_a}{\lambda T}\right),$$ (6)

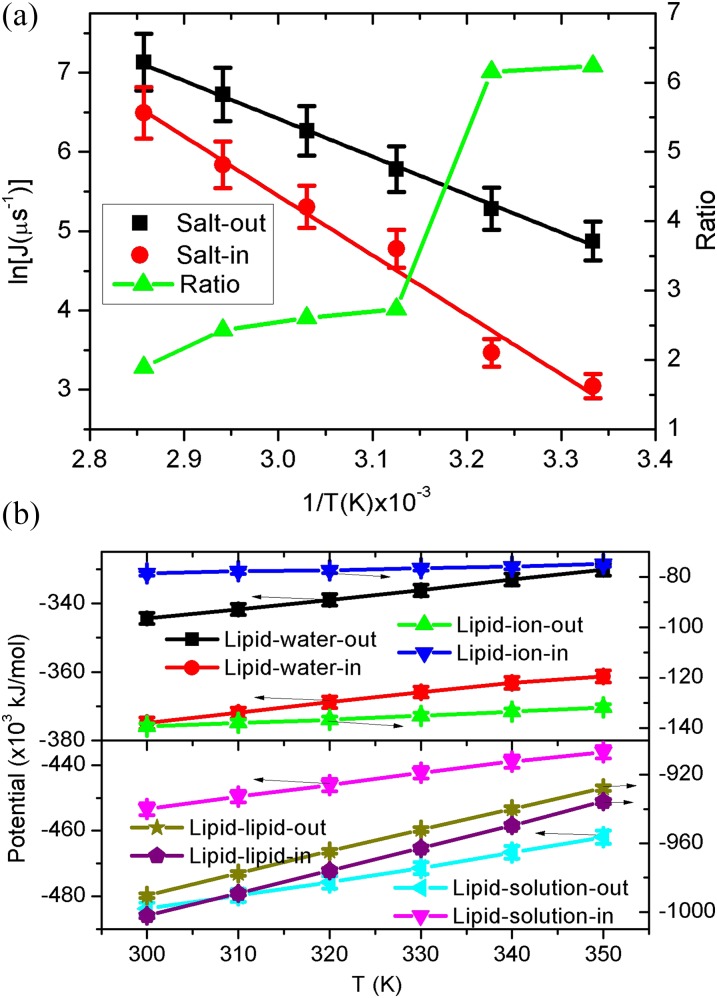
where P₀, Ea, and λ, are the pre-exponential coefficient, activation energy, and universal gas constant, respectively. The combination of Eqs. (4) and (6) will ultimately lead to the Arrhenius relation of the water flux and temperature under a given concentration difference. Interestingly, as seen in Fig. 3(a), our simulation results show excellent Arrhenius behaviors for the water flux with temperature. In addition, we also observe a clear bifurcation of the flux curves for the salt-out and salt-in, where the corresponding ratio varies from 1.9 to 6.2. The slopes for salt-out and salt-in are −4828.4 ± 115.0 and −7484.4 ± 524.3, respectively. According to Eq. (6), the slope is equal to −Ea/λ. To some extent, the active energy herein may be relevant to the potential barrier for water permeation, and the smaller value for salt-out is well corresponding to the larger water flux. Thus, besides the above salt concentration, the asymmetric water transport also exists in a broad range of temperature (300–350 K). We also note that with the increase of temperature, there is a sudden jump for the ratio at T = 320 K, which is close to the experimental melting temperature of T_m = 328 K for the current ionic bilayers.²⁶ This phenomenon indicates that although the crystalline vesicles have less water flux, it has high asymmetric transport tendency than liquid vesicles.

FIG. 3.

(a) Arrhenius plots of the water flux and temperature. Herein, the vesicle is under a given size (outside diameter R = 28 nm) and salt concentration (c = 2M). Lines are linear fittings for the same color data. (b) The corresponding potential energy of lipid-ion, lipid-water, lipid-solution, and lipid-lipid as a function of the temperature.

To further elucidate this asymmetric phenomenon, we also present the potential energy of lipid-ion, lipid-water, lipid-solution, and lipid-lipid, shown in Fig. 3(b). The bifurcation behaviors for the salt-out and salt-in cases are quite similar to those of Fig. 2(b). However, due to the competition between the kinetic and potential energy, all the potentials decrease with the temperature increasing, while a higher salt concentration leads to lower potentials except for the lipid-water. Specifically, as seen in Fig. 3(b), the lower lipid-ion-out potential also overcomes the higher lipid-water-out, resulting in the lower lipid-solution-out. As a result, due to the competition between lipid-solution and lipid-lipid interactions, the lipid-lipid-out has higher values. Meanwhile, the standard deviation of lipid-lipid-out in Fig. S1(b) of the supplementary material also exhibits high values. Thus, similar to the analysis of Fig. 2, the higher water flux for salt-out in Fig. 3(a) can be well deciphered by the higher lipid-lipid-out interaction with larger fluctuation.

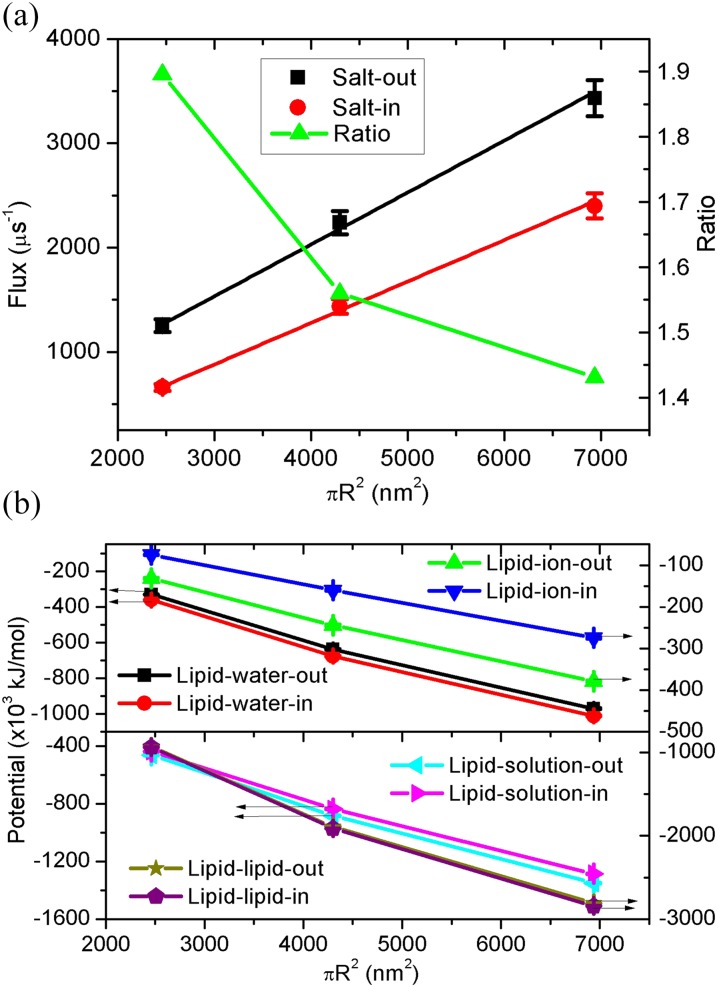
The experimental size of vesicles can be several tens nanometers to micrometers,²⁶ and thus it is necessary for us to consider the effect of the vesicle size. Due to the limitation of computational ability, we only consider the vesicle diameter up to 47 nm. The corresponding simulated system will have 1.7 × 10⁶ particles. We show in Fig. 4(a) the water flux as a function of the vesicle surface area $\text{S}={\mathrm{\pi }\text{R}}^2$. Notably, the flux exhibits a linear increase with S, i.e., J ∼ R². This is because the flux through a unit surface area should be a constant. Furthermore, the water flux of salt-out and salt-in are also distinguishable with a ratio of 1.4–1.9, implying the nontrivial role of the vesicle size in the transport symmetry. The fitting slopes for salt-out and slat-in are 0.50 + 0.03 and 0.40 + 0.02, respectively. Thus, the slat-out case also has a higher water flux and increased rate with the vesicle size. The potential energy is presented in Fig. 4(b), where the lower lipid-ion-out potential overcomes the higher lipid-water-out, leading to the lower lipid-solution-out and ultimately causes the higher values of lipid-lipid-out. Consequently, the higher water flux of salt-out can be also ascribed to the higher lipid-lipid-out potential with larger fluctuations (Fig. S1(c) of the supplementary material).

FIG. 4.

(a) Water flux through the vesicle membrane and its ratio as a function of the surface area $\text{S}={\mathrm{\pi }\text{R}}^2$ under T = 350 K and c = 2M. Lines are linear fittings for the same color data. (b) The corresponding potential energy of lipid-ion, lipid-water, lipid-solution, and lipid-lipid as a function of the surface area.

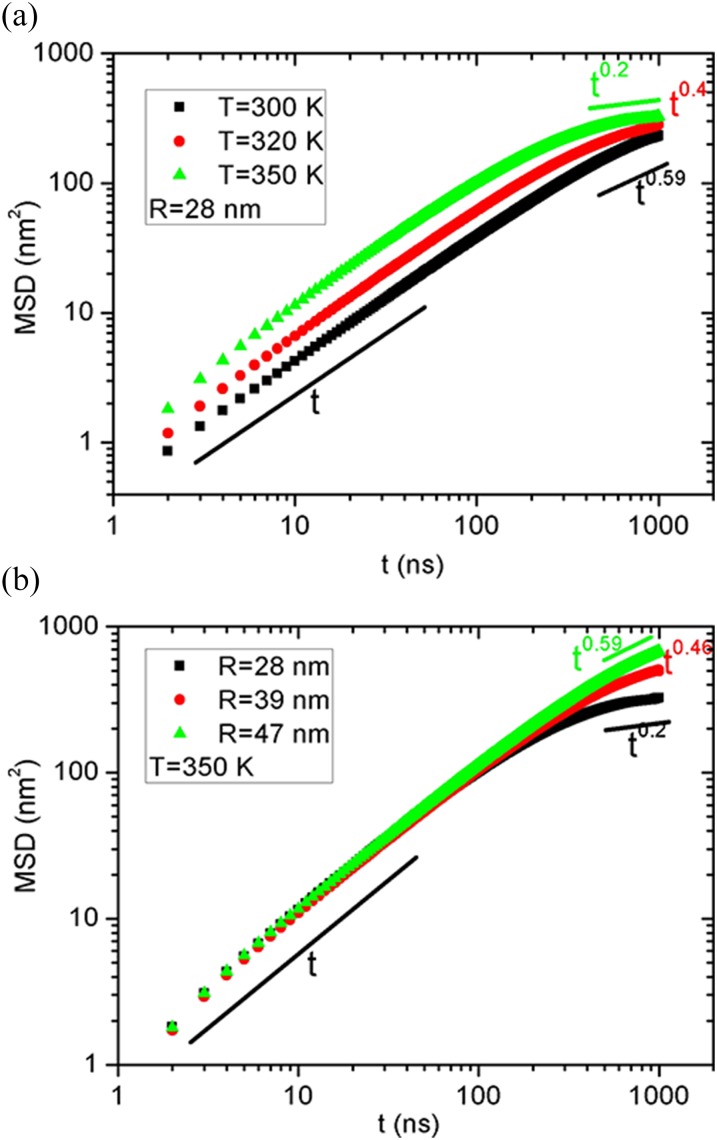
Up to now, we have investigated the permeation of water through a vesicle membrane under different salt concentrations, temperature, and vesicle size, where interesting features of the osmotic water flux are identified and interpreted by the potential energy of lipid-ion, lipid-water, lipid-solution, and lipid-lipid. Finally, we discuss the diffusion behaviors for the vesicle itself. Some recent experiments demonstrated that the motion of vesicles can be triggered by the exchange of ions,³⁶ solution pH gradient,³⁷ or catalysis.³⁸ Meanwhile, some theoretical models for active colloids and vesicles identified anomalous diffusion behaviors.^39,40 In Fig. 5, we show the mean square displacement (MSD) of vesicles under different temperatures and with different diameters. We only presented the salt-out cases since the results of salt-in are quite similar. Interestingly, at different temperatures, the MSD exhibits normal diffusion behaviors for short times; however, it bifurcates to subdiffusion after t = 500 ns. Thus, the dynamics of a vesicle will slow down for a long time. A recent work in different model also demonstrated similar dynamics slowing but the transition is from ballistic to diffusive motion.⁴⁰ Another anomalous phenomenon is that as the temperature increases, the subdiffusion power law index decreases from 0.59 to 0.2, which should be related to the transition from crystalline to liquid state for the vesicle. Similarly, we can also observe the bifurcation from normal diffusion when varying the vesicle diameter, as seen in Fig. 5(b). Notably, the subdiffusion is highly dependent on the vesicle size, and the larger vesicles exhibit more closely to the normal diffusion, observed for the hundred nanometer vesicles in experiments.⁴¹ Thus, it can be speculated that the subdiffusion behaviors may only exist in a small range of the vesicle size. To test the diffusion behavior for a longer time, we have extended the simulation time up to 2 μs for the 28 nm vesicle at two temperatures. As can be seen in Fig. S2 of the supplementary material, the MSD also exhibits subdiffusion behaviors for longer simulation times. In particular, in the duration of t = 1–1.5 μs, the power law index is further reduced. Thus, our current simulation time should be long enough to observe the subdiffusion behavior; however, more studies with different models are still needed to capture the vesicle diffusion. In a word, the diffusion behavior for vesicles is still premature and needs further investigation, while our present work focuses on the osmotic water transport.

FIG. 5.

Mean square displacement (MSD) of the vesicle as a function of the simulation time for (a) different temperatures with R = 28 nm and (b) different vesicle diameters with T = 350 K. The salt concentration is fixed as c = 2M and its effect is trivial. The results of salt-in are quite similar and are thus not shown here.

IV. CONCLUSION

In summary, we have conducted large scale coarse-grained molecular dynamics simulations to study the osmotic water permeation through a vesicle membrane. Of primary interest is that the osmotic water flux from pure water to salt solution strongly depends on the salt location (namely, salt-out and salt-in), suggesting an asymmetric transport. The flux ratio of salt-out/salt-in can be up to 6. This asymmetric phenomenon exists in a broad range of salt concentration, temperature, and vesicle size found in our work and can be deciphered by the similar asymmetric potential energy of lipid-ion, lipid-water, lipid-solution, lipid-lipid, and the lipid-lipid energy fluctuation. When the ions are outside the vesicle, they can have more attraction with the lipids than the salt-in case. The lower lipid-ion-out interaction exceeds the higher lipid-water-out, leading to the lower lipid-solution-out, which then causes the higher values of lipid-lipid-out with larger fluctuations. That is to say, the outside salt will make the vesicle conformation looser, facilitating the water permeation.

Specifically, the water flux shows a linear increase with the salt concentration, similar to the experimental flat membranes. The Nernst-Planck equation or Fick’s first law can further explain this linear relation. More surprisingly, the water flux has an excellent Arrhenius relation with the temperature. This is because the membrane permeability or water diffusion coefficient has the same behavior. Furthermore, the water flux exhibits a linear increase with the vesicle surface area. This is clearly due to the fact that the flux across a unit membrane area should be a constant. We finally presented a brief discussion on the vesicle diffusion behaviors. For different temperatures and vesicle sizes, we found a transition from normal diffusion at short times to subdiffusion at long times. It seems that further investigation perhaps in different models is needed to capture this anonymous diffusion. Our results for the first time provide a systematic understanding on the osmotic water transport through a vesicle membrane and should be helpful to predict the subsequent vesicle volume change or shape evolution. It will be quite impressive if the asymmetric phenomenon also happens in cells.

Furthermore, it will be more insightful if we can connect the water osmotic transport to the vesicle shape transformation. In our recent work,¹⁹ we directly remove some parts of the water volume inside the vesicle so as to speed up the osmotic process and change the vesicle volume. Although 1 μs is a long time simulation even for the current coarse-grained MD method, the amount of water flux is still very limited, e.g., for R = 28 nm, T = 350 K, and c = 2M, the salt-out flux is 1253/μs, while the total number of water molecules inside is 38 748. Thus, after 1 μs MD run, only 3.23% water volume is reduced. According to our work,¹⁹ the vesicle shape will be changed after at least 30% water volume is reduced. For the larger vesicles, the water volume decrease can be even smaller, e.g., 1.46% for the salt-out with R = 47 nm, T = 350 K, and c = 2M. Thus, the current 1 μs MD simulation will not change the sphere vesicle shape and we have double-checked that the final shape is a sphere. At least we should run 10 μs to observe the vesicle shape transformation, which is still inaccessible for our current computational ability. By the way, even if the vesicle shape is not a sphere, it is believed that we can still determine the number of inside water molecules by handling some techniques, e.g., let the vesicle move to another solution (perhaps oil phase) and simply judge the water location.

Finally, it is believed that the strain of the vesicle membrane should be nontrivial for the water permeation. This is because when waters are transported in/out of the vesicle, the increase/decrease of the inside water volume will affect the membrane tension, which will further affect the water permeation. In particular, the lower lipid-lipid-in interaction implies a more tightened vesicle, where the membrane tension may have more influence on preventing the increase of the inside water volume, corresponding to the lower water flux. However, due to the limited change of the inside water volume and the coarse-grained method, it is still difficult to reveal the role of strain in permeation, e.g., the Marangoni flows.⁴²

SUPPLEMENTARY MATERIAL

See supplementary material for the standard deviations of the lipid-lipid potential energy and a longer time diffusion test for the vesicles.