Anomalous barrier escape: The roles of noise distribution and correlation

Abstract

We study numerically and analytically the barrier escape dynamics of a particle driven by an underlying correlated Lévy noise for a smooth metastable potential. A “quasi-monochrome-color” Lévy noise, i.e., the first-order derivative variable of a linear second-order differential equation subjected to a symmetric α-stable white Lévy noise, also called the harmonic velocity Lévy noise, is proposed. Note that the time-integral of the noise Green function of this kind is equal to zero. This leads to the existence of underlying negative time correlation and implies that a step in one direction is likely followed by a step in the other direction. By using the noise of this kind as a driving source, we discuss the competition between long flights and underlying negative correlations in the metastable dynamics. The quite rich behaviors in the parameter space including an optimum α for the stationary escape rate have been found. Remarkably, slow diffusion does not decrease the stationary rate while a negative correlation increases net escape. An approximate expression for the Lévy-Kramers rate is obtained to support the numerically observed dependencies.

I. INTRODUCTION

Escape of a particle from a metastable potential underlies a broad range of phenomena, chemical reactions, diffusion in solids, and population extinction being examples. The well-known reaction rate theory was first developed by Kramers¹ and reviewed systematically by Hänggi et al.² The calculation of the escape rate for non-Markovian processes has a long history and appeared in different fields of science, including chemical physics,³ polymer physics,^4,5 and neuroscience.⁶ However, no general model exists for such a process, and different treatments were considered depending on whether the process is Gaussian or not, whether its trajectories are correlated or not, and so on. In the last few years, the escape dynamics has attracted much interest as a means of detecting non-Gaussian noise and potentially determining its statistics. An important question arises when replacing the Brownian particle in the barrier crossing process by a particle executing Lévy flights. This situation can be modeled by a particle subjected to a symmetric α-stable Lévy noise on the level of the Langevin equation (LE). First steps in this direction of addressing have been taken, as reported in Refs. 7–11, the prominent result in the parameter space was shown, including the optimum α for the steady escape rate.

The Lévy flight with a heavy long-tail distribution, describes a typical anomalous diffusion¹² and is connected with a non-Gaussian fluctuation, which has been observed in many systems including molecular collision,¹³ bulk-mediated surface diffusion,^14–16 particle evolutions along polymer chains,^17,18 spreading of the disease, and dispersal of banknotes.¹⁹ It is known that realistic problems are usually of high complexity and involve long-range or non-local correlations. Unfortunately, the white Lévy noise (WLN) cannot be used to drive these processes and thus one needs to take into account the non-Markovian effect, namely, time correlations underlying in Lévy flights. Moreover, the microbial motility was modeled in Ref. 20. In particular, the spontaneous electrical activity of neuronal networks has shown to adjust their activities over many time scales, based on the two basic temporal features of networks: the Lévy distribution on the time scale of interspike intervals and long-range correlations.²¹ Very recently, substantial progresses have been made in the study of Lévy flights, especially the exploration of the correlated structure of random processes with possibly infinite variances, such as the Lévy motion, white Lévy noise-driven Ornstein-Uhlenbeck (OU) process, and moving-average process.^22–26 The correlation function cascade is presented by exploiting the underlying Possonian structure of Lévy flights, which characterizes partly the correlation structure, because the approach a priori assumes that the kernel function can only be deduced with a specific case with non-negative value. Previously, the two kinds of “quasi-monochrome-color” Gaussian noises, named as the harmonic noise (HN)^27,28 and the harmonic velocity noise (HVN),^29,30 respectively, provide one an alternative train of thought. They are derived from solving a second-order stochastic differential equation driven by a Gaussian white noise, in particular, the HVN induces ballistic diffusion of a force-free particle described by the generalized Langevin equation.

All those studies open interesting perspectives and we are inspired. Usually, understanding of the stochastic process comes from its behaviors in various external potentials; for instance, the noise-driven escape of a particle from a deterministically metastable state is a theme that receives much attention in physical chemistry and related science.³¹ The barrier crossing problem in the presence of correlated-free Lévy flights was studied in Refs. 32–34, however, the non-Markovian effect of underlying correlated Lévy flights still remains open. It is significant to reflect the mechanisms of the escaping process subjected to an underlying correlated Lévy noise. Apart from numerical approaches, there exist two prominent analytical models for barrier escape: One is the Kramers approach,^1,2 which cannot be easily applied to the non-Gaussian driving noise case, and the another one is our analysis based on the reaction flux method.^35,36 With this work, we aim at extending the theory of the classical reaction rate and develop a model behind the Gaussian noise-driven metastable dynamics.

The paper is organized as follows. In Sec. II, we first investigate the barrier escape process by the numerical simulation of the Langevin equation subjected to correlated Lévy noise sources of two kinds. In particular, we analyze the dependence of the steady escape rate on the Lévy index α and the noise damping parameter Γ. In Sec. III, we present an approximate expression of the escape rate before drawing our conclusions given in Sec. IV. In the Appendix, we validate in detail these truthfully underlying correlated Lévy noises.

II. UNDERLYING CORRELATED LÉVY NOISE

A “correlated” Lévy noise can be produced by a coupled second-order LE driven by a symmetric α-stable white Lévy noise L(t), i.e.,

$$\dot{\epsilon }(t)=u(t),\dot{u}(t)+\mathrm{\Gamma }u(t)+{\mathrm{\Omega }}^2\epsilon (t)=L(t),$$ (1)

where the statistics of L(t) is determined by its characteristic function, given by

$$p(k)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\exp (ikL)p(L)dL=\exp (-D|k{|}^{\alpha })(0<\alpha <2),$$ (2)

where D measures the intensity of the noise and $\alpha$ is the Lévy index. It is known that the spectral densities of output variables $\epsilon (t)$ and u(t) are non-monotonous functions of frequency if the driven-source is a Gaussian distributed white noise in Eq. (1),^27–30 so that we call $\epsilon (t)$ as the harmonic Lévy noise (HLN) and u(t) the harmonic velocity Lévy noise (HVLN), respectively. We pay attention on the latter, and the Fourier transform of its distribution function in the long-time limit is written as

$$\stackrel{\sim }{W}(k)=\exp [-D{|k|}^{\alpha }{f}_1],$$ (3)

where the width factor of distribution $f_1={\int }_0^{\mathrm{\infty }}{|G_u(t)|}^{\alpha }dt$ and G_u(t) is the response function of Eq. (1), following Eq. (A3) in the Appendix.

Then, the stationary distribution function of the HVLN can be obtained in terms of Fox’s H function:³²

$$W_{st}(u)=\frac{\pi }{|u|}{H}_{2,2}^{1,1}\left[{\frac{{|u|}^{\alpha }}{D{f}_1}|}_{(1,\alpha ),(1,\frac{\alpha }{2})}^{(1,1),(1,\frac{\alpha }{2})}\right].$$ (4)

Its asymptotic form has a power-law long-tail behavior: $W_{st}(u)\sim D{f}_1/{|u|}^{\alpha +1}$ for $|u|\to \mathrm{\infty }$. It is obvious that Eq. (4) keeps continually the Lévy shape and exhibits a non-Gaussian nature. If $\mathrm{\Omega }\to 0$, u(t) becomes the Ornstein-Uhlenbeck Lévy noise with the underlying correlation time ${\tau }_c={\mathrm{\Gamma }}^{-1}$, and its characteristic function reads $\stackrel{\sim }{W}(k,t)=\exp [-\frac{D}{a\mathrm{\Gamma }}{|k|}^{\alpha }(1-e^{-\mathrm{\Gamma }\alpha t})]$.^22,37 It still corresponds to the symmetric α-stable Lévy process and the width $D(1-{\text{e}}^{-\mathrm{\Gamma }\alpha t})/a\mathrm{\Gamma }$ converges with time to a constant, producing a stationary distribution. In addition, the HVLN can reduce further to the white Lévy noise when $\mathrm{\Gamma }\to \mathrm{\infty }$.

Figure 1 shows the stationary distribution of the HVLN for various values of $\mathrm{\Gamma }$, $\mathrm{\Omega }$, and $\alpha$. Herein, we use point graphs to distinguish easily the distribution function under different parameters. It is seen that the distribution changes widely with the decrease of the damping coefficient $\mathrm{\Gamma }$ at a fixed value of $\mathrm{\Omega }$. When the damping parameter $\mathrm{\Gamma }$ is chosen to be a large value, the distribution of the HVLN is closer to the $\delta$ function. The distribution becomes narrower with the increase of $\mathrm{\Omega }$, but the change is not significant for a large $\mathrm{\Omega }$. We can also find that the distribution becomes wider with the decrease of Lévy index $\alpha$ for given values of $\mathrm{\Gamma }$ and $\mathrm{\Omega }$. It is worth pointing out that long-tail of the Lévy distribution will play a decisive role in the escape process, namely, less frequency but high amplitude noise spike govern the barrier crossing.

FIG. 1.

The stationary distribution of the HVLN for various parameters at D = 1.0. The parameters used are (a) $\mathrm{\Omega }=1.0$ and $\alpha =1.0$; (b) $\mathrm{\Gamma }=1.0$ and $\alpha =1.0$; and (c) $\mathrm{\Omega }=1.0$ and $\mathrm{\Gamma }=1.0$, respectively.

In the limit case of $\alpha =2$, the distribution (4) recovers to the Gaussian form $W(u)\propto \exp (-\mathrm{\Gamma }{u}^2/(2D))$ with the width factor $f_1=1/(2\mathrm{\Gamma })$. The HVLN reduces to the harmonic velocity Gaussian noise (HVGN)²⁹ with the finite variance. The autocorrelation function of the HVGN reads

$$⟨u(t)u(t^{\prime })⟩=\frac{D}{{\mu }_1^2-{\mu }_2^2}[-{\mu }_1\exp ({\mu }_1|t-t^{\prime }|)+{\mu }_2\exp ({\mu }_2|t-t^{\prime }|)],$$ (5)

where ${\mu }_1$ and ${\mu }_2$ are the two roots of the characteristic equation ${\mu }^2+\mathrm{\Gamma }\mu +{\mathrm{\Omega }}^2=0$.

In Fig. 2, we plot the correlation function of HVGN [Eq. (5)] for various values of $\mathrm{\Gamma }$. It is positive in a short period of time but becomes negative at intermediate time differences, even the plus or minus appears alternately for small damping. The previous study has demonstrated an important result: if the HVGN is regarded as an internal noise, it should lead to zero effective Markovian friction of the system and induces ballistic diffusion of a force-free particle at long times;³⁸ however, it results in the characteristic of localization of a force-free particle if the HVGN is taken as an external noise source.

FIG. 2.

The correlation function of the harmonic velocity Gaussian noise corresponding to the $\alpha =2$ limit. The parameters used are D = 1.0 and $\mathrm{\Omega }=1.0$.

In order to overcome the difficulty of infinite variance in the generic case of $0<\alpha <2$, some modifications were introduced, for instance, the implementation of a cutoff or the use of dissipative nonlinearity.^39–41 In the present work, we admit and apply the Lévy noise Green function rather than the noise correlation function, because the latter cannot be measured via the auto-covariance function.

The formal solutions for $\epsilon (t)$ and u(t) in Eq. (1) are written as

$$\{\begin{array}{cc}\hfill \epsilon (t)=F_{\epsilon }(t)+\underset{0}{\overset{t}{\int }}{G}_{\epsilon }(t-t^{\prime })L(t^{\prime })d{t}^{\prime }\hfill & \\ \hfill u(t)=F_u(t)+\underset{0}{\overset{t}{\int }}{G}_u(t-t^{\prime })L(t^{\prime })d{t}^{\prime }\hfill & \end{array},$$ (6)

where $F_{\epsilon }(t)$ and F_u(t) are two decaying functions (i.e., the coordinate and velocity solutions of the homogeneous equation under given initial conditions), and all necessary details are found in the Appendix. $G_{\epsilon }(t)$ and G_u(t) are the two Green response functions of the corresponding process. The specific form of G_u(t) is given by

$$\begin{array}{ccc}{G}_u(t)=\frac{{\mu }_1{e}^{{\mu }_{1}t}-{\mu }_2{e}^{{\mu }_{2}t}}{{\mu }_1-{\mu }_2},\hfill & \text{for}{\mu }_1\ne {\mu }_2,\hfill & \\ G_u(t)=(1+{\mu }_1)t{e}^{{\mu }_{1}t},\hfill & \text{for}{\mu }_1={\mu }_2,\hfill & \end{array}$$ (7)

where ${\mu }_{\mathrm{1,2}}=-\frac{\mathrm{\Gamma }}{2}\pm \frac{\sqrt{{\mathrm{\Gamma }}^2-4{\mathrm{\Omega }}^2}}{2}$ are the roots of the equation ${\mu }^2+\mathrm{\Gamma }\mu +{\mathrm{\Omega }}^2=0$. When $\mathrm{\Gamma }\to \mathrm{\infty }$, the HVLN reduces to the white Lévy noise with $G_u(t)=\delta (t)$; when $\mathrm{\Omega }\to 0$, it can reduce to the Ornstein-Uhlenbeck Lévy noise (OULN), and the corresponding Green function is $G_{\text{OU}}(t)=\exp (-\mathrm{\Gamma }t)$, and they are both non-negative. Note that the real part of G_u(t) is negative for this quadratic equation with positive coefficients and ${\int }_0^{\mathrm{\infty }}{G}_u(t)dt=0$.

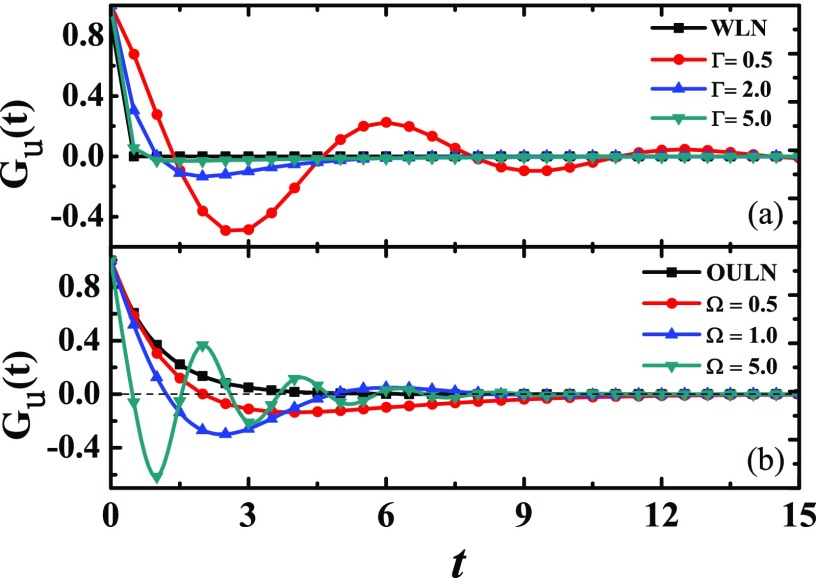
In Fig. 3, we plot the Green function of u(t) for the under-damped, critically damped, and over-damped cases. It is seen that the Green function of this noise becomes a negative value in the regime of intermediate time differences in the under-damped case, which can cross the time axis many times. In the other two cases ($\mathrm{\Gamma }\ge 2\mathrm{\Omega }$), G_u(t) can cross the time axis only once. Besides, the lower the value of $\mathrm{\Gamma }$ or the higher the value of $\mathrm{\Omega }$ is, the stronger the underlying negative correlation is. This behavior reflects the fact that a step in one direction is likely followed by a step in the other direction.

FIG. 3.

The Green functions of the HVLN for various $\mathrm{\Gamma }$ at $\mathrm{\Omega }=1.0$ (a) and various $\mathrm{\Omega }$ at $\mathrm{\Gamma }=1.0$ (b). The parameters used are D = 1.0 and $\alpha =1.0$.

We present the single noisy sequences of three kinds: WLN, HVLN, and OULN in Fig. 4, respectively. For the white Lévy noise, the random variable does not depend on its values at earlier times, L(t) can have a positive spike at this moment and then have either a negative spike or a positive spike at the next moment. However, the HVLN u(t) shows memory to its values at the latest times. As a consequence, the jump of the process cannot be quickly balanced by the jump with an opposite sign. The correlation characteristics of noise can be observed visually from Figs. 4(b) and 4(c). The OULN $\xi (t)$-driven particle needs more time to reach the stationary state even in the opposite position because there is only underlying positive correlation.

FIG. 4.

Typical trajectories for the noisy dynamics: (a) the white Lévy noise L(t); (b) the harmonic velocity Lévy noise u(t) with $\mathrm{\Gamma }=0.5$ and $\mathrm{\Omega }=0.5$; and (c) the OU Lévy noise $\xi (t)$ with ${\tau }_c=2.0$. The parameters used are $\alpha =1.2$, D = 1.0, and time step $\mathrm{\Delta }t=0.001$.

III. MONTE-CARLO SIMULATIONS OF LÉVY ESCAPE DYNAMICS

Before addressing the barrier escape problem subjected to a correlated Lévy noise analytically below, we present the results from extensive simulations. In these simulations, we employ the Langevin equation driven by a HVLN as follows:

$$\dot{x}=v,m\dot{v}=-m\gamma v-U^{\prime }(x)+u(t).$$ (8)

A type of metastable potential profile is chosen to be

$$U(x)=\{\begin{array}{cc}\frac{1}{2}m{\omega }_a^2{(x-x_a)}^2-U_b,\hfill & x\le x_c\hfill \\ -\frac{1}{2}m{\omega }_b^2{x}^2,\hfill & x>x_c\hfill \end{array},$$ (9)

where x_c is the linking point of two smooth quadratic potentials, whose frequencies correspond to ${\omega }_a$ and ${\omega }_b$, respectively, x_a is the coordinates of the potential well bottom, and U_b is the barrier height. The metastable potential used here consists of an inverse harmonic potential linking smoothly with a harmonic potential, which will be convenient for analytical derivation of the rate expression. The second-order Runge-Kutta algorithm^42–44 with a small time-step h = 0.0005 is used to solve numerically the above LE whole. All the test particles start from the bottom of the potential well. Once the trajectory of a particle crosses the exit, it is removed, and the next particle started.

The time-dependent escape rate of the particle is determined numerically by

$$r(t)=-\frac{1}{N(t)}\frac{\mathrm{\Delta }N(t)}{\mathrm{\Delta }t},$$ (10)

where N(t) denotes the overall number of resetting, and $\mathrm{\Delta }N(t)$ is the number of escapes during the interval $t\to t+\mathrm{\Delta }t$, where $\mathrm{\Delta }t$ is chosen to be much larger than the typical interval between two successive escapes, but much smaller than the characteristic time scales over which the rate may change significantly. For the latter, we chose $\mathrm{\Delta }t=0.2$ in Eq. (10) as well as $N=8\times {10}^5$ test particles. Note that the number of escape events in Eq. (10) contains the part of the test particles that return from outside to the potential well, since the exit has been chosen to be far enough.

Figure 5 shows the simulation result of the stationary escape rate for various parameters. It is seen that the stationary escape rate depends non-monotonically on $\alpha$. Because the distribution width of the particle increasing with time is faster than the movement of its peak position, a tail of the distribution behind the saddle point enters in the well again. The negative flux is formed due to the test particles recrossing the saddle point. Then, the negative flux will counteract the positive flux produced when the test particles inside the barrier cross over the saddle point. This leads to a cancellation phenomenon.

FIG. 5.

Dependence of steady escape rates of the particle induced by the HVLN and LN on $\alpha$. The remaining probability varying with time is plotted in the inset, the left for $\alpha =0.5$, and the right for $\alpha =1.2$. The parameters used are D = 1.0, m = 1.0, $\gamma =\mathrm{\Gamma }=3.0$, ${\omega }_a={\omega }_b=1.0$, $\mathrm{\Omega }=1.0$, and U_b = 4.0.

Moreover, the steady escape rate driven by the HVLN is small for large $\alpha$ but large for small $\alpha$. The phenomenon can be explained by the competition between long flights and negative correlations caused by the HVLN. We consider two different values of $\alpha =0.5$ and 1.2 as examples and make statistics on the probability of the particle still remaining in the potential well.

The left subgraph in Fig. 5 shows that the remaining probability of the particle driven by the HVLN is small for $\alpha =0.5$. This implies that more test particles escape from the potential well within a window of finite time. A strong diffusion with an underlying positive correlation in a short time helps the particle cross over the saddle point, resulting in a small number of residual test particles in the well. Thus, the steady escape rate induced by the HVLN is larger than that driven by the white Lévy noise. This result can be directly deduced from Eq. (10). On the other hand, we still find that the remaining probability is larger for the HVLN driven particle for $\alpha =1.2$. The underlying negative correlation of HVLN leads to more test particles outside the saddle point come back, and the increase of the number of test particles staying in the potential reduces the escape rate. Namely, the underlying negative correlation plays a leading role even when long jumps of the particle take place.

Notably, some peaks appear for the escape rate of the particle driven by the HVLN. It is known from Fig. 3 that the Green function of the HVLN is positive in a short period of time but becomes negative at the intermediate times. These phenomena sometimes appear alternately for various $\mathrm{\Gamma }$ and $\mathrm{\Omega }$. The underlying positive time correlation increases the probability of long jump, which is beneficial to the directional motion of the particle. In turn, the underlying negative correlation reduces the possibility of crossing the potential well after a period of time. When the effect of underlying positive correlation is most obvious, a peak appears, as shown in Figure 6. The escape rate will fall later due to the underlying negative correlation, which reflects directly the positive and negative conversions of the noise Green function shown in Fig. 3. Nevertheless, this phenomenon disappears with the increase of $\alpha$ on account of slow diffusion.

FIG. 6.

The escape rate driven by the HVLN for various values of $\alpha$. The parameters used are D = 0.5, m = 1.0, $\gamma =3.0$, $\mathrm{\Gamma }=3.0$, $\mathrm{\Omega }=1.0$, ${\omega }_a={\omega }_b=1.0$, and U_b = 4.0.

IV. THE REACTIVE FLUX FORMALISM FOR THE LÉVY-ESCAPE RATE

The alternative approach to the Gaussian noise-induced barrier crossing problem is based on the stationary flux approximation assuming that the probability current across the saddle point is equal to a constant at long times. Here, we extend this formalism to the correlated Lévy noise-driven case and present an analytical rate result for the present smooth linking metastable potential (9). We will compare the analytical result proposed here with the numerical finding from Sec. III.

The forward reaction rate is defined by the rate of disappearance of the particle from the reactant side, which is equal to the probability of the particle arriving at the barrier top multiplied by the probability of passing over the saddle point. In the spirit of reactive flux rate calculation, the initial conditions are assumed at the top of the barrier, which correspond to the ensemble of trajectories that start from identical initial preparation but experience different stochastic histories. The reactive flux approximation is based on the assumption that the barrier is high (or the noise is low), so there exists a constant probability flux across the barrier maximum. Although the reactive flux formalism for the forward rate r(t) has many different forms, perhaps the most commonly used form is^35,36,45

$$\begin{array}{cc}r(t)\hfill & =\frac{1}{hQ}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d{x}_0{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d{v}_0{v}_0\delta (x_0)W(x_0,v_0)\chi (v_0,t)\hfill \\ & =\frac{1}{hQ}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{v}_{0}W(x_0,v_0)\chi (v_0,t)d{v}_0,\hfill \end{array}$$ (11)

where Q is the partition function for reaction integration over the distribution of the ground state and given by $Q=m{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{W}_{st}(x,\upsilon )\frac{dxdv}{h}$, and h is the cell constant. W_st(x, υ) is the stationary probability distribution of the ground state, and the specific form is given by Eq. (A16) in the Appendix. Here it is noted that the effect of barrier height U_b is implied in the expression of W_st(x, υ). W(x₀, $v_0$) is the probability density function at the saddle point x₀ = x_b = 0; $\chi (v_0,t)$ is the passing probability over the saddle point. It is noticed that all the dynamics are contained in $\chi (v_0,t)$. Depending on the history of random forces that the test particle encounter, some that gets to the top of the barrier with a positive velocity will continue to reach products and others will experience random forces that cause them to recross back into the reactant region. Because of this, $\chi$ represents a generalization of the reactivity index and takes on a fractional value between 0 and 1.⁴⁵ The specific expression form of $\chi (v_0,t)$ can be written as

$$\begin{array}{cc}\chi (v_0,t)\hfill & ={\int }_0^{\mathrm{\infty }}dx{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}dv{W}_b(x,v,t;x_0=0,v_0)\hfill \\ & ={\int }_0^{\mathrm{\infty }}{W}_b(x,t)dx,\hfill \end{array}$$ (12)

where W_b is the conditional probability in an inverted harmonic oscillator potential that given the initial conditions (x₀, $v_0$) the particle will be at (x, υ) at time t. Once W_b is known, $\chi$ can be calculated by integrating W_b over the product region of phase space.

The potential around the saddle point is $U(x)=-\frac{1}{2}m{\omega }_b^2{x}^2$ for the barrier passage process. The corresponding result for this parabolic barrier has the same form as that of the harmonic potential, simply by substituting the frequency $\omega$ of the oscillator by $i\omega$. The characteristic function of the distribution W_b(x, t) is written as

$${\stackrel{\sim }{W}}_b(k_1,t)=\exp (i{k}_1⟨x(t)⟩)\exp \left(-\frac{D{|k_1|}^{\alpha }{f}_{bx}(t)}{m^{\alpha }}\right),$$ (13)

where

$$f_{bx}(t)={|R_b(t)|}^{\alpha }{f}_1+{|r_b(t){\mathrm{\Omega }}^2|}^{\alpha }{f}_0+{\int }_0^t{|R_b(s)|}^{\alpha }ds,$$ (14)

$$⟨x(t)⟩=G_{bx}(t)v_0+\left(1+{\omega }_b^2{\int }_0^t{G}_{bx}(t^{\prime })d{t}^{\prime }\right)x_0.$$ (15)

Herein, $f_0={lim}_{t\to \mathrm{\infty }}{\int }_0^t{|G_{\epsilon }(s)|}^{\alpha }ds$, $f_1={lim}_{t\to \mathrm{\infty }}{\int }_0^t{|G_u(s)|}^{\alpha }ds$, and the response functions R_b(t), r_b(t), and G_bx(t) are obtained in the Appendix.

The distribution W_b(x, t) can be expressed in terms of Fox’s H function through the inverse Laplace transformation for Eq. (13),³²

$$W_b(x,t)=\frac{\pi }{\alpha |x-⟨x(t)⟩|}{H}_{2,2}^{1,1}\left[{\frac{|x-⟨x(t)⟩|}{{(D{f}_{bx}(t))}^{\frac{1}{\alpha }}}|}_{(1,1),(1,\frac{1}{2})}^{(1,\frac{1}{\alpha }),(1,\frac{1}{2})}\right].$$ (16)

Substituting Eq. (16) into Eq. (12) and using the transformation $v^{\prime }=x/G_x(t)$, we have

$$\chi (v_0,t)=\frac{1}{2}+{\int }_0^{v_0}\frac{\pi }{\alpha |v^{\prime }|}{H}_{2,2}^{1,1}\left[{\frac{|v^{\prime }|}{{(D{f}_b(t))}^{\frac{1}{\alpha }}}|}_{(1,1),(1,\frac{1}{2})}^{(1,\frac{1}{\alpha }),(1,\frac{1}{2})}\right]d{v}^{\prime },$$ (17)

where $f_b(t)=f_{bx}(t)/{|G_{bx}(t)|}^{\alpha }$.

Under deterministic dynamics, the fate of the particle as $t\to \mathrm{\infty }$ is completely determined by the initial conditions. This means simply that the particle which arrives at the barrier top with a positive velocity will react, however, the particle with a negative velocity will not. Namely, when the limit $t\to \mathrm{\infty }$ is taken, $\chi (v_0)$ is just ${lim}_{t\to \mathrm{\infty }}\chi (v_0,t)$.

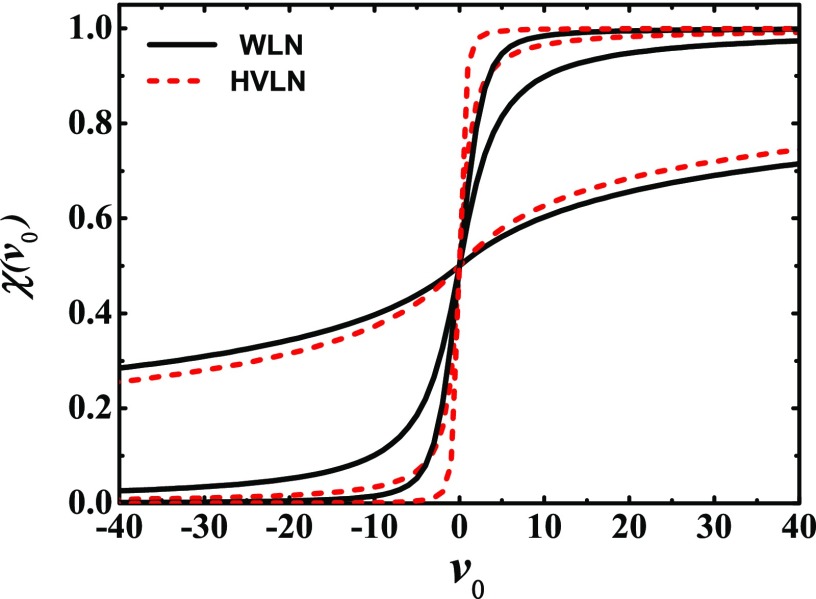
Figure 7 shows the passing probability $\chi (v_0)$ as a function of $v_0$. For the HVLN-driven case, if $v_0>0$, $\chi (v_0)$ decreases with the decrease of $\alpha$. This indicates that fast diffusion is harmful for the directional motion of the particle. On the contrary, if $v_0<0$, the passing probability increases with the decrease of $\alpha$. In the latter case, fast diffusion is beneficial for the directional motion. Besides, for a given Lévy index $\alpha$, the passing probability subjected to the HVLN is larger than that of the white Lévy noise. The above result can be interpreted by the time-evolution width of the coordinate distribution of particle, which becomes narrow due to the underlying negative correlation between two long flights. Then, the distribution becomes wider and the passing probability increases.

FIG. 7.

The steady passing probability as a function of the initial particle velocity. The white Lévy noise as a driving source (solid lines) and the harmonic velocity Lévy noise as a driving source (dashed lines) for $\alpha =1.5,1.0$, and 0.6 from top to bottom. The parameters used are D = 1.0, ${\omega }_a={\omega }_b=1.0$, $\mathrm{\Omega }=1.0$, $\gamma =2.0$, and $\mathrm{\Gamma }=3.0$.

Considering the normalized phase space distribution that corresponds to an ensemble of test particles starting at the saddle point at t = 0, the particle follows the stationary distribution W(x₀, $v_0$). Herein, we use the harmonic potential $U(x)=\frac{1}{2}m{\omega }_a^2{(x-x_a)}^2-U_b$. In terms of the inverse Fourier transform, W(x₀, $v_0$) is taken as the steady one, i.e.,

$$W(x_0,v_0)=\frac{1}{{(2\pi )}^2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}d{k}_1{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}d{k}_2\cos (k_2{v}_0)\times \exp \left[-\frac{D}{m^{\alpha }}{\int }_0^{\mathrm{\infty }}{|k_{1}R(t^{\prime })+k_{2}H(t^{\prime })|}^{\alpha }d{t}^{\prime }\right]\times \cos \left[k_1\left(x_0-\sqrt{\frac{2U_b}{m{\omega }_a^2}}\right)\right],$$ (18)

where R(t), r(t), H(t), and h(t) are four response functions, and their specific forms are given in the Appendix. Inserting Eqs. (17) and (18) into Eq. (11), we yield the analytical expression of the stationary escape rate r_st in the presence of the HVLN at long times, see Figure 8.

FIG. 8.

Dependence of the steady escape rate on the Lévy index. The parameters used are D = 1.0, ${\omega }_a={\omega }_b=1.0$, $\mathrm{\Omega }=1.0$, $\gamma =2.0$, $\mathrm{\Gamma }=3.0$, and U_b = 4.0.

In the limit case of $\alpha =2$, we have the steady escape rate driven by the Gaussian harmonic velocity noise in a special way; moreover, when the damping parameter $\mathrm{\Gamma }\to \mathrm{\infty }$, the noise Green function becomes the delta function, the driven noise reduces to the white Lévy noise. Furthermore, the steady escape rate driven by the Ornstein-Uhlenbeck Lévy noise can also be derived when $\mathrm{\Omega }\to 0$, and the width factor of distribution driven by the OU Lévy noise in the passing probability at long times can be written as

$$f_{x,OU}(t)={|Y(t)|}^{\alpha }{f}_{1,OU}+{\int }_0^t{|Y(s)|}^{\alpha }ds,$$ (19)

where $f_{1,OU}=1/(\alpha \mathrm{\Gamma })$ and the specific form of Y(t) is given in the Appendix. Besides, the probability density function induced by the OU Lévy noise reads

$$W_{OU}(x_0,v_0)=\frac{1}{{(2\pi )}^2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}d{k}_1{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}d{k}_2\cos (k_2{v}_0)\times \exp \left[-\frac{D}{m^{\alpha }}{\int }_0^{\mathrm{\infty }}{|k_{1}Y(t^{\prime })+k_{2}y(t^{\prime })|}^{\alpha }d{t}^{\prime }\right]\times \cos \left[k_1\left(x_0-\sqrt{\frac{2U_b}{m{\omega }_a^2}}\right)\right].$$ (20)

Thus, we present the stationary escape rate of the particle driven by the OU Lévy noise at long times. Figure 8 shows the dependence of the steady escape rate calculated by Eq. (11) on $\alpha$ for three kinds of noise sources. It is seen that the steady escape rate is a nonmonotonic function of the Lévy index. The optimal value of $\alpha$ is existed to make the escape rate arrive at the maximum, which is similar to the situation of white Lévy noise. This is due to the competition between the passing probability and the conditional distribution. If $\alpha$ is large, the passing probability is large, but the steady escape rate becomes small on account of the narrow velocity distribution. On the other hand, the smaller the $\alpha$ is, the wider the conditional distribution is, and then the larger the barrier escape becomes.

In comparison with the above two cases, we find that the steady escape rate of the particle subjected to the HVLN is small for a large $\alpha$, although the passing probability is large. It is noticed that the underlying negative correlation of noise makes the initial distribution narrow, which plays a decisive role and leads to a small escape rate. On the other hand, for small $\alpha$, the passing probability of the particle driven by the HVLN is large and plays a major role. Thus, the stationary escape rate is also large. For the OU Lévy noise-driven case, the probability for the occurrence of extremely long jump of the particle is reduced due to the existence of correlation, leading to the decrease of the width of the distribution. Although the underlying positive correlation increases the passing probability, the narrow initial distribution results in a small escape rate.

V. SUMMARY

We have presented an extensive analysis of generalized Kramers problem for a symmetric $\alpha$-stable correlated Lévy noise-driven metastable escape dynamics. The driving noise we proposed here is called the harmonic velocity Lévy noise, which is realized from the velocity variable of a second-order linear Langevin equation driven by a white Lévy noise. Based on the simulations and analytical derivation, we have shown that the escape rate depends nonmonotonically on the Lévy index. This is caused by recrossing the test particles outside the potential well. It is important to remake that the steady escape rate of the particle subjected to the harmonic velocity Lévy noise is larger for the small Lévy index but smaller for the large Lévy index than that driven by the white Lévy noise. This phenomenon can be explained by the competition between long flights and underlying negative correlations of noise. Besides, some peaks appear in the process of simulating the escape rate numerically in a short time. The underlying correlation of the harmonic velocity Lévy noise varies from positive to negative. The emerging non-Markovian features are that the steady escape rate reaches its maximum value when the effect of the positive correlation is most obvious and which declines because of the subsequent negative correlation. The underlying positive correlation of the harmonic velocity Lévy noise in a short time-difference leads to the increase of the passing probability, but the underlying negative correlation at the moderate time-difference makes the stationary distribution change narrow for large $\alpha$. As a consequence, the steady escape rate is a nonmonotonic function of $\alpha$. Finally, we try to promote this Lévy noise with a negative Green function to some kinds of noise through adjusting some noise parameters, like the Ornstein-Uhlenbeck Lévy noise and the Gaussian harmonic velocity noise.

The impact of the underlying correlation of the Lévy noise can be presented more intuitive along the present work. The introduction of the harmonic velocity Lévy noise provides further understanding of the non-Markovian Lévy-type processes, which can motivate further investigation in other setups such as the Lévy-type reaction dynamics subject to an electric field or biology. We believe that the present study will provide useful information for better understanding some realistic but complicated problems associated with Lévy flights.

APPENDIX: THE VARIOUS RESPONSE FUNCTIONS

From the Laplace transform of Eq. (1), we have

$$\begin{array}{ccc}\hfill \epsilon (z)& \hfill =\hfill & \frac{L(z)}{z^2+z\mathrm{\Gamma }+{\mathrm{\Omega }}^2}+\frac{u(0)}{z^2+z\mathrm{\Gamma }+{\mathrm{\Omega }}^2}+\frac{(z+\gamma )\epsilon (0)}{z^2+z\mathrm{\Gamma }+{\mathrm{\Omega }}^2},\hfill \\ \hfill u(z)& \hfill =\hfill & \frac{zL(z)}{z^2+z\mathrm{\Gamma }+{\mathrm{\Omega }}^2}+\frac{zu(0)}{z^2+z\mathrm{\Gamma }+{\mathrm{\Omega }}^2}-\frac{{\mathrm{\Omega }}^2\epsilon (0)}{z^2+z\mathrm{\Gamma }+{\mathrm{\Omega }}^2}.\hfill \end{array}$$ (A1)

For convenience, we define a simple form F(t), which is a decaying function, i.e., the solution of the homogeneous equation under given initial conditions. Then, the formal solutions for $\epsilon (t)$ and u(t) are given by

$$\begin{array}{cc}\epsilon (t)=F_{\epsilon }(t)+{\int }_0^t{G}_{\epsilon }(t-t^{\prime })L(t^{\prime })d{t}^{\prime },\hfill & \\ u(t)=F_u(t)+{\int }_0^t{G}_u(t-t^{\prime })L(t^{\prime })d{t}^{\prime },\hfill & \end{array}$$ (A2)

where $G_{\epsilon }(t)$ and G_u(t) are two response functions, $F_{\epsilon }(t)=G_{\epsilon }u(0)+\gamma G_{\epsilon }(t)\epsilon (0)+G_u(t)\epsilon (0)$, and $F_u(t)=G_u(t)u(0)-{\mathrm{\Omega }}^2{G}_{\epsilon }(t)\epsilon (0)$.

$$\begin{array}{ccc}{G}_{\epsilon }(t)=\frac{e^{{\mu }_{1}t}-e^{{\mu }_{2}t}}{{\mu }_1-{\mu }_2},\hfill & & \\ G_u(t)=\frac{{\mu }_1{e}^{{\mu }_{1}t}-{\mu }_2{e}^{{\mu }_{2}t}}{{\mu }_1-{\mu }_2},\hfill & \text{for}{\mu }_1\ne {\mu }_2,\hfill & \\ G_{\epsilon }(t)=t{e}^{{\mu }_{1}t},\hfill & & \\ G_u(t)=(1+{\mu }_1)t{e}^{{\mu }_{1}t},\hfill & \text{for}{\mu }_1={\mu }_2,\hfill & \end{array}$$ (A3)

where ${\mu }_{1,2}=-\frac{\mathrm{\Gamma }}{2}\pm \frac{\sqrt{{\mathrm{\Gamma }}^2-4{\mathrm{\Omega }}^2}}{2}$ are the roots of the equation ${\mu }^2+\mathrm{\Gamma }\mu +{\mathrm{\Omega }}^2=0$.

Similarly, the formal solutions of Eq. (8) in the presence of both the harmonic potential $U(x)=\frac{1}{2}m{\omega }_a^2{(x-x_a)}^2-U_b$ and the harmonic Lévy velocity noise read

$$\begin{array}{cc}x(t)=⟨x(t)⟩+\frac{1}{m}{\int }_0^t{G}_x(t-t^{\prime })u(t^{\prime })d{t}^{\prime },\hfill & \\ v(t)=⟨v(t)⟩+\frac{1}{m}{\int }_0^t{G}_v(t-t^{\prime })u(t^{\prime })d{t}^{\prime }.\hfill & \end{array}$$ (A4)

The response functions G_x(t) and $G_v(t)$ are given by

$$\begin{array}{ccc}{G}_x(t)=\frac{e^{{\lambda }_{1}t}-e^{{\lambda }_{2}t}}{{\lambda }_1-{\lambda }_2},\hfill & & \\ G_v(t)=\frac{{\lambda }_1{e}^{{\lambda }_{1}t}-{\lambda }_2{e}^{{\lambda }_{2}t}}{{\lambda }_1-{\lambda }_2},\hfill & \text{for}{\lambda }_1\ne {\lambda }_2,\hfill & \\ G_x(t)=t{e}^{{\lambda }_{1}t},\hfill & & \\ G_v(t)=(1+{\lambda }_1)t{e}^{{\lambda }_{1}t},\hfill & \text{for}{\lambda }_1={\lambda }_2,\hfill & \end{array}$$ (A5)

where ${\lambda }_1$ and ${\lambda }_2$ are the roots of the equation ${\lambda }_1^2+\gamma {\lambda }_1+{\omega }_a^2=0$. The average values of the particle displacement and velocity are $⟨x(t)⟩=G_x(t)v(0)+G_x(t)x_a+G_x(t)\gamma x(0)+G_v(t)x(0)$ and $⟨v(t)⟩=G_v(t)v(0)-G_x(t){\omega }_a^{2}x(0)-G_v(t){\omega }_a^2{x}_a$, respectively.

Inserting Eq. (A2) into Eq. (A4), we have

$$x(t)=⟨x(t)⟩+\frac{1}{m}{\int }_0^t{G}_x(t-t^{\prime })d{t}^{\prime }{\int }_0^{t^{\prime }}{G}_u(t^{\prime }-s)L(s)ds+\frac{1}{m}{\int }_0^t{G}_x(t-t^{\prime })G_u(t^{\prime })u(0)d{t}^{\prime }-\frac{1}{m}{\int }_0^t{G}_x(t-t^{\prime })G_{\epsilon }(t^{\prime }){\mathrm{\Omega }}^2\epsilon (0)d{t}^{\prime },$$ (A6)

and

$$v(t)=⟨v(t)⟩+\frac{1}{m}{\int }_0^t{G}_v(t-t^{\prime })d{t}^{\prime }{\int }_0^{t^{\prime }}{G}_u(t^{\prime }-s)L(s)ds+\frac{1}{m}{\int }_0^t{G}_v(t-t^{\prime })G_u(t^{\prime })u(0)d{t}^{\prime }-\frac{1}{m}{\int }_0^t{G}_v(t-t^{\prime })G_{\epsilon }(t^{\prime }){\mathrm{\Omega }}^2\epsilon (0)d{t}^{\prime }.$$ (A7)

For convenience, we write the response functions as

$$R(t)={\int }_0^t{G}_x(t-t^{\prime })G_u(t^{\prime })d{t}^{\prime },$$ (A8)

$$r(t)={\int }_0^t{G}_x(t-t^{\prime })G_{\epsilon }(t^{\prime })d{t}^{\prime },$$ (A9)

$$H(t)={\int }_0^t{G}_v(t-t^{\prime })G_u(t^{\prime })d{t}^{\prime },$$ (A10)

$$h(t)={\int }_0^t{G}_v(t-t^{\prime })G_{\epsilon }(t^{\prime })d{t}^{\prime }.$$ (A11)

Utilizing the eigenvalue function method, the characteristic function of x(t) is given by

$$\begin{array}{cc}\stackrel{\sim }{w}(k_1,t)\hfill & =⟨e^{i{k}_{1}x(t)}⟩=⟨\exp \{i{k}_1⟨x(t)⟩\}⟩\times ⟨\exp \{i{k}_1[\frac{1}{m}{\int }_0^{t}R(t-s)L(s)ds]\}⟩\times ⟨\exp [i{k}_1[-r(t){\mathrm{\Omega }}^2\epsilon (0)/m+R(t)u(0)/m]]⟩\hfill \\ & =\exp (i{k}_1⟨x(t)⟩)\exp \left(-\frac{D{|k_1|}^{\alpha }{f}_x(t)}{m^{\alpha }}\right),\hfill \end{array}$$ (A12)

where

$$f_x(t)={|R(t)|}^{\alpha }{f}_1+{|r(t){\mathrm{\Omega }}^2|}^{\alpha }{f}_0+{\int }_0^t{|R(s)|}^{\alpha }ds,$$ (A13)

Here $f_0={lim}_{t\to \mathrm{\infty }}{\int }_0^t{|G_{\epsilon }(t-s)|}^{\alpha }ds$ and $f_1={lim}_{t\to \mathrm{\infty }}{\int }_0^t{|G_u(t-s)|}^{\alpha }ds$.

Similarly, we have

$$\begin{array}{cc}\stackrel{\sim }{w}(k_2,t)\hfill & =⟨e^{i{k}_{2}v(t)}⟩=⟨\exp \{i{k}_2⟨v(t)⟩\}⟩\times ⟨\exp \{i{k}_2[\frac{1}{m}{\int }_0^{t}H(t-s)L(s)ds]\}⟩\times ⟨\exp [i{k}_2[-h(t){\mathrm{\Omega }}^2\epsilon (0)/m+H(t)u(0)/m]]⟩\hfill \\ & =\exp (i{k}_2⟨x(t)⟩)\exp \left(-\frac{D{|k_1|}^{\alpha }{f}_v(t)}{m^{\alpha }}\right),\hfill \end{array}$$ (A14)

where

$$f_v(t)={|H(t)|}^{\alpha }{f}_1+{|h(t){\mathrm{\Omega }}^2|}^{\alpha }{f}_0+{\int }_0^t{|H(s)|}^{\alpha }ds.$$ (A15)

As $t\to \mathrm{\infty }$, we can express the stationary probability distribution W(x, υ) in the ground state around the harmonic potential well $U(x)=\frac{1}{2}m{\omega }_a^2{(x-x_a)}^2-U_b$ in terms of the inverse Fourier transform technique,

$$W_{st}(x,v)=\frac{1}{{(2\pi )}^2}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}d{k}_1{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}d{k}_2\cos [k_{2}v]\times \exp \left[-\frac{D}{m^{\alpha }}{\int }_0^{\mathrm{\infty }}{|k_{1}R(t^{\prime })+k_{2}H(t^{\prime })|}^{\alpha }d{t}^{\prime }\right]\times \cos \left[k_1\left(x-\sqrt{\frac{2U_b}{m{\omega }_a^2}}\right)\right].$$ (A16)

When $\mathrm{\Omega }\to 0$, the harmonic velocity Lévy noise u(t) reduces to the OU Lévy noise with a underlying correlation time ${\tau }_c={\mathrm{\Gamma }}^{-1}$, i.e.,

$$\dot{\xi }(t)=-\mathrm{\Gamma }\xi (t)+L(t).$$ (A17)

Then, we have

$$\xi (t)=F_{\xi }(t)+{\int }_0^t{G}_{\xi }(t-t^{\prime })L(t^{\prime })d{t}^{\prime },$$ (A18)

where the Green function of OU Lévy noise is non-negative with a exponential form $G_{\xi }(t)=\exp (-\mathrm{\Gamma }t)$ for any time difference, then we have

$$x(t)=⟨x(t)⟩+\frac{1}{m}{\int }_0^t{G}_x(t-t^{\prime })d{t}^{\prime }{\int }_0^{t^{\prime }}{G}_{\xi }(t^{\prime }-s)L(s)ds+\frac{1}{m}{\int }_0^t{G}_x(t-t^{\prime })G_{\xi }(t^{\prime })\xi (0)d{t}^{\prime },$$ (A19)

and

$$v(t)=⟨v(t⟩+\frac{1}{m}{\int }_0^t{G}_v(t-t^{\prime })d{t}^{\prime }{\int }_0^{t^{\prime }}{G}_{\xi }(t^{\prime }-s)L(s)ds+\frac{1}{m}{\int }_0^t{G}_v(t-t^{\prime })G_{\xi }(t^{\prime })u(0)d{t}^{\prime }.$$ (A20)

We write the response functions as

$$Y(t)={\int }_0^t{G}_x(t-t^{\prime })G_{\xi }(t^{\prime })d{t}^{\prime },$$ (A21)

$$y(t)={\int }_0^t{G}_v(t-t^{\prime })G_{\xi }(t^{\prime })d{t}^{\prime }.$$ (A22)

Utilizing the eigenvalue function method, the characteristic function of the trajectory x(t) and the velocity $v(t)$ are given by

$$\begin{array}{cc}\stackrel{\sim }{w}(k_1,t)=\hfill & \hfill \exp (i{k}_1⟨x(t)⟩)\exp \left(-\frac{D{|k_1|}^{\alpha }{f}_{x,OU}(t)}{m^{\alpha }}\right),\\ \stackrel{\sim }{w}(k_2,t)=\hfill & \hfill \exp (i{k}_2⟨v(t)⟩)\exp \left(-\frac{D{|k_2|}^{\alpha }{f}_{v,OU}(t)}{m^{\alpha }}\right),\end{array}$$ (A23)

where

$$\begin{array}{cc}{f}_{x,OU}(t)={|Y(t)|}^{\alpha }{f}_{1,OU}+{\int }_0^t{|Y(s)|}^{\alpha }ds,\hfill & \\ f_{v,OU}(t)={|y(t)|}^{\alpha }{f}_{1,OU}+{\int }_0^t{|y(s)|}^{\alpha }ds,\hfill & \end{array}$$ (A24)

and $f_{1,OU}=1/(\alpha \mathrm{\Gamma })$.

Moreover, let us consider an inverted harmonic oscillator potential $U(x)=-\frac{1}{2}m{\omega }_b^2{x}^2$, the formal solutions of Eq. (8) driven by the harmonic Lévy noise are given by

$$x(t)=⟨x(t)⟩+\frac{1}{m}{\int }_0^t{G}_{bx}(t-t^{\prime })u(t^{\prime })d{t}^{\prime }.$$ (A25)

The response functions G_bx(t) and $G_{bv}(t)$ read

$$G_{bx}(t)=\frac{2e^{-\gamma t/2}}{m\sqrt{{\gamma }^2+4{\omega }_b^2}}\sinh (\frac{t\sqrt{{\gamma }^2+4{\omega }_b^2}}{2}),$$ (A26)

and the average displacement of the particle is $⟨x(t)⟩=G_{bx}(t)v_0+(1+{\omega }_b^2{\int }_0^t{G}_{bx}(t^{\prime })d{t}^{\prime })x_0$.

Similarly, the response functions can be written as

$$R_b(t)={\int }_0^t{G}_{bx}(t-t^{\prime })G_u(t^{\prime })d{t}^{\prime },$$ (A27)

$$r_b(t)={\int }_0^t{G}_{bx}(t-t^{\prime })G_{\epsilon }(t^{\prime })d{t}^{\prime }.$$ (A28)

Inserting Eq. (A2) into Eq. (A4), we have

$$x(t)=⟨x(t)⟩+R_b(t)u(0)/m-r_b(t){\mathrm{\Omega }}^2\epsilon (0)/m+\frac{1}{m}{\int }_0^t{R}_b(t-s)L(s)ds.$$ (A29)

Then, we have

$$\begin{array}{cc}{\stackrel{\sim }{w}}_b(k_1,t)\hfill & =⟨e^{i{k}_{1}x(t)}⟩=⟨\exp \{i{k}_1⟨x(t)⟩\}⟩\times ⟨\exp \{i{k}_1[\frac{1}{m}{\int }_0^t{R}_b(t-s)L(s)ds]\}⟩\times ⟨\exp [i{k}_1[-r_b(t){\mathrm{\Omega }}^2\epsilon (0)/m+R_b(t)u(0)/m]]⟩\hfill \\ & =\exp (i{k}_1⟨x(t)⟩)\exp \left(-\frac{D{|k_1|}^{\alpha }{f}_{bx}(t)}{m^{\alpha }}\right),\hfill \end{array}$$ (A30)

where

$$f_{bx}(t)={|R_b(t)|}^{\alpha }{f}_1+{|r_b(t){\mathrm{\Omega }}^2|}^{\alpha }{f}_0+{\int }_0^t{|R_b(s)|}^{\alpha }ds.$$ (A31)