Abstract
We propose a highly efficient method for fitting the potential energy surface of a nanocluster using a spherical harmonics based descriptor integrated with an artificial neural network. Our method achieves the accuracy of quantum mechanics and speed of empirical potentials. For large sized gold clusters (Au147), the computational time for accurate calculation of energy and forces is about 1.7 s, which is faster by several orders of magnitude compared to density functional theory (DFT). This method is used to perform the global minimum optimizations and molecular dynamics simulations for Au147, and it is found that its global minimum is not an icosahedron. The isomer that can be regarded as the global minimum is found to be 4 eV lower in energy than the icosahedron and is confirmed from DFT. The geometry of the obtained global minimum contains 105 atoms on the surface and 42 atoms in the core. A brief study on the fluxionality in Au147 is performed, and it is concluded that Au147 has a dynamic surface, thus opening a new window for studying its reaction dynamics.
I. INTRODUCTION
In the last few decades, quantum mechanical (QM) calculations have been made computationally possible for many systems. For metallic systems such as nanoclusters, the economic and accurate quantum mechanical (QM) method is density functional theory (DFT). To study the dynamics of a nanocluster theoretically, we have to run Monte Carlo (MC) or molecular dynamics (MD) simulations. This requires the calculation of energy and forces by DFT for all the structures as the simulation is processed. For larger systems (>300 atoms), it is almost near to impossible to carry out simulations using DFT1 as this will be highly computationally expensive. On the other hand, empirical potentials like the Gupta potential,2,3 Morse potential,4 Murrell–Motram potential,5 Embedded atom method (EAM),6 and Modified embedded atom method (MEAM)7 have been time and again used for the prediction of energy and forces. It has been observed that for heavy atomic systems, like gold and platinum, relativistic effects8 play an important role and therefore the empirical potentials are unable to make an accurate prediction of the structure and properties of these systems.9
Therefore, another approach is representing the atomic environments by some mathematical functions and then fitting the parameters corresponding to QM data of the atomic system. These functions are referred to as descriptors and have been proposed recently by Behler and Parrinello10 in the form of symmetric functions applied to the artificial neural network (ANN), Bartók et al.11 in the form of the bispectrum applied to gaussian ridge regression, Rupp et al.12 in form of the Coulomb matrix, and Botu and Ramprasad13 in the form of fingerprints. Recently, Behler’s approach10 has been successfully applied to generate the potential energy surface (PES) for medium sized Na clusters14 and Au clusters15 to study their dynamics and thermodynamical properties.
Behler’s symmetric functions16 contain a radial function, which is a two-body function, and an angular function which is a three-body function. The three-body function becomes exponentially time consuming for calculations with an increase in the number of atoms in the system since the number of combinations of three atoms increases with size. Therefore, we require an angular function which is independent of three-body terms for its calculation. Bartók et al. have proposed a power spectrum17 in which the atomic neighbour density is projected on the unit sphere and then it is expanded in spherical harmonics. The power spectrum is dependent only on spherical harmonics, thereby removing the radial dependence of the neighbours. To include that, Bartók et al. took a product of the radial function (a polynomial function) and the spherical harmonics in the density function expansion.17
In this work, we tend to use the technique of the ANN for fitting the PES of Au30–Au147 atom clusters. We used gaussian radial functions, unlike the polynomial function of Bartók et al.,17 and modified angular functions dependent on spherical harmonics as inputs to the ANN. All the input functions are computationally cheap as they are just two-body functions. In our approach, by taking radial functions separately, we provide the radial information around an atom such that the network has the entire atomic environment information inside it.
We consider large gold nanoclusters for our study as they have always been a subject of interest for research in various applications like plasmonics,18 biomedical applications,18,19 non-linear optics,18 and chemical applications,18 among others. The larger symmetry clusters, known as magic number clusters, for gold20 have been identified as Au13, Au55, Au147, Au309, Au561, and Au923. These clusters tend to be more stable and show different reactivities21,22 when compared to non-magic clusters. The assumed geometry of these clusters is icosahedron which has been recently published by Li et al.20 In this work, we have applied our potential to analyse the dynamics of Au147. By performing an EXAFS study23,24 on bare and supported Au147, it has been recently shown that Au147 exhibits an icosahedron geometry since the fitted parameters match with an icosahedron geometry. We have found that although being a magic cluster, Au147 does not exhibit an icosahedron geometry. Also, we have shown that according to DFT, the icosahedron geometry is 4 eV higher than the predicted global minimum (GM) structure. We have also studied the fluxional property of Au147. Our theory is given in Sec. II, followed by computational details in Section III and results and discussion in Section IV.
II. THEORY
Notation: r denotes the Cartesian vector, r denotes the magnitude of the vector, and is the unit vector.
A. Modelling of atomic neighbour density
The atomic neighbour density (ρ) of an atom i can be described using the delta function summed over all its neighbours,
| (1) |
where rij denotes the vector ri − rj. The density can be expanded in terms of spherical harmonics which form an orthonormal basis for the L2 functions on the unit sphere,17
| (2) |
where is the projection of the density in Eq. (1) on the unit sphere. The coefficients clm in Eq. (2) are obtained as
| (3) |
It can be seen from Eq. (3) that radial information is completely lost from the density projection, i.e., rij is not included in the calculation of density. Since and are only considered, when clm is obtained, the atoms lying far from the central atom and the atoms lying near to the central atom will have the same contribution. To overcome this, we do the weighting25 of the delta function with . The modified atomic density distribution function is written as
| (4) |
Different values of the factor ξ help incorporating the effects of various distances from the central atom. Since the atomic interactions over a very long range do not have much impact on energy, we restrict the number of neighbours of an atom using a cutoff function in the density distribution,
| (5) |
where fc(rij) is the cutoff function defined as10
| (6) |
where rc is the cutoff radius. The coefficients clm gets modified according to the modified atomic density distribution function (Eq. (5)). They can be calculated as follows:
| (7) |
Therefore, we get modified cnlm as
| (8) |
In another approach, as proposed by Bartók et al.,17 the radial information of a system can be incorporated in cnlm by taking a product of orthonormal radial functions and the spherical harmonics in the expansion of the density. This leads to modified basis functions,
| (9) |
On solving, cnlm is obtained as
| (10) |
These coefficients are then applied to Eq. (11) in Section II B for calculating the input coefficients to the ANN. The results using these coefficients are not accurate and are shown in Section III C.
B. Power spectrum
We can obtain a rotationally and permutationally invariant descriptor from the coefficients of the basis expansion obtained in Section II A in the form of power spectrum as follows:17
| (11) |
To normalise Pnl with respect to l, we multiply an l dependent term with the right side of Eq. (11). Thus, Eq. (11) modifies to
| (12) |
In this paper, we use the coefficients obtained in Eq. (8) to calculate Pnl above and refer to Pnl as modified angular functions. Further, we compare the results obtained by using the coefficients of Eq. (10) in Pnl and conclude that our approach is better compared to that of Bartók et al.17 (Eq. (10)) for describing the atomic environment. The coefficients obtained in Eq. (3) do not incorporate radial information; hence, they are not considered.
C. Radial functions
The angular information of an atom is not sufficient for describing an atomic environment, therefore radial environment of an atom is required for binding the system such that a correct representation of energy and forces is done.16 Radial functions of an atom i consist of a two-body interaction term summed over all the possible neighbours (j),
| (13) |
In order to probe different distances (radii), different η values are considered. Here also we need a cutoff function in order to restrict the contribution from far lying atoms.
D. Comparison of descriptors
One of the important properties of a descriptor is its ability to differentiate between two atoms that are near and far from each other. In order to fit a set of descriptors with the ANN, we have to consider those functions which follow a pattern when a change in atomic environment takes place. The change should not be too small to observe or too large to fit. So, we compare the change in descriptor functions for an atom of an Au22 cluster by varying its radial distance with its neighbouring atoms. We do the comparison between Behler’s symmetric function,16 first-order bond order parameters (Qlm),26 and Pnl of Eq. (11) using the coefficients from Eqs. (3) and (8) as shown in Fig. 1. We take an optimized cluster of Au22 such that all the bond lengths are at equilibrium distance. In the plots shown in Fig. 1, the black coloured line, red coloured line, and green coloured line correspond to the descriptor function of one atom at equilibrium distance (2.88 Å), compressed bond length (2.32 Å), and elongated bond length (4 Å), respectively, with respect to another neighbouring atom. From the plots in Figs. 1(a) and 1(b), it is observed that the variation in the functions is smooth and a pattern can be seen. In Fig. 1(a), the two-body radial functions and the three-body angular functions are plotted, whereas in Fig. 1(b), two-body radial and angular functions are plotted. On the other hand, in Fig. 1(c), we remove the weighting in the delta function and directly use the coefficients of Eq. (3) in Pnl of Eq. (11). Since the weighting is removed, the number of coefficients reduces. It can be inferred from this plot that without giving any radial information, we cannot differentiate between the atomic environments when atoms are slightly displaced from their position as the plots are almost overlapping with each other. In the bond order parameters plot (Fig. 1(d)), the functions are not rotationally invariant,17 and there are lots of variations when the atomic environment is perturbed. So, these functions should not be used as descriptors. This kind of functions does not fit well with the ANN, until a large amount of datasets is provided, which is again computationally expensive. Therefore, we have used the functions of the plot shown in Fig. 1(b).
FIG. 1.
Comparison of descriptor functions for one atom (a) Behler’s symmetric function, (b) radial function and Pnl using coefficients of Eq. (8), (c) radial function and Pnl using coefficients of Eq. (3), (d) Qlm.
III. COMPUTATIONAL DETAILS
A. Coefficients
We take 9 radial functions from Eq. (13) by varying η values given in Table I and 50 power spectrum coefficients from Eq. (12) by varying ξ values as given in Table II and l from 0 to l − 1 for describing the environment of an atom, where cnlm is given by Eq. (8). Since spherical harmonics expansion is an infinite series, we have to truncate it to a value of l which gives accurate results, i.e., a low error in the ANN weights. The maximum value of l is selected by fitting the functions and thus, the value of l which corresponds to the minimum error in energy and force predictions is then finalized. For our case, a maximum value of l = 10 gave a root mean square (RMS) error of 5 meV/atom for energy and 84 (meV/Å)/atom for forces.
TABLE I.
The values of the parameter η.
| η () | 0.005 | 0.015 | 0.0230 | 0.038 | 0.060 | 0.090 | 0.150 | 0.260 | 0.480 |
TABLE II.
The values of the parameter ξ.
| ξ () | 0.0028 | 0.0040 | 0.0110 | 0.0280 | 0.059 |
B. Economic data generation for large size clusters
The atomic environments form a primary base for fitting the PES of a cluster. The descriptor functions are used to describe these environments. In our fitting technique, i.e., ANN, we give descriptors of the atomic environment as an input and collect atomic energies as the output. For large sized clusters, where calculation of energy and forces by DFT is highly computationally expensive, fitting these clusters is a challenge. So, in order to fit large size clusters, we propose an economic approach, i.e., the split technique. According to the split technique, for any cluster, we select an atom. Then, in the cutoff distance of that atom, its neighbouring atoms along with that atom are cut from the cluster to form small sized clusters. Using this way, we generate many small sized clusters from a large atom cluster. Therefore, we restrict our database to clusters with less than 100 atoms but fit it to a cluster of 147 atoms in this work.
The cutoff distance is set as 8 Å for all the Au30–Au147 clusters for fitting the PES. We calculated the descriptor functions corresponding to different cutoff values. The contribution of the functions decreases as the cutoff increases since our descriptor has exponential weighting with respect to atomic distances. So, we optimize the value 8 Å as it had the minimum error in the fitting of energy and forces of the clusters.
C. PES fitting using neural network
Initial data for fitting are generated using MC simulations with the Gupta potential,2,3 and an initial fit is done with the ANN. The MC simulations are run for different initial geometries for 1 × 106 steps such that a variety of structures are obtained. After the first set of weights is obtained, MD simulations are run using those weights, at different temperatures at a time step of 3 fs to obtain more refined data for Au30–Au147 range of nanoclusters. All the MD simulations are performed in TINKER software.27 It is computationally expensive to run DFT based MD simulations for generating more data for a large system (Au30–Au147). Also, the empirical potentials are not accurate for the correct representation of structures of Au clusters;9 therefore, we devised a method in which we find the first set of the ANN weights to generate more data such that our potential is gradually improved. The structures are then quenched using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, and then they are included in the database. To make the calculations computationally cheap, we take 1000 clusters of Au147 and split them into small clusters. For better learning of the ANN, only 30 Au147 are taken without splitting in the dataset. Therefore, we generated 10 136 clusters containing all types of clusters below 100 atoms, and for fitting the higher atomic clusters, we use the split technique and restrict the computational calculations. The entire dataset of 10 136 clusters is shuffled and divided into a training set of 9050 clusters and a test set of 1086 clusters. The DFT calculations are performed using the Vienna Ab initio Simulation Package.28–31 The projector augmented wave method is used to describe the core electrons. It takes into account the relativistic effects in gold clusters. The electron correlation is described by generalized gradient approximation using the Perdew-Burke-Ernzerhof (PBE) functional.32,33 To sample the Brillouin zone, a gamma k-point (1 × 1 × 1) mesh is used. The cell size for clusters below 100 atoms is taken as 20 × 20 × 20 , whereas for Au147, it is kept as 25 × 25 × 25 . The threshold energy is set as 250 eV and the gradient convergence is set as 10−4. The calculation of the descriptors is done and given as an input to our ANN. The details of the ANN technique are provided in the Appendix.
It is important to mention here that the fitting of our functions with the ANN shows a very smooth decay in the RMS error of energy and forces with the iterations. The number of iterations in which the error converged is 7, which shows that fitting can be done very fast using our method. The testing and training RMS error of energy with iterations is plotted in Fig. 2. For measuring the sensitivity of our prediction model with respect to the size of training set, the PES fitting is done for different sizes of the dataset. The RMS error in energy and forces with respect to size of the training set is reported in Table III. So, with an increase in the size of dataset, the RMS error decreases and saturation in the RMS error is observed after a certain size of dataset is reached.
FIG. 2.
Decay in the RMS error of energy for training and testing dataset with iterations.
TABLE III.
RMS error in energy and forces for different sizes of training set.
| Size | RMS error energy(meV/atom) | RMS forces error ((meV/Å)/atom) |
|---|---|---|
| 1086 | 10.846 | 143.305 |
| 2172 | 7.78 | 124.332 |
| 5068 | 5.57 | 85.255 |
| 9050 | 5.00 | 84.00 |
Using the coefficients of Eq. (10) in the power spectrum and fitting them with the ANN did not give convincing results. Although the weights obtained have an RMS error of 12 meV/atom in energy prediction and 92 (meV/Å)/atom in force prediction, they were unable to provide an accurate prediction when atoms are very far and very close to an atom. Therefore, our way of providing radial functions separately and using a weighted delta function for density projection is an effective way to model interatomic potentials for metallic systems. We also applied Behler’s symmetric functions16 to our dataset and trained them using the ANN. The RMS error in energy and forces for Behler’s functions was 9 meV/atom and 112 (meV/Å)/atom, respectively. In Table IV, we present the comparison of prediction accuracy of our method, Behler’s symmetric functions16 based method, and using Bartok’s descriptor17 with the ANN. It can be seen that our proposed method achieves the minimum RMS error in energy and forces compared with both the other methods.
TABLE IV.
Comparison of the RMS error in energy and forces for different models.
| Size | RMS error energy(meV/atom) | RMS forces error ((meV/Å)/atom) |
|---|---|---|
| Our proposed method | 5.00 | 84.00 |
| Bartok’s power spectrum-ANN | 12.00 | 92.00 |
| Behler’s functions-ANN | 9.00 | 112.00 |
D. Validation of the weights
The validation of the obtained weights (an RMS error of 5 meV/atom for energy and 84 (meV/Å)/atom for force prediction) is done on refined 190 clusters obtained from MD simulations (at 400 K) of Au30–Au147. We plotted the energy per atom for these clusters for both DFT and ANN in Fig. 3(a). From this plot, it is observed that the ANN predicted energies are in an agreement with the DFT predicted energies. For a clear resolution, we also plotted the relative difference between the ANN and DFT predicted energies as shown in Fig. 3(b), in which a maximum number of clusters lie in the range of average RMS error energies, i.e., 5 meV/atom, while a few clusters lie above and below the error range. This may be due to the presence of a wide range of datasets that we have fitted for the PES. This validation helps us measuring the prediction accuracy of the optimized weights on the clusters other than the test set considered. We also compared the values of the ANN predicted and DFT predicted energies of Au147 clusters in the range of 6 eV. We perform optimization of random 10 clusters of Au147 by the DFT and ANN and compare their energies as shown in Fig. 4(a). Also, we compare the energies of 30 unoptimized clusters of Au147 using the DFT and ANN as shown in Fig. 4(b). So, it can be inferred that our ANN potential predicts energy very near to DFT for high as well as low energy clusters. We also compared the DFT and ANN energies for a set of Au58 clusters obtained from our previous work15 on PES fitting for Au17–Au58. The plot is shown in the supplementary material (Fig. 1). A trend can be seen in the energies but the prediction is not that accurate compared to Au147. One of the possible reasons for this can be the lack of atomic environments for Au58 clusters. We have provided many environments derived from larger sized clusters (Au100–Au147), and therefore their energy prediction is in agreement with the DFT as can be clearly seen in Fig. 3. So, it can be noted that for fitting any sized cluster, we have to take all the atomic environments into consideration. Since we are working with nanoclusters, we report our RMS error in energy per atom. The minimum error (mean absolute error) achieved in fitting the energy and forces in some of the recently developed techniques is 1 kCal/mol (energy) using deep tensor neural networks,34 12.7 kCal/mol (energy) using GRAPE,35 and 0.3 kCal/mol (energy and 1 (kCal/mol/)Å (forces) using Gradient domain machine learning (GDML).36 All these techniques were applied on organic molecules and, therefore, the energy error reported is not per atom. We also report the RMS error in energy and forces by using Behler’s symmetric functions16 to be 9 meV/atom and 112 (meV/Å)/atom, respectively, for the dataset Au30–Au147, which is high compared to the error that our proposed method has achieved.
FIG. 3.
(a) Comparison of the DFT and ANN predicted energies for Au30–Au147 clusters. (b) Relative difference between the DFT and ANN predicted energies (per atom) for Au30–Au147 clusters.
FIG. 4.
Comparison of the DFT and ANN predicted energies of a range of Au147 clusters. (a) Optimized clusters and (b) unoptimized clusters.
E. Computational time for energy and force calculation
The motivation behind this work was to reduce the time taken for calculation of energy and forces of a cluster accurately. We managed to reduce the time taken for calculation of energy and forces of a Au147 cluster to 3 s on a single central processing unit (CPU) [GenuineIntel 2600.0 MHz] unlike DFT, which takes around 7 h on parallelized 16 CPU [GenuineIntel 2600.0 MHz] for this calculation. Using Behler’s symmetric functions,16 the time taken for the same system is around 14 s. Therefore, we term our approach as economic since it is computationally cheap.
We have also done the parallelisation for our functions, and the time for calculation of energy and forces of one Au147 is reduced to 1.7 s on 8 CPU [GenuineIntel 2600.0 MHz].
IV. RESULTS AND DISCUSSION
A. Global optimization of Au147 cluster
Using the converged weights obtained, we perform a GM search for Au147 using the basin hopping method. The initial structures are selected from the MD simulations which are performed at 300 K, 400 K, 500 K, and 600 K. These structures are quenched first and then taken as the beginning structure for our global optimizations. We simultaneously started the GM search using 10 different initial structures of Au147 and did the optimizations for 20 000 steps each. Au147 is one of the magic number clusters, and therefore the most stable structure assumed for it is an icosahedron.20,23,24 We have generated a large number of isomers of Au147, and the structural pattern they follow is 105 atoms in the outer shell, 35 atoms in the middle shell, and 7 atoms in the inner shell, unlike an icosahedron that contains 13 atoms in the inner shell, 42 atoms in the middle shell, and 92 atoms in the outer shell. According to the ANN, and verified from DFT, the GM contains a 7-atom symmetric inner core structure, with the arrangement of the 35 atoms in the middle layer, also in a symmetric manner. The energy of the icosahedron is almost 4.0 eV higher than that of the GM structure obtained as shown in Table V. Since the converged energy error is 5 meV/atom, for a cluster of 147 atoms, it becomes 0.7 eV on an average. Therefore, the predicted ANN energy lies in the error range and is not exact in magnitude as DFT. The structure of the icosahedron geometry and the predicted GM is shown in Fig. 5.
TABLE V.
Energy of GM and icosahedron structure of Au147.
FIG. 5.
Geometries of Au147 (a) icosahedron and (b) GM.
The inner core of the predicted GM structure is shown in Fig. 6. It shows 7 atoms arranged in a capped square bi-pyramidal shape. We encountered a lot of isomers of Au147 that are very close in energy (0.5 eV) but different in the atomic arrangements. These isomers consists of 6 - 7 atoms in the inner layer, 35 - 36 atoms in the middle layer, and the overall configuration of 105 atoms in the third shell is maintained. Due to a high energy difference between the icosahedron structure and the predicted GM structure, it can be inferred that being a magic cluster, Au147 does not exhibit an icosahedron structure as the most stable isomer and there are a lot of other stable geometries possible for it.
FIG. 6.
7 atom inner core of the GM.
Recently, Xu et al.37 identified new structures of thiol protected Au68, which contains a 32-atom core. The arrangement of the atoms in the core resembles the core structure of the GM of Au147 predicted by DFT (42 atoms) as shown in Fig. 7. The core shows a layer pattern, which is also reflected in our GM core. Since the number of atoms is not equal, a resemblance can be predicted by comparing the layers in both the structures. In the top two layers (coloured red), the number of atoms in Au68 is 10 and in Au147 it is 8, but the coordination number of the capped atom is 5 in both the structures. In the same layers, a hexagonal shaped arrangement of atoms is observed for both the structures. In the orange coloured layer, there are 10 atoms in Au68 and 11 atoms in Au147, which indicates the binding of atoms in a similar way for both the clusters as atoms are varying by just one in number. The yellow coloured layer contains 14 atoms in Au147 and 9 atoms in Au68, but the coordination number of the surface atoms of the core structures is found to be same. The blue coloured layer consists of only 3 atoms in Au68 and 9 atoms in Au147. This layer is not similar, but from the pattern followed in other layers, it can be deduced that in the presence of more atoms, this layer will also exhibit the same pattern as that in Au147. So, we can conclude that on going from Au68 to Au147, a similar pattern in the core is maintained.
FIG. 7.
(a) The layer pattern in the core geometry of Au6837 and (b) the layer pattern in the core geometry of the predicted GM of Au147.
B. Temperature dependent probability of Au147 isomers
Nanoparticles are highly sensitive materials and their stability depends on numerous parameters. One of the important parameters is temperature. We collected 60 isomers of Au147, which lies at an energy gap of 0.5 eV from the predicted GM isomer. Since the GM cannot be stable at all the temperatures, to find the most probable structures at different temperatures, we calculate the probabilities of all these isomers at 3 temperatures, 300 K, 500 K, and 800 K using the method implemented by Li and Truhlar.38 This method gives the probability of a particular isomer at a temperature by implementing rotational, vibrational, and electronic partition functions in the calculation. The equation for calculating the probability of one structure is
| (14) |
The represents the relative potential energy of an isomer with respect to the GM. The rotational, vibrational, and electronic partition functions of an isomer are represented by , , and , respectively. Since the electronic transitions are of very high energy, we omit the term as the molecule preferably stay in the ground state, and the excited states have a negligible contribution to the partition function.39 Rigid rotor approximations and harmonic approximations are adopted for calculating the rotational and vibrational partition function, respectively. Eq. (14) modifies to
| (15) |
where refers to the modified probability expression. The rotational and vibrational partition functions are calculated using the formulas shown as follows:
| (16) |
| (17) |
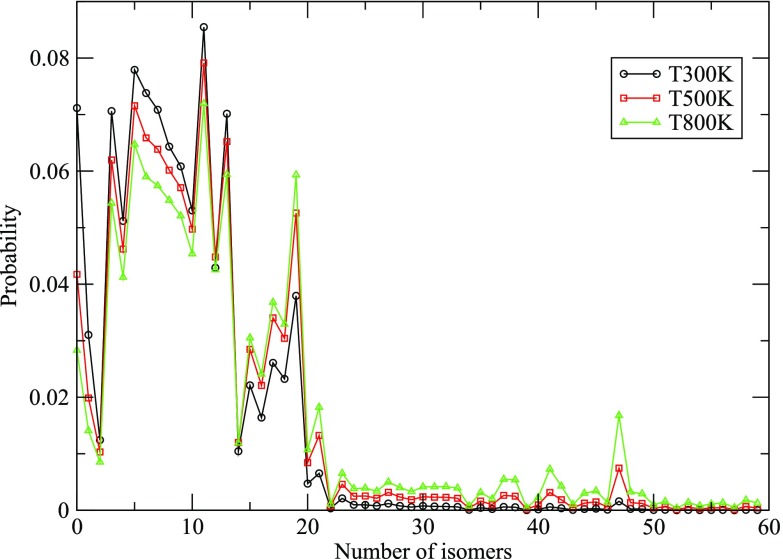
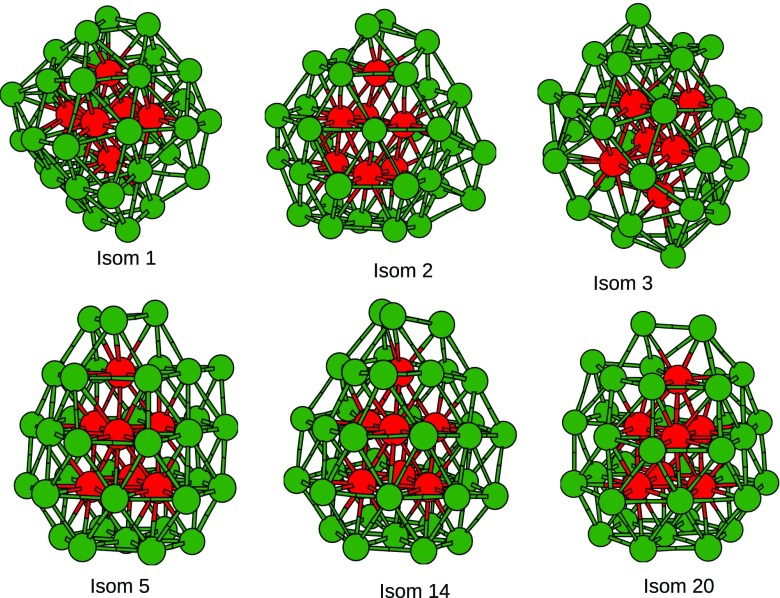
where is the wave number of the nth normal mode of an isomer and , , and are the three principle moments of inertia of the isomer. It is observed that the probability of the GM is found to be less than the other isomers at all the temperatures considered. But it is also observed that the top 20 isomers after the GM exhibit similar probability, indicating the presence of a mixture of the isomers at a particular temperature. Considering the maximum peak in the probability plot (Fig. 8), it is inferred that isomer-12 is the most probable at all the temperatures, and it is shown in Fig. 9. On comparing the core structure of the GM and the most probable isomer, a difference in the arrangement of atoms can be clearly observed as shown in Fig. 10. The most probable isomer has a more symmetric core; therefore, its probability is the greatest at all the temperatures considered. The probability of the GM along with the most probable isomer at different temperatures is given in Table VI.
FIG. 8.
Probability plot of all the isomers of Au147.
FIG. 9.
Most probable isomer at 300 K, 500 K, and 800 K.
FIG. 10.
Core structure of Au147 (a) most probable isomer and (b) GM.
TABLE VI.
Probability of the GM and most probable (mp) structure of Au147.
| T (K) | ||
|---|---|---|
| 300 | 7.1 | 8.50 |
| 500 | 4.17 | 7.90 |
| 800 | 2.8 | 7.19 |
Isomer numbers 14 and 20 have an equal probability at temperature 800 K, so we cannot predict the properties of a nanoparticle by considering just one isomer. We have to consider the most probable or nearly probable isomers for studying the dynamics of a nanoparticle at a particular temperature. The probable isomers show a stark difference in the arrangement of their core structure, some of which are shown in Fig. 11. It can be inferred that though Au147 does not exhibit an icosahedron geometry, but the GM and the most probable isomer have a symmetry in their structures.
FIG. 11.
The 42 atom core of some low lying isomers of Au147.
C. Fluxionality in Au147
Gold clusters exhibit an interesting property, fluxionality, by the virtue of which the atoms in a molecule are in a state of motion such that many low lying isomers exist at a particular temperature with a minimal energy difference between them. In a core-shell structure, the fluxionality can be due to a dynamic surface or a dynamic core. So, to study fluxionality in Au147, we run MD simulations at three temperatures—300 K, 400 K, and 700 K. Generally, the chemical reactions are carried out at room temperature; therefore, we study the dynamics of the GM at 300 K. For getting a broader picture of the structure evolution with temperature, we consider 400 K and 700 K temperature. The simulations run at a time step of 3 fs for a time duration of 1 ns. The advantage of studying gold’s fluxional behaviour is that it plays an important role in surface mediated reactions like catalysis.40–45 The fluxionality in smaller gold clusters has been investigated earlier.46,48,49 We observe a high fluxionality in Au147 clusters and notice that core atoms are highly mobile at 400 K, and both the surface and core atoms are mobile at 700 K.
To study the movements in the structures as the simulation is processed, order parameters can be calculated. The order parameters implemented in the current work are average fluctuations in the bond length,38 volume variation in the cluster,38 root mean square distance (RMSD),46 and atomic equivalence index (AEI).47
1. Average bond length fluctuation
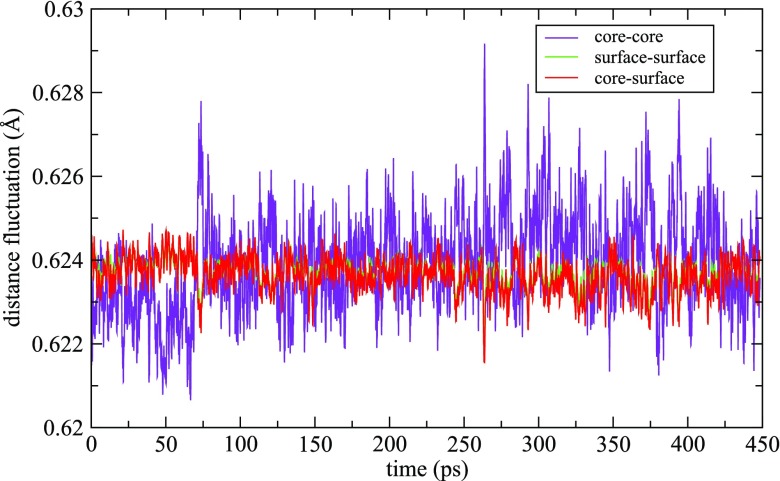
We calculate average bond length fluctuations38 for the MD trajectory of Au147 at 400 K as the time progresses. The plot of the distance fluctuations with respect to the time elapsed is shown in Fig. 12. In the plot, the fluctuations in core-core atoms, surface-surface atoms, and core-surface atoms are represented by purple color, green color, and red color, respectively. From the plot, it can be inferred that the core exhibits large fluctuations as compared to the surface of Au147 with the simulation time. Due to these fluctuations in the core, there is a change in the coordination number between the surface and core atoms, providing an evidence of rotation of the core atoms unit. So, from the average distance fluctuation calculations at 400 K, we can conclude that due to a rotation and vibration in the core, Au147 shows fluxionality.
FIG. 12.
Average bond length fluctuations of Au147 at 400 K.
2. Volume variation
We calculate the volume variation38 for Au147 clusters as the simulation progresses at 300 K, 400 K, and 700 K. The plot is shown in Fig. 13. In Fig. 13, the volume variation for temperature 300 K, 400 K, and 700 K is represented by black, red, and green, respectively. From the plots at 300 K and 400 K, it can be inferred that there is not much volume variation in the structures, such that no major movements are observed throughout the MD trajectory at these temperatures, i.e., the structures formed along the simulation do not show large variations with respect to the GM. However, at temperature 700 K, a lot of volume variation is observed. The structure of the GM is completely disturbed, and a large deviation in structures is observed. The atoms are highly mobile, and the structure changes a lot as can be seen from Fig. 13. Highest variation in the volume is observed in the structures a, b, and d in Fig. 13(b), where the clusters are more distorted as compared to our GM. Also, the structures c and e in Fig. 13(b) have a low variation in volume, and thus are near to the GM geometry.
FIG. 13.
(a) Volume variation of Au147 at 300 K, 400 K, and 700 K and (b) structural evolution with simulation time at 700 K.
3. RMSD
We calculated the RMSD46 of the clusters corresponding to the GM structure at temperatures 300 K and 700 K. Different peaks in the RMSD plots do not confirm the presence of entirely different configurations. It is a parameter to show that the atoms are moving and are not static,
| (18) |
where xi, yi, and zi are the coordinates of the GM and , , and are the coordinates of the conformation obtained from the MD trajectory; N is the number of atoms in the conformation. The relevance of the RMSD is that the atomic positions are numbered such that after every time step they change the position which can then be compared with the initial structure. Therefore, we can observe how the structure is evolving as the simulation is processed.
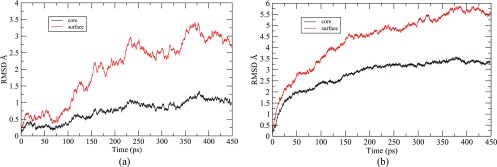
From the RMSD plots shown in Fig. 14, it is observed that the core and surface atoms are continuously moving with the simulation time. At 300 K, the RMSD of core atoms is low (Fig. 14(a)) as the structural variation of the core is less, so the movements are confined in a smaller region. On the other hand, the surface atoms have a large phase space for movement, therefore, the RMSD is more for the surface atoms. At 700 K, the initial symmetry of the structure is destroyed within 1 ps of the simulation. Since the volume variation (Fig. 13(a)) is high at 700 K, therefore, the core and surface atoms are showing a steep increase in the RMSD with the simulation time. So, from the RMSD, we can conclude that Au147 atoms are in a state of motion with the simulation time and, therefore, show fluxionality.
FIG. 14.
RMSD plot of Au147 at (a) 300 K and (b) 700 K.
4. AEI
The GM structure of Au147 consists of three layers— the inner core, middle layer, and surface. So, to visualize the behaviour of atoms with progress in simulation, we randomly select a few atoms of the surface and few atoms of the core and calculate their AEI. We calculated AEI for Au147 at 300 K and 700 K. At 300 K, the AEI plot (Fig. 15(a)) shows three distinct regions in which the bottom region refers to the inner core atoms, the middle region refers to the middle core, and the top region refers to the surface atoms. So, it can be inferred that core atoms remain in the core and surface atoms remain on the surface. The atoms are not getting exchanged between the layers.
FIG. 15.
AEI plot of Au147 at (a) 300 K and (b) 700 K.
At 700 K, in Fig. 15(b), it is observed that now the three layers of atoms are showing an intermixing. One of the core atoms, represented by the blue curve, moves from the core to the surface in the beginning of simulation and again goes back to the core after a few time steps. On further increase in the simulation time, it completely goes to the surface and then stays there. Similarly, some of the surface atoms are coming inside the core as seen from the grey and the brown plots in Fig. 15(b). The atom represented by brown color initially stays on the surface but, after some time, it breaks into the core and stays there. So, a core to surface and surface to core atom movement is observed. Therefore, we can conclude that the atoms are getting exchanged between the core and surface throughout the simulation.
V. CONCLUSIONS
In this work, we have proposed a novel technique by which accurate energy and force calculations can be achieved in accordance with quantum mechanics. We successfully fitted the PES for gold clusters ranging from Au30 to Au147 with an accuracy of 5 meV/atom for energy and 84 (meV/Å)/atom for force calculations. The spherical harmonics applied in the form of angular functions for describing the atomic environment and using it in the ANN provide us a highly efficient system for fitting the PES of a nanocluster. The computational time for accurate calculation of energy and forces of a Au147 cluster has been reduced to 1.7 s, which is very fast when compared to DFT (7 h). An extensive GM search is performed along with the MD simulations for Au147 at different temperatures. It is found that a large number of isomers are possibly lying within a narrow energy scale of 0.5 eV from the GM. The isomer obtained as the GM consists of a symmetric core and an unsymmetric surface unlike icosahedron which is a highly symmetric structure. We also confirmed that the GM of Au147 is found to be 4 eV lower in energy than the icosahedron geometry from the DFT calculations. As found in many other gold clusters, Au147 also exhibits fluxionality and it is observed that it has a dynamic surface as well as a dynamic core, thus giving a new direction for studying its reaction dynamics. Using our technique for nanoparticles in the range greater than 1.8 nm, a proper understanding of the reaction dynamics at the nanolevel can be done.
SUPPLEMENTARY MATERIAL
See supplementary material for the Cartesian coordinates of the GM of Au147 and useful figures.
ACKNOWLEDGMENTS
We thank IIT Indore for providing server facilities—OMICORN [GenuineIntel 2600.0 MHz]. S.J. thanks IIT Indore for research fellowship. S.C. thanks the University Grants Commission, India for senior research fellowship.
APPENDIX: TECHNICAL DETAILS OF ANN
ANNs are a very powerful technique for training a set of data and using the converged weights for predicting the correct properties of any system. In our case, we fitted energy and 3N force components of an N atom cluster via the ANN.
A feed-forward ANN is constructed containing two hidden layers (each having 30 neurons), one input layer (containing 59 elements per atom), and one output layer (energy as an output) as follows:
| (A1) |
This equation is a basic equation of the ANN architecture using two hidden layers to get the output value. Here, is the energy of an atom υ; n and m refers to the first and the second hidden layer, respectively; ψ represents the weights, i.e., the input layer to the first hidden layer (), the first hidden layer to the second hidden layer (), and the second hidden layer to the output layer (); fm and fn are the activation functions. We have used the sigmoid function as the activation function. and correspond to the bias layer weights of the first and the second hidden layer, respectively. The input elements are given by , which are the 59 coefficients of the υth atom. The total energy of the cluster Ecluster is calculated by taking a sum over ’s,
| (A2) |
Since, for MD simulations, we require forces of an atom; therefore, for their correct representation, we calculate forces by taking the gradient of energy as follows and fit its 3N components along with the energy:
| (A3) |
where is the force of an atom at coordinate χ and .
For optimizing the weights of the ANN, we apply the extended Kalman filter algorithm.50 The Kalman filter equations are briefly given as follows:
| (A4) |
| (A5) |
| (A6) |
| (A7) |
| (A8) |
We initialise the weight vector by random numbers (0 - 1) and update them iteratively using Eq. (A8). The error covariance matrix P is initialized as an identity matrix of the dimension weights × weight, and it is updated using Eq. (A7). Q and R are the process noise covariance matrix and measurement noise covariance matrix, respectively, and we keep them constant (Q = 0.000 02, R = 0.2) throughout the training process. H matrix contains the derivative of the energy and forces (functions that we need to minimize) with respect to weights. is an iteration dependent forgetting factor, which gives more importance to the weights of the last iteration. The parameter keeps a constant value of 0.97 and is initialized as 0.999, which gets updated iteratively using Eq. (A4). More details about the fitting of the PES using the ANN and Kalman filter can be found in our previous work.15
In order to fit the DFT data, we represent the error vector in the Kalman filter in the form of Derr,
| (A9) |
A(DFT) and represent the energy and 3N force components of a cluster predicted by DFT and the ANN, respectively. The A vector is actually a (3N + 1) element vector given as
| (A10) |
where u is DFT for A(DFT) and the ANN for , and is the Cartesian coordinate (x, y, and z) of the cluster. For validation of the weights obtained, we have a testing dataset which is not given in the training dataset. After every iteration, the weights are applied to predict the energy and forces of the testing dataset. The training is continued if the testing RMS error lies below the previous iteration error, else the training is stopped. So, the overall method can be summarized as follows:
-
(a)
calculation of descriptor functions for all the clusters in the database;
-
(b)
giving atom-wise descriptor functions as an input to the ANN, along with the DFT data of the entire cluster;
-
(c)
the weights are updated iteratively, by minimizing the error in energy and forces as the clusters are trained;
-
(d)
the training is stopped as the testing RMS error increases in comparison to the training RMS error of energy and forces;
-
(e)
the converged weights can then be applied to global optimizations, MD simulations, and many other applications.
REFERENCES
- 1.Kohn W., Phys. Rev. Lett. 76, 3168 (1996). 10.1103/physrevlett.76.3168 [DOI] [PubMed] [Google Scholar]
- 2.Gupta R. P., Phys. Rev. B 23, 6265 (1981). 10.1103/physrevb.23.6265 [DOI] [Google Scholar]
- 3.Bruma A., Ismail R., Paz-Borbon L. O., Arslan H., Barcaro G., Fortunelli A., Li Z. Y., and Johnston R. L., Nanoscale 5, 646 (2013). 10.1039/c2nr32517a [DOI] [PubMed] [Google Scholar]
- 4.Girifalco L. A. and Weizer V. G., Phys. Rev. 114, 687 (1959). 10.1103/physrev.114.687 [DOI] [Google Scholar]
- 5.Murrell J. N. and Mottram R. E., Mol. Phys. 69, 571 (1990). 10.1080/00268979000100411 [DOI] [Google Scholar]
- 6.Daw M. S. and Baskes M. I., Phys. Rev. B 29, 6443 (1984). 10.1103/physrevb.29.6443 [DOI] [Google Scholar]
- 7.Baskes M. I., Phys. Rev. B 46, 2727 (1992). 10.1103/physrevb.46.2727 [DOI] [PubMed] [Google Scholar]
- 8.Pyykko P. and Desclaux J. P., Acc. Chem. Res. 12, 276 (1979). 10.1021/ar50140a002 [DOI] [Google Scholar]
- 9.Aprá E., Ferrando R., and Fortunelli A., Phys. Rev. B 73, 205414 (2006). 10.1103/physrevb.73.205414 [DOI] [Google Scholar]
- 10.Behler J. and Parrinello M., Phys. Rev. Lett. 98, 146401 (2007). 10.1103/physrevlett.98.146401 [DOI] [PubMed] [Google Scholar]
- 11.Bartók A. P., Payne M. C., Kondor R., and Csányi G., Phys. Rev. Lett. 104, 136403 (2010). 10.1103/physrevlett.104.136403 [DOI] [PubMed] [Google Scholar]
- 12.Rupp M., Tkatchenko A., Müller K. R., and Von Lilienfeld O. A., Phys. Rev. Lett. 108, 058301 (2012). 10.1103/physrevlett.108.058301 [DOI] [PubMed] [Google Scholar]
- 13.Botu V. and Ramprasad R., Phys. Rev. B 92, 094306 (2015). 10.1103/physrevb.92.094306 [DOI] [Google Scholar]
- 14.Chiriki S. and Bulusu S. S., Chem. Phys. Lett. 652, 130 (2016). 10.1016/j.cplett.2016.04.013 [DOI] [Google Scholar]
- 15.Chiriki S., Jindal S., and Bulusu S. S., J. Chem. Phys. 146, 084314 (2017). 10.1063/1.4977050 [DOI] [PubMed] [Google Scholar]
- 16.Behler J., Int. J. Quantum Chem. 115, 1032 (2015). 10.1002/qua.24890 [DOI] [Google Scholar]
- 17.Bartók A. P., Kondor R., and Csányi G., Phys. Rev. B 87, 184115 (2013). 10.1103/physrevb.87.184115 [DOI] [Google Scholar]
- 18.Daniel M. C. and Astruc D., Chem. Rev. 104, 293 (2004). 10.1021/cr030698+ [DOI] [PubMed] [Google Scholar]
- 19.Sperling R. A., Gil P. R., Zhang F., Zanella M., and Parak W. J., Chem. Soc. Rev. 37, 1896 (2008). 10.1039/b712170a [DOI] [PubMed] [Google Scholar]
- 20.Li H., Li L., Pedersen A., Gao Y., Khetrapal N., Jónsson H., and Zeng X. C., Nano Lett. 15, 682 (2014). 10.1021/nl504192u [DOI] [PubMed] [Google Scholar]
- 21.Turner M., Golovko V. B., Vaughan O. P., Abdulkin P., Berenguer-Murcia A., Tikhov M. S., Johnson B. F., and Lambert R. M., Nature 454, 981 (2008). 10.1038/nature07194 [DOI] [PubMed] [Google Scholar]
- 22.Boyen H. G., Kästle G., Weigl F., Koslowski B., Dietrich C., Ziemann P., Spatz J. P., Riethmüller S., Hartmann C., Möller M., and Schmid G., Science 297, 1533 (2002). 10.1126/science.1076248 [DOI] [PubMed] [Google Scholar]
- 23.Duan Z., Li Y., Timoshenko J., Chill S. T., Anderson R. M., Yancey D. F., Frenkel A. I., Crooks R. M., and Henkelman G., Catal. Sci. Technol. 6, 6879 (2016). 10.1039/c6cy00559d [DOI] [Google Scholar]
- 24.Chill S. T., Anderson R. M., Yancey D. F., Frenkel A. I., Crooks R. M., and Henkelman G., ACS Nano 9, 4036 (2015). 10.1021/acsnano.5b00090 [DOI] [PubMed] [Google Scholar]
- 25.Taylor C. D., Phys. Rev. B 80, 024104 (2009). 10.1103/physrevb.80.024104 [DOI] [Google Scholar]
- 26.Steinhardt P. J., Nelson D. R., and Ronchetti M., Phys. Rev. B 28, 784 (1983). 10.1103/physrevb.28.784 [DOI] [Google Scholar]
- 27.Ponder J. W., TINKER: Software tools for molecular design 3, Washington University School of Medicine, Saint Louis, MO, 2004. [Google Scholar]
- 28.Kresse G. and Hafner J., Phys. Rev. B 47, 558 (1993). 10.1103/physrevb.47.558 [DOI] [PubMed] [Google Scholar]
- 29.Kresse G. and Hafner J., Phys. Rev. B 49, 14251 (1994). 10.1103/physrevb.49.14251 [DOI] [PubMed] [Google Scholar]
- 30.Kresse G. and Furthmüller J., Comput. Mater. Sci. 6, 15–50 (1996). 10.1016/0927-0256(96)00008-0 [DOI] [Google Scholar]
- 31.Kresse G. and Furthmüller J., Phys. Rev. B 54, 11169 (1996). 10.1103/physrevb.54.11169 [DOI] [PubMed] [Google Scholar]
- 32.Perdew J. P., Burke K., and Ernzerhof M., Phys. Rev. Lett. 77, 3865 (1996). 10.1103/physrevlett.77.3865 [DOI] [PubMed] [Google Scholar]
- 33.Perdew J. P., Burke K., and Ernzerhof M., Phys. Rev. Lett. 78, 1396 (1997). 10.1103/physrevlett.78.1396 [DOI] [PubMed] [Google Scholar]
- 34.Schütt K. T., Arbabzadah F., Chmiela S., Müller K. R., and Tkatchenko A., Nat. Commun. 8, 13890 (2017). 10.1038/ncomms13890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ferré G., Haut T., and Barros K., J. Chem. Phys. 146, 114107 (2017). 10.1063/1.4978623 [DOI] [PubMed] [Google Scholar]
- 36.Chmiela S., Tkatchenko A., Sauceda H. E., Poltavsky I., Schütt K., and Müller K. R., Sci. Adv. 3, 1603015 (2017). 10.1126/sciadv.1603015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Xu W. W., Gao Y., and Zeng X. C., Sci. Adv. 1, e1400211 (2015). 10.1126/sciadv.1400211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Li Z. H. and Truhlar D. G., Chem. Sci. 5, 2605 (2014). 10.1039/c4sc00052h [DOI] [Google Scholar]
- 39.McQuarrie D. A. and Simon J. D., Physical Chemistry: A Molecular Approach (University Science Books, 1998), Vol. 18, p. 733. [Google Scholar]
- 40.Haruta M., Catal. Today 36, 153 (1997). 10.1016/s0920-5861(96)00208-8 [DOI] [Google Scholar]
- 41.Chen M. S. and Goodman D. W., Science 306, 252 (2004). 10.1126/science.1102420 [DOI] [PubMed] [Google Scholar]
- 42.Hvolbæk B., Janssens T. V., Clausen B. S., Falsig H., Christensen C. H., and Nørskov J. K., Nano Today 2, 14 (2007). 10.1016/s1748-0132(07)70113-5 [DOI] [Google Scholar]
- 43.Haruta M. and Daté M., Appl. Catal., A 222, 427 (2001). 10.1016/s0926-860x(01)00847-x [DOI] [Google Scholar]
- 44.Li G. and Jin R., Acc. Chem. Res. 46, 1749 (2013). 10.1021/ar300213z [DOI] [PubMed] [Google Scholar]
- 45.Häkkinen H., Chem. Soc. Rev. 37, 1847 (2008). 10.1039/b717686b [DOI] [PubMed] [Google Scholar]
- 46.Vargas A., Santarossa G., Iannuzzi M., and Baiker A., Phys. Rev. B 80, 195421 (2009). 10.1103/physrevb.80.195421 [DOI] [Google Scholar]
- 47.Aguado A. and Lpez J. M., Phys. Rev. B 74, 115403 (2006). 10.1103/physrevb.74.115403 [DOI] [Google Scholar]
- 48.Arenz M., Landman U., and Heiz U., ChemPhysChem 7, 1871 (2006). 10.1002/cphc.200600029 [DOI] [PubMed] [Google Scholar]
- 49.Gu X., Bulusu S., Li X., Zeng X. C., Li J., Gong X. G., and Wang L. S., J. Phys. Chem. C 111, 8228 (2007). 10.1021/jp071960b [DOI] [Google Scholar]
- 50.Witkoskie J. B. and Doren D. J., J. Chem. Theory Comput. 1, 14 (2005). 10.1021/ct049976i [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for the Cartesian coordinates of the GM of Au147 and useful figures.