gerbil: Genotype resolution and block identification using likelihood

Abstract

The abundance of genotype data generated by individual and international efforts carries the promise of revolutionizing disease studies and the association of phenotypes with individual polymorphisms. A key challenge is providing an accurate resolution (phasing) of the genotypes into haplotypes. We present here results on a method for genotype phasing in the presence of recombination. Our analysis is based on a stochastic model for recombination-poor regions (”blocks”), in which haplotypes are generated from a small number of core haplotypes, allowing for mutations, rare recombinations, and errors. We formulate genotype resolution and block partitioning as a maximum-likelihood problem and solve it by an expectation-maximization algorithm. The algorithm was implemented in a software package called gerbil (genotype resolution and block identification using likelihood), which is efficient and simple to use. We tested gerbil on four large-scale sets of genotypes. It outperformed two state-of-the-art phasing algorithms. The phase algorithm was slightly more accurate than gerbil when allowed to run with default parameters, but required two orders of magnitude more time. When using comparable running times, gerbil was consistently more accurate. For data sets with hundreds of genotypes, the time required by phase becomes prohibitive. We conclude that gerbil has a clear advantage for studies that include many hundreds of genotypes and, in particular, for large-scale disease studies.

Most variations in the DNA sequence among individuals are at single-base sites, in which more than one nucleic acid can be observed across the population. Such differences and their sites are called SNPs (1, 2). In most cases only two alternative bases (alleles) occur at a SNP site. The total number of common human SNPs is estimated to be ≈10 million (3). The sequence of alleles in contiguous SNP sites along a chromosomal region is called a haplotype. Identification of haplotypes is a central challenge of the International HapMap Project (www.hapmap.org), because of their expected importance in disease associations (4, 5).

Recent evidence suggests that haplotypes tend to be preserved along relatively long genomic stretches, with recombination occurring mostly in narrow regions (1, 2). The stretch of SNP sites between two neighboring recombination regions is called a block. The number of different haplotypes within each block that are observed in a population is very small: typically, some 70-90% of the haplotypes within a block are identical (or almost identical) to very few (two to five) distinct common haplotypes (1).

Several studies have concentrated on the problem of block identification and partitioning in a given data set of haplotypes: Zhang et al. (6, 7) defined a block to be an interval of SNPs that minimizes the number of tag SNPs. Koivisto et al. (8) used a minimum description length criterion for block definition. Kimmel et al. (9) minimized the total number of common haplotypes when errors and missing data are allowed. The same dynamic programming approach (6) was used in all of these studies, and the main difference is in the optimization criterion used within the dynamic programming computation.

Diploid organisms, like human, have two near-identical copies of each chromosome. Most experimental techniques for determining SNPs do not provide the haplotype information separately for each of the two chromosomes. Instead, they generate for each site an unordered pair of allele readings, one from each copy of the chromosome (10). The sequence of these pairs is called a genotype. A homozygous site in the genotype of an individual has two identical bases, whereas a heterozygous site has different bases on the two chromosomal copies at that site. The process of inferring the haplotypes from the genotypes is called phasing or resolving.

In the absence of additional information, each genotype in a population can be resolved in 2^h-1 different ways, where h is the number of heterozygous sites in this genotype. Thus, one must use some model of how the haplotypes are generated to perform genotype resolving. Clark (11) proposed the first approach to haplotype resolution, which was parsimony-based. Likelihood-based expectation-maximization (EM) algorithms (12, 13) gave more accurate results. Stephens and coworkers (14, 15) and Niu et al. (16) proposed Markov chain Monte Carlo-based methods. A combinatorial model based on the perfect phylogeny tree assumption was suggested by Gusfield (17). By using this model, Eskin et al. (18) showed good performance on real genotypes with low error rates. Recently, Greenspan and Geiger (19) proposed an algorithm that performs resolution while taking into account the block structure. The method is based on a Bayesian network model.

In this study we provide an algorithm that solves block partitioning and phasing simultaneously. Our algorithm is based on a model for genotype generation. The model and preliminary analysis on its performance were reported in ref. 20. The model is based on a haplotype generation model, parts of which were suggested by Koivisto et al. (8). Within each block, we redefine common haplotypes in a probabilistic setting and seek a solution that has maximum likelihood, by using an EM algorithm. The model accounts for errors and rare haplotypes.

The algorithm was implemented in a software package called gerbil (genotype resolution and block identification using likelihood). We applied gerbil to three genotype data sets: on a data set from chromosome 5 (21) it outperformed haploblock (19) and hap (18) and gave similar results to phase (14), with much shorter run times. On the data set of Gabriel et al. (2) and on data from the International HapMap Project (www.hapmap.org), the phase algorithm was slightly more accurate than gerbil when allowed to run with default parameters, but required two orders of magnitude more time. We also simulated data with larger numbers of genotypes (500 to 1,000) based on real haplotypes. In such a scenario, when the number of genotypes increased, gerbil had a clear advantage over phase, because the latter required a prohibitively long time (and was, in fact, unable to solve the larger data sets). The gerbil software can be downloaded at www.cs.tau.ac.il/~rshamir/gerbil.

Unlike most former probabilistic approaches (12-14, 16), our algorithm reconstructs block partitioning and resolves the haplotypes simultaneously. As in refs. 14 and 19 haplotype similarity is taken into account. Although our approach has some resemblance to haploblock, there are significant differences. First, our approach computes the maximum likelihood directly and is not based on a Bayesian network. Second, once the model parameters are found, we solve the phasing problem directly to optimality, so that the likelihood function is maximized. In contrast, haploblock applies a heuristic to find the block partitioning, even though this partitioning is part of the model parameters. Third, our stochastic model allows a continuous spectrum of probabilities for each component in each common haplotype, whereas the haploblock software allows only two common probability values for all mutations. haploblock's model has the advantage of incorporating interblock transitions, whereas we handle them separately after the main optimization process.

Methods

We first concentrate on modeling and analysis of a single block. The input to the problem is n genotypes g₁,..., g_n, each of which is an m-long vector of readings g_i(1),..., g_i(m) corresponding to the SNP sites. We assume that all sites have at most two different alleles and rename the two alleles arbitrarily as 0 and 1. The genotype readings are denoted by g_i(j) ∈ {0, 1, 2}. 0 and 1 stand for the two homozygous types {0, 0} and {1, 1}, respectively, and 2 stands for a heterozygous type. A resolution of g_i is two m-long binary vectors 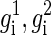satisfying 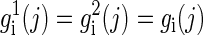if g_i(j) = 0 or 1, and 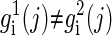if g_i(j) = 2.

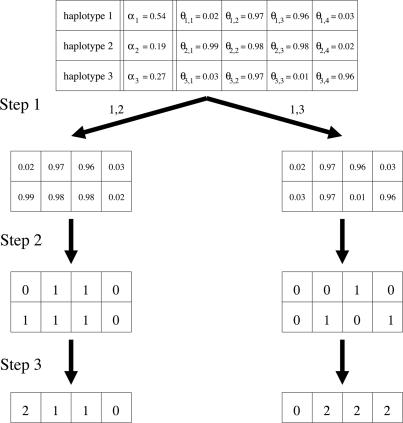
The Probabilistic Model. Our stochastic model for the genotypes generation is based on the observation that within each block the variability of haplotypes is limited (2, 21). The model assumes a set of common haplotypes that occur in the population with certain probabilities. The generation of a genotype is as follows: First, two of the common haplotypes are chosen. Second, the alleles at each site of the haplotypes are determined. Third, their confluence is formed. In our model, these common haplotypes are not deterministic. Instead, we use the notion of probabilistic common haplotype that has specific allele probabilities at each site. Such a haplotype is a vector, whose components are the probabilities of having the allele 1 in each site of a realization of that haplotype. Hence, a vector of only zeroes and ones corresponds to a standard (consensus) common haplotype, and a vector with fractional values allows for deviations from the consensus with certain (small) probabilities, independently for each site. In this way, a common haplotype may appear differently in different genotypes. A similar model was used in ref. 8 in the block partitioning of phased data. Note that the model makes the Hardy-Weinberg (22) assumption that mating is random. An illustration of the model appears in Fig. 1.

Fig. 1.

An illustration of the probabilistic model. This model has three common haplotypes covering four SNPs. In the first step, pairs of the common haplotypes are chosen according to their probabilities α_i. In this example 1,2 and 1,3 are chosen. In the second step, the alleles at each site of the haplotypes are determined according to the probabilities θ_i,j. In the third step, each genotype is formed by a confluence of two haplotypes created at the former step.

A more formal definition of the stochastic model is as follows. Assume that the genotype data contain only one block. Let k be the number of common haplotypes in that block. Let θ_i1≤i≤k be the probability vectors of the common haplotypes, where θ_i = (θ_i,1,..., θ_i,m) and θ_i,j is the probability to observe 1 in the jth site of the ith common haplotype. (Consequently, 1 - θ_i,j is the probability to observe 0 in that site.) Let α_i > 0 be the probability of the ith common haplotype in the population, with 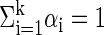. Each genotype g_t is generated as follows:

• Choose a number i between 1 and k according to the probability distribution {α₁,..., α_k}. i is the index of the first common haplotype.

• The haplotype (x₁,..., x_m) is generated by setting, for each site j independently, x_j = 1 with probability θ_i,j.

• Repeat the steps above for the second haplotype and form their confluence. The result is the genotype g_t.

For generating genotypes with several blocks, the process is repeated for each block independently.

EM. The two common haplotypes that were used to create a genotype are called its creators (the two may be identical). For a single genotype g_j, assuming its creators θ_a and θ_b are known, the probability of obtaining g_j is

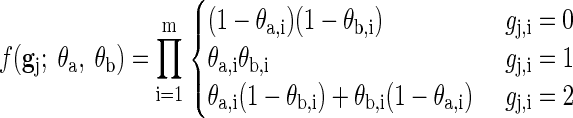We denote by I_i and J_i the index of the first and second creator of genotype g_i, respectively. The complete likelihood of all genotypes is

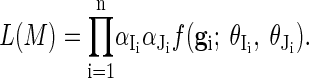Because I_i and J_i, for 1 ≤ i ≤ n, are unknown, we use the EM approach (see, e.g., ref. 23) for iteratively increasing the likelihood. We get closed-form equations for the updating of α_i in each iteration, and we use numerical methods for updating the θ_i vectors. Thus, we iteratively recalculate the parameters of the model, until convergence of the likelihood to a local maximum. For a detailed mathematical development of the solution for the optimization problem see ref. 20.

Block Partitioning and Finding the Parameter k. A simple approach that assumes independence between blocks would be to multiply the block likelihoods. However, as the parameter k is unknown, we use a minimal description length approach for finding the block partitioning and finding the parameter k for each of the blocks, in a similar fashion to ref. 8. For each pair of SNPs i,j, and for each possible k, we solve the problem as described above on the sites i through j, assuming they span a single block that contains k common haplotypes, and obtain the log likelihood score 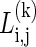. We also compute the description length 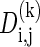of the model parameters. Note that when k is larger, the likelihood increases, but so does the description length of the model. The minimum description length of such a block is 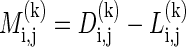. Let k(i, j) = arg min_k 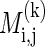. A partition P of the SNPs into b blocks is defined by 1 = i₁ < i₂ < · · · < i_b ≤ n, where the tth block is [i_t,i_t+1 - 1]. The score of such a partition according to the minimum description length criterion is 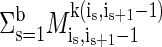. Finding the optimal partition is solved by dynamic programming (cf. refs. 6 and 8).

Speedup. Instead of checking all possible k values, we first resolve the genotype data into a preliminary haplotype matrix H^P, by using a procedure that is based on our single block resolving algorithm (see Appendix). Now, for each candidate block [i, j] the number of distinct haplotypes that appears in H^P more than once is used as an approximation for k(i, j). Also, to save time, only candidate blocks of up to 30 SNPs are considered.

Pairing Haplotypes Across Block Boundaries. To construct a full chromosome sequence, one has to determine which alleles within the block appear together with alleles in the consecutive block, on the same haplotype. We call this problem matching pairs of blocks (cf. refs. 15 and 18). Our solution is based on the fact that specific common haplotypes in neighboring blocks tend to appear together on the same chromosome (21). For each pair of neighboring blocks and for each genotype, we simply choose the pairing that occurred more often in H^P.

Initialization. When applied to a block, the EM provides only a local optimum, and starting from good initial parameter values is critical both for the solution quality and the speed of the procedure. We generate such an initial solution as follows. We randomly permute the order of the genotypes and use Clark's inference algorithm (11) to resolve as many of the genotypes as possible. In case there is still some unresolved genotype, (either because of heterozygous sites or missing data entries), we resolve that genotype arbitrarily and reapply Clark's algorithm. This procedure ends when all genotypes are resolved. The next stage is to cluster the haplotypes around k common haplotypes (where k was already determined as described above). This requires finding a set C of k haplotypes such that 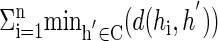is minimized, where d(...) denotes the Hamming distance. This subproblem is already hard (9), and we use the following heuristic procedure to solve it: We repeatedly select a random subset C′ of k haplotypes h₁,..., h_k, and each time calculate 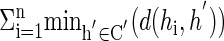. This is repeated T times and the subset C that attains the minimum score is chosen. (T = 100 was used in practice.) We use the set C to construct the initial probabilistic common haplotypes for the EM procedure, in the following way: if h_i has value 1 in SNP j, we set θ_i,j = 0.999, otherwise θ_i,j = 0.001. The α_i value is proportional to the size of the cluster containing h. We also use H^P as an additional potential starting point.

Implementation. Our algorithm was implemented in a C++ program called gerbil. Running time on a 2-GHz Pentium computer with 500 MB of memory is ≈1 min for resolving data with 100 SNPs and 150 genotypes. gerbil is available for academic use at www.cs.tau.ac.il/~rshamir/gerbil.

Evaluating and Comparing Solutions. Let the true haplotypes for genotype g_i be t = (t₁, t₂), and let the inferred haplotypes be h = (h₁, h₂). Comparison of t and h can be done only for sites that are heterozygous and are resolved in t (e.g., because of pedigree data). Suppose we restrict t and h to these sites only, and obtain l-long vectors. We use the switch test (15, 24) to evaluate the accuracy of h. The test counts the number of times η_i we have to switch from reading h₁ to h₂ or back to obtain t₁, and divides the result by d_i = l - 1 (the maximum possible of switches for this genotype). The switch test value for a set of genotypes is ∑_iη_i/∑_id_i.

Results

Chromosome 5p31. The data set of Daly et al. (21) contains 129 pedigrees of father, mother, and child, each genotyped at 103 SNP sites in chromosome 5p31. The original children data contain 13,287 typed sites, of which 3,873 (29%) are heterozygous alleles and 1,334 (10%) are missing. After pedigree resolving, only 4,315 (16%) of the 26,574 SNPs remained unknown (unresolved or missing data). When applied to the children data gerbil generated 18 blocks [compared with 11 blocks in the solution of Daly et al. (21)], and k ranged from 3 to 15 in the different blocks. The switch error rate was 3.3%.

We compared the performance of gerbil to three previously published phasing algorithms: hap (18), which uses the perfect phylogeny criterion (see also ref. 25) gave a switch error rate of 4.2%. haploblock (19), which uses a Bayesian network, gave a switch error rate of 3.6%. phase (14) (version 2.0.2 for Linux), which uses the coalescent as a Bayesian prior, gave a switch error rate of 3.1%. The run time of gerbil was 1 min, whereas phase needed 4.1 h with its default parameters. When letting phase run a comparable time to gerbil (2 min), phase achieved an error rate of 5.4%.

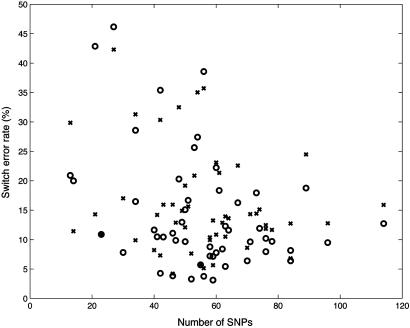
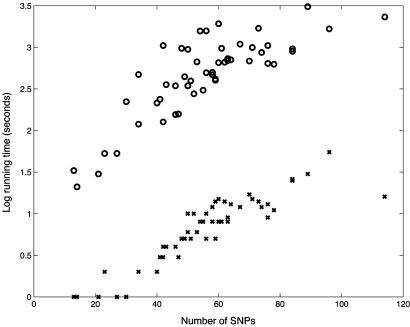
Yoruba Genotypes. Our second test focused on the Yoruba population genotypes from ref. 2. For this population there were parental genotypes that could be used to infer the true solution. We used 29 test genotypes (we removed one trio that had a high rate of missing entries). There are 52 different samples of size 13-114 SNPs from different regions of the human genome. gerbil's average switch error rate was 15% with a total run time of 8 min over all samples. phase (with default parameters) gave more accurate results, averaging 12%, with a run time of 10.1 h. The relatively high values of switch error rate compared with the results above are caused by the combination of small sample size and high missing data rate (8%). The accuracy and speed on individual samples are displayed in Figs. 2 and 3, respectively. gerbil was consistently 10-100 times faster.

Fig. 2.

Phasing accuracy on the Yoruba genotypes. The x axis shows the number of SNPs in each of the 52 data sets. The y axis shows the switch error rate of gerbil (x) and phase (○) on each data set.

Fig. 3.

Running times on the Yoruba genotypes. The x axis shows the number of SNPs in each data set. The y axis shows a logarithm (base 10) of running times (in seconds) of gerbil (x) and phase (○) on each data set.

HapMap Project Genotypes. Our third test used genotype data for 30 trios from the International HapMap Project (www.hapmap.org). As before, we used the parental information only to infer the true solution and applied the phasing algorithms to the children only. The missing entries rate in this data set was 1%, much smaller than in the former data sets.

We extracted four data sets of 70 SNPs from the beginning of each of the human chromosomes 1-22. The first data set in each chromosome contained SNPs 1-70, the second contained SNPs 71-140, etc. We applied both gerbil and phase on all 88 data sets. The average switch error rate was 11% for gerbil and 10% for phase. Overall run time was 31 min for gerbil and 22.5 h for phase.

Large Simulated Data Sets. To assess our software on data sets with a larger number of genotypes, we simulated genotypes based on the known haplotypes of chromosome 5p31 (see above). We generated six different data sets by random sampling and pairing of haplotypes from the 258 known ones. These data sets contained 500, 600, 700, 800, 900, and 1,000 genotypes. The results of gerbil and phase are presented in Table 1. On the larger data sets of 800, 900, and 1,000 genotypes, phase aborted after 12 min, because of memory allocation overload. Attempts to run phase on a larger memory machine (Pentium 3 with 2 gigabytes of memory) also were aborted. On the smaller data sets of 500, 600, and 700 genotypes, when giving phase the same amount of run time, gerbil outperforms phase in accuracy. When using the default parameters of phase, the program provides more accurate results (1% vs. 3%), but requires considerably longer run times (≈3 days vs. <1 h).

Table 1. Performance of gerbil and phase on large data sets.

	gerbil		phase
No. of genotypes	Switch error rate, %	Run time, min	Switch error rate, %	Run time, min
500	3	15	7	37
			1	4,711
600	3	20	6	47
			1	4,100
700	3	28	5	80
			1	4,525
800	3	36	No solution
900	3	42	No solution
1,000	3	59	No solution

Results are shown for different numbers of simulated genotypes generated from true chromosome 5p31 haplotypes. All runs were on a Pentium 4 computer with 500 megabytes of memory. For phase, two runs were performed, one with the default parameters and one with a short running time comparable to gerbil's. The phase processes that gave no solutions were terminated because of memory allocation overload. They also failed on a 2-gigabyte-memory machine.

Discussion

We have introduced an algorithm for haplotype resolution and block partitioning. The algorithm uses a stochastic model for genotype generation, based on the biological finding that genotypes can be partitioned into blocks of low recombination rate, and in each block, a small number of common haplotypes is found. Our model uses the notion of a probabilistic common haplotype, which can have different forms in different genotypes, thereby accommodating errors, rare recombination events, and mutations. We were able to define a likelihood function for this model. Finding the maximum-likelihood solution for genotype data under the model is achieved by using an EM algorithm. The algorithm was implemented in the gerbil program.

In tests on real data, our algorithm gave more accurate results than two recently published phasing algorithms (18, 19). Most of our comparisons concentrated on phase (15), currently the leading algorithm for haplotyping. There are two performance criteria that should be considered in such a comparison. The first and foremost is accuracy, which we measured by using the switch test (15, 24). However, when a program becomes impractically slow as one attempts to use it on larger and larger problems, one should apply the criterion of speed and test the tradeoff between accuracy and speed. Hence, we ran phase in two modes: one that used similar running times to gerbil, and another (default phase) that was run with the default parameters and required much longer run times. The tests covered 141 real data sets (2, 21) (www.hapmap.org), ranging in size between 29 and 129 genotypes and from 13 to 114 SNPs. When allowed similar run times, gerbil was consistently more accurate than phase. Default phase was slightly more accurate than gerbil but required two orders of magnitude more time (Fig. 3). The difference became more apparent on larger data sets containing 500 or more genotypes. On such data sets default phase required several days of computing time, and on 800 genotypes or more it completely failed to provide a solution (Table 1).

The next few years carry the promise of very large association studies that will use haplotypes extensively (26). Studies with 400-800 genotypes already have been reported (27), and studies with thousands of genotypes are envisioned (27). High-throughput genotyping methods are progressing rapidly (28). The number of SNPs typed is also likely to increase with technology improvements: DNA chips that can type >10,000 SNPs have been in use for over a year (29), and chips with 100,000 SNPs are already commercially available. Although clearly not all such SNPs need to be phased simultaneously, typing density would call for phasing hundreds of SNPs in up to a few thousands of genotypes. We believe that gerbil has the potential to make a unique and important contribution to the analysis of such data.

Appendix: Constructing Preliminary Haplotype Matrix

The preliminary haplotype matrix H^P is constructed in the following way: for each genotype g and for each pair of sites i, j that are heterozygous in it, we want to score the two possible phasing solutions of the two sites. This is done by applying the EM algorithm (with k = 4) on the block [i, i + 1,..., j] from which other sites that are heterozygous in g are removed. The maximum-likelihood solution gives probabilities to the four possible haplotypes that could have generated g. For example, if the genotype is g = 201102, then the four possible haplotypes are h₀₀ = 001100, h₁₁ = 101101, h₀₁ = 001101, and h₁₀ = 101100. Denote the probabilities found by the algorithm for the corresponding common haplotypes by P₀₀, P₁₁, P₀₁, and P₁₀, respectively. (Note that these are probabilities of full haplotypes and not only of the pair of sites i and j.) We use these probabilities to calculate a score, which represents the certainty level in the more probable phasing solution. Specifically, we define w(i, j) = n(P₀₀P₁₁ - P₀₁P₁₀)²/(P₀₀ + P₀₁)(P₁₀ + P₁₁)(P₀₀ + P₁₀)(P₀₁ + P₁₁), where n is the number of haplotypes in the resolved block that match one of the possible haplotypes of g. [This measure is closely related to R² (e.g., ref. 30).] For each genotype, we build a complete weighted graph G = (V, E), where each vertex corresponds to a heterozygous site, and the weight of the edge (v₁, v₂) is w(v₁, v₂). Observe that any phasing solution is obtained according to some spanning tree of G. Hence, we find a maximum spanning tree of G, and it provides a most probable phasing solution for that genotype. In practice, we set w(i, j) = 0 if |i - j| > 30.