Antibody buffering of a ligand in vivo

Abstract

Clearance is the practical limit on drug action. Here we propose a means of slowing clearance, thereby extending drug lifetime in vivo by “antibody buffering.” In this process, a drug and an anti-drug antibody are coadministered. Most of the drug is bound to the antibody, preventing the drug from acting, but also preventing its elimination. A dynamic free drug pool is established by reversible dissociation from the antibody. The free drug is active and can be eliminated, but the free pool is constantly replenished by reequilibration from the antibody-drug complex, giving a long effective lifetime. Here we explore antibody buffering experimentally by using a model compound, 2-phenyloxazol-5-one-γ-aminobutyrate (Ox), as a drug proxy. We show that antibody buffering can extend by an order of magnitude the plasma lifetime of Ox in rats, and that the steady-state Ox level depends on the molecular properties of the antibody used to buffer the Ox. In addition, the anti-Ox antibody can be recharged with drug in vivo to extend Ox lifetime without additional antibody administration, making this technique even more suitable for possible clinical application.

All drugs are cleared from the body. Clearance is nearly always a first-order process, in which the amount cleared per unit time is proportional to the amount present. Clinical dosing typically yields an initial drug level far higher than the threshold for efficacy. The level plummets because of the first-order law, and then is renewed in each subsequent dose, giving a sawtooth profile of concentration vs. time. Modern drugs usually target a saturable receptor; hence drug action follows a different law from drug clearance. Drug action increases up to a saturating concentration, several times the receptor-drug dissociation constant (K_d), but beyond the saturation point no further positive effects accrue. Indeed, undesirable effects may be manifest at higher concentrations.

The standard paradigm for antibody therapy is reaction of a specific antibody with a complementary target in vivo, causing neutralization, clearance, or destruction of the target. Yet a century of in vitro experimentation has also shown antibodies as perfect exemplars of the Law of Mass Action and the Law of Chemical Equilibrium (1). Antibodies release, as well as bind antigen, and antibody-antigen mixtures reliably partition between bound and free forms. The theory of a pH buffer is also derived most simply as a reversible binary combination, expressed by the Henderson-Hasselbalch equation:

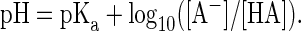[1]

A regime can be envisioned in which a ligand-specific antibody would behave like a buffering agent with respect to the ligand. Our particular interest is in whether a drug-specific antibody can maintain a long-lived pool of uncomplexed drug within the plasma of a test subject. The equation governing buffer-like behavior of such a system is a simple substitution of the Henderson-Hasselbalch equation:

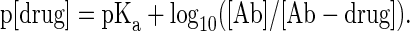[2]

(Here, and in subsequent equations, [Ab] refers to a site concentration rather than to the concentration of divalent immunoglobulin molecules.)

Work in other laboratories has demonstrated enhanced bio-activity, and in some cases prolonged lifetime, of hormones and cytokines coadministered with anti-hormone and anti-cytokine antibodies, but falls short of demonstrating a continuously replenished pool of free ligand at a concentration near the K_d (2-5). We are not aware of an antibody buffering model applied to small-molecule drugs. Our purpose here is to explore buffering behavior experimentally by using 2-phenyloxazol-5-one-γ-aminobutyrate (Ox) as a drug proxy, and to develop quantitative tools to guide design of antibody buffers for bona fide drugs.

We chose the γ-aminobutyric acid conjugate of 2-phenyloxazol-5-one as a model compound for this study because Ox has a chemical structure typical of a small-molecule drug and because an existing library of anti-Ox monoclonal antibodies has been kinetically characterized (6). We do not know the clearance mechanism of Ox, and to our knowledge it is not biologically active, but these points are immaterial to the general question of whether a specific antibody can modulate the pharmacokinetics of a small-molecule ligand in vivo.

Materials and Methods

Antibody Production. A panel of three anti-Ox hybridomas (NQ11/7.12, NQ16/113.8, and NQ22/16.4) have been described (7, 8). A control (non-Ox binding) murine anti-lysozyme antibody, D1.3 (9), was also used. These hybridomas were grown in oscillating bubble roller bottles (10), and the respective monoclonal antibodies were purified from spent culture supernatant by affinity chromatography on staphylococcal protein A-Sepharose. SDS/PAGE was performed on the antibodies to verify purity. Protein concentration was determined by UV spectroscopy, using extinction coefficients calculated from sequence (11). Antibody solutions were filter-sterilized and stored at 4°C under N₂.

Preparation of Tritiated Ox. Crude Ox was prepared essentially as described by Berek et al. (7), using γ-amino[³H]butyric acid (1 mCi/ml; 1 Ci = 37 GBq) from PerkinElmer Life Sciences. The Ox was purified by using HPLC. The reaction mixture was dissolved in PBS (25 mM NaH₂PO₄/125 mM NaCl, pH 7.0), applied to a Zorbax SB-C18 HPLC column with an analytical guard column (Agilent Technologies), and eluted with 0.1 M ammonium formate, pH 4.8 (mobile phase A), and acetonitrile (mobile phase B). A flow rate of 0.5 ml/min, a gradient of 9.5-70% mobile phase B over 26 min, and a wavelength of 348 nm were used. The Ox peak eluted at 20.5 min. Pooled fractions from the Ox peak were dried in a ThermoSavant SPD1010 SpeedVac System with no heat. After drying, the residue was resuspended in 1 ml of PBS. The radiochemical purity of the Ox was confirmed by HPLC. The concentration was determined both by quantitative HPLC and by UV spectroscopy. Specific activity was determined by diluting 1 μl of Ox into 5 ml of Scintiverse II (Fisher Scientific) and measuring radioactivity in a Beckman LS6500 scintillation counter. The specific activity of Ox was 4.4 × 10⁶ cpm/nmol.

Determination of Anti-Ox Antibody Affinity at 37°C. Antibody affinities were determined through fluorescence spectroscopy (6) using a PerkinElmer LS 50 B luminescence spectrometer. The temperature of the cuvette block was maintained by a circulating water bath heated to 37°C. A cuvette containing either 20 nM (NQ11/7.12) or 200 nM (NQ16/113.8 or NQ22/16.4) antibody in PBS was placed in the spectrometer and allowed to equilibrate to 37°C. In the case of NQ11/7.12, 30 μg/ml ubiquitin was added as a carrier. An excitation wavelength of 280 nm with a bandwidth of 5 nm and an emission wavelength of 340 nm with a bandwidth of 10 nm were used with an 8-sec integration time. Ox solution was added in 40 nM increments, and fluorescence readings were taken after allowing time for equilibration. The resulting concentration/fluorescence readings were analyzed by least squares (12) to determine the K_d of each antibody.

Determination of Anti-Ox Antibody Half-Life in Rat Plasma. NQ11/7.12 was iodinated with ¹²⁵I by using the chloramine-T method (13, 14). Iodine incorporation into the antibody was 97%, and the specific activity of the antibody solution was 1.25 × 10⁶ cpm/μg. Rats (300-g Sprague-Dawley males) implanted with a jugular vein cannula were obtained from Zivic Laboratories. ¹²⁵I-NQ11/7.12 (0.39 nmol) was mixed with unlabeled NQ11/7.12 to a final amount of 4.54 nmol. This amount was further diluted to a final volume of 1 ml in sterile PBS. The sample was infused by hand over 1 min through the jugular cannula and the cannula was flushed with 0.2 ml of heparinized saline (250 units/ml) to reduce the risk of clotting. The end of the infusion was designated as time 0. Blood samples (0.4 ml) were withdrawn from the cannula at various time points. The blood was immediately centrifuged to separate the plasma. The radioactivity of 100 μl of plasma was quantified by using a Packard Cobra AutoGamma to determine the concentration of NQ11/7.12 in the plasma.

Antibody Buffering Experiments. Samples for injection consisted of 4.54 nmol of anti-Ox antibody or control antibody and 2.27 nmol of Ox diluted to 1 ml with sterile PBS. The samples were warmed to 37°C, then infused over 1 min through the jugular vein cannula in Sprague-Dawley rats. Samples were taken at the indicated time points as described above. In addition, 100 μl of plasma was used in bound vs. free Ox experiments described below. For some rats, 0.1 ml of blood minus plasma was analyzed. These samples were first decolorized by incubating at 40°C in 0.3 ml of Scintigest (Fisher Scientific)/isopropyl alcohol (1:2, vol/vol) for 1 h. Then 0.2 ml of 30% H₂O₂ was added dropwise and the solution was incubated at room temperature for 15 min. Pipetting up and down was needed to break up some clumps. The solution was incubated at 40°C before placing it into 5 ml of Scintiverse II. The samples were allowed to sit overnight before counting to reduce chemiluminescence. Control samples were prepared by using known amounts of Ox to aid in analysis.

Separation of Bound and Free Ox by Using 187.1-Sepharose Affinity Gel. The rat anti-mouse κ antibody 187.1 (obtained from the American Type Culture Collection) (15) was isolated from spent culture medium and purified by passage over a protein A-Sepharose affinity column. Ten grams of CNBr-activated Sepharose 4 Fast Flow (Amersham Pharmacia Biosciences) was washed and coupled with 187.1 according to the manufacturer's protocol. Two milligrams of 187.1 per 10 g of swollen gel was used.

During the antibody buffering experiments, 100 μl of plasma was loaded onto the 187.1 column immediately after centrifugation. Three milliliters of PBS followed by 3 ml of 0.2 M glycine (pH 2.5) was loaded onto the column as above. All of the PBS fractions and all of the glycine fractions were collected separately for each time point and dried down in the SpeedVac. The residue was resuspended in 150 μl of PBS and then transferred to a scintillation vial with 5 ml of Scintiverse II for quantitation of radioactivity.

Long-Term Buffering Experiment. Samples of NQ11/7.12 and Ox were prepared and infused into Sprague-Dawley rats as described previously. Samples (0.4 ml) of blood were taken at 1, 10, 20, 50, 90, and 120 min. For each sample, 100 μl of plasma was counted directly and 100 μl was placed on a 187.1 column to separate bound and free Ox. At 24 h, and again at 48 h after the first administration, 2.27 nmol of Ox in 0.5 ml of PBS was infused over 1 min through the jugular cannula. Samples were taken at the indicated time points and analyzed as above.

Results

To determine its pharmacokinetic behavior, tritiated Ox was infused into a rat through a jugular cannula, and elimination of Ox was followed through blood sampling, separation of the plasma by centrifugation, and scintillation counting of the plasma. The concentration of Ox declined rapidly from the plasma, with an elimination half-life of 1.2 min (data not shown, but similar to Fig. 1). This lifetime is very short; a drug candidate with a loss rate on this scale would almost certainly be disqualified from further study.

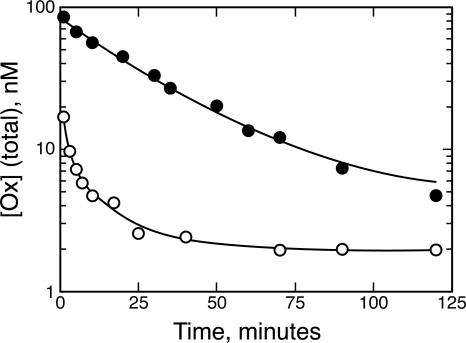
Fig. 1.

Antibody complexation opposes elimination of Ox. Elimination of Ox administered with the control antibody D1.3 (○, t_1/2 = 1.2 ± 0.2 min) occurs much more rapidly than when Ox is administered with NQ11/7.12 (•, t_1/2 = 20 ± 2 min). Each point represents data collected from five animals.

We used a set of three kinetically characterized monoclonal antibodies raised against Ox (6). The affinities of these antibodies were redetermined at 37°C by using fluorescence spectroscopy and found to be K_d = 1.3 nM (NQ11/7.12), 46 nM (NQ16/113.8), and 42 nM (NQ22/16.4). An isotype-matched (IgG1) anti-hen-egg lysozyme antibody, D1.3, was used as a control. Each rat in these studies was used only once to limit the possibility of a rat anti-mouse antibody response.

Antibodies are attractive therapeutic vehicles in part because of their long plasma half-life, which is far longer than the pharmacokinetic lifetime of most drugs. We confirmed this long residence time in the plasma by using radioiodinated NQ11/7.12. The monoclonal antibody was infused into a rat, and the elimination of the NQ11/7.12 was followed through blood sampling, separation of the plasma by centrifugation, and γ counting of the plasma. The concentration of NQ11/7.12 declined slowly, with an elimination half-life from the plasma of 20 h (data not shown). This lifetime is so long that the anti-Ox antibody concentration is effectively constant (200 ± 30 nM) over the course of all of the pharmacokinetic studies presented here, except where noted.

For an antibody to buffer a ligand, the antibody-ligand complex must form a long-lived reservoir. In other words, antibody complexation must block ligand elimination. Ox was administered with twice the molar amount of NQ11/7.12 or the control antibody through the rat's jugular cannula (Fig. 1). Administration of Ox with NQ11/7.12 showed a significant prolongation of Ox residence time, with an Ox elimination half-life of 20 ± 2 min. Comparison of the two curves indicates that much of the Ox in the control is cleared from the plasma before the sample at the first time point can be taken. The remaining Ox administered with D1.3 showed biphasic elimination kinetics; most was eliminated from the plasma with a half-life of 1.2 ± 0.2 min, and a smaller amount had a half-life of 10 ± 2 min. The 17-fold increase in half-life indicates that NQ11/7.12 binding is opposing Ox elimination from the plasma. As a control, analysis was also performed on the cellular fraction of the blood to determine whether cells are a significant repository for the Ox. The Ox concentration in the cellular fraction ranged between 1% and 2% of the total Ox concentration in the plasma (data not shown), which indicates that an insignificant amount of Ox is retained in this fraction. No adverse effects were noted in the animal subjects.

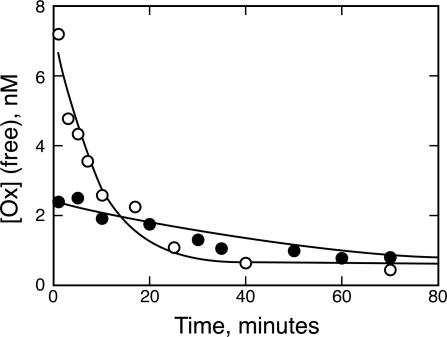
The principle of chemical equilibrium predicts that the Ox in the plasma should partition between free and antibody-bound forms. The buffering equation (Eq. 2) in particular predicts that a free pool should be constantly replenished, staying at a concentration near the antibody's K_d. To test this hypothesis, bound and free forms of Ox in plasma fractions from the previous experiment were separated on an affinity column. Samples resulting from D1.3 coadministration were processed in parallel, although no significant antibody-bound label was expected or found. An immobilized rat anti-mouse κ antibody was used to trap antibody-Ox complexes, whereas free Ox eluted from the column with a PBS wash (free Ox fraction). This analysis confirmed that a free pool of Ox does indeed exist in the rat plasma whether the Ox is administered with D1.3 or with NQ11/7.12 (Fig. 2). Initially, when Ox is administered alone or with D1.3 the amount of free Ox is high (6.8 nM), but it quickly decreases, with an elimination half-life of 6.0 ± 1 min. However, when Ox is administered with NQ11/7.12, the initial free concentration of Ox is low (2.2 nM). This low concentration remains fairly stable over time, with an Ox elimination half-life of 41 ± 6 min. Therefore, the presence of NQ11/7.12 appears to be buffering the free Ox.

Fig. 2.

NQ11/7.12 lowers the concentration of free Ox while increasing the plasma half-life of free Ox. The free concentration of Ox is initially lower when Ox is administered with NQ11/7.12 (•) versus D1.3 (○). However, this free concentration with NQ11/7.12 declines more slowly than when Ox is administered without an antibody buffer.

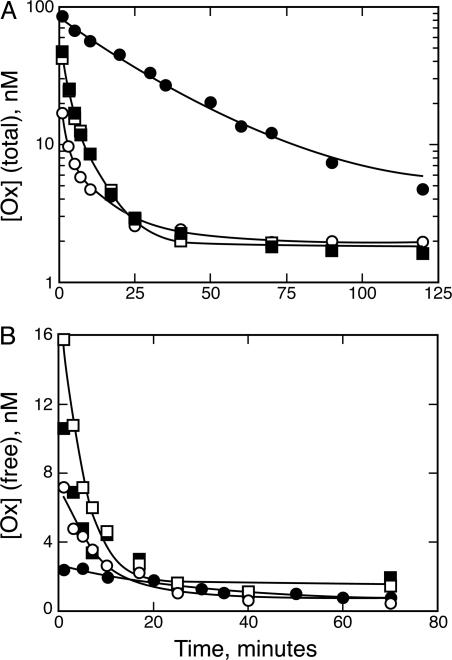
Next, we wanted to test whether antibody K_d affects the ability of an antibody to retard Ox elimination from the plasma. For this experiment, the anti-Ox antibodies NQ16/113.8 and NQ22/16.4 were used. These two antibodies have about the same K_d for Ox, but this K_d is significantly higher than that of NQ11/7.12. Ox was administered to rats with either NQ16/113.8 or NQ22/16.4. The total Ox concentration (Fig. 3A) was measured through blood sampling. The concentrations of Ox administered with NQ11/7.12 or with D1.3 are shown in Fig. 3A for comparison. Both NQ16/113.8 and NQ22/16.4 were shown to retard total Ox elimination from the plasma. This increase in Ox half-life did not match the extent of the Ox half-life increase of NQ11/7.12, which has a much higher affinity for Ox. Therefore, as predicted, antibody K_d is related to the elimination rate of total Ox in the plasma.

Fig. 3.

Antibody K_d determines the half-life of Ox and free Ox concentration. (A) Total Ox vs. time. Antibodies NQ16/113.8 (▪) and NQ22/16.4 (□), which have higher K_d than NQ11/7.12, are able to buffer Ox concentration, but to a lesser degree, than NQ11/7.12 (•). D1.3 (○) is shown for comparison. (B) Free Ox vs. time. The lower-affinity antibodies also reduce the free concentration of Ox in the plasma and are able to prolong the half-life of free Ox, but to a lesser degree than NQ11/7.12.

In addition, antibody K_d affects the free pool of Ox in the rat plasma (Fig. 3B). Plasma from the previous experiment was loaded onto the rat anti-mouse κ antibody affinity column, and free and bound Ox fractions were eluted. Initially, the free concentration of Ox administered with NQ16/113.8 or NQ22/16.4 (between 10 and 16 nM) is higher than that of Ox administered with NQ11/7.12 (2.2 nM). This free concentration declines much more rapidly than the free Ox administered with NQ11/7.12. Thus, anti-Ox antibody K_d determines the buffering capacity of the antibody.

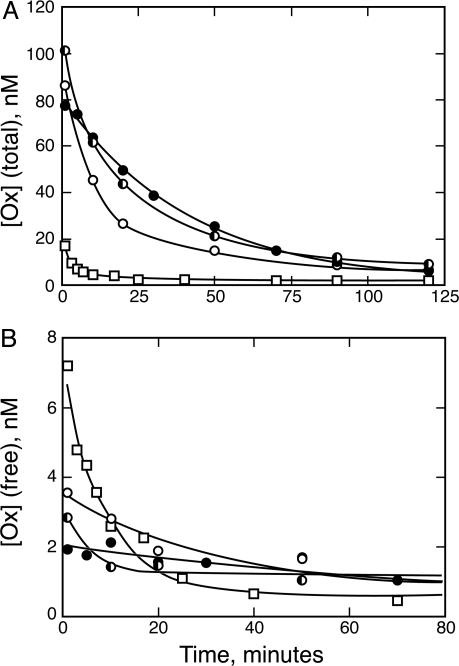
Because we had previously determined that NQ11/7.12 is retained in rat plasma for a long period compared with the elimination half-life of Ox, we wanted to test whether NQ11/7.12 retains its ability to buffer Ox concentration in the plasma days after the initial antibody infusion. For these experiments, NQ11/7.12 was administered only once. Ox was initially coadministered with NQ11/7.12, and additional aliquots of Ox alone were administered at 24 and 48 h. Blood sampling was done to follow total Ox elimination from the plasma. The Ox pharmacokinetic lifetime at 24 and 48 h showed only small changes from the kinetics after the initial NQ11/7.12 administration (Fig. 4A), which could be attributed to the slow clearance in circulating antibody over time. Ox coadministered with the D1.3 control antibody is shown for comparison. Free vs. bound Ox separation was also performed on these plasma samples (Fig. 4B). Initially, the free Ox concentration at 24 and 48 h was higher than when Ox was administered in conjunction with the antibody buffer. However, this free concentration quickly normalized as Ox was bound by the NQ11/7.12 already present in the plasma to follow an elimination pattern similar to Ox and NQ11/7.12 administered together. Therefore, an anti-Ox antibody not only can buffer the concentration of free Ox in the plasma, but it can do so even days after the initial antibody infusion.

Fig. 4.

NQ11/7.12 retains the ability to buffer Ox days after initial antibody administration. Plasma half-life of total Ox (A) and free Ox (B) is prolonged whether Ox is coadministered with NQ11/7.12 (•) or administered alone 24 h after NQ11/7.12 infusion (▪) or 48 h after NQ11/7.12 infusion (○). Ox administered with a control D1.3 antibody (□) is shown for comparison.

Discussion

In our testing of a model for antibody buffering of a small-molecule drug, several principles emerge. First, anti-Ox antibodies were able to extend the lifetime of total Ox in the plasma. Antibody complexation did not facilitate removal of Ox. This result would be expected, given that haptens do not fix complement (16) and that the major mechanism of immune complex clearance operates on aggregates of complement protein C3b and antigen-antibody complexes (17). Antibody complexation is likely to block the two major routes of drug clearance, renal filtration and hepatic metabolism. Second, the buffering mAb prevents the spike in ligand concentration characteristic of the unbuffered control. The concentration of uncomplexed Ox at the first time point in Fig. 2 is 2.4 nM, and the remaining 97% is complexed with antibody. In a drug scenario, this property of an antibody buffer might minimize high-dose toxicities because only a fraction of the administered dose is bioavailable at any one time. Third, antibody buffering increases the pharmacokinetic lifetime of the uncomplexed ligand that would be available for receptor binding. The buffered free Ox concentration in Fig. 2 declines from 2.4 to 0.8 nM over the span of an hour, whereas unbuffered Ox is more than half gone before the sample can be taken at the first time point. Fourth, a buffering mAb stabilizes a pool of free Ox near the antibody K_d. The 2.4 and 0.8 nM endpoints just cited bracket the 1.3 nM K_d of NQ11/7.12. Antibodies with higher K_d for Ox were weaker buffers in the ligand concentration range studied. The import of this for the use of antibody buffering in therapy is that one would determine the most advantageous in vivo drug level, then tune the antibody K_d to an appropriate value to stabilize that level. K_d can be manipulated conveniently with one of the display technologies (18-21).

Eq. 2 suggests that a K_d equal to the desired drug level would give the best buffer, analogous to a pH buffer exerting maximum buffering power at a pH equal to its pK_a. Indeed, the identical pharmacokinetics observed with two antibodies that differ 10-fold in kinetic constants, but with the same K_d (Fig. 3), is proof of the primacy of equilibrium in determining the free ligand level in this system. Nevertheless, scenarios can be envisioned in which rate information would be necessary to predict accurately the free ligand concentration. If we posit a steady state where dissociation of a drug (k_off) from an antibody approximately balances the rates of rebinding (k_on) and drug loss through clearance (k_loss), then

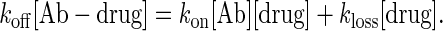[3]

If we evaluate this expression for a condition at which the antibody is half-saturated with drug, i.e., the point of maximum buffering power, and define [Ab]_1/2 as half the total antibody concentration and [drug]_ss as the steady-state free drug concentration, then

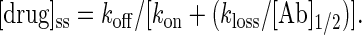[4]

The qualitative interpretation of Eq. 4 is that the antibody-drug ensemble will stay close to equilibrium so long as drug clearance is slow relative to the rate of drug rebinding by the antibody. In the case of very slow drug binding, i.e., low k_on, or very rapid elimination, i.e., high k_loss, the steady-state free drug level would deviate significantly from K_d. Eq. 4 is a tool for deciding when a steady-state model, rather than rapid-equilibrium model, is more appropriate for analysis.

Last, we have demonstrated that an antibody is able to buffer ligand concentration over multiple ligand administrations. The antibody can be “recharged” in situ. The buffered curves in Fig. 4 represent an approach to equilibrium from opposite directions. In the initial administration, the Ox and antibody are concentrated in a small volume, and nearly all of the Ox is sequestered in antibody complexes. In the readministrations, the antibody is already dispersed throughout the plasma and all of the Ox starts in the free state. The similarity of the buffered curves in Fig. 4, whether the Ox was coadministered or readministered at a later time, shows that equilibration of Ox and the antibody within the plasma is much more rapid than the elimination of free Ox. The results of the extended buffering experiment suggest a second utility of separating the antibody and drug dosing. Small-molecule drugs are in general more mobile than antibodies, and the latter are slow to penetrate structures such as tumors. An antibody cannot buffer if it is not present in a compartment. However, if a buffering antibody is administered 48 h before the buffered drug, as in Fig. 4, one could expect antibody extravasation. One would then in turn expect buffering to occur in the tissues as well as in the plasma.

In the preceding experiments, we have used a model system to demonstrate pharmacokinetic modulation of a ligand by an antibody. Antibody buffering has the potential to replace a sawtooth drug vs. time profile that is the current norm with a stable, long-lived drug level. The value of this steady-state level can be set to the optimum for drug action by genetic engineering of the antibody. Once the antibody has been administered, it can be recharged in situ multiple times with fresh drug. These attributes of an antibody buffer offer advantages over conventional delivery vehicles that are nongenetic, nonrechargeable, and work by slow release rather than equilibrium. For example, controlled-release pellets (22) or drug-loaded liposomes (23) can be introduced into the body, but they are useful for only one drug administration. In drug delivery by slow infusion, a gradient is established between the point of entry of the drug and the site of action. Antibodies, on the other hand, are able to equilibrate within a compartment, buffering the drug concentration near the desired target. While serum albumin is known to be a circulating depot for many drugs, thereby reducing the amount of drug available for biological effect (24), changing the structure of albumin to selectively bind a single drug with high affinity would be a formidable problem. Antibodies, on the other hand, can be more amenable to clinical use because they target a single drug at a therapeutically designated affinity. In short, use of antibody buffering as a method of drug delivery would improve upon methods already in place by yielding a stable, bioavailable concentration of a drug that is normally rapidly eliminated from the plasma.