Damage accumulation of bovine bone under variable amplitude loads

Abstract

Stress fractures, a painful injury, are caused by excessive fatigue in bone. This study on damage accumulation in bone sought to determine if the Palmgren-Miner rule (PMR), a well-known linear damage accumulation hypothesis, is predictive of fatigue failure in bone. An electromagnetic shaker apparatus was constructed to conduct cyclic and variable amplitude tests on bovine bone specimens. Three distinct damage regimes were observed following fracture. Fractures due to a low cyclic amplitude loading appeared ductile ( 4000 μϵ), brittle due to high cyclic amplitude loading (> 9000 μϵ), and a combination of ductile and brittle from mid-range cyclic amplitude loading (6500 –6750 μϵ). Brittle and ductile fracture mechanisms were isolated and mixed, in a controlled way, into variable amplitude loading tests. PMR predictions of cycles to failure consistently over-predicted fatigue life when mixing isolated fracture mechanisms. However, PMR was not proven ineffective when used with a single damage mechanism.

Highlights

• •A novel apparatus is considered to conduct constant and variable amplitude loading tests.
• •A wide range of forcing amplitudes are consider, such that damage mechanisms can be isolated.
• •Active damage mechanisms are identified by fracture classification and SEM imaging.
• •Palmgren-Miner Rule fails when multiple damage mechanisms are active, but does not fail when a single mechanism is active.

1. Introduction

This study considers cyclic constant and cyclic variable amplitude loading fatigue tests on bovine bone specimens, and it is motivated by the prevalence of stress fractures caused by repeated high-cycle loading. According to Verheyen et al. (2006), stress fractures occur in up to 21% of American military recruits and 45% of Israeli military recruits. Athletes such as dancers, figure skaters and gymnasts have a high incidence of stress fracture as well. However, cross country and track runners seem to experience stress fractures more often than other athletes. In a study conduct by Bennell et al. (1996), 21% of competitive runners acquired stress fractures in just a twelve month period. As we age, our bone's elastic modulus, strength and toughness decline. The elastic modulus, as well as the ultimate tensile strength, both decrease by 2% each decade between the ages of 20 and 90 years old (Mow and Hayes, 1997). These properties are extremely important to the fatigue behavior of bone, which is why the growth of microcracks is also an issue at older ages. This is especially a concern in post-menopausal, osteoporotic females. Humans are not the only mammals that acquire stress fractures; animals have a high incidence as well. Racing animals, such as horses and grey hounds, acquire stress fractures very frequently. The constant training and fatigue that human athletes, soldiers and animal athletes go through to excel at their activities is the main factor in acquiring stress fractures (Verheyen et al., 2006).

Stress fractures are microcracks within the bone that are caused from excessive fatigue. When the osteoblasts, cells that form or synthesize bone, cannot keep up with the microdamage that these continuous stresses create, the bone begins to experience fatigue. Bone fatigue is the cycle-by-cycle accumulation of damage from varying stresses and strains, so that immediate failure does not occur (Cui, 2002). The initial microcracks can eventually propagate and develop into a complete fracture in the bone. Stress fractures in humans are most commonly located in the tibia, tarsals, metatarsals and the femur (Patel et al., 2011, Sanderlin and Raspa, 2003). This type of injury is often very painful. Diagnosis is very difficult, and the best way to detect them is by plain radiography, magnetic resonance imaging, or triple-phase bone scintigraphy (Patel et al., 2011). Currently, the only way to treat a stress fracture is activity modification, analgesic drugs to relieve the pain, and pneumatic bracing to help with the healing process.

1.1. Constitutive fatigue model

When studying fatigue in bone, it is imperative to understand how bone breaks and what actually occurs as the fatigue damage accumulates. There is a strong consensus that bone acts like a fiber reinforced composite material when subjected to stresses and strains (Alto and Pope, 1979, Bell et al., 1999, Gibson et al., 1995, Guo et al., 1998, Martin et al., 1996, Moyle et al., 1978). Varvani-Farahani et al. compared the specific structures within bone and engineered composite (Varvani-Farahani and Najmi, 2010). In human cortical bone, osteons carry the brunt of the load and play the role of the reinforcing fiber within the interstitial bone tissue, which acts as the matrix. Additionally, the cement lines between the individual osteons act as the weak interfaces in fiber-reinforced composites. Bone and engineered composites display similar mechanical properties. Both are much stronger when loaded parallel to their fiber or osteonal structures. In bone, these structures run along the longitudinal axis, and are therefore stronger in the longitudinal direction.

When subjected to axial cyclic loading, bone undergoes three stages in the process leading up to, and resulting in, complete fracture (Currey, 1998, Gupta and Zioupos, 2008, Varvani-Farahani and Najmi, 2010). This is very similar to the process that composite materials undergo during characterization of fatigue damage under axial loading conditions. When loaded, both materials begin with an elastic region that strains linearly until it hits a yield point. A region of plastic flow follows this yield point. In this phase, large amounts of energy are absorbed due to a variety of toughening mechanisms. Finally, once the material cannot absorb any more energy, a catastrophic failure takes place.

1.1.1. Stage I

The first phase is a reversible deformation process prior to crack initiation that results in a very quick decline in stiffness due to the presence and initiation of microcracks in the interstitial bone, or matrix (Gupta and Zioupos, 2008, Schaffler et al., 1995, Varvani-Farahani and Najmi, 2010). Frost was the first to propose and report the idea of microcracks in 1960 (Frost, 1960). His theory was that microcracks signal and initiate their own healing due to osteocyte apoptosis. His concepts and findings were later confirmed by many studies (Bentolila et al., 1998, Mori and Burr, 1993, Verborgt et al., 2000). Researchers believe that even healthy bones contain microdamage. Burr stated that microcracks were a naturally occurring defense mechanism against extraneous forces applied to bones (Burr, 2011). Cracks are able to absorb and dissipate energy, lessening the amount of energy that the interstitial matrix and osteons have to absorb. Within healthy bone, microdamage is in equilibrium with the repair and remodeling system, osteoblasts and osteoclasts. These defects enable the bone to deform reversibly in the beginning phase until the bone hits a yield point.

1.1.2. Stage II

The slow process of stage II begins after the bone has hit this yield point. While the stiffness of the material continues to decrease, it is at a much slower rate than that of the elastic region. In this stage, the material still has its structural integrity, but is now permanently damaged (Gupta and Zioupos, 2008). The majority of this damage tends to occur at the cement lines (Varvani-Farahani and Najmi, 2010). Bone absorbs a great deal of energy in this phase and decreases in stiffness and residual strength. What is occurring during this time to cause this type of behavior, is the question that many researchers have spent their careers trying to pinpoint. It has been found that this particular behavior is primarily due to a combination of mechanisms.

Gupta and Zioupos presented two different methods in 2008 describing the failure of bone (Gupta and Zioupos, 2008). The first is the stress based method, which takes into account the stress intensity factor, K_c. This theory says that a crack is initiated when the stress at the crack tip reaches or exceeds the material's critical value. Peterlik et al. found that the fracture process depends on the direction in which the crack travels (Peterlik et al., 2006). The angle of the fibril microstructure, at the point damage originated, determines whether the crack propagates longitudinally, tangentially, or radially. Gupta and Zioupos also stated that the way in which cracks propagate through bone, and lead to complete failure, is directly influenced by the heterogeneity of the microstructure of the material (Gupta and Zioupos, 2008). The second method is an approach based on energy, including the critical strain energy release rate, and the work to fracture of a specimen. The required critical levels of energy per unit area to fracture the material are determined by these variables. Engineered composites, as well as bone, have very weak interlamellar surfaces with the ability and tendency to absorb energy and divert the main crack. This in turn slows down the start and propagation of cracks within bone. Burr stated that the ability for bone to absorb energy before failure is what determines the fracture resistance for the material (Burr, 2011).

A typical trend seen in fatigue testing is an increase in toughness as stiffness decreases. This phenomenon is precisely what is seen in this second phase of bone fatigue. Toughness is the amount of energy required to run a crack through a material. This observed toughening is due to bone's many mechanisms for deterring the propagation of cracks and damage. For this reason, Gupta and Zioupos stated that the initiation of a crack in the material is not nearly as significant as the propagation of the crack through the material (Gupta and Zioupos, 2008). Bone does not prevent the initiation of damage; it only delays the growth of fracture with its micro hierarchical structure, preventing cracks from growing to catastrophic size. The microstructure usually delays the growth of cracks long enough for the bone to repair itself. Our bodies have also developed mechanisms that attempt to prevent fracture. These toughening mechanisms increase the amount of energy that is required to grow the crack and fracture the material. Researchers have categorized the observed mechanisms into two groups, intrinsic and extrinsic (Kruzic and Ritchie, 2008, Launey et al., 2010, Nalla et al., 2003, Mar, Nalla et al., 2005, Nalla et al., 2005, Ritchie et al., 2005). Intrinsic toughening mechanisms take place ahead of the crack tip. Extrinsic toughness develops from the applied stress behind the crack tip. Along with the crack diversion or deflection, other toughening mechanisms include microdamage, nucleation, crack bridging, sacrificial bonds, interfibrillar shearing, and fiber pullout (Koester et al., 2008, Nalla et al., 2005, Ritchie et al., 2009, Ritchie et al., 2005).

Microdamage is one of the main tools that bones use to defend against crack propagation. It dissipates energy, preventing and delaying catastrophic failure. Not only are microcracks found in healthy bone, but they have also been reported to develop after crack initiation, in an attempt to slow down and deter crack growth (Hansen et al., 2008). However, this mechanism also reduces the total amount of energy that can be absorbed by the bone overall. Microdamage causes the mechanical properties of bone to decline, which in turn results in fracture. The way in which the cracks are formed, the location they are in, the stimulus that caused them to form, and the way in which they are mended are all factors that are taken into account when determining the type of microcrack that is observed. There are two types of microcracks that occur in cortical bone (Burr, 2011). The first are linear microcracks. These occur most often and are typically found in the mineralized interstitial bone. These cracks are a clear indicator that the bone tissue has deformed before the main crack initiates and are due to compressive stresses. The second is diffuse microdamage, which is a collection of small cracks that are caused by tensile loads. When these cracks are close enough, they have the tendency to nucleate, coalesce and grow in size. Vashishth reported this in 1996 and found that these mechanisms stabilized the progression of fracture by absorbing energy and taking it away from the main crack (Hansma et al., 2005).

Ritchie et al. showed that another mechanism, crack bridging, increased fracture resistance (Kruzic and Ritchie, 2008, Launey et al., 2010, Nalla et al., 2003, Mar, Nalla et al., 2005, Nalla et al., 2005, Ritchie et al., 2005). There are two forms of crack bridging. The first is collagen-fibril bridging. These by themselves do not play a large role in crack shielding. The second form is uncracked-ligament bridging which can sustain considerable loads.

Hansma et al. published a sacrificial bond theory that says the weak reformable bonds in the organic part of the biomineralized tissues are key to how bone resists fracture (Fantner et al., 2005, Hansma et al., 2005, Thompson et al., 2001). Bonds inside the organic molecules were yielding and even breaking. These sacrificial bonds absorbed high amounts of energy, and toughened the material. Gupta first proposed interfibrillar shearing (Gupta et al., 2006, Gupta et al., 2005) and later stated that irreversible bone deformation is due to the breaking of ionic bonds (Gupta et al., 2007). The breaking of the fibrils, themselves, after the yield point is due to decohesion between or inside fibrils, caused by the ionic bond breaking. Gupta determined that this bond breakage is most likely happening inside of the collagen fibrils, not in the interfibrillar matrix between two fibrils (Gupta et al., 2007).

1.1.3. Stage III

In the final stage of bone fatigue, the material has acquired a great deal of damage from the two previous stages around the matrix and cement lines. At this point, the osteons take the brunt of the load that is being applied. The toughening mechanisms are unable to absorb the necessary amount of energy to prevent the crack from propagating. The material's residual strength and stiffness decline very quickly and cause rapid crack growth. This results in the osteons debonding and catastrophic failure of the material. Some researchers have reported osteon pullout at this stage (Braidotti et al., 1997, Hiller et al., 2003). In a living bone, the final stage also occurs because the repair system cannot keep up with accumulating damage.

Our study, however, did not use living tissue; therefore there is an absence of this remodeling process. Further research with living bone tissue is necessary to understand the damage accumulation in vivo, but the current study will allow for quantification of the direct effects of cyclic loading.

1.2. Damage accumulation

The fatigue limit of a material is the maximum stress amplitude that can be withstood, for an infinite number of cycles, without failing. Cyclic Amplitude Loading and Variable Amplitude Loading are methods used to determine the fatigue limit of different types of materials (Carter and Caler, 1983, Anon, 1995, Evans, 2007, Pattin et al., 1996). Both of these methods are typically applied during a three or four-point bending test. During Cyclic Amplitude Loading (CAL), the force applied to the specimen is periodic and consistent. Variable Amplitude Loading (VAL) is the process of applying loads to a specimen, while varying the amplitude of the exerted force. In reality, bones are more likely to undergo varying external stresses as opposed to repetitive consistent stresses. The summation of microcracks developed from repetitive loading is referred to as damage accumulation.

1.2.1. Palmgren-Miner rule

The Palmgren-Miner rule is a linear cumulative damage hypothesis and is the best estimation of the fatigue limit available to date (Schijve, 2003). It states that the summation of the ratio of the number of cycles at a given amplitude and the number cycles to failure is equal to the damage accumulated,

$$D_p=\sum _{i=1}^k\frac{n_i}{N_i},$$ (1)

where n_i is the number of cycles under a constant amplitude, N_i is the total number of cycles to failure at that amplitude, and D_p is the damage parameter. Failure occurs when the damage parameter is equal to one. This is the point at which 100% of the fatigue life is expended. Under this theory, it is assumed that the order in which the various loads and cycles are applied does not affect the outcome of failure, and that damage accrues at the same rate at a given stress level without respect to the history of the material (Collins, 1981). Palmgren first published this hypothesis in 1923. It was later reinforced by Miner in 1945 when he used it to predict the fatigue life of materials in the aerospace industry (Miner, 1945, Palmgren, 1924). Deviations from the prediction have been reported in the literature (Anon, 1995, Cui, 2002, Fatemi and Yang, 1998, Todinov, 2001). Todinov presented a thorough explanation for why the resulting endurance limits differ from the Palmgren-Miner rule (Todinov, 2001). Reasons for such deviation are associated with the prediction being independent of the load-level, the load-sequence, and the load-interaction (Cui, 2002, Fatemi and Yang, 1998). Murakami and Matsuda reported that the fatigue limit stress and the critical stress play very important roles in the prediction of fatigue life and need to be taken into account (Ravichandran, 1999). Murakami and Matsuda found that the effect of the applied stress changes at every moment with the change in the crack length. These factors are not considered in the Palmgren-Miner rule, thus it can be expected that the Palmgren-Miner rule will have limited success in predicting bone fatigue and failure. However, the simplicity of this rule is the reason it is widely accepted throughout industry, and a more accurate prediction does not yet exist (Collins, 1981, Schijve, 2003).

2. Materials and methods

2.1. Bone preparation

Bovine femora were purchased from Animal Technologies, Inc. (Tyler, TX). The gender, body weight, and health of the cows from which the bones were harvested were unknown. It was known, however, that the cows were skeletally immature, and between the ages of eight and thirty months. To eliminate one possible source of error, specimens were only cut from the lateral side. The tissue on the outside of the bones was removed and the epiphyses were cut off using a band saw. The diaphysis was then cut into two sections, separating the medial and the lateral sides of the bone. The marrow was removed, and the lateral half of the diaphysis was then longitudinally cut into three sections, so that the grain of the bone ran along the length of the specimen. A Buehler IsoMetTM 1000 precision saw with an IsoMetTM 15 LC diamond wafering blade was used to cut the lateral longitudinal pieces into specimens that were 2 in. long, by 0.5 in. wide, by 0.1 in. thick. Fig. 1 provides a schematic of the number of specimens cut per bone and their location with respect to the bone. A 3:33 ratio of Buehler Cool 2 cutting fluid to water was used as the cutting fluid for the saw. The diamond blade allowed for a smooth, polished finish on the faces of the specimens. Four femurs were used to machine twenty-eight total lateral specimens. Any specimens that were cut to the specific dimensions but had visible surface defects were not used in order to eliminate variability.

Fig. 1.

Schematic of where specimens were extracted from bovine tibia. M refers to the medial side of the bone, and L refers to the lateral side of the bone.

Specimens were notched with a triangular file on both sides centered within a 1′′ test section to create a stress concentration and assure that the bone would break in a specific area. An 11/64′′ hole was drilled in the bone at one end (designated as bottom of specimen) to allow for attachment of a steel pendulum. To keep the specimens hydrated until testing, the bones were wrapped in gauze, soaked in 0.9% saline solution, and stored at 1.4 °C in a ZiplockTM bag in a compact refrigerator. If the bones were not intended to be used for an extended period of time, they were instead stored in a commercial freezer at −20 °C, and then allowed to thaw in the compact refrigerator for at least 24 h before testing. All specimens were allowed to dry out for 7 h immediately preceding testing. Preliminary testing found that after 7 h, the bone samples were fully dried (sample properties no longer affected by further drying).

2.2. Test apparatus

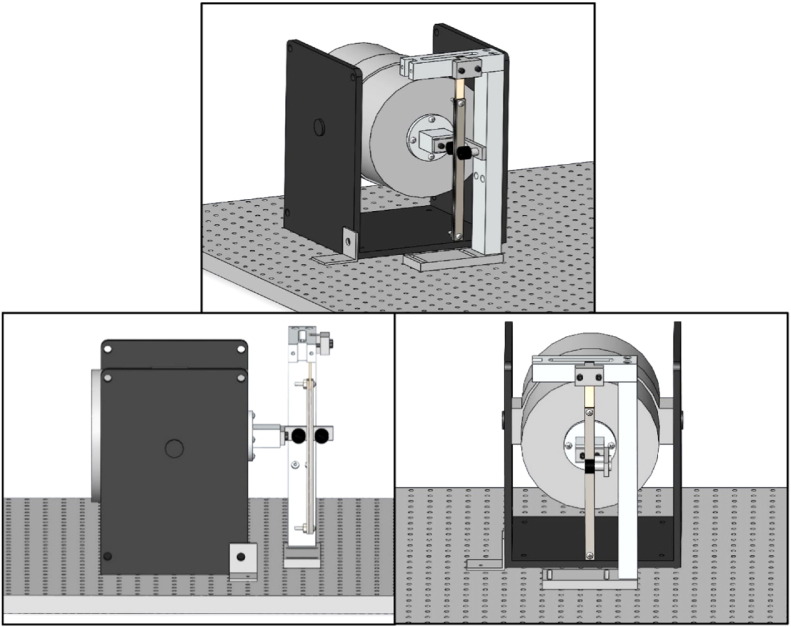
The experimental setup is shown in Fig. 2. A VTS-100 electromagnetic shaker (Vibration Test Systems) was used in this study to conduct both constant amplitude and variable amplitude loading tests. The translational movement of the shaker apparatus was used to apply a load to a pendulum that acted as a reversible single cantilever beam. Two 3/4′′ cams were fixed to an aluminum jig that was attached to and extended out from the shaker. These cams applied the load to the pendulum as the shaker forced them back and forth. The use of a roller at the tip of the actuator allowed for the pendulum to bend without creating a torque on the shaker itself. To hold the pendulum in place between the two cams, a three piece C-arm apparatus was machined out of aluminum. To create the long pendulum, the bone specimen was clamped between two 91/4′′ ×1/2′′ ×1/8′′ steel plates and secured by bolts. An aluminum plate spacer was used to fill the gap between the steel plates below the bone. The top of the bone specimen was clamped in the side of the C-arm with an aluminum cap. The pendulum was clamped such that 1′′ of the bone specimen was being tested. The testing region was from the bottom of the C-arm clamp to the top of the steel plates of the pendulum. The shaker and C-arm were bolted to a vibration isolation table to eliminate noise from the surrounding environment. The C-arm was aligned so that the pendulum fell directly between the two cams, and was slightly touching both.

Fig. 2.

The pendulum is positioned directly between the two cams. The three images show different views of the apparatus to visualize the positioning of the pendulum.

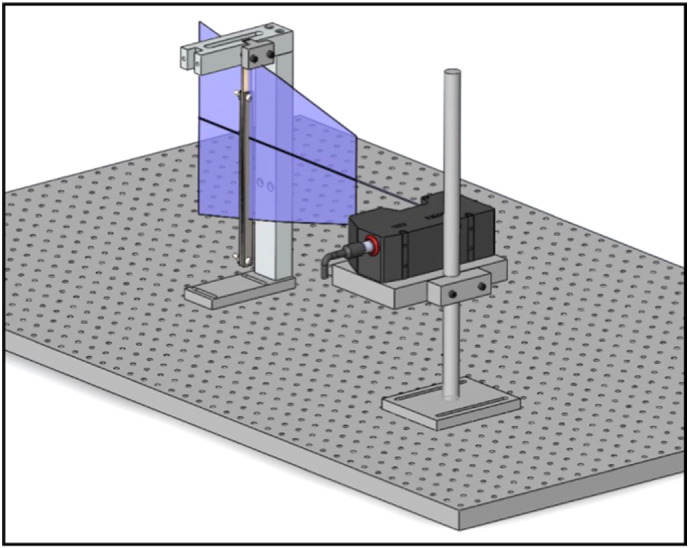
Initial experiments with strain gages mounted over the narrowed region of the bone specimen were performed with the intent to measure strain directly; however, the strain gages prevented the pendulum from deflecting to its maximum displacement and reinforced the specimen. Thus, deflection of the pendulum was measured with a laser displacement sensor (LJ-V7300, Keyence) to estimate strain. The stand and the sensor head are illustrated in Fig. 3. A custom stand was machined from aluminum to dissipate heat generated by the laser and to properly orient it relative to the testing apparatus. Along with the shaker and C-arm, the stand was also bolted to the vibration isolation table. The stand was designed so that the height of the laser stage was adjustable. The laser stage was carefully positioned to ensure that the pendulum, when mounted in the C-arm, was positioned directly in the center of the beam to ensure accurate displacement measurement at a critical point on the pendulum and on the C-arm. The stand was placed so that the face of the sensor head was 17.5" from the face of the steel clamp on the pendulum.

Fig. 3.

The laser sensor head is positioned so that the pendulum is in the middle of the laser beam.

2.3. Methodology

2.3.1. Constant amplitude

Fourteen specimens from the lateral half of the diaphysis of bovine femurs were cyclically loaded at four different constant amplitudes, each at a frequency of 5 Hz. Four specimens at “low” amplitude (≈ 4000 μϵ), six at “mid” amplitude (≈ 6500–6750 μϵ) and four at “high” amplitude (≈ 9000 μϵ). These specimens were cycled until complete failure, and the number of cycles to failure was counted and recorded. The deflections of the bone were continuously measured with a laser vibrometer, and these values were used to calculate the strain profile for each of the specimens. Then the fracture surface was examined to determine fracture type. The average endurance limits at each of the cyclic amplitudes were used to calculate N_i in the Palmgren-Miner (Eq. (1)) rule for a particular forcing amplitude and this information was used to design variable amplitude forcing experiments.

2.3.2. Variable amplitude

Six specimens were prepared from the lateral half of the diaphysis of bovine femurs and were tested under variable amplitude loading. The Palmgren-Miner rule (Eq. (1)) was used to predict when specimens tested under variable amplitude loading would fail (i.e., when the damage accumulated, D_p, was predicted to equal one). The chosen variable amplitude loading pattern consisted of 1000 cycles at low amplitude followed by 100 cycles at high amplitude. This pattern was continuously repeated until complete failure of the bone occurred. As described in the Results section, this pattern was chosen as a representative case that mixed different fracture mechanisms which were isolated in the constant amplitude loading experiments.

2.4. Analysis

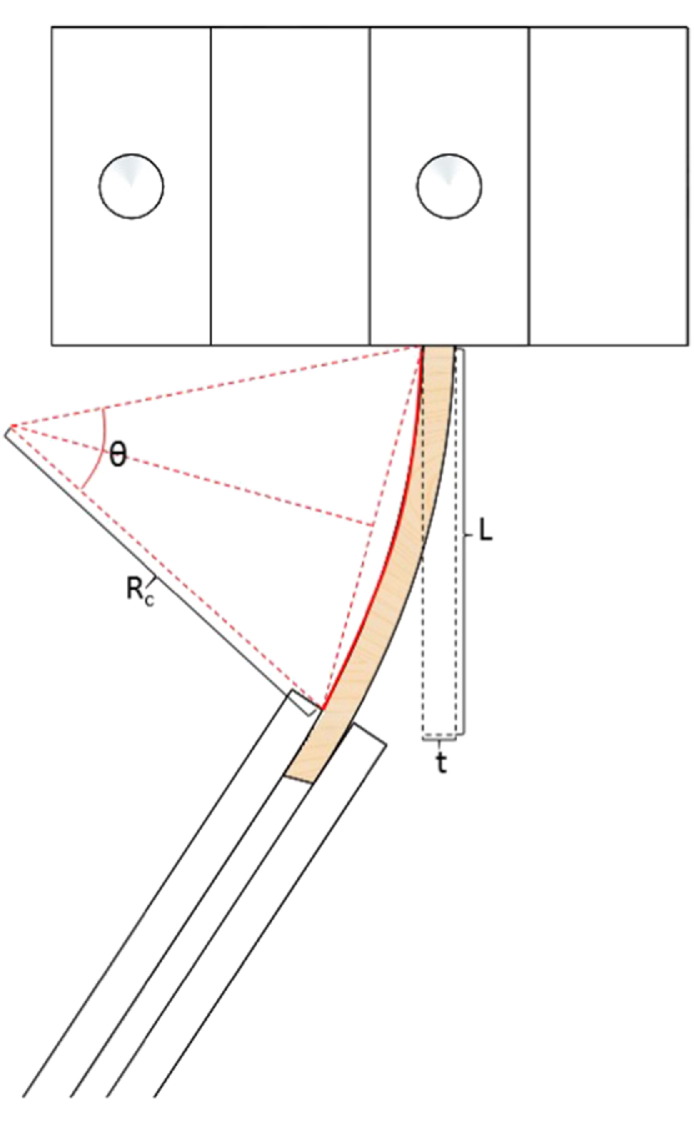
The voltage output from the laser vibrometer was collected at 200 Hz using a custom LabVIEW program. Data was post processed using a custom MATLAB program. The number of cycles to failure was calculated by multiplying the time of testing by the driving frequency. Fig. 4 shows a schematic of the bone in bending and the parameters used in calculating the initial strain on the specimen.

Fig. 4.

Schematic of bone in bending between clamp and pendulum indicating the parameters used to calculate strain.

The strain, ϵ, on the bone was calculated (Eq. (2)) by using the acquired laser profile data to first determine the radius of curvature, R_c, of the specimen. The radius of curvature was then used to calculate the arc angle, θ, where L was the gage length of the bone test section. The change in length, dL, was then calculated using the specimen thickness, t. Finally strain was calculated by dividing the change in length of the specimen by the initial length of the test section.

$$\begin{array}{l}\hfill R_c=\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{\frac{3}{2}}}{\frac{d^{2}y}{d{x}^2}}\\ \hfill \theta =2\sin \left(\frac{L}{2R_c}\right)\\ \hfill dL=\left(\frac{t}{2}\right)\theta \\ \hfill ϵ=\frac{dL}{L}\end{array}$$ (2)

After testing, the fracture surface of each specimen was imaged with an 8 megapixel camera and visually classified by the type of break (i.e. ductile vs. brittle). Scanning Electron Microscope (JEOL) images were taken of representative specimens from each of the fracture classifications. Outliers specimens were also imaged.

3. Results

3.1. Constant amplitude

3.1.1. Low amplitude

Four of the specimens were tested at low-amplitude forcing (≈ 4000 μϵ). The number of cycles to failure, or endurance limit, for each specimen was recorded (see Table 1). Failure was considered to be after the bone had broken into two pieces and the pendulum fell to the table. Together the specimens resulted in very high endurance limits with a mean of approximately 140,000 cycles.

Table 1.

Results from cyclic low amplitude testing.

Specimen	Endurance limit	Fracture type
1	116,846	Ductile
2	159,775	Ductile
3	145,661	Ductile
4	129,801	Ductile

Following failure, each specimen was examined and categorized by their fracture surfaces. All of the specimens cycled at the low amplitude displayed a ductile break. Fig. 5 (left) contains photographs of both sides of a specimen tested at low amplitude. The crack formed on this specimen originated from the notch and propagated across the width of the specimen. This represented a slow break with a high cycle fatigue limit.

Fig. 5.

Left: Fracture of a specimen tested at a constant low amplitude that displayed a ductile break. Center: Fracture of a specimen tested at a constant mid-range amplitude that displayed a combination of brittle and ductile breaks. Right: Fracture of a specimen tested at a constant high amplitude that displayed a brittle break.

3.1.2. Medium amplitude

A total of six samples were tested at mid-amplitude (≈6500–6750 μϵ). The number of cycles to failure, or endurance limit, for each specimen was recorded (see Table 2). Together the bones cycled at a mid-amplitude resulted in a mean endurance limit of 39,632 cycles.

Table 2.

Results from cyclic mid-amplitude testing.

Specimen	Endurance limit	Fracture type
1	66,061	Ductile/brittle
2	34,287	Ductile/brittle
3	28,152	Ductile/brittle
4	36,447	Ductile/brittle
5	45,482	Ductile/brittle
6	27,362	Ductile

All but one of the specimens tested at this amplitude displayed a combination of ductile and brittle breaks. Fig. 5 (center) shows an example of a sample with a ductile to brittle fracture classification. As seen in the top image, the crack originated at the bottom notch and propagated across the width of the specimen. Once the stress became too much for the material to handle, a fast fracture occurred which can be observed in the bottom image of Fig. 5 (center).

3.1.3. High amplitude

Four samples were tested at high-amplitude (≈9000 μϵ), which was the highest stress tested. These specimens resulted in much lower endurance limits than that of all of the previous amplitudes tested, as seen in Table 3. These bones together resulted in a mean endurance limit of 9970 cycles to failure.

Table 3.

Results from cyclic high-amplitude testing.

Specimen	Endurance limit	Fracture type
1	15,804	Brittle
2	7592	Ductile/brittle
3	11,054	Brittle
4	5428	Brittle

One of the specimens displayed a combination of ductile and brittle failure, similar to those seen in the specimens run at the mid-amplitudes. The remaining three specimens showed brittle breaks, an example of which can be seen in Fig. 5 (right). The distinct characteristic observed in the brittle fracture classification is the straight, or flat, break. There is no evidence of crack propagation, only fast fracture across the thickness of the specimen.

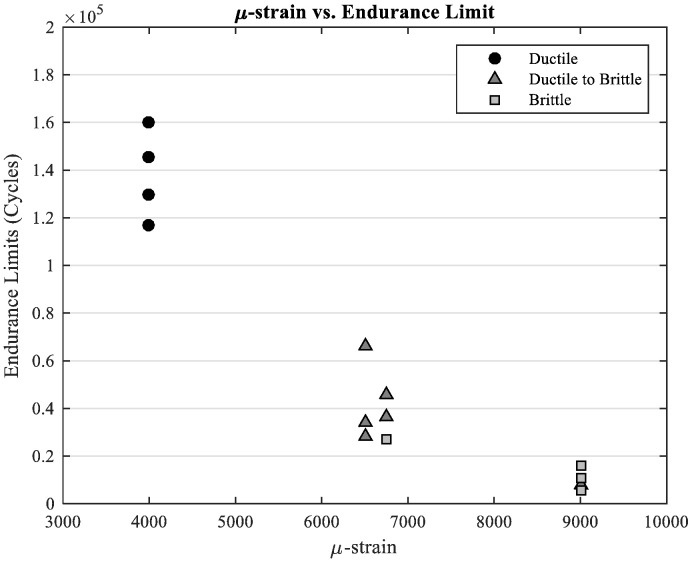
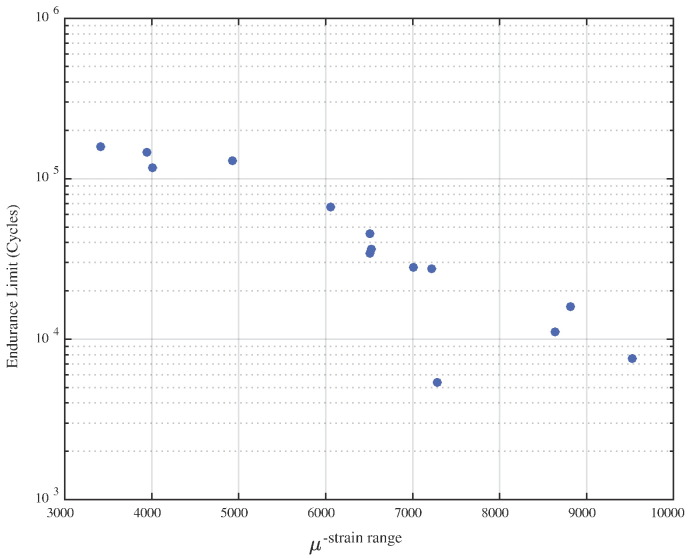
Fig. 6 is a plot of the endurance limits of all of the specimens tested under cyclic amplitude loading. The bones that were fatigued at a lower average initial microstrain level were associated with higher endurance limits and displayed ductile breaks. The bones that were fatigued at a medium average initial microstrain level resulted in lower endurance limits and displayed mostly a combination of ductile and brittle breaks. The bones that were fatigued at a high average initial microstrain resulted in much lower endurance limits in comparison to the rest of specimens tested. These specimens displayed mostly brittle, fast fracture breaks.

Fig. 6.

Endurance limits of bones tested under cyclic amplitude loading.

3.2. Variable amplitude

Six specimens were tested under variable amplitude loading with a cycle pattern designed using only the low- and high-amplitudes tested in the cyclic amplitude loading cases. The pattern of 1000 cycles at low-amplitude followed by 100 cycles at high-amplitude, was continuously repeated until complete failure of the bone occurred. The endurance limit for VAL specimens, according to the Palmgren-Miner rule, was predicted to be 63,780 cycles. Table 4 displays the endurance limits of the specimens run in this test. Endurance limit represents the total number of cycles to failure and damage accumulated represents the endurance limit of the specimen relative to the predicted endurance limit.

Table 4.

Results from variable amplitude load testing.

Specimen	Endurance limit	Damage accumulated	Fracture type
1	23,016	0.361	Ductile/brittle
2	10,916	0.171	Ductile/brittle
3	2110	0.033	Ductile/brittle
4	1006	0.016	Brittle
5	36,275	0.569	Ductile/brittle
6	61,556	0.965	Ductile

Of the six specimens tested, five of them resulted in low cycle endurance limits, ranging from 1006 to 36,275 cycles to failure. One of the specimens resulted in an endurance limit of 61,556 cycles. Most of the specimens tested showed a combination of ductile and brittle breaks with the exception of one specimen with a brittle break and one with a ductile break. There are numerous causes for sample to sample variability including (but not limited to) the history of the bone, machining/cutting damage and procedural damage due to experimental protocol. It is unclear if one or more of these factors was responsible for difference in fracture type of these two specimens. The fracture surface of the specimen that broke in a ductile manner was found to display a similar appearance to those run at a low cyclic amplitude. The fracture surface of the specimen that failed after 1006 cycles was found to display a brittle break fracture pattern similar to those seen in the specimens run at a high cyclic amplitude.

Most of the specimens tested under variable amplitude loading displayed a combination of ductile and brittle fracture patterns as seen in Fig. 7. These fractures showed a very close resemblance to those of the specimens tested at mid-amplitudes. On this specimen, the top image indicates that the crack originated at the notch and propagated across the width of the surface. The bottom image shows the fast fracture surface that broke brittlely once the stress applied to the material became too much for the undamaged bone to handle.

Fig. 7.

Fracture of a specimen tested under variable amplitude loading that displayed a combination of brittle and ductile breaks.

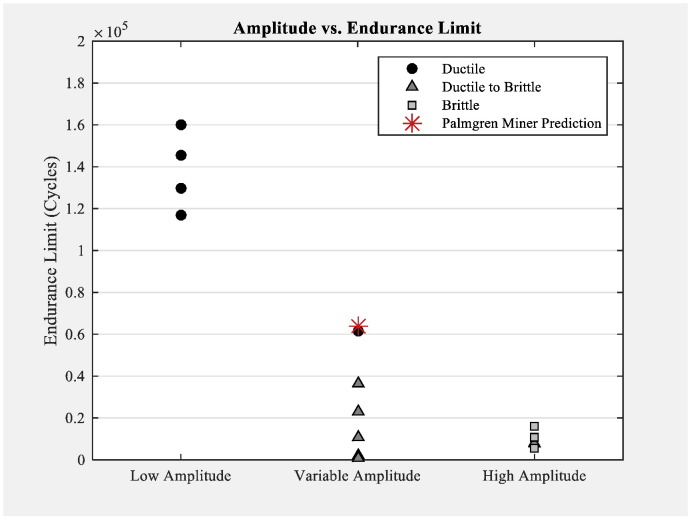
Fig. 8 displays the endurance limits of the specimens run at low-, variable-, and high-amplitudes. The number of cycles to failure predicted by the Palmgren-Miner rule is represented by the red asterisk for the variable-amplitude case. This value was calculated to be 63,780 cycles, which was very near the middle of the range of endurance limits seen in the specimens tested at the high and low amplitudes. The prediction range calculated using the extreme endurance limit values of the low- and high-amplitude forcings was 46,476 to 99,573 cycles. All but one of the variable amplitude loading specimens fell well below the prediction

Fig. 8.

Endurance limits of specimens tested at low, variable, and high amplitudes compared to the Palmgren-Miner prediction.

3.3. Fracture surfaces

The results gathered from the cyclic-amplitude tests showed three distinct fracture types: ductile, brittle, and a combination of both ductile and brittle. The specimens were first classified by their appearance to the naked eye, but further investigation of the fracture surfaces of the failed specimens was conducted by imaging one representative specimen of each fracture classification tested under both cyclic- and variable-amplitude loading by scanning electron microscopy (SEM). The higher magnification revealed distinct fracture characteristics and allowed for better understanding of the different fracture mechanisms.

3.3.1. Cyclic amplitude loading specimens

3.3.1.1. Brittle fracture

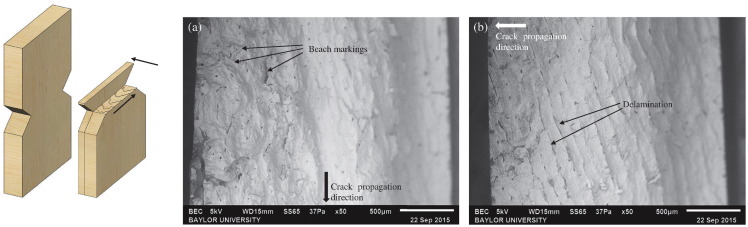
All of the bone specimens run at high-amplitude displayed a brittle break and were accompanied by a very low number of cycles to failure. To the naked eye, a brittle break appeared as a relatively smooth fracture surface with straight edges, demonstrating evidence of a fast fracture. This was confirmed with SEM imaging, which revealed a delamination of layers indicative of a fast fracture. This delamination of the layers is due to the applied high force which separated the individual layer of the bone along the thickness of the specimen, shown schematically in Fig. 9 (left) and along side the SEM image (right). Not only was the crack growing through the interstitial matrix due to high stress, but the interfaces between the layers of the bone were weakening as well. Multiple toughening mechanisms were imaged, including void coalescence and ligament crack bridging. Both of these are extrinsic toughening mechanisms, meaning they occur behind the crack tip. Higher magnification images and more discussion of these two mechanisms can be found in the Discussion section.

Fig. 9.

Left: Schematic of the fracture surface of a brittle break. Right: SEM image of a specimen tested at constant high-amplitude that displayed a brittle break.

3.3.1.2. Ductile fracture

The specimens run at the low-amplitude displayed a very distinct type of break. All of the specimens broke after a very high number of cycles, and their fracture surfaces all displayed a ductile break. A major distinguishing factor between the ductile break and other fracture classifications was the evidence of beach markings. Beach markings are distinct progression marks on the fracture surface that point directly back to the point of crack initiation. These markings also showed the route of travel of the crack propagation. Fig. 10 (left) displays an example of what is seen in a ductile break and how the beach markings give a representation of how the crack propagated through the specimen. The arrow indicates the direction in which the crack grew. Almost every specimen that exhibited a ductile fracture also had a crack that propagated along the width of the bone. Due to the greater distance traveled, the crack took more time to form and, in turn, resulted in a higher number of cycles before failure. Beach markings can be clearly observed in this SEM image (Fig. 10 right), which shows crack propagation across the width of the specimen. No delamination is observed on this specimen, which indicates that this was a purely ductile break.

Fig. 10.

Left: Schematic of the fracture surface of a ductile break. Right: SEM image of a specimen tested at constant low amplitude that displayed a ductile break.

3.3.1.3. Combination of fracture modes

The specimens run at a mid-amplitude displayed a combination of both ductile and brittle fractures. Fig. 11 (left) shows an example of what was noted in these combination fractures. Beach markings were observed, indicating that the main crack originated from one of the notches. However, unlike the purely ductile break, beach markings were not observed along the entire surface of the specimen. In these specimens, part of the fracture surface displayed a smooth surface with straight edges paired with delamination of the interstitial layers. This indicated that the main crack propagated until the remaining undamaged bone could no longer withstand the applied force. The specimen then fractured quickly, broke the weaker bonds between the layers, and pulled the lamina apart. Regions of ductile and brittle fracture can clearly be seen in the SEM image. Fig. 11 (center: a) displays the ductile portion of the fracture surface where beach markings can be seen, indicating a slower crack propagation along the width of the specimen. Fig. 11 (right: b) shows the brittle portion of the fracture surface where separation of layers and delamination can be seen. These display a fast fracture across the thickness of the specimen, perpendicular to that of the crack propagation in the ductile region.

Fig. 11.

Left: Schematic of the fracture surface of a combination of ductile and brittle breaks. Right: SEM image of a specimen tested at constant mid amplitude that displayed a combination of ductile and brittle breaks. (a) Ductile type break can be observed. (b) Brittle type break can be observed.

3.3.2. Variable amplitude loading specimens

Of the six specimens tested under variable amplitude loading, most displayed a combination of both ductile and brittle fracture mechanics. One of these specimens was imaged with SEM (Fig. 12). This image distinctly shows characteristics of both fracture mechanisms. Directly in the center of the image, delamination was observed. The right side of the image showed clear beach markings. This mixed mode fracture of distinct brittle and ductile regions, was the standard fracture type for the specimens tested at the mid-range amplitudes.

Fig. 12.

SEM image of a specimen tested under variable amplitude loading that displayed a combination of brittle and ductile breaks.

Note that two of the variable amplitude specimens did not show this combination ductile-brittle break. One specimen resulted in a higher number of cycles until failure than the others. This specimen was imaged and found to display only ductile fracture patterns. The other specimen resulted in a very low number of cycles until failure than the others. This specimen was imaged and found to display only brittle fracture patterns. It is unknown what caused the difference in the behavior of these two specimens and further testing is need to improve the statistical significance of these results.

4. Discussion

Stress fractures are a very prevalent and painful injury due to microcracks within the bone that are caused by excessive fatigue of the material (Bennell et al., 1996, Patel et al., 2011, Verheyen et al., 2006). Studies conducted in the past have shown that bone's mechanical properties change and weaken due to cyclic testing (Carter and Caler, 1983, Pattin et al., 1996). Therefore, damage in bone is observable and measureable. However, more advanced testing methods are needed because current methods do not properly simulate realistic loading situations that bones experience in everyday activity. Simple constant amplitude tests are not sufficient and do not provide enough information to predict when a bone will break if subjected to certain activity levels. An accurate prediction method for the amount of damage accumulated by the material is necessary to determine the state of the bone and hypothesize its eventual failure. To provide insight into this problem and more accurately simulate the everyday forces that bones experience, a novel testing apparatus was modified to conduct fatigue tests on bone (Chelidze et al., 2002, Chelidze and Liu, 2005, Chelidze and Liu, 2008).

The Palmgren Miner rule is a damage accumulation hypothesis that is often used in the aerospace and mechanical industries to predict the endurance limit of metals. In this study, the Palmgren Miner rule was used to predict when the failure of bone would occur. The results showed that the simplicity of a linear relationship is not accurate or sufficient enough to predict failure under variable amplitude loading conditions.

4.1. Cyclic amplitude loading

4.1.1. Toughening mechanisms

There are multiple toughening mechanisms that occur in bone during fatigue loading (Kruzic and Ritchie, 2008, Launey et al., 2010, Nalla et al., 2003, Mar, Nalla et al., 2005, Nalla et al., 2005, Ritchie et al., 2005), but they are typically placed into two categories: intrinsic and extrinsic. Intrinsic mechanisms occur in front of the crack tip, while extrinsic mechanisms act behind the crack tip in the wake. Both intrinsic and extrinsic mechanisms were observed when tests were conducted under cyclic amplitude.

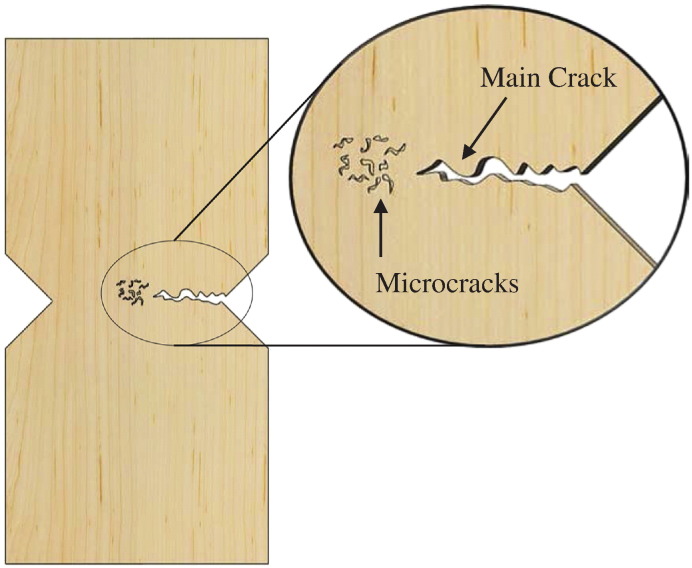
Intrinsic toughening mechanisms: A ductile fracture classification is typically observed with intrinsic toughening mechanisms, such as beach marking. This microdamage occurs in front of the crack tip and slows down the crack propagation by absorbing and dissipating energy. Fig. 13 shows a schematic representation of this toughening mechanism occurring in the ductile fracture. The main crack propagated along the width of the specimen with microcracks forming directly in front of the main crack. This mechanism typically occurs during strain hardening and can be compared to the plastic zone formed in front of the crack tip in other materials. In metals, for example, the plastic zone absorbs and dissipates energy away from the main crack, which helps to slow down the growth of the crack. This same mechanism is employed by bone when subjected to low amplitude stresses. The microcracks increase the amount of energy necessary to propagate the crack and to fracture the bone.

Fig. 13.

Schematic of microcracks occurring in front of the main crack tip.

Extrinsic toughening mechanisms: All of the specimens tested at the high-amplitude fractured with a brittle break. This type of break is typically accompanied by extrinsic toughening mechanisms, such as crack bridging and void coalescence. Both of these mechanisms were observed by SEM in the specimens that fractured with brittle breaks, as seen in Fig. 14. Crack bridging occurs behind the crack tip and is utilized to keep the cracking material in a unified state for as long as possible. Fig. 14a shows collagen-fibril bridging in which the collagen fibrils were pulled in tension. The high elasticity of the collagen fibrils allowed them to stretch a relatively large amount in an attempt to keep the crack closed. Once the stress became too much, the collagen fibril broke and allowed the crack to propagate further. Void coalescence occurs in the wake of the crack and acts to reduce the local stress intensity applied at the crack tip, which in turn toughens the material. This can be seen in Fig. 14b where two preexisting voids coalesced together in an attempt to absorb and dissipate energy away from the main crack.

Fig. 14.

SEM images of (a) collagen-fibril bridging and (b) void coalescence.

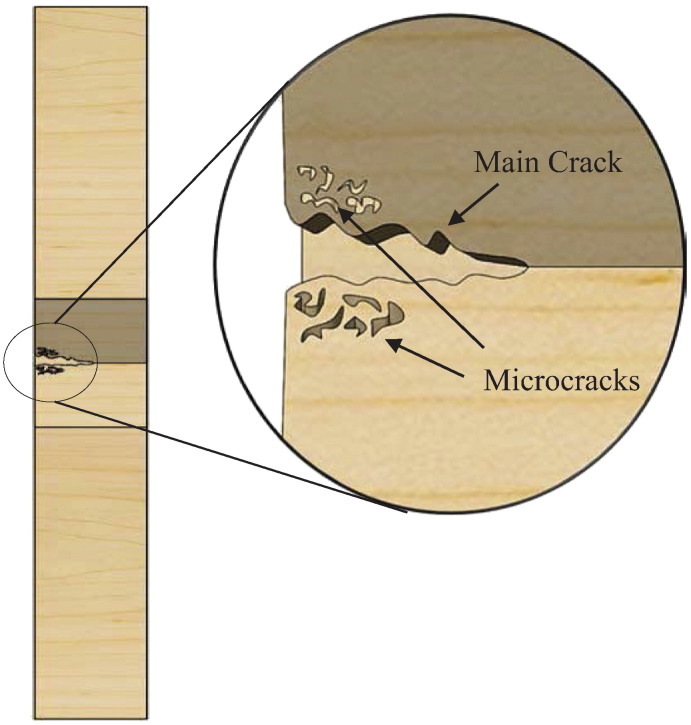
Combination of toughening mechanisms: The mid-amplitude loading resulted in a combination of both brittle and ductile fractures and displayed evidence of a combination of toughening mechanisms. Vashnisth described the semi-contradictory phenomenon of a specimen observed to have a brittle type fracture with a high fatigue limit (Vashishth et al., 1997). This can be explained by the extrinsic mechanisms working along with microdamage accumulating in the wake of the crack. This microdamage absorbs and dissipates energy as seen in the ductile breaks, but is not able to slow down the crack propagation as much as if it were located in front of the crack tip. If the microdamage had occurred in front of the crack tip as opposed to in the wake of the crack, a ductile fracture surface would have primarily been seen. Fig. 15 shows a schematic of an extrinsic toughening mechanism occurring in a specimen that resulted in a combination of ductile and brittle fractures. As the main crack propagates, microcracks begin to occur in the wake of the crack. These very small cracks form in the attempt to redistribute the stress applied on the main crack to try to prevent it from growing.

Fig. 15.

Schematic of microcracks occurring in the wake of the main crack.

4.2. Variable amplitude loading

The cyclic amplitude tests run at a low-amplitude or a high-amplitude both resulted in very repeatable endurance limits with common fracture characteristics within each group. The specimens run at the low-amplitude all resulted in very high cycles to failure with ductile fracture surfaces. The specimens run at the high-amplitude all resulted in very low cycles to failure with brittle fracture surfaces. However, the cyclic amplitude tests run at the mid-amplitudes were more variable in their results. The specimens tested at these amplitudes tended to result in a combination of the two fracture types.

The aim of this research project was to run variable amplitude tests that isolated the different toughening and failure mechanisms. The low-amplitude selected resulted in primarily ductile fractures, while the high-amplitude selected resulted in primarily brittle fractures. For this reason, a cycle pattern including only the low- and high-amplitudes was chosen to test whether the Palmgren-Miner rule could predict the failure of specimens undergoing two types of fracture mechanisms. The cycle pattern consisted of 1000 cycles at a low-amplitude, followed by 100 cycles at a high-amplitude and was repeated continuously until failure. This ensured that the specimens were being subjected to intrinsic toughening mechanisms followed by extrinsic mechanisms.

Application of the Palmgren Miner rule predicted that the bone would break at approximately 63,780 cycles. Most of the specimens, however, broke much sooner than the predicted endurance limit. The fracture surfaces displayed a combination of both brittle and ductile fracture patterns, the same combination observed in the specimens tested at mid-amplitudes under constant amplitude loading. Typically, in metals, an overload early in the test creates a large plastic zone in front of the crack tip, which slows the crack propagation and extends the endurance limit of the material (McEvily and Kasivitamnuay, 2013, Stephens et al., 2001). The opposite was observed in bone. The tests run in this study showed that this overload created more damage in the material and caused the crack to propagate more rapidly and thus the endurance limit to shorten.

All of the specimens broke during the high-amplitude component of the variable amplitude forcing function. This indicated that the specimens had accumulated too much damage to withstand the higher amplitude loading but not enough damage to fracture during the lower amplitude loading. The combination of fracture types was seen in the majority of the variable amplitude specimens. The main crack propagated during the lower amplitude cycles, but once a critical level of damage had occurred, the specimens were not able to withstand the high-amplitude loading and a brittle fracture occurred. All but one of the variable amplitude specimens broke much earlier than predicted. It was concluded that the Palmgren-Miner rule was not sufficient for failure prediction when multiple fracture mechanisms are active.

Zioupos and Casinos also found that the Palmgren-Miner rule was not adequate enough as a linear accumulation rule (Zioupos and Casinos, 1998). They discovered that when the cycle pattern used for variable amplitude loading went from all low amplitude cycles to all high amplitude cycles, the damage accumulated was less than that of the prediction. They also found that when the amplitude pattern went from all high amplitude cycles to all low amplitude cycles, the damage accumulated was greater than that of the prediction. Damage is highly dependent upon stress level and stress history. However, in their study, the deviations from the prediction found were not explained in terms of dynamics and the fracture mechanisms taking place. Zioupos and Casinos applied strain levels in their tests that ranged between 5000 and 10,000 μϵ. Thus, the intrinsic and extrinsic toughening mechanisms were not necessarily isolated.

Fig. 16 shows micro-strain versus endurance limits for the specimens tested under constant amplitude loading for the current study. The brittle fracture regime began to take effect at approximately 9000 μϵ, the combination regime at approximately 6000 to 7000 μϵ, and the ductile regime at less than 5000 μϵ. In the current study, not only were both of the toughening mechanisms isolated, but the cycle pattern incorporated a true mixing of the two otherwise isolated failure modes. This was done by applying a loading pattern that alternated between low to high cycle forcing, as opposed to applying all of the low-amplitude cycles followed by all of the high-amplitude cycles, as in the Zioupos and Casinos study. Theoretical damage accumulation, D_P, calculated using the Palmgren Miner rule (Eq. (1)), was considerably less than predicted for the variable amplitude specimens. Therefore, the current study unambiguously confirms that when bone is subjected to both intrinsic and extrinsic toughening mechanisms, a more sophisticated prediction method is necessary.

Fig. 16.

Endurance limits of specimens run under constant amplitude loading dependent upon their original micro-strain levels.

4.3. Statistical analysis

Following the testing of the specimens run under the cyclic amplitude loading, an ANOVA was performed that indicated there was a significant difference among the specimens run at the four different amplitudes (p < 0.0001). A multiple comparison Tukey-Kramer test run at α = 0.05 indicated a significant difference in the specimens run at the low amplitude compared to the rest of the groups, including the mid-range and high amplitudes. There were no significant differences among the other groups.

A second ANOVA was performed comparing the specimens tested under cyclic amplitude loading at the low and high amplitudes and the specimens tested under variable amplitude loading. This test indicated a significant difference (p < 0.0001) among the groups. A multiple comparison Tukey-Kramer test run at α = 0.05 indicated there was a significant difference in the specimens run at the low amplitude compared to the other two groups. There was no significant difference between the specimens run at the high amplitude and the specimens tested under variable amplitude loading.

These finding establish the validity of the general approach and the importance of interactions between different fracture mechanisms involved in the fatigue process. A limitation of the current study is the sample size. A statistical power calculation was conducted, based on the presented results, that suggests a 35 specimen sample size is optimal for improved statistical significance. Among other things, improving the sample size to gain better statistical significance is part of ongoing work.

5. Conclusion

From the results of this study, it is clear that bone displayed three different fracture modes: brittle, ductile, and a combination of the two. The amplitude of strain applied to the bone specimen is a key variable in determining the type of fracture that would occur. Low amplitudes that applied an original micro-strain of 5000 or lower resulted in a ductile fracture and very high cycles to failure. High amplitudes that applied an original micro-strain of 9000 or higher resulted in a brittle fracture and very low cycles to failure. These fracture classifications, both brittle and ductile, are typically accompanied by a certain type of toughening mechanism. Brittle fractures are associated with extrinsic toughening mechanisms that occur behind or in the wake of the crack. Ductile fractures are associated with intrinsic toughening mechanisms that occur in front of the main crack. The combined results of the cyclic amplitude loading tests showed a nonlinear trend. The results did not disprove that the Palmgren-Miner rule works when testing in only one fracture regime. However, if multiple fracture mechanisms are active, the number of cycles to failure cannot be predicted using a linear damage accumulation hypothesis, such as the Palmgren-Miner rule. Thus, future efforts should be made to seek new methodologies to improve bone health monitoring and failure prediction.

Conflict of Interest

The authors of this manuscript have no existing conflicts of interest related to the researchpresented in this manuscript.