A robust measurement point for dose verification in delivery quality assurance for a robotic radiosurgery system

Abstract

In this CyberKnife® dose verification study, we investigated the effectiveness of the novel potential error (PE) concept when applied to the determination of a robust measurement point for targeting errors. PE was calculated by dividing the differences between the maximum increases and decreases in dose distributions by the original distribution after obtaining the former by shifting the source-to-axis and off-axis distances of each beam by ±1.0 mm. Thus, PE values and measurement point dose heterogeneity were analyzed in 48 patients who underwent CyberKnife radiotherapy. Sixteen patients who received isocentric dose delivery were set as the control group, whereas 32 who received non-isocentric dose delivery were divided into two groups of smaller PE (SPE) and larger PE (LPE) by using their median PE value. The mean dose differences (± standard deviations) were 1.0 ± 0.9%, 0.5 ± 1.4% and 4.1 ± 2.8% in the control, SPE and LPE groups, respectively. We observed significant correlations of the dose difference with the PE value (r = 0.582, P < 0.001) and dose heterogeneity (r = 0.471, P < 0.001). We concluded that when determining a robust measurement point for CyberKnife point dose verification, PE evaluation was more effective than the conventional dose heterogeneity-based method that introduced optimal measurement point dose heterogeneity of <10% across the detector.

INTRODUCTION

The CyberKnife® robotic radiosurgery system (Accuray Inc., Sunnyvale, CA, USA) yields a conformal dose distribution around the target and causes relatively less damage to normal structures. Several authors have described the clinical effects of CyberKnife stereotactic radiosurgery (SRS) and stereotactic radiotherapy (SRT) at various disease sites [1–4] and suggest that these techniques could improve local control rates, with few side effects. The CyberKnife system delivers the intended dose via isocentric or non-isocentric dose delivery; in the former, every radiation beam should intersect at a single isocenter, whereas in the latter, peripheral doses are superimposed to improve dose conformity at the target site [5]. Therefore, for non-isocentric dose delivery, targeting accuracy is a very important parameter with regard to ensuring delivery of the prescription dose, given the steep peripheral dose fall-off. Using a CyberKnife G4 system, Antypas et al. reported a targeting accuracy of within 0.25 mm and an overall targeting accuracy of 0.29 ± 0.10 mm for fiducial tracking [6]; however, even a submillimeter targeting error could significantly affect the accuracy of dose delivery in a non-isocentric treatment plan.

Despite the importance of intended dose delivery robustness, a consensus beam-by-beam quality assurance test has not been established. A report from task group (TG) No. 135 of the American Association of Physicists in Medicine (AAPM) recommended conducting a delivery quality assurance (DQA) test for patients intending to undergo CyberKnife SRS or SRT, in order to comprehend the overall accuracy of dose delivery [7]. For this test, the acceptance criteria would include a 90% pass rate and a gamma index of 2%/2 mm for the tumor, critical structures, and high-dose region (down to the 50% isodose line) [7], although the absolute point dose has not yet been described. As CyberKnife radiotherapy uses multidirectional beams and fluctuating beam intensities to achieve complex dose distribution, the overall dose prescription accuracy should be verified similarly to that of intensity-modulated radiation therapy (IMRT) (i.e. practical patient-specific QA testing) [8]. However, point-dose verification of CyberKnife radiotherapy is challenging with respect to dosimetry in a small field and dosimetric point determination.

CyberKnife G4 robotic radiosurgery involves transport of an unflattened photon beam from a linear accelerator at the end of the robotic arm; secondary collimators, which feature various aperture sizes (12 diameters, range: 5–60 mm) at a distance of 800 mm from the source are generally smaller than the conformal radiotherapy irradiation field, and subsequently collimate the beam to irradiation field size [5, 9]. Small-field dosimetry is associated with a lack of photon fluence, reduced photon energy, lateral electronic disequilibrium, and steep dose fall-off [10, 11], which are likely to interfere with an accurate evaluation [12]. Therefore, special attention is needed for the DQA of CyberKnife radiotherapy.

Regarding the measurement point determination for IMRT, Low et al. defined the optimal measurement point as where the expected dose heterogeneity is <10% across the detector using a volume-averaged dose-based comparison [13]. However, the resulting complex dose distribution might cause difficulties for the DQA of CyberKnife radiotherapy. For non-isocentric dose delivery, two mixture dose distribution regions are generally observed: (i) a high dose is predominantly delivered from the collimator center, with low doses from the periphery, and (ii) multiple low doses from the collimator periphery predominate, with a low collimator-center dose. Accordingly, the dosimetric uncertainty differs between these regions, even if the deposited doses are identical. The steep peripheral dose fall-off at the lateral dose profile and targeting uncertainty strongly affect the dose prescription accuracy in the latter situation. Even a situation in which the calculated dose homogeneity in the detector volume of interest (VOI) is satisfied within a certain range might impede the detector and reduce the robustness of the determination method described by Low et al. [13].

A vulnerable measurement point would lead to an evaluation error because the collimator periphery dose delivery accuracy is sensitive to targeting errors [14]. As total-targeting errors are controlled by Delta-manipulator vectors, followed by a daily automatic quality assurance test and monthly end-to-end tests, targeting uncertainties are not needed in total beam intensity evaluations. Therefore, a measurement point determination method for robust CyberKnife DQA point dose evaluations should be established [15]. Here, we introduce the potential error (PE) concept as a novel measurement point determination method for CyberKnife DQA and assess whether PE is effective for determining a robust measurement point by comparing it with the determination method of Low et al. [13].

MATERIALS AND METHODS

Patients

Performance details of the CyberKnife G4 image-guided robotic stereotactic radiosurgery system have been reported previously [6]. Although this system can employ an optional IRIS^TM variable-aperture collimator, size-fixed collimators were used in this study. Characteristics of the 48 enrolled patients who underwent CyberKnife radiotherapy of the brain, lung, liver, prostate and spine between February 2014 and March 2015 are described in Table 1. Although several disease sites were included to assess the overall versatility of our approach, disease site variability is considered to have little impact because DQA was conducted using a homogeneous I'mRT Phantom (IBA Dosimetry GmbH, Schwarzenbruck, Germany) with a beam arrangement identical to that used in patient treatment (see below for PE evaluation and point dose measurement details). This study was approved by our institutional review board and conducted in accordance with the principles of the Declaration of Helsinki.

Table 1.

Description of 48 study plans enrolled in this study

Description of 48 study plans	Value (range)
# Isocentric plans	16
# Non-isocentric plans	32
# Treatment site of brain	26
# Treatment site of lung	8
# Treatment site of liver	4
# Treatment site of prostate	9
# Treatment site of spine	1
Mean (range) size of PTV	29.3 cm3 (0.4–142.3 cm3)
Mean (range) #nodes	43 (18–75)
Mean (range) #beams	68 (18–136)
Mean (range) collimator	15 mm (7.5–60 mm)
Mean (range) absolute point dose difference	0.41% (−4.05% – 2.84%)

Absolute point dose measurement

We performed CyberKnife DQA using an I'mRT Phantom and PinPoint^® ionization chamber (0.016 cm³; model PTW31016; PTW, Freiburg, Germany) for absolute point dose verification. This chamber was cross-calibrated against a reference standard ionization chamber and electrometer system calibrated by the Japan Calibration Service System laboratory. For phantom set-up, 10 fiducial markers of 2.0-mm diameter (Beekley Spots, Beekley, Bristol, USA) were attached to the top of the phantom for automatic fiducial tracking; an end-to-end test demonstrated an overall accuracy of within 0.50 mm (data not shown). A schematic layout of absolute point dose measurement is shown in Fig. 1.

Fig. 1.

Schematic layout of the process of absolute point dose measurement using the I'mRT Phantom and the PinPoint ionization chamber. A total of 10 fiducial markers were attached to the top of the I'mRT Phantom to facilitate automatic phantom set-up via fiducial marker tracking.

In all 48 patients, the absolute point dose was measured at the center of the planning target volume (PTV) without reference to Low et al. [13]. Fiducial tracking and automatic phantom set-up requires two steps before dosimetry. Because a large difference between the I'mRT Phantom dosimetric point and the imaging center of the treatment locating system could inhibit the projection of fiducial markers onto electronic portal imaging devices, the authorized treatment plan imaging center was first moved to the PTV center. Subsequently, beam information (e.g. robotic manipulator node coordinates, target coordinates, collimator size, monitor unit weight) was identically transferred to computed tomography (CT) images of the I'mRT Phantom, (1.25-mm slice thickness). Finally, dose distribution was recalculated using the Ray-tracing algorithm with 0.59 × 0.59 × 1.25 mm³ voxel size. The measured point dose was compared with the calculated mean dose at the volume of interest (VOI) in the PinPoint ionization chamber, using a MultiPlan^® version 4.6.1 (Accuray Inc., Sunnyvale, CA, USA) treatment planning system (TPS). Dose differences were calculated as follows:

$$\mathit{Dose}\mathit{difference}=\frac{D_{\mathit{meas}}-D_{\mathit{calc}}}{D_{\mathit{calc}}}\times 100,$$ (1)

where D_meas is the measured point dose, and D_calc is the calculated mean dose at the VOI in the PinPoint ionization chamber in the MultiPlan TPS.

Potential error calculation

ShioRIS2.0 (RADLab Co. Ltd, Osaka, Japan) software incorporates several CyberKnife radiotherapy analytical functions: superimposition of dose distributions from several TPSs, robust simulation against intra/interfractional motion, Ray-tracing algorithm dose recalculation, and PE evaluation of CyberKnife DQA [16–18]. For the analysis, the Digital Imaging and Communications in Medicine – Radiation Therapy (DICOM RT) dose, the DICOM RT structure set, and a CT image series from the original treatment plan file (xml format) were imported into ShioRIS2.0.

The CyberKnife radiotherapy point dose was given by the following equation [19]:

$$\begin{array}{c}\mathit{Dose}=\mathit{MU}\times {\left(\mathit{SAD}/800\right)}^{-2}\times {\mathit{TPR}}_{(A_d,\mathit{depth})}\hfill \\ \times {\mathit{OAR}}_{(\mathit{Coll},\mathit{OAD},\mathit{depth})}\times \mathit{OPF}\left(A_d\right),\hfill \end{array}$$ (2)

where MU represents the monitor unit, SAD the source-to-axis distance in millimeter, A_d the irradiation field size at depth d, OAR the off-axis ratio, Coll the corresponding collimator size, and OAD the off-axis distance. The result indicated that the point dose was sensitive to SAD and OAD. In particular, OAD strongly affected the dose prescription accuracy as a result of steep dose fall-off at the lateral dose profile periphery. Accordingly, total targeting errors could cause major discrepancies in TPS calculations. Therefore, a PE evaluation approach was introduced to identify robust measurement points against targeting errors, as follows:

$$\begin{array}{c}\mathit{PE}=\hfill \\ \frac{{\mathit{Dose}}_{\left(\right(\mathit{SAD}-1\mathit{mm}),(\mathit{OAD}-1\mathit{mm}),\mathit{depth})}-{\mathit{Dose}}_{\left(\right(\mathit{SAD}+1\mathit{mm}),(\mathit{OAD}+1\mathit{mm}),\mathit{depth})}}{{\mathit{Dose}}_{(\mathit{SAD},\mathit{OAD},\mathit{depth})}}\hfill \end{array}$$ (3)

where Dose_{((SAD − 1 mm),(OAD − 1 mm),depth)} represents the maximum dose increase, and Dose_{((SAD + 1 mm),(OAD + 1 mm),depth)} the maximum dose decrease, thus denoting the worst-case dose prescription scenario. Negative SAD and OAD values represent the directions facing the target and facing the central beam axis, respectively. The PE map was generated by dividing the difference between the maximum-increased and maximum-decreased dose distributions by the original distribution; this calculation is represented by a flowchart in Fig. 2. The corresponding measurement point PE value was then extracted from the mean value in the VOI of the PinPoint ionization chamber. In the PE evaluation, the dose calculation accuracy, determined using the Ray-tracing algorithm implemented in the ShioRIS software, would affect the PE value accuracy. Therefore, we first verified the compatibility of ShioRIS and MultiPlan TPS calculations by comparing the percentage depth dose (PDD) with the lateral dose profile at a 100-mm depth using the mode collimator sizes of the enrolled patients’ treatment plans.

Fig. 2.

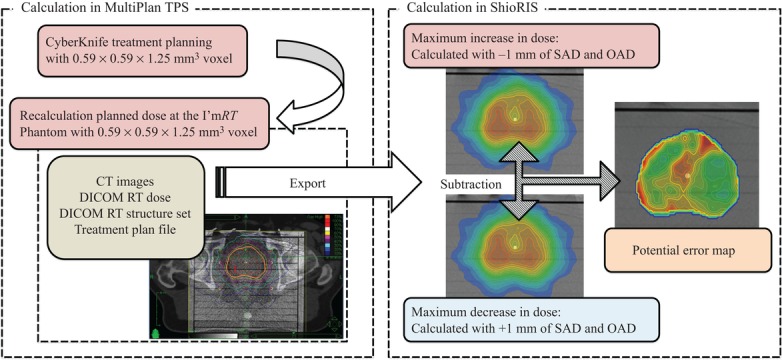
A flowchart of potential error (PE) calculation. Four individual pieces of data are required for PE calculation: a series of CT images, DICOM RT dose, DICOM structure set, and the treatment plan file in xml format. SAD: source-to-axis distance; OAD: off-axis distance.

Applicability of a dose-heterogeneous approach to CyberKnife DQA

Low et al. proposed that the optimal IMRT measurement point is where the expected dose heterogeneity is <10% across the detector [13]. This approach could be theoretically applied to CyberKnife DQA, despite the complex dose distribution. Dose heterogeneity was determined as follows:

$$\mathit{Dose}\mathit{heterogeneity}=\frac{D_{\mathit{Max}}-{\mathit{D}}_{\mathit{Min}}}{D_{\mathit{Mean}}}\times 100,$$ (4)

where the D_max, D_min and D_mean represent the respective maximum, minimum and mean doses at the measurement point. To determine whether this indication of dose heterogeneity can effectively predict a robust dosimetric point for absolute point dose verification, we evaluated the correlation between dose difference and dose heterogeneity at the measurement point.

Statistical analysis

As isocentric radiation beams intersect at a single isocenter and have low dosimetric uncertainty, doses measured after isocentric dose delivery were used as controls. By contrast, doses measured using non-isocentric dose delivery were divided into two groups of smaller PE (SPE) and larger PE (LPE) by using their median PE value. Snedocor's F-test was used to compare the range of dose differences in each group. Relationships in the dose differences between PE values and dose heterogeneity were determined using Pearson correlation analysis or Spearman rank correlation analysis depending on sample normality (Shapiro–Wilk test). P < 0.05 was considered significant. All statistical analyses were performed using JMP^® 11 statistical software (SAS Institute Inc., Cary, NC, USA).

RESULTS

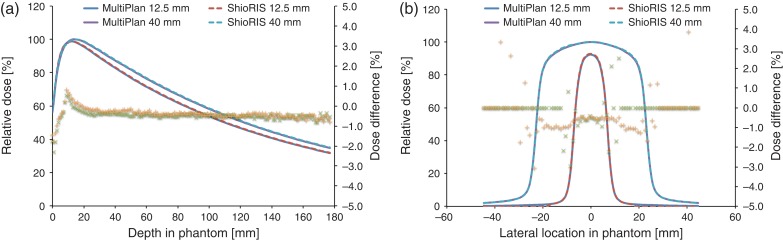
The PDD and dose differences between ShioRIS and MultiPlan TPS, determined using fixed collimators with diameters of 12.5 mm and 40 mm, are shown in Fig. 3a. The maximum and mean dose differences were −2.3% and −0.5%, respectively, for the 12.5-mm collimator and −1.8% and −0.4%, respectively, for the 40-mm collimator; the maximum dose difference was observed at the phantom entrance area, but the dose difference at the measurement depth (5 cm) was <0.5%. Similarly, lateral dose profiles and dose differences between ShioRIS and MultiPlan TPS are shown in Fig. 3b. The maximum and mean dose differences for the 12.5-mm and 40-mm collimators were −3.0% and −0.4%, and 3.9% and −0.4%, respectively. Most dose discrepancy was observed in the penumbra area.

Fig. 3.

Differences in the PDD and percentage dose (a) and the lateral dose profile and percentage dose (b) calculated using ShioRIS and MultiPlan. Horizontal axes represent the depth (a) and lateral location in the I'mRT Phantom (b). The left vertical axis represents the relative dose, and the right represents the percentage dose difference. Solid line: dose calculated by MultiPlan using the Ray-tracing algorithm (12.5 mm and 40 mm); dashed line: dose calculated by ShioRIS (12.5 mm and 40 mm); cross mark: percentage dose differences for 12.5 mm collimator between ShioRIS and MultiPlan; plus mark: percentage dose difference for 40 mm collimator between ShioRIS and MultiPlan.

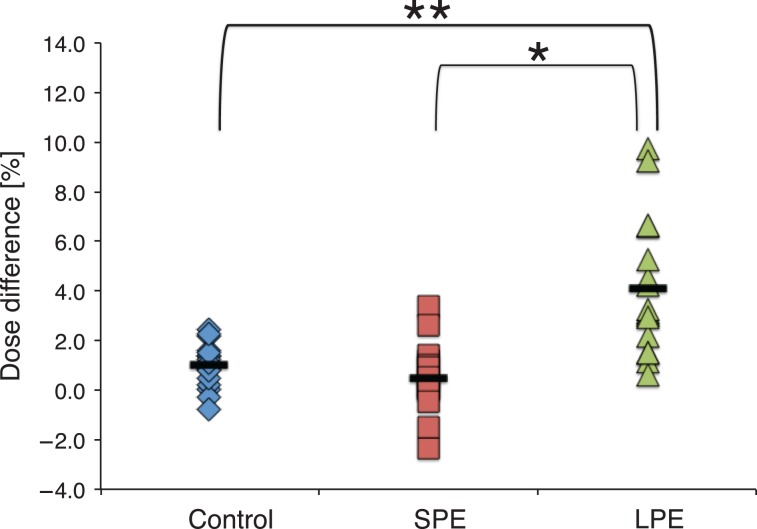
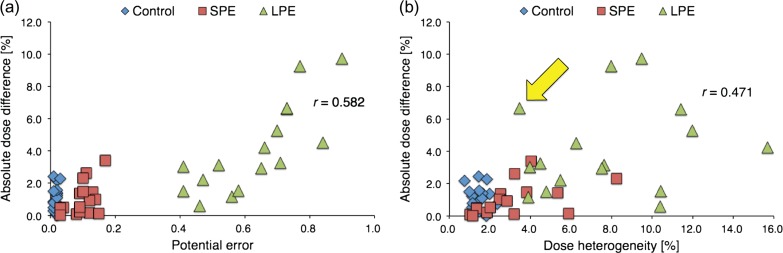
Figure 4 displays the ranges of differences between measured and MultiPlan-calculated doses per group. The mean PTV sizes of the SPE and LPE groups, divided according to a median PE threshold of 0.29, were 75.4 cm³ (26.8–142.3 cm³) and 6.0 cm³ (0.91–14.4 cm³), respectively. The control, SPE and LPE groups had mean dose differences ± standard deviations of 1.0 ± 0.9%, 0.5 ± 1.4% and 4.1 ± 2.8%, respectively. F-test comparisons revealed significant differences in dose difference ranges between control and LPE (P < 0.001) and between SPE and LPE (P < 0.05). Figure 5a illustrates the relationship between PE values and absolute dose differences; the latter were determined between measured and MultiPlan-calculated doses. Figure 5b similarly presents the relationship between dose heterogeneity and absolute dose difference. Significant correlations of dose difference with the PE value (r = 0.582; P < 0.001) and dose heterogeneity (r = 0.471; P < 0.001) were observed.

Fig. 4.

Distribution of point dose differences for each group. The vertical axis represents the percentage dose difference between the PinPoint ionization chamber measured doses and the MultiPlan-calculated doses. Solid black bars represent the mean dose differences for each group. *: P < 0.05, **: P < 0.001, SPE: group with smaller potential errors, LPE: group with larger potential errors.

Fig. 5.

Relationships between the absolute dose difference and the potential error (PE) value (a) and dose heterogeneity (b). The horizontal axis represents the PE value (a) and dose heterogeneity (b), and the vertical axis represents the absolute dose differences (in percentages) between the measured and MultiPlan-calculated doses. The yellow arrow in Fig. 5b indicates an outlier with a small dose heterogeneity and a large dose difference (a detailed dose distribution of this case is provided in the Discussion). SPE: group with smaller potential errors; LPE: group with larger potential errors.

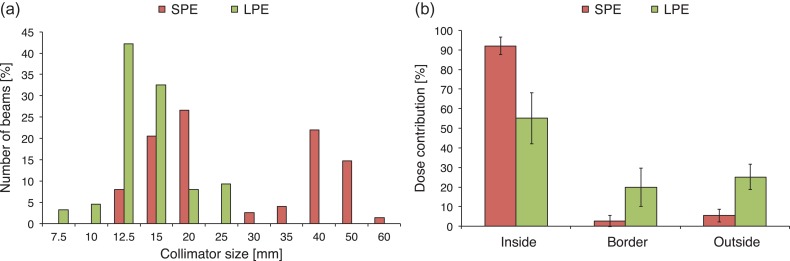
Figure 6a shows collimator size distributions in the SPE and LPE groups. Mode collimator diameters were 20 mm and 40 mm for the SPE group and 12.5 mm for the LPE group. Figure 6b shows the dose contribution to total dose prescription for each treatment plan; here, ‘inside’ indicates the passage of the beam from the collimator through the reference point. ‘Border’ indicates contact of the beam periphery with the reference point, resulting from the dose prescription from the collimator periphery. ‘Outside’ indicates that the beam does not pass through the reference point but contributes to the total dose by penumbra dose superimposition. The mean (± standard deviation) inside, border and outside values in the SPE group were 92.0 ± 4.4%, 2.5 ± 2.8% and 5.4 ± 3.3%, respectively. The corresponding values in the LPE group were 55.1 ± 13.0%, 19.9 ± 9.8% and 25.0 ± 6.5%.

Fig. 6.

Collimator size distributions with respect to the total number of beams per group (a). The horizontal axis represents the fixed collimator diameter, and the vertical axis indicates the number of beams per group (percentage). Similarly, the dose contribution to the total dose prescription is shown for each treatment plan (b). The horizontal axis represents the relative position of the beam path to the reference point. Black bars represent one standard deviation from the mean dose contribution. SPE: group with smaller potential errors; LPE: group with larger potential errors.

DISCUSSION

ShioRIS and MultiPlan PDDs correlated well except at the phantom entrance area, in agreement with the findings of Inoue et al. [17], who suggested that this PDD originated from a different recognition algorithm on the phantom surface in CT images. MultiPlan searches the surface along the central beam axis in a voxel-by-voxel manner to consistently determine the exact phantom surface from CT images, whereas ShioRIS searches the target surface along the central beam axis in 1-mm steps from the plane that includes the reference point. Accordingly, the ShioRIS recognition algorithm tends to slightly overestimate the phantom surface; however, this effect was small in our study, as the phantom measurement point was located at a depth of 5 cm. By contrast, certain dose differences in the lateral dose profile were observed between ShioRIS and MultiPlan. As seen in Fig. 3b, most large dose differences were observed in the penumbra region; these would affect the accuracy of non-isocentric dose delivery calculations, and thus compromise the accuracy of PE calculations.

CyberKnife radiotherapy is affected by multiple systematic and random error-related uncertainties. In the present study, we introduced PE, which considers the worst-case dose prescription scenario by calculating the maximum dose increase and decrease via modification of the SAD and OAD for each beam by −1.0 mm and +1.0 mm (the ±1.0 mm modification value was doubled for the overall targeting accuracy of our CyberKnife system; 0.50 mm, details not shown). As the delta-manipulator vector parameter can control systematic errors, the modification value of ±1.0 mm might vary depending on the vector precision (i.e. targeting accuracy) at individual institutions.

In small-field dosimetry, radiation-induced leakage resulting from chamber stem/cable irradiation can reduce verification accuracy. Agostinelli et al. indicated that for Pinpoint ionization chamber dosimetry, the stem effect for 100 × 100 mm² could be negligible, although this has been reported for coplanar dose delivery [20]. Furthermore, the spherical beam geometry around the target prevents full application of the conventional stem effect in the CyberKnife DQA. Therefore, we presumed that the stem effect of radiation-induced leakage would be negligible. By contrast, angular dependence resulting from the passage of multidirectional beams through the PinPoint ionization chamber presents a challenge. A maximum change in detector response of ~11% was observed in accordance with the beam incident angle [21]. Although this study did not correct the angular dependence output factor [22], future studies should evaluate the dosimetric impact of this factor.

The significant correlation between dose heterogeneity and dose difference (r = 0.471, P < 0.001; Fig. 5b) suggests that dose heterogeneity across the detector could effectively predict the robustness of dosimetry for CyberKnife DQA. Therefore, the determination method reported by Low et al. [13] can be used for point dose verification in CyberKnife DQA, even though the accuracy of non-isocentric dose prescription is sensitive to targeting errors. However, the yellow arrow in Fig. 5b suggests a large discrepancy between the measured and calculated doses, despite the small dose heterogeneity at the measurement point. The dose distribution in this case is presented in Fig. 7; as shown, the 100% isodose line was normalized at 7.0 Gy. We observed that dose heterogeneity across the detector bordered the region of steep dose elevation, despite remaining within the definition devised by Low et al. [13]. Because the dose heterogeneity–based determination method does not incorporate the impact of targeting errors, the measurement point might locate a point that is vulnerable to dose shifting. By contrast, a stronger correlation was observed between the PE value and the dose difference (r = 0.582, P < 0.001; Fig. 5a). The collimator size distributions for the SPE and LPE groups revealed a tendency to use a larger collimator size for patients in the SPE group. Furthermore, the dose contribution rate revealed that in this group, the measured doses were mainly contributed from inside the collimator. As the steep dose fall-off indicates that targeting errors affect the peripheral dose prescription accuracy, we concluded that the SPE measurement point was located in a region where a major portion of the deposited dose is delivered from inside the collimators, leading to a homogeneous dose distribution. Thus, the PE evaluation approach can predict locations robust to targeting errors by considering the worst-case dose prescription scenario, in contrast to the determination method introduced by Low et al [13]. This difference in the correlation coefficients obtained using the PE evaluation approach and the determination method of Low et al. [13] suggests that the PE evaluation approach could identify a more robust measurement point when compared with the earlier determination method, given the ability of the former to include targeting errors in predictions.

Fig. 7.

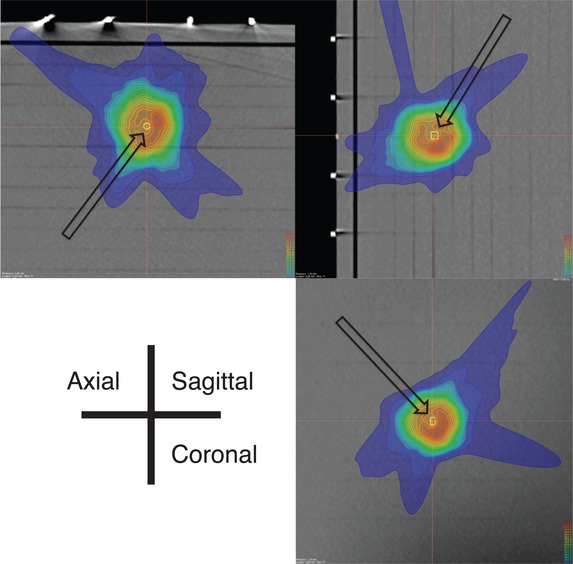
Three-dimensional dose distribution in a single case (indicated by a yellow arrow in Fig. 5b). The 100% isodose line was normalized at 7.0 Gy, and the solid white line indicates the PinPoint ionization chamber voxel of interest. The solid orange and yellow lines represent the 90% and 80% isodoses, respectively.

The significant difference between the control and LPE groups suggests that PE evaluation can effectively determine a robust dosimetric point and can thus be expected to reduce dose difference variability. Furthermore, the significant difference between the SPE and LPE groups indicates the usefulness of the PE value magnitude for predicting the measurement point stability. Consequently, the measurement point should be determined at the location of the lowest PE value. We note that the maximum and mean PE values of isocentric dose delivery were 0.030 and 0.017, respectively. This variation in PE values was quite small; therefore, PE evaluation would instead be particularly effective for absolute point dose measurements from non-isocentric dose delivery.

Additionally, PE-guided DQA was conducted for five cases in the LPE group that exhibited large differences between calculated and measured doses to confirm the efficacy of this method. The lowest PE value measurement point was identified on a PE map that was obtained by subtracting the dose distributions of the maximum dose increases and decreases (Fig. 2). Subsequently, the overlaid dose distribution on the I'mRT Phantom was transferred and used to adjust the VOI in the PinPoint ionization chamber to the location of the lower PE point, after which dose recalculation was performed (see Table 2 for a summary). Although PE-guided DQA reduced the differences between the calculated and measured doses, Cases 4 and 5 still exhibited large differences, indicating that for such cases, a perfect measurement point could not be determined in the context of a highly complex treatment plan. In other words, when a higher dose region is condensed in a small PTV, spots robust to targeting errors might be unavailable. Under such a complex dose distribution, large-volume ionization chambers, which are less sensitive to geometrical errors, would be effective for dose difference evaluations. A previous report involving a Farmer chamber (sensitive volume of 0.6 cm³) indicated that this chamber reduced variations in dose differences to a greater extent when compared with small-volume detectors such as the PinPoint ionization chamber [23]. In this situation, measured and calculated doses are compared with volume-averaged doses to account for the effect of volume averaging.

Table 2.

Result of PE-guided DQA for five cases in the LPE group

		Measurement at center of PTV			Measurement with PE-guidance
# Cases	PTV (cm3)	DD (%)	PE	DH (%)	DD [%]	PE	DH (%)
1	2.68	6.61	0.73	11.40	−0.20	0.26	5.73
2	3.62	6.65	0.73	3.45	−0.68	0.30	5.32
3	3.36	5.27	0.70	11.97	0.09	0.39	8.77
4	0.91	9.73	0.90	9.49	−7.56	0.62	13.60
5	3.60	9.25	0.77	7.98	−6.79	0.29	5.13

DD = dose difference between measurement and calculation by MultiPlan; DH = dose heterogeneity.

PE evaluation is limited by its inability to incorporate the impacts of random errors into the prediction. Such errors would affect the precision of a dose prescription because a minor vertical positioning error for an oblique-incident beam will cause a major lateral locating error, and vice versa. However, the total impact of random errors was assumed to be small because CyberKnife radiotherapy delivers multidirectional beams to the target. If the robotic manipulator experienced a minor random error in the irradiation location, the prescribed dose via non-isocentric dose delivery would differ greatly because of the steep dose fall-off in the lateral dose profile. Therefore, the uphill and downhill dose regions could be observed through an interplay effect, similar to the effect observed in the IMRT cases [24]. On the other hand, the uphill and downhill dose regions, if superimposed during irradiation, could also cancel each other out. Consequently, a large dose difference might result from an interplay of random errors, even though an area of small PE is measured.

IMRT treatment plans incorporate multiple abutted treatment fields to improve dose conformity, especially for large targets. During a DQA of the IMRT treatment plan, a leaf-positioning or phantom set-up error could significantly affect the dosimetry accuracy in abutting step-and-shoot IMRT fields [25]. PE, which is intended to determine a robust measurement point in the worst-case dose prescription scenario, can be applied to a robust dosimetry that includes abutting step-and-shoot IMRT fields.

In conclusion, PE evaluation was more effective than the conventional dose heterogeneity–based method for determining a robust measurement point for CyberKnife point dose verification.

FUNDING

This work was supported by a grant from the Japan Society for the Promotion of Science (JSPS) Core-to-Core program (Grant No. 23003) and JSPS KAKENHI Grant Number JP16K19230.

CONFLICT OF INTEREST

The authors declare that there are no conflicts of interest.