Climatic suitability influences species specific abundance patterns of Australian flying foxes and risk of Hendra virus spillover

Abstract

Hendra virus is a paramyxovirus of Australian flying fox bats. It was first detected in August 1994, after the death of 20 horses and one human. Since then it has occurred regularly within a portion of the geographical distribution of all Australian flying fox (fruit bat) species. There is, however, little understanding about which species are most likely responsible for spillover, or why spillover does not occur in other areas occupied by reservoir and spillover hosts. Using ecological niche models of the four flying fox species we were able to identify which species are most likely linked to spillover events using the concept of distance to the niche centroid of each species. With this novel approach we found that 20 out of 27 events occur disproportionately closer to the niche centroid of two species (P. alecto and P. conspicillatus). With linear regressions we found a negative relationship between distance to the niche centroid and abundance of these two species. Thus, we suggest that the bioclimatic niche of these two species is likely driving the spatial pattern of spillover of Hendra virus into horses and ultimately humans.

1. Introduction

Spillover of wildlife pathogens is a recurrent and often unpredictable phenomenon with important consequences for human and domestic animal health. Bats (Mammalia: Chiroptera) have been focus of considerable attention for their seemingly disproportionate diversity of viruses that are pathogenic to other mammal orders [1]. A few well known bat borne zoonotic viral diseases include Ebola, Marburg virus disease and SARS [2], [3], [4]. Despite their importance, spillover of these viral diseases is difficult to predict [5], [6], [7], partly due to the poor understanding of the viruses in their specific reservoir hosts and the ecological interaction of these hosts with the spillover hosts.

The abundance of reservoir hosts is an important determinant of the risk of pathogen spillover as it is a key driver of pathogen prevalence and disease transmission [8], [9]. Spatial patterns of species abundance can be influenced by the climatic characteristics of the geographic areas inhabited by species [10]. At the very least, climate can predict where abundance is more likely to be higher [11].

Ecological niche modelling (ENM) is a field of ecology that studies the environmental requirements of species. By using spatially referenced environmental and climatic data ENM is frequently used to identify geographic areas where species can survive and persist [12], [13]. The abundance patterns of species within the predicted geographic ranges are often related to its location within the ecological and climatic niche [10]. The different locations within climatic niches can be estimated by finding its multivariate centroid, which is formed by the mean of each environmental/climatic dimension of the niche. For instance the average of the maximum temperature or rainfall of wettest season across a species geographical range might represent a bi-variate niche centroid. Departures from the centroid in any direction are measured as environmental distance from the niche centroid (DNC).1 Consequently the DNC of reservoir host species could be used to better understand and predict the risk of spillover of emerging zoonotic pathogens.

One of these emerging zoonoses is Hendra virus (HeV),2 belonging to the genus Henipavirus (Paramyxoviridae). It was discovered in Australia in 1994 after a respiratory disease outbreak involving the death of 20 horses and one human [14]. Hendra virus has been found to naturally infect the four Australian fruit bat species (genus Pteropus, also known as flying foxes, FF),3 the black flying fox, P. alecto; grey headed flying fox, P. poliocephalus; spectacled flying fox, P. conspicillatus; and the little red flying fox, P. scapulatus [15]. To date, infection in horses is rare and sporadic. Fifty-one spillover events have been recorded since September 1994, spanning nearly 1500 km of the east coast of Australia. The case fatality rates in horses and humans are approximately 75 and 50%, respectively [16].

Recent analyses suggest that black (P. alecto, BFF)4 and spectacled FF (P. conspicillatus, SFF)5 are more likely to be responsible for the HeV spillover events. This is based on the observation that the density of records of these two species is higher in areas where spillover has occurred [17], [18], and that HeV is more likely to be detected in these species [19], [20]. Spillover events seem to be expanding south, coinciding with the southwards expansion of P. alecto during the last few decades [21]. Although these correlations are statistically significant, an ecological explanation is still missing. For instance, the southwards increase of spillover cases can result from either the expanding range of P. alecto, or confounded by improved reporting and surveillance after the first New South Wales spillover case was detected in 2006 [22]. One way to address the uncertain role of these four FF species is to look at the ecological suitability of spillover sites for each of the four potential reservoir host species.

One of the key determinants of ecological suitability for FF are their preferred food resources, which are dependent on climate. For example, the flowering status of several Eucalyptus species, the main food source for FF, is determined by climatic factors [23]. In addition, the spillover pathway of Hendra virus from FF to horses is directly linked to FF food resources, as transmission appears to be due to FF shedding virus in trees inside horse paddocks while foraging [24], [25]. This provides an ecological basis for investigating the spatial suitability and abundance patterns of FF in relation to climate with correlative methods. Moreover, it is well known that FF have limited thermal tolerance that differs among the four Australian species, indicating that their fundamental niche is a key component of their potential distribution, making climate an important factor limiting their geographic distribution [26], [27].

Three previous studies have modelled the distribution of henipaviruses, first Peterson [28] sought to identify conditions that allow transmission and persistence of Nipah virus (NiV)6 among hosts. Second, Daszak et al. [29] modelled the present and future potential distributions of Henipavirus hosts; and, Smith et al. [18] identified geographical correlates of HeV spillover. Other studies of bat borne zoonotic viruses have focused strictly on finding geographic areas of risk to human populations [e.g., [7], [30]]. In this study we modelled the climatic requirements of HeV reservoir hosts. The models were then used to establish a relationship between suitability for FF and risk of HeV spillover based on the observed geography of spillover. Our results provide further evidence of the association of FF species with HeV spillover and potential drivers of the spatial pattern of spillover.

2. Methods

Predictions from niche models are a series of smoothed surfaces in the form of maps whose accuracy depends largely on the explanatory environmental variables [13], [31]. Correlative niche modelling relies on statistical relationships between environmental characteristics and geographical records of species presence [32]. In many cases reliable records of species absence are not available which has led to the development of algorithms that use presence only data, like Maxent [32]. Similarly, validation techniques have been adapted to this kind of presence only data. For example some model testing methods use the proportion of the study area predicted to be occupied by the species and the proportion of predicted presences; like the Partial ROC and Jacknife test [33], [34]. These methods compare prediction rates of the model on testing data by comparing prediction rates with a random spatial predictor (proportion of area predicted to be occupied). Maxent is a machine learning algorithm based on maximum entropy, that is similar to a Poisson regression [35], but has a logistic-like output and is capable of fitting non-linear relationships. The result is a series of response functions that provide an estimate of probability of species presence in relation to the assumed proportion of grid cells occupied by the species [36]. Below we describe the methods we used to select the variables to model the niche of each FF species, validate the models and calculate the DNC of FF species of all pixels across the area where HeV spills over to horses and determine its relation to HeV spillover.

2.1. Niches of flying fox species

We obtained flying fox presence localities from the global biodiversity database (http://www.gbif.org), the Atlas of Living Australia (http://www.ala.org.au) and Roberts et al. [21]. The three databases were combined to maximise the number of records. We then used an iterative method to eliminate localities within a pre-specified threshold distance to reduce spatial autocorrelation. The filtered presence localities were then used to sample climatic raster data from the Worldclim bioclimatic variables (http://www.worldclim.org) [37]. In addition, points that were dubious or very far from the known distributional limits were removed. For each bat species we selected a set of layers based on pairwise correlations between climatic variables and how the presence points were distributed within each plot of variable pairs [13]. We sought to include the variables where presences had a unimodal distribution and occupied a limited range within the scope of possible values of the variable.

To validate models by means of measuring its performance on independent data we selected training and testing data spatially. To do so we created a chess board grid with squares of 40,000 km² approximately, and 200 km wide horizontal and vertical bands (along longitude and latitude). We used points lying within contiguous bands or squares for training and testing with a partial ROC analysis [33], [38]. Given that we did not verify flying fox occurrence records for accuracy we allowed a 50% omission rate of testing points for the partial ROC analysis. Because the final data set for P. conspicillatus contained < 30 occurrence records, we validated this model with a Jacknife test [34]. For the Jacknife test we calibrated N-1 models (N = number of presence localities), leaving one of the presence localities out in each model run. Then from the scores assigned by the algorithm to each locality we used the minimum of these values as a threshold to see if the omitted locality had been predicted as present (had a probability of occurrence ≥ threshold). The predictions/non-predictions and thresholds were used as probabilities to run the validation test with the “pValueCompute” tool from Pearson et al. [34].

Because niche models should only encompass the areas where species can move (areas colonisable by species = M [Movement]) [39], [40], we assumed that the climatic regions of Australia (Bureau of Meteorology of Australia, http://www.bom.gov.au) occupied by each FF species are the boundaries of the areas accessible to colonise. The same assumption helped identify the HeV M area. All climatic regions containing at least one presence point of the final presence database were combined to mask the climatic variables for each species. All the FF niche models were generated with Maxent without clamping and extrapolation [32]. To generate the binary models necessary for the subsequent analyses we applied a threshold corresponding to the 50th percentile of model scores at presence localities, which represents the same criterion used in model testing. The resulting binary maps represent areas where each FF species has a probability ≥ 0.5 of being present. All models and analyses were performed with the statistical programming language R 3.1.1 [41] (R-Core-Team 2014) with packages “dismo” and “raster” [42], [43].

2.2. Proximity of HeV spillover events to the centroid of flying foxes

To calculate the centroid we extracted the variables' values contained within each of the FF predicted distributions that overlap with the HeV spillover M area [10]. The centroid of all the climatic dimensions is found with the arithmetic mean of each variable. Then we calculated the Mahalanobis distance (Euclidean times covariance matrix, to correct for variable's correlations) from each pixel within the HeV M area to the centroid of each bat species. In other words, the centroid was obtained with the climatic data after we removed the FF areas that do not overlap with the HeV M area. In doing this we assumed that FF have multiple centroids and that the centroids within the HeV M area are independent from the centroids from the areas that were not included. This assumption was based on other climatic envelope modelling algorithms that assume that all presence localities represent optimal conditions [44], [45]. Finally we extracted the resulting distances to each FF species' centroid at the location of spillover events. To avoid comparing DNC at different scales, distances to FF species centroids were calculated using the same set of climatic variables selected with the procedure described in the previous section using the HeV presence records.

To confirm that distances to the niche centroid at the location of spillover differed between the four bat species we performed a Kruskal-Wallis test. To assess if the frequency of occurrence within each of the calculated centroid distances departed from random expectations we identified which FF species centroid was closer to each spillover location. To calculate the expected frequencies, the maximum value from all these minimum DNC scores was used as a threshold to calculate the proportion of pixels occupied by each FF species within an equal or smaller distance to the centroid. With these values we calculated the probability of finding each species using the proportion of pixels predicting its presence with respect to the total number of pixels occupied by all FF species. These probabilities were used as the expected frequencies of any species' DNC being lowest in the location of spillover. We used a chi squared test to compare expected and observed frequencies (number of times each species had the minimum DNC at the location of spillover). We assumed that all spillover localities were independent from each other after filtering for spatial autocorrelation of spillover events. The independence assumption might not be true, however after using the distance threshold of 0.5° we were left with 27 presence records, and we did not want to lose any more statistical power.

Finally to determine if the selected FF species occur at higher densities in areas closer to the niche centroid, we registered the coordinates and all the abundance categories for each flying fox roost site (camp) in the National FF monitoring program of Australia (http://www.environment.gov.au/node/16393) using the interactive FF web viewer. We then performed linear regressions between the average abundance category, the maximum category for each camp and the standard deviation. Additionally we performed a kernel density estimation weighted by the maximum abundance category for each camp. We then ran a correlation test between these density models and the DNC models.

3. Results

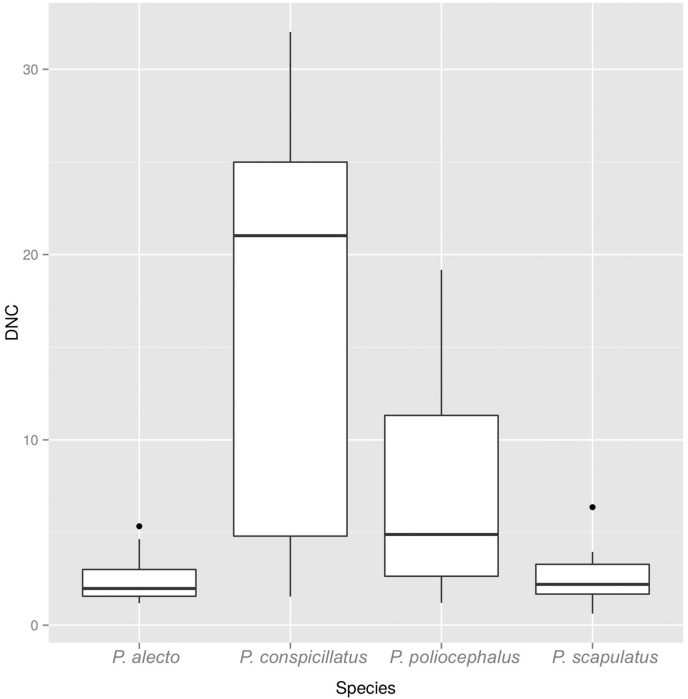
We were able to calibrate at least one model that performed better than random (table of AUC ratios in Supplementary data 1) for each FF species (Fig. 1). Although the model for P. conspicillatus could only be validated with the Jacknife test, it also performed better than random. Variables describing niches differed across species and are listed in the supporting information. As for the DNC models, we found that sixteen out of 27 HeV spillover events that remained in the data set after filtering were closer to the niche centroid of P. alecto than to the centroid of the other three species. In 7 events, the distance was smaller to the centroid of P. scapulatus, and for the remaining four events, the distance was smaller to the centroid of P. conspicillatus. The DNC at spillover sites were significantly different among species (one way Kruskal-Wallis, χ² = 43.31, d.f. = 3, P = 2.11 × 10^− 9; Fig. 2, Fig. 3), indicating that some species are more likely involved in spillover.

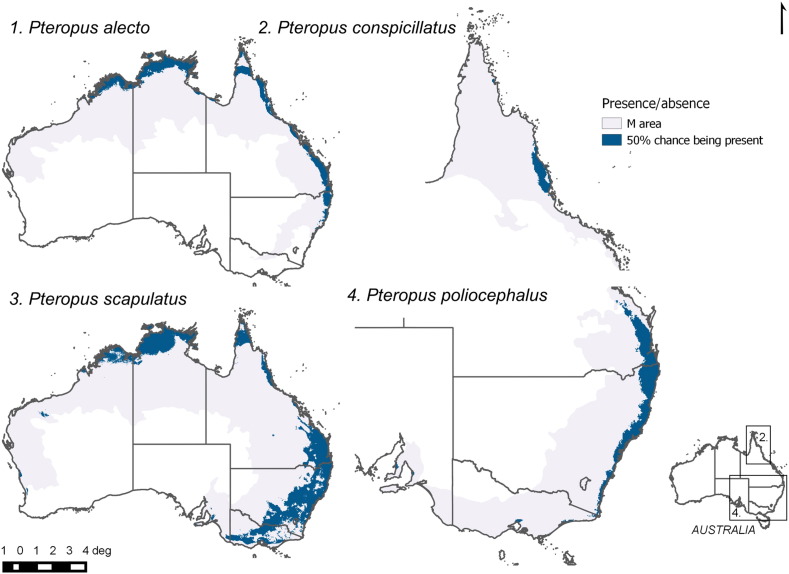
Fig. 1.

Maps of predicted potential distributions of the four Australian FF. Dark blue indicates areas where each species has at least a 0.5 probability of being present. Grey shaded areas correspond to the available geographic space for each species (M areas).

Fig. 2.

Box plots of the Mahalanobis distance to the centroid of each species from the locations of spillover events.

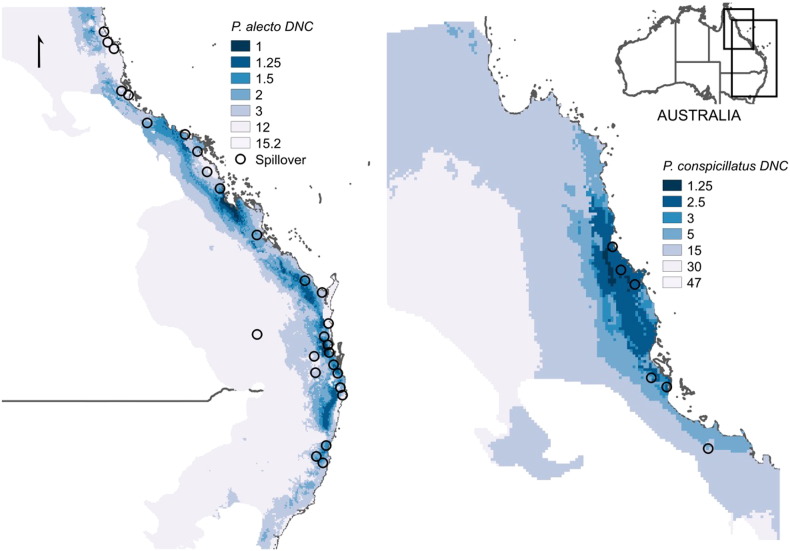
Fig. 3.

Map of distance categories to the niche centroid of P. alecto and P. conspicillatus and spillover events. According to the distribution of DNC categories and hence abundance in space of FF, spillover events have occurred closer to these two species compared with P. poliocephalus and P. scapulatus.

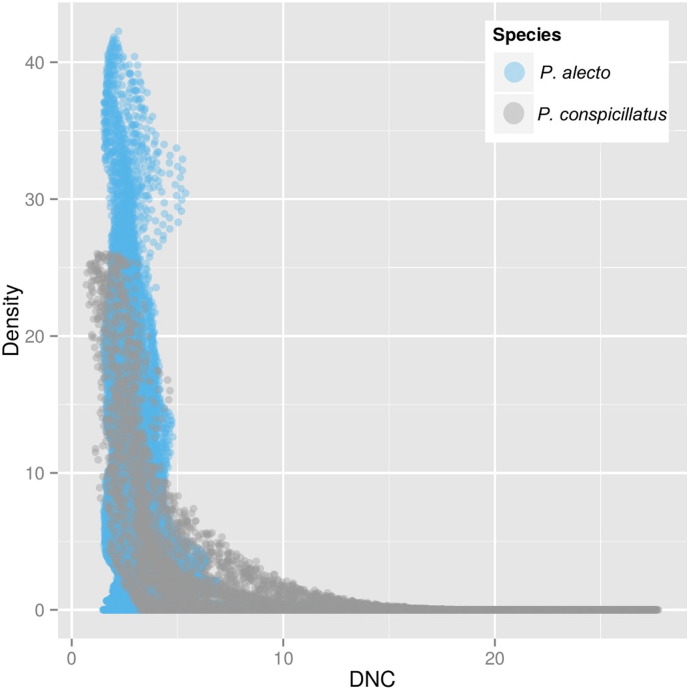
Because most of the events (16/27) have occurred closer to the niche centroid of P. alecto, we tested this association with the chi squared test which was highly significant (χ² = 49.9, d.f. = 3, P = 8.09 × 10^− 11). The probability of randomly selecting a pixel with conditions suitable for P. alecto, P. conspicillatus and P. scapulatus in the geographic space of the Hendra M area was 0.26, 0.016 and 0.61, respectively. The linear regressions confirm a decreasing trend of abundance with DNC only for P. alecto especially the maximum camp size (Table 1). Similarly the correlation between weighted density of P. alecto and P. conspicillatus and DNC were − 0.28 (P < 0.05) and − 0.39 (P < 0.05) respectively (Fig. 4).

Table 1.

Relationship between DNC and size categories of FF camps. The categories used were: 1 (1–499), 2 (500–4999), 3 (5000–9999), 4 (10,000–19,999), 5 (20,000–49,999) and 6 (> 50,000).

Species	Average camp size		R2	P	Maximum camp size		R2	P	S.D. camp size		R2	P
	Intercept	Slope			Intercept	Slope			Intercept	Slope
P. alecto	0.37	− 0.15	0.03	0.01	0.94	− 0.15	0.08	≪ 0.05	0.87	− 0.11	0.05	≪ 0.05
P. conspicillatus	1.13	− 0.22	0.09	0.2	1.12	− 0.05	− 0.06	0.7	1.10	− 0.013	≈ 0	0.9

Fig. 4.

Scatter plot between weighted density and DNC of P. alecto and P. conspicillatus. Despite the lack of a significant relationship between P. conspicillatus and the abundance categories in Table 1, there is a significant negative correlation between DNC and weighted density.

4. Discussion

The climatic characteristics of HeV spillover locations are similar to the conditions suitable for P. alecto and P. conspicillatus. In areas where conditions permit the presence of other species, spillover events have occurred mostly in areas closer to the centroid of P. alecto. Density of P. alecto and P. conspicillatus records are higher in areas where spillover to horses has occurred, suggesting these species were more likely to be responsible for spillover than P. poliocephalus and P. scapulatus [18]. None of the events occurred closer to the centroid of P. poliocephalus than to the centroid of other species, and the presence of spillover closer to seven out of 27 events to the niche of P. scapulatus is possibly because it has the widest distribution of all FF species. Hence, the majority of the Hendra M area was suitable for them. Pteropus scapulatus are highly mobile and unpredictable, they are nectarivorous and thus rely strictly on flowering trees [46], [47]. HeV antibodies are distributed throughout P. scapulatus populations [46]. Yet, no spillover events have been reported in areas where P. scapulatus is the only species present, and P. alecto has been consistently found in proximity to spillover events [17]. Nevertheless, their intermittently combined densities have important implications for spillover [17], [18].

An important feature of HeV spillover is the timing of events. Spillover tends to cluster in space and time, most events usually occur in winter in the southernmost part of the distribution of P. alecto. The reasons for this are still unknown, and are probably multifactorial [25]. Given the movement patterns of P. poliocephalus, it is possible that they play a role in spillover because they tend to move towards the northern areas of their distribution during the southern hemisphere winter [48], which will create higher concentrations of FF in areas highly suitable for P. alecto according to our models.

To confirm the climatic suitability-abundance correlation for FF we were able to demonstrate a negative relationship between DNC and maximum abundance of FF. Furthermore, the negative relationship between the standard deviation of the camp size and DNC provides more support; meaning that the higher the DNC the smaller and less variable with respect to maximum size the camp sizes tend to be through time. In the case of P. conspicillatus, the regressions were not significant, however the significant negative correlation between the weighted kernel density model and DNC suggests that the relationship is negative (Fig. 4). Our results show stronger relationships between climatic suitability and maximum size of populations (number of FF in camp sites), a phenomenon observed in several different species [11]. This indicates that the areas closest to the smaller DNC have greater potential to harbor either large or several FF camps, and hence timing of such densities might be a key determinant of risk of spillover.

Throughout this study we made two key assumptions: 1) FF do not have a single range-wide DNC that influences abundance patterns, but multiple independent DNCs; and 2) that spillover cases used in analyses are independent from each other and from the FF camp records used to train the models. The assumption of local DNC independence from a range-wide DNC is based on similar assumptions made by some modelling algorithms. For example, the Mahalanobis distance algorithm [44] and BIOCLIM [45] assume that all localities used in model training are as suitable as is the niche centroid. The second assumption appears reasonable given that spillover events appear to be independent of one another and FF localities.

There are obvious limitations in our methods. First, climatic data used by our niche models are averages over space and time rather than the specific conditions that occur at the time and place of a spillover event. Second, presence records of FF mostly reference the location of bat roosting sites, whereas HeV spillovers usually occur where FF forage. Therefore, there is a spatial lag between the areas chosen by FF to camp and the areas where HeV is transmitted to horses. These areas could well be outside of the preferred conditions by P. alecto to establish a colony [47] but within the preferences of other FF species that could be present. Despite this shortcoming, the aim of the study is to identify where climatic characteristics allow the presence of larger flying fox populations. Given the methods we used, we do not aim to understand small scale interactions such as choosing to camp in a specific tree and forage in another [12]. A clear example of the implications of climate on persistence of species are the heat waves that exceed the limits of the temperature tolerance of FF [26], [27]. For example, P. scapulatus has lower evaporation rates and higher thermal tolerance than P. alecto and P. poliocephalus, which explains its wider distribution into drier and warmer areas [47], (Fig. 1). These relationships represent the ecological scale of organisation on which our results should be interpreted [40]. Therefore, the DNC models do not represent areas where FF are constantly more abundant, but are areas with certain climatic characteristics that have greater potential to harbor larger populations given the temperature tolerance and preference of the species and its food resources [11].

The relationships between climatic suitability and abundance are typically weak as we found here. Additional factors contribute to abundance patterns such as geographical barriers, biotic interactions and ecological changes [10], [11]. In the specific case of FFs, density is affected by the presence of food resources (biotic interactions) that can be spatiotemporally sporadic [48]. In addition, sampling bias can greatly affect the strength of the DNC-abundance relationship. In particular, the timing of a census is important for highly mobile and gregarious species. We suspect that the DNC-abundance relationship was altered by the increasing width of the abundance categories in the national FF monitoring program. The higher the category reported the broader the difference between the upper and lower limits. However, the non-random distribution of spillover among FF niches suggests there is a strong relationship between spillover and P. alecto and P. conspicillatus numbers and/or presence. Further analyses of habitat suitability and abundance should be performed with raw values of FF abundance that better account for variability than categories of abundance.

Our modelling suggests that there is a bioclimatic effect driving the spatial patterns of P. alecto and P. conspicillatus abundance. The location of urban settlements in geographical proximity to the NC of P. alecto may contribute to urban habituation of this species. Our models can be used for guiding future research, to address key questions in understanding the dynamics of spillover. The effect that climatic variations in areas close to the niche centroid have on HeV dynamics and FF population levels could be investigated to better understand the risk of HeV spillover to horses.

5. Conclusions

According to the DNC analyses, P. alecto and P. conspicillatus are more likely to have been present in proximity to spillover events and therefore responsible for transmission of Hendra virus to horses. Our results indicate that the bioclimatic suitability for P. scapulatus is very high in almost 25% of HeV spillover events, which requires further investigation.

Disclosure

GM and CY conceived and designed the study. BR collected Pteropus alecto and P. poliocephalus presence localities. CC provided statistical advice during the design. RP and LS helped to develop the theoretical background, and RW collected the flying fox abundance data.

Conflicts of interest

None.

Supplementary data

Supplementary material