Vortices formed on the mitral valve tips aid normal left ventricular filling

Abstract

For the left ventricle (LV) to function as an effective pump it must be able to fill from a low left atrial pressure. However, this ability is lost in patients with heart failure. We investigated LV filling by imaging the cardiac blood flow using 2D phase contrast magnetic resonance imaging and quantified the intraventricular pressure gradients and the strength and location of vortices. In normal subjects, blood flows towards the apex prior to the mitral valve opening, and the mitral annulus moves rapidly away after the valve opens, with both effects enhancing the vortex ring at the mitral valve tips. Instead of being a passive by-product of the process as was previously believed, this ring facilitates filling by reducing convective losses and enhancing the function of the LV as a suction pump. The virtual channel thus created by the vortices may help insure efficient mass transfer for the left atrium to the LV apex. Impairment of this mechanism contributes to diastolic dysfunction, with LV filling becoming dependent on left atrial pressure, which can lead to eventual heart failure. Better understanding of the mechanics of this progression may lead to more accurate diagnosis and treatment of this disease.

Introduction

The left ventricle normally functions as a suction pump[22], filling rapidly during early diastole, and can increase the rate of filling during stress (such as exercise) without an elevation of left atrial (LA) pressure [28, 34, 8]. Many conditions including aging, coronary artery disease, hypertension, LV hypertrophy, myocardial ischemia, dilated cardiomyopathy and restrictive cardiomyopathy impair early diastolic filling, diminishing the ability of the LV to function as a suction pump [14, 41, 40, 27]. In these conditions filling becomes dependent on increased LA pressure [27, 9, 28], such as that generated by elevated pulmonary pressure or LA contraction during late diastole. This diastolic dysfunction (LVDD) is present in patients with heart failure whether their LV ejection fraction is preserved or decreased [3, 29] making it a unifying element of the condition. Furthermore, abnormalities of LV filling dynamics in asymptomatic subjects indicate groups with increased risk for subsequently developing heart failure [38]. There is thus a clear clinical need to understand what characteristics are needed to create strong diastolic suction, and how disease-induced changes in the heart impair the ability of the LV to fill at low atrial pressures.

Previous studies have revealed a great deal about the basic features of LV filling, and much of this work, along with an overview of fluid dynamics of the heart in general, is summarized in Pasipoularides’ 2010 book (see in particular Ch. 6, 7, and 14) [36]. However, these studies have provided only limited explanation as to whether or how the observed fluid dynamics help ensure normal LV function, or if they are merely a byproduct of normal heart motion. For example, Kilner et al. found that the configuration of the LV aids in redirecting the late diastolic inflow from the left atrium toward the LV outflow tract, contributing to efficient pumping [25]. It has also been shown that early diastole can be divided into two phases which are resolvable using Color M-mode echocardiography [48]. In the first phase, as the mitral valve opens blood is accelerated nearly simultaneously along the entire length of the ventricle by the passage of a pressure wave. Shortly thereafter, in the second phase high speed blood from the atrium through the mitral annulus forms an inflow jet which advances more slowly; the motion of this structure has been linked to the formation of a vortex ring in the LV [44, 52], and its speed may be related to LV stiffness [53]. In-vitro work by Shortland et al. showed that the growth and motion of this vortex ring is sensitive to heart geometry, valve diameter, and the filling pattern, but made little mention of possible consequences of these flow changes on the health of normal left ventricles other than to speculate certain patterns might reduce blood residence time at the apex [43]. Later work by Gharib et al. using in-vivo ultrasound scans and in-vitro experimental observations suggested that the duration of diastole in a healthy heart maximizes the momentum captured in the vortex ring without forcing it to pinch off from the jet [15, 24, 23]. The authors hypothesized that this allows the vortex ring to move blood efficiently from the LV inflow tract to the apex, enhancing the efficiency of overall LV filling. In-vivo measurements by Töger et al. using 4-D pcMRI scans showed that the these vortex rings capture roughly the same volume of fluid in healthy and diseased patients, and that this occurs primarily during the rapid filling part of the cycle, but that percentage of the total LV volume was much higher for healthy volunteers than for patients with dilated cardiomyopathy. Also, the vortex boundary more closely matched the LV endocardial walls for healthy volunteers. The difference was attributed to a closer matching between cardiac motion and blood flow, but the analysis focused on the measure of vortex properties as a diagnostic measure of diastolic function, rather than as active components of efficient filling, except as they related to increased thrombus formation in diseased hearts[50]. Sengupta et al. found that regional differences in relaxation timing from apex to base and between the subepicardium and subendocardium lead to a preferential lengthening and enlargement of the LV apex during isovolumic relaxation [42] even as basal regions may be continuing to contract [42, 5]. These wall motions may be in part responsible for the initiation of apically-directed blood flow within the LV prior to opening of the mitral valve [41, 20], which has been linked by Ohte et al. to normal function during both systole and diastole [35]. However, none of these studies established whether the observed fluid motions were important for the normal function of the heart, or merely the consequence. Pasipoularides and his collaborators conducted some of the few studies to suggest that proper filling patterns are necessary to normal function of the heart using patient-specific computer simulations of canine right ventricle (RV) flow. This work seemed to indicate that, although no vortices at all formed during the accelerating portion of early diastole (the “upstroke” of the E-wave), once the flow began decelerating (the “downstroke”) the development of an adverse pressure gradient along the ventricle forced the establishment of a recirculating vortex ring around the inflow jet, constraining it and mitigating the pressure losses due to convective deceleration. This mechanism was hypothesized to help maintain higher filling velocities later into diastole, but was dependent on the presence of normal heart geometry and motion[36]. Furthermore, he hypothesizes that these vortices formed behind heart valve leaflets (including both the atrioventricular and aortic valves) act to aid in proper valve closure by applying inward forces as the flow decelerates. Additionally, in this model no vortices were formed in healthy ventricles by shear layer roll-up (the mechanism by which vortex rings are typically formed by jets) during early diastole. However, although it was proposed that this model should also apply in the LV of human hearts, it does not appear that the work has been corroborated yet in-vivo.

Accordingly, based on our clinical observations and the existing literature we hypothesized a new mechanism by which the configuration and contraction pattern of the LV also contributes to early diastolic LV filling. Specifically, the transient flow towards the LV apex prior to opening of the mitral valve initiates the formation of a ring vortex at the tips of the mitral valve leaflets that is enhanced by the rapid movement of the mitral annulus away from the apex as the mitral valve opens. The resulting ring vortex begins forming while the jet is still accelerating and creates a virtual hydrodynamic channel extending from the mitral valve towards the apex of the heart. This channel, in concert with the elliptical shape of the healthy LV, prevents spreading of the filling jet and loss of momentum to convective deceleration. In contrast, in patients with diastolic dysfunction these mechanisms remain present but are impaired. Accordingly, early rapid filling of the LV continues to be initiated by LV suction whose magnitude is not sufficient to keep mean left atrial pressure within the normal range. Hence, as a compensatory mechanism intended to maintain stroke volume and cardiac output, the heart becomes dependent on elevated LA pressure to create the necessary pressure gradient to fill the chamber to its diastatic (equilibrium) volume. (This is the ‘pseudonormal’ Doppler echocardiographic filling pattern in clinical cardiology). We tested these hypotheses in normal subjects and a variety of patients with diastolic dysfunction using phase contrast MRI (magnetic resonance imaging).

Materials and Methods

Phase Contrast MRI

Phase contrast MRI measurements were performed on an Avanto 1.5T Scanner from Siemens Medical Solutions, located at the Wake Forest University Baptist Medical Center in Winston-Salem, NC. 2D pcMRI scans were acquired of 14 patients in various stages of LVDD (as determined by physicians) in accordance with IRB guidelines pre-established for the study. Velocity encoding (VENC) for each scan was 100–130 cm/s, with a TR of about 20 ms and 40, 45, or 50 reconstructed phases (depending on patient heart rate). TE was 3.3, and there was 1 view per segment. Flip angle was 20 degrees, and the resolution was 320×256 at 1.25 mm/pixel in plane with a 5 mm slice thickness. Three signal averages were used for each scan.

In addition, a separate high-SNR imaging scan was acquired immediately following each pcMRI over the same field of view and used to perform image segmentation on the velocity portraits, as noise in the real part of the pcMRI images often made boundary detection difficult. These images were registered to the pcMRI scans via common anatomical landmarks, and the boundaries of the left ventricle (LV), left atrium (LA), aortic outflow tract, right ventricle, and descending aorta were mapped and transferred to the pcMRI images.

Patient Population

The fourteen patients selected for this study were selected from patients undergoing clinically indicated cardiac MRI procedures. Information about the group is shown in Table 1. More detailed information on each patient is given in Table S1 in the Supplementary Material available online.

Table 1.

Patient cohort information

	all (n=14)	healthy (n=4)	diseased (n=10)
age (mean±std.dev)	50±17	28±25	58±12
sex (% male)	43%	75%	30%

Statistics

Comparisons were made using a Wilcoxon signed-rank nonparametric test in order to avoid assumptions on the distribution of values (such as Normal, etc.). Differences were defined as statistically significant if the p-value was less than 0.05.

Pressure Difference Calculations

A number of different methods have traditionally been used with pcMRI data to derive relative pressure data, including line-integration along a single path [13, 49], iterative approaches [49, 6, 51], and the solution of a Poisson equation minimizing the curl of the resulting pressure gradient field [6]. However, our previous work with derivation of pressure fields from noisy particle image velocimetry fields indicated that the iterative, omni-directional line integral pressure solver as suggested by Liu and Katz [30], when applied to a particle image velocimetry fields and paired with a reduced order model derived from proper orthogonal decomposition (POD) [2], yielded superior results to many other similar algorithms [7]. Consequently, this was the method chosen for this study.

In brief, the algorithm begins with the location and removal of velocity measurements that failed a local median test. In the experimental fluid dynamics community, such a technique is typically referred to as a “universal outlier detection” method [54] and serves to replace velocity measurements that are obviously out of character with the surrounding measurements, usually due to low signal-to-noise ratios in the original measurement volume. This filtered field was then used in the construction of a low-order model using POD [2]. This method constructs an efficient spanning of the sampled field, sorted by relative contribution to the total kinetic energy of the flow, from which can be selected the modes of interest. This sorting by kinetic energy is one of the reasons the pre-smoothing of the velocity field with a median filter was important, because spurious velocity measurements typically have large kinetic energy relative to the surrounding fluid and thus make accurate decomposition more difficult since a few large incorrect measurements will pollute many of the resulting modes.

Typically in noisy experimental data, the primary modes contain most of the flow information, while the higher modes contain information about the random noise, and can therefore be excluded. From this decomposition, a minimum of 10 of the most energetic modes were kept, spanning at least 95% of the original energy in the flow; most cases required only 10 modes to meet this criterion. A typical eigenvalue spectrum can be seen in Fig. S2 for the healthy patient shown in Fig. 1 for which 10 modes made up 97% of the total energy.

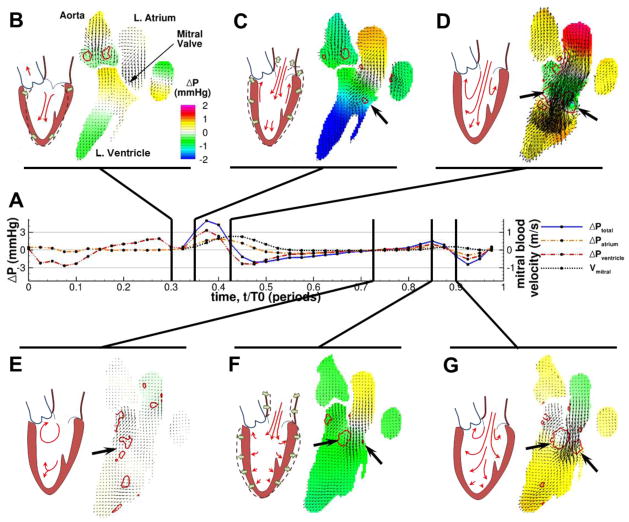
Fig. 1. Filling patterns for a representative healthy patient during diastole (approximately 0.3<t/T₀<1).

Pressure differences are larger during early filling than during the atrial contraction, and a higher velocity is developed during the initial relaxation. (A) Time history of relative pressure differences within and between the chambers of the left heart, with the velocity and pressure fields at several time points called out. t=0 is the beginning of systole. (B–G) Snapshots of the pcMRI velocity vectors within the blood pool at different instants throughout diastole. Background color indicates pressure relative to the MV, and the red contours identify the borders of vortex structures. The black arrows indicate the vortices near the MV leaflets. For reference, a cartoon of the idealized flow patterns in each snapshot is drawn next to each snapshot.

Pressure calculations were then performed on this reduced-order model. The omnidirectional method of Liu and Katz [30] works by constructing a virtual boundary outside the flow field, and then integrating along straight paths between all possible combinations of points on this boundary. This is shown schematically in Fig. S1 Only integrals within the fluid domain are performed, and the solution is initialized by integrating around the true fluid boundaries. The resulting pressure information is averaged between all paths. This information is then used to update the pressure boundary information, and the process is repeated until the field converges. This method has the advantage of localizing the effect of any errors in the velocity field.

These relative pressure readings were used to analyze the time histories of the pressure differences within the left heart in comparison to the measured transmitral flow velocity (measured at the mitral valve centerline at the level of the leaflet tips), in a manner similar to that originally employed by Courtois et al. in-vivo using pressure catheters [10]. Due to the regional variation in pressure along the LV during filling[10] for accurate comparisons it was necessary to choose consistent locations within the heart; in this study the top of the LA and the lowermost point of the LV apex were selected, with the mitral annulus chosen as the division between atrial and ventricular flow regions and the pressure set to zero as a reference.

Vortex Identification

Analysis of the measured velocity vectors was supplemented by identification of the primary vortical flow structures using the imaginary parts of any complex eigenvalues of the velocity gradient tensor (a λ_ci method) [55]. These λ_ci values correspond to the local swirling strength of the flow, and the method is Galilean invariant. Vortices were identified as connected regions with the absolute value of their swirling strengths above 2% threshold of the maximum value measured over the entire heart cycle. For each vortex, circulation (denoted by Γ) was then calculated as the area integral of the vorticity within the connected region. Vorticity was calculated using a second-order central difference method, and is calculated as the curl of the velocity field.

Lagrangian Coherent Structures (LCS)

Finite time Lyapunov exponents (FTLE) were calculated from the experimental velocity fields using a technique similar to that described by Haller [17, 18]. In brief, virtual particles were placed at the center of each voxel in the pcMRI velocity fields. Then, using a 4^th order Runge-Kutta-Feldberg integrator with 5^th order corrector step to perform time marching, the resulting trajectories of each virtual particle in the domain were calculated over a period of one heartbeat. This process was repeated for each time step to obtain forward trajectories anchored at each instant in time. Using the resulting trajectories, a map of the FTLE values for each time step in the recorded pcMRI scan was calculated to generate Movie S4 through Movie S6 (see the Supporting Information online). In general, a Lyapunov exponent can be considered a measure of the rate that two closely-spaced particles diverge from each other in time. A value greater than one indicates exponential divergence (growth in distance); local maximums suggest that the flow is separating and that the increase in the distance of two adjacent fluid elements becomes unbounded. To calculate the FTLE plots shown in Fig. 4, integration was limited to the periods of either early filling (isovolumic relaxation through diastasis), or late filling (beginning of the atrial contraction to the closure of the mitral valve). This was done to isolate only the contribution of the filling process to the increasing separation of the blood element paths. The rapid discharge of blood during the systolic emptying tended to further divide the flow and obscure the effect of the filling waves.

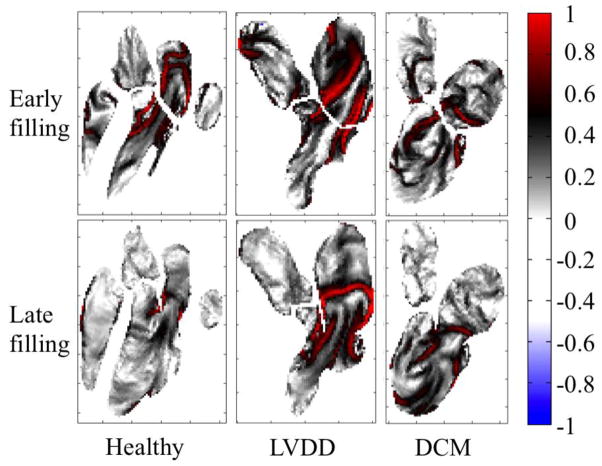
Fig. 4. Maps of finite-time Lyapunov exponents.

The maps are calculated over the early (top) and late (bottom) filling periods for healthy, diastolic dysfunction, and dilated cardiomyopathy patients. Exponents are normalized with the peak value in the LV. Healthy and LVDD patients are the same as shown in Fig. 1 and Fig. 2. Regions marked with red indicate areas of high, exponential rates of separation of adjacent fluid elements, and connected areas of maximum spreading are known as Lagrangian coherent structures. These structures coincide with the inner boundaries of strong inflow vortex rings, and indicate that their presence creates boundaries that entering blood does not easily cross, helping to direct it in a smooth jet toward the apex of the heart. In contrast, the DCM patient shows patterns that reflect the circular, clockwise path of blood through the LV.

A similar technique was previously used by Töger et al. to measure vortex ring volumes during LV filling from the LCS boundaries[50]. The main difference between their approach and that used here is that to calculate the vortex ring volumes backward-time FTLE were utilized, whereas in this study forward-time FTLE values were found; therefore the patterns observed cannot be directly compared.

Results

Observed flow patterns and heart motion

Comparison of phase contrast MRI scans of patients with LVDD and normal filling revealed clear differences between the two groups. (Fig. 1 and Fig. 2, also Movie S1 and Movie S2 in the Supporting Information). Fourteen patients were studied, four with normal filling, and ten with various filling disorders, including eight with various stages of diastolic dysfunction, one with left ventricular hypertrophy, and one with dilated cardiomyopathy (DCM, an enlargement of the LV).

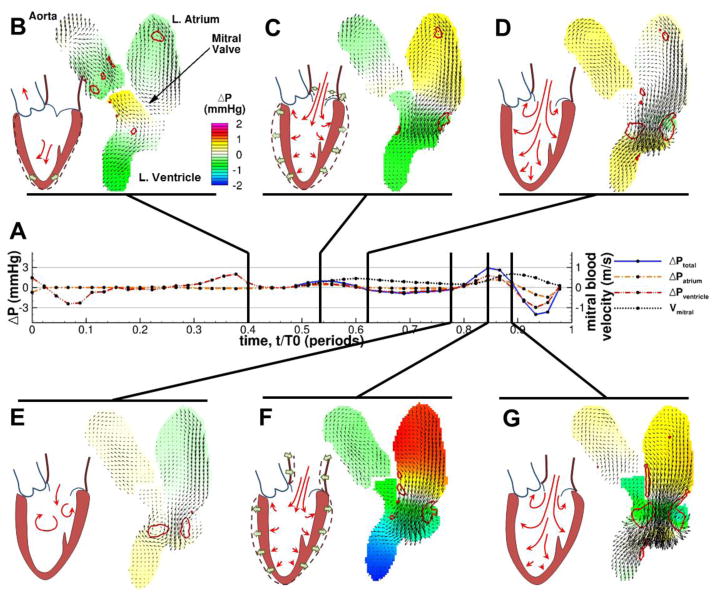
Fig. 2. Filling patterns for a representative LVDD patient during diastole (approximately 0.4<t/T₀<1).

Pressure differences are smaller during early filling than during the atrial contraction, and more vigorous velocity is developed in late diastole. Layout and notation are the same as in Fig. 1.

The primary vortical flow structures were identified using the eigenvalues of the velocity gradient tensor (λ_ci method) [55]. The circulation (Γ) of each vortex was then calculated via the integral of vorticity (a measure of fluid rotation) over its area. Furthermore, using an omnidirectional pressure integration scheme [30] on the velocity fields in combination with a reduced-order model constructed using proper orthogonal decomposition [7] we estimated the relative pressure distributions within the left heart and aortic root of each patients over a single heartbeat. A complete listing of calculated pressures and circulations is given in Table S2.

The results of this analysis are shown in Fig. 1 and Fig. 2 for two representative patients, one with normal filling and one suffering from LVDD (see also Movie S1 and Movie S2 in the Supporting Information for animations of this behavior). In each figure, the time history of the pressure difference between the top of the LA and the apex of the LV (ΔP_total) is shown in (A), as are the pressure differences across each chamber (ΔP_atrium, ΔP_ventricle). The ΔP_total is plotted for the period when the MV is open, while the ΔP_atrium and ΔP_ventricle are plotted throughout the cycle. Blood velocity parallel to the axis of the LV at a level just beyond MV leaflet tips is also given (V_mitral). Several snapshots (B–G) of the pcMRI velocity vector fields and vortex contours are shown to illustrate events of interest in the blood flow.

In healthy hearts we observed that the residual myocardial contraction at the base of the LV and the untwisting motion of the apex induce a downward blood current prior to opening of the mitral valve [41, 20] (Fig. 1B). As the myocardium relaxed, opening of the mitral valve and lengthening of the LV quickly followed, coincident with recoil of the mitral annulus away from the nearly stationary apex (Fig. 1C) and the formation of a large pressure difference along the left heart (ΔP_total = 4.93 mmHg). These motions initiated a strong inflow jet from the LA into the LV and a strong vortex pair (Γ_peak=268 m²/s) behind the mitral valve leaflets appeared (Fig. 1D). This vortex pair is the two-dimensional projection of the ring vortex forming at the mitral valve leaflets and is asymmetric, with a larger core near the anterior side adjacent to the aortic valve. The inflow jet penetrated into the LV without spreading until it passed the end of the vortex ring. As the early filling ended, the development of an adverse pressure gradient beyond the mitral valve caused the deceleration of the filling jet (Fig. 1D), but the vortex ring persisted near the mitral valve tips throughout diastasis (Fig. 1E). The atrial contraction (Fig. 1F) gave rise to a similar but smaller jet and vortex ring (Fig. 1F and G) with correspondingly smaller driving pressure gradients (Γ_peak=89 m²/s, ΔP_total = 1.49 mmHg), but the expansion of the ventricle appeared to be primarily across the short axis, as opposed to the long axis lengthening of early filling. The beginning of the ventricular contraction forced the mitral valve closed and brought the filling process to an end.

In contrast, patients with diastolic dysfunction showed a weaker initial apical flow prior to mitral valve opening (Fig. 2B). After the opening of the mitral valve (Fig. 2C), the early filling inflow jet was weaker with lower peak velocity and atrioventricular pressure gradient (for this patient, ΔP_total = 0.95 mmHg), and the associated ring vortex at the mitral valve tips was reduced in size and strength and was located closer to the base of the ventricle (Γ_peak=78 m²/s). Additionally, the mitral annulus exhibited less motion away from the apex and the overall expansion of the LV was more lateral than longitudinal, as has been previously reported [19, 39]. The inflow jet also began to diverge earlier than in the typical healthy filling pattern (Fig. 2D). As before, the tip vortices persisted through diastasis and lasted until the atrial contraction (Fig. 2E). Also, slow inflow continued throughout diastasis, suggesting that elevated atrial and pulmonary pressures are assisting in filling. Unlike in healthy filling, the atrial contraction was strong, and gave rise to a filling jet and atrioventricular pressure differences as strong or stronger than the relaxation-driven early filling (here, ΔP_total = 2.88 mmHg, Γ_peak=146 m²/s) but still less vigorous than typical healthy early filling.

In the case of the patient with severe dysfunction and dilated cardiomyopathy, the filling process is noticeably disrupted (Movie S3). Instead of distinct early and late filling periods, the two processes are fused. With the opening of the mitral valve, a vortex ring forms around the jet and propagates toward the center of the LV. Although the lateral vortex appears to diffuse into the wall, the vortex formed on the anterior side of the mitral valve remains strong and is continually fed by the inflow jet. This behavior, paired with a shift in the jet direction toward the posterio-lateral wall of the LV, creates a swirling motion during diastole that allows the filling wave to proceed toward the aortic valve, much like Kilner’s description of LV flow at elevated heart rates [25]. This swirling motion in this patient becomes attenuated by the end of systole, but never completely ceases. In contrast, like the patients in Fig. 1 and Fig. 2, Kilner’s scans at normal heart rates show the blood coming nearly to rest between each filling and ejection event.

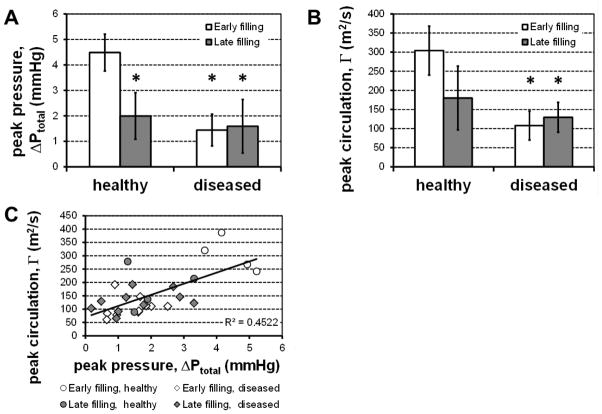
Taken together, the velocity and pressure fields reveal a drastic change in the dynamics of diastole governed by LV relaxation-driven early filling in healthy patients, to an atrially-driven late filling in those with diastolic dysfunction. This is exemplified by the dramatic drop of the early filling peak intraventricular pressure difference (ΔP_total = 4.49±0.72 mmHg vs. 1.44±0.62 mmHg, p<0.005) and vortex circulation (Γ_peak = 304±64 m²/s vs. 108±38 m²/s, p<0.005) (Fig. 3A and B). In fact, in diseased patients the developed pressure and vorticity during early filling assume magnitudes that are on the same order as the respective values measured during the atrially-driven late filling in both healthy and diseased patients. This is shown clearly by plotting pressure and vorticity versus each other for each patient (Fig. 3C). The values corresponding to healthy early filling occupy the upper right corner of the plot clearly separated from both healthy and diseased late filling and diseased early filling, which are all in the lower left with no clear distinction between them. These results demonstrate that in the presence of diastolic dysfunction the early filling is driven by pressure-driven atrio-genic processes instead of the LV relaxation.

Fig. 3. Comparison of pressure differences and vortex strength.

Whiskers indicate ±1 standard deviation. (A) Peak atrioventricular pressure difference was on average much higher during the relaxation-driven early filling process than either healthy late filling (N=4), or either period in diseased hearts (N=10, *: p<0.05 vs. healthy early filling). (B) A similar trend was observed for the magnitude of the peak circulation measured in the proximal mitral tip ring vortex (*: p<0.05 vs. healthy early filling). (C) These differences appear because not only are the developed pressure difference and the vortex strength strongly coupled (R²=0.45, p<0.001), healthy early filling appears to fall in a separate regime from late and unhealthy filling processes.

Finally, to better elucidate the dominant structures present around the inflow jet and the ring vortex at the mitral valve tips, the measured velocity fields were used to calculate the forward finite-time Lyapunov exponents (FTLE) [18] in the left heart through diastole for patients with both healthy and abnormal filling (Fig. 4, Movie S4 through Movie S6). Connected regions with high FTLE values are often referred as Lagrangian Coherent Structures (LCS) and indicate barriers to transport. Using the FTLE fields, we observed that such barriers existed in each flow field for both early and late filling, and independent of the disease state of the individual. These structures aligned closely with the inner borders of the vortices previously identified, and could be considered to represent virtual channels that extended the effective length of the mitral annulus to well beyond the ends of the tips of the leaflets. In general, like the vortices, these structures were larger and penetrated farther into the ventricle for early filling in healthy individuals than for late filling or flow in the diseased patients.

Discussion

Ventricular motion and the enhancement of vortex ring growth

Phase contrast MRI scans of subjects with and without diastolic dysfunction reveal a dramatic difference between the normal LV diastole with suction-driven early rapid filling and normal LA pressures, versus diastole with impaired LV suction and increased LA pressure - or as seen in the setting of significant diastolic function impairment, diastole where LA contraction-driven filling volume exceeds suction initiated filling volume.. The representative scans of LV filling and heart motion presented in Fig. 1 and Fig. 2 help explain these changes. In healthy patients (Fig. 1), diastole begins prior to mitral valve opening with the completion of a residual contraction in the subendocardial layers at the base of the heart and a lengthening of those same layers at the apex [42, 5], creating a preferential apical expansion of the LV cavity[39] and an initial apically-directed current [41, 20, 35]. This motion strengthens the filling jet and prevents the heart from having to overcome the inertia of static blood, or worse, residual upward blood motion toward the aortic outflow tract. Subsequently, the relaxation of the myocardium drives an expansion of the left ventricle that is primarily longitudinal [19, 47], with the mitral annulus moving vigorously away from the apex, creating a pressure gradient that rapidly refills the LV. This motion accelerates the blood near the LV walls upward, counter-cyclically to the energetic inflow jet forming near the middle of the chamber. The two opposing currents further feed the growth of the mitral vortices to a greater size and strength compared to what would be expected for a static chamber. This is consistent with prior investigations of the effect of counter flow on the development of a vortex ring around an impulsively started jet; bulk motion of the fluid surrounding the jet orifice in a direction counter to the jet delays vortex pinch-off, enhancing the vortex strength and the amount of fluid entrained into the vortex ring [11]. In contrast, expansion of the LV during late filling is primarily due to the contraction of the left atrium driving fluid into the LV [14]; by this point most of the relaxation of the myocardium is complete [4]. This creates a more balloon-like, radial expansion, which does not enhance the formation of a mitral vortex ring, and results in weaker vortices during late filling.

Diastolic dysfunction, however, disrupts the timing of left ventricular relaxation and filling, causing major alterations in flow patterns [41] and wall motions [32]. Asynchrony in the LV wall motion between the end of the ejection phase and the opening of the mitral valve has been strongly associated with a decrease or absence of this apically-directed flow, and reductions in the propagation velocity of the diastolic inflow [35]. One of the earliest changes to occur is an increased delay between the end of the systolic contraction and the relaxation of the left ventricle [14], and the progression of diastolic dysfunction is also associated with a decrease in the velocity of the mitral annulus during early filling (typically termed E′) [19]. Both effects were observed in the patients in our study. Furthermore, it has been shown that in patients with LV hypertrophy (one condition commonly associated with LVDD) that even though the volume change is preserved during early diastole, there is a shift in how that volume is accommodated, leading to smaller longitudinal volume changes, and increased radial volumes[39]. Additionally, LVDD is linked to increases in left atrial and pulmonary pressures [1, 34], which however were not directly measured here. These changes deprive the LV of the ability to enhance the formation of the ring vortices at the mitral valve tips. Instead, LV motion becomes more radial even during early filling [19], leading to reduced vortex strengths. Additionally, increased LV wall stiffness and lower compliance [33] reduce the amount of low pressure filling that occurs during the first part of diastole, further reducing the amount of energy in the filling jet available to feed the growth of the mitral inflow vortices.

The active role of vortices at mitral valve tips

Previous works suggested that vortex rings are associated with the efficiency of the filling process[15, 36, 50, 37] but did not explain their role. Here, we found that these vortices actively sustain the filling wave and enhance the efficient filling of the ventricle. It is clear from the calculated FTLE maps that the inner borders of the mitral valve tip vortices constitute a LCS, and act as a virtual channel for the incoming blood flow, guiding the jet toward the apex. As a result, in both healthy patients and those with diastolic dysfunction the expansion of the jet is postponed, hence delaying the development of an adverse pressure gradient until past the vortex ring (see Fig. 1 and Fig. 2). The difference is that with reduced participation by the mitral vortices, the early filling wave in diseased patients encounters this gradient sooner, slowing or stopping the flow of blood into the ventricle, and larger LA contractions or elevated LA pressures are required to achieve the same filling. This early termination of the filling wave has also been observed in restricted filling patients using both echocardiography and pcMRI scans [26, 46].

This new mechanism is similar to, but different than that previously proposed to explain flow patterns seen in computer simulations of RV flow built from flow and tissue measurements of canine hearts [36]. In that model, vortices did not form by vortex sheet roll-up during the initial accelerating inflow portion of the early filling wave, but instead were produced primarily by adverse pressure gradient-driven flow reversal along the endocardium after the peak flow. In contrast, for the present results the vortex ring clearly begins to form prior to the deceleration of the early filling wave (see Fig. 1 and Fig. 2 as well as Movie S1 and Movie S2). However, in both models of ventricular filling, once the vortex rings were established they acted to constrain and stabilize the jet, limiting convective deceleration and allowing the filling jet to be preserved longer into diastole. The discrepancy can likely be attributed in large part to the significant differences in chamber geometry and motion between the right and left ventricles. It is possible though that the early filling wave in the LV may become more similar to that observed by Pasipoularides et al.[36] as diastolic dysfunction progresses and the original vigorous longitudinal motion of the mitral annulus is lost [19, 39, 32, 47].

This proposed active role for the vortices helps to explain why clinical metrics that include only measures of inflow velocity (such as the early and late filling velocities, E and A, or their ratio) yield poorer predictive power than metrics that also include tissue motion (such as the ratio of E to mitral annulus velocity E′, E/E′, or measures derived from speckle tracking echocardiography) [40, 31]. In healthy early filling patterns, organized directed motion of the ventricle walls and mitral annulus feed and amplify the creation of vortices that ease the flow of the jet into the ventricle. Without such motion, even for an equivalent filling velocity, the filling is less efficient and the pressure difference required to drive the flow must be made up by increased atrial pressure. Thus, as has been observed clinically[31], using the inflow velocity alone is insufficient for accurate diagnosis.

One additional interesting observation is that in the majority of patients we did not observe significant propagation of the vortex pair away from the mitral valve leaflets until the inflow from the LA ended. This is consistent with clinical observations [26] and experimental and computer simulations that model realistic LV proportions and motion [12] but contradicts simulations featuring stationary mitral valves and symmetric ventricles [53, 52]. The exception to this was the patient with dilated cardiomyopathy (see Movie S3 in the Electronic Supplementary Material). Most of the blood entered the heart as a result of atrial contraction, and the vortex pair formed behaved much more like a classic vortex ring around an impulsively started jet. Furthermore, due to the vortex motion, the FTLE plots show the jet is less constrained and is redirected clockwise around the LV (Fig. 4, and more clearly in Movie S6). Pressure distributions were also quite different, and the vortex cores showed clear local pressure minimums, a feature that was not usually seen here in hearts with more normal ventricular widths. In patients with typical geometry, pressure distributions were more similar to flow through a channel, with pressure drops only occurring lengthwise along the ventricle, and not across its short axis, despite the presence of the vortex ring (Fig. 1, Fig. 2). Although pressure minima are common in vortex cores, they are not necessary, especially if the centrifugal forces are largely balanced by axial strain or viscous forces [21]. Thus, in these cases any small local pressure drop was not resolvable by the pressure estimation algorithm in contrast to the large longitudinal pressure gradients established by the shear layers of the filling jet.

This vortex ring propagation is typically associated with vortex ring pinch off from the filling jet [15, 24, 23], and it has been proposed that the formation time of these vortices are synchronized with the total length of diastole [15], but in other recent work by our group evidence points toward vortex formation being unaffected by disease stage with pinch off occurring at a consistent time within, rather than at the end of, diastole [45]. However, in this study due to the limited temporal and spatial resolution of the pcMRI scans a determination of this pinch off was not attempted. Regardless of the true answer, the formation of a virtual channel in LV filling should be independent of when and whether the vortex ring pinches off from the jet, as the presence of the vortex should act to assist in limiting the spreading of the jet in either case.

Limitations

Several limitations may have affected the results of this study. First, due to the cost and time involved in scanning with pcMRI, only a small number of patients were included in the study (N=14). Additionally, since only patients that were already referred for clinically indicated MRI studies were included in the study, it was not possible to perform full 3D scans due to the significant additional time such scans take. For the same reason, only partial echocardiographic data was available for many of the patients since there were no clinically-indicated ultrasound scans performed within a reasonable interval of the pcMRI scan (see Table S1).

This lack of volumetric data could potentially affect the conclusions of this study, especially the calculation of the FTLE fields. However, several factors mitigate the impact of this limitation. Firstly, we are mostly concerned with the behavior of the filling jet and the surrounding vortex ring during diastole. Since the scanning plane was positioned to align with the inflow jet and bisect both the mitral valve and the ventricle, the flow can be assumed to mostly planar for the portion of the heartbeat we are concerned about. Away from the valve and after filling is complete the flow becomes more three-dimensional, but this should have little effect on the peak intraventricular pressure differences calculated along the path of the jet presented here. Additionally, in [7] it was shown that using the present methodology, pressure errors remain under 10% for vortical flow off-axis tilts of up to 30°, and under 20% for 45°. Above that angle, performance rapidly degrades. Furthermore, it has been shown using simulations that for similar pressure calculations made on echocardiographic data that calculated intraventricular pressure differences in the ventricle are also relatively insensitive to misalignment of the scanning plane – both magnitude and time history were closely matched for scanlines placed anywhere within the central 60% of the ventricle and misaligned less than 20% [16]. Secondly, much of the three dimensionality is bound up in the smaller structures, especially near the mitral valve. This means it will have limited effect on the large-scale structures that we are discussing here. This is true also for the FTLE fields, as the shape of the LCS boundaries is governed primarily by the large-scale structures, and even if we fail to resolve out of plane motion, this will only result in missing possible flow boundaries, but the in-plane features we detect will be nearly unaffected.

Conclusions

We found that diastolic mechanics are governed by the following principles. First, in normal hearts, left ventricular shape change during isovolumic relaxation and the translation of the mitral valve annulus away from the apex combine to aid vortex ring formation, making early diastolic filling different than pressure-driven filling during normal atrial contraction or during either period in the presence of diastolic dysfunction. In LVDD there is a shift from a left ventricular, suction-driven early filling to a process driven by elevated left atrial pressures – a change which accounts for the similarity in the vortex dynamics between the two atrially-driven processes (late filling due to atrial contraction, and abnormal early filling boosted by elevated atrial pressures). Secondly, vortex ring formation behind the mitral valve leaflets actively constrains and channels the filling and maintains the momentum of the inflow jet. This is in contrast to a simple vortex ring model where the ring builds as a side effect of the jet only, until the angular momentum is maximized and the ring pinches off. This pattern is seen only in severely dilated hearts. Finally, impaired relaxation and reduced compliance in early and late filling lead to passive and reduced vortex ring formation, resulting in increasing convective deceleration and forcing the heart to work against adverse pressure gradients earlier and closer to the mitral valve. The gross morphological alterations that occur in dilated cardiomyopathy further exacerbate these problems. The vortex-induced flow channeling we observed helps to explain why the changes in myocardial motion with diastolic dysfunction lead to impaired heart function and eventual heart failure. This channeling effect seems to be an important component of the heart’s strategy for maximizing rapid mass transport from the atrium to the LV apex during the filling process, and its loss in diastolic dysfunction may prove to be a key player in the loss of efficiency as the dysfunction progresses. As the primary means for diagnosing this condition rely heavily on measurements of heart and blood motions, better understanding of these changes in cardiovascular mechanics should lead to more accurate diagnosis and treatment options for this disease.

Abbreviations

DCM

dilated cardiomyopathy

FTLE

finite time Lyapunov exponents

LA

left atrium

LCS

Lagrangian coherent structures

LV

left ventricle

LVDD

left ventricular diastolic dysfunction

MV

mitral valve

MRI

magnetic resonance imaging

pcMRI

phase contrast MRI

POD

proper orthogonal decomposition

RV

right ventricle

SNR

signal to noise ratio