Perfect chemomechanical coupling of F_oF₁-ATP synthase

Significance

Peter D. Mitchell, a Nobel awardee in 1978, proposed that F_oF₁-ATP synthase converts energy between electrochemical potential of H⁺ across biological membrane ($\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{{\text{H}}^{+}}$), which is established by respiratory chain complexes, and chemical potential of adenine nucleotide [ΔG_(ATP)]. However, the efficiency of the energy conversion has been a matter of debate for over 50 years. In this study, with a highly reproducible analytical system using F_oF₁-ATP synthase from thermophilic Bacillus, apparently perfect energy conversion was observed. Mitchell’s prediction thus has quantitative evidence.

Abstract

F_oF₁-ATP synthase (F_oF₁) couples H⁺ flow in F_o domain and ATP synthesis/hydrolysis in F₁ domain through rotation of the central rotor shaft, and the H⁺/ATP ratio is crucial to understand the coupling mechanism and energy yield in cells. Although H⁺/ATP ratio of the perfectly coupling enzyme can be predicted from the copy number of catalytic β subunits and that of H⁺ binding c subunits as c/β, the actual H⁺/ATP ratio can vary depending on coupling efficiency. Here, we report actual H⁺/ATP ratio of thermophilic Bacillus F_oF₁, whose c/β is 10/3. Proteoliposomes reconstituted with the F_oF₁ were energized with ΔpH and Δψ by the acid−base transition and by valinomycin-mediated diffusion potential of K⁺ under various [ATP]/([ADP]⋅[Pi]) conditions, and the initial rate of ATP synthesis/hydrolysis was measured. Analyses of thermodynamically equilibrated states, where net ATP synthesis/hydrolysis is zero, show linear correlation between the chemical potential of ATP synthesis/hydrolysis and the proton motive force, giving the slope of the linear function, that is, H⁺/ATP ratio, 3.3 ± 0.1. This value agrees well with the c/β ratio. Thus, chemomechanical coupling between F_o and F₁ is perfect.

Most of cellular ATP is provided by F_oF₁-ATP synthase (F_oF₁) that is located in bacterial membranes, inner membranes of mitochondria, and thylakoid membrane of chloroplast. It synthesizes ATP from ADP and inorganic phosphate (Pi) by the energy of H⁺ flow driven by proton motive force (pmf) across membranes (1–4). The enzyme is composed of two rotary motors, membrane-peripheral F₁ and membrane-embedded F_o. The simplest version of F_oF₁ is found in bacteria where subunit composition of F₁ is α₃β₃γδε and that of F_o is ab₂c_x (x is variable among species). In F₁ motor, γε rotates against a stator part, α₃β₃δ-ring by the energy of ATP hydrolysis (5). It also catalyzes reverse reaction, ATP synthesis, when the rotor is forced to rotate in the opposite direction (6, 7). F_o motor is driven by H⁺ flow, where a c ring formed by multimeric c subunits rotates as a rotor relative to the stator, ab₂. Because stators and rotors of the two motors are respectively connected in the whole F_oF₁ architecture, F_oF₁ achieves energy conversion between pmf and chemical potential of ATP hydrolysis/synthesis via rotation, the direction of which is determined by the balance of the two energies.

The number of protons moving across membranes coupled with a single ATP synthesis/hydrolysis, defined as H⁺/ATP ratio, is crucial to understand not only the coupling mechanism of F_oF₁ but also the energy balance of cells. During one revolution of the motor, each of three catalytic β subunits in F₁ synthesizes/hydrolyzes one ATP molecule, and each of the c subunits in c ring of F_o transports one proton. Therefore, if the coupling is perfect, the H⁺/ATP ratio is determined by the stoichiometric ratio of c subunits per β-subunits in F_oF₁, c/β. The number of c subunits in the c ring is dependent on the species: 14 of spinach chloroplast (8, 9), 8 of bovine (10), and 10 of yeast mitochondria (11), thermophilic Bacillus PS3 (12), and Escherichia coli (13). The approximate c/β value is 4.7 for chloroplast, 2.7 for bovine, and 3.3 for yeast, E. coli, and Bacillus PS3. However, reported values of H⁺/ATP ratios are 4.0 ± 0.3 of chloroplast (14), 2.9 ± 0.2 of yeast (15), and 4.0 ± 0.3 of E. coli (16). The ratios obtained experimentally were similar to but different from their theoretical values, all of which were outside error limit of the experimental values, although the ratios were roughly correlated to the multimeric numbers of c rings. The reason for the disagreement may be intrinsic, such as slippage of the motor, activation of the inactive F_oF₁, and leak of protons, or may be related to insufficient accuracy of measurements. Recently, we have developed a reconstituted proteoliposome (PL) system for thermophile F_oF₁ (TF_oF₁) from Bacillus PS3 that shows a reasonable rate of ATP synthesis/hydrolysis at room temperature with high stability and reproducibility (17). The improved experimental procedures of the system include a simple preparation of stable PLs, and extensive removal of contaminating K⁺ from phospholipids and of ATP from ADP preparations. In this report, we used this system to determine the actual H⁺/ATP ratio. The results show the perfect agreement of H⁺/ATP ratio to c/β, indicating tight coupling efficiency of proton translocation in F_o and ATP synthesis/hydrolysis in F₁. In addition, kinetic and energetic equivalence of transmembrane difference of pH (ΔpH) and electric potential (Δψ) was supported with unprecedented certainty over a wide range of pmf values.

Results

ATP Synthesis/Hydrolysis by TF_oF₁ Under Varying pmf.

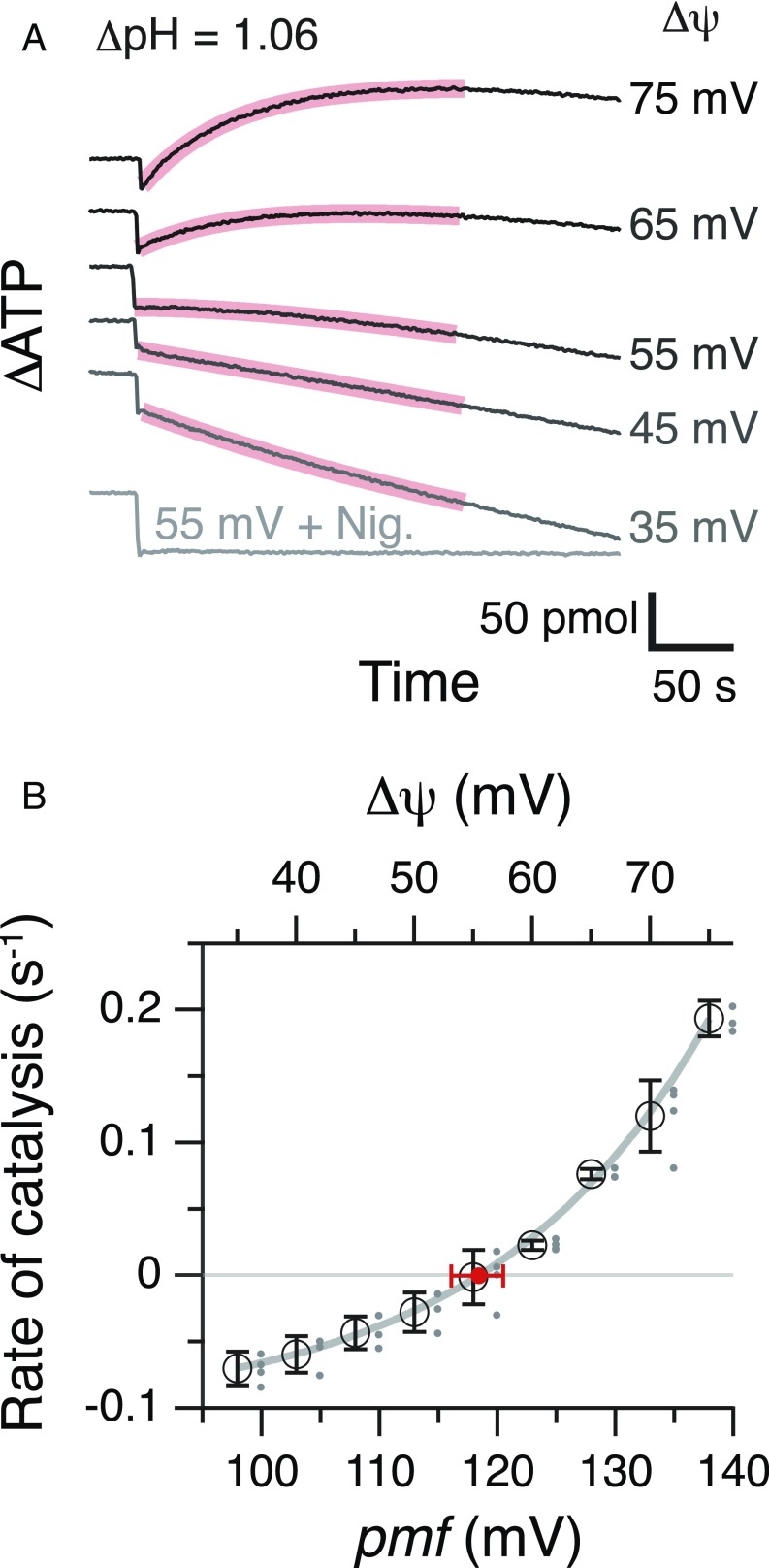
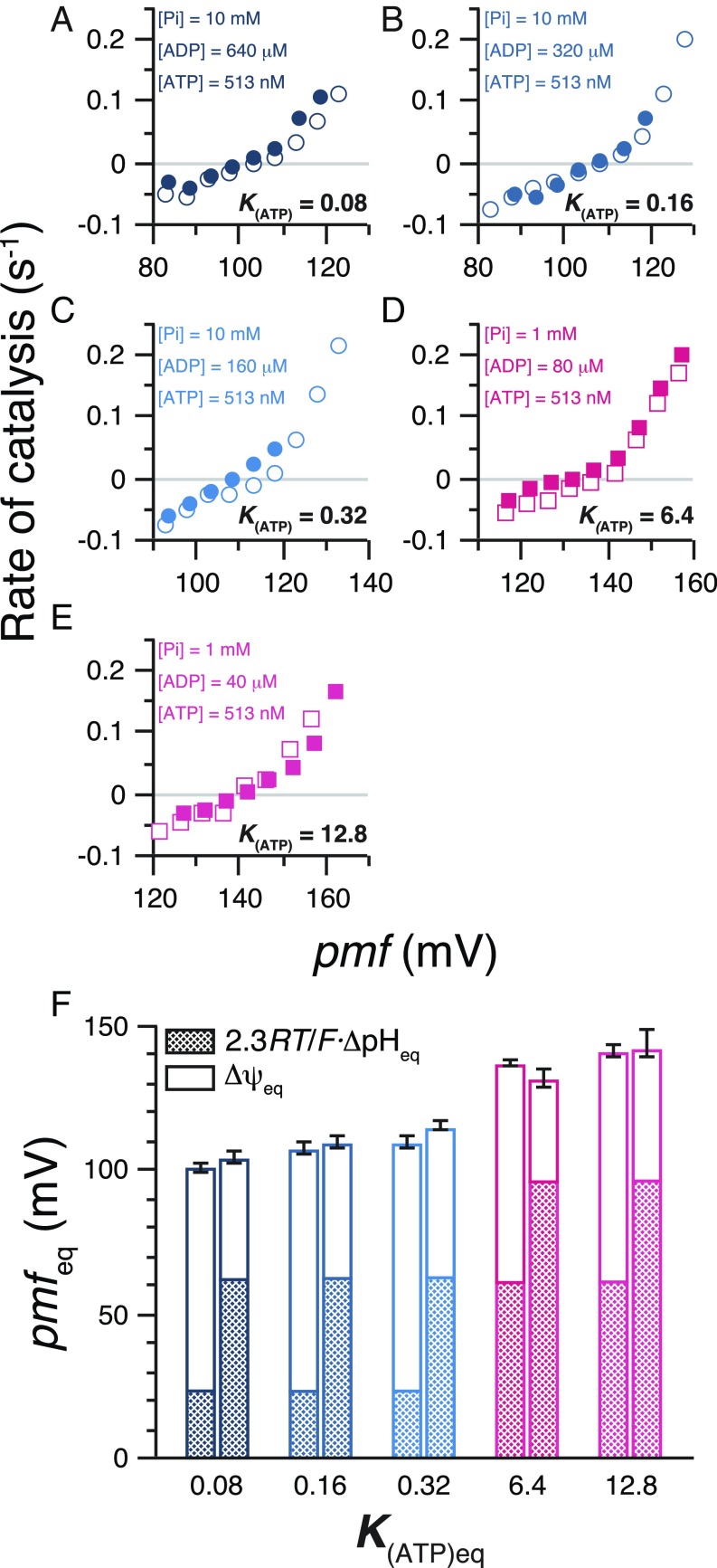
We imposed pmf of varying magnitude across membranes of PLs in the presence of 80 μM ADP, 10 mM Pi, and 512 nM ATP, and measured the initial rates of ATP synthesis/hydrolysis catalyzed by TF_oF₁. The rates were plotted against pmf, and the pmf_eq value where no net catalysis occurred (the rate was zero) was obtained from interpolation of the rate-vs.-pmf plots (Fig. 1). At the point of pmf_eq, K_(ATP) (= [ATP]/[ADP]·[P_i]) corresponds to an equilibrium constant, K_(ATP)eq. In the experiments, PLs were equilibrated in the acidic medium, in which [K⁺] was 5 mM and pH was 6.98. In the following data analysis, [K⁺]_in is [K⁺] in the acidic medium, and pH_in is the actually measured pH of the acidified PLs solution. The reaction was initiated by rapid injection of the acidified PLs into a base medium containing luciferin, luciferase, and valinomycin. [K⁺] (20 mM to 93 mM) and actually measured pH (8.04) of the resulting reaction mixture correspond to [K⁺]_out and pH_out, respectively. By mixing, one unit of ΔpH (pH_out − pH_in) was established across membranes of the PLs. Transmembrane voltage, Δψ, generated by valinomycin-mediated diffusion potential of K⁺, was calculated to be 35 mV to 75 mV by the Nernst equation based on the difference between [K⁺]_out and [K⁺]_in. Change in [ATP] was monitored with luminescence from luciferin/luciferase system (Fig. 1A), and the initial rate of the change was obtained. The negative rates values correspond to hydrolysis of ATP by TF_oF₁. In the upper two traces, [ATP] reaches a plateau and then starts decreasing, reflecting that TF_oF₁ switches the direction of net catalysis from ATP synthesis to hydrolysis as pmf decays below pmf_eq. The magnitude of pmf_eq was obtained as 118 ± 2 mV from interpolation of the rate-vs.-pmf plot (Fig. 1B).

Fig. 1.

ATP synthesis/hydrolysis at different pmf and determination of pmf_eq. (A) Typical time courses of ATP synthesis/hydrolysis at different pmf. Reaction was started by the injection of acidified PLs into the base medium containing luciferin/luciferase at t = 0. Vertical axis shows the amount of ATP in the reaction mixture quantified from the intensity of the luciferin luminescence. K_(ATP) is 0.64; [ADP] = 80 μM, [Pi] = 10 mM, and [ATP] = 512 nM. ΔpH was 1.06 (pH_out 8.04 − pH_in 6.98), and Δψ was varied ([K⁺]_in = 5 mM; [K⁺]_out = 20–93 mM), giving 95 mV to 135 mV of pmf. Nigericine (500 nM) was added at Δψ of 55 mV. (B) The pmf dependency of ATP synthesis/hydrolysis and determination of pmf_eq. The initial rate of synthesis/hydrolysis was calculated from the exponential fit 0–200-s portions (red curves in A) and plotted against their pmf values. Experiments were repeated at least three times (dots beside the circle) and averaged (black open circles). The data points were fitted with an exponential function, and pmf_eq (red circle) was obtained at the point of rate = 0. An error bar of pmf_eq (red horizontal bar) was made from the fitting curves for the largest or the smallest rates at each pmf.

ATP Synthesis/Hydrolysis by TF_oF₁ at Various [ATP], [ADP], and [Pi].

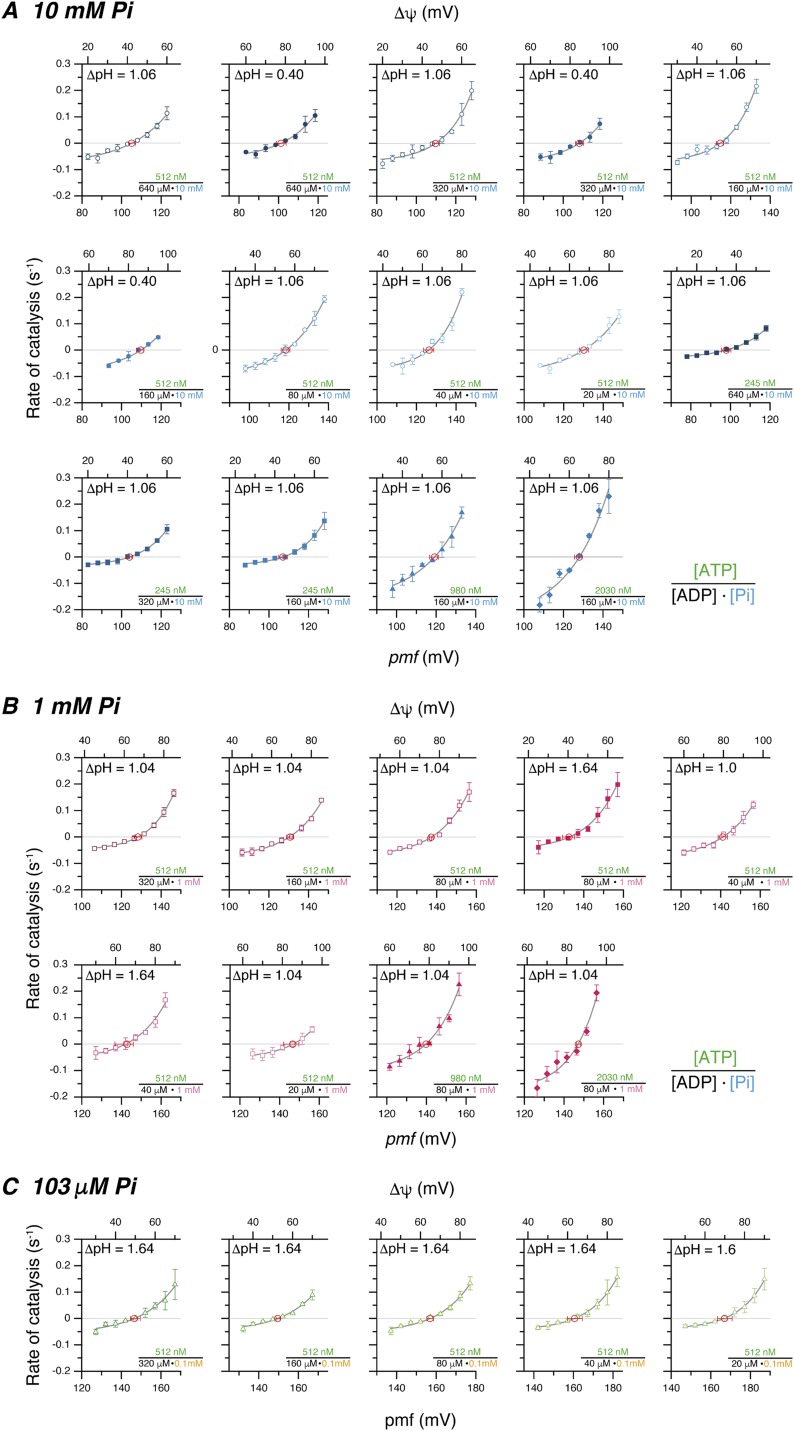
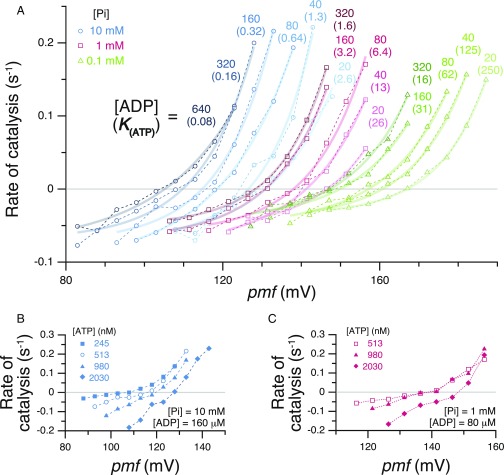
Many series of measurements similar to those of Fig. 1 were carried out at different combinations of substrate concentrations (Tables S1 and S2). [ADP], [Pi], and [ATP] were varied in the range 20 μM to 640 μM, 0.1 mM to 10 mM, and 245 nM to 2,030 nM, respectively, and pmf ranging from 83 mV to 187 mV was imposed with 0.40, 1, or 1.64 units of ΔpH and 25 mV to 95 mV of Δψ (see also Fig. S1). The rate-vs.-pmf plots at 512 nM ATP and different [ADP] and [Pi] are shown in Fig. 2A, and those at different [ATP] are shown in Fig. 2 B and C. The traces are positioned roughly in parallel by the order of magnitudes of K_(ATP). The pmf_eq and K_(ATP)eq are obtained from each curve and used for the following analyses.

Table S1.

Summary of composition of mixtures used for ATP hydrolysis/synthesis measurements

Components	Reconstitution	Acidification*			Reaction (outside liposomes)
pH	8.03	6.37	6.98	7.62	8.02–8.04
Tricine, mM	20		6		0.6
Mes, mM	—	28	0	0	0.6 or 0
Hepes, mM	—	0	28	28	280
MgCl2, mM	2.5		5		5
NaH2PO4, mM	—		10 or 1 or 0.1		10 or 1 or 0.1
KCl, mM	5		5		5
NaCl, mM	25		11.8		11.5
Sucrose,† mMa	500		500		50
KOH, mM	—		—		0–202
NaOH, mM	15		10–50		202–0
ADP,‡ mM	—		0.02–0.64		0.02–0.64
Valinomycin, nM	—		200		20
ATP,§ nM	—		245–2,030		245–2,030
Osmolarity, mosmol/L	610		610–650		600

^*The three columns show three kinds of acidification solutions.

^†Added for osmotic balance.

^‡The purified ADP contained 0.0005% of ATP.

^§ATP concentration is average value from actual measurements in each condition.

Table S2.

Summary of analytical condition for all measurements performed in this study

No.	ADP, μM	Pi,* mM	ATP,† nM	K(ATP) ([ATP]/[ADP][Pi])	pHin, unit	ΔpH,‡ unit	[K+]out, mM	Δψ,‡ mV	Imposed pmf,§ mV	pmfeq (mV)
1	640	10	513	0.0802	6.98	1.06	10.9–51.8	20–60	82.9–123	105
2	640	10	513	0.0802	7.62	0.40	51.8–202	60–95	83.5–119	101
3	320	10	513	0.160	6.98	1.06	10.9–62.9	20–65	82.9–128	110
4	320	10	513	0.160	7.62	0.40	62.9–202	65–95	88.5–119	108
5	160	10	513	0.321	6.98	1.06	16.1–76.5	30–70	92.9–133	115
6	160	10	513	0.321	7.62	0.40	76.5–202	70–95	93.5–119	110
7	80	10	513	0.642	6.98	1.06	19.6–92.9	35–75	97.9–138	118
8	40	10	513	1.28	6.98	1.06	28.9–113	45–80	108–143	126
9	20	10	513	2.57	6.98	1.06	28.9–137	45–85	108–148	130
10	640	10	245	0.0383	6.98	1.06	10.9–51.8	20–60	77.9–118	98
11	320	10	245	0.0766	6.98	1.06	10.9–51.8	20–60	82.9–123	104
12	160	10	245	0.153	6.98	1.06	13.2–62.9	25–65	87.9–128	107
13	160	10	980	0.613	6.98	1.06	19.6–76.5	35–70	97.9–133	119
14	160	10	2030	1.27	6.98	1.06	28.9–113	45–80	108–143	127
15	320	1	513	1.60	6.98	1.04	28.9–137	45–85	106–146	128
16	160	1	513	3.21	6.98	1.04	28.9–137	45–85	106–146	130
17	80	1	513	6.41	6.98	1.04	42.6–202	55–95	116–156	137
18	80	1	513	6.41	6.37	1.64	10.9–51.8	20–60	117–157	133
19	40	1	513	12.8	6.98	1.04	51.8–202	60–95	121–156	141
20	40	1	513	12.8	6.37	1.64	16.1–62.9	30–65	121–156	143
21	20	1	513	25.7	6.98	1.04	62.9–202	65–95	126–156	147
22	80	1	980	12.3	6.98	1.04	51.8–202	60–95	121–156	140
23	80	1	2030	25.3	6.98	1.04	62.9–202	65–95	126–156	147
24	320	0.103	513	15.6	6.37	1.64	16.1–76.5	30–70	127–167	147
25	160	0.103	513	31.1	6.37	1.64	19.6–76.5	35–70	132–167	150
26	80	0.103	513	62.3	6.37	1.64	23.8–113	40–80	137–177	157
27	40	0.103	513	125	6.37	1.64	28.9–137	45–85	142–182	161
28	20	0.103	513	249	6.37	1.64	35.1–167	50–90	147–187	167

^*Contamination of Pi in the reaction mixture (3 μM) was considered only for measurements under low Pi conditions (103 μM).

^†The ATP concentration was assessed by monitoring the luminescence intensity of reaction mixture just after adding acidified PLs.

^‡For all measurements, pH_out and [K⁺]_in were ∼8.02 to 8.04 (actual measurement) and 5 mM, respectively.

^§Imposed pmf was calculated using the equation pmf = 2.3RT/FΔpH + Δψ.

Fig. S1.

Raw data of pmf dependency of catalytic activity of F_oF₁ under various conditions; [Pi] of (A) 10 mM, (B) 1 mM, and (C) 103 μM. Open and closed circles in A are with ΔpH of 1.06 and 0.40, open and closed squares in B are of 1.04 and 1.64, and open triangles in C are 1.64. Analytical conditions for pH, [ATP], [ADP], and [Pi] are indicated in each panel. Δψ was varied as indicated. Center red open circles with error bars represent equilibrated states between ATP synthesis and ATP hydrolysis under the analytical condition, which were obtained from interpolating on fitted function. The pmf at the equilibrated state corresponds to pmf_eq. Error bars represented in all data are SD obtained from at least three measurements.

Fig. 2.

The pmf dependency of ATP synthesis/hydrolysis at different K_(ATP). (A) [ATP] = 512 nM. [Pi] = 10 mM (cyan circles), 1 mM (magenta squares), or 0.1 mM (green triangles). [ADP] and K_(ATP) are shown on the top of each trace (the latter is in parentheses). (B and C) [ATP] was changed. [ATP], [ADP], and [Pi] are shown in the figure. Error bars are omitted for clarity (plots with error bars are shown in Fig. S1).

Tight Correlation Between Chemical Potential and pmf, and Determination of H⁺/ATP Ratio.

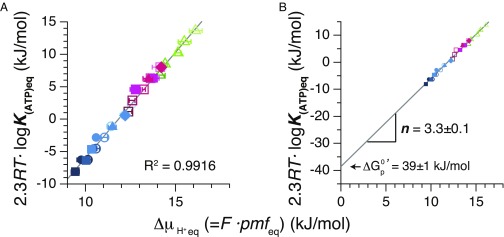
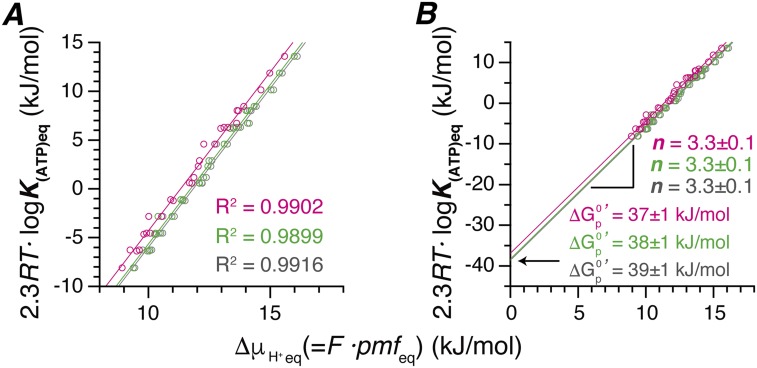
Both pmf_eq and K_(ATP)eq were converted to the energy units of measurement (kilojoules per mole) according to the Eq. 5 and were plotted (Fig. 3A). All of the points fitted well to a linear function. A numerical value of the slope of the linear function gives the thermodynamic H⁺/ATP ratios, n, and the y intercept of the function corresponds to the standard free energy of ATP synthesis, $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$. The n value thus determined is 3.3 ± 0.1 (Fig. 3B). This value appears to be a perfect match with the c/β ratio of TF_oF₁ that is 10/3, indicating that TF_oF₁ achieves perfect coupling between downhill/uphill H⁺ flow through F_o portion and ATP synthesis/hydrolysis in F₁ portion. The magnitude of $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$ is estimated, from y intercept, to be 39 ± 1 kJ·mol⁻¹. Similar values are reported from the experiments of chloroplasts (36 ± 3 kJ·mol⁻¹) (14), yeast (36 ± 3 kJ·mol⁻¹) (15), and E. coli (38 ± 3 kJ·mol⁻¹) (16). Contamination of damaged TF_oF₁ in PLs that hydrolyzes ATP without H⁺ pumping would be minimal. Even in the case where there is some contamination, the plots in Fig. 2 shift downward in parallel, making values of pmf_eq slightly larger, but the slope of the line in Fig. 3A remains almost the same whereas $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$ becomes slightly larger.

Fig. 3.

Chemical potential of ATP synthesis at different electrochemical potentials of H⁺ across membrane. (A) Chemical potential of ATP synthesis calculated from K_(ATP)eq and electrochemical potential of H⁺, F⋅pmf_eq, of all datasets are shown. The plots were fitted with a linear function by the least squares method. The error bars in A were made as in Fig. 1B. (B) The trace in A is extrapolated to its y intercept region. From the slope and y-intercept point, n and $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$ were determined as 3.3 ± 0.1 kJ/mol and 39 ± 1 kJ/mol.

Consideration of Possible Error in Δψ Estimation.

In the above analysis, magnitude of Δψ was estimated from the Nernst equation. Possible error of the estimate was carefully discussed for experiments of chloroplast F_oF₁ by Turina et al. (18). As follows, we adhered to similar considerations in our case and verified that the main conclusion, H⁺/ATP ratio = 3.3 ± 0.1, stands unaffected, although $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$ becomes slightly smaller after the considerations. (i) The generation of the Δψ requires the flow of K⁺ ions into PLs, and this flow induces the change in [K⁺]_in. For example, when the maximum Δψ (95 mV, [K⁺]_out = 202 mM, [K⁺]_in = 5 mM) is induced by K⁺ influx, the increase in [K⁺]_in is calculated to be 0.4 mM, taking into account membrane capacitance (∼1 μF/cm⁻²) and size of PLs (average diameter 170 nm). The change in [K⁺]_out is neglected because of the large volume of the solution outside of PLs. The increase in [K⁺]_in from 5.0 mM to 5.4 mM leads to generating weaker Δψ (93 mV) than in the case where K⁺ influx is not assumed. Similarly, we recalculated [K⁺]_in, Δψ, pmf_eq, and K_(ATP)eq of all measurements, and generated a new plot (Fig. S2). The slope of the simulated line remains the same (H⁺/ATP ratio = 3.3 ± 0.1) whereas $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$ becomes slightly smaller (38 ± 1 kJ/mol). (ii) The proton efflux coupled with ATP synthesis (and by simple H⁺ leak) leads to a charge compensating K⁺ influx, and this influx changes [K⁺]_in. The amount of K⁺ influx caused by proton efflux was calculated under the condition where maximum ΔpH is applied (pH_in = 6.37, pH_out = 8.02, H⁺/ATP-ratio = 3.3, time period = 5 s). It leads to 0.069 mM increase in [K⁺]_in at t = 5 s. The increase is over 70-fold smaller than the original [K⁺]_in, 5 mM, and is negligible. (iii) By definition, the Nernst equation uses activities instead of concentrations of ion. Taking into account all inorganic ion species in the reaction mixtures, we estimated activities of K⁺ according to the Debye−Huckel equation and calculated Δψ values with the Nernst equation using the activities of K⁺. Then, new sets of K_(ATP)eq and pmf_eq were obtained and plotted in Fig. S2. Compared with Fig. 3, the plots shifted slightly leftward in parallel, keeping the slope of the simulated line the same (H⁺/ATP ratio = 3.3 ± 0.1). $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$ became slightly smaller (37 ± 1 kJ/mol). Altogether, the error range of simple application of the Nernst equation to estimate Δψ is very small and does not change the value of the H⁺/ATP ratio.

Fig. S2.

Effects of several factors on H⁺/ATP-ratio and $\mathrm{\Delta }{\mathit{G}}_{\mathit{p}}^{0^{\mathit{\text{'}}}}$. (A) Chemical potential of ATP synthesis vs. electrochemical potential of H⁺ at the point of equilibrium (no net ATP synthesis/hydrolysis). All data of the present study are plotted. Values of Δψ were calculated by the Nernst equation (gray, the same as Fig. 3) using K⁺ concentrations, [K⁺]_in and [K⁺]_out, (magenta) using the activities of K⁺ instead of the concentrations, or (green) after taking into account the increase in [K⁺]_in caused by K⁺ influx to PLs upon addition of valinomycin. Plots were fitted with a linear function by the least squares method. (B) The traces in A are extrapolated to their y-intercept region. The resulting coefficient of determination (R²), n value (H⁺/ATP-ratio),y and $\mathrm{\Delta }{G}_p^{0^{\text{'}}}$ are shown beside of the traces.

Kinetic and Energetic Equivalence of ΔpH and Δψ.

During this study, kinetic and energetic equivalence of two terms that define the energy of H⁺ flow, ΔpH and Δψ, was confirmed with certainty. Their kinetic equivalence was previously reported (17), but this study demonstrates it under a wider range of conditions, including ATP hydrolysis. As shown (Fig. 4 A−E), a pair of experiments under the same conditions but a different combination of ΔpH and Δψ that gives the same pmf shows indistinguishable rate-vs.-pmf profiles. Energetic equivalence is obvious from Fig. 3A where energy for ATP synthesis/hydrolysis is defined solely by the value of pmf irrespective of the relative contribution of ΔpH and Δψ to pmf. When pairs with the same K_(ATP)eq and pmf_eq are selected from all data, the difference in the relative ratio of the ΔpH and Δψ in the pmf_eq has no significant effect on the K_(ATP)eq in each pair (Fig. 4F). This confirms the previous study of chloroplast F_oF₁ (18) that ΔpH and Δψ quantitatively contribute to pmf exactly as predicted by the established thermodynamic equation.

Fig. 4.

Equivalent contribution of ΔpH and Δψ to ATP synthesis/hydrolysis. (A−E) Kinetic equivalence of ΔpH and Δψ. A pair of rate-vs.-pmf plots under the same conditions except different combinations of ΔpH and Δψ that gives the same pmf. [ATP], [ADP], and [Pi] are indicated. ΔpH was set to 1.04 or 1.06 (open circles and open squares in A−E), 0.40 (filled circles in A−C), and 1.64 units (filled squares in D and E), and Δψ was changed by changing [K⁺]_out. Error bars are omitted for clarity. (F) Thermodynamic equivalence of ΔpH and Δψ terms. Pairs of datasets with the same K_(ATP)eq and pmf_eq were selected, and contributions of Δψ and ΔpH in each dataset (bar) are shown with opened and meshed areas, respectively. Colors of the bars are same as those in A−E. Detailed conditions of the measurements are summarized in Tables S1 and S2.

Discussion

H⁺/ATP ratio is a key parameter of energy production of the cell and has been extensively investigated by using F_oF₁s of E. coli, yeast, and chloroplasts (14–16, 18). The studies have established valuable technique and theory, which enable us to make estimates of H⁺/ATP ratio. The reported values of H⁺/ATP ratios, however, did not fit the ratio of copy number of c subunit/β-subunit. In this report, we adopted and further optimized the procedures. Stable TF_oF₁ enabled us to develop a simple, unique method for PL preparation (17, 19), which does not use preformed liposomes as other studies did (14–16). PLs thus prepared are highly active and stable, allowing many measurements using the same PL preparation for several tens of hours, and give reproducible results (17). Measurements were repeated, and error bars of each result, as well as error range (±0.1) of the H⁺/ATP ratio, are much smaller than those in the previous reports. Elimination of ATP contamination from commercial ADP down to 0.0005% also contributed significantly to setting accurate K_(ATP) value, especially at high [ADP]. By virtue of these procedures that take advantage of the stable nature of TF_oF₁, the determined value of H⁺/ATP ratio (3.3 ± 0.1) is now in close agreement with the c/β ratio (3.33...). A long-anticipated, but unproved, conception that F_oF₁ achieves a perfect coupling between transmembrane H⁺ translocation and ATP synthesis/hydrolysis has direct experimental evidence now. A brief comment should be added concerning the reason why the values of H⁺/ATP ratio of F_oF₁s of E. coli and chloroplasts do not match the c/β ratio. It was reported that chloroplast F_oF₁ needs activation by ΔpH and Δψ (18) and E. coli F_oF₁ needs activation by Δψ (20). The maximum rate of ATP synthesis by E. coli F_oF₁ is limited by the magnitude of Δψ. It is possible that their measurements were accurate but that these regulatory activation processes could cause deviation of the observed H⁺/ATP ratio from the c/β values.

In a thermodynamic view, the perfect coupling means perfect energy conversions between chemiosmotic (H⁺ translocation), mechanical (rotary motion), and chemical energy (ATP synthesis/hydrolysis). A near-perfect energy conversion from ATP hydrolysis to rotary motion of γ-subunit in F₁ was recently demonstrated in a thermodynamically defined manner (21), and this study predicts that other conversions should also be highly efficient. In a mechanistic view, the perfect coupling means that there is no slippage within and between F_o motor and F₁ motor. Atomic structures of F₁ are convincing that rotary motion of the γ-subunit could not occur without conformation change of the catalytic subunits. Structural basis for rotation of F_o motor without slippage has been suggested recently by atomic structures of whole F_oF₁ revealed by cryoelectron microscopy (22). The connection of the two motors should also be strong enough to endure the twisting force of torque. Crystal structures of F₁·c-ring complexes indicate that the connection appears to be held by a small number of interactions between the bottom portion of F₁’s rotor and polar loops in the c ring (11). Interestingly, this connection must be versatile, because the chimera TF_oF₁ with replaced F_o from Propionegenium modestum (23) that has 11 c subunits shows good coupled activity.

Materials and Methods

Chemicals.

ATP, ADP, valinomycin, and Pi were purchased from Sigma (A2383, A2754, and V0627) and Wako Pure Chemical (198-14505). As the commercial ADP contained ∼0.05% ATP contamination (molar ratio), the contaminated ATP was eliminated by anion exchange column chromatography (MonoQ 5/50 GL; GE Healthcare) as follows: After loading 4 mL of 20 mM ADP dissolved in 10 mM Tricine/NaOH (pH 8.03), the column was washed with the buffer, and ADP was eluted with the buffer supplemented with 150 mM NaCl. Only the initial 1.5 mL of the ADP peak was collected. ATP contamination in the purified ADP solution decreased 100-fold (0.0005% ATP relative to ADP). Contamination of Pi in the reaction mixture used for measurement of the catalytic activity was quantified to be 3 μM by EnzCheck phosphate assay kit (Thermo Fischer).

Preparation of F_oF₁, Lipids, and PLs.

A mutated F_oF₁ of Bacillus PS3, F_oF₁-εΔc (17, 19, 24), was used throughout this study. The F_oF₁ has a histidine tag composed of 10 histidine residues at N terminus of β and lacks C-terminal domain of the ε subunit, of which the mutations have no significant effect on catalytic function (17, 24). The mutated F_oF₁ is named as just TF_oF₁ in this paper. TF_oF₁ was overexpressed in F_oF₁-deficient E. coli strain DK8 using plasmid pTR19-ASDS-εΔc. Preparation of membrane fraction and purification of TF_oF₁ were performed as described previously (17).

Lipid and PLs reconstituted with TF_oF₁ were prepared by the methods in ref. 17, with a modification: for preparation of PLs, dioleoyl l-α-phosphatidylethanolamine (Wako Pure Chemical Industries) was supplemented at a final concentration of 4 mg/mL to 36 mg/mL (5 mM) of the soybean lipid that was previously washed repeatedly to eliminate contamination of K⁺ ions (17). Contamination of uncoupled TF_oF₁ in PLs was minimal because ATP hydrolysis activity of PLs was inhibited nearly completely (92 to 98% inhibition) by a proton translocation inhibitor, dicyclohexylcarbodiimide.

Measurement of ATP Synthesis/Hydrolysis Activity and Data Analysis.

Measurement of ATP synthesis/hydrolysis activity was performed using the method of acid/base transition with valinomycin-induced Δψ, as described previously (17). Briefly, PLs were acidified as follows: 30 μL of the PLs (40 mg lipid per milliliter) was mixed with 70 μL of acidification buffer (40 mM buffer containing 0.147 mM to 14.7 mM NaH₂PO₄, 6 mM MgCl₂, 5 mM KCl, 4 mM NaCl, 0.5 M sucrose, 0.03 mM to 0.9 mM purified ADP, 0.04 μM to 3 μM ATP, and 0.3 μM fresh valinomycin), and pH was adjusted with NaOH. The mixture was incubated for 10 h to 20 h at 23 °C to 27 °C to acidify inside PLs. Base medium was prepared by mixing 25 μL of the luciferin/luciferase mixture (2× concentration of CLSII solution in ATP bioluminescence assay kit; Roche) supplemented with 5 mM luciferin (L9504; Sigma), 800 μL of base buffer (350 mM Hepes, 11.3, 1.13, or 0.113 mM NaH₂PO₄, 5.6 mM MgCl₂, 5.6 mM KCl, 11.25 mM NaCl, and 272 mM mixture of KOH + NaOH to keep total concentration of Na⁺ plus K⁺ in the solution), 18 μL of 1 mM to 32 mM ADP, and 57 μL of water. Details of the acidification buffer and base medium are summarized in Table S1. For the assay, base medium (900 μL) was incubated at 25 °C for 8 min for equilibrium. The catalytic reaction, ATP synthesis and hydrolysis, was initiated by injecting 100 μL of the acidified PLs suspension into the base medium (time t = 0 s). The final TF_oF₁ concentration was 8.5 nM. This acid−base transition should lead to transmembrane fluxes of all permeable ions, but, by the assist of valinomycin, K⁺ ions are selectively and efficiently transported into PLs several orders of magnitude faster than all other ions, and diffusion potential of K⁺ ion is established instantaneously. Change in the ATP concentration was monitored in real time by luminescence light from luciferin/luciferase using a luminometer (Luminescencer AB2200 with sample injection apparatus; ATTO). Upon injection, the intensity of luminescence showed a negative jump. Magnitude of the jump fluctuated from one measurement to another for unknown reasons, but the luminescence intensity per unit amount of ATP calibrated in each measurement was reproducible. Initial ATP concentration at t = 0 was obtained from the light intensity just after the negative jump. At t = 200 s, 10 μL of 10 μM ATP was added three times for calibrating luminescence light intensity to ATP concentration. Maximum ATP concentration measurable by this luciferin/luciferase method is ∼2 nmol/mL. The initial rate at 0 s was calculated by regression analysis of the time courses (0 s to 200 s) with sum of a single-exponential function and linear function (14). All experiments we performed contribute to the statistics (every point in the graphs shows the average over at least three measurements using three or more independent preparations of PLs, and the error bar indicates the SD). The pH_in and pH_out were determined by directly measuring pH, respectively, of the acidified PLs solution and of reaction mixture (base medium supplemented with acidified PLs) for every condition using the same glass electrode. ΔpH was obtained by subtracting pH_in from pH_out. Transmembrane electrical potential, Δψ, was calculated using the Nernst equation, Δψ = 2.3RT/Flog([K⁺]_out/[K⁺]_in) = 59.1·log([K⁺]_out/[K⁺]_in), where [K⁺]_in and [K⁺]_out were K⁺ concentrations in the acidification buffer containing PLs and in the reaction mixture after adding acidified PLs, respectively. As carefully examined in our previous report (figure S4 of ref. 17), when [K⁺]_in is above 1 mM, initial rates of TF_oF₁-catalyzed ATP synthesis are consistently simulated by a function of pmf, in which Δψ is estimated from the Nernst equation. However, they start to show some deviation from the function when [K⁺]_in is deceased below 1 mM. In the present study, [K⁺]_in was fixed to 5 mM in all experiments, and the Nernst equation should be valid for estimation of Δψ values.

Functions and Calculations.

Determination of K_(ATP)eq, pmf_eq, and n was performed as follows. In Peter Michel's chemiosmotic coupling theory (1), ATP synthesis/hydrolysis catalyzed by F_oF₁-ATP synthase should be coupled with translocation of n protons, in which n is the required number of protons in a single ATP catalysis reaction,

$$\text{ADP}+\text{Pi}+\hspace{0.17em}n{\text{H}}_{\text{in}}^{+}\rightleftharpoons \text{ATP}+{\text{H}}_2\text{O}+n{\text{H}}_{\text{out}}^{+}.$$ [1]

The Gibbs free energy of the coupled reactions, $\mathrm{\Delta }G\prime$, is expressed by

$$\begin{array}{l}\mathrm{\Delta }G\prime =\mathrm{\Delta }{G}_p^{\prime }-n\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{H^{+}}\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\mathrm{\Delta }{G}_p^{\prime }-n\left(2.3RT\mathrm{\Delta }\text{pH}+F\mathrm{\Delta }\psi \right)\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\mathrm{\Delta }{G}_p^{\prime }-nF\mathrm{\cdot }pmf,\hfill \end{array}$$ [2]

where $\mathrm{\Delta }{G}_{\text{p}}$ is the Gibbs free energy of ATP synthesis, and $\mathrm{\Delta }{\stackrel{\sim }{\mu }}_{H^{+}}$ is the transmembrane electrochemical potential difference of the proton, which can be converted to proton motive force (referred to as pmf in this study) in millivolts comprising transmembrane difference of pH, ΔpH = pH_out – pH_in, and transmembrane difference of electrical potential, Δψ = ψ_in – ψ_out, and R, T, and F are gas constant, absolute temperature, and Faraday constant, respectively. The Gibbs free energy of ATP synthesis, $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$, is given by

$$\mathrm{\Delta }{G}_p^{\prime }=\mathrm{\Delta }{G}_p^{0\prime }+2.3RT\mathrm{\cdot }\log \frac{\left[\text{ATP}\right]c^0}{\left[\text{ADP}\right]\left[\text{Pi}\right]}=\mathrm{\Delta }{G}_p^{0\prime }+2.3RT\mathrm{\cdot }\log K_{\left(\text{ATP}\right)},$$ [3]

where $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$ is the Gibbs free energy at the biochemical standard state, c⁰ is the standard concentration (equal to 1M), and K_(ATP) is a ratio, [ATP]/([ADP]·[P_i]. Therefore, Eq. 4 is obtained by the sum of Eqs. 2 and 3,

$$\mathrm{\Delta }G\prime =\mathrm{\Delta }{G}_{\text{p}}^{0\prime }+2.3RT\mathrm{\cdot }\log K_{\left(\text{ATP}\right)}-nF\mathrm{\cdot }pmf.$$ [4]

At the energetic equilibrium point of the coupled reactions ($\mathrm{\Delta }G\prime$= 0), Eq. 4 can be converted to

$$2.3RT\mathrm{\cdot }\log K_{\left(\text{ATP}\right)\text{eq}}=-\mathrm{\Delta }{G}_{\text{p}}^{0\prime }+nF\mathrm{\cdot }pm{f}_{\text{eq}},$$ [5]

in which pmf_eq is a variable and experimentally measurable value. Therefore, with data sets of K_(ATP)eq and its corresponding pmf_eq, $\mathrm{\Delta }{G}_{\text{p}}^{0\prime }$ and n can be determined by the linear regression analysis.