Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 May 5;8(10):2310–2315. doi: 10.1021/acs.jpclett.7b00848

A Blind Test of Computational Technique for Predicting the Likelihood of Peptide Sequences to Cyclize

Jonathan Booth †, Christina-Nicoleta Alexandru-Crivac ‡,§, Kirstie A Rickaby ‡, Ada F Nneoyiegbe ‡, Ugochukwu Umeobika ‡, Andrew R McEwan ‡,§, Laurent Trembleau ‡, Marcel Jaspars ‡,*, Wael E Houssen ‡,§,∥,*, Dmitrii V Shalashilin †,*
PMCID: PMC5441752  PMID: 28475844

Abstract

graphic file with name jz-2017-00848b_0005.jpg

An in silico computational technique for predicting peptide sequences that can be cyclized by cyanobactin macrocyclases, e.g., PatGmac, is reported. We demonstrate that the propensity for PatGmac-mediated cyclization correlates strongly with the free energy of the so-called pre-cyclization conformation (PCC), which is a fold where the cyclizing sequence C and N termini are in close proximity. This conclusion is driven by comparison of the predictions of boxed molecular dynamics (BXD) with experimental data, which have achieved an accuracy of 84%. A true blind test rather than training of the model is reported here as the in silico tool was developed before any experimental data was given, and no parameters of computations were adjusted to fit the data. The success of the blind test provides fundamental understanding of the molecular mechanism of cyclization by cyanobactin macrocyclases, suggesting that formation of PCC is the rate-determining step. PCC formation might also play a part in other processes of cyclic peptides production and on the practical side the suggested tool might become useful for finding cyclizable peptide sequences in general.

Being able to predict folded shapes and biochemical properties of proteins and other biological molecules simply from their amino-acid sequences is one of the central problems in computational biochemistry. With the development of efficient methods of atomistic simulations, substantial progress has been made in this direction. For example, fast protein folding has been accurately simulated by molecular dynamics (MD).1,2 In general, predicting the properties of biomolecules solely from their chemical structure remains a challenge.

In this paper we demonstrate that cyclizable peptide sequences can be reliably predicted computationally. The propensity for cyclization correlates with the probability of the sequence to adopt the so-called pre-cyclization conformation (PCC) in which its termini are close to each other. The probabilities of adopting PCC [P(PCC)] have been calculated with the help of boxed dynamics3−5 for 25 peptides previously studied experimentally. The calculations performed in the manner of a blind test, i.e., without prior knowledge of the experimental data, resulted in an 84% success rate.

Cyclic peptides are attractive scaffolds for the pharmaceutical industry as they are capable of interacting with larger binding sites than small molecules. They can target protein–protein interactions (PPis) involved in infections (e.g., gramicidin S) and diseases such as cancer (e.g., somatostatin) and autoimmune disorders (e.g., cyclosporine).6,7 Cyclic peptides are now considered as cheaper and more practical medium-sized pharmaceutical alternatives to biologics.8−10 Cyclic peptides have a number of advantages over their linear counterparts, which include reduced susceptibility to rapid metabolism, improved membrane permeability, and better binding affinity.11

Unfortunately, the production of cyclic peptides is often difficult and costly. Most processes rely on the cyclization of a linear peptide under high dilution conditions to prevent oligomerization side-reactions. The success of this method is largely dependent on the sequence and the length of the peptide, and its viability as a production method has not yet been proven. Epimerization of the activated residue during cyclization can present additional difficulty.7 An alternative approach is to carry out cyclization on polymeric support, which also helps minimize the production of cyclo-oligomers. This method is complicated as it requires attachment of the peptide to a solid support via an amino acid side chain and needs an orthogonal protecting group strategy.12 Another recent method of peptide cyclization, which has had some success, relies on incorporation of conformational elements, such as proline or pseudoprolines, that help the peptides adopt the appropriate folded conformations. Other strategies involve the use of cavities created by polymeric scaffolds, or assistance of the cyclization by metal-ions. Another important biochemical method makes use of a sortase, but this technique leads to the incorporation of a LPXTG sequence in the cyclic peptide product where X is variable.13

Previously, a new biosynthetic approach to making cyclic peptides in vitro was proposed.14 The new method uses a macrocyclase, PatGmac, to catalyze N- to C- cyclization, and in the current paper an in silico tool for finding peptide sequences cyclizable by PatGmac will be described.

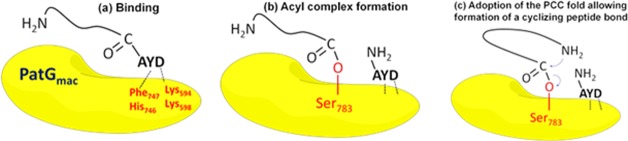
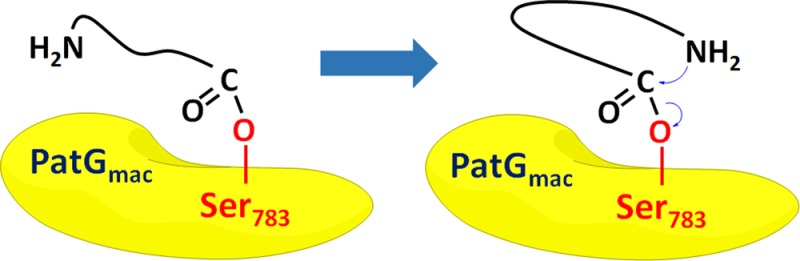
Mechanism of Cyclization, Experimental Data, and Computations. PatGmac is an enzyme involved in biosynthesis of the marine cyclic peptides, patellamides. It is a subtilisin-like protease, which recognizes a C-terminal three-residue recognition signal (AYD) attached to the core sequence, cleaves it off, and cyclizes the substrate. To favor cyclization over proteolysis, the substrate has to adopt a bent conformation in which its amino terminus is in close proximity to the enzyme–substrate acyl complex.15 In this paper, this conformation is called the pre-cyclized conformation (PCC) (Figure 1).

Figure 1.

Figure 1

Open in a new tab

A cartoon showing the steps of cyclization by PatGmac. (a) Binding of the substrate recognition signal AYD to the enzyme. (b) Formation of the acyl complex with the catalytic Ser783 and proteolytic cleavage of the AYD signal. (c) Adoption of PCC allows the substrate amino terminus to attack the acyl complex forming a new cyclizing peptide bond. The enzyme-bound AYD signal prevents water from attacking the acyl complex.

All cyclizable substrates contain a core sequence ending either by proline (Pro) or thiazoline (ThH) before the AYD enzyme recognition signal.16 Structural data and computations17 shows that the aspartate in the AYD signal binds to the basic residues Lys594 and Lys598 in the enzyme, preventing water from attacking the acyl complex. Instead, the free N-terminal amino group of the peptide substrate attacks the acyl complex, resulting in cyclization of the core peptide sequence.15,17 This attack can occur only if the PCC conformation is adopted. Thus, the formation of PCC may be the rate-limiting step for cyclization by PatGmac.

Although PatGmac from the patellamide biosynthetic pathway is the most studied, other homologues were identified later, e.g., LynGmac from an aestuaramide biosynthetic pathway,18,19 and assumed to work through the same mechanism.

We have previously developed an approach to simulating nonenzymatic peptide cyclization5 that successfully reproduced the kinetics of cyclization and was able to calculate the potential of the mean force (PMF), which is the free energy as a function of the distance between two termini. To apply the methodology5 to enzymatic cyclization, our working hypothesis here was that the formation of the PCC (stage c in Figure 1) is the limiting step of the process, and the enzymatic environment does not strongly influence this step. If this is the case, then the likelihood of cyclization should correlate with the free energy of the PCC fold when C and N termini of the cyclizing sequence are close to each other. Only the peptide sequences with low free energy of PCC and high probability P(PCC) can be cyclized by PatGmac. The formation of PCC may play an important part in the processes of cyclization other than by PatGmac, which makes this study potentially applicable to other models of peptide macrocyclization.

To test this hypothesis, a data set of 25 peptides of varying length (5–17 amino acid residues) and containing mainly L and in some instances 1–3 D-amino acids were prepared by solid-phase synthesis, and the sequences were confirmed by liquid chromatography–mass spectrometry LC-MS and MS/MS analyses (see Supporting Information). Peptides incorporating thiazoline residues were obtained by treatment of the cysteine-containing linear peptides by LynD heterocyclase.20 These sequences were designed to cover the 20 natural amino acids as well as few unnatural and modified amino acids. Most of these sequences were derived from cyanobactin sequences found in the literature,19 while some others were designed to study the substrate tolerance of the enzyme. The substrates were treated with PatGmac under identical conditions (see Supporting Information for the details), and the reactions were analyzed by (LC-MS). It was found that 11 out of 25 sequences were cyclizable. The experimental information was withheld from our simulation team until predictions had been made, ensuring blind test conditions.

For all 25 sequences, their probabilities of PCC formation were calculated, and it was shown that that correlation between the calculated probability and cyclization indeed exists. Although some computational studies21−23 of peptide cyclization have been reported, to the best of the authors’ knowledge, no predictive model has been rigorously tested against an experimental data set.

Calculating P(PCC), the probability of the PCC formation was not a trivial task because the ability of MD to simulate rare events, characterized by high free energy and long time scales, is severely limited.3−5,24,25 We have used boxed molecular dynamics (BXD), a method that overcomes the long time scale and high free energy problem. Previously BXD has been successfully employed to simulate a wide range of difficult processes such as protein unfolding in atomic force microscopy experiments, nonenzymatic peptide cyclization, and diffusion.3−5,24,26

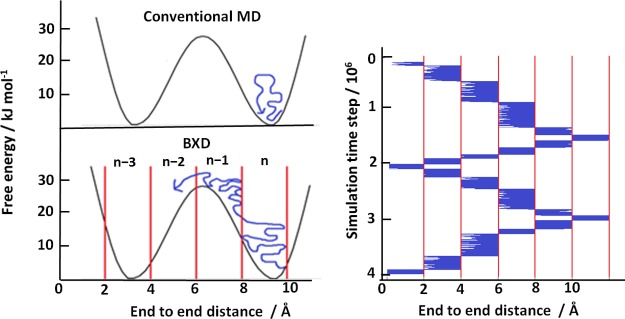
In BXD, a reaction coordinate is defined first to describe the process of interest. Then, BXD places boundaries along the reaction coordinate, splitting the phase space into boxes. As the simulation progresses, the value of the reaction coordinate is monitored. If the trajectory crosses a boundary between two neighboring boxes, the velocity in the direction of the reaction coordinate is inverted, confining the trajectory within a box. After a set amount of time, the trajectory is allowed to proceed into the next box where it is again confined. In this way the trajectory cannot roll back downhill into a free energy minimum; free energy barriers are crossed efficiently because the boxes act as a thermal ratchet as shown below in the Figure 2a. In practice, multiple passage of the boxes are allowed back and forth in the reaction coordinate as shown by Figure 2b.

Figure 2.

Figure 2

Open in a new tab

Sketch of the BXD method is shown on the left. With conventional MD a simulated trajectory (blue line) will not be able to cross large free energy barriers so sampling is poor. With BXD, reflecting boundaries are placed along the reaction coordinate chosen to describe the process, splitting the phase space into boxes (n, n+1, n+2···). By restricting the trajectory within a box for a length of time, and then allowing it to pass into the next box and restricting it there, the boxes act as a thermal ratchet and allow free energy barriers to be crossed. On the right, a plot of the reaction coordinate value against simulation time from a BXD simulation shows how the trajectory (blue) moves through the boxes and samples the space. The boxes’ boundaries are shown by vertical lines.

For the BXD trajectory shown in Figure 2b, a box-to-box rate constant can be found simply as the average time between two subsequent trajectory inversions on the border between the boxes, using also the decorrelation procedure.4 Decorrelation is needed to remove the contribution of the inversions that are separated by a very short time and therefore are not independent from each other. When all box-to-box rate constants are determined, it is then possible to construct the free energy profile along the reaction coordinate for the process of interest. With BXD it is possible to obtain free energies in the regions that cannot be reached by standard MD, as well as detailed kinetics for processes occurring on a time scale as long as seconds, many orders of magnitude beyond the reach of conventional MD.

BXD belongs to the class of methods that deal with the long time scale problem by considering only the motion along a reaction coordinate and therefore have their origin in the umbrella sampling.27−29 The advantage of BXD is that it provides both kinetic and thermodynamic information without any biasing forces or modification of the potential energy landscape. Another advantage is that it uses very simple language of the transition state theory familiar to chemists. BXD relies on a good choice of reaction coordinate, which for peptide cyclization is chosen naturally as the C and N termini end-to-end distance. A more detailed description of BXD, along with many of its applications may be found in the literature,3−5,24,26 where it is also compared with other similar techniques.

Results and Discussion. We have used BXD implemented in CHARMM code30 to simulate the propensity of 25 different peptide substrates to adopt the PCC. The reaction coordinate was chosen as the distance between C and N termini of the cyclizing peptide sequence. For each peptide sequence, 20 trajectories similar to the one shown in Figure 3 were run until converged, usually after 20 to 40 cycles through the reaction coordinate. 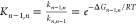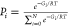The free energy difference ΔGn–1,n between the adjacent boxes n–1 and n was then calculated as the equilibrium constant is related to the rate constants of box-to-box transition calculated by BXD: Inline graphic. A typical trajectory converged in around 2 days of CPU time, orders of magnitude faster than what could be achieved with conventional MD. BXD can be parallelized trivially and actual calculation time can be reduced greatly. Knowing ΔGn–1,n the box free energy Gi and the probability Inline graphic of finding a peptide in the ith box can be found. Then the probability of finding the peptide in its PCC can be calculated. Defining the PCC as occurring when the termini are within 4 Å of each other, the probability of finding a peptide in the PCC fold is given as

graphic file with name jz-2017-00848b_m003.jpg 1

where the numerator is the sum of the Boltzmann factors in the M boxes below 4 Å and the denominator is the sum of the Boltzmann factors over all N boxes present in the simulation. The assumption that the C–N bond is formed at the distance of 4 Å, which is a reasonable estimate for the transition state. In ref (5), a slightly longer parameter (5 Å) was used because there the process of “recyclization”, in which the bond is first broken and then recombines, was considered. The kinetics of such recombination is almost independent of the position of the transition state.

Figure 3.

Figure 3

Open in a new tab

Cyclization free energy profile (PMF) for a typical pair of sequences tested, showing a peptide that cyclizes readily (18, red) and one that does not cyclize (17, blue). The 4 Å threshold that defines the separation of the termini in the PCC is shown by the gray line. In the native state of the peptide 18 its termini are close to each other. This is not the case for the peptide 17, which needs to overcome 20 kJ mol–1 barriers to reach PCC.

The peptides were simulated in isolation without the presence of any enzyme for three reasons:

  • (1)

    It is not known to what extent the enzyme assists with the formation of the PCC (frame c, Figure 1), or if this step is diffusional, i.e., the bound substrate randomly explores its conformational space and finds the PCC. However, if the mechanism described previously is accurate and the cyclization of a peptide depends on the free energy of cyclization in the absence of an enzyme, then the PCC formation step (frame c in Figure 1) is confirmed as the rate-limiting step.

  • (2)

    If the predictions are accurate without an enzyme being simulated then similar predictions can be valid for nonenzymatic methods of N to C cyclization as well, making this method even more generally useful.

  • (3)

    Without an enzyme, the simulations are significantly faster. This is important if a practical high-throughput in silico screening tool is to be produced.

As it is not known to what extent the bound substrate is exposed to water, a low-cost implicit solvent model31 was used to approximate the effects of real water.

The free energy along the cyclization coordinate was calculated for each of the 25 peptides. Figure 3 shows the cyclization free energy profiles (PMF) for a peptide that cyclizes readily (Peptide 18) and one that does not cyclize (Peptide 17).

The full list of sequences presented along with their cyclization free energy profiles can be found in Table 1 and in the Supporting Information, which also present experimental LC-MS data.

Table 1. List of Peptides Tested and Comparison of BXD Prediction with Experimenta.

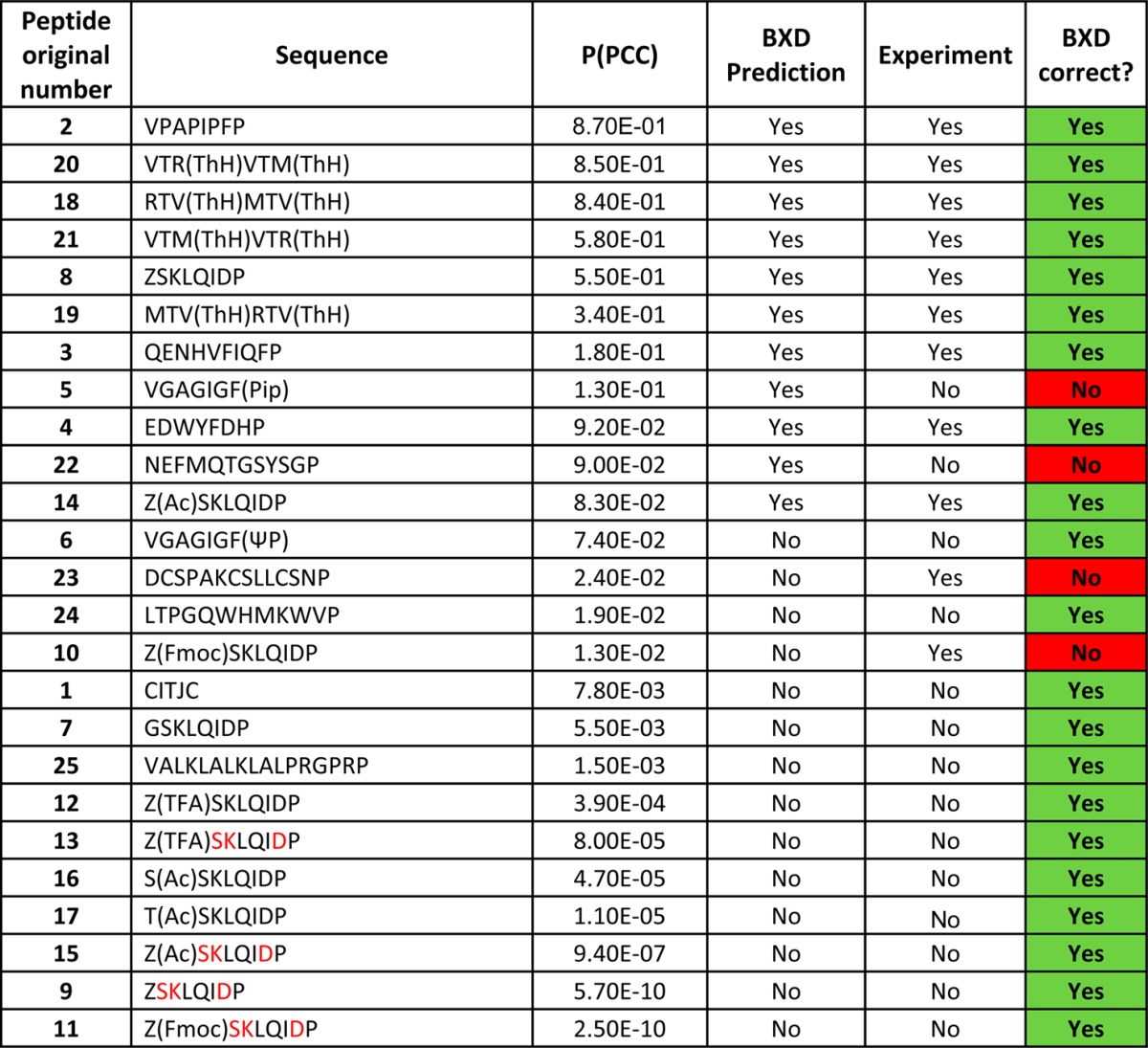
graphic file with name jz-2017-00848b_0004.jpg

Open in a new tab
a

The peptides in the table are arranged in the order of descending P(PCC). Substrates were synthesized with an AYDG recognition signal at the C-terminal of each sequence. This signal is then cleaved by the enzyme before cyclisation occurs. J = Fmoc-l-propargylglycine; Pip = Piperidine; ΨP = pseudo Proline; Z = Amino alanine; Fmoc = Fmoc protected; TFA = TFA protected; Ac = Acetylated; Amino acids in red are in D conformation.

BXD ranks the peptides in order of their PCC probability, whereas the experimental data consists of a binary yes/no on whether the peptide can be cyclized. Sequences with the highest PCC probability were predicted to cyclize. The results of calculating the PCC probability given by eq 1 are shown in Table 1, which summarizes the predictions of the blind test. To compare the predictions of BXD with experiment, we have used additional information that only 11 of the 25 peptide sequences were found to be cyclizable experimentally and therefore 11 sequences with the highest P(PCC) were predicted to cyclize.

According to Table 1, BXD was correct in 21 out of 25 cases, giving an accuracy of 84%. Very importantly, all predictions with a high or a low score were correct, and all mismatches occurred only for the medium probability P(PCC). This is ideal for a computational screening tool. When faced with a large set of candidate sequences, a developer of cyclic peptides could use the model presented here and be highly confident that the top ranked sequences would cyclize, allowing the development to proceed on these peptides with a high degree of certainty that the final cyclization step is possible. Conversely, there would be a set of peptides with lower predicted P(PCC) that the developer would know not to invest any more time in, as it is highly likely that they can not be cyclized. Thus, even though the model is not 100% accurate, it could be used to make large savings in time and cost for a producer of cyclic peptides.

The success of our blind test gives insight into the mechanism of enzyme-mediated cyclization by suggesting that the PCC formation, shown in Figure 1c, is indeed the rate-limiting step. Also the fact that the predictions were accurate without including any details of the enzyme itself means that the PCC formation is diffusional and occurs with little or no mechanical assistance from the enzyme. To test whether the cleavage of the AYD tag (frame b, Figure 1) occurs before or after the formation of the PCC, additional simulations were performed:

  • (1)

    First, in order to test the hypothesis that PCC could be formed in solution before binding, we performed calculations of free energies of all core sequences given in Table 1 but with the AYD tag attached to them. The reaction coordinate was still the distance between C and N termini of the cyclizing core sequence, but the AYD tag was attached to its C terminus.

  • (2)

    Second, we tested the hypothesis that the PCC can also be formed right after the binding of AYD to the surface of PatGmac at the stage shown by Figure 1a, before the cleavage of the AYD tag. To simulate the AYD tag attached to the surface of the enzyme, CHARMM dihedral constraints were used, which apply a very large potential energy penalty to rotation around a dihedral, preventing the rotation from happening. The constraints around the dihedrals in the backbone of the AYD tag and on the backbone bond between the tag and the first residue of the core sequence were applied. For example, for the sequence X1-X2-A-Y-D, the backbone bonds in AYD and the peptide bonds between D-Y, Y-A, and A-X2 were restrained, rendering the AYD tag immobile.

Both types of simulation performed very badly, achieving an accuracy of around 50%, the worst possible score. Thus, our calculations support the proposed mechanism of cyclization shown in Figure 1, where PCC is formed after AYD tag being detached from the cyclizing sequence as shown in Figure 1c. It also supports the assumption that after forming the acyl complex the enzyme does not influence the conformational dynamics of the core sequence forming PCC and this dynamics is similar to that in solution. The role of the enzyme is to protect the acyl complex from water and allow its attack by the N-terminus amino group. Thus, the success of the reported blind test sheds light on the mechanism of cyclization by cyanobactin macrocyclase.

On the practical side, the high accuracy of the predictions in Table 1 suggests that we have developed a computational tool that can reliably find peptide sequences with high P(PCC) for cyclization by PatGmac. It also can discard noncyclisable sequences, characterized by low probability P(PCC). The top and bottom of Table 1 were predicted correctly, with the uncertainty occurring only in the middle of Table 1 for medium probabilities of the PCC formation. As explained above, this is an important factor in a screening tool, as, when a data set is presented, the model can make confident and reliable findings of the most and the least favorable sequences. The simplicity and speed of the model makes it suitable for broad use. As PCC formation can be one of the stages of cyclization processes other than by cyanobactin macrocyclase, the developed computational tool may be of more general use.

Currently more work is under way in our groups. Experimentally we are focusing on obtaining kinetic information on the rate of cyclization as opposed to simply a yes/no indication of the presence of the cyclic product. Experimental information about cyclization kinetics would allow ranking peptides according to their cyclization rate and making a more thorough comparison of the experimental rank with that of theoretical calculations given in Table 1.

There are a number of new theoretical tasks on our list. First, the role of the enzyme needs to be investigated in more detail. While it seems that the PatGmac enzyme does not actively bring the ends of the peptide together, it is possible that it offers some small assistance, which would make the simulation of isolated peptides less reliable for the peptides in the medium range of P(PCC) in Table 1. Also, other enzymes that assist folding may be found in the future. In this case, obtaining correlation between theory and experiment will require taking into account the dynamics of enzyme, not just that of the substrate sequence as has been done here. Second, we are looking at a large number of new sequences trying to expand our data set. We also hope that with some optimizations of the code and the algorithm we will be able to scan peptide sequences systematically and predict many new cyclizable peptides. With the help of new improvements of the BXD algorithm,32 a systematic scan of ALL four or perhaps even five residue peptides may be within the reach.

Finalizing this paper, we conclude that even the limited data set presented in this work provides mechanistic details for peptide cyclization by PatGmac. A computational technique for screening peptide sequences and scoring their likelihood to cyclize has been developed and can be used as a screening tool for future cyclic peptide production. Our in silico tool requires only peptide sequences as an input. To the best of the authors’ knowledge, this is the first time that peptide cyclization has been predicted quickly and accurately against an experimental data set.

Acknowledgments

J.J.B. acknowledges his EPSRC support from Grants EP/J019240/1 and EP/J001481/1. The work done at the University of Aberdeen was funded by the European Research Council (ERC 339367 (NCB-TNT)). A.F.N. and U.U. acknowledge the support from the Tertiary Education Trust Fund (TETFUND), Nigeria. K.A.R. was supported by the AstraZeneca studentship. We would like to acknowledge David Glowacki for his useful comments and help.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b00848.

Author Present Address

⊥ Croda International Plc, Cowick Hall, Snaith, Goole, East Yorkshire, DN14 9AA

Author Contributions

# Equal contribution

The authors declare no competing financial interest.

Supplementary Material

jz7b00848_si_001.pdf (1.3MB, pdf)

References

  1. Lindorff-Larsen K.; Piana S.; Dror R. O.; Shaw D. E. How Fast-Folding Proteins Fold. Science 2011, 334 (6055), 517–520. 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
  2. Shaw D. E.; Maragakis P.; Lindorff-Larsen K.; Piana S.; Dror R. O.; Eastwood M. P.; Bank J. A.; Jumper J. M.; Salmon J. K.; Shan Y.; Wriggers W. Atomic-Level Characterization of the Structural Dynamics of Proteins. Science 2010, 330 (6002), 341–346. 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
  3. Glowacki D. R.; Paci E.; Shalashilin D. V. Boxed Molecular Dynamics: A Simple and General Technique for Accelerating Rare Event Kinetics and Mapping Free Energy in Large Molecular Systems. J. Phys. Chem. B 2009, 113 (52), 16603–16611. 10.1021/jp9074898. [DOI] [PubMed] [Google Scholar]
  4. Glowacki D. R.; Paci E.; Shalashilin D. V. Boxed Molecular Dynamics: Decorrelation Time Scales and the Kinetic Master Equation. J. Chem. Theory Comput. 2011, 7 (5), 1244–1252. 10.1021/ct200011e. [DOI] [PubMed] [Google Scholar]
  5. Shalashilin D. V.; Beddard G. S.; Paci E.; Glowacki D. R. Peptide kinetics from picoseconds to microseconds using boxed molecular dynamics: Power law rate coefficients in cyclisation reactions. J. Chem. Phys. 2012, 137 (16), 165102. 10.1063/1.4759088. [DOI] [PubMed] [Google Scholar]
  6. Mallinson J.; Collins I. Macrocycles in new drug discovery. Future Med. Chem. 2012, 4 (11), 1409–1438. 10.4155/fmc.12.93. [DOI] [PubMed] [Google Scholar]
  7. Driggers E. M.; Hale S. P.; Lee J.; Terrett N. K. The exploration of macrocycles for drug discovery - an underexploited structural class. Nat. Rev. Drug Discovery 2008, 7 (7), 608–624. 10.1038/nrd2590. [DOI] [PubMed] [Google Scholar]
  8. Kotz J.Bringing Macrocycles Full Circle. SciBX.20125 (45), 1176. 10.1038/scibx.2012.1176 [DOI] [Google Scholar]
  9. Scannell J.; Blanckley A.; Boldon H.; Warrington B. Nat. Rev. Drug Discovery 2012, 11, 191–200. 10.1038/nrd3681. [DOI] [PubMed] [Google Scholar]
  10. Giordanetto F.; Kihlberg J. J. Med. Chem. 2014, 57, 278–295. 10.1021/jm400887j. [DOI] [PubMed] [Google Scholar]
  11. Glas A.; Bier D.; Hahne G.; Rademacher C.; Ottmann C.; Grossmann T. N. Constrained Peptides with Target-Adapted Cross-Links as Inhibitors of a Pathogenic Protein–Protein Interaction. Angew. Chem., Int. Ed. 2014, 53 (9), 2489–2493. 10.1002/anie.201310082. [DOI] [PubMed] [Google Scholar]
  12. White C. J.; Yudin A. K. Contemporary strategies for peptide macrocyclization. Nat. Chem. 2011, 3 (7), 509–524. 10.1038/nchem.1062. [DOI] [PubMed] [Google Scholar]
  13. Wu Z.; Guo X.; Guo Z. Sortase A-catalyzed peptide cyclization for the synthesis of macrocyclic peptides and glycopeptides. Chem. Commun. 2011, 47 (32), 9218–9220. 10.1039/c1cc13322e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Houssen W. E.; Bent A. F.; McEwan A. R.; Pieiller N.; Tabudravu J.; Koehnke J.; Mann G.; Adaba R. I.; Thomas L.; Hawas U. W.; Liu H.; Schwarz-Linek U.; Smith M. C. M.; Naismith J. H.; Jaspars M. An Efficient Method for the In Vitro Production of Azol(in)e-Based Cyclic Peptides. Angew. Chem., Int. Ed. 2014, 53 (51), 14171–14174. 10.1002/anie.201408082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Koehnke J.; Bent A.; Houssen W. E.; Zollman D.; Morawitz F.; Shirran S.; Vendome J.; Nneoyiegbe A. F.; Trembleau L.; Botting C. H.; Smith M. C. M.; Jaspars M.; Naismith J. H. The mechanism of patellamide macrocyclization revealed by the characterization of the PatG macrocyclase domain. Nat. Struct. Mol. Biol. 2012, 19 (8), 767–772. 10.1038/nsmb.2340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. McIntosh J. A.; Robertson C. R.; Agarwal V.; Nair S. K.; Bulaj G. W.; Schmidt E. W. Circular Logic: Nonribosomal Peptide-like Macrocyclization with a Ribosomal Peptide Catalyst. J. Am. Chem. Soc. 2010, 132 (44), 15499–15501. 10.1021/ja1067806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Bras N. F.; Ferreira P.; Calixto A. R.; Jaspars M.; Houssen W.; Naismith J. H.; Fernandes P. A.; Ramos M. J. The Catalytic Mechanism of the Marine-Derived Macrocyclase PatGmac. Chem. - Eur. J. 2016, 22 (37), 13089–13097. 10.1002/chem.201601670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Donia M. S.; Ravel J.; Schmidt E. W. A global assembly line for cyanobactins. Nat. Chem. Biol. 2008, 4 (6), 341–343. 10.1038/nchembio.84. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Sivonen K.; Leikoski N.; Fewer D. P.; Jokela J. Cyanobactins-ribosomal cyclic peptides produced by cyanobacteria. Appl. Microbiol. Biotechnol. 2010, 86 (5), 1213–1225. 10.1007/s00253-010-2482-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Koehnke J.; Mann G.; Bent A. F.; Ludewig H.; Shirran S.; Botting C.; Lebl T.; Houssen W. E.; Jaspars M.; Naismith J. H. Structural analysis of leader peptide binding enables leader-free cyanobactin processing. Nat. Chem. Biol. 2015, 11 (8), 558–U48. 10.1038/nchembio.1841. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Cavelierfrontin F.; Pepe G.; Verducci J.; Siri D.; Jacquier R. PREDICTION OF THE BEST LINEAR PRECURSOR IN THE SYNTHESIS OF CYCLOTETRAPEPTIDES BY MOLECULAR MECHANIC CALCULATIONS. J. Am. Chem. Soc. 1992, 114 (23), 8885–8890. 10.1021/ja00049a021. [DOI] [Google Scholar]
  22. Besser D.; Olender R.; Rosenfeld R.; Arad O.; Reissmann S. Study on the cyclization tendency of backbone cyclic tetrapeptides. J. Pept. Res. 2000, 56 (6), 337–345. 10.1034/j.1399-3011.2000.00735.x. [DOI] [PubMed] [Google Scholar]
  23. Yongye A. B.; Li Y. M.; Giulianotti M. A.; Yu Y. P.; Houghten R. A.; Martinez-Mayorga K. Modeling of peptides containing D-amino acids: implications on cyclization. J. Comput.-Aided Mol. Des. 2009, 23 (9), 677–689. 10.1007/s10822-009-9295-y. [DOI] [PubMed] [Google Scholar]
  24. Booth J.; Vazquez S.; Martinez-Nunez E.; Marks A.; Rodgers J.; Glowacki D. R.; Shalashilin D. V. Recent applications of boxed molecular dynamics: a simple multiscale technique for atomistic simulations. Philos. Trans. R. Soc., A 2014, 372 (2021), 20130384. 10.1098/rsta.2013.0384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Bolhuis P. G.; Chandler D.; Dellago C.; Geissler P. L. Transition path sampling: Throwing ropes over rough mountain passes, in the dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. 10.1146/annurev.physchem.53.082301.113146. [DOI] [PubMed] [Google Scholar]
  26. Booth J. J.; Shalashilin D. V. Fully Atomistic Simulations of Protein Unfolding in Low Speed Atomic Force Microscope and Force Clamp Experiments with the Help of Boxed Molecular Dynamics. J. Phys. Chem. B 2016, 120 (4), 700–708. 10.1021/acs.jpcb.5b11519. [DOI] [PubMed] [Google Scholar]
  27. Kaestner J. Umbrella sampling. Wiley Interdisciplinary Reviews-Computational Molecular Science 2011, 1 (6), 932–942. 10.1002/wcms.66. [DOI] [Google Scholar]
  28. Torrie G. M.; Valleau J. P. MONTE-CARLO STUDY OF A PHASE-SEPARATING LIQUID-MIXTURE BY UMBRELLA SAMPLING. J. Chem. Phys. 1977, 66 (4), 1402–1408. 10.1063/1.434125. [DOI] [Google Scholar]
  29. Torrie G. M.; Valleau J. P. NON-PHYSICAL SAMPLING DISTRIBUTIONS IN MONTE-CARLO FREE-ENERGY ESTIMATION - UMBRELLA SAMPLING. J. Comput. Phys. 1977, 23 (2), 187–199. 10.1016/0021-9991(77)90121-8. [DOI] [Google Scholar]
  30. Brooks B. R.; Brooks C. L. III; Mackerell A. D. Jr.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; Caflisch A.; Caves L.; Cui Q.; Dinner A. R.; Feig M.; Fischer S.; Gao J.; Hodoscek M.; Im W.; Kuczera K.; Lazaridis T.; Ma J.; Ovchinnikov V.; Paci E.; Pastor R. W.; Post C. B.; Pu J. Z.; Schaefer M.; Tidor B.; Venable R. M.; Woodcock H. L.; Wu X.; Yang W.; York D. M.; Karplus M. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30 (10), 1545–1614. 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lazaridis T.; Karplus M. Effective energy function for proteins in solution. Proteins: Struct., Funct., Genet. 1999, 35 (2), 133–152. . [DOI] [PubMed] [Google Scholar]
  32. O’Connor M.; Paci E.; McIntosh-Smith S.; Glowacki D. R. Adaptive free energy sampling in multidimensional collective variable space using boxed molecular dynamics. Faraday Discuss. 2016, 195 (0), 395–419. 10.1039/C6FD00138F. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz7b00848_si_001.pdf (1.3MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES