Significance
This report combines kinetic and spectroscopic data with state-of-the-art theoretical methods to provide insights into the stability of covalently bound species ubiquitous as intermediates in hydrocarbon and alcohol reactions on solid acids [e.g., coupling, alkyl(methyl)ation, isomerization, cracking, dehydration,…]. In doing so, the study addresses the long-standing search for a systematic analysis of the effects of the size and shape of organic guests (alkoxides) and inorganic hosts (catalysts). It reveals how framework distortions act to balance the requirements for covalency with the need for optimal void geometries that maximize van der Waals contacts. These details are essential to understand the stability and reactivity of bound alkoxides, prevalent as reactive intermediates in host–guest systems of catalytic interest.
Keywords: zeolites, alkene adsorption, heterogeneous catalysis, density functional theory
Abstract
This study reports the thermodynamics of bound species derived from ethene, propene, n-butene, and isobutene on solid acids with diverse strength and confining voids. Density functional theory (DFT) and kinetic data indicate that covalently bound alkoxides form C–C bonds in the kinetically relevant step for dimerization turnovers on protons within TON (0.57 nm) and MOR (0.67 nm) zeolitic channels and on stronger acids HPW (polyoxometalate clusters on silica). Turnover rates for mixed alkenes give relative alkoxide stabilities; the respective adsorption constants are obtained from in situ infrared spectra. Tertiary alkoxides (from isobutene) within larger voids (MOR, HPW) are more stable than less substituted isomers but are destabilized within smaller concave environments (TON) because framework distortions are required to avoid steric repulsion. Adsorption constants are similar on MOR and HPW for each alkoxide, indicating that binding is insensitive to acid strength for covalently bound species. DFT-derived formation free energies for alkoxides with different framework attachments and backbone length/structure agree with measurements when dispersion forces, which mediate stabilization by confinement in host–guest systems, are considered. Theory reveals previously unrecognized framework distortions that balance the C–O bond lengths required for covalency with host–guest distances that maximize van der Waals contacts. These distortions, reported here as changes in O-atom locations and dihedral angles, become stronger for larger, more substituted alkoxides. The thermodynamic properties reported here for alkoxides and acid hosts differing in size and conjugate-anion stability are benchmarked against DFT-derived free energies; their details are essential to design host–guest pairs that direct alkoxide species toward specific products.
Hydrocarbon reactions on solid Brønsted acids often involve bound alkene-derived intermediates. Their reactivity and selectivity in C–C bond formation and cleavage and in hydrogen transfer reactions depend on their thermodynamic properties, which reflect, in turn, the properties of the conjugate anion and of the confining voids in microporous solid acids. Weakly bound adsorbed alkanes interact with void walls via dispersion forces at low temperatures without molecular transformations; their unreactive nature allows accurate assessments of their binding properties (1–4). Alkenes interact with protons via H bonding or π-interactions, as well as by proton transfer from strong acids to form alkoxides; the intermediate between these states is a positively charged carbenium ion. The thermodynamics of alkoxide formation remain uncertain because of their very fast oligomerization and β-scission reactions (5, 6), thus requiring indirect inferences from kinetic, spectroscopic, or theoretical methods. This uncertainty is particularly prevalent in isobutene-derived species, for which steric effects may disfavor the formation of covalently bound butoxides (7–9). Infrared spectra that lack intact or perturbed O–H stretches (10, 11) during oligomerization of propene or isobutene on TON and MFI (12) indicate the proton has been transferred to the stable species, which is consistent for either the covalently bound alkoxide or carbenium ion. However, density functional theory (DFT) shows that alkoxides acquire carbenium ion character only at the transition states that mediate their transformations during catalysis on solid acids, but not at their lowest energy stable bound states (13–19), which suggests the prevalence of bound alkoxides at near saturation coverages during catalysis.
The presence, catalytic involvement, and spectral features of bound alkoxides on solid acids have been reported, but we have not found any systematic studies that combine kinetic and spectroscopic data with theoretical treatments that account for dispersion forces in assessing adsorption constants for conditions and solids of practical interest. We combine here these methods to report the thermodynamics of alkoxides derived from C2–C4 alkenes during their co-oligomerization on acids of diverse strength and confining environments (H-TON [10-membered ring (MR)] zeolite; H-MOR (12-MR) zeolite; Keggin polyoxometalates dispersed on mesoporous SiO2 (H3PW12O40; HPW)). Theory (DFT) and experiment show that C–C bond formation rates are limited by the addition of an alkene to bound alkoxides, present at saturation coverages at all alkene pressures (10–500 kPa) (12). At lower pressures, absolute alkoxide formation equilibrium constants for ethoxide and propoxides are measured from homodimerization rates and from the integration of infrared bands that are dependent on alkene pressure; their relative values agree with DFT-derived adsorption free energies and values measured from heterodimerization where competition for surface sites exists. The oligomerization of alkene mixtures gives relative alkoxide stabilities for all C2–C4 alkenes and thus ratios of their adsorption constants. In large voids (MOR, HPW), alkoxide stabilities increase with chain length and substitution, but bulkier alkoxides (e.g., tert-isobutoxide) are sterically hindered within smaller concave environments (TON). DFT-derived free energies for alkoxide formation, ensemble-averaged over all alkoxide-binding configurations (i.e., primary, secondary, or tertiary) from a given alkene, accurately capture experimental trends.
The proper accounting of dispersive interactions in DFT reveals an unexpected and previously unrecognized flexibility of zeolite frameworks, which allows lattice distortions that enhance van der Waals contacts between alkoxides and the surrounding inorganic framework, while preserving the C–O distances required for covalent attachment of alkoxides. DFT-derived energies show how these lattice distortions are compensated by more favorable dispersive interactions; these geometric rearrangements are evident from the displacement of framework O atoms and from changes in their dihedral angles upon alkoxide formation. These geometric distortions become more prevalent as alkoxides become larger and more substituted, thus accounting for the unfavorable formation of bulkier alkoxides on TON relative to HPW measured experimentally. These crystalline framework distortions are likely to become more significant on nanometer-sized crystals and in near-surface regions, plausibly giving rise to observed diffusion and catalytic phenomena typically denoted as surface barriers (20–22) and pore mouth catalysis (23–25), respectively.
Experimental Methods
Alkoxide Adsorption Constants from Kinetic Data.
TON (Si/Al = 39) (26, 27), MOR [H45Na55MOR (28); Zeolyst; Si/Al = 10], and H3PW12O40/SiO2 (29) were pelleted, crushed, and sieved to retain 180- to 250-μm aggregates. Their proton densities are 0.22, 0.44, and 0.043 mmol H+⋅g−1, respectively, as determined by a combination of NH3 evolution from NH4+-exchanged zeolitic samples, Al-NMR, deconvolution of FTIR spectra, and in situ titrations, which have been reported previously for these samples (6, 28). Alkene turnover rates (per H+) were measured on samples (0.015–0.100 g) held within a plug-flow tubular reactor (316 stainless steel, 12-mm i.d.). Temperatures were set using a three-zone resistive furnace (ATS 3210; Watlow controllers 96 series) and measured with a concentric K-type thermocouple. NH4-TON and H45Na55MOR were treated in 5% O2/He (83.3 cm3⋅g−1⋅s−1; Praxair) by heating to 818 K (at 0.025 K⋅s−1; 3-h hold) before rate measurements at 503 K. HPW was treated in He (50 cm3⋅g−1⋅s−1; 99.999%; Praxair) by heating to 503 K (at 0.083 K⋅s−1) to desorb adsorbed H2O. Ethene (99.9%; Praxair), propene (99.9%, Praxair, or 5% in He, Praxair), trans-2-butene (99.9%; Praxair), and isobutene (99.9%; Praxair) were metered into He flow using electronic mass controllers, and products were brought into a gas chromatograph (Agilent 6890) through lines held at 373 K. Concentrations were measured by flame ionization after chromatographic separation in a methyl silicone capillary (Agilent HP-1 column; 50 m × 0.32 mm × 1.05-μm film). The system pressure was maintained using a dome-loaded regulator (Tempresco).
Infrared Assessment of OH Groups and Adsorbed Species During Catalysis.
Infrared spectra were collected using a Nicolet NEXUS 670 spectrometer with a Hg–Cd–Te (MCT) detector. Wafers (∼20–40 mg) were held within a quartz infrared cell fitted with NaCl windows and treated in dry air (20.8 cm3⋅g−1⋅s−1; zero grade; Praxair) by heating to 818 K (at 0.033 K⋅s−1; 3-h hold) and cooled in He to 503 K. Ethene (99.9%; Praxair), propene (99.9%; Praxair), or isobutene (99.9%; Praxair) was introduced into He flow (99.999%; Praxair) to set the desired alkene reactant pressure (3–70 kPa). Spectra were collected with 2 cm−1 resolution at 4,000–400 cm−1 using 64 scans.
DFT Methods.
Periodic DFT, as implemented in the Vienna ab initio simulation package (30–33), was used to determine optimized structures and energies for transition states and stable intermediates along the dimerization reaction coordinate using a periodic plane-wave basis set expansion (cutoff energy, 396 eV) and projector-augmented wave (PAW5) pseudopotentials (34, 35). Exchange and correlation energies were derived from generalized gradient approximation using revised Perdew–Burke–Ernzerhof functionals (36–38). Dispersive energies and forces were calculated by DFT-D3 during each energy minimization (39, 40). A 1 × 1 × 1 Monkhorst–Pack k-point mesh was used to sample the first Brillioun zone (41).
Accurate descriptions of TON frameworks required five unit cells (as defined in Database of Zeolite Structures; www.iza-structure.org/databases/) to capture the details of the void network and to provide an appropriate vacuum region that prevents interactions among periodic images. The Al2-O3(H) (notation as in Database of Zeolite Structures; www.iza-structure.org/databases/) site was used as the location for the alkoxides. HPW clusters were described as full clusters (∼1-nm diameter) placed at the center of 3 × 3 × 3 nm3 cells to prevent intercluster interactions. Convergence criteria were <0.05 eV⋅Å−1 for forces and <1 × 10−6 eV for energies. Electronic energies (E0) were used to determine Gibbs free energies by including zero-point vibrational energies and vibrational free energies (Gvib) from frequencies of optimized structures; gaseous free energies also include translational and rotational free components (Gtrans and Grot). Low-frequency modes were excluded, because of their anharmonic nature, and replaced with a fraction (0.7) of the translational and rotational entropies of the gaseous alkene using statistical mechanics, a method shown to provide accurate entropy estimates for adsorbed molecules on oxide surfaces (42). All energies are referenced to that of the H form of the acid () and the gaseous alkene, unless indicated otherwise. The formation energy of species i () is given by the following:
| [1] |
where is the Gibbs free energy of the alkoxide i, is the protonated form of the catalyst (), and is the gaseous alkene. Charges of individual atoms of optimized structures were determined by transforming the converged wavefunctions into a set of localized quasi-atomic orbitals (QUAMBO) (43–46).
Results and Discussion
Kinetic Measurement of Alkoxide Stabilities.
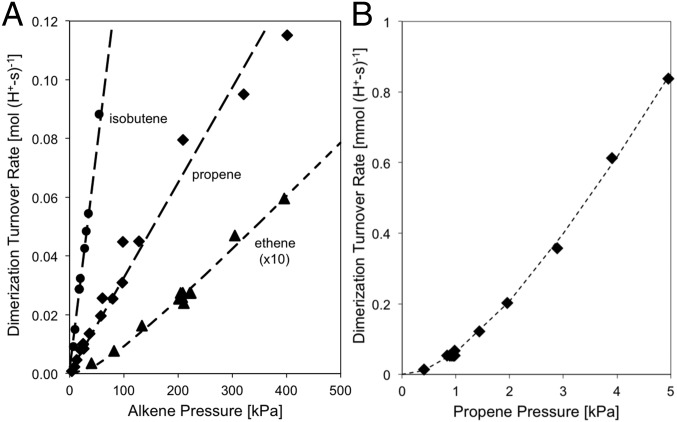
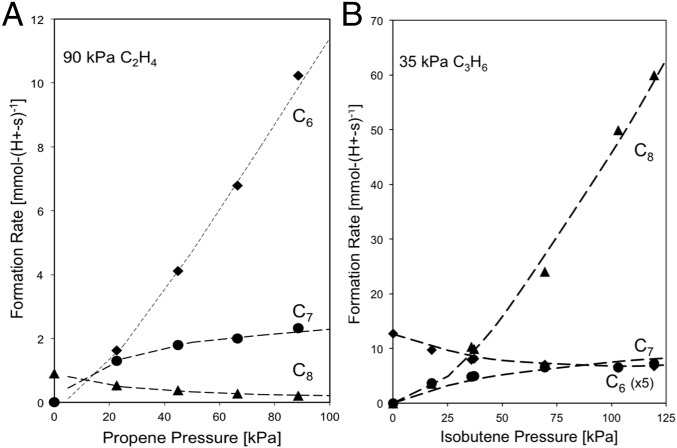
Propene and isobutene dimerization turnover rates on TON [per H+, 0.22 mmol H+⋅g−1 from NH4+ decomposition (6)] are proportional to the alkene pressure (10–500 kPa; 503 K) (Fig. 1A), consistent with the kinetic relevance of the alkene–alkoxide reactions that form the C–C bond (12). At lower propene pressures (1–5 kPa), dimerization rates deviate from first order (Fig. 1B), as they do for ethene reactions even at higher pressures (Fig. 1A). Such kinetic trends indicate that alkoxides reach saturation coverages as alkene pressure increases and do so at lower pressures as the alkene size increases.
Fig. 1.
(A) Alkene dimerization turnover rates on TON for C2H4 (▲; ×10 for clarity), C3H6 (◆), and i-C4H8 (●) as a function of alkene pressure. (B) Propene dimerization turnover rates on TON at low pressures [503 K; (A) 0–400 kPa, (B) 0–5 kPa; <5% alkene conversion; dashed lines represent linear regression fits].
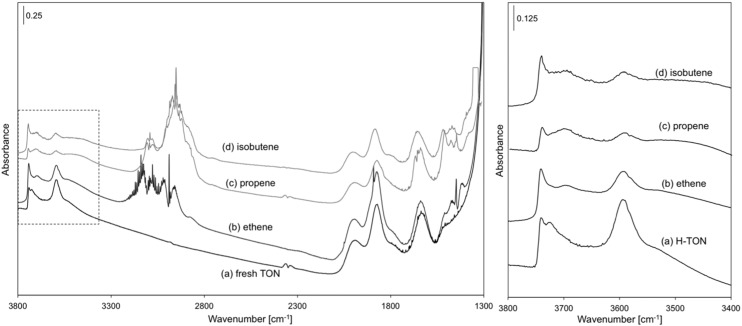
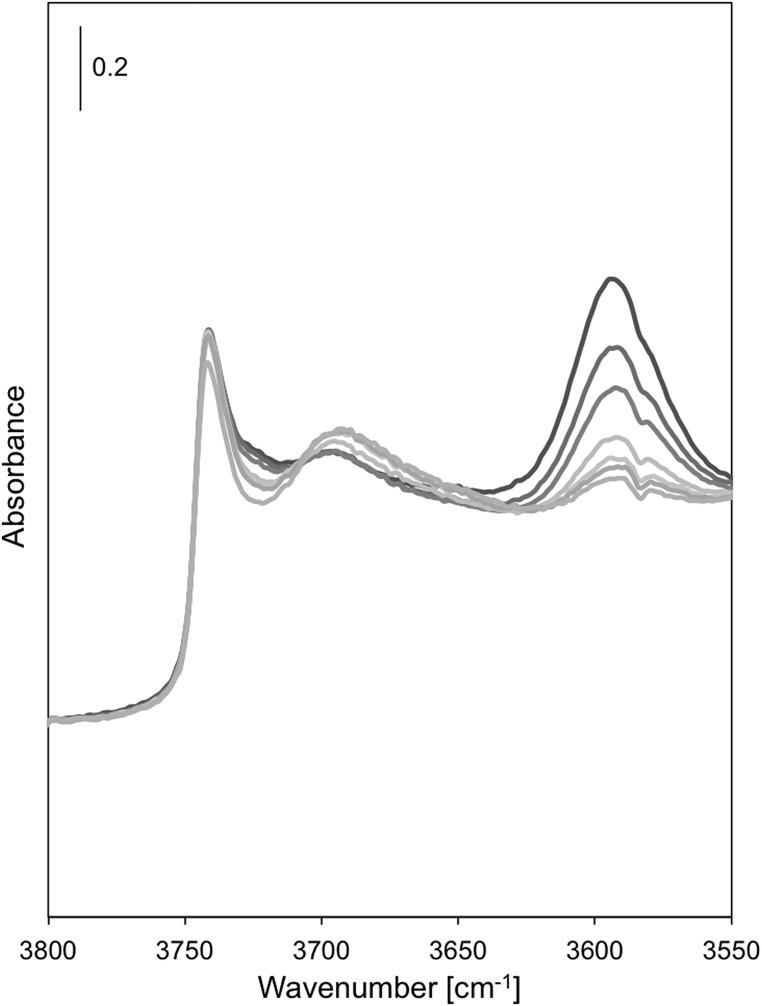
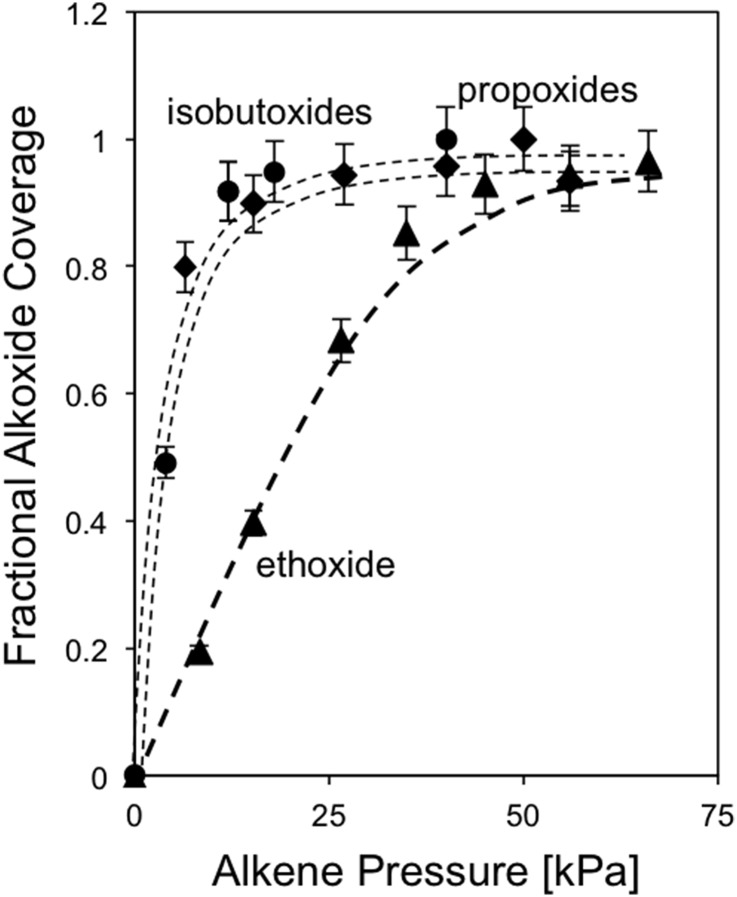
Infrared spectra also show that O–H stretching bands [3,600 cm−1 (47)], indicative of free H+ without bound species, become less intense with increasing ethene pressure (Fig. 2, 8-kPa ethene, 503 K; Fig. S1, 8–70 kPa), whereas bands for alkoxide species (–O–CnH2n+1) at 1,500–1,450 cm−1 (7, 31, 32) concurrently emerge. These spectra do not show broad bands near 2,800 cm−1, the frequency range expected from theoretical treatments for π-bonded alkenes at protons (7, 12). Thus, bound species predominantly consist of covalently bound alkoxides. This conclusion is discussed in more detail in DFT-Derived Free Energies of Alkoxide Formation. The fractional ethoxide coverages derived from these O–H band intensities exhibit Langmuirian adsorption behavior, reaching saturation values above 50 kPa (Fig. 3); propoxides and isobutoxides reach saturation coverages at much lower pressures [10 kPa, TON (Fig. 3)]. Alkoxide coverages (fi) derived from species i are expected to obey a Langmuir-type equation (dashed curves in Fig. 3) because of the isolated nature of zeolitic protons:
| [2] |
Here, Ci is the concentration of species i in the gas phase, which determines the coverage of the respective bound alkoxide through the magnitude of <Ki>, the equilibrium constant ensemble-averaged over all potential binding configurations j (primary, secondary, tertiary; Scheme 1) of the alkoxide derived from species i (discussed more thoroughly below). These different binding configurations are not individually accessible from experiments, thus requiring the theoretical assessments described in DFT-Derived Free Energies of Alkoxide Formation. <Ki> values from infrared spectra are less certain for propene and isobutene (0.35 ± 0.19 kPa−1 and 0.41 ± 0.16 kPa−1, respectively) than for ethene (0.07 ± 0.006 kPa−1) because coverages well below saturation are achieved only at very low pressures.
Fig. 2.
Infrared spectra of TON (Left) and enhanced spectral region in box (Right) at 503 K in H form (a), 8-kPa C2H4 (after 0.18 ks; b), 6.5-kPa C3H6 (after 0.18 ks; c), and 4-kPa i-C4H8 (after 0.18 ks; d).
Fig. S1.
Infrared spectra of TON at 503 K under C2H4 (8–70 kPa; dark gray to light gray).
Fig. 3.
Fractional alkoxide coverage measured from the decrease in the intensity of the 3,600 cm−1 OH band in the infrared spectra of TON (Si/Al = 40) at 503 K during C2H4 (▲), C3H6 (◆), or i-C4H8 (●) dimerization reactions. Dashed lines indicate regression fits to the functional form of Eq. 2.
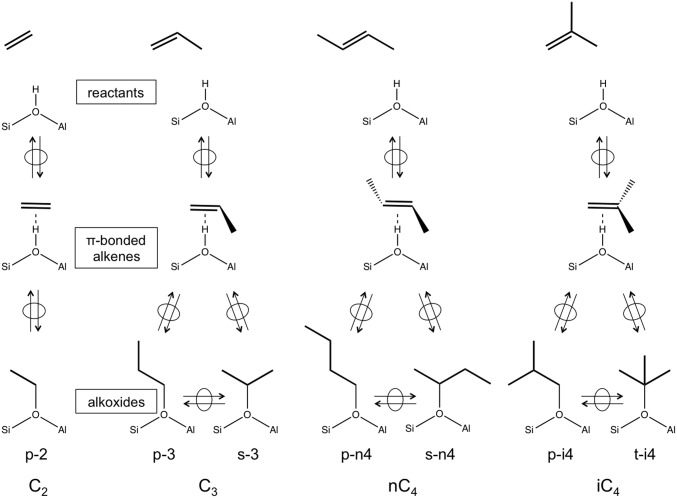
Scheme 1.
Alkoxide formation with available attachments from ethene (primary ethoxide; p-2), propene (primary and secondary propoxide; p-3 and s-3), trans-2-butene (primary and secondary butoxide; p-n4 and s-n4), and isobutene (primary and tertiary isobutoxide; p-i4 and s-i4) via π-bonded intermediate on an aluminosilicate. Double arrows with ovals indicate quasi-equilibrated steps.
These <Ki> values can also be measured from dimerization rates at alkoxide coverages below saturation coverage for each alkene reactant or from heterodimerization rates of two or more alkenes (Eq. 3A). Heterodimerization rates measured at pressures when H+ sites are saturated with mixtures of their respective alkoxides yield relative alkoxide equilibrium constants (Eq. 3B).
| [3A] |
| [3B] |
Here, the two terms in the numerator account for the coverages of the Ci and Cn alkoxides during catalysis. Homodimerization rates are given Eqs. 3A and 3B when i = n. ki and kn are the intrinsic rate constants for the coupling of two alkenes with i or n carbons, where the subscript represents which alkene is in the alkoxide form; kin,eff is the rate constant extracted from kinetic analysis of measured rate data. The rate constants and equilibrium constants reflect ensemble averages for the formation and subsequent reaction of alkoxides with different binding configurations (primary, secondary, tertiary). The rigorously averaged equilibrium constants (<Ki>, <Kn>) depend on the Gibbs free energy for the ensemble average of all alkoxide-binding configurations <>:
| [4] |
| [5] |
where (Eq. 6) depends on the Gibbs free energy of alkoxide formation () with i carbons and binding configuration j referenced to the protonated form of the catalyst () and the gaseous alkene with i carbons (), and is the probability of each binding configuration:
| [6] |
These j different binding configurations reflect the different attachment points of alkoxides derived from a given alkene (j = 1, 2, 3 for primary, secondary, and tertiary C atoms bound to framework O atoms; Scheme 1). Their ensemble-averaged free energies, instead of those for any given attachment, determine measured <Ki> values. Comparisons between theory and experiment thus require the theoretical calculation and the appropriate averaging of Kij values for each configuration j of each alkoxide with i C atoms derived from a Ci alkene (DFT-Derived Free Energies of Alkoxide Formation).
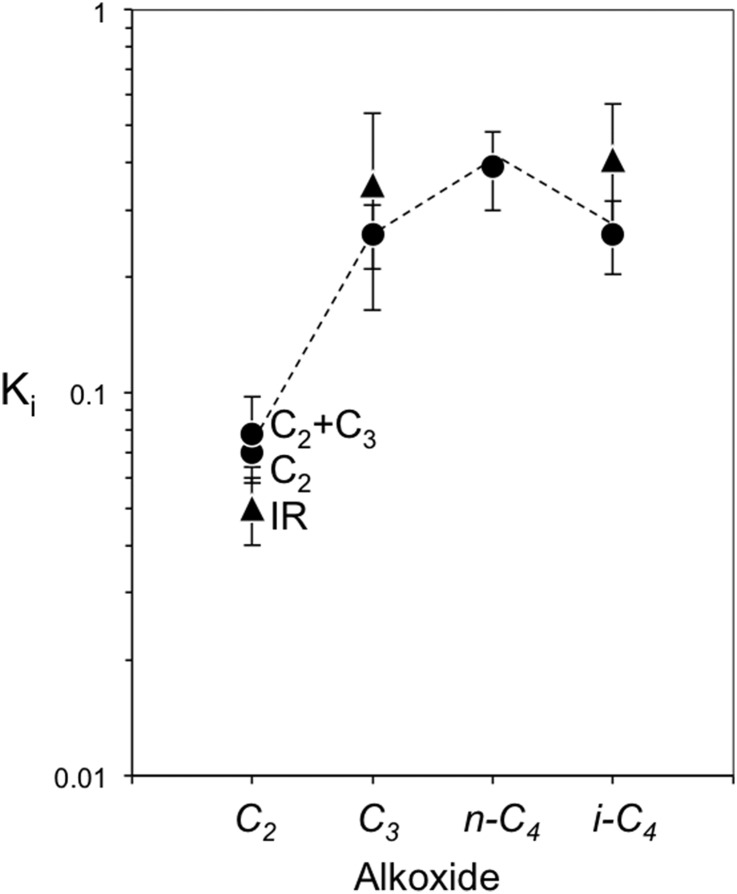
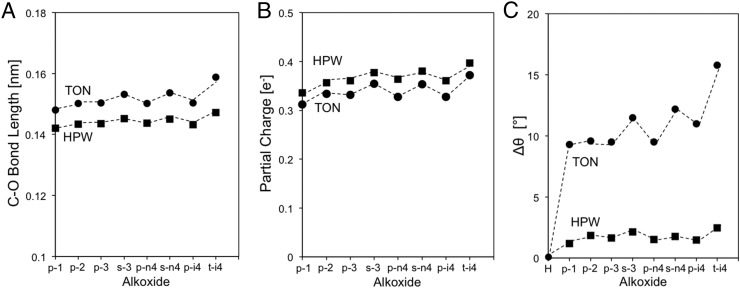
Fig. 4 shows <Ki> values on TON obtained from the value of <K3> derived from the data in Fig. 1B and the (<Ki>/<K3>) values regressed from rates of the heterodimerization reactions of ethene, isobutene, and trans-2-butene with propene (Fig. 5) to the functional form of Eq. 3B. These data show that C3 and C4 alkoxides are more stable than C2 alkoxides and that the K2 values derived from independent measurements of ethene homodimerization rates (0.05 ± 0.01) and infrared spectra during ethene dimerization (0.07 ± 0.006) and ethene–propene heterodimerization (0.078 ± 0.02) lie well within their respective experimental uncertainties. Similar conclusions are evident for propene (0.26 ± 0.05 and 0.35 ± 0.19 from homodimerization and infrared, respectively) and isobutene (0.26 ± 0.06 and 0.41 ± 0.16 from heterodimerization and infrared data, respectively). The measured <Ki> values for alkoxides formed from n-butenes (denoted so because trans-2-butene reactants equilibrates with all linear regioisomers) are slightly larger than for propoxides, indicating that larger chains are more stable, possibly because of more effective van der Waals contacts within TON channels. However, isobutoxides are less stable than n-butoxides on TON, apparently because of steric hindrance imposed by the concave environment of small TON channels [10-MR; 0.46 nm × 0.57 nm (Database of Zeolite Structures; www.iza-structure.org/databases/)]. Such conjectures are confirmed by the observed effects of chain length and substitution on <Ki> for larger voids (MOR) and convex surfaces (HPW), as we describe next.
Fig. 4.
Measured equilibrium constants for alkoxide formation on TON [503 K; <5% alkene conversion during kinetic rate measurement (●); during IR (▲); dashed lines connect data points to guide the eye]. Parameters from least-squares fit of co-oligomerization rate equations with respect to propoxide and multiplied by propoxide formation measured from low-pressure kinetic data. Ethoxide formation also measured from fitting single-feed oligomerization kinetic data.
Fig. 5.
Formation rates of homodimers and heterodimers from (A) ethene and propene and (B) isobutene and propene mixtures on TON (503 K; <5% alkene conversion). Dashed lines indicate regression fits to the functional form of Eq. 3B.
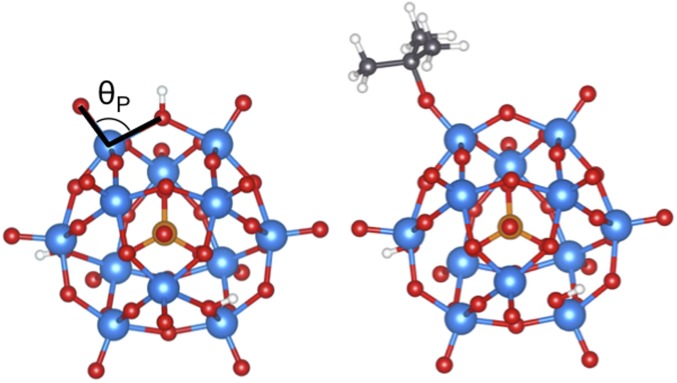
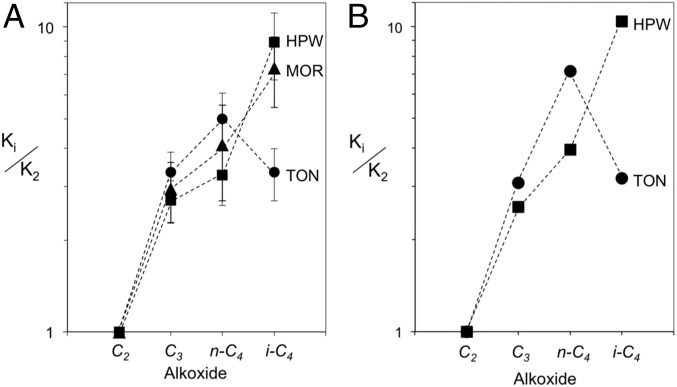
MOR frameworks contain 12-MR channels (0.70 × 0.65 nm) with 8-MR side pockets (Database of Zeolite Structures; www.iza-structure.org/databases/). H+ species in the smaller 8-MR side pockets were selectively titrated with Na+ in these sample such that 83% of the 0.53 mmol H+⋅g−1 in this sample reside within the 12-MR pockets in MOR (28); thus, the observed reactivity arises predominantly from protons within the larger cylindrical channels in MOR. Keggin HPW clusters [0.043 mmol H+⋅g−1; 2,6-di-tert-butylpyridine titration (12)] consist of 1.1-nm WO3 shells surrounding a PO43− anion (structure in Fig. 6) and are supported, here, on mesoporous SiO4 silica with 2.4-nm pores. Fig. 7A shows <Ki> values relative to those for ethoxide (from <Ki>/<K3> values multiplied by <K3>/K2) to reference equilibrium constants to those of the smallest and least stable alkoxide on TON, MOR, and HPW. <Ki>/K2 values are larger than unity for all alkoxides on all samples, but the steric hindrance that led to smaller <Ki> values for isobutoxides than n-butoxides on TON is no longer evident for H+ present within the larger channels in MOR or the mesopores in the SiO2 supports used to disperse HPW, suggesting that the distances required for covalent attachments can be achieved with less consequential repulsion or lattice distortions as surfaces become convex (in SiO2) or at least less concave (in MOR) than those in TON channels.
Fig. 6.
Structures of HPW in H form (Left) and t-isobutoxide (Right). O–W–O angle (Left) shows the angle (θP) used for characterization in Fig. 11.
Fig. 7.
(A) Measured relative equilibrium constants (<Ki>) with respect to ethoxide (K2) on TON (●), MOR (▲), and HPW (■) (503 K; <5% alkene conversion; dashed lines connect data points to show trend). <Ki> values from regression of rate data to the function form of Eq. 3B with respect to propoxide were renormalized to ethoxide. (B) DFT-derived <Ki> values calculated as relative alkoxide stabilities with respect to ethoxide on TON (●) and HPW (■). Multiple alkoxide attachment points were ensemble-averaged according to the alkoxide ΔG at 503 K according to Eqs. 4–6. All energies are referenced to the H form of each catalyst and alkene precursors.
<Ki>/K2 values are similar on MOR and HPW for each alkoxide, despite their very different void structures and also their different acid strength; the latter is evident from their different deprotonation energies [HPW: 1,090 kJ/mol (48); MOR (and other aluminosilicate frameworks): 1,190–1,222 kJ/mol (49)]. These data suggest that more stable anions (in stronger acids) do not lead to more stable alkoxides, an experimental demonstration of the covalent nature of the alkoxide structures, which is consistent with DFT-derived formation energies and partial charges for s-propoxides that are independent of acid strength for a series of Keggin POM clusters with different central atoms and very different acid strength (HPW, HSiW, HAlW) (12). These data also show that stabilization by confinement is similar among different alkoxides and not very consequential for their stability within 12-MR MOR channels, but becomes detectable within smaller 10-MR TON channels. These measured <Ki> values, essential for the interpretation of alkoxide reactivity, reflect ensemble averages of all alkoxide configurations that can form for each given alkene (Eqs. 4–6); their comparison with theory and the dissection of the relative contributions of each configuration to surface coverages and to oligomerization rates require DFT-derived free energies for each species and their rigorous ensemble averaging.
DFT-Derived Free Energies of Alkoxide Formation.
Gibbs free energies and enthalpies were calculated using DFT methods, as described in Experimental Methods, DFT Methods, for π-bound alkenes and for each configuration of bound alkoxides derived from alkenes with i C-atoms to assess their relative stability (Table 1; TON, HPW). The values shown in Table 1 show that the π-bound alkene is less stable than the respective alkoxide configurations for each alkene, except for isobutene-derived alkoxides on TON. In this latter case, the π-bound alkene configuration is more stable than the t-isobutoxide and similar in stability to the p-isobutoxide; similar conclusions were reported for bound isobutene-derived species on MOR and FER (7–9) and for pentene-derived species on MFI (17). The absence of bands for π-bonded alkenes in the infrared spectra (Results and Discussion, Kinetic Measurement of Alkoxide Stabilities), however, indicates a preference for bound alkoxides over π-bound isobutene. The similar DFT-derived free energies for alkoxides and π-bonded alkenes render them interchangeable in our analysis of their stability and involvement as intermediates and make comparisons with experiment independent of which is chosen. In what follows, we choose the covalently bound butoxides as the prevalent form of isobutene-derived surface species in light of the experimental evidence.
Table 1.
DFT-derived enthalpies and Gibbs free energies of formation for bound alkene-derived species on TON and HPW from respective alkenes (503 K; 1 bar)
| TON | HPW | |||
| Species | ∆H, kJ⋅mol−1 | ∆G, kJ⋅mol−1 | ∆H, kJ⋅mol−1 | ∆G, kJ⋅mol−1 |
| π-Ethene | −62.5 | −8.90 | −19.3 | 8.94 |
| p-Ethoxide | −93.8 | −17.7 | −98.1 | −22.5 |
| π-Propene | −82.7 | −13.1 | −20.3 | −11.7 |
| p-Propoxide | −99.1 | −21.8 | −81.5 | −9.50 |
| s-Propoxide | −105 | −23.2 | −100 | −31.0 |
| π-trans-2-Butene | −96.5 | −22.0 | −17.3 | −12.5 |
| p-n-Butoxide | −119 | −18.5 | −82.9 | −5.10 |
| s-n-Butoxide | −119 | −28.4 | −93.1 | −31.1 |
| π-Isobutene | −104 | −24.4 | −21.4 | −17.9 |
| p-Isobutoxide | −91.5 | −24.8 | −76.9 | 13.1 |
| t-Isobutoxide | −58.3 | 3.88 | −116 | −38.1 |
Comparisons between DFT-derived energies and measured equilibrium constants require ensemble-averaging of theory-derived energies over all binding configurations (primary, secondary, tertiary; Scheme 1) to obtain the <Ki> values that molecules sample in the experiments (Eqs. 4–6). Fig. 7B and Table 2 show these DFT-derived <Ki>/K2 ratios at 503 K on TON and HPW; the optimized structures are shown in Fig. 8 for TON (Fig. S2 for HPW). These DFT-derived <Ki>/K2 ratios agree well in both their magnitude and their sensitivity to chain length and substitution with measured values (Fig. 7 and Table 2) when all binding configurations are included. The π-bonded isobutene-derived species is similar in energy to the p-isobutoxide (Table 1); thus, DFT-derived <Ki4>/K2 values would be similar irrespective of which configuration prevailed in practice. The data shown in Fig. 7 also indicate that the simulations used capture the measured effects attributed to steric hindrance and to the concave or convex surfaces on the stability of covalently bound bulkier alkoxides.
Table 2.
Measured (K) and DFT-derived (KDFT) equilibrium constants for alkoxide formation on TON, MOR, and HPW relative to ethoxide (503 K)
| Alkoxide | KTON | KDFT,TON | KMOR | KHPW | KDFT,HPW |
| C3 | 3.3 (0.55) | 3.1 | 2.9 (0.65) | 2.7 (0.43) | 2.6 |
| n-C4 | 5.0 (1.06) | 7.1 | 4.1 (1.24) | 4.6 (0.94) | 3.9 |
| i-C4 | 3.3 (0.65) | 3.2 | 7.4 (1.93) | 8.2 (2.04) | 10.4 |
Errors in measurement are in parentheses.
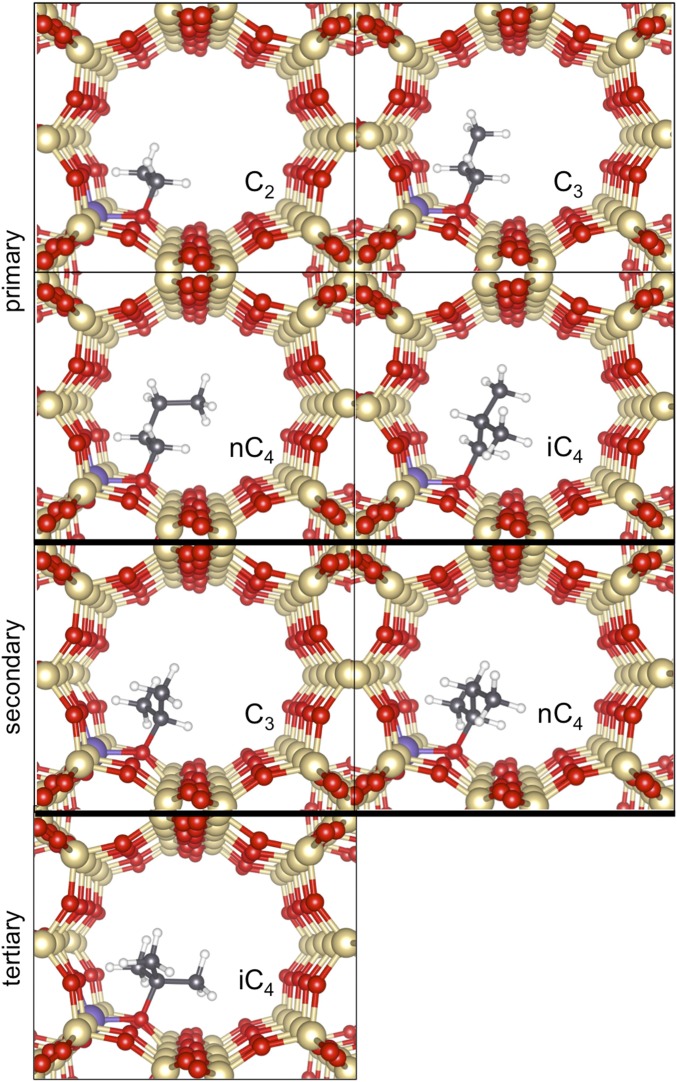
Fig. 8.
DFT-derived alkoxide structures in TON (Al2 site) with increasing chain length and substitution of alkene precursor (C2H4, C3H6, n-C4H8, and i-C4H8). Primary alkoxides are shown in the top two rows; secondary alkoxides, in the third row; and tertiary alkoxide, in the bottom row.
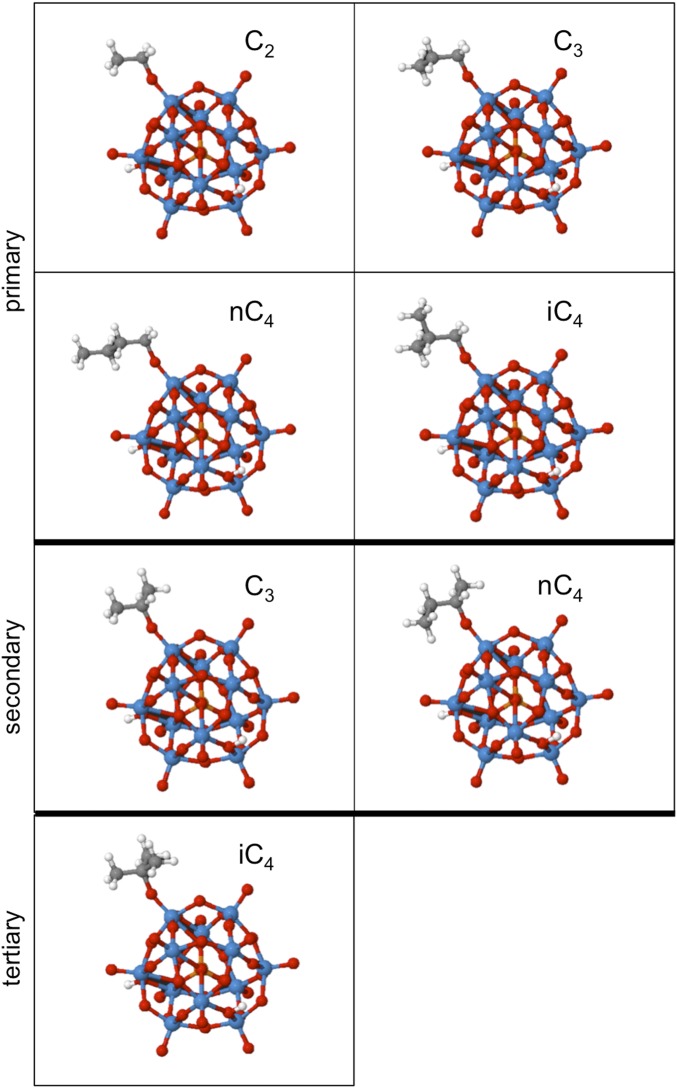
Fig. S2.
DFT-derived alkoxide structures on terminal HPW site with increasing chain length and substitution of alkene precursor (C2H4, C3H6, n-C4H8, and i-C4H8). Primary alkoxides are shown in the top two rows; secondary alkoxides, in the third row; and tertiary alkoxide, in the bottom row.
The inclusion of a (separable) dispersion component in the total energies (Etotal) derived from DFT-D3BJ functionals (39, 40) for zeolitic structure optimizations allows energies to be separated into their quantum mechanical (EQM) and attractive van der Waals (EvdW) components, where the repulsive components of interatomic potentials are included in the quantum-mechanical treatments through Pauli exclusion principles:
| [7] |
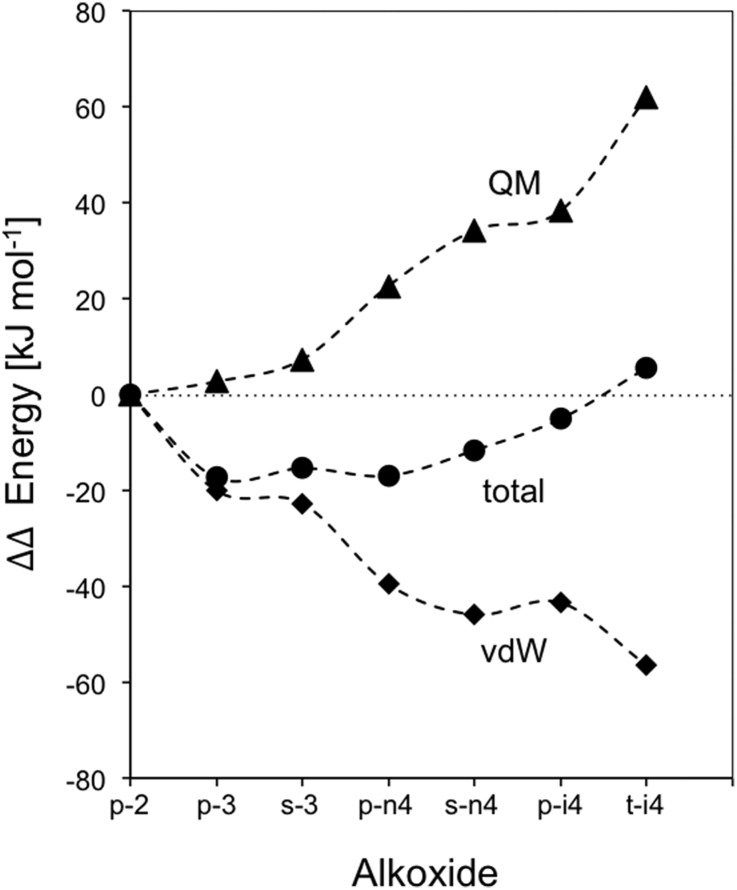
Both the EQM and the EvdW terms are referenced to the gaseous alkene and the H-TON form for each attachment isomer of each alkoxide. All alkoxides show negative formation energies with respect to bare protons and their respective gaseous alkenes; their energies are also lower than that for ethoxide on TON and become more so as their chain length increases, except for t-isobutoxide, which has a higher energy than propoxides, n-butoxides, and p-isobutoxides (Fig. 9). These trends with size reflect, in part, the more effective van der Waals contacts between larger alkoxides and TON channels, as evident from EvdW values that decrease with increasing chain length and substitution; the EvdW remains more favorable for t-isobutoxides than for the smaller and less substituted alkoxides, despite their higher total energy (Fig. 9). Clearly, such van der Waals stabilization of larger chains comes at an energy penalty, because of the need to balance the C–O bond lengths required for covalency with the lattice or molecular distortions required to preserve such covalency; such energy costs are compensated by the more effective van der Waals contacts created from such lattice distortion in a manner that leads to a lower total energy for the system.
Fig. 9.
Calculated alkoxide total electronic energies (●) and its two components [van der Waals (vdW; ◆) and quantum mechanical (QM; ▲)] for p-propoxide, s-propoxide, p-n-butoxide s-n-butoxide, p-isobutoxide, and t-isobutoxide relative to ethoxide on TON (∆∆Energy) (nomenclature as in caption of Scheme 1). Energies are referenced to H-TON and respective gaseous alkene precursors and dashed lines are to guide the eye.
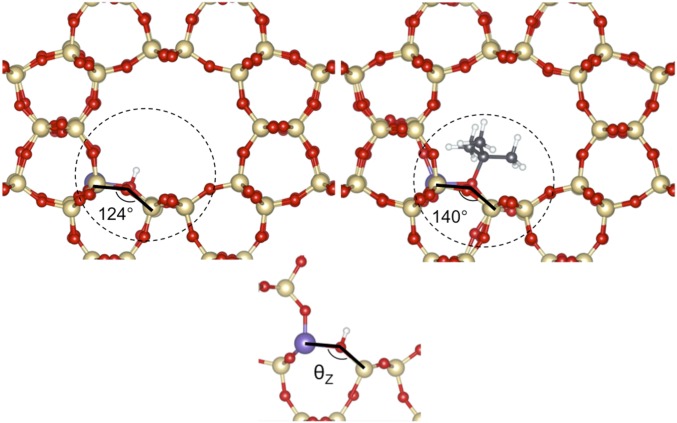
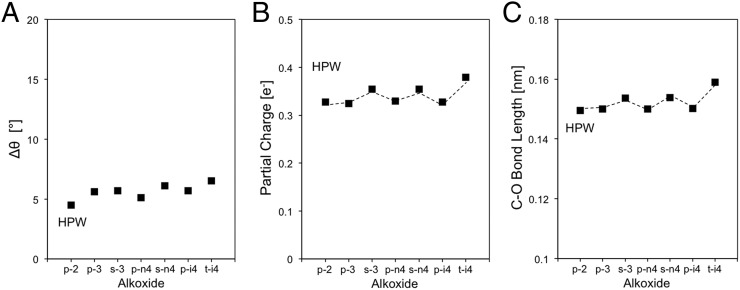
The geometric distortions and the energetic consequences for the alkoxide and the framework components are considered next. For the alkoxide, the C–O bond length in TON (at the O atom in Al–O–Si; Figs. 8 and 10) and HPW (at the terminal O atom; Fig. 6; or at the bridging O atom, Fig. S3) is similar for alkoxides with a given substitution even when their chain lengths differ (TON primary alkoxides, 0.1502–0.1504 nm, and secondary alkoxides, 0.1532–0.1537 nm; HPW primary alkoxides, 0.1439–0.1440 nm, and secondary alkoxides, 0.1458–0.1463 nm; Fig. 11A). The charge at the alkoxide is also essentially invariant with carbon number (TON primary alkoxides, 0.327–0.334 nm, and secondary alkoxides, 0.353–0.354 nm; HPW primary alkoxides, 0.356–0.363 nm, and secondary alkoxides, 0.377–0.381 nm; Fig. 11B); these similar charges and bond distances are consistent with the sharing of electrons and with the strict requirements in orbital overlap required for covalent bonds. Both the C–O bond length and the partial charge increase slightly with substitution, but their small and similar charge and C–O bond lengths lead to measured <Ki> values that do not depend on acid strength (Fig. 7A and Table 2), because of the predominantly covalent nature of bound alkoxides.
Fig. 10.
Structures of TON (Al2 site) in H-form (Top Left) and t-isobutoxide (Top Right) with portion of most displacements highlighted in the dashed circle. The Si–O–Al bridge (Bottom) shows the angle used for characterization in Fig. 11.
Fig. S3.
Properties of optimized alkoxide structures on HPW (bridging; ■): (A) Δθ between H form and alkoxide form of W–O–W in HPW, (B) partial charge of organic atoms, and (C) C–O bond length (nomenclature as in caption of Scheme 1).
Fig. 11.
Properties of optimized alkoxide structures on TON (Al2; ●) and HPW (terminal; ■): (A) C–O bond length, (B) partial charge of organic atoms, and (C) Δθ between H form and alkoxide form of Si–O–Al bridge in TON and O–W–O in HPW (nomenclature as in caption of Scheme 1).
DFT-Derived Measures of Structural Flexibility of Aluminosilicate Frameworks and Associated Energy Costs upon Alkoxide Formation.
These similar alkoxide structures on solids with different acid strength and confining voids indicate that the energetic cost of the lattice distortions that enhance van der Waals contacts is imposed on the inorganic framework; such phenomena are most evident for t-isobutoxide. These distortions are assessed here by comparing optimized structures for the inorganic framework in its proton form and with a bound alkoxide. We show that such distortions can occur, and thus become evident, only when structures are optimized using functionals that rigorously account for dispersive forces. The angle (θ) subtended by the lattice O atom that forms the C–O with either the bound alkoxide (Si–O–Al for TON, Fig. 10; O–W–O for HPW, Fig. 6) or the H–O bond in the unperturbed acid differ significantly in the H and alkoxide forms of these acids. Fig. 11C shows how these angles are affected by the binding of each alkoxide on TON and HPW. The dihedral angles (O–W–O) for terminally bound alkoxides (and for bridge-bound alkoxides (W–O–W); Fig. S3) on HPW change with their size (structures in Fig. S2) to a much lesser extent than on TON (Si–O–Al) (Fig. 11C). The primary alkoxides derived from ethene, propene, and n-butenes changed the dihedral angle on TON (Si–O–Al; 9.5–9.6°; Fig. 11C) to similar extents, but such distortions were smaller than those observed upon formation of the bulkier p-isobutoxides (11°; Fig. 11C). On TON, lattice distortions upon alkoxide formation increased more strongly with substitution than with the chain length of alkoxides; tert-isobutoxides disrupt Si–O–Al bridges most strongly (15.8°, optimized structure in Fig. 10; distortion highlighted by circle), in contrast with the minimal distortion imposed by the formation of tert-isobutoxides on HPW (15.8°, optimized structure in Fig. 6). The lack of distortion at the terminal O atom in HPW reflects its convex nature, which allows the formation of even bulky t-isobutoxides at the optimal distances imposed by covalency without significantly disrupting the inorganic solid structure. This evidence suggests that these systems respond to steric effects by distorting the inorganic structure to preserve orbital overlap without requiring more energetic distortion of the alkoxide organic moiety; the extent of such framework distortions to accommodate the alkoxide is much more evident for concave than convex geometries (e.g., TON vs. HPW).
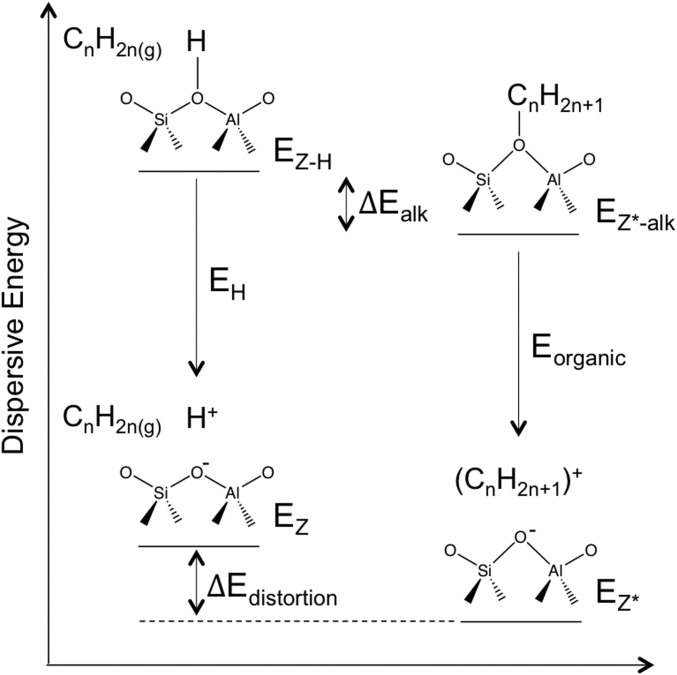
Next, we address the energetic consequences of such framework distortions by determining the energy differences between the initial framework with the charge-proton and the same framework containing a bound alkoxide. These energies are calculated using the two-body interaction models implemented in the D3BJ functional (39, 40) and include the effects of distortions on all atoms in the inorganic catalyst (Si, Al, and O), but excludes those with the organic moieties and those among the atoms in the organic moieties, so as to rigorously isolate the energetic costs of distortions. These methods give the framework energies in both alkoxide (EZ*) and the proton (EZ) forms (Scheme 2); larger deviations from the proton form reflect larger distortions of the inorganic host. The distortion energy is defined as follows:
| [8] |
where EZ*-alk and EZ-H are the D3BJ (attractive) interaction energies of the fully optimized alkoxide and proton structures, respectively; Eorganic and EH represent the dispersive energies of the organic component and proton, respectively.
Scheme 2.
Dissection of distortion energy (Eq. 8) in terms of dispersive energies. The distortion energy (Edistortion) depends on the difference in dispersive energy between optimized inorganic component from the alkoxide (EZ*) and proton (EZ) form, which are defined as the difference in dispersive energy between the fully optimized structure (Ealk-Z* and EH-Z) and the organic component (Eorganic and EH, respectively).
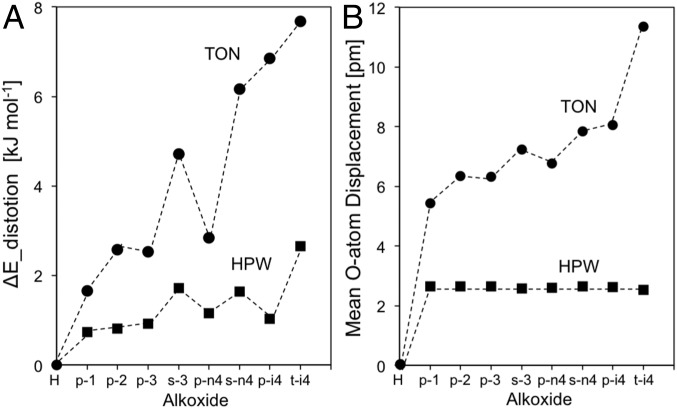
These distortion energies are shown in Fig. 12A; their magnitude is larger for all alkoxides on TON than on HPW, indicating that the inorganic host adapts to the inclusion of the alkoxide to preserve the length of the covalent bond required for effective orbital overlap in the case of concave environments and that it does so specially for bulkier alkoxides. These distortion energies become larger as substitution increases, but they vary only slightly with chain length on HPW acids, as also observed for dihedral angles upon alkoxide formation (Fig. 11C). For instance, all primary alkoxides on HPW exhibit similar distortion energies (0.81–1.2 kJ⋅mol−1), irrespective of chain length, and such distortions are only slightly smaller than for secondary alkoxides (1.6–1.7 kJ⋅mol−1). In contrast, alkoxide formation on TON frameworks results in distortion energies that are sensitive to both chain length and substitution, because van der Waals contacts can be significantly enhanced through lattice distortions away from the binding T site, the extent of which depends on the size and shape of the bound alkoxides.
Fig. 12.
(A) Framework distortion energies (Eq. 8) and (B) mean displacements of oxygen atoms (Eqs. 9 and 10) of alkoxide formation on TON (Al2; ●) and HPW (terminal; ■) relative to the H form of each catalyst (nomenclature as in caption of Scheme 1).
The larger distortion energies for TON compared with those in HPW are consistent with the magnitude of the mean displacements () of the atoms in the framework, defined as follows:
| [9] |
where do,m is given by the following:
| [10] |
Here, each O-atom m has coordinates of (xalk, yalk, zalk)m and (xH, yH, zH)m in the alkoxide and the H form, respectively, and the displacement of each O atom is then averaged over all O atoms in the unit cell (M) (Eq. 9). These O-atom displacements are the most sensitive descriptors of distortion because O atoms are most strongly displaced and their shifts cause the largest effects on van der Waals interactions. The O-atom displacement upon alkoxide binding on HPW (<do> = 2.58–2.65 pm) is insensitive to alkoxide chain length and much smaller for all alkoxides than on TON (Fig. 12B). For TON, <do> increase slightly with chain length but more strongly with substitution (p-ethoxide: 6.34 pm; t-isobutoxide: 11.3 pm; Fig. 12B), consistent with values for ΔEdistortion in Fig. 12A that vary slightly with chain length each attachment configuration but more so with substitution.
Distortion energies (ΔEdistortion) and O-atom displacements (<do>) reflect rearrangements that seek to maximize van der Waals contacts between the TON framework and the alkoxide. In contrast, dihedral angles of alkoxide attachment (Δθ; TON: Si–O–Al; HPW: O–W–O) reflect local distortions required to maintain orbital overlap in the covalent C–O bond between the alkoxide and the framework. Their combined effects cause particularly large distortions for p-isobutoxides than for other primary alkoxides or for s-propoxide and s-n-butoxide (Fig. 12 A and B: ΔEdistortion: p-isobutoxide, 6.9 kJ⋅mol−1; s-propoxide, 4.7 kJ⋅mol−1); yet, Δθ on TON values for p-isobutoxide were smaller than for normal s-alkoxides (Fig. 11C). We conclude that O atoms distant from the binding T site are more strongly displaced for p-isobutoxides than for the smaller alkoxides, because such distortions lead to more effective van der Waals contacts as the alkoxide size approaches that of the confining voids (structures depicted in Fig. 8).
The strong effects of covalent bond distances on alkoxide energies require the framework distortions that we observe, especially for bulky alkoxides. The energy costs of framework distortions are recovered by enhanced van der Waals contacts, in a manner that decreases the overall energy of the system and leads to more stable bound alkoxide configurations. The quantum-mechanical portion of the total energy increases with increasing “bulkiness” (Fig. 9, QM), whereas the van der Waals component becomes more negative (Fig. 9, vdW). Thus, the van der Waals interactions more than compensate for the energetic penalties of framework distortions required to preserve covalency, up to the point where alkoxides become sufficiently bulky, at which point they become less stable relative to ethoxides (t-isobutoxide ΔΔE = 5.59 kJ⋅mol−1; Fig. 9, “total”).
The high reactivity of alkenes for C–C bond formation necessitates clever and thorough kinetic experiments to identify the elusive nature of alkene-derived species on solid Brønsted acids. Here, we have benchmarked kinetic and spectroscopic measurements with state-of-the-art DFT to resolve experimentally inaccessible information. The use of DFT has also led to the previously unrecognized phenomenon of local distortion to the crystalline, yet flexible lattice, which occurs upon formation of bound species in zeolitic materials.
Conclusions
Stabilities of bound alkene-derived species were investigated by combining kinetic and spectroscopic data with DFT. Relative alkoxide stabilities were measured experimentally as the ratio of equilibrium constants from alkene coupling reactions of ethene, n-butene, and isobutene with propene using microporous [TON (10-MR), MOR (12-MR)] and mesoporous [Keggin polyoxometalate clusters on silica (HPW)] solid acids with different acid strength and void size and shape; absolute adsorption constants were extracted from low-pressure measurement of turnover rates and infrared spectra using homogenous feeds. These measurements indicate that alkoxides formed in large voids (MOR, HPW) have similar stabilities despite differences in acid strength, consistent with the covalent nature of these species, but bulkier alkoxides formed within these larger voids are more stable than less substituted ones. These bulkier alkoxides become destabilized within smaller concave environments (TON), a trend that is corroborated by DFT when functionals account for the pertinent dispersion forces ubiquitous in these host–guest systems. We propose this destabilization is, in part, caused by framework distortions required to avoid steric repulsion while maintaining the C–O distance of the alkoxide bond requisite for covalency. These distortions (quantified in terms of O-atom displacement, alkoxide dihedral angles, and distortion energies) increase with increasing chain length and substitution of the alkoxide within TON, but are mostly insignificant on HPW. This restructuring of the inorganic host to optimize interaction with the organic guest as well as the stability of these bound guest species are necessary to extrapolate to other host–guest pairs and to control reactivity and selectivity through changes in acid strength and the geometry of the confining voids.
Acknowledgments
We thank Drs. David Hibbitts (University of California, Berkeley; University of Florida), Will Knaeble (University of California, Berkeley), Matthew Neurock (University of Minnesota), and Craig Plaisance (University of Virginia) for advice on matters of theory, and Drs. Eric Doskocil (BP), Glenn Sunley (BP), and John Shabaker (BP) for extensive technical discussions throughout the course of these studies. We also acknowledge with thanks the financial support from the National Science Foundation for a Graduate Research Fellowship (to M.L.S.) and from the BP XC2 Program for all research activities leading to the results reported in this article. Computational resources were provided by BP High Performance Computing (BP, p.l.c.) and by the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation (Grant CHE-140066).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1619557114/-/DCSupplemental.
References
- 1.Eder F, Stockenhuber M, Lercher JA. Brønsted acid site and pore controlled siting of alkane sorption in acidic molecular sieves. J Phys Chem B. 1997;101:5414–5419. [Google Scholar]
- 2.Eder F, Lercher JA. Alkane sorption in molecular sieves: The contribution of ordering, intermolecular interactions, and sorption on Brønsted acid sites. Zeolites. 1997;18:75–81. [Google Scholar]
- 3.Lercher JA, Seshan K. Sorption and activation of hydrocarbons by molecular sieves. Curr Opin Solid State Mater Sci. 1997;2:57–62. [Google Scholar]
- 4.Gorte RJ, White D. Interactions of chemical species with acid sites in zeolites. Top Catal. 1997;4:57–69. [Google Scholar]
- 5.Grady MC, Gorte RJ. Adsorption of 2-propanol and propene on H-ZSM-5: Evidence for stable carbenium ion formation. J Phys Chem. 1985;89:1305–1308. [Google Scholar]
- 6.Sarazen ML, Doskocil E, Iglesia E. Effects of void environment and acid strength on alkene oligomerization selectivity. ACS Catal. 2016;6:7059–7070. [Google Scholar]
- 7.Tuma C, Sauer J. Protonated isobutene in zeolites: tert-Butyl cation or alkoxide? Angew Chem Int Ed Engl. 2005;44:4769–4771. doi: 10.1002/anie.200501002. [DOI] [PubMed] [Google Scholar]
- 8.Chu Y, Han B, Zheng A, Yi X, Deng F. Pore selectivity for olefin protonation reactions confined inside mordenite zeolite: A theoretical calculation study. J Phys Chem C. 2013;117:2194–2202. [Google Scholar]
- 9.Tuma C, Kerber T, Sauer J. The tert-butyl cation in H-zeolites: Deprotonation to isobutene and conversion into surface alkoxides. Angew Chem Int Ed Engl. 2010;49:4678–4680. doi: 10.1002/anie.200907015. [DOI] [PubMed] [Google Scholar]
- 10.Spoto G, et al. IR study of ethene and propene oligomerization on H-ZSM-5—hydrogen-bonded precursor formation, initiation and propagation mechanisms and structure of the entrapped oligomers. J Chem Soc Trans. 1994;90:2827–2835. [Google Scholar]
- 11.Geobaldo F, Spoto G, Bordiga S, Lamberti C, Zecchina A. Propene oligomerization on H-mordenite: Hydrogen-bonding interaction, chain initiation, propagation and hydrogen transfer studied by temperature-programmed FTIR and UV-VIS spectroscopies. J Chem Soc Trans. 1997;93:1243–1249. [Google Scholar]
- 12.Sarazen M, Doskocil E, Iglesia E. Catalysis on solid acids: Mechanism and catalyst descriptors in oligomerization reactions of light alkenes. J Catal. 2016;344:553–569. [Google Scholar]
- 13.Aronson MT, Gorte RJ, Farneth WE. An infrared spectroscopy study of simple alcohols adsorbed on H-ZSM-5. J Catal. 1987;105:455–468. [Google Scholar]
- 14.Aronson MT, Gorte RJ, Farneth WE, White D. Carbon-13 NMR identification of intermediates formed by 2-methyl-2-propanol adsorption in H-ZSM-5. J Am Chem Soc. 1989;111:840–846. [Google Scholar]
- 15.Bhan A, Joshi YV, Delgass WN, Thomson KT. DFT investigation of alkoxide formation from olefins in H-ZSM-5. J Phys Chem B. 2003;107:10476–10487. [Google Scholar]
- 16.van Santen RA. Quantum-chemistry of zeolite acidity. Catal Today. 1997;38:377–390. [Google Scholar]
- 17.Hajek J, et al. On the stability and nature of adsorbed pentene in Brønsted acid zeolite H-ZSM-5 at 323 K. J Catal. 2016;340:227–235. [Google Scholar]
- 18.Boronat M, Zicovich-Wilson CM, Viruela P, Corma A. Influence of the local geometry of zeolite active sites and olefin size on the stability of alkoxide intermediates. J Phys Chem B. 2001;105:11169–11177. [Google Scholar]
- 19.Boronat M, Viruela PM, Corma A. Reaction intermediates in acid catalysis by zeolites: Prediction of the relative tendency to form alkoxides or carbocations as a function of hydrocarbon nature and active site structure. J Am Chem Soc. 2004;126:3300–3309. doi: 10.1021/ja039432a. [DOI] [PubMed] [Google Scholar]
- 20.Kärger J, Bülow M, Millward GR, Thomas JM. A phenomenological study of surface barriers in zeolites. Zeolites. 1986;6:146–150. [Google Scholar]
- 21.Kocirik M, Struve P, Fiedler K, Bulow M. A model for the mass-transfer resistance at the surface of zeolite crystals. J Chem Soc Faraday Trans 1 Phys Chem Condens Phases. 1988;84:3001–3013. [Google Scholar]
- 22.Vigne´-Maeder F, El Amrani S, Ge’lin P. An approach to the surface barrier concept in diffusion in zeolites by computer simulation. J Catal. 1992;134:536–541. [Google Scholar]
- 23.Fraenkel D, Cherniavsky M, Ittah B, Levy M. Shape-selective alkylation of naphthalene and methylnaphthalene with methanol over H-ZSM-5 zeolite catalysts. J Catal. 1986;101:273–283. [Google Scholar]
- 24.Derouane EG, Andre J-M, Lucas AA. Surface curvature effects in physisorption and catalysis by microporous solids and molecular sieves. J Catal. 1988;110:58–73. [Google Scholar]
- 25.Martens JA, et al. Evidences for pore mouth and key–lock catalysis in hydroisomerization of long n-alkanes over 10-ring tubular pore bifunctional zeolites. Catal Today. 2001;65:111–116. [Google Scholar]
- 26.Barri SAI, Young D. 1984. Eur Patent Appl EP0124998A3 and Publ EP0124998 A2.
- 27.Ball WJ, Barri SAI, Young D. 1986. Eur Patent Appl EP19830305073 and Publ EP0104800 B1.
- 28.Gounder R, Iglesia E. Catalytic consequences of spatial constraints and acid site location for monomolecular alkane activation on zeolites. J Am Chem Soc. 2009;131:1958–1971. doi: 10.1021/ja808292c. [DOI] [PubMed] [Google Scholar]
- 29.Knaeble W, Carr RT, Iglesia E. Mechanistic interpretation of the effects of acid strength on alkane isomerization turnover rates and selectivity. J Catal. 2014;319:283–296. [Google Scholar]
- 30.Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys Rev B Condens Matter. 1993;47:558–561. doi: 10.1103/physrevb.47.558. [DOI] [PubMed] [Google Scholar]
- 31.Kresse G, Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys Rev B Condens Matter. 1994;49:14251–14269. doi: 10.1103/physrevb.49.14251. [DOI] [PubMed] [Google Scholar]
- 32.Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci. 1996;6:15–50. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- 33.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- 34.Blöchl PE. Projector augmented-wave method. Phys Rev B Condens Matter. 1994;50:17953–17979. doi: 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
- 35.Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B. 1999;59:1758–1775. [Google Scholar]
- 36.Hammer B, Hansen LB, Nørskov JK. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys Rev B. 1999;59:7413–7421. [Google Scholar]
- 37.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 38.Zhang Y, Yang W. Comment on “Generalized Gradient Approximation Made Simple.”. Phys Rev Lett. 1998;80:890. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 39.Grimme S, Antony J, Ehrlich S, Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 40.Grimme S, Ehrlich S, Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J Comput Chem. 2011;32:1456–1465. doi: 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- 41.Monkhorst HJ, Pack JD. Special points for Brillouin-zone integrations. Phys Rev B. 1976;13:5188–5192. [Google Scholar]
- 42.Campbell CT, Sellers JRV. Enthalpies and entropies of adsorption on well-defined oxide surfaces: Experimental measurements. Chem Rev. 2013;113:4106–4135. doi: 10.1021/cr300329s. [DOI] [PubMed] [Google Scholar]
- 43.Qian X, et al. Quasiatomic orbitals for ab initio tight-binding analysis. Phys Rev B. 2008;78:245112. [Google Scholar]
- 44.Chan T-L, et al. Highly localized quasiatomic minimal basis orbitals for Mo from ab initio calculations. Phys Rev B. 2007;76:205119. [Google Scholar]
- 45.Lu WC, Wang CZ, Chan TL, Ruedenberg K, Ho KM. Representation of electronic structures in crystals in terms of highly localized quasiatomic minimal basis orbitals. Phys Rev B. 2004;70:41101. [Google Scholar]
- 46.Lu WC, et al. Molecule intrinsic minimal basis sets. I. Exact resolution of ab initio optimized molecular orbitals in terms of deformed atomic minimal-basis orbitals. J Chem Phys. 2004;120:2629–2637. doi: 10.1063/1.1638731. [DOI] [PubMed] [Google Scholar]
- 47.Corma A. Inorganic solid acids and their use in acid-catalyzed hydrocarbon reactions. Chem Rev. 1995;95:559–614. [Google Scholar]
- 48.Macht J, Janik MJ, Neurock M, Iglesia E. Catalytic consequences of composition in polyoxometalate clusters with Keggin structure. Angew Chem Int Ed Engl. 2007;46:7864–7868. doi: 10.1002/anie.200701292. [DOI] [PubMed] [Google Scholar]
- 49.Jones AJ, Iglesia E. The strength of Brønsted acid sites in microporous aluminosilicates. ACS Catal. 2015;5:5741–5755. [Google Scholar]