Visual working memory buffers information retrieved from visual long-term memory

Significance

How do we retrieve long-term memory? Here, we show that by measuring subjects’ electroencephalogram (EEG), we can directly observe the dynamic process of long-term memory retrieval. Our findings suggest that retrieved information becomes consciously available by being represented in a working-memory format that is similar to that used to represent new perceptual inputs. Furthermore, we show that our EEG measures can track the process of retrieving and combining two long-term memories acquired separately (e.g., image of a horse and a pair of wings) into one working-memory representation (e.g., a Pegasus). Thus, our results not only provide direct neural support for a long-assumed theory of memory retrieval but also demonstrate how flexible retrieval allows for creative thought.

Abstract

Human memory is thought to consist of long-term storage and short-term storage mechanisms, the latter known as working memory. Although it has long been assumed that information retrieved from long-term memory is represented in working memory, we lack neural evidence for this and need neural measures that allow us to watch this retrieval into working memory unfold with high temporal resolution. Here, we show that human electrophysiology can be used to track information as it is brought back into working memory during retrieval from long-term memory. Specifically, we found that the retrieval of information from long-term memory was limited to just a few simple objects’ worth of information at once, and elicited a pattern of neurophysiological activity similar to that observed when people encode new information into working memory. Our findings suggest that working memory is where information is buffered when being retrieved from long-term memory and reconcile current theories of memory retrieval with classic notions about the memory mechanisms involved.

Humans are capable of storing an essentially limitless amount of information in long-term memory and can remember specific pieces of information when needed to guide behavior. For over a century, researchers have proposed that, when humans retrieve information from long-term memory, we do this by bringing the information back into working memory (1–3). This has become so engrained in the dogma regarding how human memory works that retrieving information from long-term memory into working memory is described in introductory textbooks (e.g., refs. 4 and 5). However, although there is behavioral evidence in line with the notion that information retrieved from long-term memory is brought back into working memory (ref. 6; see ref. 7 for a review of additional classic evidence; refs. 8–10), a direct demonstration that this is occurring in brain is needed. If we were able to track this cognitive process, we could use it to understand the fine-grained dynamics of memory retrieval.

In the present study, we took advantage of the fact that encoding new sensory information into working memory is capacity limited (11–16). Neuroscientific studies have established that the encoding of a subset of the available visual information into working memory can be measured by frequency-specific oscillations of subjects’ electroencephalograms (EEGs) (17–20). Specifically, the magnitude of suppression of alpha-band oscillations (8–13 Hz) measured across parieto-occipital channels as new information is held in working memory changes as additional information is loaded into working memory and hits an asymptote at a subject’s working-memory capacity estimated from behavioral performance. We chose this neural correlate of working memory over other correlates (e.g., the contralateral delay activity in ref. 12) because it allowed the estimation of working-memory load without necessitating the presentation of to-be-ignored distractors. Here, we asked whether the neural and behavioral metrics of visual working-memory storage that have been studied when new information is presented are also observed when old information is retrieved from long-term memory.

The basic logic of our approach was simple. If information is brought back into visual working memory when it is retrieved from long-term memory, then we should see retrieval marked by the similar capacity limits and neurophysiological markers that characterize the storage of perceptual information in working memory. For example, if a subject’s behavior and brain activity indicate that they can encode no more than three objects’ worth of visual information from a scene into visual working memory when this information is first viewed, then even after a detailed representation of that scene has been built up in long-term memory, we should find that they retrieve no more than three objects’ worth of information at a time when trying to remember the scene.

Results

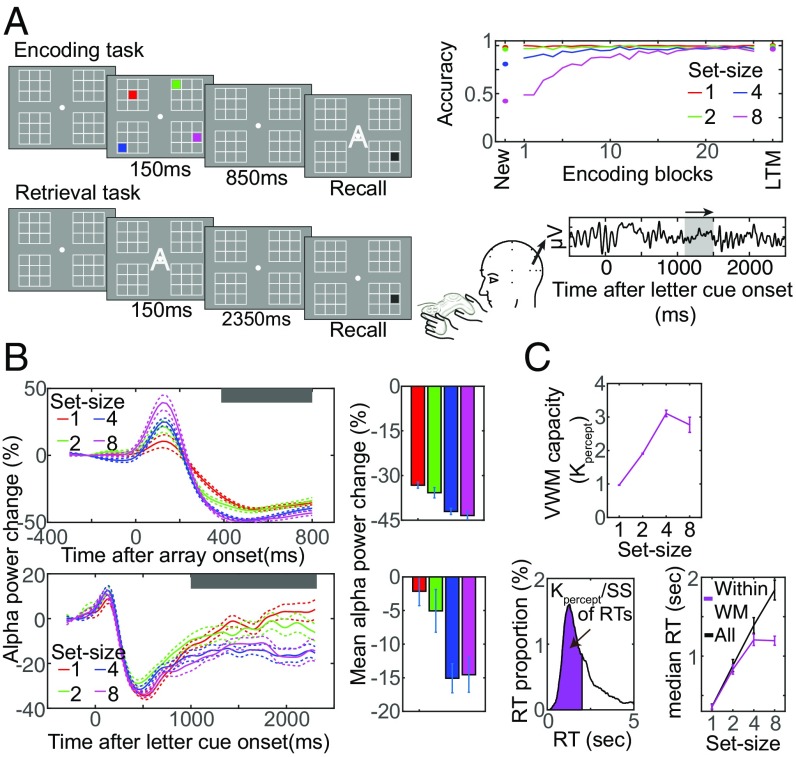
In experiment 1, we first had subjects learn four spatial arrays of colored squares. We used these simplified scenes so that we could estimate the amount of information stored and retrieved from long-term memory. The arrays consisted of one array of each set size 1, 2, 4, and 8 colored squares (Fig. 1A for an example array of four squares). During the learning phase, each to-be-learned array was presented for eight times in a row, interleaved with new arrays to measure visual working-memory capacity (as described later in this section), across 25 blocks (meaning each to-be-learned array was presented 200 times in total). We used this repeated presentation to ensure that even the arrays with eight objects were learned. Subjects’ task was to press one of eight possible color buttons on a handheld game pad to indicate the color that had appeared at the location probed by the gray cue at the end of the trial (Fig. 1A). The probe remained visible until they responded, and during the period that this memory probe appeared, we also showed letters at fixation to serve as labels for each of the to-be-learned arrays (the letters A–D, for each array, and N for “new” if it was a new, randomly generated array). Subjects were instructed to learn these labels for the repeated arrays. As shown in Fig. 1A, recall accuracy reached ceiling within these 200 trials across all set sizes. Learning these four arrays took this extended period due to interference created by our randomly interleaving nonrepeating arrays to measure subjects’ working-memory capacity for new visual input. Finally, we tested subjects’ memory for the learned arrays with a retrieval task at the end of the experiment. Each trial of the retrieval task began with the presentation of the white letter cue for one of the arrays. Then, 2.4 s after the letter cue, the gray probe appeared and subjects had to report the color of the object at that location with a button press, just like in the learning task. Recall that classic theories of human memory predict that retrieving information from long-term memory in the final phase of the experiment should exhibit the similar signatures of working-memory storage that we measure during the temporary storage of new arrays of objects.

Fig. 1.

The experimental paradigm and the results for experiment 1. (A) Left panel shows example schematics of the encoding and the retrieval task for set size 4 array in experiment 1. Top Right panel shows the behavioral result for the encoding of new arrays (New) and old arrays across encoding blocks as well as retrieval performance for old arrays [long-term memory (LTM)]. Bottom Right panel demonstrates the schematic of our oscillatory analysis. The waveform represents an EEG signal obtained from a single trial, and the gray box indicates the 400-ms-long sliding window used to estimate the oscillatory activity at the central time point of the sliding window. (B) Electrophysiological results for the encoding and the retrieval task. Waveforms on the Left show the modulation of parieto-occipital alpha power during the encoding task (Top) and the retrieval task (Bottom). The doted margins indicate the within-subject SEM at a given time point, and the time value on x axis for the alpha-power suppression reflects the center of 400-ms-long sliding window. The gray boxes indicate the time window with which the mean alpha-power suppression was calculated. The bar graphs show the mean alpha-power suppression during corresponding retention intervals. (C) The top line graph shows the set size function of visual working-memory (WM) capacity estimates (K_percept) that were calculated for each set size based on the encoding performance for nonrepeating (new) arrays. The bottom left panel depicts the schematic of correct recall RT analysis for a set size SS array that isolated the correct recall RTs for an item that was actively represented within WM at the moment of recall prompt (within-WM RTs, shown in purple) from all correct RTs. K was estimated by the initial encoding performance for new arrays of the corresponding set size SS. The line graph on the Right shows the median RTs for within-WM trials and all trials. The error bars show the within-subject SEM.

During the learning phase of experiment 1, we presented four to-be-learned arrays repeatedly. Critically, they were interleaved with nonrepeating unique arrays (i.e., “new arrays”). The new arrays allowed us to determine each subject’s working-memory capacity for new visual information by testing their memory for a probe item after a retention interval of only 1 s. For these new arrays, behavioral performance on this working-memory test monotonically declined as a function of set size [F_(3,84) = 406.1, P < 0.001]. The working-memory load estimates across set sizes increased up to three objects, and then leveled off, resulting in a significant quadratic effect [t₍₂₇₎ = 22.2, P < 0.001 for K1_percept < K4_percept; t₍₂₇₎ = 13.6, P < 0.001 for K2 _percept < K4 _percept; t₍₂₇₎ = 2.1, P < 0.05 for K4_percept > K8_percept; Fig. 1C; see SI Results for further discussion]. This is consistent with numerous previous findings that individuals' visual working-memory capacity is about three to four simple objects’ worth of information. Our electrophysiological data exhibited the same capacity-limited signature of storage in working memory that we saw with the subjects’ behavior (18). As shown in Fig. 1B, Top, shortly following a transient increase in the parieto-occipital alpha power reflecting low-level perceptual encoding of the to-be-remembered stimuli (but see also ref. 21 for an alternative explanation), we observed a strong parieto-occipital alpha-power suppression that monotonically increased in magnitude up to the subjects’ working-memory capacity measured behaviorally, with no further increase thereafter [t₍₂₇₎ = 4.6, P < 0.001 for set size 1 < set size 4; t₍₂₇₎ = 2.6, P < 0.05 for set size 2 < set size 4; t₍₂₇₎ = 1.3, not significant (NS) for set size 4 > set size 8, Fig. 1B].

The key prediction derived from the classic memory models is that the parieto-occipital alpha activity should show the similar pattern of the capacity-limited power reduction we just observed elicited by these new arrays when the learned arrays are retrieved from long-term memory. Although we anticipated that it might take longer for the capacity-limited set size effect to emerge because it generally takes longer to retrieve and represent information from long-term memory based on a sparse retrieval cue than it does for the visual system to process new inputs, we did not have a precise prediction as to when it would emerge. However, what we did predict was that, once the capacity-defined set size effect emerged, it would be persistent throughout the retention interval.

To test this prediction, we had subjects perform a retrieval task after learning was complete as described briefly above. Recall that, in the retrieval task, we presented letter cues that subjects learned in association with the learned arrays. Subjects were instructed to retrieve the array from long-term memory when the cue was presented so that they could report the color of the memory probe that would follow (Fig. 1A). As Fig. 1B, Bottom, shows, the parieto-occipital alpha-power suppression exhibited the similar capacity-defined set size function that we saw when these same subjects held information from new arrays in working memory [t₍₂₇₎ = 3.7, P < 0.001 for set size 1 < set size 4; t₍₂₇₎ = 2.1, P < 0.05 for set size 2 < set size 4; t₍₂₇₎ = 0.5, NS for set size 4 > set size 8]. These findings are consistent with the hypothesis that the information retrieved from long-term memory is buffered in working memory, thus facing the similar capacity limit as perceived information.

Behavioral results from the retrieval task further supported the conclusion that information is brought back into working memory when retrieved from long-term memory. If the classic idea of retrieval from long-term memory into working memory is correct, then the correct retrieval of the probed item can result from two types of retrieval (22–24). On some trials, the probed item was actively represented within working memory at the time the gray memory probe was presented, making it readily accessible, thus producing fast reaction times (RTs) (within–working-memory RTs). The other type of trials is that in which the probed item was not represented within working memory when the memory probe was presented, and thus, it had to be retrieved from long-term memory into working memory so that the color can be reported. Thus, the RTs for such trials will be longer. When we isolated within–working-memory RTs by using the set size-specific working-memory load estimate for new perceptual input obtained from the encoding task (K_percept), they revealed the classic capacity-defined set size effect (Fig. 1C, Bottom; Materials and Methods) [t₍₂₇₎ = 8.8, P < 0.001 for set size 1 < set size 4; t₍₂₇₎ = 5.6, P < 0.001 for set size 2 < set size 4; t₍₂₇₎ = 0.2, NS, for set size 4 > set size 8]. Taken together, our results suggest that the amount of information retrieved into working memory from long-term memory at a given time is limited to three objects’ worth of information.

Now that we established that information retrieved from long-term memory is maintained in working memory just like newly perceived information, we next used our ability to electrophysiologically track retrieval from long-term memory to understand the flexibility of this process. Specifically, in experiment 2, we tested the hypothesis that subjects can selectively retrieve a subset of a learned array, and in experiment 3, we tested the hypothesis that subjects can combine two representations that were learned separately. After subjects learned arrays of colored squares, as in experiment 1, we had subjects perform different retrieval tasks in experiments 2 and 3.

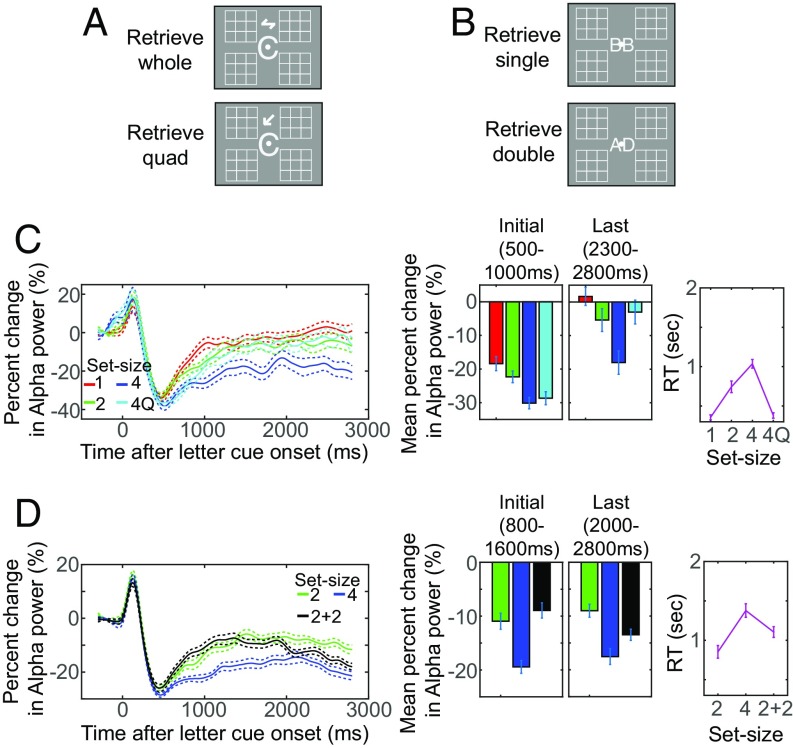
In experiment 2, subjects either retrieved an entire array indicated by a letter cue or a part of the array indicated by an arrow cue presented together with the letter cue (Fig. 2A). When subjects retrieved entire arrays of set size 1, 2, and 4 in experiment 2, the parieto-occipital alpha-power suppression showed the capacity-defined set size function (Fig. 2C), thus replicating experiment 1. When subjects were cued to retrieve one item from a set size 4 array, the alpha-power suppression was initially identical to that for the retrieval of all four items [t₍₁₉₎ = 0.7, NS for set size 4 whole > set size 4 quad; t₍₁₉₎ = 3.3, P < 0.01 for set size 1 < set size 4 quad]. However, toward the end of the retrieval interval, the level of alpha suppression shifted to be identical to the level we measured during the retrieval of a set size 1 array [t₍₁₉₎ = 2.3, P < 0.05 for set size 4 whole > set size 4 quad; t₍₁₉₎ = 1.2, NS for set size 1 < set size 4 quad]. These findings suggest that the time course of alpha suppression could be used to measure when the contents of working memory have been focused on a target memory when multiple memories compete for retrieval. Our analyses of RT provided converging evidence for these conclusions drawn from the brain activity as subjects’ ultimate behavioral response for one-object arrays was the same as when subjects selected one object from arrays of four objects [Fig. 2C, Right, t₍₁₉₎ = 18.8, P < 0.001 for set size 4 whole > set size 4 quad; t₍₁₉₎ = 1.1, NS, for set size 1 < set size 4 quad]. These results indicate that individuals initially retrieve entire arrays of information within working-memory capacity and then remove the task-irrelevant items from working memory. This measure of human brain activity is consistent with computational models of memory that propose long-term memory retrieval involves the initial reinstatement of a learned context when a specific item needs to be remembered (25).

Fig. 2.

The experimental paradigms and the results for experiments 2 and 3. (A) The retrieval cues used in experiment 2. (B) The retrieval cues used in experiment 3. (C and D) The results for the retrieval task in experiments 2 and 3. Waveforms on the Left show the modulation of the parieto-occipital alpha power during the retrieval task for experiment 2 (C) and experiment 3 (D). The dotted margins indicate the within-subject SEM at a given time point, and the time value on x axis for the alpha-power suppression reflects the center of 400-ms-long sampling window. The bar graphs show the mean alpha-power suppression during corresponding retention intervals. The line graphs on the Right shows set size functions derived from median RT during the retrieval task for experiment 2 (C) and experiment 3 (D). The error bars show the within-subject SEM.

In experiment 3, we presented two letter cues simultaneously indicating that subjects were to remember two entire arrays (Fig. 2B). When two matching letter cues prompted the retrieval of a set size 4 array, the parieto-occipital alpha-power suppression was larger than the retrieval of a set size 2 array. However, when two different letter cues prompted the simultaneous retrieval of two set size 2 arrays, the alpha-power suppression was initially identical to that for the retrieval of one set size 2 array [t₍₁₉₎ = 1.0, NS for set size 2 additive > set size 2; t₍₁₉₎ = 4.7, P < 0.001 for set size 2 additive < set size 4; Fig. 2D], but it grew larger toward the end of the retrieval interval [t₍₁₉₎ = 2.5, P < 0.05 for set size 2 additive > set size 2; t₍₁₉₎ = 2.0, P = 0.06 for set size 2 additive < set size 4; Fig. 2D]. A RT analysis corroborated this finding [t₍₁₉₎ = 7.4, P < 0.001, for set size 2 + 2 > set size 2; t₍₁₉₎ = 4.9, P < 0.001, for set size 2 + 2 < set size 4 quad]. These results indicate that, with our electrophysiological measures, we can track the additional time it takes to combine two separately learned representations in working memory. The method that we introduce here appears to provide a much-needed tool with which to precisely measure memory retrieval dynamics in a host of other tasks and subject populations.

SI Results

Experiment 1.

The encoding task.

Behavioral analyses.

First, the accuracy for new arrays was examined. A repeated-measures ANOVA revealed that there was a main effect of set size [F_(3,84) = 406.1, P < 0.001] such that the accuracy declined monotonically as a function of set size. We then transformed the accuracy to calculate the estimate of visual working-memory (WM) load (i.e., the number of colored squares maintained in visual WM) for each set size as the following assumptions. Let SS be the set size of interest, and K_percept be the amount of visual information maintained in visual WM at the set size SS. If the tested item was represented in visual WM, participants should be able to report its color correctly. Otherwise, they would guess the correct color by chance. Because there were eight colors to choose from, the chance level would be 1/8. These assumptions lead to the equation below. Accuracy = K_percept/SS + (SS − K_percept)/SS × 1/8. Solving this equation for K_percept, K_percept = 8/7 × SS × (Accuracy − 1/8). The K_percept estimate for each set size was then subjected to a repeated-measures ANOVA. This revealed a significant effect of set size [F_{(3, 84)} = 81.1, P < 0.001]. Planned simple comparisons revealed that K_percept estimate plateaued at set size 4 [t₍₂₇₎ = 22.2, P < 0.001 for K1_percept < K4_percept; t₍₂₇₎ = 13.6, P < 0.001 for K2_percept < K4_percept; t₍₂₇₎ = 2.1, P < 0.05 for K4 > K8]. This is consistent with numerous previous findings. Interestingly, there was a decrease in the K_percept estimate from set size 4 to set size 8. This has also been reported in the previous studies, and it is thought to be caused by perceptual overload at the encoding stage (48–50).

Next, we examined accuracy data for to-be-learned arrays. A repeated-measures ANOVA revealed a significant main effect of set size [F_(3,84) = 58.6, P < 0.001] and blocks [F_(24,672) = 26.9, P < 0.001] as well as their significant interaction [F_(72,2,016) = 19.0, P < 0.001]. This shows that the large accuracy differences across set sizes diminished by the end of the encoding blocks (accuracy for all set sizes > 94%), thus showing successful learning for all four arrays.

Electrophysiological analyses.

The parieto-occipital alpha-power suppression was calculated as the mean percentage change of alpha power (8–13 Hz) of posterior channels (P3/4, PO3/4, OL/R, O1/2, and Pz) in 300- to 1,000-ms window after the array onset. A repeated-measures ANOVA revealed that there was a main effect of array types (i.e., new and to-be-learned) [F_(1,27) = 38.4, P < 0.001] and set size [F_(3,81) = 30.4, P < 0.001]. More importantly, there was no significant interaction between array type and set size [F_(3,81) = 2.6, NS]. Planned simple comparisons revealed that the alpha-power suppression for both new and to-be-learned arrays approximated the expected capacity-defined set size function just like the behavioral capacity estimate [values of t₍₂₇₎ > 4.6, P < 0.001 for set size 1 < set size 4; t₍₂₇₎ > 2.6, P < 0.05 for set size 2 < set size 4; t₍₂₇₎ = 2.1, P < 0.05 for set size 4 < set size 8 for to-be-learned array and t₍₂₇₎ = 1.3, NS for set size 4 < set size 8 for new array]. Of note, we did not find a statistically significant difference between the alpha-power suppression for set size 1 and set size 2 conditions for new arrays [t₍₂₇₎ = 2.8, P < 0.01 for set size 1 < set size 2 for to-be-learned array but t₍₂₇₎ = 0.7, NS for set size 1 < set size 2 for new array]. This is likely simply due to noise because other studies that used very similar WM tasks (i.e., change detection tasks) have found that alpha suppression increased from set size 1 to set size 2 (18, 20).

The retrieval task.

Electrophysiological analyses.

The time window used in the retrieval task was different from the encoding task. Although we anticipated that it might take longer for the capacity-limited set size effect to emerge due to the visual system processing inputs faster than long-term memory (LTM) retrieval can operate, we did not have a precise prediction as to when it would emerge. However, what we did predict was that once the capacity-defined set size effect emerged, it would be persistent throughout the retention interval. That is clearly what we see in the data and reflected in our measurement window. The parieto-occipital alpha-power suppression was calculated as the mean percentage change of alpha power (8–13 Hz) of the same posterior channels (P3/4, PO3/4, OL/R, O1/2, and Pz) in 800- to 2,500-ms window after the letter cue onset. Planned simple comparisons showed that the alpha-power suppression showed the expected capacity-defined set size effect [t₍₂₇₎ = 3.7, P < 0.001 for set size 1 < set size 4; t₍₂₇₎ = 2.1, P < 0.05 for set size 2 < set size 4; t₍₂₇₎ = 0.5, NS for set size 4 > set size 8], whereas the sustained negativity did not.

Behavioral analysis.

The accuracy showed that participants were near ceiling at retrieving the learned arrays from LTM (accuracy > 94% for all four arrays). A repeated-measures ANOVA revealed that the RTs for correct trials monotonically increased as a function of set size [F_(3,81) = 96.2, P < 0.001]. We hypothesized that this is a result of two types of accurate recall trials. One type of trials is when the probed item was actively maintained in mind when recall is prompted and therefore readily accessible. The other is when the probed item was not held actively in mind when recall is prompted but stored inactively in LTM, and therefore the participants had to activate it for retrieval. As a result, the recall RTs for the former trial type are systematically faster than RTs for the latter type of trials because one has to know whether the probed item is already available for recall in mind before executing more effortful retrieval from LTM. Furthermore, the recall RT for the former type of trials should be the fast K_retrieval/SS portion of the entire correct RTs where K_retrieval is the amount of retrieved information for an array of set size SS that can be held active at a given time. Based on these assumptions, we made the following prediction. If the same WM is used to represent new perceptual information as well as previously learned retrieved information, then K_retrieval should be the same as K estimated with new perceptual information (K_percept) for the same set size SS during the encoding task. To test this, we extracted the fast K_percept/SS portion of accurate recall RTs for each set size as within-WM recall RTs and examined whether these within-WM RTs would exhibit the characteristic capacity-defined set size function. That is, we predicted that there should be a monotonic increase in the recall RTs as a function of set size until their visual WM capacity is saturated and there would be no further increase in the RTs for larger set sizes. A repeated-measures ANOVA confirmed this prediction. In addition to a significant main effect of set size [F_(3,81) = 79.2, P < 0.001], planned simple comparisons showed that search RT within WM showed the capacity-limited set size function [t₍₂₇₎ = 12.8, P < 0.001 for set size 1 < set size 4; t₍₂₇₎ = 5.6, P < 0.001 for set size 2 < set size 4; t₍₂₇₎ = 0.2, NS for K4_percept < K8_percept]. These results, taken together with the alpha-power results, suggest that the amount of information retrieved from LTM at a given time is limited by WM capacity.

The Retrieval Task in Experiment 2.

Behavioral analyses.

The accuracy showed that participants were near ceiling at retrieving the learned arrays from LTM (accuracy > 96% for all four conditions).

Electrophysiological analyses.

To capture the time course of partial retrieval, we tested the parieto-occipital alpha-power suppression in early (500–1,000 ms after the letter cue onset) and late (2,300–2,700 ms after the letter cue onset) time window separately. First of all, planned simple comparisons revealed that the alpha-power suppression replicated the results of experiment 1 for both early and late retention periods [values of t₍₁₉₎ > 3.6, P < 0.01 for set size 1 < set size 4 whole retrieval; t₍₁₉₎ > 3.3 P < 0.01 for set size 2 < set size 4 whole retrieval]. Another set of planned simple comparisons revealed that quadrant retrieval initially yielded the same level of alpha-power suppression as set size 4 whole retrieval [t₍₁₉₎ = 0.7, NS for set size 4 whole > set size 4 quad; t₍₁₉₎ = 3.3, P < 0.01 for set size 1 < set size 4 quad], but it declined to the same level as set size 1 by the late retention period [t₍₁₉₎ = 2.3, P < 0.05 for set size 4 whole > set size 4 quad; t₍₁₉₎ = 1.2, NS for set size 1 < set size 4 quad].

The Retrieval Task in Experiment 3.

Behavioral analyses.

The accuracy showed that participants were near ceiling at retrieving the learned arrays from LTM (accuracy > 92% for all three conditions).

Electrophysiological analyses.

To capture the time course of partial retrieval, we tested the parieto-occipital alpha-power suppression in early (800–1,600 ms after the letter cue onset) and late (2,000–2,700 ms after the letter cue onset) time window separately. First of all, planned simple comparisons revealed that the alpha-power suppression replicated the results of experiments 1 and 2 for both early and late retention periods [values of t₍₁₉₎ > 3.5, P < 0.01 for set size 2 < set size 4]. Another set of planned simple comparisons revealed that additive retrieval initially yielded the same level of alpha-power suppression as set size 2 retrieval [t₍₁₉₎ = 1.0, NS for set size 2 additive > set size 2; t₍₁₉₎ = 4.7, P < 0.001 for set size 2 additive < set size 4], but it amplified to the same level as set size 4 by the late retention period [t₍₁₉₎ = 2.5, P < 0.05 for set size 2 additive > set size 2; t₍₁₉₎ = 2.0, P = 0.06 for set size 2 additive < set size 4].

Discussion

Our results provide direct electrophysiological evidence for the classic theoretical proposal that information retrieved from long-term memory is represented in capacity-limited working memory. In doing so, our results also effectively rule out three alternative explanations, as we discuss next.

The first potential alternative explanation that we considered is that the parieto-occipital alpha-power suppression indexes the degree to which subjects relied on automatic activation of stimulus–response mappings acquired through extensive training (26–30). It is worth considering because we trained subjects to produce a given set of manual responses for a specific stimulus (e.g., when they saw the letter cue “A,” they could have activated a certain set of responses). Although it seems plausible, at least four aspects of our data are inconsistent with this account. First, the parieto-occipital alpha-power suppression showed the capacity-limited set size effect such that there was no further suppression of the alpha power once working-memory capacity was reached (i.e., at set size 4) despite the increase in the number of responses associated with the stimulus (i.e., set size 8). Second, we saw similar capacity-limited set size function for stimuli on which subjects received no training (i.e., new arrays presented during encoding task). These results are inconsistent with the automaticity account as there was not opportunity to learn specific responses for these new arrays. Third, in the retrieval task of experiment 2, the parieto-occipital alpha-power suppression was significantly greater for the first second of retrieval when participants tried to retrieve one item from a set size 4 array than when they retrieved a set size 1 array. The automaticity account has difficulty in explaining this result because, in both cases, the number of responses that are associated with the retrieval cue is 1. Fourth, in the retrieval task of experiment 3, the parieto-occipital alpha-power suppression was no different for the first 2 s of retrieval when participants tried to retrieve two set size 2 arrays and one set size 2 array. Again, this result cannot be explained by the automaticity account because it would predict greater alpha-power suppression for the retrieval of two set size 2 arrays due to the increased number of responses to activate. Taken together, our interpretation that the degree of the parieto-occipital alpha-power suppression reveals the dynamic process of representing a limited amount of visual information in working memory regardless of the origin of the information (i.e., perceived through vision input or retrieved from long-term memory).

Second, the parieto-occipital alpha-power suppression might index the spatial extent of visual field from which task-relevant information was processed instead of the amount of information represented in visual working memory. Although the working-memory load correlated with the spatial extent of task-relevant visual field in experiment 1, our results from experiments 2 and 3 directly contradict with this alternative explanation. In these latter experiments, the arrow cue concurrently presented with the letter cue at the beginning of the trial unambiguously predicted the spatial extent of the task-relevant visual field. However, in experiment 2, the magnitude of the alpha-power suppression was not differentiated between whole and partial retrieval of set size 4 arrays for the first second of the retention interval even though the spatial extent of task-relevant visual field was drastically different. In addition, in experiment 3, the alpha-power suppression was statistically identical for the first 2 s of the retention interval when individuals retrieved one set size 2 array subtending one visual hemifield or two set size 2 arrays subtending two hemifields. These results clearly demonstrate the dissociation between the parieto-occipital alpha-power suppression and the spatial extent of the task-relevant visual field.

The third potential alternative explanation that we considered is that participants might have engaged in configural learning that allowed them to chunk each array of colored squares into one configural representation (7, 31–34). This is plausible given that what participants had to learn were simply spatial configurations of colored squares. However, the capacity-defined set size effect of the parieto-occipital alpha-power suppression challenges this idea because the configural learning explanation would predict that each array, regardless of its set size, should be learned as one configuration. This being said, we have no intention to argue that configural learning is impossible. Instead, we suspect that our task demands discouraged the use of configural learning. We had participants recall an individual item from a learned configuration. To correctly report a cued item, participants had to access the individualized representation of the cued item. This test procedure likely encouraged participants to maintain multiple individualized representations of colored squares rather than one configural representation of the colored squares. However, in future studies, it will be useful to determine whether we observe neural evidence of configural learning when task demands allow participants to engage in such a learning strategy (e.g., testing memory with a whole report procedure).

Our demonstration of two distinct memory states (i.e., actively represented working memory and inactively stored long-term memory) challenges theories that propose human memory consists of a single memory storage mechanism that is unlimited in capacity (35–38). Furthermore, our results demonstrate that the behavioral benefits of representing well-learned information come from additional iterations of retrieval from long-term memory rather than expanded working-memory capacity (39–41).

Although our findings appear to falsify some models of human memory, our findings appear to reconcile other classes of models. One class of theories of human memory proposes that working memory is the capacity-limited activated portion of long-term memory (7, 42, 43). Our results show how the classic theories of human memory that propose retrieved long-term memories are brought back into working memory can be reconciled with the class of theories in which working memory is the active portion of long-term memory. Specifically, we show that alpha-band oscillations can be used to track when a memory representation changes its state from a passive long-term memory to an active working memory (44). Given the evidence that the similar patterns of neural activity represent perceptual inputs and maintain those representations in working memory (45–47), we propose that the alpha-band activity we measured indicates a shift to the same active state by the neurons that store long-term memories.

We believe that our metric of alpha suppression during memory retrieval represents a vital tool for investigating the extent of maneuverability and creativity our memory system supports. For instance, experiment 3 showed that our mind is capable of integrating two separately learned long-term memory representations into one never-seen working-memory representation. More precisely, our results suggest that such retrieval is best characterized as sequential or cascading retrieval of each component representation. Such transformation of mental representations (e.g., combining a pair of wings and then a horse into a Pegasus) is a fundamental asset of our creative mind. Thus, future studies are now better equipped to examine the nature and extent of the flexibility that our mind possesses.

Materials and Methods

Subjects.

We first obtained informed consent for procedures approved by the Vanderbilt University Institutional Review Board. In experiments 1, 2, and 3, 28 (16 males), 20 (12 males), and 20 (11 males) subjects with normal or correct-to-normal vision contributed data, respectively. The sample size was larger in experiment 1 because of the additional number of conditions that each subject completed. They were compensated $10/h for their participation. In experiment 1, five additional subjects’ data were excluded from analyses due to an excessive number of trials contaminated by ocular artifacts (more than 30% of trials in any condition) or an inability to follow instructions. Similarly, four and three additional subjects were excluded in experiments 2 and 3, respectively.

Procedure.

Experiment 1.

Subjects first performed an encoding task (Fig. 1). Before the experiment, four to-be-learned arrays (set size 1, 2, 4, and 8) were created by randomly selecting a location from 3 × 3 grids (each grid 4.3 × 4.3° of visual angle) in each quadrant with a constraint that every quadrant has to have at least one square before a second square is allocated to any quadrant. After square locations are selected, colors were assigned to the selected locations without repetition from a set of eight colors [red (x = 0.592, y = 0.367, 9.60 cd/m²), green (x = 0.299, y = 0.579, 27.6 cd/m²), blue (x = 0.15, y = 0.08, 4.35 cd/m²), yellow (x = 0.396, y = 0.509, 35.5 cd/m²), magenta (x = 0.295, y = 0.171, 13.3 cd/m²), cyan (x = 0.219, y = 0.315, 31.2 cd/m²), black (x = 0.393, y = 0.423, 0.31 cd/m²), and white (x = 0.293, y = 0.323, 38.5 cd/m²]. One hundred new arrays for each set size were also created using the same procedure. We verified that none of the new arrays was identical to the to-be-learned arrays.

A central fixation dot (0.2° × 0.2° in visual angle) and a 3 × 3 gray grid (4.3° × 4.3° in visual angle) centered 3.8° eccentric to the center of the screen in each quadrant were presented and remained visible throughout the experiment. Seven hundred milliseconds after subjects initiated each trial with a button press, an array of colored squares was presented for 150 ms, which was followed by a 850-ms-long retention interval. After the retention interval, a gray probe was presented in one of the locations previously occupied by a colored square (i.e., the test square). Subjects indicated the color of the test square with a button press on a handheld game pad on which each of the eight buttons mapped to the eight possible colors. Subjects were provided with a response key throughout the experiment to minimize the memory load needed to press the appropriate button. At the same time that the gray probe was shown, a letter cue (A, B, C, or D for to-be-learned arrays and N for new arrays) was presented so that subjects learned the letter cue associated with each array. The assignment of the letter cues to set sizes was randomized across subjects. Auditory feedback was provided after each trial to aid learning. Each to-be-learned array was presented in miniblocks of eight trials to also aid learning. Subjects completed 25 blocks of 48 trials (32 to-be-learned trials and 16 new trials).

The learning phase described above took place over 1.5 h. Beginning 5 min after completing the learning phase, subjects performed the retrieval task (Fig. 1). The 3 × 3 grids and a central fixation cross served as a standing background on the screen. Seven hundred milliseconds after subjects initiated each trial with a button press, a white letter cue (0.75° × 1.5°) was presented for 150 ms, which was followed by a 2,350-ms-long retrieval interval. Subjects were instructed to retrieve and maintain the learned array associated with the cue during this retrieval interval. After the retrieval interval, a gray test probe was presented, and subjects reported the color presented at the probed location in the retrieved array by pressing one of eight buttons on the handheld game pad. Subjects performed 120 trials for each learned array.

Experiment 2.

Subjects performed the encoding task first just as in experiment 1 with the following exceptions. First, subjects learned three arrays of set size 1, 2, and 4. Second, there were no new arrays introduced, and to-be-learned arrays were presented four trials in a row in each block. Subjects performed six blocks of 24 trials. The retrieval task was also identical to that of experiment 1 except for following. A letter cue accompanied a white arrow cue. A bidirectional arrow cue prompted the retrieval of the entire array associated with the letter cue, and a diagonal arrow cue prompted the retrieval of just the quadrant of the array indicted by the arrow cue. Subjects performed 120 trials of whole-array retrieval for set size 1, 2, and 4 array and 240 trials of quadrant retrieval of the set size 4 array.

Experiment 3.

Subjects performed the encoding task first just as in experiment 2 with the following exceptions. Subjects learned two arrays each of set size (i.e., 2, 4). For construction of the set size 2 arrays, an additional constraint was that the two arrays appeared in different hemifields. Subjects performed eight blocks of 24 trials. The retrieval task was also identical to that of experiment 2 except for following. Two letter cues were presented simultaneously to prompt the retrieval. Two matching letter cues were presented to prompt the retrieval of the associated array, and two different letter cues prompted the retrieval of a combined array of two associated arrays. Subjects performed 200 trials of retrieval for a single set size 2 and 4 arrays and 200 trials of combined retrieval of set size 2 arrays.

EEG Acquisition and Preprocessing.

The EEG was recorded using a right-mastoid reference on-line and rereferenced off-line to the average of the left and right mastoids. The signals were amplified with a gain of 20,000, a bandpass of 0.01–100 Hz, and digitized at 250 Hz. We used the 10–20 electrode sites (Fz, Cz, Pz, F3, F4, C3, C4, P3, P4, PO3, PO4, O1, O2, T3, T4, T5, and T6) and a pair of custom sites, OL (halfway between O1 and OL) and OR (halfway between O2 and OR). Eye movements were monitored using electrodes placed 1 cm lateral to the external canthi for horizontal movement and an electrode placed beneath the right eye to detect blinks and vertical eye movements.

For each experiment, the continuous EEG data were first segmented into trial epochs. For experiment 1, the trial epoch was defined as −400 to 1,000 ms after the array onset for the encoding task, and −400 to 2,500 ms after the letter cue onset for the retrieval task. For experiments 2 and 3, the retrieval trial epoch was defined as −400 to 3,000 ms after the letter cue onset. Trials accompanied by horizontal eye movements (>30-μV mean threshold across observers) or blinks (>75-μV mean threshold across observers) were rejected before further analyses. Subjects’ data with more than 30% of trials rejected for ocular or motor artifacts in any given condition were replaced.

EEG Analyses.

To examine the oscillatory responses, EEG from each trial was subjected to spectral decomposition with a fixed window size of 400 ms and a window overlap of 380 ms using spectrogram.m in Matlab (please see Fig. 1A for a schematic). We measured the parieto-occipital alpha-power suppression in the following manner. First, the baseline power spectrum was defined as the mean power spectrum observed in the pretrial time window (−400 to 0 ms relative to an array or a letter cue onset, depicted as the data at −200 ms in Fig. 1B due to our 400-ms-wide windowing procedure). This baseline spectrum was subtracted from the entire epoch, and the resultant spectral difference was divided by the baseline spectrum and then multiplied by 100. This allowed us to calculate the percentage change in power at each frequency. The alpha-power percentage change was thus the average percentage of power change between 8 and 13Hz. This alpha-power percentage change was averaged across the parieto-occipital channels (PO3/4, P3/4, O1/2, OL/R, and Pz). For experiment 1, the mean percentage change from 200 to 1,000 ms after the array onset (depicted as 400- to 800-ms data points in Fig. 1B due to our 400-ms-wide windowing procedure) was used as the measure of the parieto-occipital alpha-power suppression for the encoding task, and that from 800 to 2,500 ms (depicted as 1,000- to 2,300-ms data points in Fig. 1B due to our 400-ms-wide windowing procedure) after the letter cue onset for the retrieval task.

Estimating Visual Working-Memory Capacity During Encoding in Experiment 1.

To estimate working-memory capacity for new visual inputs (K_percept), we transformed the encoding accuracy for new arrays with the following assumptions. Let SS be the set size of interest, and K_percept be the visual working-memory capacity given set size SS. If the tested item was represented in visual working memory, participants should be able to report its color correctly. Otherwise, they would guess the correct color by chance. Because there were eight colors to choose from, the chance level would be 1/8. Based on these assumptions, we derived the following equation:

$$\text{Accuracy}={\text{K}}_{\text{percept}}/\text{SS}+\left(\text{SS}-{\text{K}}_{\text{percept}}\right)/\text{SS}\times 1/8.$$

Solving this equation for K_percept,

$${\mathrm{K}}_{\text{percept}}=8/7\times \mathrm{SS}\times \left(\text{Accuracy}-1/8\right).$$

RT Analysis for the Retrieval Task in Experiment 1.

The accuracy data showed that participants were near ceiling at retrieving the learned arrays from long-term memory (accuracy > 94% for all four arrays). We hypothesized that this was a result of two types of accurate trials. One trial type was when the probed item was held actively in working memory when memory was probed and therefore readily accessible. The other trial type was when the probed item was not held actively in working memory when memory was probed, but stored inactively in long-term memory, and therefore the participants had to retrieve this representation. Thus, the RTs for the former trial type are systematically faster than RTs for the latter type of trials because one has to know whether the probed item is already available for recall in mind before executing more effortful retrieval from long-term memory. Furthermore, the RT for the former type of trials should be the fast K_retrieval/SS portion of the entire correct RT distribution where K_retrieval is the amount of retrieved information for an array of set size SS that can be held active at a given time.

Based on the assumptions outlined above, we made the following prediction. If working memory is used to represent new perceptual information as well as previously learned information retrieved from long-term memory, then K_retrieval should be the same as K_percept estimated with new perceptual information for the same set size (SS) during the encoding task. K_percept for each set size was available from initial encoding performance for new arrays. To test this, we extracted the fast K_percept/SS portion of accurate report RTs for each set size as within–working-memory recall RTs and examined whether these within–working-memory RTs would exhibit the characteristic capacity-defined set size function. That is, we predicted that there should be a monotonic increase in within–working-memory RTs as a function of set size until their working-memory capacity is saturated and there would be no further increase in the RTs for larger set sizes.

To evaluate the set size effect of within-working-memory recall RTs, we chose median RTs instead of mean-based measurements of RTs because a median-based measure is robust against the very likely possibility that within–working-memory recall RTs cannot be crisply isolated, as illustrated in Fig. 1C, due to the trial-to-trial variation in the time it takes to terminate the within–working-memory search before executing long-term memory search. In other words, a median RT is invariant to the exact RT values of the fast and slow ends of the RT distribution, whereas the mean-based RT measures are. Thus, our median-based RT analysis of within–working-memory recall can be interpreted without specifying the exact RT boundary of within–working-memory recall.