Significance
Circadian rhythms influence most aspects of physiology and behavior. However, how do we apply this knowledge in medicine? Identifying molecular mechanisms in humans is challenging as existing large-scale datasets rarely include time of day. To address this problem, we combine understanding of periodic structure, evolutionary conservation, and unsupervised machine learning to order unordered human biopsy data along a periodic cycle. We show this works using ordered mouse and human data and that it gives consistent results when applied to populations on different continents. Then, we investigate molecular rhythms in normal human lung and liver and cancerous liver. Finally, we demonstrate proof of concept by finding the best time to administer a chemotherapeutic drug in an animal model.
Keywords: gene expression, biological rhythms, machine learning, autoencoder, circadian rhythms
Abstract
Circadian rhythms modulate many aspects of physiology. Knowledge of the molecular basis of these rhythms has exploded in the last 20 years. However, most of these data are from model organisms, and translation to clinical practice has been limited. Here, we present an approach to identify molecular rhythms in humans from thousands of unordered expression measurements. Our algorithm, cyclic ordering by periodic structure (CYCLOPS), uses evolutionary conservation and machine learning to identify elliptical structure in high-dimensional data. From this structure, CYCLOPS estimates the phase of each sample. We validated CYCLOPS using temporally ordered mouse and human data and demonstrated its consistency on human data from two independent research sites. We used this approach to identify rhythmic transcripts in human liver and lung, including hundreds of drug targets and disease genes. Importantly, for many genes, the circadian variation in expression exceeded variation from genetic and other environmental factors. We also analyzed hepatocellular carcinoma samples and show these solid tumors maintain circadian function but with aberrant output. Finally, to show how this method can catalyze medical translation, we show that dosage time can temporally segregate efficacy from dose-limiting toxicity of streptozocin, a chemotherapeutic drug. In sum, these data show the power of CYCLOPS and temporal reconstruction in bridging basic circadian research and clinical medicine.
Circadian rhythms are nearly ubiquitous in nature. In animals, much of physiology and behavior is under circadian control. Body temperature, hormonal rhythms, blood pressure, and locomotor activity are just a few of the processes displaying daily rhythms. In circadian model systems (e.g., cyanobacteria, Neurospora, Arabidopsis, Drosophila, and mice), high-resolution time sampling is straightforward, and experiments show that a substantial fraction of the transcriptome is under clock control. For example, in mice, a majority of genes are clock regulated in at least 1 of 12 different organs (1).
Circadian rhythms are also critical for humans. Shift work-induced circadian misalignment is associated with higher rates of metabolic, cardiovascular, and neoplastic disease. Clinical experience suggests time of day can have a marked effect on disease severity (2–4). Indeed, the majority of the best-selling prescription drugs and World Health Organization essential medicines target molecules that oscillate in mice (1). However, translation of these findings to clinical medicine remains slow. How does human molecular physiology change with circadian time? In mice, and presumably humans, circadian output genes are markedly different in each tissue. Obviously, repeated sampling from most human organs is not possible. As a result, we have limited ability to study human molecular rhythms and relate them to either normal or disease physiology.
One approach is to analyze temporally annotated clinical samples, where time of sample collection is recorded. There are >1 million human gene expression samples in the National Center for Biotechnology Information Gene Expression Omnibus (GEO) repository. Unfortunately, the sample collection time is almost never reported. Ueda et al. (5) first used transcriptional “time-stamping” to reconstruct the circadian phase of tissue samples from mouse liver, and supervised learning methods continue to improve (6, 7). However, supervised learning requires a training library of samples with known circadian time. With the exception of blood (8, 9) and brain (10), temporally annotated human samples are lacking. Although theoretically possible, scheduling people for internal organ biopsies every 2 h for 2 d is both dangerous and impractical.
Alternatively, in single-cell biology, unsupervised algorithms are being used to reconstruct the relative temporal order of samples, for example, in cellular development and differentiation (11). Orderings that minimize the distance between adjacent samples or maximize the smoothness of the trajectories connecting them are calculated directly from gene expression data. For example, Oscope is designed to extract oscillatory (cell cycle) dynamics from single-cell data (12). To do this, Oscope compares every gene-by-gene pairing in the genome to identify those that best approximate an ellipse. In addition to being computationally taxing, this approach is highly sensitive to systematic (nonrhythmic) intersubject variation found in clinical samples.
Here, we describe a method, cyclic ordering by periodic structure (CYCLOPS), that uses global descriptors of expression structure, unsupervised machine learning, and evolutionary conservation, to order periodic data. We show CYCLOPS is robust by analyzing legacy mouse and human data, where time is known. We also demonstrate remarkably consistent results when analyzing unordered human data from different geographical populations. We report the cycling of hundreds of human disease genes and drug targets. We also analyze the altered circadian function of hepatocellular carcinoma (HCC) samples. Finally, for proof of concept, we used this information to design a dosing scheme that temporally segregates efficacy from toxicity for streptozocin (STZ), a cytotoxic chemotherapeutic agent.
Results
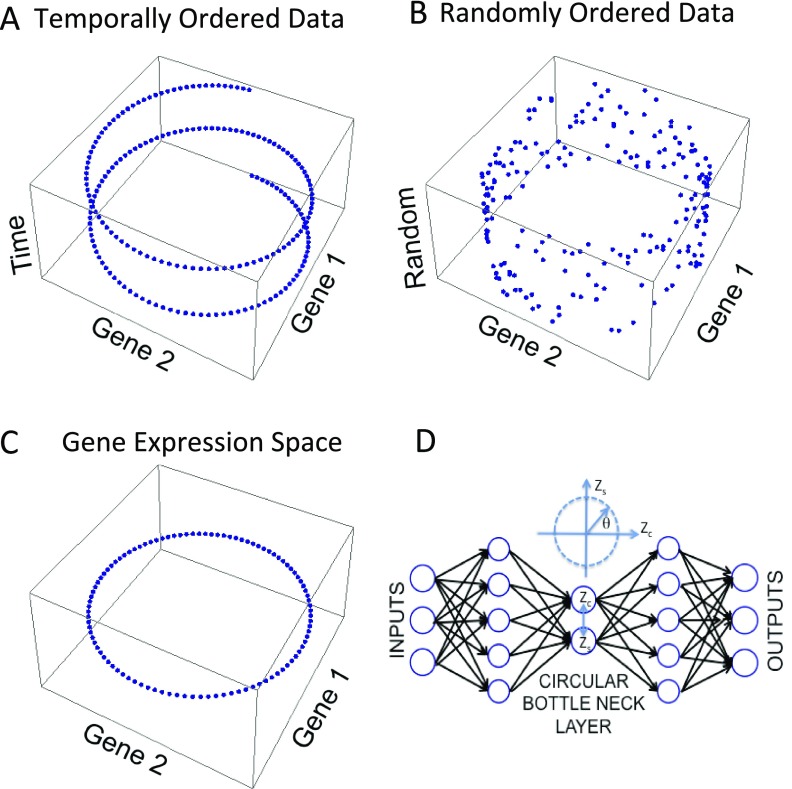
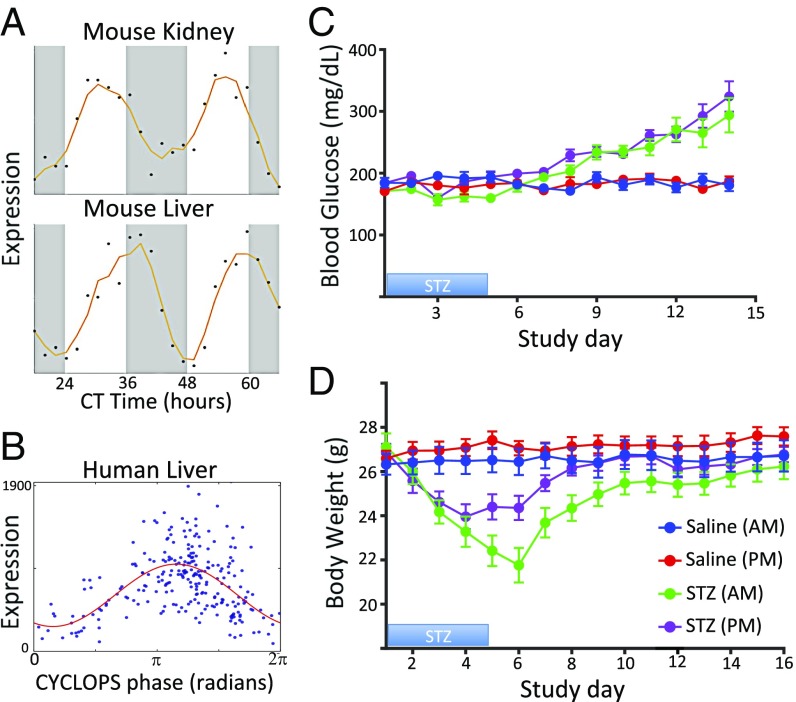
Data generated by a common periodic process have a defined structure. Analyzing the yeast cell cycle, Alter, Brown, and Botstein (13) used singular value decomposition to reduce the dimensionality of the data and identify “eigengenes,” characteristic expression patterns, that span the global expression profiles. Alter et al. recognized the first eigengenes as out-of-phase sinusoidal oscillations. When plotted in expression space, they form an ellipse. Importantly, this result is independent of the annotated collection time and can be used to determine the relative order of samples in the dataset (Fig. S1).
Fig. S1.
Graphical depiction of CYCLOPS. (A) The expression of two, out-of-phase genes periodic with a common frequency are plotted in the X and Y dimensions. Time is depicted in the Z dimension. (B) The same expression data are plotted with temporal information replaced with a random index. (C) The same data are plotted in expression space. The structure forms a circle. (D) CYCLOPS autoencoder: The neural network is trained so that its output reproduces its input with minimal error. Linear neurons project the data onto the circular bottleneck layer. The circular bottleneck layer is composed of two coupled neurons constrained to encode the data on a closed elliptical curve. Data from each sample are represented by a single angular phase representing the sample’s position on the ellipse.
With human data, confounds such as genetic differences, age, gender, exercise, diet, etc., all add significant noise and limit this approach. Circadian and noncircadian patterns can be mixed and distributed among the various eigengenes. CYCLOPS optimally weights and combines the eigengenes patterns to reveal underlying elliptical structure, and then uses this structure to order the data. CYCLOPS couples our prior knowledge of rhythms in model organisms with use of a circular node autoencoder (Fig. S1D). Autoencoders are feedforward neural networks trained so that the network’s output reproduces its input (14). By constraining the size of the intervening “bottleneck layer,” the network is forced to encode the data in a reduced number of dimensions. Here, we combine linear encoding and decoding neurons with a circular bottleneck node (15). The outputs of the two coupled circular bottleneck nodes represent a single angular phase. CYCLOPS linearly projects the data and encodes it on a simple elliptical curve (15). In this way, CYCLOPS identifies a closed curve that best represents the characteristic expression patterns. An angular phase represents the position of each sample on the ellipse and its temporal phase in the reconstructed periodic cycle. Circular autoencoders have been used to generate nonlinear models of periodic processes in nature (16, 17). To our knowledge, their use in ordering these data are novel.
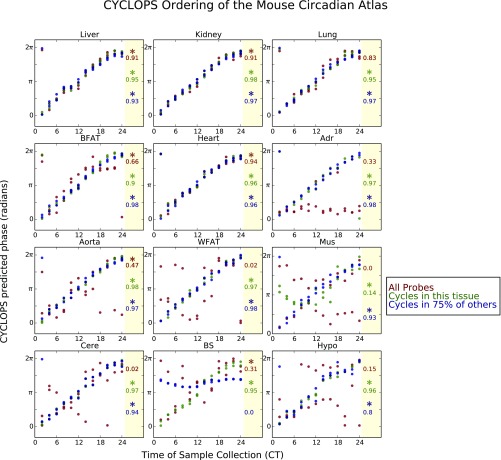
We first applied CYCLOPS to mouse time course expression data (1, 18). With no prior knowledge, CYCLOPS correctly ordered the samples from mouse liver (Fig. 1A). The circular correlation (ρc) (19) and the circular rank correlation(ηc) (19) between the CYCLOPS-estimated phases and true circadian times were both greater than 0.9. CYCLOPS also ordered data from other highly rhythmic organs (e.g., lung, kidney, and adrenals) but failed to correctly order data from tissues with weaker circadian signals (e.g., skeletal muscle, cerebellum, and brainstem; Fig. S2). Reasoning that prior biological knowledge could increase the signal-to-noise ratio and improve ordering, we restricted the analysis to either a list of transcripts that cycled in that tissue or a list of transcripts found to cycle in >75% of other tissues. With this method, CYCLOPS was able to correctly order samples for all mouse tissues (Fig. S2).
Fig. 1.
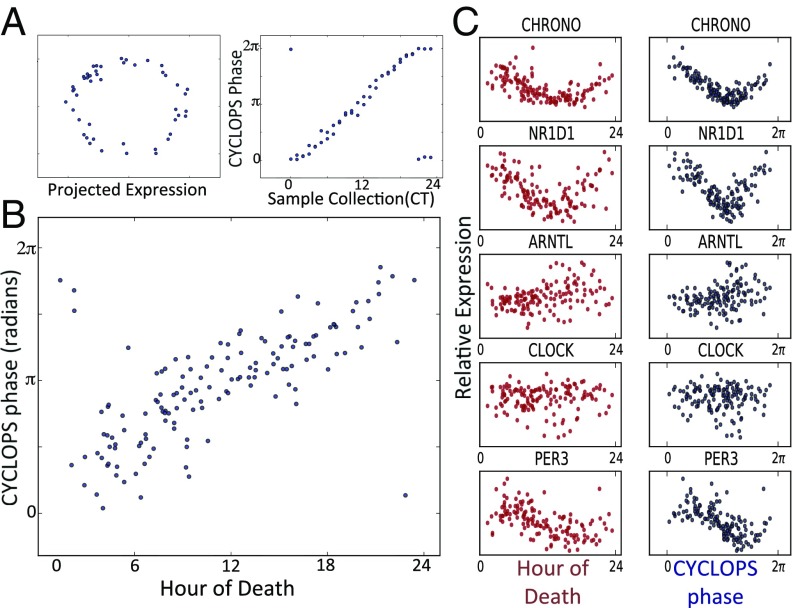
Validation of CYCLOPS. Time course expression data from the mouse liver (18) were encoded with CYCLOPS. (A, Left) The linear encoding is visualized as a projection onto a plane where the data approximates an ellipse. (A, Right) Sample collection phase is plotted along the horizontal axis, whereas the CYCLOPS-estimated phase is plotted on the vertical axis. (B) Expression data from 146 human prefrontal cortex samples (10) encoded with CYCLOPS. The hour of death for each sample is plotted on the horizontal axis. The CYCLOPS-derived phases are plotted on the vertical axis. Time 0 is the same as 24 and phase 0 is the same as 2π; samples plotted near the corners of the graph are actually “near” the diagonal line of identity. (C) Expression of select transcripts is plotted as a function of both TOD (red) and CYCLOPS phase (blue).
Fig. S2.
Application of CYCLOPS to the Mouse Circadian Atlas. Time course expression data (1) from each of 12 mouse tissues (samples obtained every 2 h for 2 d) were encoded with the CYCLOPS neural network. The CYCLOPS-determined phases for each sample are plotted as a function of the true sample collection time. Temporal reconstruction was based on or “seeded with” (A) all well-expressed probes within coefficient of variation between 0.07 and 0.14 (shown in red); (B) the list of probes that were found to cycle in that tissue (shown in green); or (C) the list of probes that were found to cycle in 75% of the other tissues (shown in blue). Because time 0 is the same as 24 and phase 0 is the same as 2π, samples plotted near the corners of the graph are actually “near” the diagonal line of identity. To the Right of each graph, stars denote orderings that had a smoothness metric, and a significant (P < 0.05) error statistic, . The circular correlation between each CYCLOPS ordering and the true time of data collection are also shown. Adr, adrenals; BFAT, brown fat; BS, brain stem; Cere, cerebellum; Hypo, hypothalamus; Mus, skeletal muscle; WFAT, white fat.
CYCLOPS was developed to analyze data without an annotated order. Thus, assessing the quality of CYCLOPS orderings when the true order is unknown is important. CYCLOPS computes a quickly interpretable smoothness metric, Metsmooth, and a more computationally intensive error statistic, Staterr, the significance of which is assessed by bootstrap. Metsmooth compares the smoothness of the reconstructed circular trajectory in expression space to the smoothness of a linear ordering based on the first principal component. Staterr describes the improvement in the residual sum of squares error when encoding the data onto a closed, one-dimensional elliptical manifold compared with the residual error when encoding the data onto a one-dimensional linear manifold. In the cases where Metsmooth < 1 and Staterr differed from background (P < 0.05), the ordering was generally well correlated to ground truth (Fig. S2).
Next, we applied CYCLOPS to expression data derived from human prefrontal cortex samples obtained at autopsy (10). Following the CYCLOPS methodology, we used evolutionary conservation and knowledge of murine rhythms to sharpen the expected circadian signature. We restricted the list of transcripts used for temporal reconstruction to human homologs of genes found to cycle in >75% of mouse tissues. CYCLOPS produced a high-quality ordering (Metsmooth < 1, P < 0.05) that provides an excellent estimate of time of death (TOD) (ρc = 0.68, ηc = 0.55, median absolute error = 1.69 h) (Fig. 1B). When the expression of individual transcripts is plotted as a function of either CYCLOPS phase or TOD (Fig. 1C), CHRONO (20) was found to have the strongest circadian cycling. Known clock genes NR1D1 and PER3 also showed clear rhythms. More generally, transcripts that cycled as a function of TOD also cycled as a function of CYCLOPS phase, whereas nonrhythmic transcripts by TOD were also nonrhythmic by CYCLOPS phase. Sinusoidal fits to CYCLOPS phase were slightly better than sinusoidal fits to TOD (Fig. 1C). We hypothesize that CYCLOPS better accounts for interindividual differences in circadian entrainment to the terrestrial day, for example, due to shift work, biological variation, or the poor entraining conditions of hospitals.
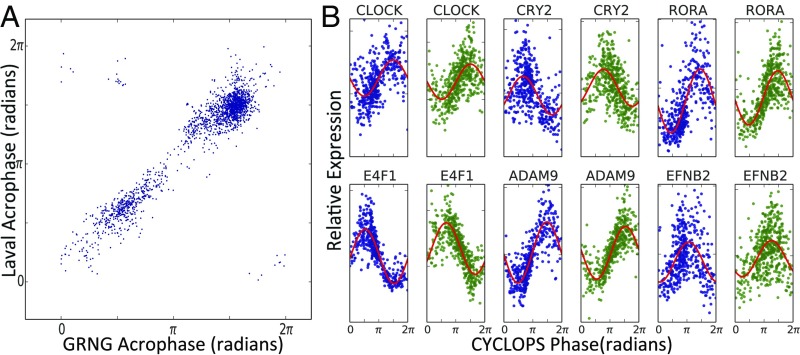
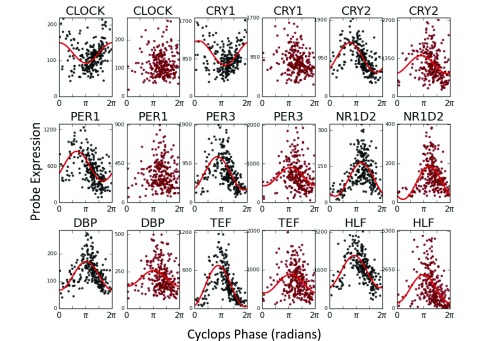
Then we applied CYCLOPS to biopsy data describing the normal human pulmonary transcriptome (21). Human pulmonary physiology demonstrates clear circadian rhythms. However, to our knowledge, molecular rhythms in the human lung remain unexamined. We confined the CYCLOPS reconstruction to human homologs of genes that cycle in the mouse lung. We independently analyzed data from Groningen and Quebec City (22) and used modified cosinor regression to identify transcripts well described by a sinusoidal function of CYCLOPS phase in both datasets (23) (Dataset S1). The phase of peak expression of each transcript was remarkably consistent between research sites (ρc = 0.66, median absolute discrepancy = 0.32 radians ∼1.2 h) (Fig. 2A). Known circadian genes, including CLOCK, CRY1, and CRY2 were periodic with phase relationships similar to those seen in mouse (Fig. 2B).
Fig. 2.
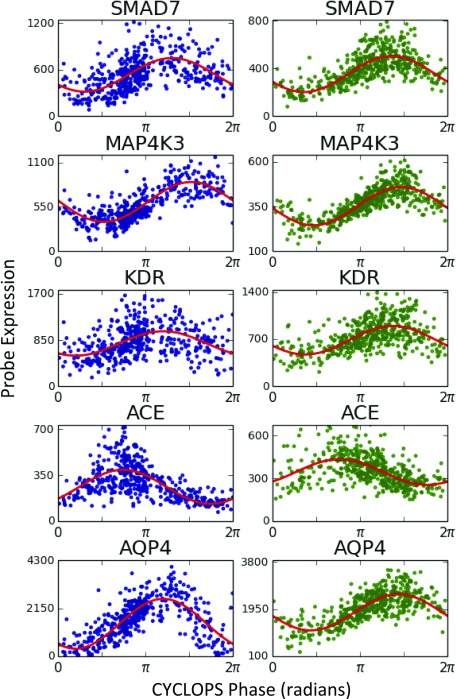
CYCLOPS analysis of circadian transcriptome in human lung. Using independent biopsy data sets (21) from the University of Groningen (GRNG) (Groningen, The Netherlands) and the University of Laval (Quebec City, QC, Canada), we used CYCLOPS to generate two reconstructions of the circadian transcriptome in the human lung. Modified cosinor regression was then used to identify cycling transcripts. (A) Results from the transcripts found to cycle in both datasets are shown. For each transcript, the acrophase in the Laval dataset is plotted against the transcript acrophase as determined from the Groningen data. (B) CYCLOPS-ordered expression data from Groningen and Quebec City are plotted in blue and green, respectively.
Clinically important transcripts also showed strong cycling (Fig. 2B and Fig. S3). For example, ADAM9 is implicated in lung cancer and is a risk marker for distant metastases (24). EFNB2, a receptor tyrosine kinase (TK), also cycled strongly and may have prognostic significance in both small cell lung cancer and nonpulmonary cancers (25). We used the Drug Signatures Database to identify rhythms in drug targets (Dataset S2) (26). Several drug target classes in asthma treatment were rhythmic, including β-adrenergic receptors (targeted by β-agonists) and glucocorticoid receptors (targeted by inhaled and systemic steroids). Various TKs cycled (e.g., MAP4K1, MAP4k3, SLK, FYN, KDR, PKN2, TAOK, and TAOK2). Several of these are targeted in the treatment of non–small-cell lung cancer and pulmonary fibrosis (22, 27).
Fig. S3.
Expression of selected clock-controlled transcriptional outputs in human lung as determined by CYCLOPS. Using independent biopsy datasets (21) from the University of Groningen (Groningen, The Netherlands) and the University of Laval (Quebec City, QC, Canada), we used CYCLOPS to generate two reconstructions of the circadian transcriptome in the human lung. Expression data from human homologs of genes found to be cycling in mouse lung (1) were used in the ordering. Expression data for the labeled transcripts are plotted as a function of CYCLOPS phase. CYCLOPS-ordered expression data from Groningen are plotted in blue. CYCLOPS-ordered expression data from Quebec City are plotted in green.
Drugs used for nonrespiratory conditions that act via the pulmonary system also target rhythmic molecules. Angiotensin-converting enzyme (ACE) inhibitors are used in the treatment of hypertension and heart failure. Inhibiting ACE reduces the production of the potent vasoconstrictor Angiotensin II (28). ACE is predominantly localized to the pulmonary and renal vasculatures and, per CYCLOPS, demonstrates a marked diurnal fluctuation in human lung. Night-time dosing of ACE inhibitors improves nocturnal blood pressure control without sacrificing daytime efficacy (29). The cycling of pulmonary ACE may provide the underlying molecular mechanism for this findings.
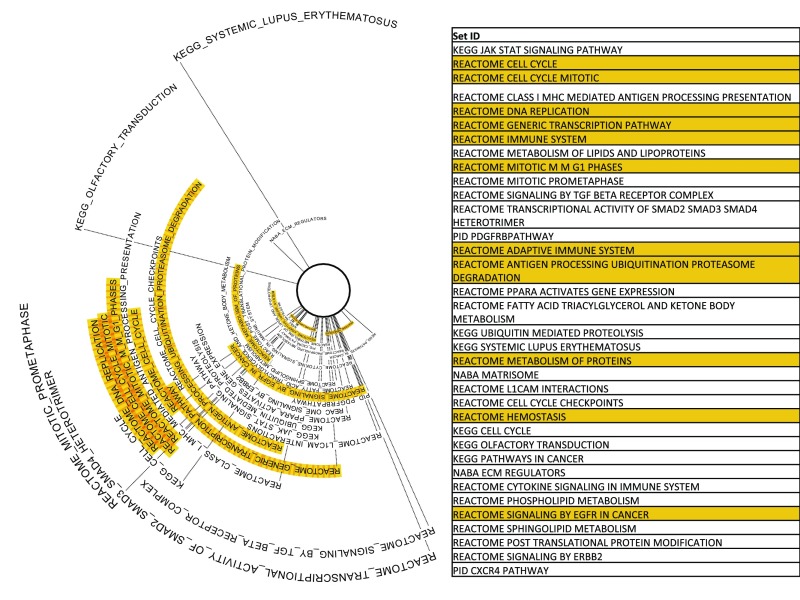
To identify biological pathways and processes that show circadian coordination in the human lung, we applied phase set enrichment analysis (PSEA) (30). As in the mouse (30), pathways describing cell cycle regulation, adaptive immune function, and channel-mediated transport demonstrate phase-synchronized expression (Fig. S4). These data are consistent with clinical evidence demonstrating diurnal variation in the symptoms of asthma (31) and the efficacy of cell cycle-targeting chemotherapeutic agents (32). The SMAD and TGF-β pathways were among those that demonstrated the strongest phase clustering. Both have recently been highlighted in the pathogenesis of pulmonary fibrosis and nonsmall cell lung cancer (33, 34).
Fig. S4.
Phase synchronized pathways and gene sets in human lung as determined by CYCLOPS: phase set enrichment analysis (30) was applied to the CYCLOPS-ordered human pulmonary transcriptome. Gene sets showing phase-clustered expression are shown. Sets further from the center of the circle display more unimodal phase clustering/synchronization. Gene sets and pathways that were also found to have phase clustered expression in the mouse lung (30) are highlighted in orange.
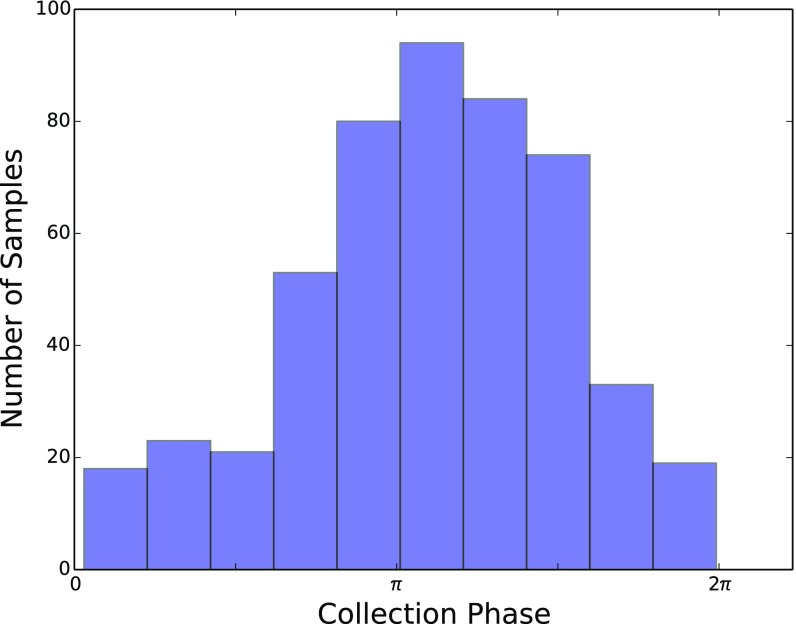
Of note, temporal reconstruction with CYCLOPS did not uniformly distribute samples across the circadian cycle (Fig. S5). Biopsies are obtained during surgical working hours (∼6:00 AM to 6:00 PM). However, samples obtained from shift workers during the terrestrial day likely provide data describing the circadian night (sleep period). The phase distribution of samples is consistent with US data that ∼15–20% of the population are shift workers (35). Of course, the effect of shift work on local tissue clocks remains incompletely understood. It is possible that circadian perturbations alter local molecular timekeeping in a tissue-dependent manner, resulting in intertissue (36) or intratissue (30) desynchrony.
Fig. S5.
Distribution of lung biopsy sample collection times: Histogram showing the number of samples assigned to different CYCLOPS phases. As expected, most samples were collected in one of the four phase bins likely corresponding to the working day when the biopsies were collected.
Next, we wanted to examine circadian rhythms in a cancerous and paired normal organ. We applied CYCLOPS to expression data from 249 patient biopsies of noncancerous (NC) liver tissue (37). The vast majority (n = 243) were of the “normal margin” adjacent to tumor. Using homologs of the transcripts that cycle in the mouse liver (1), CYCLOPS was able to order the samples (Metsmooth < 1, P < 0.05). Core clock components showed similar phase relationships to those observed in mouse (Fig. 3A). A full list of transcripts and pathways found to cycle in NC human liver are presented in (Datasets S3 and S4). Pathways describing metabolism, lipid and cholesterol processing, and cell cycle regulation all demonstrated strong circadian cycling.
Fig. 3.
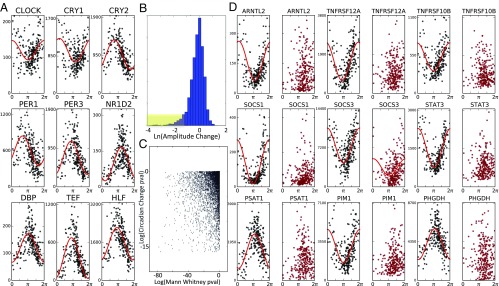
CYCLOPS analysis of noncancerous (NC) and cancerous (HCC) human liver. Expression data from biopsy-derived NC tissue was processed using CYCLOPS. (A) Reconstructed expression profiles of selected clock genes are plotted as a function of CYCLOPS phase. Expression data from samples with HCC were projected onto the eigenvectors established in the NC samples before CYCLOPS ordering. (B) Histogram of circadian amplitude differences between NC and HCC samples. A long tail, highlighted in yellow, shows transcripts with reduced amplitude in HCC. (C) A scatter plot compares the statistical significance of testing for a change in mean expression (Mann–Whitney test) with the statistical significance of testing for a circadian expression change. (D) Expression of selected genes as a function of CYCLOPS phase in both NC (black) and HCC (red) samples.
We used data from biopsies of HCC to explore transcriptional rhythms in an intact solid human tumor (37). HCC is the most common primary liver cancer. We initially analyzed the HCC data as we did the normal margin data, seeding the ordering on the human homologs of mouse cycling genes (1). However, we were not able to generate a quality ordering in this way. We reasoned that HCC might compromise clock function or that the increased interindividual variation between neoplastic samples may have confounded CYCLOPS. To reduce the influence of neoplastic variability and emphasize circadian variation, HCC expression data were projected onto the eigenvectors established by the NC samples. Applying CYCLOPS to these data produced a high-quality fit (P < 0.05). We then used cosinor regression analysis to identify cycling transcripts.
Surprisingly, most “core clock” components continued to cycle in HCC samples. Notable exceptions were PER1 and CRY1 (Fig. S6). Nearly one-half of the genes cycling in NC samples were not well fit by cosinor regression in the HCC data. Again, we wondered whether this might reflect increased “noise” among HCC samples rather than a true change in circadian expression. We used a nested modeling approach to better distinguish these possibilities. Pooled, ordered expression data from both HCC and NC samples were first fit with a single (sinusoidal) model. We then tested whether adding additional sinusoidal terms dependent on histological status significantly improved fit. The combined modeling framework allowed us to identify transcripts that cycled in NC samples but (i) were not well fit by a sinusoidal function when HCC samples were fit in isolation, (ii) were significantly better fit by a nested model with different circadian parameters for HCC and NC samples, and (iii) had at least a twofold reduction in amplitude among HCC samples in the pooled model (Fig. 3 B and C). Based on these combined criteria, we estimate that ∼15% of the transcripts that cycled in NC samples lost rhythmic expression in HCC.
Fig. S6.
Expression of selected core-clock genes in noncancerous (NC) and cancerous human liver as determined by CYCLOPS. As described in the main text, expression data from tissue obtained at biopsy was processed using CYCLOPS to reconstruct the circadian transcriptome in NC human liver samples and matched histologic samples with hepatocellular carcinoma (HCC). Reconstructed temporal expression profiles of selected “core” clock genes are plotted as a function of CYCLOPS phase. Expression of various clock genes is plotted as a function of CYCLOPS phase in both NC (black) and HCC (red) samples.
Using DAVID (38), we identified pathways overrepresented among genes that lost rhythmicity in HCC. In a related analysis, we ranked all circadian genes in NC samples by the reduction of their amplitude in HCC. The ranked list was analyzed with gene set enrichment analysis (GSEA) (39). Reassuringly, these analyses yielded overlapping results (Table S1). There was temporal deregulation of key circadian outputs including overlapping apoptotic pathways and JAK–STAT signaling. We also find evidence for reduced cycling among transcripts related to hypoxia and redox metabolism. Of note was loss of rhythmicity in TKs targeted by several latest-generation antineoplastic agents. Also notable was a loss of cycling in ARNTL2, which has been implicated in several neoplastic diseases (40, 41).
Table S1.
Pathway level analysis of circadian changes with HCC
 |
After temporal reconstruction with CYCLOPS, transcripts having lost rhythmicity in HCC were identified. This required (i) significant cycling in NC samples by the following criteria: (ii) the lack of significant cycling in HCC samples; (iii) the significance of tumor specific circadian parameters in a nested model; and (iv) a more than twofold reduction in amplitude. KEGG, Reactome, and GO biological (direct) processes sets that were overrepresented among those genes that lost rhythmicity in HCC are shown. Separately, genes were ranked by the change in amplitude when comparing HCC and NC samples. GSEA was used to identify pathways enriched with amplitude reduction. For both analyses, the false-discovery rate (FDR) as output from the corresponding programs are shown for each gene set. Gene sets highlighted in the same color represent overlapping physiological pathways.
Chronotherapy is an immediate area of interest for clinical translation. Earlier, we proposed that drugs that target rhythmic, high-amplitude gene products represent a path for mechanism-driven chronotherapy. With CYCLOPS, we can now identify drug targets that oscillate in humans. Among the many transcripts with high-amplitude oscillations in normal human liver was SLC2A2 (Fig. 4A). Murine Slc2a2 cycles with similar temporal phasing in both the liver and kidney (1). SLC2A2 encodes GLUT2, a glucose transporter highly expressed in pancreas, liver, and kidney. STZ is a GLUT2 substrate and is standard of care in patients with locally advanced pancreatic neuroendocrine tumors (pNETs) (42). Although pNETS are rare, the incidence has nearly doubled in the last decades (43). STZ is cytotoxic to GLUT2-expressing cells, including islet cells and pNETS, with renal and hepatic toxicity being dose-limiting and potentially lethal (42).
Fig. 4.
Prospective chronotherapy for streptozocin (STZ). STZ is a cytotoxic agent used to treat pancreatic neuroendocrine tumors. STZ is actively transported into cells by the protein product of SLC2A2 and is associated with renal and hepatic toxicity. (A) The expression of Slc2a2 in mouse kidney and liver (1) is plotted as a function of circadian time. (B) Expression of SLC2A2 in human liver samples is plotted as a function of CYCLOPS phase. (C) Eleven-week-old male mice were dosed with STZ (green and purple) or saline (blue and red) at 7:00 AM (blue and green) or 7:00 PM (red and purple). Dosing time did not significantly impact the induction of hyperglycemia and expected treatment efficacy. (D) Body weight was used as a measure of gross toxicity. There was less weight loss among mice administered STZ at 7:00 PM.
As STZ has a remarkably short half-life (<15 min), it is an excellent candidate for chronotherapy. We reasoned dosing STZ during the nadir of hepatic SLC2A2 abundance could preserve STZ efficacy while minimizing renal and hepatic toxicity. The same dose of STZ was administered in the morning [Zeitgeber time (ZT) 0] or evening (ZT 12) to DBA/2J mice (44) for 5 consecutive days. We measured blood glucose levels as a surrogate marker for the efficacy of STZ in killing islet cells. Body weight was used as a simple measure of animal health and gross toxicity. Mice treated with STZ at either time were equally susceptible to hyperglycemia (Fig. 4B). However, mice administered STZ in the morning, when Slc2a2 transcript expression is low and GLUT2 protein abundance is high (1, 45), had a much greater loss in body mass compared with mice receiving STZ in the evening (−19.8 g vs. –12.9 g, P = 0.015). Thus, we temporally separated apparent efficacy (hyperglycemia) from toxicity (loss of body weight).
Discussion
Much of the molecular mechanics underlying circadian rhythms has been revealed in the last two decades. Much less progress has been made in converting these findings into actionable clinical knowledge. The lack of human time course data has presented a key barrier to translation. CYCLOPS aims to address this deficiency, using global descriptors of gene expression, evolutionary conservation, and machine learning to order unordered data within a periodic cycle. CYCLOPS builds on the foundation of Alter et al. (13) and the computational structure of Kirby and Miranda (15) to order high-throughput data and identify latent periodic oscillations in transcription. We validated CYCLOPS using ordered mouse and human data. We also demonstrated the consistency of CYCLOPS using human lung data from two distinct patient populations on separate continents.
CYCLOPS has advantages and disadvantages compared with existing methods. Supervised methods (e.g., ZeitZeiger) continue to improve but require time course training data. Obtaining blood and skin samples is straightforward. Serial biopsies of internal human organs are not practical. Unsupervised methods, like Oscope, have recovered cell cycle rhythms from unordered single-cell data. However, Oscope works on the single transcript level and requires thousands more computations than does CYCLOPS. Furthermore, Oscope is highly sensitive to the intersubject variability inherent to human data. Supervised methods are tissue specific and are similarly sensitive to biologic variability (as might be expected in cancer), as they have been optimized to use only a small number of highly informative transcripts. CYCLOPS uses global descriptors of expression structure, making it both robust and efficient for population-based human data. However, as with other high-dimensional bioinformatics methods, the particular data normalization scheme and descriptors of expression structure used can influence the final results.
CYCLOPS also has several limitations. It requires data from the entire periodic cycle to form an ellipse. Biopsies are almost exclusively obtained during the day. A large patient population, including shift workers, is necessary to fill in underrepresented times of day. Our experience suggests that >250 samples are required to order biopsy samples (Table S2). We also leveraged evolutionary conservation and mouse data to focus the genes used for human temporal reconstruction. CYCLOPS does not require that rhythms in mice and men are identical but does assume that the human homologs of mouse cycling genes are more likely to cycle. Importantly, CYCLOPS identifies features that are consistent with oscillations with respect to a latent variable, assumed to be time. Several findings lend confidence to our reconstructions. First, we recovered oscillations consistent with known circadian biology (e.g., phase relationships of core clock genes). We also recovered sample collection phases consistent with biopsy collection times and smooth orderings that well explain the data. CYCLOPS orderings are also relative. Additional information is needed to assign a circadian time to any particular CYCLOPS phase. In ordering the human lung and liver transcriptomes, we used the average acrophase of the PAR bZip transcription factors to fix time “π.” In the lung and liver of nocturnal mice, these factors show peak expression near ZT12 (1), the beginning of the peak activity period.
Table S2.
Description of datasets ordered in this manuscript
| Ref. | Tissue | Species | Sample collection | N samples |
| 18 | Liver | Mus musculus | Time course (every hour for 2 d) | 48 |
| 1 | Liver | Mus musculus | Time course (every 2 h for 2 d) | 24 |
| Kidney | — | — | 24 | |
| Lung | — | — | 24 | |
| Brown fat | — | — | 24 | |
| Heart | — | — | 24 | |
| Adrenal | — | — | 24 | |
| Aorta | — | — | 24 | |
| White fat | — | — | 24 | |
| Skeletal muscle | — | — | 24 | |
| Cerebellum | — | — | 24 | |
| Brainstem | — | — | 24 | |
| Hypothalamus | — | — | 24 | |
| 10 | Cortex (B11) | Homo sapiens | Autopsy | 202* |
| 21 | Lung (Groningen) | Homo sapiens | Biopsy | 445 |
| Lung (Laval) | Homo sapiens | Biopsy | 499 | |
| 37 | Liver (noncancerous) | Homo sapiens | Biopsy | 249 |
| Liver (cancerous) | Homo sapiens | Biopsy | 268 |
Table providing a brief summary of the different datasets analyzed, including the method of sample collection and the number of samples.
140 had an annotated time of death.
Circadian rhythms persist in the absence of environmental cues. The observation of rhythms under normal conditions is not sufficient to classify a rhythm as circadian. Pending further study, the human transcriptional oscillations identified by CYCLOPS are more properly labeled as diurnal.
A final caveat lies in the identification of periodic transcripts from CYCLOPS-ordered data. Regression and other rhythm detection methods are predicated on time as a variable independent of expression. CYCLOPS phases are derived from gene expression. As a result, standard statistical significance tests tend to be too liberal. To mitigate this concern, we have imposed an unusually strict numerical cutoff for statistical significance. We also require cycling with sufficient amplitude to suggest physiologic importance.
Despite these limitations, we have successfully used CYCLOPS to explore diurnal rhythms in human lung, liver, and HCC. Our analyses of normal lung and liver present clear translational opportunities. We found strong circadian cycling of the cell cycle and immune pathways in human lung. ACE, well expressed in the pulmonary vasculature and a key drug target for hypertension, appeared rhythmic. We also found cycling in members of the SMADs and the JAK–STAT pathways along with various TKs, many of which are important targets in idiopathic pulmonary fibrosis.
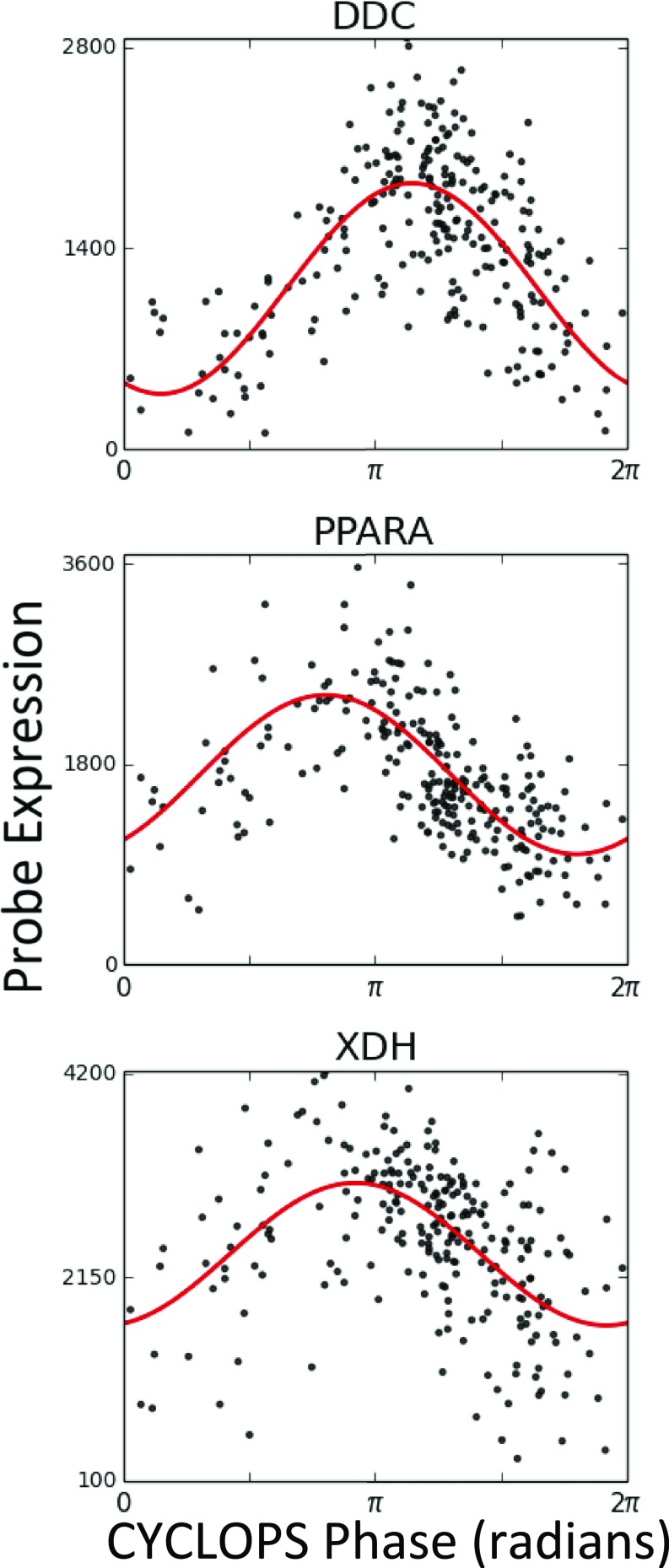
In liver, PPARA, DDC, and XDH, targets of the fibrates, dopamine decarboxylase inhibitors, and xanthine oxidase inhibitors, respectively, all display high-amplitude rhythms (Fig. S7). SLC2A2, the target of STZ, also displayed strong cycling in human liver. In a proof-of-concept experiment, we leveraged these data to time STZ administration and segregate gross toxicity from efficacy. In sum, this approach presents a straightforward path from genome-scale human data to hypothesis-driven opportunities in chronotherapy.
Fig. S7.
Expression of selected clock-controlled drug targets in noncancerous liver as determined by CYCLOPS. Expression data from tissue obtained at biopsy was processed using CYCLOPS to reconstruct the circadian transcriptome in noncancerous (NC) human liver samples. Expression of selected drug targets is plotted as a function of CYCLOPS phase.
An important aspect of chronotherapy is the accurate circadian assessment or “phasing” individual patients. However, how accurate must this be? The answer likely depends on the kinetics of the drug and the dynamics of its target. For STZ and other fast-acting drugs that target molecules with high-amplitude rhythms, there may be a broad window of acceptable dosing times. For other drugs, more temporal precision might be required.
CYCLOPS is an algorithm that temporally reconstructs population-based human organ data. Applying CYCLOPS to over 2,000 human samples, we observe clear, high-amplitude molecular rhythms in lung, liver, brain, and HCC. Despite disparities in patient age, gender, genetics, diet, and environment, CYCLOPS extracted significant periodic signatures. For a large subset of genes, circadian variability in expression was larger than the variability attributable to these aggregated genetic and environmental variables. By implication, circadian control may offer a powerful tool for precision medicine.
Finally, we investigated the state of circadian rhythms in a human cancer, HCC. The circadian clock is believed to gate the cell cycle. In HCC, we find that, despite continued oscillator function, there is circadian deregulation of JAK–STAT, apoptotic, and metabolic pathways. To catalyze the further pursuit of translational chronobiology, we have posted the CYCLOPS program and associated scripts on GitHub. We hope this and related approaches will propel investigation into the role of circadian biology in clinical medicine.
Methods
All animal studies were done under Charles River Laboratories study number 20091523 under Institutional Animal Care and Use Committee protocol P01182016A.
Microarray Processing.
CEL files containing raw data were downloaded from NIH GEO and processed with RMA in R (version 3.2.3) Bioconductor.
Computational Methods.
The CYCLOPS autoencoder and downstream analysis were implemented in Julia 0.3.10. The associated files are available for download on GitHub.
Data Scaling and Normalization.
For temporal reconstruction, we first restricted the list of probes used to the top 10,000 highest expressed probes (as sorted by mean probe value). For each probe, we impute extreme expression values at the top/bottom 2.5th percentile. The expression of each probe i in sample j was scaled as follows:
where Mi is the mean expression of probe i across samples: .
The Si,j data were expressed in eigengene coordinates following the methods of Alter et al. The number of eigengenes (singular values) retained was set so as to preserve 85% of the variance of the data. The autoencoder was applied to these characteristic expression patterns for the purposes of temporal reconstruction.
CYCLOPS Autoencoder.
The activated value of neuron j in layer l is denoted by and for linear neurons is given by , where weight from the kth neuron in layer l − 1 to the jth neuron in layer l is represented by . The bias in jth neuron in layer l is denoted (46).
A single, circular node was used in the bottleneck layer. The single circular neuron was implemented as two coupled neurons (15). The preactivation values of these neurons and are given by the following:
Activated values are obtained by mapping these onto the unit circle:
with phase
linear neurons were used in both the encoding and decoding steps. The autoencoder was trained by backpropagation using stochastic batch gradient descent with momentum (46). Default training parameters were set as set batch size = 10, rate = 0.3, and momentum = 0.5.
Training is repeated multiple times (default = 40) starting at different, randomly set initial weighting conditions. The result with minimal sum of squares output error is used.
The fully trained autoencoder was used to encode the characteristic expression data . The value of the circular node assigned each sample j ( was the phase assigned to that sample.
The same autoencoder training parameters were used for all reconstructions.
Additional methodological details can be found in SI Methods.
SI Methods
CYCLOPS Quality Metrics.
Two metrics were used to assess the quality of the CYCLOPS ordering.
compares the total sum of squares error of the circular autoencoder in reconstructing characteristic expression patterns with the residual variance/error unexplained by the first principal component. The first principal component analytically reproduces the results of a fully linear autoencoder with a single bottleneck node (47). Thus, compares the improvement in model fit when a circular rather than linear bottleneck node is used. mirrors the definition of the F statistic in nested regression models used to evaluate the inclusion of additional parameters with increasing model complexity. Defining as the autoencoder reconstruction error and as the variance remaining unexplained by the first principal component:
is a measure of the smoothness of the ordered expression trajectory. It compares the mean distance, in expression space, between sequential samples when using a circular ordering to the distance between sequential samples assuming a linear ordering. Given the samples j and associated CYCLOPS phases , we create circular ordering c, which is a permutation of the indexes j such that for all c. Similarly, we define a linear ordering l based on the magnitude of the first eigengene so that for all l. Denoting as the Euclidean norm and the as the eigengenes expression profile of sample j:
Evaluating Significance of Error Metric.
The significance of was assessed by bootstrap. To create a background distribution for , each row i of was independently permuted. This removed any fixed phase relationship between the probes while maintaining their marginal distributions. These data were then expressed eigengenes and the CYCLOPS autoencoder was retrained and the error metric recomputed. This process is repeated to create a background distribution used to assess the significance of .
Identification of “Seed Genes” by Homology.
To identify genes that are more likely to cycle in a specified human tissue, we use the data of Zhang et al. (1) and identified genes with cycling expression using JTK-Cycle (48) (value of q < 0.05). The gene identifiers were matched to their human homolog using Homologene.
Modified Cosinor Regression.
Cosinor regression has long been used to identify circadian processes (23). The datasets typically analyzed in this way include more than a single cycle so that monotonic expression patterns are not misidentified as circadian. CYCLOPS, however, assigns each sample a phase along a single reconstructed cycle
To better exclude monotonic trends, we compared the fit of a best-fit line with the fit of nested model including both that line and sinusoidal functions of CYCLOPS phase.
For each probe (i), we fit the data to two models:
| [M1] |
| [M2] |
The are first optimized in M1 by a brute-force search. The F test is used to evaluate the null hypothesis 0.
The amplitude and acrophase of each probe are given by and using the standard regression model .
Identification of Probes That “Lost Cycling” in HCC.
Given the CYCLOPS-ordered expression data from NC and HCC samples, we first used modified cosinor regression to identify the set of probes that appeared to cycle in NC data (Bonferroni-corrected P value < 0.05, amplitude > 33% mean expression) but not in HCC data.
We then sought to identify probes for which there appeared to be a change in circadian expression rather than an increase in noncircadian noise. For each probe identified above, we then pooled the NC and HCC data and corresponding phase assignments and fit the data with two nested models:
| [MPool1] |
| [MPool2] |
where I is an indicator variable equal to 0 for NC sample and 1 for HCC samples.
An F test is used to evaluate the null hypothesis 0. We restricted our results to probes for which the Bonferroni-corrected P value < 0.05.
Finally, we compared the amplitude for NC samples and HCC samples from Eq. MPool2 and further restricted our list to those probes that had a more than twofold reduction in normalized amplitude.
Set/Pathway Level Analysis.
PSEA was applied to reconstructed pulmonary and liver expression data as previously described (30). The JAVA application was downloaded from GitHub and default application settings were used. The “Canonical Pathways Gene sets (CP)” were downloaded from the molecular signatures database (49).
GSEA was used to identify pathways enriched for amplitude loss in HCC (39). We analyzed all probes that were found to cycle in NC samples (as described above) and ranked them by the change in amplitude in HCC compared with NC samples as assessed by Eq. MPool2. The JAVA version of GSEA (version 1.0) was used to test the “Hallmark Pathways” using the “Pre-ranked” analysis function and the “classic” enrichment statistic.
The NIH David web application (version 6.8) was used to evaluate the list of probes that “lost cycling” as described above (38). To mirror GSEA and PSEA results, the search for overrepresented pathways was limited to KEGG, REACTOME, and Gene Ontology (GO) Biological Process (BP) gene sets. This full list of genes that cycled in the NC liver were used as a custom background.
STZ Experiments.
Mice.
Male DBA/2J mice were procured from The Jackson Laboratory (stock number 000671) and entrained to a 12-h light/12-h dark, light cycle for 2 wk before dosing. All studies were done under Charles River Laboratories study number 20091523 under Institutional Animal Care and Use Committee protocol P01182016A.
Intraperitoneal injections.
STZ (Sigma; S0130) was formulated in 0.05 M sodium citrate (pH 4.5) on ice. Sodium citrate was added to preweighed STZ. The solution was kept on ice and protected from light. Dosing was performed within 20 min of final formulation. Treatment was administered by i.p. injection. The dose volume per animal (5 mL/kg) was based on morning body weight measurements.
Study design.
Forty male DBA/2J mice were randomized to one of four treatment groups (n = 10/group) at 11 wk of age. Morning (7:00 AM—just after lights on) vehicle, morning drug, evening (7:00 PM—just before lights off) vehicle, or evening drug groups received an i.p. injection of either saline (vehicle groups), or low-dose STZ (40 mg⋅kg−1⋅d−1), on 5 consecutive days (day 1 through day 5). Mice were monitored for 2 wk following the first i.p. injection. During the treatment period, mice were given 10% sucrose in water until day 6 to prevent fatal hypoglycemia that often occurs during dosing. Body weight and nonfasting blood glucose measurements were recorded daily. Mice were killed on day 16.
Statistical analyses.
The largest change from baseline body weight was determined for each animal in the study. A two-tailed t test was used to compare responses in the AM and PM STZ treatment groups. An identical analysis was performed for blood glucose.
Supplementary Material
Acknowledgments
We thank Gang Wu, Robert Schmidt, and Marc Ruben for their critical reading of the manuscript and testing of the CYCLOPS program. We are grateful to researchers who generated the original datasets. This work is supported by Defense Advanced Research Projects Agency Grants D17AP00003 (to R.C.A.) and in part by D12AP00025, National Institute of Neurological Disorders and Stroke Grant 5R01NS054794-08 (to J.B.H.), in part by National Institute on Aging Grant 2P01AG017628-11, and the Penn Genome Frontiers Institute under a Health Research Formula Fund grant with the Pennsylvania Department of Health.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 5069.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1619320114/-/DCSupplemental.
References
- 1.Zhang R, Lahens NF, Ballance HI, Hughes ME, Hogenesch JB. A circadian gene expression atlas in mammals: Implications for biology and medicine. Proc Natl Acad Sci USA. 2014;111:16219–16224. doi: 10.1073/pnas.1408886111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hetzel MR, Clark TJ. Comparison of normal and asthmatic circadian rhythms in peak expiratory flow rate. Thorax. 1980;35:732–738. doi: 10.1136/thx.35.10.732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Straub RH, Cutolo M. Circadian rhythms in rheumatoid arthritis: Implications for pathophysiology and therapeutic management. Arthritis Rheum. 2007;56:399–408. doi: 10.1002/art.22368. [DOI] [PubMed] [Google Scholar]
- 4.Ferrell JM, Chiang JYL. Circadian rhythms in liver metabolism and disease. Acta Pharm Sin B. 2015;5:113–122. doi: 10.1016/j.apsb.2015.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ueda HR, et al. Molecular-timetable methods for detection of body time and rhythm disorders from single-time-point genome-wide expression profiles. Proc Natl Acad Sci USA. 2004;101:11227–11232. doi: 10.1073/pnas.0401882101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hughey JJ, Hastie T, Butte AJ. ZeitZeiger: Supervised learning for high-dimensional data from an oscillatory system. Nucleic Acids Res. 2016;44:e80. doi: 10.1093/nar/gkw030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Agostinelli F, Ceglia N, Shahbaba B, Sassone-Corsi P, Baldi P. What time is it? Deep learning approaches for circadian rhythms. Bioinformatics. 2016;32:i8–i17. doi: 10.1093/bioinformatics/btw243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Möller-Levet CS, et al. Effects of insufficient sleep on circadian rhythmicity and expression amplitude of the human blood transcriptome. Proc Natl Acad Sci USA. 2013;110:E1132–E1141. doi: 10.1073/pnas.1217154110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Arnardottir ES, et al. Blood-gene expression reveals reduced circadian rhythmicity in individuals resistant to sleep deprivation. Sleep. 2014;37:1589–1600. doi: 10.5665/sleep.4064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen C-Y, et al. Effects of aging on circadian patterns of gene expression in the human prefrontal cortex. Proc Natl Acad Sci USA. 2016;113:206–211. doi: 10.1073/pnas.1508249112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Trapnell C, et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat Biotechnol. 2014;32:381–386. doi: 10.1038/nbt.2859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Leng N, et al. Oscope identifies oscillatory genes in unsynchronized single-cell RNA-seq experiments. Nat Methods. 2015;12:947–950. doi: 10.1038/nmeth.3549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Alter O, Brown PO, Botstein D. Singular value decomposition for genome-wide expression data processing and modeling. Proc Natl Acad Sci USA. 2000;97:10101–10106. doi: 10.1073/pnas.97.18.10101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kramer MA. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 1991;37:233–243. [Google Scholar]
- 15.Kirby MJ, Miranda R. Circular nodes in neural networks. Neural Comput. 1996;8:390–402. doi: 10.1162/neco.1996.8.2.390. [DOI] [PubMed] [Google Scholar]
- 16.Scholz M. 2007. Analysing periodic phenomena by circular PCA. Bioinformatics Research and Development (Springer, Berlin), pp 38–47.
- 17.Hsieh WW. Nonlinear principal component analysis by neural networks. Tellus A. 2001;53:599–615. doi: 10.1016/j.neunet.2007.04.018. [DOI] [PubMed] [Google Scholar]
- 18.Hughes ME, et al. Harmonics of circadian gene transcription in mammals. PLoS Genet. 2009;5:e1000442. doi: 10.1371/journal.pgen.1000442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jammalamadaka SR, Sengupta A. Topics in Circular Statistics. World Scientific; Singapore: 2001. [Google Scholar]
- 20.Anafi RC, et al. Machine learning helps identify CHRONO as a circadian clock component. PLoS Biol. 2014;12:e1001840. doi: 10.1371/journal.pbio.1001840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bossé Y, et al. Molecular signature of smoking in human lung tissues. Cancer Res. 2012;72:3753–3763. doi: 10.1158/0008-5472.CAN-12-1160. [DOI] [PubMed] [Google Scholar]
- 22.Sgambato A, et al. The role of EGFR tyrosine kinase inhibitors in the first-line treatment of advanced non small cell lung cancer patients harboring EGFR mutation. Curr Med Chem. 2012;19:3337–3352. doi: 10.2174/092986712801215973. [DOI] [PubMed] [Google Scholar]
- 23.Refinetti R, Lissen GC, Halberg F. Procedures for numerical analysis of circadian rhythms. Biol Rhythm Res. 2007;38:275–325. doi: 10.1080/09291010600903692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lin C-Y, et al. ADAM9 promotes lung cancer metastases to brain by a plasminogen activator-based pathway. Cancer Res. 2014;74:5229–5243. doi: 10.1158/0008-5472.CAN-13-2995. [DOI] [PubMed] [Google Scholar]
- 25.Brantley-Sieders DM. Clinical relevance of Ephs and ephrins in cancer: Lessons from breast, colorectal, and lung cancer profiling. Semin Cell Dev Biol. 2012;23:102–108. doi: 10.1016/j.semcdb.2011.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yoo M, et al. DSigDB: Drug signatures database for gene set analysis. Bioinformatics. 2015;31:3069–3071. doi: 10.1093/bioinformatics/btv313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Richeldi L, et al. Efficacy of a tyrosine kinase inhibitor in idiopathic pulmonary fibrosis. N Engl J Med. 2011;365:1079–1087. doi: 10.1056/NEJMoa1103690. [DOI] [PubMed] [Google Scholar]
- 28.Bader M. Tissue renin-angiotensin-aldosterone systems: Targets for pharmacological therapy. Annu Rev Pharmacol Toxicol. 2010;50:439–465. doi: 10.1146/annurev.pharmtox.010909.105610. [DOI] [PubMed] [Google Scholar]
- 29.Hermida RC, Ayala DE. Chronotherapy with the angiotensin-converting enzyme inhibitor ramipril in essential hypertension: Improved blood pressure control with bedtime dosing. Hypertension. 2009;54:40–46. doi: 10.1161/HYPERTENSIONAHA.109.130203. [DOI] [PubMed] [Google Scholar]
- 30.Zhang R, Podtelezhnikov AA, Hogenesch JB, Anafi RC. Discovering biology in periodic data through phase set enrichment analysis (PSEA) J Biol Rhythms. 2016;31:244–257. doi: 10.1177/0748730416631895. [DOI] [PubMed] [Google Scholar]
- 31.Mehra R. Understanding nocturnal asthma. The plot thickens. Am J Respir Crit Care Med. 2014;190:243–244. doi: 10.1164/rccm.201406-1130ED. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lévi F, Okyar A, Dulong S, Innominato PF, Clairambault J. Circadian timing in cancer treatments. Annu Rev Pharmacol Toxicol. 2010;50:377–421. doi: 10.1146/annurev.pharmtox.48.113006.094626. [DOI] [PubMed] [Google Scholar]
- 33.Warburton D, Shi W, Xu B. TGF-β-Smad3 signaling in emphysema and pulmonary fibrosis: An epigenetic aberration of normal development? Am J Physiol Lung Cell Mol Physiol. 2013;304:L83–L85. doi: 10.1152/ajplung.00258.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jeon H-S, Jen J. TGF-beta signaling and the role of inhibitory Smads in non-small cell lung cancer. J Thorac Oncol. 2010;5:417–419. doi: 10.1097/JTO.0b013e3181ce3afd. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.McMenamin TM. Time to work: Recent trends in shift work and flexible schedules, A. Monthly Lab Rev. 2007;130:3. [Google Scholar]
- 36.Archer SN, et al. Mistimed sleep disrupts circadian regulation of the human transcriptome. Proc Natl Acad Sci USA. 2014;111:E682–E691. doi: 10.1073/pnas.1316335111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lamb JR, et al. Predictive genes in adjacent normal tissue are preferentially altered by sCNV during tumorigenesis in liver cancer and may rate limiting. PLoS One. 2011;6:e20090. doi: 10.1371/journal.pone.0020090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Huang W, Sherman BT, Lempicki RA. Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nat Protoc. 2009;4:44–57. doi: 10.1038/nprot.2008.211. [DOI] [PubMed] [Google Scholar]
- 39.Subramanian A, et al. Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci USA. 2005;102:15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ha N-H, Long J, Cai Q, Shu XO, Hunter KW. The circadian rhythm gene Arntl2 is a metastasis susceptibility gene for estrogen receptor-negative breast cancer. PLoS Genet. 2016;12:e1006267. doi: 10.1371/journal.pgen.1006267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Brady JJ, et al. An Arntl2-driven secretome enables lung adenocarcinoma metastatic self-sufficiency. Cancer Cell. 2016;29:697–710. doi: 10.1016/j.ccell.2016.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chan JA, Kulke M, Clancy TE. 2016 Metastatic well-differentiated pancreatic neuroendocrine tumors: Systemic therapy options to control tumor growth and symptoms of hormone hypersecretion. UpToDate. Available at www.uptodate.com/index. Accessed August 10, 2016.
- 43.Hallet J, et al. Exploring the rising incidence of neuroendocrine tumors: A population-based analysis of epidemiology, metastatic presentation, and outcomes. Cancer. 2015;121:589–597. doi: 10.1002/cncr.29099. [DOI] [PubMed] [Google Scholar]
- 44.Furman BL. Streptozotocin-induced diabetic models in mice and rats. Curr Protoc Pharmacol. 2015;70:5.47.1–5.47.20. doi: 10.1002/0471141755.ph0547s70. [DOI] [PubMed] [Google Scholar]
- 45.Lamia KA, Storch K-F, Weitz CJ. Physiological significance of a peripheral tissue circadian clock. Proc Natl Acad Sci USA. 2008;105:15172–15177. doi: 10.1073/pnas.0806717105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bishop CM. Pattern Recognition and Machine Learning. 20th Ed Springer; New York: 2007. [Google Scholar]
- 47.Baldi P, Hornik K. Neural networks and principal component analysis: Learning from examples without local minima. Neural Netw. 1989;2:53–58. [Google Scholar]
- 48.Hughes ME, Hogenesch JB, Kornacker K. JTK_CYCLE: An efficient nonparametric algorithm for detecting rhythmic components in genome-scale data sets. J Biol Rhythms. 2010;25:372–380. doi: 10.1177/0748730410379711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Liberzon A, et al. Molecular signatures database (MSigDB) 3.0. Bioinformatics. 2011;27:1739–1740. doi: 10.1093/bioinformatics/btr260. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.