Shape-driven solid–solid transitions in colloids

Significance

Despite the fundamental importance of solid–solid transitions for metallurgy, ceramics, earth science, reconfigurable materials, and colloidal matter, the details of how materials transform between two solid structures are poorly understood. We introduce a class of simple model systems in which the direct control of local order, via colloid shape change, induces solid–solid phase transitions and characterize how the transitions happen thermodynamically. We find that, within a single shape family, there are solid–solid transitions that can occur with or without a thermal activation barrier. Our results provide means for the study of solid–solid phase transitions and have implications for designing reconfigurable materials.

Abstract

Solid–solid phase transitions are the most ubiquitous in nature, and many technologies rely on them. However, studying them in detail is difficult because of the extreme conditions (high pressure/temperature) under which many such transitions occur and the high-resolution equipment needed to capture the intermediate states of the transformations. These difficulties mean that basic questions remain unanswered, such as whether so-called diffusionless solid–solid transitions, which have only local particle rearrangement, require thermal activation. Here, we introduce a family of minimal model systems that exhibits solid–solid phase transitions that are driven by changes in the shape of colloidal particles. By using particle shape as the control variable, we entropically reshape the coordination polyhedra of the particles in the system, a change that occurs indirectly in atomic solid–solid phase transitions via changes in temperature, pressure, or density. We carry out a detailed investigation of the thermodynamics of a series of isochoric, diffusionless solid–solid phase transitions within a single shape family and find both transitions that require thermal activation or are “discontinuous” and transitions that occur without thermal activation or are “continuous.” In the discontinuous case, we find that sufficiently large shape changes can drive reconfiguration on timescales comparable with those for self-assembly and without an intermediate fluid phase, and in the continuous case, solid–solid reconfiguration happens on shorter timescales than self-assembly, providing guidance for developing means of generating reconfigurable colloidal materials.

Despite wide-ranging implications for metallurgy (1), ceramics (2), earth sciences (3, 4), reconfigurable materials (5, 6), and colloidal matter (7), fundamental questions remain about basic physical mechanisms of solid–solid phase transitions. One major class of solid–solid transitions is diffusionless transformations. Although in diffusionless transformations, particles undergo only local rearrangement, the thermodynamic nature of diffusionless transitions is unclear (8). This gap in our understanding arises from technical details that limit what we can learn about solid–solid transitions from standard laboratory techniques, such as X-ray diffraction or EM (9). The use of a broader array of experimental, theoretical, and computational techniques could provide better understanding of solid–solid transitions if an amenable class of models could be developed (10). To develop minimal models, it is important to note that solid–solid transitions are accompanied by a change in shape of the coordination polyhedra in the structure (11). Coordination polyhedra reflect the bonding of atoms in a crystal, which suggests that minimal models of solid–solid transitions could be provided by systems in which the shape of coordination polyhedra is directly manipulated. Direct manipulation of coordination polyhedra may be achieved in systems of anisotropically shaped colloids (12, 13). Anisotropic colloids manifest an emergent, shape-dependent entropic valence (12, 13) that is responsible for the stabilization of a wide variety of structures, even in the absence of direct interparticle forces (12, 14–23). Moreover, colloids are amenable to a wide range of observational and experimental techniques, and colloids have been widely used to investigate melting (24, 25), sublimation (26), crystallization (27–29), and vitrification (30). Pioneering realizations of solid–solid phase transitions in colloids (6, 10, 31–35) have revealed detailed information about the transition mechanisms, including showing experimentally a first-order transition that goes through an intermediate fluid (10, 32), an experimental system that showed a variety of different transition pathways (33), and the experimental observation of a pressure-dependent transition in colloidal superballs (35). Recently, interaction shifting via DNA programing has been used to construct colloidal solid–solid transitions (36), including showing that a single solid mother phase can be reprogrammed to yield multiple daughter phases through diffusionless transitions (37).

Here, we change particle shape in situ to directly control particle coordination in colloidal crystals to create minimal models of solid–solid phase transitions. Our models mimic the changes in coordination that occur indirectly in conventional atomic solid–solid transitions through changes in temperature, pressure, or density. We find isochoric solid–solid transitions in “shape space” in a simple two-parameter family (38) of convex colloidal polyhedra with fixed point group symmetry that exhibits transitions between crystals with one [simple cubic (SC)], two [body-centered cubic (BCC)], and four [face-centered cubic (FCC)] particles in a cubic unit cell. We study the thermodynamics of the transitions using a consistent thermodynamic parametrization of particle shape via the recently proposed approach of “digital alchemy” (39) combined with the rare event sampling technique of umbrella sampling (40), which is commonly used to calculate free energy difference between two different states (41). We investigate solid–solid transitions between BCC and FCC crystals and between BCC and SC crystals. We find that both transitions are diffusionless transformations between lattices that are continuously related by linear mathematical transformations. We study four cases of the BCC$\leftrightarrow$FCC transition and find that, in all cases, the transition is thermodynamically discontinuous (i.e., first order). We also study two cases of the BCC$\leftrightarrow$SC transition and find, in contrast, that, in both cases, the transition is thermodynamically continuous (i.e., second or higher order). We study the dynamics of the solid–solid transitions and find no evidence of intermediate fluid states, regardless of whether the transition is discontinuous or continuous. Our results show that diffusionless solid–solid phase transitions can be thermodynamically discontinuous or continuous, even in cases where transitions are induced by symmetry-invariant shape change driven solely by entropy maximization and where transitions are between cubic crystals with four or fewer particles in a unit cell. More generally, our approach opens up a wide array of systems for studying solid–solid transitions by using particle shape to directly manipulate coordination polyhedra. Finally, we find systems in which solid–solid transitions occur on timescales that are comparable with those for self-assembly, suggesting approaches for rationally designing reconfigurable colloidal materials.

Model and Methods

A goal of this study is to determine if shape-driven solid–solid transitions are viable for developing reconfigurable materials. Our study considers scenarios in which structural reconfiguration happens on much longer timescales than particle shape change. Moreover, because particle shape change can occur in systems of colloidal particles that are on the scale of hundreds of nanometers (42), shape variability is typically small at those scales, and therefore, we will model all particles as having the same shape.

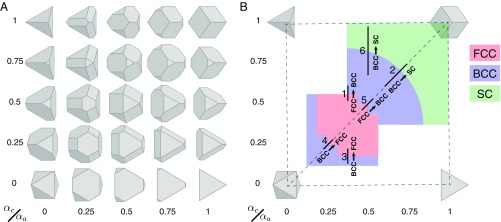
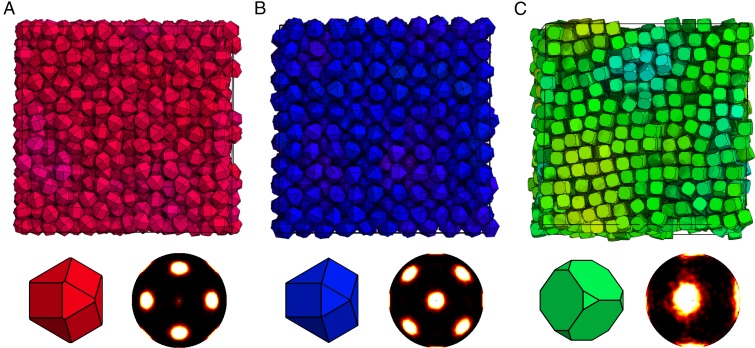
A family of shapes that have the same point group symmetry and self-assemble crystals with small unit cells (1-SC, 2-BCC, and 4-FCC) in adjacent regions of shape space is found in the spheric triangle invariant 323 family (${\mathrm{\Delta }}_{323}$) of hard polyhedra (38) (Fig. 1 shows shapes); ${\mathrm{\Delta }}_{323}$ is formed by subjecting cubes to two distinct sets of tetrahedral truncations and includes the cube, tetrahedron, and octahedron. These shapes as well as intermediate shapes in ${\mathrm{\Delta }}_{323}$ have been synthesized at the colloidal scale (6, 18, 20, 43). Simulations of hard colloidal polyhedra in ${\mathrm{\Delta }}_{323}$ have shown them to have rich self-assembly behavior (Fig. 2 shows three examples) with both wide and narrow regions of thermodynamic stability for a number of different bulk structures (22). We denote shapes according to the conventions $({\alpha }_a\text{,}{\alpha }_c)$, where $0\le {\alpha }_{a\text{,}c}\le 1$ defines the boundaries of shape space in this shape family. With these conventions, $(\mathrm{0,0})$ is an octahedron, $(0\text{,}1)$ and $(1\text{,}0)$ are tetrahedra (which is self-dual), and $(1\text{,}1)$ is a cube (dual to the octahedron). We use conventions in which all particles have unit volume.

Fig. 1.

(A) Spheric triangle invariant (${\mathrm{\Delta }}_{323}$) polyhedra form a continuous two-parameter (${\alpha }_a$, ${\alpha }_c$) family of symmetric convex shapes that are bounded by the octahedron [$({\alpha }_a\text{,}{\alpha }_c)=$(0,0)], tetrahedron [(0,1) and (1,0)], and cube (1,1). (B) We show six lines indicating regions of shape space in which there is a change in the equilibrium structure at a packing density of $\eta =0.55$. The lines are annotated with the relevant structural transition and direction. The colors indicate the self-assembled structures, where FCC is red, BCC is blue, and SC is green. The self-assembled phases indicated are an approximated representation from the actual self-assembled phases. Phases in the white region are not of interest in this paper. Results for transitions 1 and 2 are given in Figs. 4 and 5, respectively. Results for transitions 3–6 are in SI Text.

Fig. 2.

Sample self-assembled colloidal crystals formed by shapes in the ${\mathrm{\Delta }}_{323}$ triangle-invariant family of hard polyhedra, with images showing particle shape and bond order diagram. (A) An FCC crystal self-assembled from shape $({\alpha }_a\text{,}{\alpha }_c)=(0.4\text{,}0.525)$. (B) A BCC crystal self-assembled from shape $({\alpha }_a\text{,}{\alpha }_c)=(0.4\text{,}0.59)$. (C) An SC crystal self-assembled from shape $({\alpha }_a\text{,}{\alpha }_c)=(0.76\text{,}0.76)$. Note the similarity of shapes in A and B; even small shape differences can affect the bulk self-assembly of hard polyhedra. Shapes in A and B are both on line 1 in Fig. 1, and the shape in C is on line 2 in Fig. 1.

We investigate shape change-induced solid–solid transitions in ${\mathrm{\Delta }}_{323}$ in the regions indicated in Fig. 1, focusing on BCC, FCC, and SC structures. FCC and BCC as well as BCC and SC can be found in neighboring regions of ${\mathrm{\Delta }}_{323}$. We study FCC$\leftrightarrow$BCC and BCC$\leftrightarrow$SC transitions, and the regions of investigation indicated in Fig. 1 are all known boundaries between the phases of interest in ${\mathrm{\Delta }}_{323}$.

We study the thermodynamics of solid–solid transitions using both the Ehrenfest and Landau approaches (44). All Monte Carlo (MC) simulations and computations were done at fixed packing fraction $\eta =0.55$, which is sufficiently dense to observe the spontaneous assembly of each of the target phases (22) and sufficiently dilute so as to avoid the complicated infinite pressure behavior of this family of shapes (22, 38). All simulations were performed with HOOMD-Blue (45) using the HPMC-plugin (46), and we use units in which $k_{\mathrm{B}}T=1$.

First, to estimate the location of phase boundaries, we use the notion of generalized “alchemical” structure–property relationships (39). Alchemical structural–property relationships are derived from a consistent statistical mechanics treatment of particle attributes (here shape) as thermodynamic quantities. These thermodynamic quantities enter extended $NVT{\mu }_a{\mu }_c$ ensembles that, for ${\mathrm{\Delta }}_{323}$, have the form

$$\mathcal{Z}(N,V,T,{\mu }_a,{\mu }_c)\equiv e^{-\beta \varphi }=\int d{\alpha }_{a}d{\alpha }_c[dp][dq]e^{-\beta (H-{\mu }_{a}N{\alpha }_a-{\mu }_{c}N{\alpha }_c)}\text{,}$$ [1]

where the integral is taken over shape space as well as the ordinary (translational and rotational) phase space of the particles and where $\beta =1/k_{B}T$ and ${\mu }_{a\text{,}c}$ are thermodynamically conjugate to the shape variables ${\alpha }_{a\text{,}c}$ and referred to as “alchemical potentials” (39). The use of the term alchemical here comes from the fact that ${\mu }_{a\text{,}c}$ encodes the free energy cost of modifying the basic attributes (here shape) of the particles in the system in analogy with the (failed) attempts of the ancient alchemists to transmute the chemical elements. It is convenient to make a Legendre transformation of the free energy $\varphi$ from the $NVT{\mu }_a{\mu }_c$ ensemble to the free energy $F=\varphi +{\mu }_{a}N{\alpha }_a+{\mu }_{c}N{\alpha }_c$ of the $NVT{\alpha }_a{\alpha }_c$ ensemble, from which we can extract the constitutive relation

$$P({\alpha }_a\text{,}{\alpha }_c)=-{\left(\frac{\partial F}{\partial V}\right)}_{N,T,{\alpha }_a,{\alpha }_c}.$$ [2]

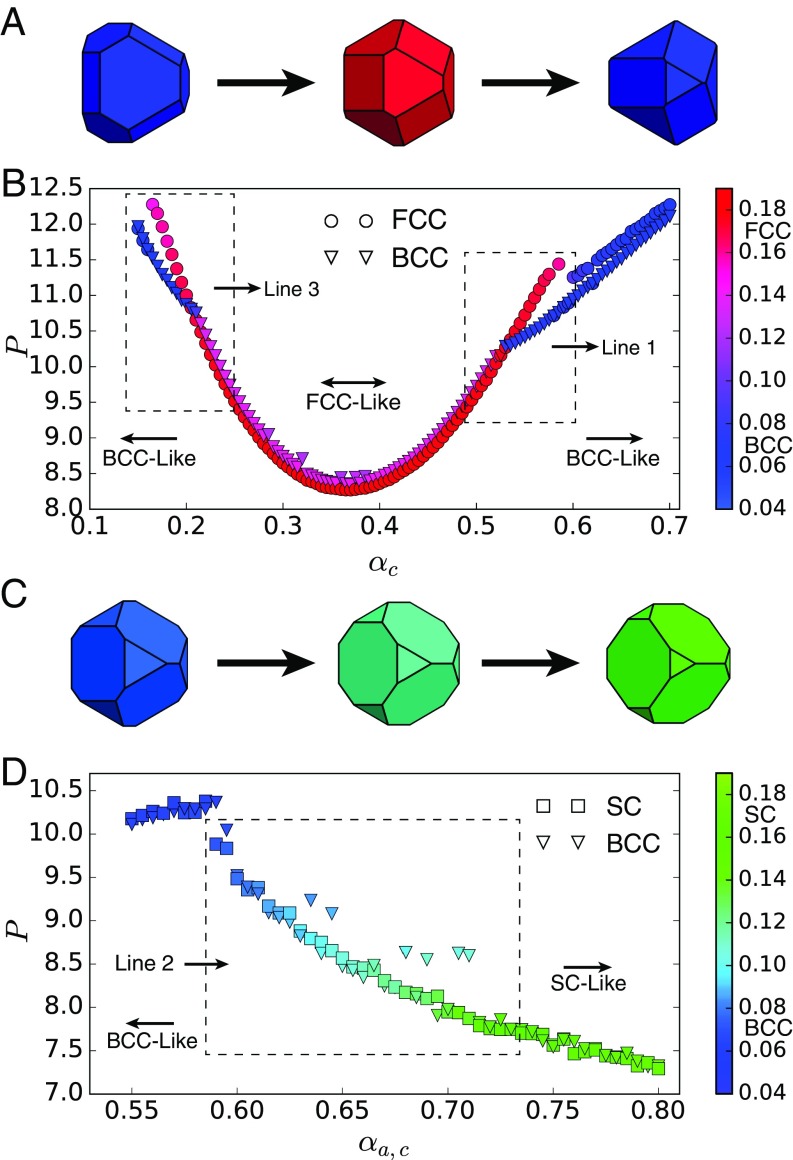
A thermodynamic phase transition, by the standard approach of Ehrenfest (44), is indicated if a thermodynamic quantity [e.g., $P({\alpha }_a,{\alpha }_c)$] or any of its derivatives is discontinuous. A discontinuity of $P({\alpha }_a,{\alpha }_c)$ signals a thermodynamic phase transition in shape space because of the explicit shape dependence in this relation. Accordingly, we searched for discontinuities by initializing systems with different building blocks (examples are in Fig. 3 A and C) in perfect BCC ($N=2\text{,}000$), FCC ($N=2\text{,}048$), or SC ($N=2\text{,}197$) structures and computed $P({\alpha }_a,{\alpha }_c)$ (Fig. 3 B and D) after $1.5\times {10}^7$ MC steps to ensure that systems reach equilibrium or metastable equilibrium using standard techniques (47).

Fig. 3.

Pressure–shape constitutive relation for ${\alpha }_a=0.4$ and ${\alpha }_a={\alpha }_c$. (A) Shape evolution in ${\alpha }_c$ at fixed ${\alpha }_a=0.4$. Shapes vary from self-assemble into BCC (blue) to FCC (red) and then back to BCC (blue). (B) Pressure–shape constitutive relation at fixed ${\alpha }_a=0.4$. Circles indicate FCC system initialization, and triangles indicate BCC system initialization. Marker colors indicate the value of the order parameter ${\overline{Q}}_4$ computed in the final structure of the system after equilibration. Boxed regions show the BCC$\leftrightarrow$FCC boundaries corresponding to lines 1 and 3 in Fig. 1. Errors are smaller than marker size. (C) Shape evolution for ${\alpha }_a={\alpha }_c$. Shapes vary from self-assemble into BCC (blue) to SC (green). (D) Pressure–shape constitutive relation for ${\alpha }_a={\alpha }_c$. Squares indicate SC system initialization; triangles indicate BCC initialization. Marker colors indicate the value of the order parameter ${\overline{Q}}_4$ computed in the final structure of the system after equilibration. Boxed regions show BCC$\leftrightarrow$FCC and BCC$\leftrightarrow$SC boundaries corresponding to lines 2, 4, and 5 in Fig. 1. Errors are smaller than marker size. Outliers are systems that did not equilibrate in $2\times {10}^7$ MC steps.

Second, having located discontinuities in $P({\alpha }_a,{\alpha }_c)$ and its derivatives, we computed the free energy as a function of order parameter (i.e., the Landau free energy) (44) for a series of fixed particle shapes near the solid–solid transition using umbrella sampling (40). To quantify the system crystal structure, we used a neighbor-averaged (48) version of the standard spherical harmonic bond order parameters (49). To achieve good order parametric separation of our crystal phases of interest, we used the second neighbor-averaged $l=4$ parameter ${\overline{Q}}_4$, which distinguishes BCC from FCC, SC, and hexagonally close-packed (HCP) phases in our systems as shown in Figs. 4B and 5B. To confirm the validity of ${\overline{Q}}_4$ as an order parameter for monitoring the FCC$\leftrightarrow$BCC transitions, we plot thermal averages of ${\overline{Q}}_4$ computed in BCC, HCP, and FCC in Fig. 4B. Data indicate that BCC crystals have a peak near ${\overline{Q}}_4=0.06$, that HCP has a peak near ${\overline{Q}}_4=0.09$ and a second smaller peak around ${\overline{Q}}_4=0.13$ because of mixed HCP–FCC stacking, and that FCC has a peak near ${\overline{Q}}_4=0.17$. The peaks are well-separated, and therefore, ${\overline{Q}}_4$ is a good distinguishing measure of a crystal phase. Umbrella sampling calculations used $5\times {10}^4$ samples in $32$ equally spaced windows in ${\overline{Q}}_4$ across each transition with a harmonic constraint of spring constant $k=3.5\times {10}^4$. [$k$ is parametrically large because it scales like the inverse square of the resolution of the order parameter, $\delta {\overline{Q}}_4$. For our crystals of interest, ${\overline{Q}}_4$ falls in the range of $0.05$–$0.2$, so that we need to be able to resolve order parameter intervals of $\delta {\overline{Q}}_4\approx 0.005$. The value $k=3.5\times {10}^4$ that we found to be consistent with efficient sampling is consistent with a naive estimate $k\approx {(\delta {\overline{Q}}_4)}^{-2}$.] We study FCC$\leftrightarrow$BCC transitions in four distinct regions of shape space, in each case using six polyhedra with shapes near the solid–solid transition; all systems contained $N=500$ particles (Fig. 4A). For BCC$\leftrightarrow$SC transitions, we studied two distinct regions of shape space, in both cases using different polyhedra in systems of $N=432$ particles (Fig. 5A). In all cases, five independent replicates were used to generate umbrella samples. Umbrella samples were used to reconstruct free energy curves using the weighted histogram analysis method (50), and errors were estimated using jackknife resampling (51). Additional methodological details are in SI Text. Data, documentation, simulation code, and analysis code are available on request from S.C.G.

Fig. 4.

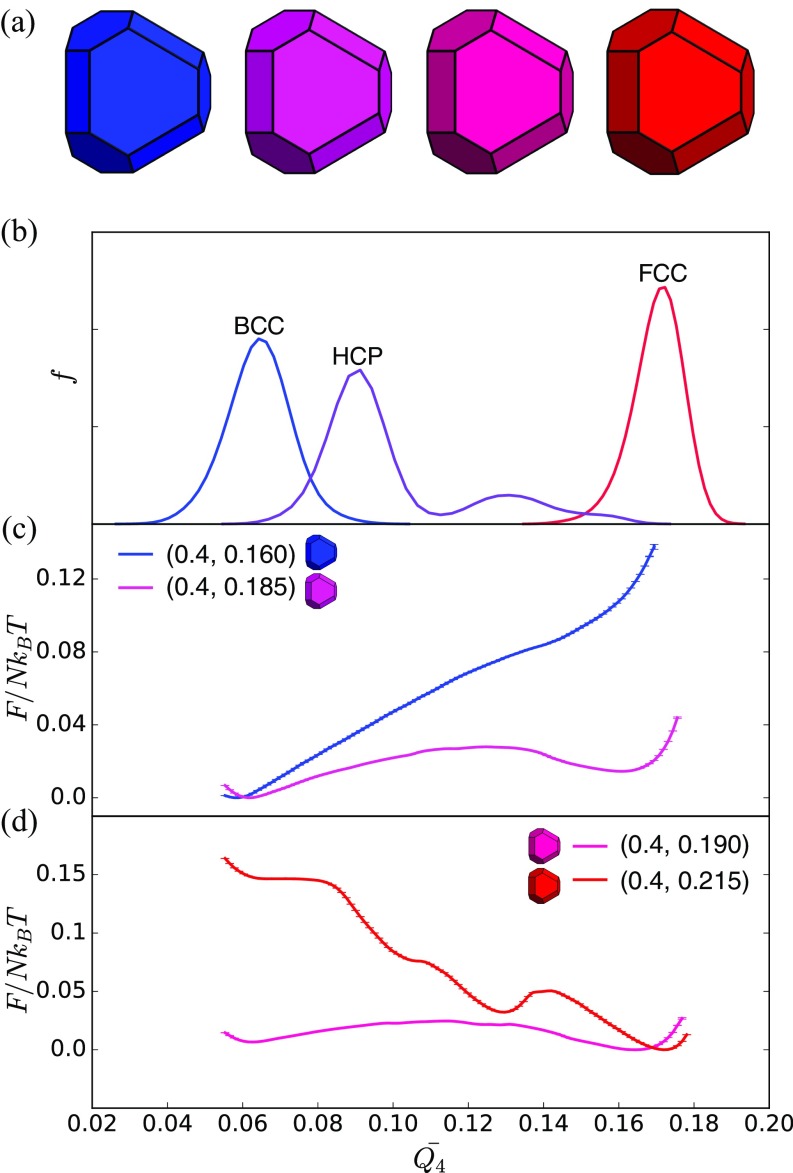
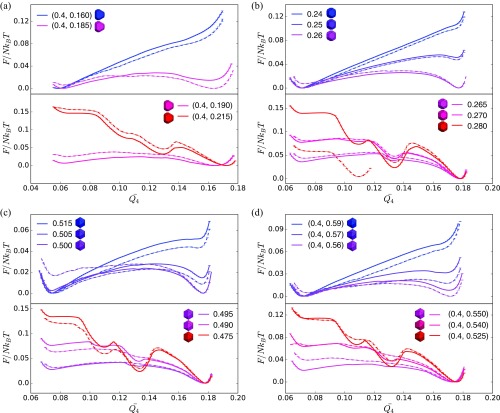
Shape-induced structural FCC$\leftrightarrow$BCC reconfiguration is accompanied by a first-order thermodynamic phase transition in spheric triangle invariant hard polyhedra. (A) Shapes used in umbrella sampling calculations. (B) Second neighbor-averaged $l=4$ spherical harmonic order parameter ${\overline{Q}}_4$ distinguishes BCC, FCC, and HCP crystal phases in thermal systems of spheric triangle invariant polyhedra. (C) Above the transition (${\alpha }_c>{\alpha }_c^{\ast }$), a metastable FCC free energy basin develops near ${\alpha }_c=0.58$. (D) Below the transition (${\alpha }_c<{\alpha }_c^{\ast }$), the FCC free energy basin becomes dominant (${\alpha }_c=0.55$), and well above the transition (${\alpha }_c=0.54$), the BCC free energy basin becomes unstable, and a second metastable HCP basin appears.

Fig. 5.

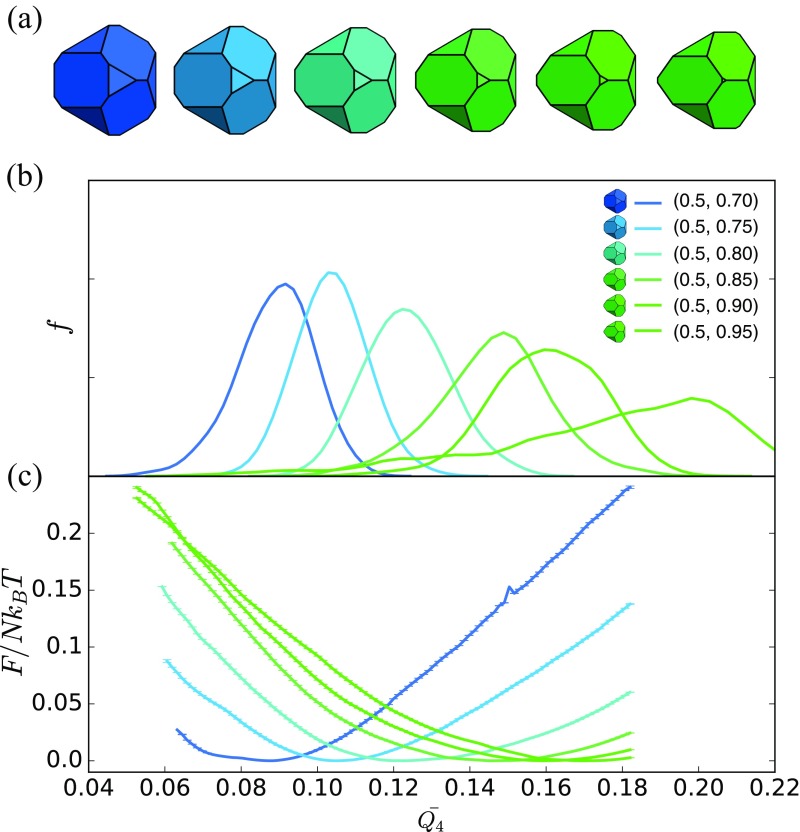
Shape-induced structural BCC$\leftrightarrow$SC reconfiguration occurs continuously in spheric triangle invariant hard polyhedra. (A) Sample shapes used in umbrella sampling calculation from the start to end in equal space. C shows all shapes. (B) Second neighbor-averaged $l=4$ spherical harmonic order parameter ${\overline{Q}}_4$ shows a series of structures between BCC and SC. (C) Umbrella sampling shows a continuous phase transition. (D) Location of free energy minima extracted from umbrella sampling simulations as a function of ${\alpha }_{a\text{,}c}$.

SI Text

Averaged Bond Order Parameter.

The averaged bond order parameter (49) associates a set of spherical harmonics with every fictitious bond connecting one particle to its near neighbors. Here, a “bond” refers to a vector from a particle to a neighboring particle. The mathematical formalism of this parameter is as follows.

Following ref. 51, we denote

$$Q_{lm}(\overrightarrow{r})\equiv Y_{lm}(\theta (\overrightarrow{r}),\varphi (\overrightarrow{r})),$$ [S1]

where $\overrightarrow{r}$ is the vector that indicates the bond, and $Y_{lm}(\theta ,\varphi )$ are spherical harmonics. To determine the local environment, we consider the average

$${\overline{Q}}_{lm}\equiv ⟨Q_{lm}(\overrightarrow{r})⟩\hspace{0.17em}\left(\text{nearest neighbor average}\right)$$ [S2]

over all near neighbors within some $r_{\text{cut}}$, which is often the cutoff radius of the first neighbor shell. Because ${\overline{Q}}_{lm}$ for a given $l$ can change drastically when changing the orientation, one should use the rotationally invariant combination, which is

$$Q_l\equiv {\left[\frac{4\pi }{2l+1}\sum _{m=-l}^l{|{\overline{Q}}_{lm}|}^2\right]}^{1/2}.$$ [S3]

$Q_l$ has been shown to be a useful order parameter for describing certain crystal structures (49). However, for the structures of interest in this study, BCC, FCC, HCP, and SC have similar $Q_l$ values, and therefore, it is problematic to use this definition of $Q_l$ as the order parameter in umbrella sampling simulation.

Lechner and Dellago (48) have introduced a second neighbor-averaged $Q_l$ that reduces noise, and it is a suitable order parameter for our investigation. In this modified version, after ${\overline{Q}}_{lm}$ is calculated, the values are again averaged over all particles and their neighbors, which gives

$$\text{Ave}{\overline{Q}}_{lm}\equiv ⟨{\overline{Q}}_{lm}(\overrightarrow{r})⟩.\hspace{0.17em}(\text{nearest neighbor}+\text{1 average})$$ [S4]

The final average $Q_l$ has the form

$$\overline{Q_l}\equiv {\left[\frac{4\pi }{2l+1}\sum _{m=-l}^l{|\text{Ave}{\overline{Q}}_{lm}|}^2\right]}^{1/2}.$$ [S5]

After comparing different $l$ values, we found ${\overline{Q}}_4$ with a next nearest neighbor average gave the best order parametric separation of our structures of interest. We chose a cutoff based on the number of nearest neighbors rather than a cutoff distance because we found that ${\overline{Q}}_4$ for different cutoff distances was highly sensitive to the thermal noise inherent in our systems.

Umbrella Sampling.

The basic idea of umbrella sampling (40, 41) is to divide the order parameter space (here, ${\overline{Q}}_4$) into different state points (windows) and apply a biased potential to the system that favors the target state point. To sample the system, we computed the biased energy for the target state point every 50 unbiased MC sweeps and apply a Metropolis criterion to decide whether to accept or reject the series of moves. After the system is equilibrated at the target state point, we sampled the biased distribution. Using the biased distribution with the known bias, we can recover the unbiased free energy. Below, we discuss how to apply the formalism of umbrella sampling (following ref. 62) to recover the free energy in the case of shape change-driven structural reconfiguration.

In the following derivation, superscript $b$ denotes biased quantities, whereas superscript $u$ denotes unbiased quantities, and $w_i({\overline{Q}}_4)$ is the bias potential of window $i$, which depends solely on ${\overline{Q}}_4$ in our case. The total energy of the system in window $i$ will then be

$$E^b(r)=E^u(r)+w_i({\overline{Q}}_4)=w_i({\overline{Q}}_4).$$ [S6]

Because our system only contains hard particles, the unbiased total energy of the system is $0$.

To obtain the unbiased free energy $A_i({\overline{Q}}_4)$, we need the unbiased distribution, which is

$$\begin{array}{c}{P}_i^u({\overline{Q}}_4)=\frac{\int \exp [-\beta E(r)]\delta [{\overline{Q}}_4^{\prime }(r)-{\overline{Q}}_4]d^{N}r}{\int \exp [-\beta E(r)]d^{N}r}\\ =\frac{\int \delta [{\overline{Q}}_4^{\prime }(r)-{\overline{Q}}_4]d^{N}r}{\int d^{N}r}.\end{array}$$ [S7]

During the umbrella sampling simulation, we can get the biased distribution $P_i^b$ along the order parameter ${\overline{Q}}_4$. Assuming that the system is ergodic, we have

$$\begin{array}{c}{P}_i^b({\overline{Q}}_4)=\frac{\int \exp \{-\beta [E(r)+w_i({\overline{Q}}_4^{\prime }(r))]\}\delta [{\overline{Q}}_4^{\prime }(r)-{\overline{Q}}_4]d^{N}r}{\int \exp \{-\beta [E(r)+w_i({\overline{Q}}_4^{\prime }(r))]\}{d}^{N}r}\\ =\frac{\int \exp \{-\beta [w_i({\overline{Q}}_4^{\prime }(r))]\}\delta [{\overline{Q}}_4^{\prime }(r)-{\overline{Q}}_4]d^{N}r}{\int \exp \{-\beta [w_i({\overline{Q}}_4^{\prime }(r))]\}{d}^{N}r}.\end{array}$$ [S8]

Because the bias potential only depends on ${\overline{Q}}_4$ and because the integration in the numerator is over all df but ${\overline{Q}}_4$, we have

$$\begin{array}{c}{P}_i^b({\overline{Q}}_4)=\exp [-\beta w_i({\overline{Q}}_4)]\times \frac{\int \exp [-\beta E(r)]\gamma [{\overline{Q}}_4^{\prime }(r)-{\overline{Q}}_4]d^{N}r}{\int \exp \{-\beta [E(r)+w_i({\overline{Q}}_4^{\prime }(r))]\}{d}^{N}r}\\ =\exp [-\beta w_i({\overline{Q}}_4)]\times \frac{\int \gamma [{\overline{Q}}_4^{\prime }(r)-{\overline{Q}}_4]d^{N}r}{\int \exp \{-\beta [w_i({\overline{Q}}_4^{\prime }(r))]\}{d}^{N}r}.\end{array}$$ [S9]

Combining Eqs. S7 and S9, we get

$$P_i^u({\overline{Q}}_4)=P_i^b({\overline{Q}}_4)\exp [\beta w_i({\overline{Q}}_4)]⟨\exp [-\beta w_i({\overline{Q}}_4)⟩.$$ [S10]

Using the definition of free energy, we obtain

$$A_i({\overline{Q}}_4)=-\left(\frac{1}{\beta }\right)\ln P_i^b({\overline{Q}}_4)-w_i({\overline{Q}}_4)+F_i.$$ [S11]

$F_i$ does not depend on ${\overline{Q}}_4$ and has the following form:

$$F_i=-\left(\frac{1}{\beta }\right)\ln ⟨\exp [-\beta w_i({\overline{Q}}_4)]⟩.$$ [S12]

This result is exact up to numerical sampling errors, which depends on the choice of the bias potential $w_i({\overline{Q}}_4)$. Here, we chose a standard harmonic potential:

$$w_i({\overline{Q}}_4)=\frac{1}{2}k{({\overline{Q}}_4-\overline{Q_4^i})}^2.$$ [S13]

In all cases, we used the range ${\overline{Q}}_4\in [0.055,0.179]$, which evenly divides into 32 windows.

Pressure $\text{𝑷}({𝜶}_{\text{𝒂}}\mathit{\text{,}}{𝜶}_{\text{𝒄}})$ Plots.

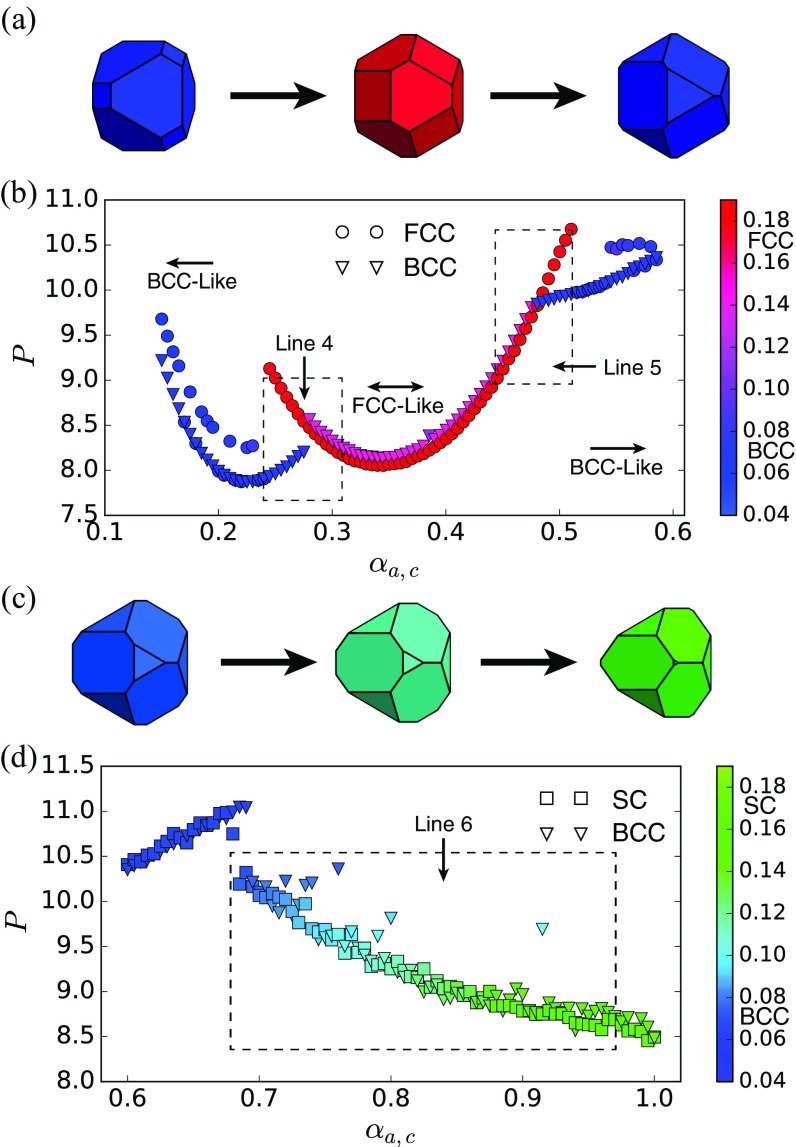
Six different groups of polyhedra were used in umbrella sampling and chosen from three different slices of the 323 family (38). The pressure $P({\alpha }_a,{\alpha }_c)$ plots of the first five groups are shown in the text. Fig. S1 shows the group indicated by lines 4–6.

Fig. S1.

Pressure–shape constitutive relation of the vertical slice ${\alpha }_a=0.5$ and ${\alpha }_a={\alpha }_c$. (A) Shape evolution for ${\alpha }_a={\alpha }_c$. Shapes vary from a BCC former (blue) to an FCC former (red) and then back to a BCC former (blue). (B) Pressure–shape constitutive relation for ${\alpha }_a={\alpha }_c$. Circles indicate FCC system initialization; triangles indicate BCC initialization. Marker colors indicate the value of the order parameter ${\overline{Q}}_4$ computed in the final structure of the system after equilibration. Boxed regions show the BCC$\leftrightarrow$FCC boundaries corresponding to lines 4 and 5 in Fig. 1. Errors are smaller than marker size. C shows the shape evolution on the vertical slice ${\alpha }_a=0.5$. The shapes vary from a BCC former to an SC former. D shows the pressure–shape constitutive relation of the vertical slice ${\alpha }_a=0.5$. All points in the shape of a square indicate that the system was initialized to be an SC structure; triangles mean a BCC initialization, regardless of particle shape. The color of the points indicates the final structure of the system after equilibration. The color bar is based on the order parameter $\overline{Q_4}$. The boxed region shows the BCC$\leftrightarrow$SC boundary, which corresponds to transition line 6 in Fig. 1. Error is smaller than the tick size. Outliers are systems that did not equilibrate in $2\times {10}^7$ MC steps.

Free Energy Plots.

Similar to Figs. 2 and 3, which show the free energy calculation for two groups of polyhedra, Figs. S2–S5 show the free energy calculation of the remaining four groups. Figs. S2–S5 follow the same style, with Figs. S2A, S3A, S4A, and S5A indicating the polyhedra used, Figs. S2B, S3B, S4B, and S5B showing the pressure–shape constitutive relationship, and Figs. S2 C and D, S3 C and D, S4 C and D, and S5C showing the free energy calculation.

Fig. S2.

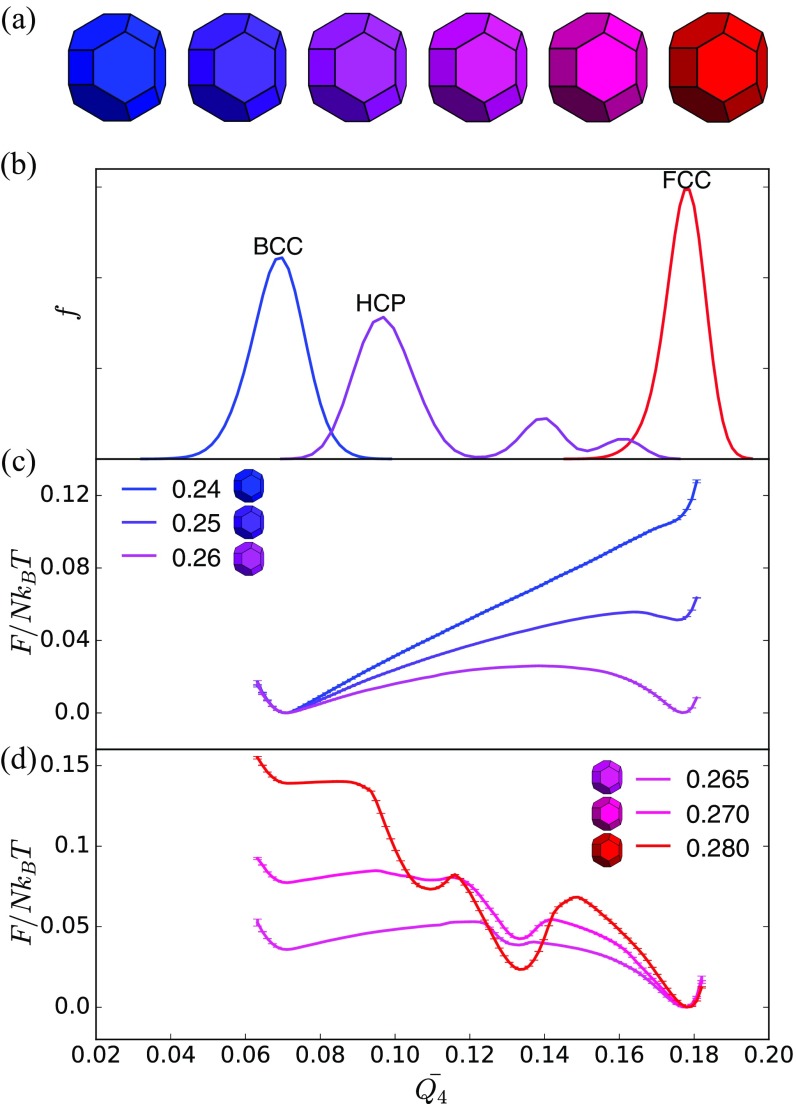
Shape change-driven FCC$\leftrightarrow$BCC reconfiguration is accompanied by a first-order thermodynamic phase transition in spheric triangle invariant hard polyhedra. (A) Shapes used in umbrella sampling calculation. (B) Second neighbor-averaged $l=4$ spherical harmonic order parameter ${\overline{Q}}_4$ distinguishes BCC, FCC, and HCP crystal phases in thermal systems of spheric triangle invariant polyhedra. (C) Below the transition (${\alpha }_c<{\alpha }_c^{\ast }$), a metastable FCC free energy basin develops below ${\alpha }_c=0.185$. (D) Above the transition (${\alpha }_c>{\alpha }_c^{\ast }$), the FCC free energy basin becomes dominant above (${\alpha }_c=0.190$). Well above the transition (${\alpha }_c=0.215$), the BCC free energy basin becomes unstable, but there is a second metastable HCP basin.

Fig. S5.

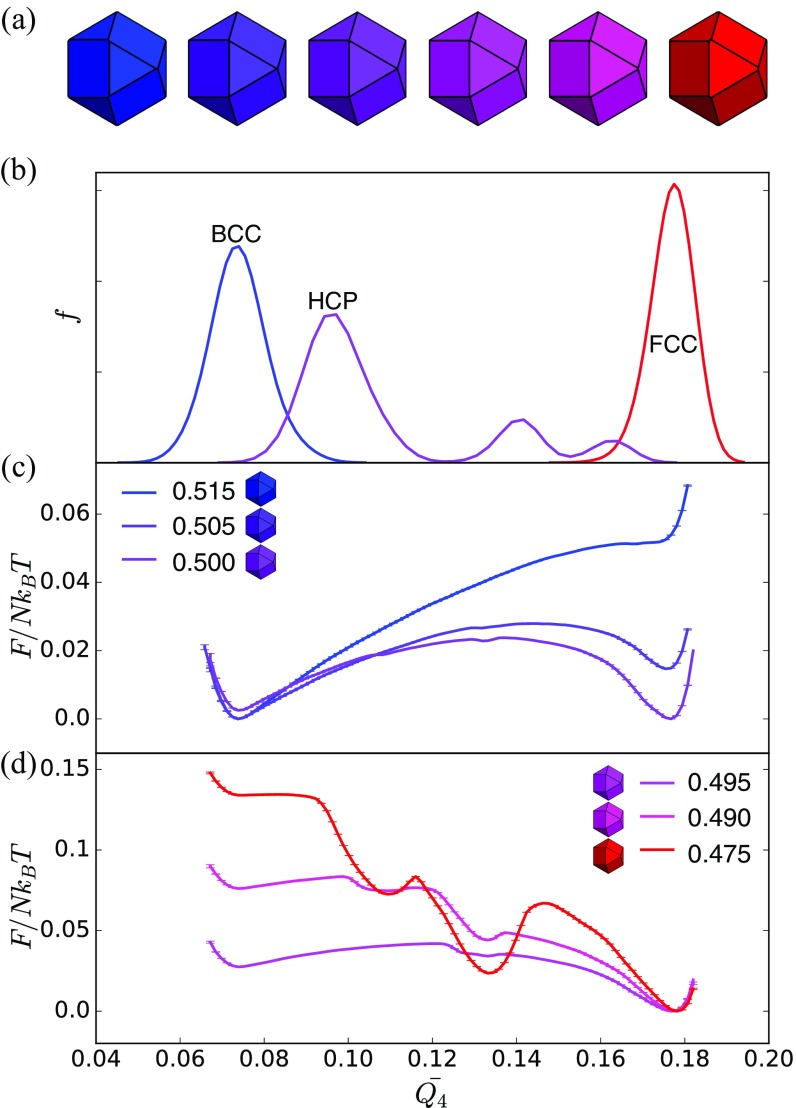
Shape change-driven BCC$\leftrightarrow$SC reconfiguration occurs continuously in spheric triangle invariant hard polyhedra. (A) Shapes used in umbrella sampling calculation. (B) Second neighbor-averaged $l=4$ spherical harmonic order parameter ${\overline{Q}}_4$ indicates a series of structures intermediate between BCC and SC. (C) Umbrella sampling shows no evidence of a thermodynamic phase transition.

Fig. S3.

Shape change-driven FCC$\leftrightarrow$BCC reconfiguration is accompanied by a first-order thermodynamic phase transition in spheric triangle invariant hard polyhedra. (A) Shapes used in umbrella sampling calculation. (B) Second neighbor-averaged $l=4$ spherical harmonic order parameter ${\overline{Q}}_4$ distinguishes BCC, FCC, and HCP crystal phases in thermal systems of spheric triangle invariant polyhedra. (C) Below the transition (${\alpha }_c<{\alpha }_c^{\ast }$), a metastable FCC free energy basin develops at ${\alpha }_{a\text{,}c}=0.25$. (D) Above the transition (${\alpha }_c>{\alpha }_c^{\ast }$), the FCC free energy basin becomes dominant above (${\alpha }_{a\text{,}c}=0.265$). Well above the transition (${\alpha }_c=0.280$), the BCC free energy basin becomes unstable, but there is a second metastable HCP basin.

Fig. S4.

Shape change-driven FCC$\leftrightarrow$BCC reconfiguration is accompanied by a first-order thermodynamic phase transition in spheric triangle invariant hard polyhedra. (A) Shapes used in umbrella sampling calculation. (B) Second neighbor-averaged $l=4$ spherical harmonic order parameter ${\overline{Q}}_4$ distinguishes BCC, FCC, and HCP crystal phases in thermal systems of spheric triangle invariant polyhedra. (C) Above the transition (${\alpha }_c>{\alpha }_c^{\ast }$), a metastable FCC free energy basin develops at ${\alpha }_{a\text{,}c}=0.505$. (D) Below the transition (${\alpha }_c<{\alpha }_c^{\ast }$), the FCC free energy basin becomes dominant above (${\alpha }_{a\text{,}c}=0.495$). Well above the transition (${\alpha }_c=0.475$), the BCC free energy basin becomes unstable, but there is a second metastable HCP basin.

Error Analysis.

All of the error bars in the free energy plots are generated using jackknife resampling. We selected 10 different subsets of all of the data from the replica runs and stitched together the resulting free energy curves from the subsets. The error from the weighted histogram analysis method (50) is negligible. However, jackknife resampling can only compute the statistical error; because of the large sample size (50,000 × 5 = 250,000), the statistical error is still small. The largest and most difficult error to calculate is the systematic error of umbrella sampling. This systematic error can come from multiple sources. First, because of the equilibration routine of the umbrella sampling simulation, for each individual window, the final distribution can be shifted slightly to the left or right of the target ${\overline{Q}}_4$ value for each independent run. Second, the initial state of the system can also affect the end result slightly. Because of the complexity of systematic error, we conducted simulations from two extreme cases, initializing the system with the two solid phases that we wish to study, and compared the free energy of the end result. In Figs. S6 and S7, we can see that the free energy curves shift slightly with different initialization, but the macroscopic behavior of the phase transitions stay the same.

Fig. S6.

Shape change-driven FCC$\leftrightarrow$BCC reconfiguration is accompanied by a first-order thermodynamic phase transition in spheric triangle invariant hard polyhedral shown here with both BCC (solid lines) and FCC (dashed lines) initialization. Differences between curves indicate systematic errors in computing the location of the transition but that the thermodynamic nature of the transition is robust. (A) Free energy curves of hard polyhedra as in Fig. S2. (B) Free energy curves of hard polyhedra as in Fig. S3 (gaps in red dotted lines indicate insufficient statistics in one umbrella sampling window). (C) Free energy curves of hard polyhedra as in Fig. S4. (D) Free energy curves of hard polyhedra as in Fig. 2.

Fig. S7.

Shape change-driven BCC$\leftrightarrow$SC reconfiguration occurs continuously by continuous transition in spheric triangle invariant hard polyhedra shown here with both BCC (solid lines) and SC (dashed lines) system initialization. Differences between curves indicate systematic errors in computing the location of the transition but that the thermodynamic is robust. (A) Free energy curves of hard polyhedra as Fig. 3. (B) Free energy curves of hard polyhedra as Fig. S5.

Results

We first present thermodynamic findings followed by dynamics results for the FCC$\leftrightarrow$BCC transition. Next, we present the same for the BCC$\leftrightarrow$SC transition.

FCC$\mathbf{\leftrightarrow }$BCC Transition.

We investigated the thermodynamics of shape change-driven FCC$\leftrightarrow$BCC solid–solid phase transitions in four distinct regions of shape space (indicated by lines 1 and 3–5 in Fig. 1). In each region, at the FCC$\leftrightarrow$BCC cross-over, we find that the $P({\alpha }_a,{\alpha }_c)$ constitutive relation exhibits a discontinuous first derivative (Fig. 3B), indicating a phase transition that is either first or second order in the Ehrenfest classification (44). Additional investigation via umbrella sampling yields the Landau free energy near the putative solid–solid transition for six different shapes depicted in Fig. 4A. Note that the similarity in particle shapes makes them difficult to distinguish by eye but is most clearly indicated by the relative size of the square face. Particles are colored from blue (BCC) to red (FCC) according to the structures that they spontaneously self-assemble. More blue (more red) shapes are more likely to form BCC (FCC). Shapes colored purple exhibit an almost equal probability to form either BCC or FCC. We computed the Landau free energy using the order parameter ${\overline{Q}}_4$ defined above. In Fig. 4 C and D, we plot Landau free energies obtained from umbrella sampling after averaging from five independent replica runs on both sides of the solid–solid phase transition. Calculations at ${\alpha }_c>{\alpha }_c^{\ast }$ (i.e., above the FCC$\leftrightarrow$BCC transition) (Fig. 4C) show that, sufficiently far into the BCC phase, there is no metastable FCC free energy basin; however, as ${\alpha }_c$ approaches ${\alpha }_c^{\ast }$, a metastable FCC basin appears. At ${\alpha }_c<{\alpha }_c^{\ast }$ (Fig. 4D), umbrella sampling calculations show that FCC becomes the stable free energy basin and that the BCC basin becomes metastable. Well below the transition, the BCC basin disappears, but a metastable basin develops that corresponds to mixed FCC and HCP stacking. Corresponding plots that lead to the same conclusions for the other regions of shape space are shown in SI Text. Together, our results show that shape change-driven FCC$\leftrightarrow$BCC solid–solid phase transitions in ${\mathrm{\Delta }}_{323}$ are first-order thermodynamic phase transitions.

We investigated the dynamics of the FCC$\leftrightarrow$BCC solid–solid phase transition by modeling how the system responds to a sudden change in particle shape. Several experimental techniques exist for dynamically altering colloid shape (5, 42, 52, 53). Here, we model a process in which particle shape reconfiguration occurs on a much shorter timescale than structural relaxation by initializing FCC-forming particles in BCC lattices (and vice versa) and simulating at fixed particle shape and packing density for $1.5\times {10}^7$ MC sweeps (example simulation results are shown in Movie S1). On these simulation timescales, which are long compared with typical structural relaxation times and much longer than needed for the solid–solid transition outside the metastable region, we did not observe structural transformation for any systems that our umbrella sampling computation indicated as metastable. Homogeneous nucleation is inherently a rare event, and our MC simulations in metastable regions of shape space suggest that the driving force for structural reconfiguration is not sufficient to overcome the free energy barrier to observe a first-order solid–solid phase transition on timescales that are typically sufficient to observe first-order fluid–solid phase transitions in systems of this type (12, 15, 17, 19). However, we did observe a spontaneous solid–solid transition when systems were initialized with shapes beyond the metastable region, in which case we observed structural reconfiguration with no discernible intermediate fluid phase. The existence of metastability in shape space provides an additional confirmation that the solid–solid transition is first order. Moreover, by measuring the order parameter evolution in MC simulation, our results indicate that the transition pathway in MC simulation follows the order parameter that we chose in umbrella sampling, providing additional confirmation that it appropriately parametrizes the FCC$\leftrightarrow$BCC solid–solid transition.

BCC$\mathbf{\leftrightarrow }$SC Transition.

We investigated the thermodynamics of BCC$\leftrightarrow$SC solid–solid phase transitions in two distinct regions of shape space (lines 2 and 6 in Fig. 1). In Fig. 3D, we plot the $P({\alpha }_a,{\alpha }_c)$ constitutive relation with ${\alpha }_a={\alpha }_c\equiv \alpha$ for region 2, which shows a discontinuity in pressure near $\alpha \approx 0.6$ consistent with a phase transition that is, at most, second order in the Ehrenfest classification. A close-up view of these data is presented in Fig. 6B. Fig. 6A shows ${\overline{Q}}_4$ order parameter measurements that suggest a discontinuous first derivative with respect to $\alpha$, which is also consistent with a continuous (i.e., second or higher order) thermodynamic phase transition. Corroborating evidence is provided by computing the Landau free energy as a function of the order parameter ${\overline{Q}}_4$ near the putative solid–solid transition via umbrella sampling for a range of shapes indicated in Fig. 5A. Particles are colored from blue (BCC) to green (SC) according to the value of the order parameter ${\overline{Q}}_4$ of the structures into which they self-assemble. Computed thermal averages (Fig. 5B) of the order parameter ${\overline{Q}}_4$ in BCC and SC crystals show that BCC crystals have a peak near $0.08$ and that SC has a peak near $0.17$; however, our results also suggest the existence of structures with intermediate ${\overline{Q}}_4$ for intermediate particle shapes, where their self-assembled structures are in between BCC and SC as shown in their ${\overline{Q}}_4$ distribution. Landau free energies computed via umbrella sampling are plotted in Fig. 5C and show no evidence of secondary local minima that would indicate a discontinuous (i.e., first-order) phase transition. Umbrella sampling computations were performed at a higher resolution of shape space below the putative transition ($\alpha \lesssim 0.6$) to extract the expected value of the order parameter ${\overline{Q}}_4$ (Fig. 5D) and are consistent with the self-assembled ${\overline{Q}}_4$ measurements (Fig. 6), suggesting that ${\overline{Q}}_4$ has a discontinuous derivative at the transition. Together, the $P({\alpha }_a,{\alpha }_c)$ constitutive relation, the direct evaluation of the order parameter ${\overline{Q}}_4$, and the umbrella sampling results all indicate that the BCC$\leftrightarrow$SC solid–solid phase transition is a continuous (i.e., second- or higher-order) thermodynamic phase transition in ${\mathrm{\Delta }}_{323}$. Evidence that the BCC$\leftrightarrow$SC solid–solid phase transition is also continuous in shape space region 6 (Fig. 1) is given in SI Text.

Fig. 6.

BCC$\leftrightarrow$SC solid–solid phase transition is a continuous (i.e., second- or higher-order) thermodynamic phase transition. (A) Order parameter $\overline{Q_4}$ vs. shape suggests the derivative of the order parameter changes discontinuously near ${\alpha }_{a\text{,}c}=0.6$. (B) $P({\alpha }_a\text{,}{\alpha }_c)$ also indicates a discontinuous derivative near ${\alpha }_{a\text{,}c}$ also consistent with a continuous phase transition.

As in the FCC$\leftrightarrow$BCC case, we investigated the dynamics of the BCC$\leftrightarrow$SC solid–solid phase transformation by modeling how the system responds to a sudden change in particle shape. We model a process in which particle shape reconfiguration occurs on a much shorter timescale than the structural relaxation by initializing BCC-forming particles in SC lattices (and vice versa) and simulating at fixed particle shape and packing density for $1.5\times {10}^7$ MC sweeps (example simulation results are shown in Movie S2). On these simulation timescales, in all cases, we observed dynamic solid–solid phase transformations via a transition pathway through intermediate structures that follow the order parameter that we used for umbrella sampling. Moreover, we observe that, for $\alpha$ above the transition, any shape perturbation induces a structural change with no evidence of metastability. We also observe that the dynamics of the solid–solid transformation occurs on typical timescales of $2\times {10}^6$ MC sweeps. Taken together, these results provide additional corroboration of our observation that BCC$\leftrightarrow$SC is a continuous thermodynamic phase transition in ${\mathrm{\Delta }}_{323}$ at fixed packing fraction $\eta =0.55$, and the timescale under which the solid–solid transition occurs dynamically is shorter by nearly an order of magnitude than in the case of FCC$\leftrightarrow$BCC.

Discussion

Motivated by the need for minimal models to study solid–solid transitions (10), the observation that, in these transitions, coordination polyhedra change shape (11), the connection between anisotropic colloid shape and valence (12, 13), the large body of work on entropy-driven ordering in systems of colloids with anisotropic shape (12–23), and recently developed techniques for treating particle shape thermodynamically (39), we studied a class of minimal model systems exhibiting solid–solid phase transitions driven by changes in particle shape. We showed that particle shape change gives rise to several distinct solid–solid transitions in a single family of shapes and via MC simulation and umbrella sampling techniques. We investigated FCC$\leftrightarrow$BCC and BCC$\leftrightarrow$SC transitions. Both FCC$\leftrightarrow$BCC and BCC$\leftrightarrow$SC are solid–solid transitions that are related by linear transformations of the positions of the particle centers. BCC and FCC are related by elongation in one direction (54); BCC and SC are related by a shear transformation within the unit cell (55). Both transitions are expected to be diffusionless. Surprisingly, despite both being diffusionless transitions and the common point group symmetry of the particle shape, we find that the FCC$\leftrightarrow$BCC transition is thermodynamically discontinuous (i.e., first order) and that BCC$\leftrightarrow$SC is thermodynamically continuous (i.e., second or higher order). Our results suggest several directions for additional investigation.

The physics of FCC$\leftrightarrow$BCC solid–solid phase transitions is of longstanding interest in metallurgy [e.g., in the transition between the so-called $\gamma$ (FCC) and $\alpha$ (BCC) forms of iron (54)]. We found that, for several distinct regions of shape space, the FCC$\leftrightarrow$BCC solid–solid phase transition is discontinuous. It is possible that, for particles with other paths of shape shifting, there could be less/no thermal activation; we will address this question in future work. Additionally, although our focus here was on solid–solid transitions between cubic crystals with four or fewer particles per cubic unit cell, studies of noncubic crystals or crystals with more complicated unit cells require only straightforward generalizations of our approach. We expect that the approach that we have developed here will provide a powerful setting for the study of the basic physics of solid–solid phase transitions between a wide array of technologically relevant structures.

Constructing shape-driven solid–solid transitions furthers the aim of developing minimal models of these transitions because it allows the direct manipulation of coordination polyhedra. As we noted above, coordination polyhedra also reconfigure in solid–solid transitions in metallurgy with changes in pressure, density, or temperature. An additional complicating factor in those transitions is that both enthalpy and entropy play a role, and decoupling their effects is difficult (8). A side benefit of this approach is that, in the hard particle systems that we present here, the behavior is entirely driven by entropy. Future studies of systems with controllable shape and enthalpic interactions (12) could allow enthalpic and entropic contributions to be disentangled. An important question for additional investigation is whether the physics of solid–solid transitions is determined by the structures, the particle shapes, or an interplay between the two.

Another fundamental question that calls for additional investigation is the study of the kinetics of colloidal solid–solid phase transformations through nonclassical nucleation and growth. It is expected that the nucleation and growth of solid–solid transitions will be rich because crystals break the rotational symmetry required by classical nucleation theory, and recent experimental evidence (10, 56) shows evidence for two-step nucleation in quasi-2D systems. Minimal colloidal models of the type constructed here provide an avenue for the study of full 3D transformations.

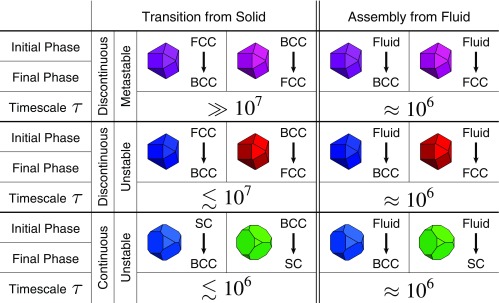
Our results can also help to guide the synthesis of reconfigurable colloidal material (Fig. 7). Experiments have shown systems with changeable building block shape either directly (5, 52, 53, 57, 58) or effectively via depletion (34). Here, we show that, for colloidal particles that can be synthesized in the laboratory (18, 20), changing particle shape can be used to induce transformations between FCC$\leftrightarrow$BCC and BCC$\leftrightarrow$SC. What implications are there for the rational design of reconfigurable colloidal materials? To answer this question, it is important to understand how structural reconfiguration compares with self-assembly in terms of typical timescales. We obtain “timescales” via MC simulations involving local translations and rotations of individual particles to approximate the Brownian dynamics (59) of physical colloids (60). In the case of FCC$\leftrightarrow$BCC, for shapes near the discontinuous transition ($|\alpha -{\alpha }^{\ast }|\lesssim 0.05$), we did not observe spontaneous structural reconfiguration in systems of $N\sim 2\text{,}000$ particles on timescales of $\tau \lesssim {10}^7$ MC sweeps. This timescale is much longer than the typical time that it takes to observe spontaneous crystallization or melting in MC simulations of the self-assembly of $N\sim 2\times {10}^3$ particles, for which $\tau \sim {10}^7$. The contrasting timescales for self-assembly vs. solid–solid reconfiguration suggest that, for small shape deformations of $|\alpha -{\alpha }^{*}|\lesssim 0.05$, spontaneous, shape change-driven, dynamic FCC$\leftrightarrow$BCC reconfiguration in ${\mathrm{\Delta }}_{323}$ can be achieved on shorter timescales by completely melting and then recrystallizing the system. However, for larger shape changes $|\alpha -{\alpha }^{*}|\gtrsim 0.05$, we observed spontaneous FCC$\leftrightarrow$BCC reconfiguration on timescales of $\tau \sim {10}^6$ MC sweeps. The relatively short timescales observed for reconfiguration suggests that, for sufficiently large shape deformations, although the phase transition is first order, direct solid–solid reconfiguration without an intermediate fluid can occur on comparable physical timescales to self-assembly and therefore, is a viable means of designing reconfigurable colloidal materials. In the BCC$\leftrightarrow$SC case, the continuous nature of the transition implies that there is no nucleation barrier, and indeed, we observed structural reconfiguration in MC simulations of $N\sim 2\times {10}^3$ particles on typical timescales of $\tau \sim {10}^6$, which are less than what is typically observed for self-assembly of comparably sized systems of hard anisotropic colloids. The relatively fast speed at which structural reconfiguration occurs in this case of a continuous solid–solid transition suggests that a broader search for other systems of anisotropic colloids that exhibit continuous solid–solid phase transitions could yield candidate systems for developing rapidly switchable reconfigurable colloidal materials.

Fig. 7.

Shape-driven solid–solid reconfiguration and self-assembly timescales for BCC, FCC, and SC structures. Thermodynamically discontinuous FCC$\leftrightarrow$BCC solid–solid phase transitions occur dynamically in MC simulations on timescales ($\tau \lesssim {10}^7$ MC sweeps) that are similar to self-assembly timescales ($\tau \approx {10}^6$ MC sweeps) beyond the metastable region. In the metastable region, solid–solid reconfiguration does not occur on timescales ($\tau \gg {10}^7$ MC sweeps) that are much longer than typical self-assembly times. Thermodynamically continuous BCC$\leftrightarrow$SC solid–solid phase transitions occur dynamically in MC simulations on timescales ($\tau \lesssim {10}^6$ MC sweeps) that are comparable with or less than typical self-assembly times.