Universal transition from unstructured to structured neural maps

Significance

To save wiring, neurons in the brain that are connected to one another should be located in close vicinity. We use computational models based on multidimensional scaling to explore the implications of this simple premise regarding the organization of the visual cortex. Assuming only that neurons with similar orientation preference are more strongly connected, we predict the emergence of characteristic pinwheels where preferred orientations organize in a continuous circular manner. We find that a universal transition exists between completely unstructured and such structured neural maps when increasing neuron numbers even without changing the selectivity of the connections. Our results are a simple explanation for the existence of salt-and-pepper arrangements in rodents and pinwheel arrangements in cat visual cortex.

Abstract

Neurons sharing similar features are often selectively connected with a higher probability and should be located in close vicinity to save wiring. Selective connectivity has, therefore, been proposed to be the cause for spatial organization in cortical maps. Interestingly, orientation preference (OP) maps in the visual cortex are found in carnivores, ungulates, and primates but are not found in rodents, indicating fundamental differences in selective connectivity that seem unexpected for closely related species. Here, we investigate this finding by using multidimensional scaling to predict the locations of neurons based on minimizing wiring costs for any given connectivity. Our model shows a transition from an unstructured salt-and-pepper organization to a pinwheel arrangement when increasing the number of neurons, even without changing the selectivity of the connections. Increasing neuronal numbers also leads to the emergence of layers, retinotopy, or ocular dominance columns for the selective connectivity corresponding to each arrangement. We further show that neuron numbers impact overall interconnectivity as the primary reason for the appearance of neural maps, which we link to a known phase transition in an Ising-like model from statistical mechanics. Finally, we curated biological data from the literature to show that neural maps appear as the number of neurons in visual cortex increases over a wide range of mammalian species. Our results provide a simple explanation for the existence of salt-and-pepper arrangements in rodents and pinwheel arrangements in the visual cortex of primates, carnivores, and ungulates without assuming differences in the general visual cortex architecture and connectivity.

Models assuming short cables and fast signal propagation in the circuit predict the precise placement of neurons and brain areas (1–4), the existence of topographic maps (5), and the existence of ocular dominance (OD) columns and orientation preference (OP) maps in the visual cortex (6, 7). The latter examples have become model systems to study structured neural maps because of the combination of striking striped patterns of OD and the intricate arrangement of OPs in a radial symmetry around pinwheel-like structures (8–11). A number of modeling approaches have been shown to predict different map properties and their possible biological origin (12–15). Examples are the link between the shape of the visual cortex and the overall stripe pattern of OD columns (16, 17) as well as the link between monocular deprivation and stripe thickness (16, 18). In accordance with these observations, the enlargement of specific brain areas has been predicted by competitive Hebbian models (Kohonen maps) in regions with increased input (19) and has been found in monkeys and cats (20, 21). Furthermore, the order of OD and OP map development has been linked to the ratio between OD and OP wavelength (22), and a constant density of pinwheels relative to the cortical hypercolumn size has been predicted in models and confirmed by experiments (14, 23).

Although particular models can predict some properties of visual cortex maps very well (7), other properties are absent or contradictory to experimental observations (24, 25). Structured maps in the visual cortex have been described in primates, carnivores, and ungulates but are reported to be absent in rodents, which instead exhibit unstructured, seemingly random arrangements commonly referred to as salt-and-pepper configurations (26–28). Phase transitions between an unstructured and a structured map have been described in a variety of models as a function of various model parameters (12, 13). Still, the biological correlate of the phase transition and therefore, the reason for the existence of structured and unstructured neural maps in closely related species remain unknown. Models in which minimal wiring constraints are applied to neurons arranged on a grid show that switching from a nonselective to a selective connectivity between neurons of similar OP can lead to a transition between salt-and-pepper and pinwheel arrangements (6). The results from these models indicate that a difference in selective connectivity could lead to the formation of unstructured vs. structured maps. However, similar grid-like arrangements using Ising-like XY models that also can predict pinwheel arrangements as well as OD columns (29, 30) show an alternative transition of unstructured to structured maps. This phase transition occurs even with a fixed connection selectivity while varying the so-called temperature, a measure that relates to the entropy or the amount of noise in the system (Methods). These results indicate that a simple transition to organized neural maps could occur without a direct alteration of the connectivity (31). Such a transition would be compatible with the pronounced selective connectivity between neurons of similar OP observed in mice with their salt-and-pepper organization (32–35). We show here by using a neural placement model based on multidimensional scaling (MDS) and a modified XY model that, in both models, changes in a parameter characterizing the amount of interconnectivity between orientation-selective neurons can lead to the phase transition. We further show that this parameter is directly related to the temperature in our XY model. We conclude that increasing the interconnectivity, which is reflected in higher total numbers of neurons, may lead to structured maps without changing the connection selectivity, a theory that we support with biological data, which we curated from the available literature.

Results

In the following section, we use a general method to predict the optimal placement of neurons given an arbitrary connectivity based on MDS (36). MDS can be used to find locations with pairwise distances that match a given set of target values by minimizing a respective stress function. To predict the positions of neurons, we use their corresponding connection similarities as distances. Thus, we ensure that neurons with similar connectivity in the circuit are located in close vicinity and hence, that the amount of wiring length is optimized (Methods). This model allowed us to dissect the variables leading to the organization of neural maps. To show our method, we first used a surrogate binary connection matrix that we obtained from the geometric proximity of randomly distributed points in a square arrangement arbitrarily divided into six layers. Because the connection matrix then reflects the spatial relations between nearby points, it should be possible to retrieve the location of all points from the binary connectivity matrix alone. Using MDS, we were indeed able to faithfully recover the original locations (Fig. 1A), indicating that our optimal placement method conserved neighborhood relations present in the connectivity and favored short distances between connected points. Under these conditions, the mean deviation between original and recovered positions was about 2.4% of the side length of the square after careful alignment of the points (average over 51 trials). Using the optimized locations, the amount of cable required to connect the points according to the binary matrix was then only about 35% of the cable required when using a random placement. The reconstruction worked precisely over a wide range of levels of connection sparsities.

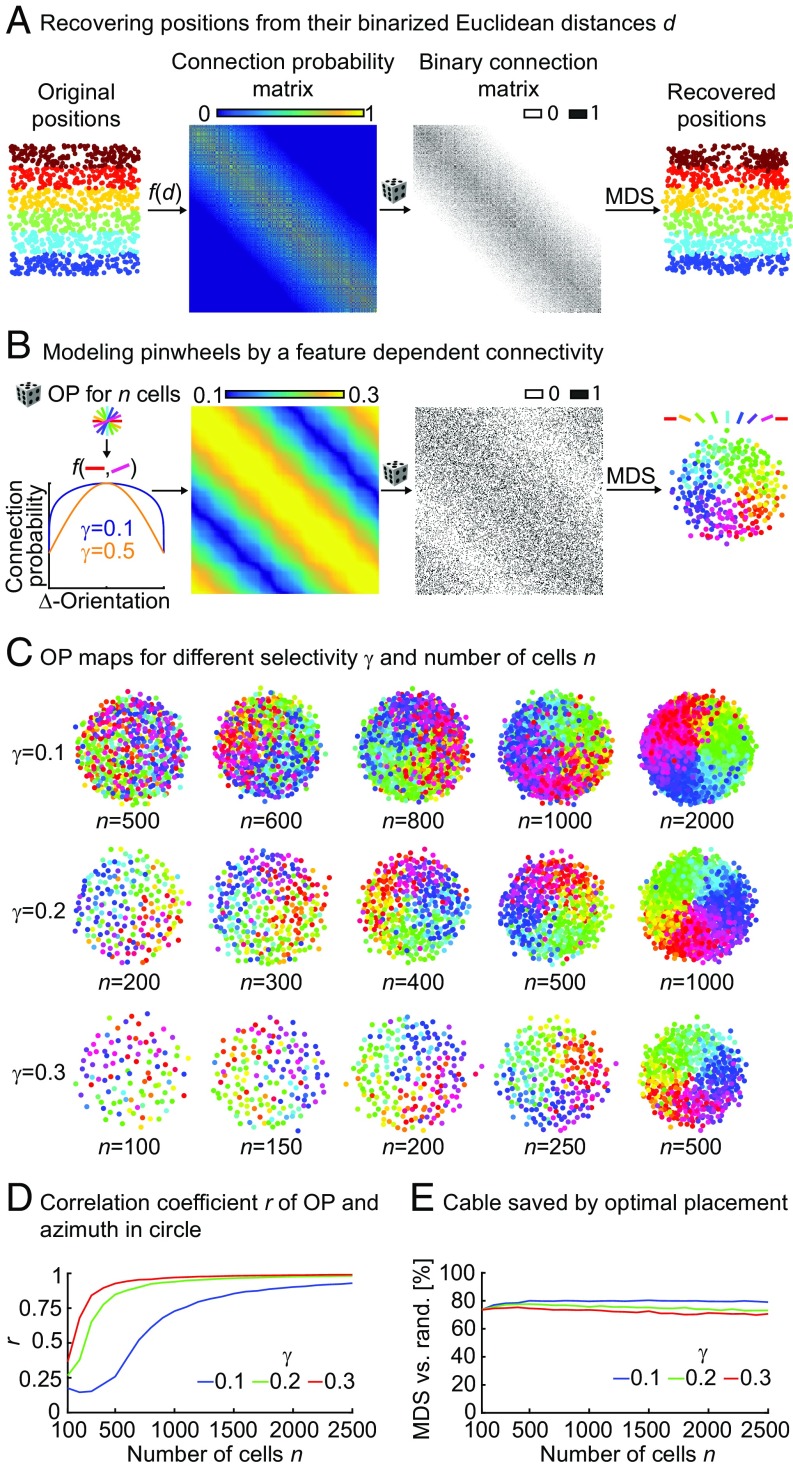
Fig. 1.

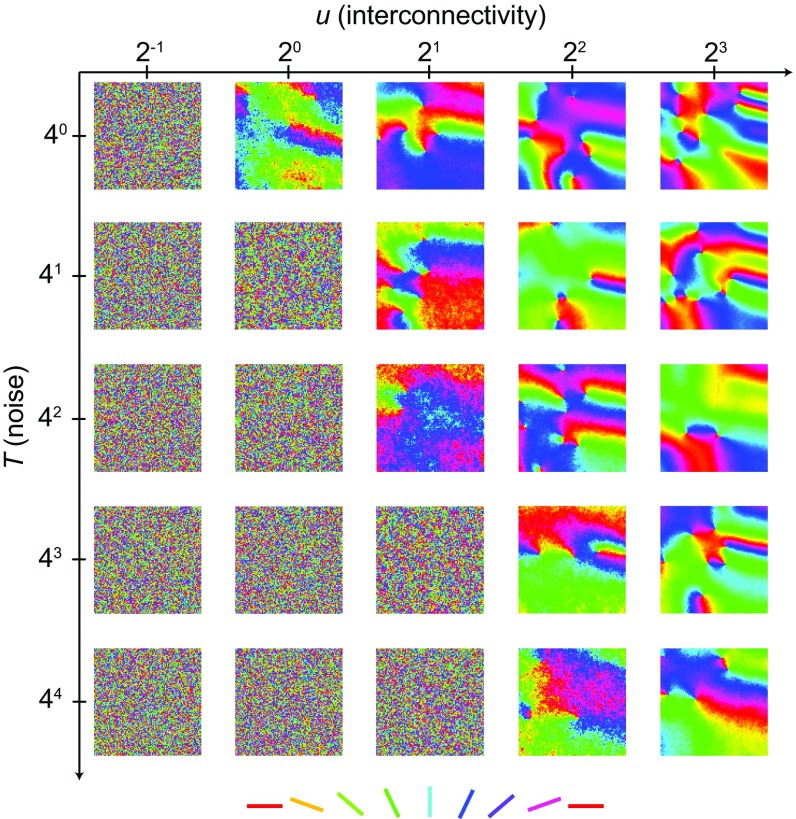
Optimal placement of orientation-selective neurons switches from salt and pepper to pinwheel. (A) Validation of optimal placement using MDS (Methods). From left to right, random locations in a unit square divided into six layers by color, connection probabilities obtained from Euclidean distances [f(d)], binary connection matrix obtained by random instantiation from the connection probability matrix, and recovered positions of neurons using MDS to minimize the amount of cable for the binary connectivity matrix. Colors correspond to layers in the original locations. (B) Optimal placement for orientation-selective neurons. From left to right, connection probability obtained as a periodic function of the difference between randomly selected OPs between n neurons illustrated here for different values of γ, the selectivity of the connection (constants a and b are set to 0.1 and 0.2, respectively); connection probability matrix for γ = 0.6 and 300 neurons with uniformly distributed random OPs; randomly instantiated binary connectivity from connection probability matrix; and positions of neurons as determined using MDS. (C) Transition between salt and pepper and pinwheels. Optimal placement for different numbers of neurons n and different selectivity values γ. (D) Absolute values of correlation coefficients r between OP and azimuth for three values of γ from C using the mean of 40 instantiations of connectivity matrices (in steps of 100 cells) for each parameter combination. (E) Amount of cable used after optimal placement using MDS compared with random (rand) placement (same data as D).

Using the same method, we then predicted the optimal placement of orientation-selective neurons. With the simple assumption that neurons with similar OPs are selectively connected, we predicted the arrangement of a single pinwheel (Fig. 1B). As expected from previous optimal wiring models (6), increasing the specific selectivity in the connection probability (γ in Fig. 1B) resulted in the appearance of pinwheel arrangements. Unexpectedly, however, we observed a transition from a salt-and-pepper to a pinwheel configuration when increasing the number of neurons (Fig. 1C, left to right and Fig. S1) for any fixed selectivity. Increasing the number of neurons effectively increases the interconnectivity (i.e., the overall number of neurons that a neuron is connected to) without altering the specificity. Interestingly, total interconnectivity is reduced when increasing selectivity γ in our connection function, indicating that seemingly opposing forces determine how much structure is in the final neural map (SI Text and Figs. S2 and S3). We quantified the amount of resulting structure by calculating correlation coefficients between OP and azimuth in the putative pinwheels, clearly visualizing the transition in the parameter space (10) (Methods, Fig. 1D, and Fig. S1). Incidentally, when using relatively unselective connection functions, we still predicted pinwheels for cell numbers above 1,000, thereby matching the numbers found in the cat visual cortex (10). Also, the amount of cable used was around 75% compared with random placements for all parameter values, with a slight improvement for more selective connectivities (Fig. 1E). Seemingly unstructured salt-and-pepper arrangements, therefore, still minimize the amount of cable used and are precisely ordered (6), albeit at higher spatial frequencies compared with the lower spatial frequencies found in pinwheel maps.

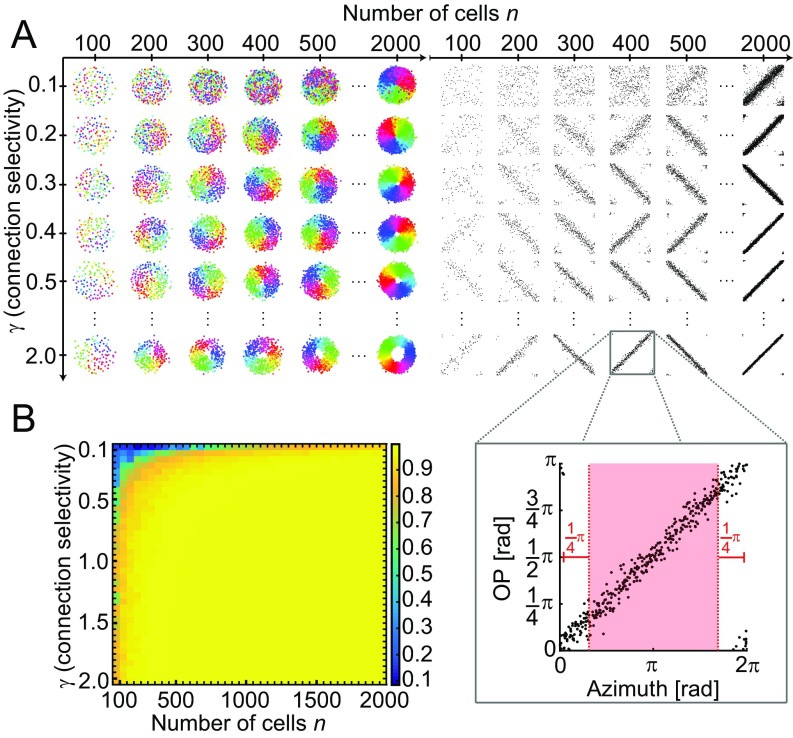
Fig. S1.

Optimal placement of orientation-selective neurons for a wide range of connection selectivity values γ and numbers of neurons n. (A) Transition between salt and pepper and pinwheels. (Left) Optimal placement for different numbers of neurons n and different connection selectivity values γ. (Right) Plots with OP and azimuth for each neuron (black dots; one representative case is shown in Inset) in all combinations of γ and n from Left. (B) Absolute values of correlation coefficients between OP and azimuth for the parameter space from A but using the mean of five different instantiations of each parameter combination. Bins are 50 wide and 0.05 tall, with blue being salt and pepper (no correlation) and yellow being pinwheel (strong correlation). All correlation coefficients were calculated for the red area in B, Right to avoid the edge effects caused by the periodicity of the data. The constants a and b were set to 0.1 and 0.2, respectively, for all of the shown calculations.

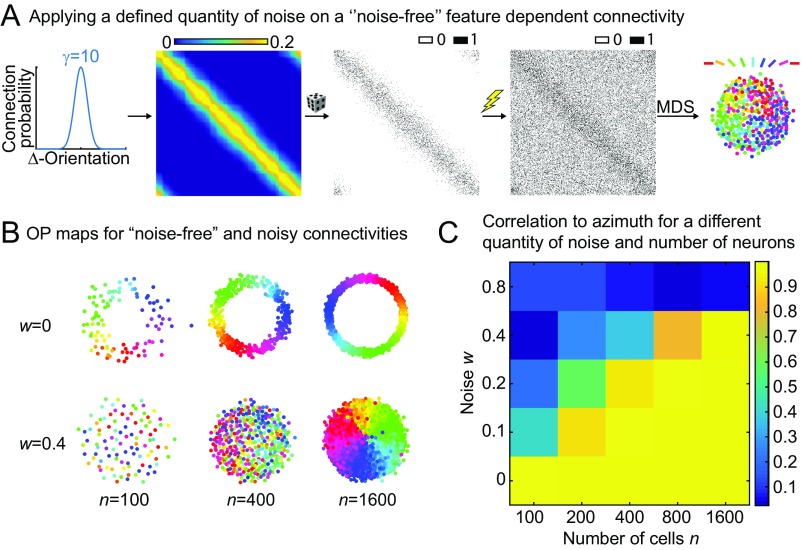
Fig. S2.

Influence of noise on the optimal placement of orientation-selective neurons. (A) A highly selective noise-free connection function is used (γ = 10) to generate a connection matrix that accordingly is also noise-free. Noise is then applied by randomly setting a bin in the connection matrix to either zero or one, where the probability to change a bin is given by the noise parameter w. (B) OP maps for noise-free and noisy connectivities (w = 0.4). (C) Correlation to azimuth for more extensive parameter values of n and w. The constants a and b were set to 0 and 0.2, respectively, for all of the shown calculations.

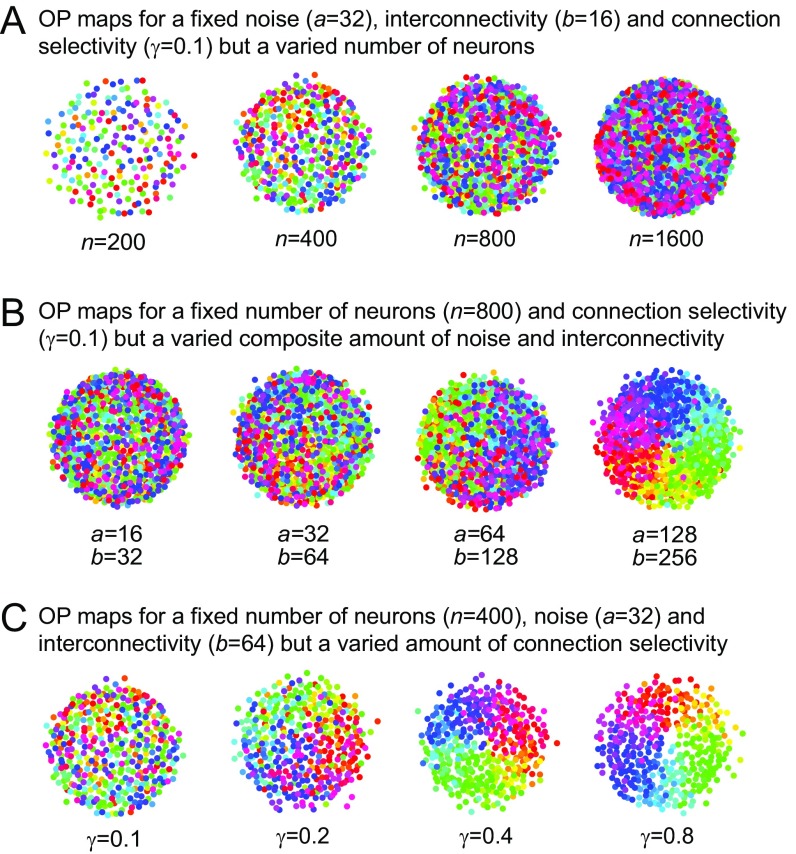
Fig. S3.

Relationship between the interconnectivity and the number of neurons in the MDS model. (A) OP maps for different numbers of neurons but fixed parameters for noise, interconnectivity, and connection selectivity. (B) OP maps for a varied composite amount of interconnectivity and noise but a fixed number of neurons and connection selectivity. (C) OP maps for a varied connection selectivity but a fixed number of neurons, noise, and interconnectivity.

Although the MDS model robustly showed a structural transition with increasing interconnectivity, it did not become clear why this transition occurred or how general it was with respect to other neural arrangements. To address these questions, we used XY models from statistical mechanics that calculate interactions of continuous periodic spins on a lattice. These models are known to exhibit well-defined characteristic phase transitions in the resulting geometric arrangements of their spins (37, 38). Such Ising-like models have previously been shown to predict OP and OD maps when using a nonlocal type of interactions with a “Mexican-Hat” shape, corresponding to neural models of lateral inhibition (29, 30, 39).

In our XY model, we considered n neurons with the following pairwise interaction between two neurons i and j:

$${\mathbf{J}}_{\mathbf{i}\mathbf{j}}\sim {\left(\frac{d\left(i,j\right)}{u}\right)}^{-\alpha },$$

where d(i,j) is the distance from neuron i to j, α is the decay power of the interaction strength with distance, and $u=\rho \cdot {\lambda }^{1/\alpha }$ is the degree of interconnectivity. Here, the interconnectivity is composed of the neuronal density ρ and the average neuronal span λ as described later. The interaction strength can be interpreted as the connection probability between two neurons that increases with neuronal interconnectivity and decays with distance as a power law. It was previously shown that, when the decay power α is greater than or equal to four, this class of models becomes similar to a short-range XY model described previously (37, 38) and exhibits similar phase transitions (40, 41). Incorporating the connection probabilities into the partition function (details are in Methods)

$$Z={\displaystyle \sum _{\theta }\exp \left(\frac{u^{\alpha }}{T}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^{n}d{(i,j)}^{-\alpha }\text{cos}(2{\theta }_i-2{\theta }_j)}}\right)}$$

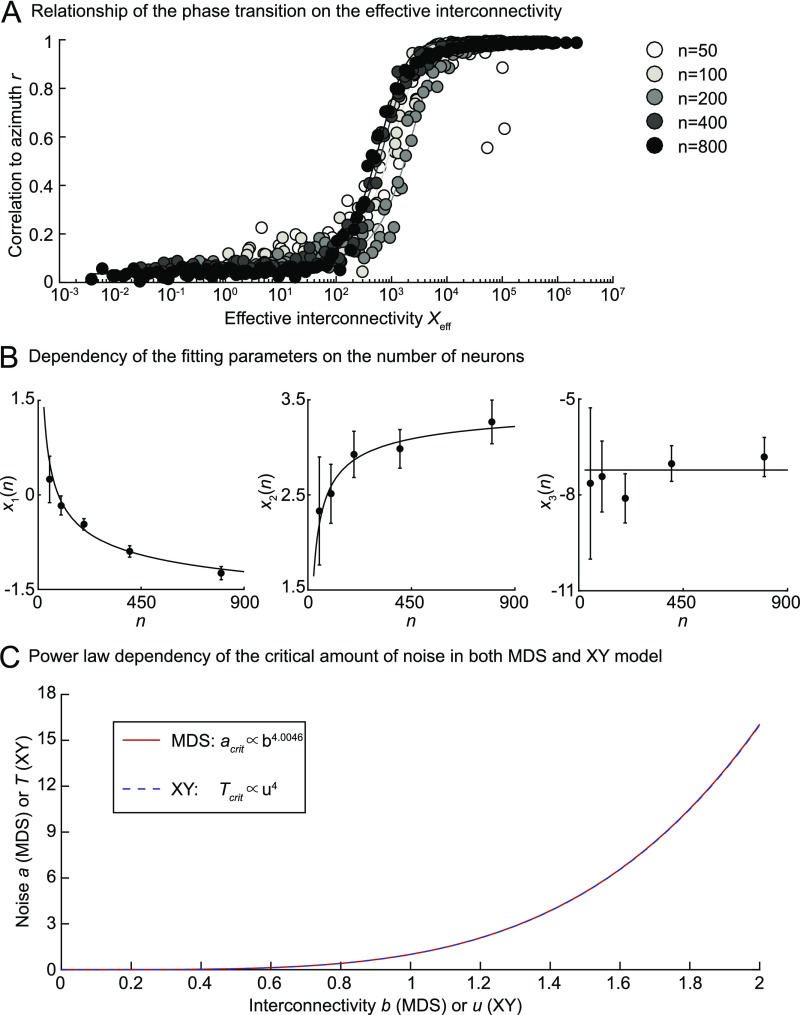
allows the study of phase transitions in the XY model that are known to occur when changing the temperature T, a model parameter that is related to the entropy of the system and therefore, the amount of disorder in the resulting map. Varying the amount of interconnectivity u is inversely proportional to varying T, because they both combine to an effective temperature $T/u^{\alpha }$ in the partition function. Therefore, the same phase transitions that are known to occur when changing the temperature will occur when changing either the neuronal span or the density. To illustrate this relationship, we performed numerical simulations using a hybrid Monte Carlo algorithm to produce output patterns for a range of different values of u and T (Methods and Fig. 2). The transition was clearly observed when changing not only T but also the amount of interconnectivity u.

Fig. 2.

Phase transitions in the XY model with network interconnectivity. Single realizations for 25 different combinations of two parameters T and u of our adaptation of the XY model after evolving the spins on a regular lattice with up to 10 million iterations using a hybrid Monte Carlo algorithm (as described in Methods). Values are given in arbitrary units.

Our results show a phase transition that is dependent on the interconnectivity, the connection selectivity, and the noise of the system. In both models, map structure can be influenced by changing the interconnectivity by varying either n in the MDS model or u in the XY model. We provide a detailed explanation of the relationship between our MDS and XY models as well as the role of all parameters involved in SI Text (Figs. S2–S4).

Fig. S4.

Relationship between phase transitions in the MDS and the XY models. (A) Fit of the correlation to the azimuth r of OP maps calculated with our MDS model for different numbers of neurons (shown as different shades of gray) and a large range of values for a and b. Original data points are shown in the space of the effective interconnectivity X_eff, which was calculated using the fitted parameters. The following ranges of a and b values have been used to obtain the fits for different numbers of neurons: n = 50 (a = [1.4236, 34.1995]; b = [1.3594, 21.5443]), n = 100 (a = [1.4236, 69.3145]; b = [1.3594, 39.8107]), n = 200 (a = [1.4236, 140.4844]; b = [1.3594, 73.5642]), n = 400 (a = [1.4236, 200]; b = [1.3594, 100]), and n = 400 (a = [1.4236, 200]; b = [1.3594, 100]). (B) Dependency of the fitting parameters (Left) x₁, (Center) x₂, and (Right) x₃ on the number of neurons n. Data points show the mean values, and the error bars show the lower and upper limits of the respective fitting parameters. Lines are fits of the dependency of x₁, x₂, and x₃ on logarithmic [$x_1\left(n\right)=A+B/\log \left(N\right)$ with A = −3.56 and B = 15.96], square root [$x_2\left(n\right)=A+B/\sqrt{N}$ with A = 3.54 and B = −9.46], and constant [$x_3\left(n\right)=A$ with A = −7.22] functions. (C) Critical noise has a power law dependence on the interconnectivity in the MDS and the XY models as shown by the curves and the given relationship in Inset. The power law of the MDS model depicted here was obtained for n = 284.

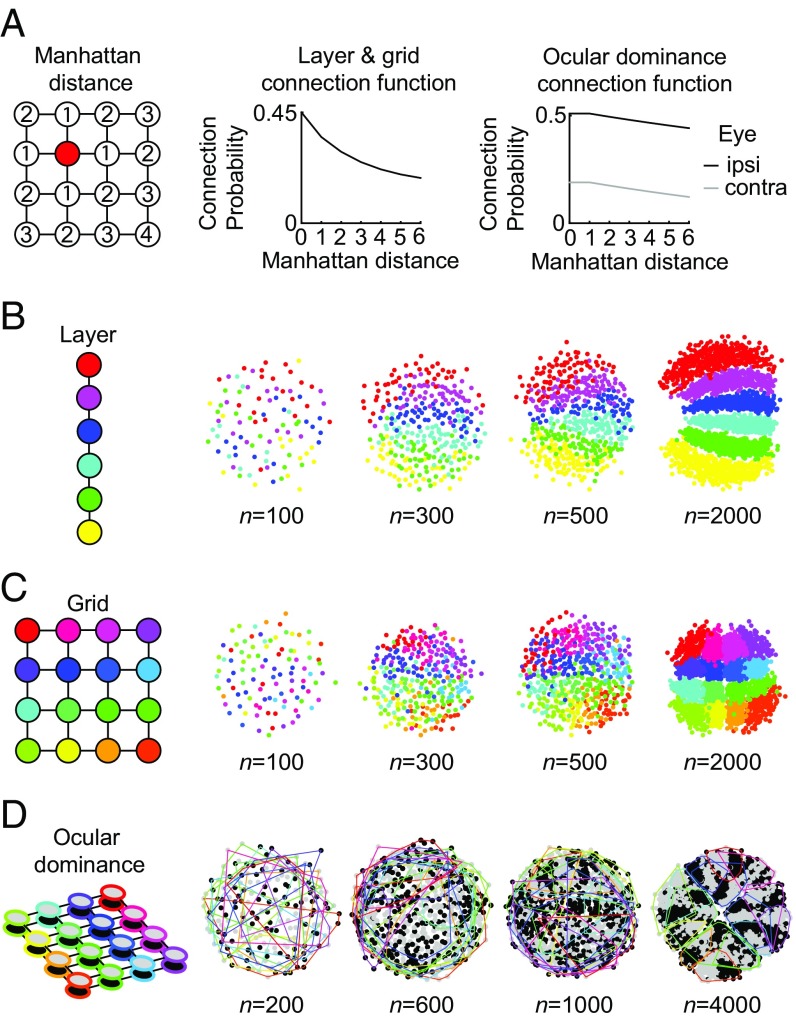
The progression from unstructured to structured arrangements seen in both the XY model and the MDS model for OP arrangements is, therefore, likely to be a general feature of neural maps. To show that this is also the case for simple topographic arrangements, we calculated the optimal placement of neurons selectively connected as groups on various grid configurations with a probability that decayed as a function of the Manhattan distance (Fig. 3A). Neural maps conserving neighborhood relations from the grid configurations emerged in all cases. A 1D chain of six groups of neurons led to six distinct layers (Fig. 3B), a 2D 4 × 4 connectivity led to a typical topographic map as observed in various systems throughout the brain (Fig. 3C), and a 3D grid connecting a 4 × 4 grid input from one eye with a 4 × 4 grid from the other eye (Fig. 3A, Right shows connection probability) led to a 2D arrangement conserving the neighborhood relations in both grids and forming a map of OD columns typical of the ones observed in the visual system (Fig. 3D). As is the case with OP maps, OD maps in biology exist in cats and monkeys (5) but are absent in rodents (42, 43) and tree shrews (44), adding to the evidence that the transition that we observe in the model could be pertinent to neural maps in general. In all three cases shown in Fig. 3, higher interconnectivity through a larger number of neurons led to more structure in the resulting topographic maps. Incidentally, increasing the feature space (i.e., from one to three dimensions between Fig. 3 B–D) also seemed to increase the threshold number of neurons required for the emergence of structured maps, indicating that the number of features also played a role in determining the amount of structure in the neural map.

Fig. 3.

Emergence of topographic maps with increasing interconnectivity. (A, Left) Distances in the topographic arrangements were defined using the Manhattan distance. (A, Center) Connection probability for the layer and grid arrangements in B and C. (A, Right) Individual connection probabilities to ipsilateral (black) and contralateral (gray) eye. (B–D) Neural placement similar to Fig. 1C as a function of numbers of cells using the connection probabilities from A. (B) 1D connectivity leading to layers. (C) 2D grid leading to a topographic map. (D) OD arrangement connecting two 4 × 4 grids. Colors of the neurons in all panels correspond to the colors in the sketch of the connectivity arrangement on the left. For D, eye preferences are plotted in black and gray, whereas assignment to the grid is shown as convex hulls around all neurons of the same groups in their respective colors. In B–D, the resulting maps were rotated and flipped manually to best match the schematic layout.

To support our theory with experimental data, we curated the available literature for numbers of neurons in mammalian V1 (Table S1) and their corresponding expression of OP and OD maps (Table S2) in a broad range of species and body sizes. According to our curated data, map structure seems to be critically dependent on the number of neurons in V1 (Fig. 4A), which directly relates to neuron numbers and interconnectivity in our models (Discussion).

Table S1.

Visual cortex metrics for mammalian species of different orders

Species	T, mm	V1 area A, mm2	No. of V1 neurons n	Density n/A, mm−2	Method	Ref.
Glires
Musa	0.7	2.5b	280,000c	112,200	Stereology	72d
Mus musculus	0.67	2.5b	216,500c	86,600	Stereology	73
Mus musculus	0.73	2.5b	352,500c	141,000	Stereology	74e
Mus musculus	0.87	2.5b	250,000c	100,000	Stereology	75
Mus musculus	0.583	5.258f	475,913	90,650	Isotropic fractionator	76
Mesocricetus auratus	0.7			75,101.37	Stereology	77g
Rattus norvegicus	1.49	8.5h	1,022,380c	120,280	Stereology	78e
Rattusa	1	8.5h	916,300c	107,800	Stereology	72d
Rattus norvegicus	1.2	8.5h	771,800	90,800	Stereology	73
Rattus norvegicus	1.34	8.5h	510,000c	60,000	Stereology	79e
Rattus norvegicus	1.74	8.5h	335,716c	39,496	Stereology	80e
Rattus norvegicus	1.342	8.5h	738,650c	86,900	Stereology	81
Sciurus carolinensis		32i	2,694,816c	84,213j	Estimatej	Estimatej
Oryctolagus cuniculus	2.1	74k	5,920,000c	80,000	Stereology	82e
Dasyprocta azarae	1.55	280l	12,121,536c	43,291.2	Stereology	77g
Cuniculus paca	1.67			39,521.35	Stereology	77g
Artiodactyla
Ovis aries	1.7m	1,000n	18,000,000c	18,000o	Estimateo	Estimateo
Carnivora
Felis catus (binocular)	1.62	345p	27,061,800c	78,440	Stereology	83e
Felis catus (monocular)	1.24	345p	21,355,500c	61,900	Stereology	83e
Felisa	1.5	345p	37,881,000c	109,800	Stereology	72d
Felis catus	1.67	345p	34,224,000c	99,200	Stereology	73
Mustela putorios furo	1.45q	80r	7,665,040c	95,813q	Estimateq	Estimateq
Scandentia
Tupaiaa (monocular)	0.71	42s	4,603,200c	109,600	Stereology	72d
Tupaiaa (binocular)	1.24	42s	8,097,600c	192,800	Stereology	72d
Primata
Callithrixa	1.52	205b	56,785,000c	277,000	Stereology	72d
Saguinus midas	1.34	314	36,119,106c	115,029	Stereology	77g
Aotus nancymae	1.49t	327.4	81,210,938	145,288	Isotropic fractionator	84
Aotus trivirgatus	1.56	275u	31,920,345c	116,073.98	Stereology	77g
Saimiria	1.49	637b	174,283,200c	273,600	Stereology	72d
Galagoa	1.24	200r	55,480,000c	277,400	Stereology	72d
Otolemur garnettii	1.5	206.649	34,770,894	168,261	Isotropic fractionator	84
Otolemur garnettii	1.18t	206.649v	35,481,013c	171,697w	Isotropic fractionator	84
Cebus apella	1.4	1,344x	162,294,720c	120,755.5	Stereology	77g
Macaca fascicularis and Macaca mulatta	1.59	841	169,882,000c	202,000	Stereology	85e
Macaca mulatta	1.48	1,269b	339,965,100c	267,900	Stereology	72d
Macaca fascicularis	1.8	1,090b	211,460,000c	194,000	Stereology	86e
Macaca fascicularis	1.4	1,090b	244,160,000c	224,000y	Stereology	87e
Papio c. anubis	1.87t	2,674x	567,029,722c	212,053z	Isotropic fractionator	84
Papioa	1.48	3,379x	906,923,600c	268,400	Stereology	72d
Pan troglodytes	1.8	2,805aa	670,648,152	239,043aa	Stereology and isotropic fractionator	88aa
Pana	1.59	3,331x	929,349,000	279,000	Stereology	72d
Homo sapiens	1.91	3,871x	1,002,201,900c	258,900	Stereology	72d
Homo sapiens	1.93	3,830x	574,500,000c	150,000	Stereology	89e

Data for V1 thickness (T), V1 area, number of neurons in V1, number of neurons under 1 mm² of cortex (n/A) in V1, and the counting method are shown. The data were curated from the literature (see references).

^aExact species not specified.

^bFrom ref. 73.

^cCalculated from V1 area and numbers of neurons per 1 mm².

^dData similarly normalized to densities as in refs. 73 and 90. Normalization to densities has been done differently (91), leading to higher cell numbers, probably because it does not account for shrinkage. We used the normalization of refs. 73 and 90, because these studies were specifically carried out to verify the results of ref. 72.

^eNormalized and corrected data taken from ref. 91.

^fAreas in atlas V1, V1M, and V1B.

^gDensity for the most caudal part of the cortex.

^hMeans of 7.1 (92), 9.4 (78), and 9 mm² (93).

ⁱMean of 30 mm² obtained from measuring flattened cortical pieces using ImageJ in figure 8 in ref. 94 and mean of 34 mm² obtained from measuring flattened cortical pieces using ImageJ in figures 4 and 5 in ref. 95 contradict the estimated size of 80 mm² in ref. 27.

^jHigher-bound estimate by using mean density of rats.

^kMean of 58 mm² obtained from graphical reconstructed transverse series in figure 5 of ref. 96 and mean of 90 mm² obtained from various figures of flattened albino rabbit cortices in ref. 97 using ImageJ.

^lMeasured from figure 1B in ref. 98 using ImageJ.

^mCortical thickness measured from figures 3 and 4 in ref. 99 using ImageJ.

ⁿEstimate of binocular (V1) and monocular (V1 and V2) segments in figure 1 in ref. 100 respecting cortical convolutions for sections A–C using ImageJ; approximately matches the V1 area size given in ref. 73 but contradicts the given size in ref. 101.

^oEstimate of density by calculating neurons per 1 mm³ in cortex of a similar sized Artiodactyla species (Damaliscus dorcas phillipsi) from table 1 in ref. 62, multiplying by cortical thickness to get a value of density in cortex, and multiplying this value by a factor of two to incorporate the generally higher neuronal density in V1 (77).

^pMeans of 380 (102) and 310 mm² (103).

^qLower-bound estimate by using mean density of cats (excluding monocular); cortical thickness estimated from figure 12D in ref. 116 using ImageJ.

^rFrom ref. 104.

^sMeans of 34 mm² obtained from figure 7 in ref. 63 using ImageJ and 50 mm² obtained from figure 4 in ref. 105 using ImageJ.

^tCalculated by division of neurons per 1 mm² by neurons per 1 mm³.

^uFrom ref. 27.

^vV1 size taken from the other tested Otolemur in ref. 84.

^wMeans of tube i.d. 1–5.

^xCalculated by dividing V1 gray matter volume data from ref. 106 by the cortical thickness.

^yDensity is estimated by multiplying numbers of neurons per 1 mm³ with cortical thickness.

^zMeans of tube i.d. 10, 13, and 16–19.

^aaTotal neuron count is mean of flow cytometry, Neubauer chamber, and optical fractionator results; density is estimated by multiplying numbers of neurons per 1 mm³ with cortical thickness. V1 size is estimated by dividing the total number of neurons by the estimated value for density.

Table S2.

Characterization of visual cortex map structure for different mammalian species

Species	OP	OD	Description
Mouse	Absent	Absent	No OP columns by electrophysiological recordings found (107), although indications for the clustering of cells of similar OPs were found
			No OD columns by autoradiography (108) and electrophysiological recordings (107, 109) found
Rat	Absent	Absent	No OP columns by calcium imaging (26) and electrophysiological recordings (110) found (ref. 28 has a review)
			No OD columns present (ref. 43 has a review), although inputs from both eyes are largely segregated in the binocular region of V1 (111)
Rabbit	Absent	Absent	No OP columns by electrophysiological recordings found (112), although OPs appeared to be arranged in clusters
			No OD columns found by autoradiography (96)
Gray squirrel	Absent	Absent	No OP columns by electrophysiological and optical imaging found (27)
			No OD columns by autoradiography found (113)
Agouti	Unknown	Unknown	Manifestation of visual cortex maps is unknown
Sheep	Present	Present	The presence of OP columns was shown by a gradual shift in OP in ref. 61, but the exact characteristic of the map is unknown
			The presence of OD columns was also found electrophysiologically in ref. 61, although the existence of an OD map is controversial, because the work in ref. 100 could find only slight indications for a structured map by autoradiography
Ferret	Intermediate	Intermediate	The presence of OP maps has been described by optical recordings (114, 115) but categorized as less regular and more discontinuous than the cat map. Therefore, we classified it as intermediate
			The presence of OD columns has been described by autoradiography (116) and optical recordings (117) and characterized as less pronounced than in primates (117). Therefore, we classified it as intermediate (44)
Cat	Highly developed	Intermediate	OP map found by optical recordings (9, 115, 117, 118) and calcium imaging (10)
			OD map found by optical recordings (117, 118) and autoradiographic and electrophysiological recordings (21) but characterized as less pronounced than in primates (117). Therefore, we classified it as intermediate (44)
Tree shrew	Intermediate	Absent	OP map has been shown by optical recordings (14, 63), but map contains extensive regions of a stripe-like pattern instead of the classical pinwheel pattern. Therefore, we classified it as intermediate
			No OD columns found by the pattern of LGN projections (64), electrophysiologically (65), and by autoradiography (66)
Marmoset	Highly developed	Intermediate	OP map has been shown by optical recordings (ref. 119 has a review)
			OD map in some species but not in others found by optical recordings and if it appeared relatively weak and as a mosaic of irregular bands or islands (120). Expression of OD maps has been reported (121) but remains controversial (ref. 119 has a discussion). Therefore, we classified it as intermediate
Galago	Highly developed	Intermediate	OP map has been reported by optical recordings (14, 122)
			OD map has been reported by optical recordings in most of the tested animals but not all (122), and CO blobs are not centered to OD columns (122). Therefore, we classified it as intermediate
Owl monkey	Highly developed	Intermediate	OP map has been shown by optical imaging (123, 124)
			OD map is cryptic, because there is no known anatomical substrate of OD columns except for one reported owl monkey (125), but a functional OD map is visible in the superficial layers (124). OD columns in owl monkeys are more patch-like or circular than the stripe-like OD columns seen in other monkeys, and CO blobs are not centered to OD columns (124). Therefore, we classified it as intermediate
Squirrel monkey	Highly developed	Intermediate	OP map has been reported by ref. 126
			Intermediate OD columns, because they are less well-segregated than in macaques (43) and capriciously expressed in different individuals (57). Furthermore, CO domains have been reported to not adhere strictly to the center of OD domains (43). Therefore, we classified it as intermediate (44)
Macaque	Highly developed	Highly developed	Reference example of OP and OD map
			OP map has been found by electrophysiological (127) and optical recordings (8)
			OD map has been found by electrophysiological recordings in combination with a silver staining method (128), by autoradiography (129), and by optical recordings (8)
			Map shows pinwheel singularities at the center of OD columns and linear zones at the edges of OD columns; isoorientation bands tend to intersect the borders of OD columns at angles of 90°, and CO blobs are in the center of OD columns (58, 130, 131)
Chimpanzee	Unknown	Highly developed	Presence of OP map is unknown
			OD map has been found by autoradiography (132)
Human	Highly developed	Highly developed	OP map has been reliably reported by fMRI, and striking similarities with the known spatial features of monkeys were found (133)
			OD map has been reliably reported by fMRI (133, 134) and cytochrome oxidase staining of human postmortem tissue (135). A similar network of patches as in macaque has been described (58, 135)

Map structure for OP and eye preference (OD) is characterized as absent, unknown, present, intermediate, or strong. The explanation for the characterization is given by the description that contains the supporting references. CO, cytochrome oxidase; LGN, lateral geniculate nucleus.

Fig. 4.

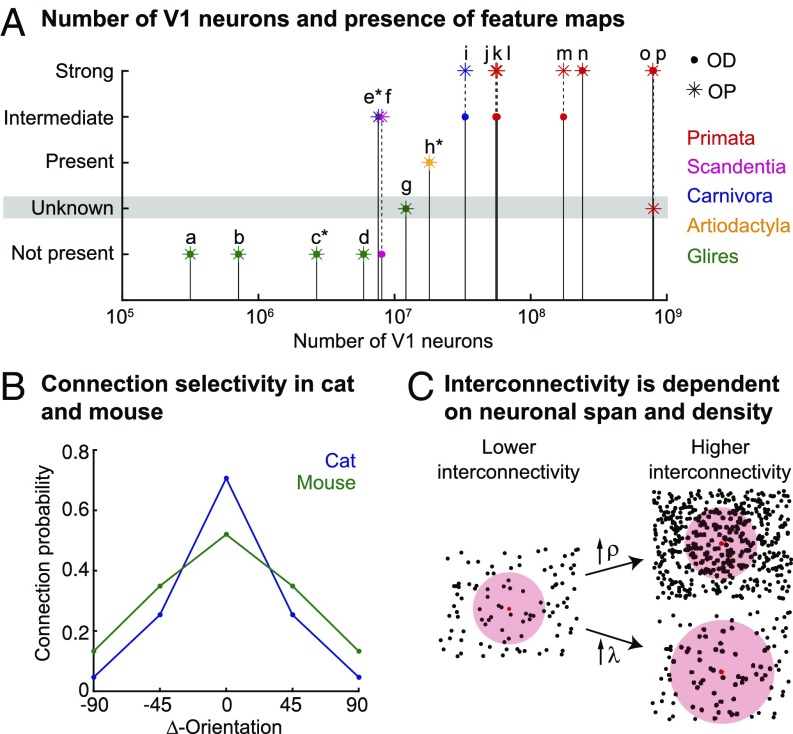
Interpretation of the parameters and biological data. (A) Numbers of neurons in visual cortex (V1) of species from different orders (color-coded) and their relation to map structure. OD and OP map structure are given by the positions of the dot and star symbol, respectively on the y axis of the plot. Number of V1 neurons and map structure were both curated from the literature and are summarized in Tables S1 and S2. The following species are shown: (a) mouse, (b) rat, (c) gray squirrel, (d) rabbit, (e) ferret, (f) tree shrew, (g) agouti, (h) sheep, (i) cat, (j) marmoset, (k) galago, (l) owl monkey, (m) squirrel monkey, (n) macaque, (o) human, and (p) chimpanzee. Neuronal numbers for species denoted with a star are only estimates (Table S1). (B) Connection selectivity given by the connection probability between orientation-selective neurons in the visual cortices of mouse and cat (estimated mean of curated data from figure 3 in ref. 28; original data from refs. 34, 35, and 71). (C) The amount of interconnectivity is dependent on both the cell density ρ and the neuronal span λ when the probability of connection within λ is constant. This relationship is illustrated as an example for one neuron (red dot) that has a fixed connection probability to other neurons (black dots) within its neuronal span (red-shaded area).

Discussion

We have shown that connectivity and neural placement are consistent with optimal wiring as has been previously suggested (5, 6) but that a phase transition between an unstructured and a structured map can occur without changing the selectivity of the connections. This finding is in line with recent experimental measurements that indeed have shown a selective connectivity in the salt-and-pepper arrangements in rodents (32–35) (Fig. 4B).

Phase transitions between unstructured and structured maps have previously been observed in a number of modeling studies (12, 13), including those using elastic net models (7, 16, 22) and competitive Hebbian models (Kohonen map models) (45). There, phase transitions depending on receptive field (7, 16, 22) and neighborhood size (19, 45) are reminiscent of the phase transition depending on the interconnectivity in our models. Elastic net models have been shown to predict the order of map development for a set of given features with respect to the sizes of their particular cortical hypercolumn, indicating a possible link between the phase transition and cell numbers similar to our own results (22). The similarity of the resulting neural maps and the corresponding phase transitions in all of these models (46–49) indicate a common underlying theme. Accordingly, the XY and the MDS model are related. It is, therefore, not surprising that we find analogous relationships regarding the phase transition in both models, and we would predict equivalent phase transitions with interconnectivity to be present in other models. However, despite their similarities, different models highlight different aspects of visual cortex maps (12, 50).

In our MDS model, the relationships between interconnectivity, neuron numbers, and maps became particularly visible. Changing the number of neurons n in the MDS model naturally led to an increase in the number of connections per neuron (i.e., the interconnectivity) if the connection selectivity was fixed. Likewise, in the XY model, the interconnectivity was proportional to the cell density ρ and the neuronal span λ if one assumes a fixed connection probability within the interaction range of a neuron (Fig. 4C). Therefore, changing the interconnectivity u in the XY model was analogous to changing the number of neurons n in the MDS model. To better study this relationship, we also decoupled the interconnectivity from the number of neurons in the MDS model (Fig. S3). This study confirmed that changing the number of neurons without increasing the interconnectivity has no visible effect on the obtained map layouts. However, direct application of noise in the MDS model, analogous to changing the temperature T in the XY model, unsurprisingly resulted in unstructured maps. A higher number of neurons then increased the resistance to such noise (Fig. S2) similarly to increasing u in the XY model. Overall, the numerical analysis of the phase transition in the MDS model showed that noise and interconnectivity affect the map structure similarly as in the XY model, indicating a similarity of the phase transition in both models (Fig. S4).

We validated our model prediction by curating absolute numbers of neurons in mammalian V1 from the available literature (Fig. 4 A and B and Table S1) and found that neuronal map structure increases with the number of neurons. The question then emerges as to how the number of neurons in V1 relates to neuronal interconnectivity. Because V1 represents the visual field in a retinotopic manner, for potential pinwheels (or any type of cortical hypercolumns) to exist, these pinwheels should not exceed a maximum relative size. Otherwise, no part of the visual field would represent the entire feature space (51). The absolute number of neurons in V1, therefore, directly determines the maximum number of neurons available to form a pinwheel. Accordingly, for a fixed relative connectivity, the amount of interconnectivity would increase with the absolute number of neurons in V1.

Based on our findings, we believe that cortical maps did not “evolve” to fulfill a certain function (52). Our results rather indicate that cortical maps emerge as a consequence of optimal wiring and connectivity requirements. This conclusion is also supported by a number of strong arguments. From an evolutionary perspective, it is unlikely that fundamental differences in neural maps in closely related species are caused by differences in the visual cortex architecture (53). Our theory is further supported by experimental studies, which show that the emergence of visual cortex map patterns depends on the input (54–56) and that OD columns are capriciously expressed in some New World monkeys, excluding functional consequences from having structured OD maps (57, 58). OP maps have also been observed in birds (59), which altogether lack a cortical architecture (60), further indicating that neural maps in the visual system are more likely to be a product of neuronal optimization principles based on the afferent input. These findings may lead to the conclusion that structured maps could be a sign of increased neural organization or superior optimization compared with homologous areas without structured maps in different species. We would argue against such a conclusion based on our MDS model results, because wiring length is similarly optimized in unstructured and structured map layouts (Fig. 1E). In conclusion, our model results suggest a simple explanation for the difference of visual cortex maps between rodents and primates, carnivores, ungulates, and tree shrews without assuming a difference in the general functional architecture or how optimal the network layout is.

Although data for connection selectivity between neurons of similar tuning are available only for cats and mice, a higher connection selectivity in carnivores and possibly, primates and tree shrews together with a generally higher number of neurons could explain the presence of structured visual cortex maps in those species and their absence in rodents. However, it has been shown that sheep show some form of a structured map (61) and that ungulates in general possess similar neuronal scaling rules as rodents (62). The emergence of a structured map in larger rodents is, therefore, likely. The agouti is a rodent with neuronal numbers in V1 that are as high as those of other species with structured OP maps (Fig. 4A and Tables S1 and S2). Although occurrences of structured maps in the agouti and the even larger capybara have not yet been reported, they likely possess OP maps. The existence of structured visual cortex maps in rodents has mainly been questioned because of a study that showed the presence of an unstructured map in the gray squirrel—a highly visual rodent (27). Here, it has been claimed that ferret, tree shrew, and gray squirrel possess similar V1 sizes and visual acuity, leading to the conclusion that visual cortex map structure cannot be determined by these factors (27). However, the gray squirrel has a smaller V1 than the tree shrew and the ferret (Table S1). Most likely, it also has a smaller neuronal density than tree shrew and ferret and as a consequence, a much lower number of neurons in V1. Thus, the results obtained for the gray squirrel (27) do not contradict our results.

In addition to a sharp separation of map structures given by the neuronal numbers in V1, there seems to be a progression in the strength of the expression of the maps depending on the number of neurons (Tables S1 and S2). For example, tree shrews that are on the lower end of the spectrum show an intermediate OP map pattern, which is characterized by a more stripe-like appearance in large parts of their V1 (63). Additionally, they lack an OD map entirely (64–66). New World monkeys with V1 neuron numbers between those of tree shrews and macaques (Table S1) show a robust OP map (Table S2) but an intermediate OD map pattern, which is, furthermore, erratically expressed between different individuals (57, 58). Also, carnivores seem to show a progression of map structure depending on the number of neurons in V1. The OP and OD map of the ferret have been described as less structured and regular than those of the cat, and neuronal numbers in cat V1 are very likely to be greater than those in the ferret V1 (Tables S1 and S2).

Our models suggest that a certain number of neurons per hypothetical hypercolumn are necessary to form a structured OP map. The area of V1 required for a pinwheel should, therefore, vary with neuronal density, and hypercolumn sizes would scale accordingly (14, 23). In the light of our results, the different hypercolumn sizes observed in different species could be explained by individual neuronal densities in visual cortex. In line with this argument, neuronal density in cat was shown to be about one-half of the density measured in macaque, but hypercolumn sizes were twice as large (Table S1) (44). Although we provide biological data that are as reliable and comprehensive as possible, the collected data are largely fragmented over more than a dozen different studies and confined in the diversity of species that they provide (Tables S1 and S2). To confirm our theory, additional experiments providing better data for more species are necessary. Neuronal numbers and connection selectivities should be obtained by standardized methods, ideally in the same individuals where the map structure is assessed. However, it would be particularly interesting to see whether structured visual cortex maps are expressed in the largest existing rodent, the capybara, and conversely, whether they are missing in the smallest primates, carnivores, or ungulates.

Methods

To show the transition between unstructured and structured circuit arrangements, we take advantage of two separate models that generate the patterns of OP maps. The first model is our own model based on optimal placement of neurons to minimize wiring in the circuit using MDS; the second model is based on an adaptation of the Ising-like XY model, where spatial patterns emerge from interactions between nodes on a regular lattice.

Determining Connection Probabilities from Euclidean Distances.

The connection probabilities in Fig. 1A were calculated from the Euclidean distances between each pair of nodes i,j using the following function:

$$p\left(i,j\right)=\left(1-\min \left(1,\frac{d\left(i,j\right)}{d_{\max }}\right)\right),$$ [1]

where d(i,j) is the Euclidean distance between nodes i and j, and d_max is the maximum distance to establish a connection. In Fig. 1A, we used 1,000 neurons uniformly distributed in a square area. We divided the square into six layers of the same size and attributed to each layer a unique color that we correspondingly assigned to the neurons of the respective layer. For calculating the connection probabilities, a d_max of 0.4 was used.

Calculating Connection Dissimilarity for the MDS Model.

Given a binary connectivity matrix C for n neurons, we determined the connection dissimilarity δ_i,j of two connected neurons i and j by calculating the Jaccard distance

$$JD=1-JC(C_i,C_j)=1-\frac{|C_i\cap C_j|}{|C_i\cup C_j|},$$ [2]

where $C_i=\{k:{\mathbf{C}}_{i,k}=1,\hspace{0.5em}k\in \{1,\dots ,n\}\}$ denotes the set of nonvanishing indices of the ith row of C, and C_i,k is the entry at the ith row and kth column of C. After calculating the dissimilarity for all connected neurons, we obtained the remaining dissimilarities by summing up the calculated dissimilarity values over the shortest paths between nonconnected neurons.

Optimal Placement Using MDS.

MDS finds positions X of n nodes in r dimensions, such that the Euclidean distances d(i,j) between the nodes i and j best match given dissimilarity values δ_i,j. For calculating the optimal neural placement, we used the dissimilarity of the connectivity between neurons i and j as defined above to calculate their 2D positions by ordinal MDS. The positions X are calculated in MDS by minimizing the stress function σ:

$$\sigma ≔{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n{\left(f\left({\delta }_{i,j}\right)-d(i,j)\right)}^2}},$$ [3]

where f(δ_i,j) transforms the dissimilarity values into spatial distances. In ordinal MDS, this function f has to be monotonic, must only fulfill the condition ${\delta }_{i,j}<{\delta }_{k,j}\iff f\left({\delta }_{i,j}\right)\mathrm{\le }f\left({\delta }_{k,j}\right)$, and is also computed such that it minimizes σ (36). We used the MATLAB function mdscale to perform the ordinal MDS.

Optimal Placement for a Single Pinwheel Using MDS.

Random OPs θ ∈ [0, π] were associated with n neurons used for one pinwheel. The probability p of connecting two neurons i and j was determined by

$$p({\theta }_i,{\theta }_j)=a+b\cdot {\left[\frac{(\cos (2{\theta }_i-2{\theta }_j)+1)}{2}\right]}^{\gamma },$$ [4]

a function of the preferred orientations θ_i and θ_j of both neurons. This type of periodic connectivity is analogous to previous models predicting OP maps (6). Here, a defines the constant connection probability between all n neurons, and b is the maximum connection probability between two neurons i and j. The selectivity of the connection is given by γ, a parameter of crucial importance in Fig. 1.

Estimation of Cable Saved by Optimal Placement.

To quantify the amount of cable that was saved by the optimal placement of n neurons, we compared the arrangement obtained using MDS with the arrangement of n randomly located neurons in an area with similar dimensions. Random positions were obtained using a uniform distribution within the bounding box around the positions determined using MDS (Fig. 1A) or for a circular bounding box (Fig. 1C). For any connectivity matrix C that has been used to calculate the neuronal positions using MDS and the distance matrix D of the positions determined by MDS, we calculated the total wiring length L as follows:

$$L={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{C}_{ij}\cdot D_{ij}}}.$$ [5]

For the distances of the random positions D_rand, the total wiring length connecting the random positions L_rand was calculated analogously. The proportion of wiring length compared to random was then defined in percentage by 100⋅L/L_rand.

Correlation Coefficient Between Preferred Orientation and Pinwheel Azimuth.

To quantify how much the MDS neural placement followed a pinwheel arrangement, we calculated the correlation between OP and azimuth for all neurons in each modeled arrangement. A reference vector was defined by the mean direction of the coordinates of the first 10 neurons, with a preference to the smallest orientations greater than or equal to 0. For each neuron, the azimuth was then calculated with respect to the reference vector and plotted against the preferred orientation (Fig. 1C). The Pearson correlation coefficients for Fig. 1D were then calculated for data points with an azimuth in the range between 1/4π and 7/4π to avoid data points that possess an OP near π but reside near the 0 azimuth and vice versa. For the results shown in Fig. 1D, 40 modeled neural arrangements were calculated for each parameter pair, and we used the average of the absolute values of the corresponding correlation coefficients.

XY Model for Studying the Phase Transition with Interconnectivity.

The 2D XY model is an Ising-like model (67), where the state of a single spin s_i can take values θ from $0$ to $\pi$. The interaction between two spins s_i⋅s_j then is equal to the scalar product of the two corresponding orientation vectors: cos(2θ_i − 2θ_j). The system is described by the following Hamiltonian operator:

$$H=-J\hspace{0.5em}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n\cos (2{\theta }_i-2{\theta }_j)}},$$ [6]

where J is a positive constant. We modified the original XY model (67) to be able to better compare it with variables from the MDS model and better study the effect of interconnectivity by replacing the constant J with an n × n matrix J that incorporates the strength of the interaction J_ij between all pairs of neurons i,j ∈ {1, …, n}. Assuming that neuronal connection probability decays strongly with distance, we used a simple power law relationship: J_ij ∼ λ(d(i,j)⋅ρ⁻¹)^−α, where d(i,j) is the distance between two neurons, ρ is the neuronal density, and λ represents the neuronal span. For ease of notation, we considered the following connection function:

$${\mathbf{J}}_{\mathbf{i}\mathbf{j}}\sim {\left(\frac{d\left(i,j\right)}{u}\right)}^{-\alpha },$$ [7]

where we introduced the interconnectivity as parameter $u=\rho \cdot {\lambda }^{1/\alpha }$. It is important to note that, when increasing the density of neurons, the average distance between them will decrease. Increasing either the density ρ or the average neuronal span λ will, therefore, increase the amount of interconnectivity u. The Hamiltonian operator then becomes

$$H=-{\displaystyle \sum _{i=1}^n\frac{1}{k_i}{\displaystyle \sum _{i=j+1}^n{\left(\frac{d\left(i,j\right)}{u}\right)}^{-\alpha }\hspace{0.17em}\cos \left(2{\theta }_i-2{\theta }_j\right)}},$$ [8]

where the factor $k_i={\displaystyle {\sum }_{k\ne i}d{(i,k)}^{-\alpha }}$ has been introduced to ensure the thermodynamic limit of the system and its asymptotic independence on the number of neurons (68).

In the limit of α → ∞, this model becomes equivalent to the common short-range XY model that only takes into account interactions with the nearest neighbors.

Increasing Radius of Interaction Is Equivalent to Decreasing Temperature.

In a statistical system, such as the Ising XY model that we used, the properties of the system, including its characteristic phase transitions, can be obtained from the partition function Z. This function is defined as the sum over all possible configurations of its Boltzmann weights:

$$Z={\displaystyle \sum _{\left\{\theta \right\}}{e}^{-\frac{H(\theta ,u)}{T}}}.$$ [9]

Inserting Eq. 8 into Eq. 9 leads to

$$Z={\displaystyle \sum _{\left\{\theta \right\}}\exp \left(\frac{u^{\alpha }}{T}{\displaystyle \sum _{i=1}^n\frac{1}{k_i}{\displaystyle \sum _{j=i+1}^{n}d{(i,j)}^{-\alpha }\text{cos}(2{\theta }_i-2{\theta }_j)}}\right)}.$$ [10]

It was shown previously (40, 41, 69) that, when α is greater than or equal to four, the system described by Eq. 10 belongs to the Kosterlitz–Thouless universality class (37, 38). The system thereby exhibits phase transitions driven by the temperature T, a model parameter that is related to the entropy of the system. Below the critical temperature, the system exhibits long-range correlations that decay as a power law and share similarities with cortical OP maps, including alternating clockwise and anticlockwise pinwheel formations. Above the critical temperature, the correlation length decays exponentially, and mesoscopic patterns can exist only on a short scale. Eq. 10 can be rewritten in terms of effective temperature: $T_{eff}=T/u^{\alpha }$, and it follows directly that changing the interconnectivity u is inversely proportional to changing the temperature T. Increasing the interconnectivity as well as decreasing the temperature, therefore, both lead to a phase transition in this class of systems (40, 41).

Numerical Simulations for XY Model Using a Hybrid Monte Carlo Technique.

To visualize the phase transition in the XY model with increasing interconnectivity, we performed numerical simulations based on a standard method for XY model predictions using a hybrid Monte Carlo method (70). The original Hamiltonian operator of the system (Eq. 8) was considered as a potential that depends on the n OPs of all neurons in the system. We introduced an additional parameter ϕ for each of these dfs representing the velocity of each orientation:

$$H\left(\left\{\theta \right\},\left\{\varphi \right\},u\right)=-{\displaystyle \sum _{i=1}^n\frac{1}{k_i}{\displaystyle \sum _{j=i+1}^n{\left(\frac{d\left(i,j\right)}{u}\right)}^{-\alpha }}}\cos \left(2{\theta }_i-2{\theta }_j\right)+\frac{1}{2}{\displaystyle \sum _{i=1}^n{{\varphi }_i}^2}.$$ [11]

At each Monte Carlo iteration, all of the nodes of the grid evolved according to the equation, whereas the system returned to its previous state with a probability

$$P_{reject}=1-\min \left(1,\exp \left(-\frac{\mathrm{\Delta }H}{T}\right)\right);$$ [12]

10,000 neurons on a grid were associated with random initial orientations, and up to 1,000 iterations were performed according to the following algorithm.

Algorithm.

• i)Select n parameters from a normal distribution centered around zero with an SD of T.
• ii)Numerically integrate

$$\begin{array}{c}{\varphi }_i\left(\frac{\mathrm{\Delta }t}{2}\right)={\varphi }_i\left(0\right)-\frac{\mathrm{\Delta }t}{2}\frac{\partial H}{\partial {\theta }_i}\\ {\theta }_i\left(\mathrm{\Delta }t\right)={\theta }_i\left(0\right)+\mathrm{\Delta }t\frac{\partial H}{\partial {\varphi }_i}\\ {\varphi }_i\left(\mathrm{\Delta }t\right)={\varphi }_i\left(\frac{\mathrm{\Delta }t}{2}\right)-\frac{\mathrm{\Delta }t}{2}\frac{\partial H}{\partial {\theta }_i}\end{array}$$ [13]

• for each node.

• iii)Calculate the difference between the new and the old Hamiltonian operators and accept the new values θ if the change is not rejected according to the rejection probability (Eq. 12).

The resulting θ produced by this algorithm follows the same statistics as the partition function. Fig. 2 was generated in this way for α = 4 and 25 different combinations of temperature and levels of interconnectivity.

SI Text

Extended Data for Fig. 1.

In Fig. S1, we show a larger range of OP map realizations for our MDS model similar to Fig. 1. Fig. S1A focuses on the region where the phase transition is most pronounced. Fig. S1A, Right describes the type of data used for the correlation measure r in Fig. 1D in greater detail. Note that both right- and left-handed pinwheels were predicted (Fig. 1C and Fig. S1A) with corresponding points along the diagonal or antidiagonal in the OP vs. azimuth plot (Fig. S1A, Right). The entire parameter range is shown in Fig. S1B.

Noise in the MDS Model.

Noise is represented by the temperature T in the XY model, but there is no explicit parameter in the MDS model used in the manuscript that determines the amount of noise in the system. However, noise is introduced by the random nature of the connectivity and the distortions in the development of a structured map caused by unselective connections. To better understand the relationship between connectivity and noise in the MDS model, we designed an initial highly selective noise-free connectivity that we subsequently subjected to noise (Fig. S2A). Similar to decreasing connection selectivity, increasing noise leads to an unstructured map. This relationship suggests that noise and unselective connections can be considered equivalent with respect to their effect on resulting map patterns (Fig. S2B).

Neuronal Numbers, Interconnectivity, and Connection Selectivity in the MDS Model.

In the manuscript, we showed a phase transition in our MDS model with number of neurons n and discussed in depth the relationship of n to the interconnectivity. To more formally compare the XY model with the MDS model, we introduce here a modified connection function that decouples interconnectivity from the number of neurons:

$$p({\theta }_i,{\theta }_j)=\frac{1}{n}\left(a+b\cdot {\left[\frac{\left(\cos (2{\theta }_i-2{\theta }_j)+1\right)}{2}\right]}^{\gamma }\right).$$ [S1]

Here, the connection function is defined similarly as in Eq. 4, but the connection probability is normalized by the number of neurons. Because we showed that there is no difference between noise and unselective connectivity, we define a as the amount of noise and b as the amount of selective interconnectivity. Note that the results obtained by this connection function are representative of the results that can be obtained using the original connection function, because there is a one to one correspondence between both functions. Because both parameters are normalized by the number of neurons n, interconnectivity can be set independently from n. Hence, we are able to analyze the effect of numbers of neurons, interconnectivity, and connection selectivity separately. However, we want to clarify that, although the interconnectivity can be set independently of the number of neurons, the maximum amount of interconnectivity is dependent on the number of neurons (because the maximum interconnectivity refers to the maximum amount of possible connections, which are limited by n), and therefore, increasing the latter is indispensable for reaching certain amounts of interconnectivity. Furthermore, it is also not our intention to suggest that structured maps arise because of a higher interconnectivity for a fixed number of neurons. We rather believe that higher numbers of neurons (e.g., in V1) increase the interconnectivity for a fixed relative connectivity, which then leads to the phase transition. In agreement with our expectations, varying the number of neurons but keeping the other parameters fixed does not lead to a change in map structure (Fig. S3A). However, varying the amount of interconnectivity by uniformly increasing noisy and selective connections (by increasing a and b) leads to a transition from a salt-and-pepper to a pinwheel organization (Fig. S3B). Thus, we show that the effect of the numbers of neurons on the phase transition seems to depend only on the interconnectivity. Furthermore, we show that the effect of the connection selectivity on map structure is unsurprisingly not affected using the connection function given in Eq. S1 (Fig. S3C).

MDS and XY Model Relationship.

Although we have shown that the phase transitions of the MDS and the XY models are based on similar parameters, their exact relationship is still not clear. The phase transition in the XY model is a Kosterlitz–Thouless transition of infinite order, and the interdependence of the critical noise T_crit and the interconnectivity u is analytically given by $T_{crit}\propto u^4$. However, for the MDS model, a complete analytical description of the phase transition is beyond the scope of this article. The connection function given in Eq. S1 enabled us to numerically study the effects of the amount of unselective interconnectivity [i.e., of noise (a), the amount of selective interconnectivity (b), and the number of neurons (n)] on the phase transition separately. The correlation to the azimuth r that quantifies the amount of structure in the OP map depends on the set values for a and b, which we have shown to correspond to T and u in the XY model. We analytically showed that the phase transition in the XY model is determined by the effective temperature T_eff = T/u^α (Methods). To show a similar relationship between noise and interconnectivity, we fitted the calculated correlation values r for the results of different values of a, b, and n and a fixed γ = 1 to a sigmoid function given by

$$r\left(a,b\right)=\left(1-\frac{1}{\sqrt{n}}\right)\left[\frac{a^{x_1}{b}^{x_2}{e}^{x3}}{\sqrt{{\left(a^{x_1}{b}^{x_2}{e}^{x3}\right)}^2+1}}-1\right]+1,$$ [S2]

where r is the correlation to the azimuth (definition are in Methods), and x₁, x₂, and x₃ are the fitting parameters.

According to the fit function in Eq. S2, the order parameter that corresponds to the effective temperature in the MDS model is given by $X_{eff}=a^{x_1}\cdot b^{x_2}$, which we define as the effective interconnectivity. Furthermore, the critical value of the phase transition is given by $X_{crit}=\exp (-x_3)$. In Fig. S4A, we show the results of the fit and the data that have been fitted in the space of X_eff and r. To show an analogous behavior of the MDS and XY models regarding the phase transition, the fitting parameters x₁ and x₂ should have the same sign in both models, and x₃ should be constant. Because the phase transition is analytically given by T_eff = T/u^α, it follows that x₁ = −4 and x₂ = 1 for α = 4 in the XY model. Accordingly, we found numerically that the phase transition observed in the MDS model matches the characteristics of the XY model phase transition. Specifically, we found that x₁ is always negative (Fig. S4B, Left), that x₂ is always positive (Fig. S4B, Center), and that x₃ is constant (Fig. S4B, Right). Thus, similar to in the XY model, where the order parameter of the phase transition is given by a power law between noise T and interconnectivity u, the critical amount of noise a in the MDS model is also given by a power law in dependence on the interconnectivity

$$a_{crit}\propto b^{\frac{x_2}{x_1}}.$$

The power law of the XY model is best matched for n = 284 in the MDS model and shown for a wide range of interconnectivity and noise values in Fig. S4C.

The constancy of x₃ confirms more systematically what we have shown in Fig. S3: the number of neurons has no effect on the phase transition, at least regarding the effective interconnectivity. This relationship can also be seen in the fitted curves in Fig. S4A, because there is no discernible regular shift of these curves regarding the respective number of neurons. However, because the values of x₁ and x₂ change with the number of neurons, the critical composite amount of noise and interconnectivity fluctuates when changing the number of neurons. Thus, the identical relationship between noise and interconnectivity in the XY model cannot be replicated in the MDS model.

In conclusion, the two models exhibit two different phase transitions, but these transitions are driven by similar parameters representing the noise and the interconnectivity, which affect the order parameters X_eff and T_eff in a similar way.

Biological Data.

To support our model results by biological data, we curated the available literature to obtain the number of neurons in V1. Thereby, we obtained a dataset from a wide range of species containing thickness, area, number of neurons, and neuronal density in V1 (Table S1). Furthermore, we characterized the visual cortex map structures for all of the mammalian species given in Table S1 when available (Table S2).