Explaining negative kin discrimination in a cooperative mammal society

Significance

Kin selection theory predicts that animals will direct altruism toward closer genetic relatives and aggression toward more distantly related individuals. Our 18-y study of wild banded mongooses reveals that, unusually, dominant individuals target females who are more closely related to them for violent eviction from the group. This puzzling result can be explained by selection for unrelated individuals to resist eviction and for related individuals to submit more easily. In support of this idea, we show that kin are targeted for aggression only when individuals are capable of resisting. Our results suggest that, where potential victims can oppose aggression, the usual predictions of kin selection theory can be reversed.

Abstract

Kin selection theory predicts that, where kin discrimination is possible, animals should typically act more favorably toward closer genetic relatives and direct aggression toward less closely related individuals. Contrary to this prediction, we present data from an 18-y study of wild banded mongooses, Mungos mungo, showing that females that are more closely related to dominant individuals are specifically targeted for forcible eviction from the group, often suffering severe injury, and sometimes death, as a result. This pattern cannot be explained by inbreeding avoidance or as a response to more intense local competition among kin. Instead, we use game theory to show that such negative kin discrimination can be explained by selection for unrelated targets to invest more effort in resisting eviction. Consistent with our model, negative kin discrimination is restricted to eviction attempts of older females capable of resistance; dominants exhibit no kin discrimination when attempting to evict younger females, nor do they discriminate between more closely or less closely related young when carrying out infanticidal attacks on vulnerable infants who cannot defend themselves. We suggest that in contexts where recipients of selfish acts are capable of resistance, the usual prediction of positive kin discrimination can be reversed. Kin selection theory, as an explanation for social behavior, can benefit from much greater exploration of sequential social interactions.

Kin selection theory aims to understand how selection acts on social traits, such as altruism and selfishness, that affect the fitness of social partners and local group members (1, 2). The theory predicts that where animals can discriminate between more closely and less closely related individuals within their social group, they will preferentially direct altruism toward closer genetic relatives and aggression toward less closely related targets (1–3). Instances of such positive kin discrimination are taxonomically numerous and widespread (4), whereas reported examples of negative kin discrimination are rare (5, 6).

Contrary to the predictions of traditional kin selection theory, we show below that banded mongooses exercise negative kin discrimination during attempts at eviction and that this result is not readily explained by inbreeding avoidance or local kin competition. However, a simple and very general sequential game model of selfish behavior that takes into account the possibility of active resistance on the part of recipients does provide a potential explanation for negative kin discrimination. We first describe the model and then test predictions of the model using our data.

Explaining Negative Kin Discrimination: A Model

Consider the interaction between two individuals, the first of whom (player 1) may perform a selfish act at the other’s expense, such as stealing a food item, killing offspring, or, in the case with which we are concerned, evicting the other from the territory or group. We suppose that this act entails some fitness cost to the actor, denoted c₁, but that the cost is outweighed by the benefit to be gained, b₁ > c₁. The act, if carried out, also deprives the recipient, player 2, of a benefit b₂ that it would otherwise enjoy. If the two individuals are related by a coefficient r, then Hamilton’s rule tells us that the act will be favored by selection provided that b₁ – c₁ – r b₂ > 0. Consequently, selfishness will never be directed toward a closer relative where it would not also be directed toward a more distant one.

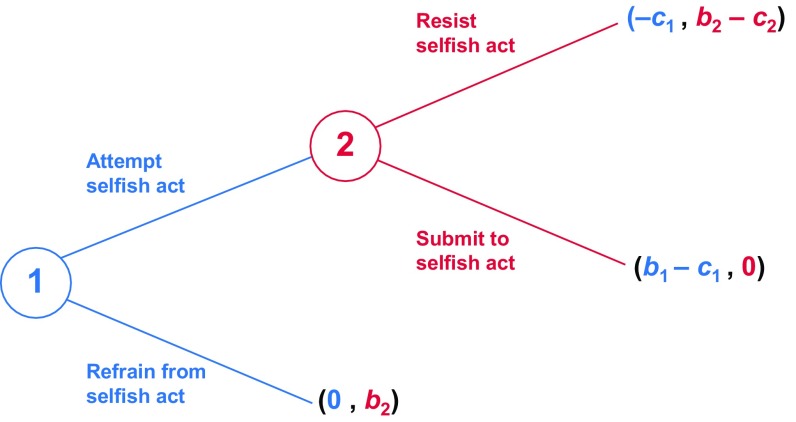
Suppose, however, that if player 1 attempts the selfish act, player 2 may then choose to resist. Resistance ensures that the act will fail; player 1 will still suffer the cost c₁ of attempting the act, but will not enjoy the benefit b₁ of success, nor will player 2 suffer the consequent loss of benefit b₂. At the same time, resistance entails a fitness cost to player 2 of c₂. This situation may be modeled as a two-step, sequential game, as illustrated in Fig. 1 (SI Models for a population genetic formulation of the model; Fig. S1).

Fig. 1.

A sequential model of selfishness and resistance. Player 1 (blue) first chooses whether or not to attempt a selfish act at the expense of player 2 (red); in the event of such an attempt, player 2 then chooses whether or not to resist. Direct fitness payoffs to both players are shown in their respective colors.

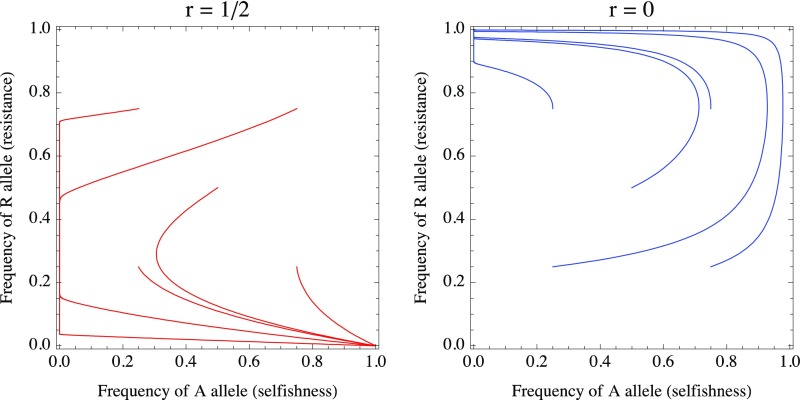
Fig. S1.

Evolutionary trajectories converge from multiple initial conditions to nonresistance and selfishness (f_Ar = 1, f_AR = f_aR = f_ar = 0) when r = 1/2, but to resistance and nonselfishness (f_aR = 1, f_AR = f_Ar = f_ar = 0) when r = 0. In both cases, parameter values are otherwise identical, with b₁ = b₂ = 1, c₁ = 0.25, c₂ = 0.75, and ε = 0.01.

How does relatedness affect the outcome of this game? Applying Hamilton’s rule once again, if c₂ > b₂ – r b₁, then the cost of resistance to player 2 outweighs the benefit of preventing a selfish act. Under these circumstances, player 2 will submit, and selection once again favors performance of the selfish act provided that b₁ – c₁ – r b₂ > 0. If, by contrast, c₂ < b₂ – r b₁, then player 2 will resist, and selection consequently does not favor the selfish act. Because a more closely related recipient of the selfish act may prefer to submit where a more distantly related recipient would resist, it follows that selfishness may be directed toward a closer relative where it would not be directed toward a more distant one. To be precise, if we consider two levels of relatedness, r_high and r_low (r_low < r_high), then provided that

$$\frac{b_1-c_1}{b_2}>r_{\text{high}}>\frac{b_2-c_2}{b_1}>r_{\text{low}},$$

then the subgame-perfect equilibrium of the game features targeting of a selfish act toward a recipient related to the actor by r_high, but not toward a recipient related by r_low. To illustrate, suppose b₁ = b₂ = 1, c₁ = 0.25, and c₂ = 0.75; then the model predicts that a recipient of low relatedness (r_low < 0.25) would resist a selfish act and hence should not be targeted, whereas a recipient of higher relatedness (0.75 > r_high > 0.25) will submit and so should be targeted.

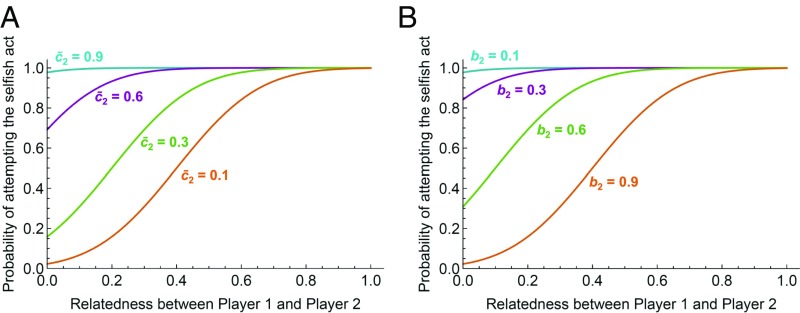
Unrelated recipients are more likely to resist a selfish act, favoring preferential targeting of more closely related victims, when c₂ (the cost of resistance) is small and b₂ (the benefit to be retained) is large. These effects are illustrated in Fig. 2. If c₂ is typically too large, or b₂ too small, even unrelated recipients are unlikely to resist, favoring indiscriminate selfishness; only for smaller values of c₂ or larger values of b₂ is negative kin discrimination predicted.

Fig. 2.

Impact of model parameters on patterns of kin discrimination. Here we focus on a region of parameter space in which player 1 should carry out the selfish act when unopposed, but in which player 2 may do best to resist (i.e., b₁ – c₁ – r b₂ > 0). We show the probability that, at equilibrium, the actor attempts a selfish act, as a function of relatedness, when c₂ is drawn from a normal distribution with specified mean and SD equal to 0.2. (A) Probability that a selfish act is attempted at equilibrium, assuming that b₁ = 1, c₁ = 0.1, b₂ = 0.5, and mean c̄₂ as specified for the plotted curves. (B) Probability that a selfish act is attempted at equilibrium, assuming that b₁ = 1, c₁ = 0.1, c̄₂ = 0.5, and b₂ is as shown in the plot.

SI Models

In the main text we analyze a simple, game-theoretical model of selfishness and resistance. Here, we present two population genetic analyses of the same situation, in which we explicitly model the evolutionary dynamics of alleles that influence both traits. These two models differ in the specific assumptions they make regarding the genetic basis of selfishness and resistance and the nature of mutation. In both cases, the two traits are under the control of distinct (unlinked) loci, but in the first, “adaptive dynamic” model, we assume that evolution proceeds through the successive substitution of mutations of small effect at one or the other locus that slightly alter the probability either of acting selfishly or of resisting such action. In the second model, by contrast, we assume that there are two alleles present in the population at each locus that determine whether or not individuals act selfishly or resist and focus on evolutionary changes in the frequencies of the possible genotypes. Both models confirm the findings of the game-theoretical analysis.

An Adaptive Dynamic Model.

We focus on a large (effectively infinite), sexual population with nonoverlapping generations. For simplicity, we assume haploid genetics. In each generation, adult breeding members of the population mate at random to produce many offspring. Members of this offspring generation then collectively engage in pairwise interactions with one another. Each offspring interacts with a single partner, and in any given pairwise interaction, one individual is randomly assigned the role of actor and the other the role of recipient. The actor may choose whether or not to attempt a selfish act; if it chooses to do so, the recipient may choose whether or not to resist. An individual’s genetically determined strategy specifies the probability of selfish action p and the probability of resistance q. We allow, however, for a small degree of error in implementation of actors’ choices, such that with probability ε (where 0 < ε << 0.5), an individual actor acts contrary to the behavior specified by its strategy. Individuals (both actors and recipients) receive payoffs from this interaction as specified in the main text: actors incur an additive cost of c₁ (relative to the baseline fitness value of 1) if they act selfishly, and recipients incur an additive cost of c₂ if they resist a selfish act (where 0 < c₁, c₂ ≤ 1); at the same time, actors obtain an additive benefit of b₁ if they perform a selfish act that is not resisted, whereas recipients obtain an additive benefit of b₂ unless they fail to resist a selfish act against them. After offspring have interacted with one another in this way, all compete for breeding opportunities in the next generation, with probabilities of success proportional to their payoffs, and the cycle then repeats.

To model the evolution of this population, we take an adaptive dynamic approach, in which the behavioral strategy adopted by members of the population is assumed to change through the successive substitution of mutations of small effect, each of which affects either the probability of selfish action or the probability of resistance.

Because our focus is on the impact of relatedness on the evolution of selfishness and resistance, we suppose that offspring may interact preferentially with kin, with whom they share a degree of genetic similarity by virtue of common descent. The probability that an individual and its partner share alleles at a given locus that are identical by descent is denoted r. If, for instance, interactions always involve full sibs, then r = 1/2 (compared with r = 0 if interaction occurs at random within the population as a whole). We do not explicitly model the processes that give rise to interactions among kin, as these might take different forms in different contexts (such as familial interaction, preferential assortment, or limited dispersal); instead, we simply specify the value of r.

Suppose, then, that the population currently adopts the strategy (p, q), and consider the fate of a mutant allele that specifies a probability of resistance $q_m\equiv q+{\delta }_q$ that differs slightly from q. Let

$$\stackrel{\sim }{p}=\left(1-\epsilon \right)p+\epsilon \left(1-p\right)$$

denote the probability of a randomly chosen individual in this population acting selfishly when the chance of error ε is taken into account and

$$\overline{q}=f_m{q}_m+\left(1-f_m\right)q$$

denote the probability of a randomly chosen individual resisting a selfish act, given the current frequency f_m of the mutant allele. The expected payoff from pairwise interaction to an individual in this population bearing a mutant allele is given by

$$w_m=1+\frac{1}{2}\left(\stackrel{\sim }{p}\left(1-\left(r{q}_m+\left(1-r\right)\overline{q}\right)\right)b_1-\stackrel{\sim }{p}{c}_1\right)+\frac{1}{2}\left(\left(1-\stackrel{\sim }{p}\left(1-q_m\right)\right)b_2-\stackrel{\sim }{p}{q}_m{c}_2\right),$$

whereas the expected payoff to an individual bearing a resident allele is given by

$$w_r=1+\frac{1}{2}\left(\stackrel{\sim }{p}\left(1-\left(rq+\left(1-r\right)\overline{q}\right)\right)b_1-\stackrel{\sim }{p}{c}_1\right)+\frac{1}{2}\left(\left(1-\stackrel{\sim }{p}\left(1-q\right)\right)b_2-\stackrel{\sim }{p}q{c}_2\right).$$

Following competition for breeding opportunities and random mating, the frequency of the mutant allele in the next generation is then given by

$$f_m^{\prime }=\frac{f_m{w}_m}{f_m{w}_m+\left(1-f_m\right)w_r},$$

implying that

$$\mathrm{\Delta }{f}_m\equiv f_m^{\prime }-f_m=f_m\left(1-f_m\right)\left(w_m-w_r\right),$$

i.e., that the mutant allele will increase (or decrease) in frequency if its bearers enjoy a greater (or smaller) mean payoff from pairwise interaction than do bearers of the resident allele.

Now,

$$w_m-w_r=\frac{1}{2}\stackrel{\sim }{p}{\delta }_q\left(-r{b}_1+b_2-c_2\right),$$

which, because $\stackrel{\sim }{p}$ is always positive, implies that if

$$c_2<b_2-r{b}_1,$$ [S1]

then bearers of any mutant allele that specifies an increased probability of resistance (i.e., for which ${\delta }_q$ > 0) will enjoy a greater expected payoff than bearers of the resident allele at all frequencies, and the allele will thus increase monotonically in frequency and spread to fixation, regardless of the value of p. By contrast, bearers of a mutant allele that specifies a decreased probability of resistance (i.e., for which ${\delta }_q$ < 0) will suffer a reduced payoff at all frequencies, and the allele will thus be eliminated, again regardless of the value of p. If condition [S1] is not met, then the reverse conclusions hold true.

We conclude that when condition [S1] is satisfied, any convergently stable evolutionary equilibrium must feature q = 1, whereas when condition [S1] is not satisfied, such an equilibrium must feature q = 0.

Now, consider the fate, if a population currently adopts the strategy (p, q), of a mutant allele that specifies a probability of selfish action $p_m\equiv p+{\delta }_p$ that differs slightly from p. Let

$${\stackrel{\sim }{p}}_m=\left(1-\epsilon \right)p_m+\epsilon \left(1-p_m\right)$$

denote the probability of a mutant individual in this population acting selfishly when the chance of error ε is taken into account,

$$\stackrel{\sim }{p}=\left(1-\epsilon \right)p+\epsilon \left(1-p\right)$$

denote the probability of a resident individual acting selfishly, and

$$\stackrel{\sim }{\overline{p}}=f_m{\stackrel{\sim }{p}}_m+\left(1-f_m\right)\stackrel{\sim }{p}$$

denote the probability of a randomly chosen individual acting selfishly, given the current frequency f_m of the mutant allele. Then the expected payoff to an individual in this population bearing a mutant allele is given by

$$w_m=1+\frac{1}{2}\left({\stackrel{\sim }{p}}_m\left(1-q\right)b_1-{\stackrel{\sim }{p}}_m{c}_1\right)+\frac{1}{2}\left(\left(1-\left(r{\stackrel{\sim }{p}}_m+\left(1-r\right)\stackrel{\sim }{\overline{p}}\right)\left(1-q\right)\right)b_2-\left(r{\stackrel{\sim }{p}}_m+\left(1-r\right)\stackrel{\sim }{\overline{p}}\right)q{c}_2\right),$$

whereas the expected payoff to an individual bearing a resident allele is given by

$$w_r=1+\frac{1}{2}\left(\stackrel{\sim }{p}\left(1-q\right)b_1-\stackrel{\sim }{p}{c}_1\right)+\frac{1}{2}\left(\left(1-\left(r\stackrel{\sim }{p}+\left(1-r\right)\stackrel{\sim }{\overline{p}}\right)\left(1-q\right)\right)b_2-\left(r\stackrel{\sim }{p}+\left(1-r\right)\stackrel{\sim }{\overline{p}}\right)q{c}_2\right).$$

It follows that

$$w_m-w_r=\frac{1}{2}\left(1-2\epsilon \right){\delta }_p\left(\left(1-q\right)b_1-c_1-r\left(1-q\right)b_2-rq{c}_2\right),$$ [S2]

which, when q = 1, reduces to

$$w_m-w_r=\frac{1}{2}\left(1-2\epsilon \right){\delta }_p\left(-c_1-r{c}_2\right).$$

Under these circumstances, therefore, bearers of a mutant allele that specifies an increased probability of selfishness (i.e., for which ${\delta }_p$ > 0) will suffer a reduced payoff compared with bearers of the resident allele at all frequencies, and the mutant allele will thus decrease monotonically in frequency and eventually be eliminated, whereas bearers of a mutant allele that specifies a decreased probability of selfishness (i.e., for which ${\delta }_p$ < 0) will enjoy a payoff advantage at all frequencies, so that the mutant allele in this case will spread to fixation. Consequently, at an equilibrium that features resistance (q = 1), actors will refrain from selfishness (p = 0).

When q = 0, by contrast, condition [S2] reduces to

$$w_m-w_r=\frac{1}{2}\left(1-2\epsilon \right){\delta }_p\left(b_1-c_1-r{b}_2\right).$$

Under these circumstances, therefore, if

$$b_1-c_1-r{b}_2>0,$$ [S3]

then bearers of any mutant allele that specifies an increased probability of selfishness (i.e., for which ${\delta }_p$ > 0) will enjoy a payoff advantage over bearers of the resident allele at all frequencies, and the mutant allele will thus spread to fixation, whereas bearers of a mutant allele that specifies a decreased probability of resistance (i.e., for which ${\delta }_p$ < 0) will suffer a payoff disadvantage at all frequencies, and in this case the mutant allele will thus be eliminated. If condition [S3] is not met, then the reverse conclusions hold true.

We conclude that at an equilibrium that does not feature resistance (q = 0), actors will act selfishly (p = 1) if condition [S3] is satisfied and refrain from doing so (p = 0) if condition [S3] is not satisfied.

Because r may be interpreted as the coefficient of relatedness between interacting offspring, these results are identical to those of the game-theoretical model presented in the main text and lead to the same conclusion that selfishness may be directed toward a closer relative where it would not be directed toward a more distant one. To be precise, if we consider two levels of relatedness, r_high and r_low (r_low < r_high), then provided that

$$\frac{b_1-c_1}{b_2}>r_{\text{high}}>\frac{b_2-c_2}{b_1}>r_{\text{low}},$$

selfishness persists at equilibrium when actors interact with a recipient related to them by r_high, but not when they interact with a recipient related to them by r_low.

A Classical Population Genetic Model.

We consider a large (effectively infinite), sexual population with nonoverlapping generations. For simplicity, we assume haploid genetics. In each generation, adult breeding members of the population mate at random to produce many offspring. Members of this offspring generation then collectively engage in pairwise interactions with one another. Each offspring interacts with a single partner, and in any given pairwise interaction, one individual is randomly assigned the role of actor and the other the role of recipient. The actor may choose whether or not to attempt a selfish act; if it chooses to do so, the recipient may choose whether or not to resist. Behavior in the actor role is determined by an individual’s genotype at the A locus; those bearing the A allele typically act selfishly, whereas those bearing the a allele typically do not. Similarly, behavior in the recipient role is determined by an individual’s genotype at the (unlinked) R locus; those bearing the R allele resist a selfish act, whereas those bearing the r allele do not. We allow for a small degree of error in implementation of actors’ choices, such that with probability ε (where 0 < ε << 0.5), an individual actor acts contrary to the behavior typical of its genotype. Individuals (both actors and recipients) receive payoffs from this interaction as specified in the main text: actors incur an additive cost of c₁ (relative to the baseline fitness value of 1) if they act selfishly, and recipients incur an additive cost of c₂ if they resist a selfish act (where 0 < c₁, c₂ ≤ 1); at the same time, actors obtain an additive benefit of b₁ (>0) if they perform a selfish act that is not resisted, whereas recipients obtain an additive benefit of b₂ (>0) unless they fail to resist a selfish act against them. After offspring have interacted with one another in this way, all compete for breeding opportunities in the next generation, with probabilities of success proportional to their payoffs, and the cycle then repeats.

Our focus is on the impact of relatedness on the evolution of selfishness and resistance. We therefore suppose that offspring may interact preferentially with kin, with whom they share a degree of genetic similarity by virtue of common descent. The probability that an individual and its partner share alleles at a given locus that are identical by descent is denoted r. If, for instance, interactions always involve full sibs, then r = 1/2 (compared with r = 0 if interaction occurs at random within the population as a whole). We do not explicitly model the processes that give rise to interactions among kin, as these might take different forms in different contexts (such as familial interaction, preferential assortment, or limited dispersal); instead, we simply specify the value of r.

Let f_AR, f_Ar, f_aR, and f_ar denote the frequencies of the four possible genotypes in the population immediately before pairwise interaction (where f_AR + f_Ar + f_aR + f_ar = 1). The probability that a randomly chosen actor in this population acts selfishly is then given by

$$A=\epsilon +\left(1-2\epsilon \right)\left(f_{AR}+f_{Ar}\right),$$

whereas the probability that a randomly chosen recipient resists a selfish act is given by

$$R=\left(f_{AR}+f_{aR}\right).$$

Expected payoffs obtained by individuals of the four genotypes are thus given by

$$w_{AR}=1+r\left[-\frac{1}{2}\left(1-\epsilon \right)c_1+\frac{1}{2}\left(b_2-\left(1-\epsilon \right)c_2\right)\right]+\left(1-r\right)\left[\frac{1}{2}\left(1-\epsilon \right)\left(\left(1-R\right)b_1-c_1\right)+\frac{1}{2}\left(b_2-A{c}_2\right)\right]$$

$$w_{Ar}=1+r\left[\frac{1}{2}\left(1-\epsilon \right)\left(b_1-c_1\right)+\frac{1}{2}\epsilon b_2\right]+\left(1-r\right)\left[\frac{1}{2}\left(1-\epsilon \right)\left(\left(1-R\right)b_1-c_1\right)+\frac{1}{2}\left(1-A\right)b_2\right]$$

$$w_{aR}=1+r\left[-\frac{1}{2}\epsilon c_1+\frac{1}{2}\left(b_2-\epsilon c_2\right)\right]+\left(1-r\right)\left[\frac{1}{2}\epsilon \left(\left(1-R\right)b_1-c_1\right)+\frac{1}{2}\left(b_2-A{c}_2\right)\right]$$

$$w_{ar}=1+r\left[\frac{1}{2}\epsilon \left(b_1-c_1\right)+\frac{1}{2}\left(1-\epsilon \right)b_2\right]+\left(1-r\right)\left[\frac{1}{2}\epsilon \left(\left(1-R\right)b_1-c_1\right)+\frac{1}{2}\left(1-A\right)b_2\right],$$

leading to frequencies of the four genotypes among breeders of

$$f_{AR}^{\prime }=\frac{f_{AR}{w}_{AR}}{\overline{w}},\hspace{1em}{f}_{Ar}^{\prime }=\frac{f_{Ar}{w}_{Ar}}{\overline{w}},\hspace{1em}{f}_{aR}^{\prime }=\frac{f_{aR}{w}_{aR}}{\overline{w}},\hspace{1em}{f}_{ar}^{\prime }=\frac{f_{ar}{w}_{ar}}{\overline{w}},$$

where

$$\overline{w}=f_{AR}{w}_{AR}+f_{Ar}{w}_{Ar}+f_{aR}{w}_{aR}+f_{ar}{w}_{ar}$$

denotes the mean payoff. Following random mating, the frequencies of the four genotypes in the next generation (immediately before pairwise interaction) are then given by

$$f_{AR}^{″}=f_{AR}^{\prime 2}+f_{AR}^{\prime }{f}_{Ar}^{\prime }+f_{AR}^{\prime }{f}_{aR}^{\prime }+\frac{1}{2}{f}_{AR}^{\prime }{f}_{ar}^{\prime }+\frac{1}{2}{f}_{Ar}^{\prime }{f}_{aR}^{\prime }$$

$$f_{Ar}^{″}=f_{Ar}^{\prime 2}+f_{AR}^{\prime }{f}_{Ar}^{\prime }+f_{Ar}^{\prime }{f}_{ar}^{\prime }+\frac{1}{2}{f}_{AR}^{\prime }{f}_{ar}^{\prime }+\frac{1}{2}{f}_{Ar}^{\prime }{f}_{aR}^{\prime }$$

$$f_{aR}^{″}=f_{aR}^{\prime 2}+f_{aR}^{\prime }{f}_{ar}^{\prime }+f_{AR}^{\prime }{f}_{aR}^{\prime }+\frac{1}{2}{f}_{AR}^{\prime }{f}_{ar}^{\prime }+\frac{1}{2}{f}_{Ar}^{\prime }{f}_{aR}^{\prime }$$

$$f_{ar}^{″}=f_{AR}^{\prime 2}+f_{aR}^{\prime }{f}_{ar}^{\prime }+f_{Ar}^{\prime }{f}_{ar}^{\prime }+\frac{1}{2}{f}_{AR}^{\prime }{f}_{ar}^{\prime }+\frac{1}{2}{f}_{Ar}^{\prime }{f}_{aR}^{\prime }.$$

Iteration evaluation of the above equations allows us to track changes in genotype frequencies from one generation to the next.

Illustrative trajectories are shown in Fig. S1, which highlights parameter values for which the system converges (from multiple initial starting conditions) to an equilibrium featuring selfishness and nonresistance for a higher level of relatedness (r = 0.5), but to resistance and nonselfishness for a lower level of relatedness (r = 0), demonstrating that (as we argue in the main text) interactions between closer kin may feature more selfish behavior than between more distant kin or between nonrelatives.

Beyond the above example, we can further demonstrate a close correspondence between the results of the genetic model and of our game-theoretical analysis from the main text. The game-theoretical model yields three types of equilibria: (i) When b₂ − c₂ – rb₁ > 0, recipients resist and actors refrain from selfishness; (ii) when b₂ − c₂ – rb₁ < 0 and b₁ – c₁ – rb₂ > 0, recipients do not resist and actors behave selfishly; and (iii) when b₂ − c₂ – rb₁ < 0 and b₁ – c₁ – rb₂ < 0, recipients do not resist but actors nevertheless refrain from selfishness. The fourth possible pure-strategy equilibrium at which recipients resist and actors behave selfishly is never stable.

In the genetic model, because f_AR + f_Ar + f_aR + f_ar = 1, it is necessary to specify only three frequencies to determine the state of the system. Below, therefore, we set f_ar = 1 − f_AR – f_Ar – f_aR and evaluate the stability of the equilibria suggested by the game-theoretical analysis, by calculating the eigenvalues of the Jacobian

$$J=\left(\begin{array}{ccc}\frac{\partial f_{AR}^{″}}{\partial f_{AR}}& \frac{\partial f_{AR}^{″}}{\partial f_{Ar}}& \frac{\partial f_{AR}^{″}}{\partial f_{aR}}\\ \frac{\partial f_{Ar}^{″}}{\partial f_{AR}}& \frac{\partial f_{Ar}^{″}}{\partial f_{Ar}}& \frac{\partial f_{Ar}^{″}}{\partial f_{aR}}\\ \frac{\partial f_{aR}^{″}}{\partial f_{AR}}& \frac{\partial f_{aR}^{″}}{\partial f_{Ar}}& \frac{\partial f_{aR}^{″}}{\partial f_{aR}}\end{array}\right)$$

at each candidate equilibrium point.

• i)At the candidate equilibrium f_aR = 1, f_AR = f_Ar = f_ar = 0 (at which recipients resist and actors refrain from selfishness), these eigenvalues are

$$\begin{array}{l}\frac{2+b_2-\epsilon \left(c_1+b_2-r{b}_1\right)}{2+b_2-\epsilon \left(c_1+c_2\right)},\\ \frac{2+b_2-c_1-r{c}_2+\epsilon \left(c_1-\left(1-2r\right)c_2\right)}{2+b_2-\epsilon \left(c_1+c_2\right)},\\ \frac{2+r{b}_1+\left(1-r\right)b_2-c_1+\epsilon \left(c_1-r{b}_1-\left(1-2r\right)b_2\right)}{4+2b_2-2\epsilon \left(c_1+c_2\right)}.\end{array}$$

• The equilibrium is stable if all eigenvalues are of magnitude less than 1; considering the first eigenvalue, this yields the necessary and sufficient condition

$$b_2-c_2-r{b}_1>0,$$

identical to the condition for stability in the game-theoretical model. In the limit as $\epsilon$→0 the above condition also proves sufficient to ensure that the other two eigenvalues are of magnitude less than 1.

• ii)At the candidate equilibrium f_Ar = 1, f_AR = f_aR = f_ar = 0 (at which recipients do not resist and actors behave selfishly), these eigenvalues are

$$\frac{2+b_1-c_1+b_2-c_2-r{b}_1}{2+b_1-c_1},\hspace{1em}\frac{2+r{b}_2}{2+b_1-c_1},\hspace{1em}\frac{2+b_2-c_2+r{c}_2}{4+2b_1-2c_1}.$$

• The first eigenvalue is of magnitude less than 1 if and only if

  $$b_2-c_2-r{b}_1<0,$$

  the second if and only if

$$b_1-c_1-r{b}_2>0,$$

• conditions that are identical to those for stability in the game-theoretical model. Moreover, these two conditions suffice to ensure that the third eigenvalue is also of magnitude less than 1.

• iii)At the candidate equilibrium f_ar = 1, f_AR = f_Ar = f_aR = 0 (at which recipients do not resist but actors nevertheless refrain from selfishness), these eigenvalues are

$$\begin{array}{l}\frac{2+b_2+\epsilon \left(b_1-c_1-r{b}_1-c_2\right)}{2+b_2+\epsilon \left(b_1-c_1-b_2\right)},\\ \frac{2+b_1-c_1+b_2-r{b}_2-\epsilon \left(b_1-c_1+b_2-2r{b}_2\right)}{2+b_2+\epsilon \left(b_1-c_1-b_2\right)},\\ \frac{2+b_1-c_1+b_2-r{b}_1-r{c}_2-\epsilon \left(b_1-c_1+c_2-r{b}_1-2r{c}_2\right)}{2\left(2+b_2+\epsilon \left(b_1-c_1-b_2\right)\right)}.\end{array}$$

• The first eigenvalue is of magnitude less than 1 if and only if

$$b_2-c_2-r{b}_1<0,$$

• whereas in the limit as $\epsilon$ →0 the second is of magnitude less than 1 if and only if

$$b_1-c_1-r{b}_2<0,$$

• conditions that are identical to those for stability in the game-theoretical model. Moreover, in the same limit, these two conditions suffice to ensure that the third eigenvalue is also of magnitude less than 1.

• iv)At the candidate equilibrium f_AR = 1, f_Ar = f_aR = f_ar = 0 (at which recipients resist and actors behave selfishly), these eigenvalues are

$$\frac{2+b_2-c_2+r{c}_2}{2+b_2-c_2-c_1},\hspace{1em}\frac{2+r{b}_2}{4+2b_2-2c_1-2c_2},\hspace{1em}\frac{2-c_1+r{b}_1}{2-c_1+b_2-c_2}.$$

• Because the first of the expressions above is of magnitude greater than 1 for all permissible parameter values, this equilibrium is always unstable, as in the game-theoretical model.

Negative Kin Discrimination in Banded Mongooses

We examine kin discrimination in the context of a conspicuous form of intragroup aggression in cooperatively breeding banded mongooses, Mungos mungo: the violent eviction of males and females from the group. Banded mongooses live in highly cooperative groups with limited dispersal and varying levels of relatedness between group members (7). In our study population in Uganda, groups consist of around 20 adults, plus offspring, and breed on average four times per year (8). Multiple females give birth synchronously to a communal litter that is cared for by members of both sexes (typically not the parents) (7). Each group contains a cohort of multiple dominant females (median = 4) that are older than the other females, breed more regularly and more successfully, and aggressively evict younger females (7, 9, 10). Older males monopolize mating with estrus females by mate guarding them and aggressively driving away younger, subordinate males (10, 11). Previous work shows that both sexes are capable of kin discrimination in the context of mating, supporting the assumption of our model that such discrimination is possible in this system (12). Evictions are relatively common, involve intense, targeted aggression, and result in the forcible mass exclusion of groups (median = 6 individuals) of females (female-only evictions) and, in around half of cases, groups (median = 9 males) of males alongside them (mixed-sex evictions) (13). These mass evictions are triggered by high levels of intrasexual reproductive competition: females are evicted when there are many breeding females in the group, and males are evicted alongside females when there are many breeding males (13). Evictions are very violent, and evictees are often left with serious injuries as a result of the aggression they receive (Movie S1).

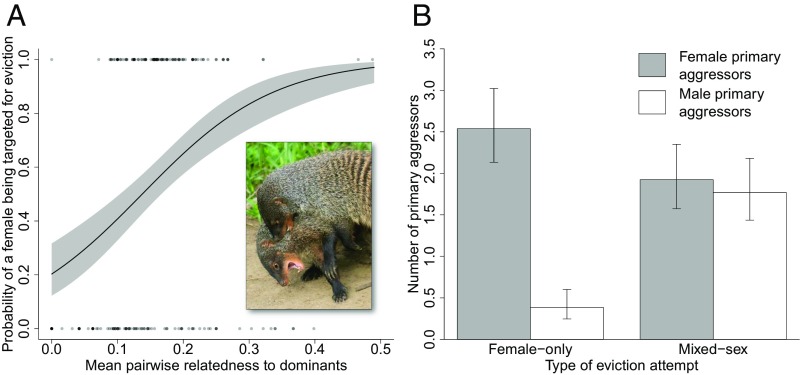
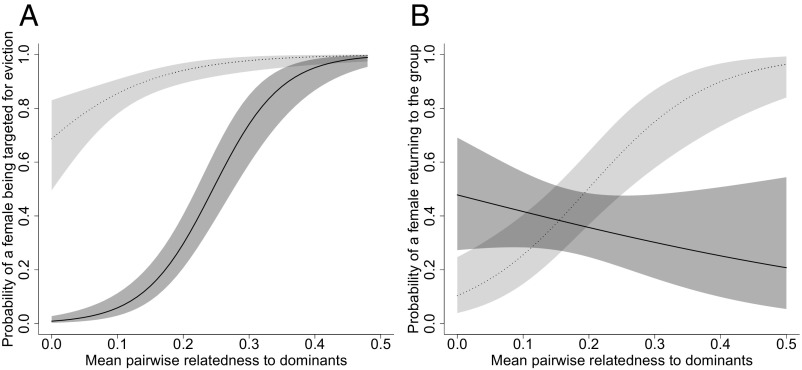
Among adult female banded mongooses, those more closely related to dominant individuals of both sexes (that is, males and females older than 3 y) in the group were more likely to be targeted for eviction [generalized linear mixed model (GLMM), β ± SE = 9.95 ± 3.36, χ²₁ = 9.51, P = 0.002; Fig. 3A and Table S1]. Younger females were also more likely to be subject to an eviction attempt (GLMM, β ± SE = −0.003 ± 0.0005, χ²₁ = 39.98, P < 0.0001; Table S1), but there was no effect of a female’s pregnancy status or nonpregnant weight on her probability of being targeted for eviction (pregnancy status, GLMM, β ± SE = −0.61 ± 0.49, χ²₁ = 1.63, P = 0.20; weight, GLMM, β ± SE = 0.002 ± 0.001, χ²₁ = 2.59, P = 0.11; Table S1). For a subset of eviction attempts we had data on the identity of “primary aggressors” (individuals that were recorded as being notably more aggressive than other group members toward potential evictees). Females that were more closely related to primary aggressors were more likely to be targeted for eviction (GLMM, β ± SE = 5.47 ± 2.87, χ²₁ = 3.85, P = 0.0498; Table S2).

Fig. 3.

Negative kin discrimination and sex-specific aggression in banded mongooses. (A) The effect of mean pairwise relatedness to dominants (males and females older than 3 y) on the probability of a female being targeted for eviction (n = 207 females in 29 eviction attempts in five groups). The line shows the prediction from the GLMM (±SE). (A, Inset) Eviction attempts are highly aggressive and involve biting, chasing, and wrestling (photo courtesy of Dave Seager) (Movie S1). (B) The number of female (gray bars) and male (white bars) primary aggressors in female-only and mixed-sex eviction attempts (n = 26 eviction attempts in six groups). The bars show the predictions from the GLMM (±SE).

Table S1.

Investigating the effect of mean pairwise relatedness to dominants (males and females older than 3 y) on eviction

Model	Response	Fixed effect	β	SE	χ2	P
Female	Probability of a female being targeted for eviction	Intercept	−1.53	1.81
		Relatedness to dominants, males and females >3 y	9.95	3.36	9.51	0.002
		Age, d	−0.003	0.0005	39.98	<0.0001
		Weight, g	0.002	0.001	2.59	0.11
		Pregnancy status	−0.61	0.49	1.63	0.20
		Rainfall, mm	−0.08	0.18	0.21	0.65
		Group size	0.02	0.03	0.23	0.63
Male	Probability of a male being targeted for eviction in a mixed-sex eviction attempt	Intercept	−5.01	2.88
		Relatedness to dominants, males and females >3 y	0.84	3.08	0.07	0.79
		Age, d	−0.0004	0.0003	2.12	0.15
		Weight, g	0.002	0.002	1.65	0.20
		Male breeding status	−0.43	0.49	0.80	0.37
		Rainfall, mm	0.16	0.20	0.57	0.45
		Group size	0.03	0.04	0.42	0.52

Shown are models predicting the probability of being targeted for eviction for females (GLMM, n = 207 females in 29 eviction attempts in five groups) and males (GLMM, n = 177 males in 15 eviction attempts in five groups). Models were fitted using a binomial error structure and logit-link function and with individual ID, eviction attempt, and group as random intercepts. Significant terms are in boldface type.

Table S2.

Investigating the effect of mean pairwise relatedness to known primary aggressors on eviction

Model	Response	Fixed effect	β	SE	χ2	P
Female	Probability of a female being targeted for eviction	Intercept	2.99	2.87
		Relatedness to primary aggressors	5.47	2.87	3.85	0.0498
		Age, d	−0.002	0.0006	12.85	<0.001
		Weight, g	−0.0005	0.002	0.06	0.80
		Pregnancy status	−1.07	0.68	2.72	0.10
		Rainfall, mm	−0.29	0.26	1.28	0.26
		Group size	0.03	0.04	0.33	0.57
Male	Probability of a male being targeted for eviction in a mixed-sex eviction attempt	Intercept	−5.28	1.32
		Relatedness to primary aggressors	2.30	3.24	0.54	0.46
		Age, d	−0.0001	0.0004	0.06	0.80
		Weight, grams	0.002	0.002	0.64	0.42
		Male breeding status	−0.58	0.64	0.86	0.35
		Rainfall, mm	0.21	0.24	0.74	0.39
		Group size	0.06	0.05	1.52	0.22

Shown are models predicting the probability of being targeted for eviction for females (GLMM, n = 131 females in 19 eviction attempts in 4 groups) and males (GLMM, n = 130 males in 11 eviction attempts in 4 groups). Models were fitted using a binomial error structure and logit-link function and with individual ID, eviction attempt, and group as random intercepts. Significant terms are in boldface type.

We did not find evidence that this pattern of negative kin discrimination was an attempt to reduce inbreeding between targeted females and dominant males. We found that it was relatedness of females to female dominants (not male dominants) that predicted whether they were targeted for eviction. Females were more likely to be targeted if they were more closely related to female dominants (females older than 3 y: GLMM, β ± SE = 5.10 ± 2.65, χ²₁ = 4.07, P = 0.044; Table S3), but not if they were more closely related to male dominants (males older than 3 y: GLMM, β ± SE = 3.69 ± 2.55, χ²₁ = 2.09, P = 0.15; Table S3). Behavioral data indicate that females are almost entirely responsible for the attempts at eviction of other females: males rarely attacked females in female-only eviction attempts (GLMM, β ± SE = 1.80 ± 0.56, χ²₁ = 12.48, P < 0.001; Fig. 3B and Table S4). Previous work indicates that eviction attempts are triggered when the level of reproductive competition in the group is high, not when the potential for inbreeding is high (13), and that both sexes use kin discrimination during mating to avoid inbreeding (12).

Table S3.

Investigating the effect of mean pairwise relatedness to same-sex and opposite-sex dominants (individuals older than 3 y) on eviction

Model	Response	Fixed effect	β	SE	χ2	P
Female	Probability of a female being targeted for eviction	Intercept	0.39	1.72
		Relatedness to male dominants, males >3 y	3.69	2.55	2.09	0.15
		Age, d	−0.002	0.005	34.49	<0.0001
		Weight, g	0.002	0.001	0.66	0.20
		Pregnancy status	−0.67	0.50	1.91	0.17
		Rainfall, mm	−0.03	0.18	0.021	0.88
		Group size	0.002	0.04	0.001	0.98
Female	Probability of a female being targeted for eviction	Intercept	−0.01	1.78
		Relatedness to female dominants, females >3 y	5.10	2.65	4.07	0.044
		Age, d	−0.002	0.0005	32.58	<0.0001
		Weight, g	0.002	0.001	1.80	0.18
		Pregnancy status	−0.59	0.51	1.45	0.23
		Rainfall, mm	−0.05	0.18	0.06	0.81
		Group size	0.0004	0.04	−0.01	1.00
Male	Probability of a male being targeted for eviction in a mixed-sex eviction attempt	Intercept	−4.90	2.93
		Relatedness to male dominants, males >3 y	−0.82	2.87	0.08	0.77
		Age, d	−0.0004	0.0003	2.41	0.12
		Weight, g	0.002	0.002	1.70	0.19
		Male breeding status	−0.48	0.49	0.97	0.33
		Rainfall, mm	0.18	0.20	0.71	0.40
		Group size	0.03	0.04	0.48	0.49
Male	Probability of a male being targeted for eviction in a mixed-sex eviction attempt	Intercept	−5.34	2.84
		Relatedness to female dominants, females >3 y	2.88	2.50	1.41	0.24
		Age, d	−0.0003	0.0003	1.26	0.26
		Weight, g	0.002	0.002	1.78	0.18
		Male breeding status	−0.47	0.50	0.89	0.35
		Rainfall, mm	0.11	0.22	0.25	0.62
		Group size	0.02	0.04	0.34	0.56

Shown are models predicting the probability of being targeted for eviction for females (GLMM, n = 198 females in 27 eviction attempts in five groups) and males (GLMM, n = 177 males in 15 eviction attempts in five groups). Models were fitted using a binomial error structure and logit-link function and with individual ID, eviction attempt, and group as random intercepts. Significant terms are in boldface type.

Table S4.

Sex-specific aggression during eviction attempts

Fixed effect	β	SE	χ2	P
Intercept	0.93	0.17
Sex of primary aggressor*	−1.89	0.48
Eviction type†	−0.28	0.27
Sex of primary aggressor* × eviction type†	1.80	0.56	12.48	<0.001

Shown is a model predicting the number of male and female primary aggressors in female-only and mixed-sex eviction attempts (GLMM, n = 26 eviction attempts in six groups). The model was fitted using a Poisson error structure and a log-link function and with eviction attempt and group as random intercepts. Significant terms are in boldface type.

^*Reference level: males.

^†Reference level: mixed-sex eviction attempt.

We also did not find evidence for the alternative hypothesis that closer relatives are targeted for eviction because they inflict higher costs on the reproductive success of dominants. Dominant females did not suffer greater reproductive costs when cobreeding with more closely related females. There was no difference in the number of emergent pups to which dominant females gave birth when cobreeding with more closely related vs. less closely related females (GLMM, β ± SE = −0.06 ± 0.12, χ²₁ = 0.23, P = 0.63; Table S5); nor was there a difference in the proportion of the emergent litter that was assigned maternity to dominant individuals (GLMM, β ± SE = −0.08 ± 0.14, χ²₁ = 0.27, P = 0.60; Table S5).

Table S5.

Investigating whether closer relatives inflict higher reproductive costs on dominants

Response	Fixed effect	β	SE	χ2	P
No. of emergent pups to which a dominant female (aged over 3 y) is assigned maternity	Intercept	−1.57	0.37
	Relatedness to female cobreeder	−0.06	0.12	0.23	0.63
	Female cobreeder age, d	0.000002	0.00003	−0.004	1.00
	No. of breeding females	0.04	0.06	0.55	0.46
	Dominant female age, d	0.0001	0.00009	1.63	0.20
	Rainfall, mm	−0.08	0.06	1.66	0.20
	Relatedness to female cobreeder × female cobreeder age	0.00002	0.0002	−0.07	1.00
Proportion of emergent litter to which a dominant female (aged over 3 y) is assigned maternity	Intercept	−0.3	0.20
	Relatedness to female cobreeder	−0.08	0.14	0.27	0.60
	Female cobreeder age, d	−0.00003	0.00004	0.53	0.47
	No. of breeding females	−0.20	0.03	58.58	<0.0001
	Dominant female age, d	0.0002	0.00007	11.93	<0.001
	Rainfall, mm	−0.06	0.03	4.40	0.036
	Relatedness to female cobreeder × female cobreeder age	−0.00005	0.0002	0.08	0.78

Shown are models predicting the number of emergent pups to which each dominant breeding female is assigned maternity (GLMM, n = 2,719 pairs of dominant females and female cobreeders, involving 131 dominant females giving birth to 337 litters in 17 groups) and the proportion of an emergent litter to which each dominant breeding female is assigned maternity (GLMM, n = 2,719 pairs of dominant females and female cobreeders, involving 131 dominant females giving birth to 337 litters in 17 groups). Models were fitted using a Poisson error structure and log-link function and a binomial error structure and logit-link function, respectively. Dominant female, cobreeder female, litter, and group ID were included as random intercepts. Significant terms are in boldface type.

Among males, by contrast with females, there was no effect of an individual’s mean pairwise relatedness to dominant group members (males and females older than 3 y) on the probability of being subject to an eviction attempt (mixed-sex eviction attempts: GLMM, β ± SE = 0.84 ± 3.08, χ²₁ = 0.07, P = 0.79; Table S1). We found no evidence of any discrimination as to which males were targeted for eviction (Table S1). There was also no discrimination of any kind when we restricted our analysis to cases where the identity of primary aggressors was known (Table S2) or when we tested the effect of mean pairwise relatedness to same-sex and opposite-sex dominants (Table S3). Unlike the case for female-only eviction attempts, both males and females were primary aggressors in eviction attempts directed at both sexes (GLMM, β ± SE = 1.80 ± 0.56, χ²₁ = 12.48, P < 0.001; Fig. 3B and Table S4).

Testing Model Predictions

Two specific predictions of the model are (i) that selfish acts will be directed preferentially toward closer relatives only when recipients can resist and (ii) that resistance to selfish acts offered by recipients should decrease as their relatedness to the actor increases. After we developed the model, we tested these predictions. To test the first prediction, we examined how the effect of relatedness varied with the age and weight of potential evictees. Our reasoning was that younger or lighter females should be less able to resist eviction attempts and that the pattern of negative kin discrimination should therefore be more pronounced when eviction is targeted at older or heavier individuals. We found that older females were indeed more likely to be targeted for eviction when more closely related to dominants, but that no such effect of relatedness was apparent for younger females (interaction between relatedness and age: GLMM, β ± SE = 0.008 ± 0.004, χ²₁ = 5.98, P = 0.014; Fig. 4A and Table S6). The strong overall positive relationship between the probability of being targeted for eviction and relatedness was thus driven almost entirely by the pattern in older females (SI Methods, Fig. S2, and Fig. 4A). A similar interaction was also found between relatedness and weight (GLMM, β ± SE = 0.03 ± 0.02, χ²₁ = 5.63, P = 0.018; Table S6). Consistent with prediction i, therefore, negative kin discrimination was restricted to cases in which the targets of eviction were older or heavier and potentially more capable of offering resistance. As predicted by our model, we found no discrimination on the basis of relatedness for cases where the targets of eviction were younger or lighter and therefore likely to suffer high costs of resistance (a high value of ${\overline{c}}_2$; Fig. 2A).

Fig. 4.

Patterns of kin discrimination toward recipients capable of offering varying levels of resistance. (A) In eviction attempts, dominants (males and females older than 3 y) exhibit negative kin discrimination only toward older females (n = 207 females in 29 eviction attempts in five groups). The lines show the predictions from the GLMM (±SE) for younger females (dotted line and area with light shading, 25th percentile of age = 522 d) and older females (solid line and area with dark shading, 75th percentile of age = 1,636 d). (B) Following an attempt at eviction, older females who were more related to dominants (males and females older than 3 y) were less successful in regaining entry to the group (n = 76 females in 14 eviction attempts in four groups); this pattern was reversed in younger females. The lines show the predictions from the GLMM (±SE) for younger females (dotted line and area with light shading, 25th percentile of age = 446 d) and older females (solid line and area with dark shading, 75th percentile of age = 922 d).

Table S6.

Investigating how the effect of relatedness varies with age and weight of potential evictees

Fixed effect	β	SE	χ2	P
Intercept	5.88	3.31
Relatedness to dominants, males and females >3 y	−39.36	19.14
Age, d	−0.005	0.001
Weight, g	−0.001	0.002
Pregnancy status	−0.60	0.52	1.41	0.24
Rainfall, mm	−0.10	0.19	0.20	0.65
Group size	−0.0003	0.04	−0.08	1.00
Relatedness to dominants, males and females >3 y, × age, d	0.008	0.004	5.98	0.014
Relatedness to dominants, males and females >3 y, × weight, g	0.03	0.02	5.63	0.018

Shown is a model predicting the probability of being targeted for eviction for females (GLMM, n = 207 females in 29 eviction attempts in five groups). The model was fitted using a binomial error structure and logit-link function and with female ID, eviction attempt, and group as random intercepts. Significant terms are in boldface type.

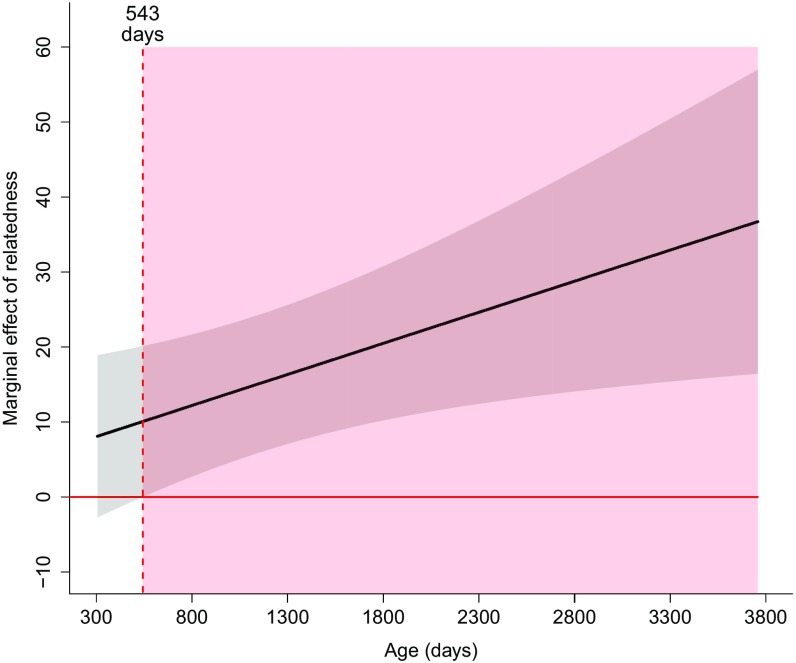
Fig. S2.

Johnson–Neyman plot of the marginal effect of relatedness on the probability of a female being targeted for eviction for varying ages. The gray shaded region shows the 95% confidence interval of the marginal effect of relatedness. The horizontal solid red line shows where the marginal effect of relatedness is zero. The vertical dashed red line shows the age at which the marginal effect of relatedness is significantly different from zero (at 543 d), and the red shaded region shows the region of significance for the marginal effect of relatedness.

We found no evidence for the alternative hypothesis that the pattern of negative kin discrimination among older females arises because older, more closely related females inflict higher reproductive costs on dominants (number of emergent pups assigned to dominant female, GLMM, interaction between female cobreeder age and relatedness to dominant female, β ± SE = 0.00002 ± 0.0002, χ²₁ = −0.07, P = 1.00; proportion of emergent litter assigned to dominant female, GLMM, interaction between female cobreeder age and relatedness to dominant female, β ± SE = −0.00005 ± 0.0002, χ²₁ = 0.08, P = 0.78; Table S5).

To test further whether negative kin discrimination depends on the capacity of recipients to resist, we examined kin discrimination in cases of infanticide of newborn pups. Between 1 and 12 females reproduce in each breeding attempt (14) and birth is highly synchronized, with pregnant females giving birth on exactly the same morning in 63% of cases (15). Experimental and observational evidence suggests that asynchronous litters are often killed by dominant females (14, 15) and that in asynchronous litters the death of a litter in the first week after birth can be used as a proxy for infanticide (15, 16). In contrast to the pattern of negative kin discrimination in the eviction of adult females, there was no evidence of kin discrimination in cases of presumed infanticide (GLMM, β ± SE = −0.64 ± 2.00, χ²₁ = 0.10, P = 0.75; Table S7). This is again consistent with our model, which predicts zero or positive kin discrimination where resistance is impossible or prohibitively costly (Figs. 1 and 2A).

Table S7.

Investigating whether negative kin discrimination depends on the recipient’s capacity to resist

Fixed effect	β	SE	χ2	P
Intercept	0.39	1.29
Mother’s relatedness to female dominants, females >3 y	−0.64	2.00	0.10	0.75
Mother’s age, d	−0.0002	0.0005	0.26	0.61
Rainfall, mm	0.29	0.23	2.01	0.16
Group size	−0.04	0.04	0.95	0.33

Shown is a model predicting the probability of a female’s litter being killed in an infanticidal attack by dominant females in the first week after birth (GLMM, n = 57 females giving birth to 50 communal litters in 11 groups). The model was fitted using a binomial error structure and logit-link function and with female ID, litter, and group as random intercepts.

To test the second prediction, that resistance to the selfish act should decrease as the recipient’s relatedness to the actor increases, we examined the effects of relatedness to dominants (males and females older than 3 y) and age on the probability of females targeted for eviction overcoming efforts to permanently exclude them from the group. After being targeted for eviction, some individuals leave the group, splitting into single-sex cohorts and dispersing separately in cases where males and females are evicted together. Other targeted individuals, however, actively resist eviction: they persist in following the rest of the group, despite being aggressively driven away, until efforts to expel them eventually cease (9). Some attempts at eviction may thus be said to “fail,” largely due to sheer persistence on the part of the potential evictees. We predicted, therefore, that the probability of resisting eviction and regaining entry to the group should decline with increasing relatedness to dominant individuals, particularly among older females who are potentially more capable of resisting eviction. There was a significant interaction between the effect of relatedness and the age of targeted females on the probability of regaining entry (interaction between relatedness and age: GLMM, β ± SE = −0.03 ± 0.01, χ²₁ = 5.96, P = 0.015; Fig. 4B and Table S8). Among older females, individuals that were more closely related to dominants were less likely to regain entry to the group, although this slope was not significantly different from zero (SI Methods, Fig. S3, and Fig. 4B). By contrast, among younger females, more closely related targets were significantly more likely to regain entry (SI Methods, Fig. S3, and Fig. 4B).

Table S8.

Investigating whether resistance offered by the recipient decreases as relatedness increases

Fixed effect	β	SE	χ2	P
Intercept	−4.09	1.95
Relatedness to dominants, males and females >3 y	23.36	9.76
Age, d	0.004	0.002
Relatedness to dominants, males and females >3 y, × age, d	−0.03	0.01	5.96	0.015

Shown is a model predicting the probability of targeted females overcoming efforts to permanently evict them (GLMM, n = 76 females in 14 eviction attempts in four groups). The model was fitted using a binomial error structure and logit-link function and with female ID, eviction attempt, and group as random intercepts. Significant terms are in boldface type.

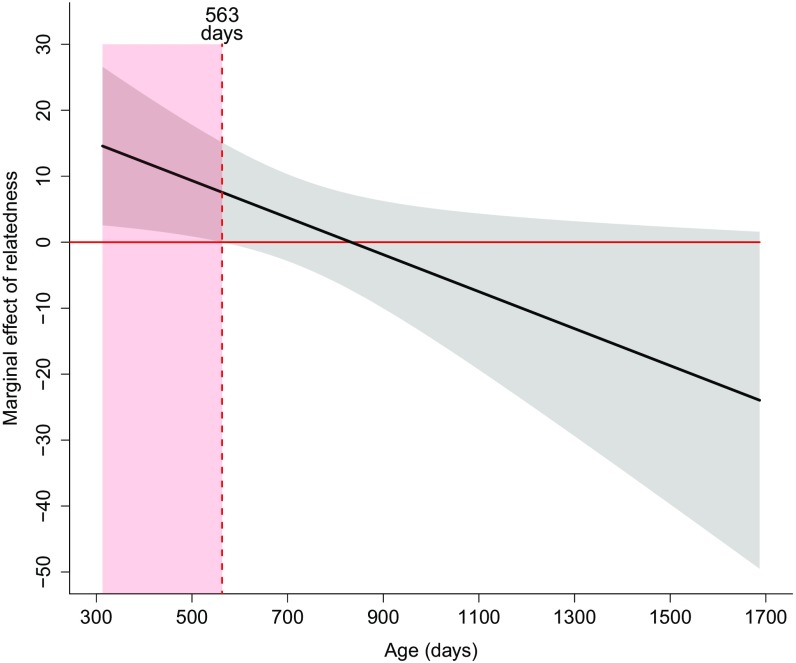
Fig. S3.

Johnson–Neyman plot of the marginal effect of relatedness on the probability of a targeted female returning to the group following an eviction attempt for varying ages. The gray shaded region shows the 95% confidence interval of the marginal effect of relatedness. The horizontal solid red line shows where the marginal effect of relatedness is zero. The vertical dashed red line shows the age at which the marginal effect of relatedness is not significantly different from zero (at 563 d), and the red shaded region shows the region of significance for the marginal effect of relatedness.

SI Methods

Genetic Analyses and Calculating Relatedness.

DNA was extracted from tail tips and genotyped at up to 43 microsatellite loci isolated from a variety of carnivore species, including the banded mongoose. Genotyping was conducted following ref. 10 or (post-2010) using multiplex PCRs (Qiagen Multiplex PCR Kit) with fluorescent-labeled forward primers and was visualized through fragment size analysis on an ABI 3730 DNA analyzer. For full details of genotyping methods, see ref. 12. We assigned parentage using MasterBayes 2.51 (44), implemented in R 3.1.1 (details in ref. 12). Estimates of pairwise relatedness were calculated from a nine-generation deep pedigree constructed using a combination of parentage and sibship assignments from MasterBayes 2.51 (44) and COLONY 2.0.5.7 (45). Full details of pedigree construction are given in ref. 12.

Analysis of Negative Kin Discrimination to Avoid Inbreeding.

To investigate whether the attempted eviction of relatives was in fact the result of inbreeding avoidance, we repeated the first analysis of negative kin discrimination outlined in Methods, i) Negative Kin Discrimination in Banded Mongooses, but instead of including the mean pairwise relatedness to both male and female dominants in the group, we used the mean pairwise to same-sex dominants aged over 3 y and the mean pairwise relatedness to opposite-sex dominants aged over 3 y as the measure of relatedness in separate models. All other fixed and random effects used in the original male and female analyses remained the same. We fitted the female models to data on 198 females in 27 eviction attempts in five groups and the male models to data on 177 males in 15 eviction attempts in five groups.

Analysis of Negative Kin Discrimination by Primary Aggressors.

To investigate the effect of relatedness to known aggressors on the probability of a female (or male) being targeted for eviction, we repeated the first analysis of negative kin discrimination outlined in Methods, i) Negative Kin Discrimination in Banded Mongooses, but restricted our analysis to eviction attempts where we had data on the identity of primary aggressors. In each of the female and male models we replaced mean pairwise relatedness to dominants in the group with mean pairwise relatedness to primary aggressors. All other fixed and random effects used in the original male and female analyses remained the same. We fitted the female model to data on 131 females in 19 eviction attempts in four groups and the male model to data on 177 males in 11 eviction attempts in four groups.

Analysis to Investigate Whether Closer Relatives Inflict Higher Reproductive Costs on Dominants.

We examined whether dominant females suffered higher reproductive costs when cobreeding with more closely related females. We measured a dominant female’s reproductive success in two ways: (i) as the number of emergent pups in a litter to which a dominant female was assigned maternity and (ii) as the proportion of an emergent litter to which a dominant female was assigned maternity. For the first analysis, we fitted the number of emergent pups to which each dominant breeding female (females over 3 y of age) was assigned maternity as the Poisson response variable with a log-link function in a GLMM. We included each dominant female’s pairwise relatedness to cobreeding females (other females that contributed to the communal litter), the age (days) of cobreeding females, and the interaction between these two variables as fixed effects. We also included the dominant female’s age (days), the number of females that contributed to the litter, and mean rainfall (millimeters) in the 30 d before birth. We controlled for repeated measures by including dominant female, cobreeder female, litter, and group ID as random intercepts and fitted the model to data on 2,719 pairs of dominant females and female cobreeders, involving 131 dominant females giving birth to 337 litters in 17 groups. This model was checked for overdispersion of the response variable (39). For the second analysis, we fitted the proportion of an emergent litter to which each dominant breeding female (females over 3 y of age) was assigned maternity as the binomial response variable with a logit-link function in a GLMM. We included the same fixed and random effects as in the first analysis and fitted the model to data on 2,719 pairs of dominant females and female cobreeders, involving 131 dominant females giving birth to 337 litters in 17 groups.

Johnson–Neyman Technique to Investigate Significant Interactions.

To further investigate the nature of the significant interaction (i) between relatedness and age on the probability of a female being targeted for eviction and (ii) between relatedness and age on the probability of a targeted female returning to the group following an eviction attempt we used the Johnson–Neyman technique (46–48). This enabled us to evaluate the conditional effect of relatedness on each of the respective response variables with respect to age by calculating the region of significance and 95% confidence intervals for the marginal effect of relatedness across all possible ages (47, 49).

i) Investigating the nature of the significant interaction between relatedness and age on the probability of a female being targeted for eviction.

Fig. S2 shows that the marginal effect of relatedness on the probability of a female being targeted for eviction is positive for all ages and is significantly different from zero at ages greater than 543 d. We also performed a test of significance on the regression slopes of the effect of relatedness on the probability that a female is targeted for eviction for younger vs. older females to determine whether these slopes were significantly different from zero. Using noncentered variables and values of age plotted in Fig. 4A, the slope of regression for younger females was not significantly different from zero (age at 25th percentile = 522 d, t₁₉₈ = 1.92, P = 0.057) and the slope of regression for older females was significantly different from zero (age at 75th percentile = 1,636 d, t₁₉₈ = 3.81, P < 0.001). Using mean-centered variables, the slope of regression for both younger and older females was significantly different from zero (age at mean − 1 SD, t₁₉₈ = 2.11, P = 0.036; age at mean + 1 SD, t₁₉₈ = 4.98, P < 0.0001).

ii) Investigating the nature of the significant interaction between relatedness and age on the probability of a targeted female returning to the group following an eviction attempt.

Fig. S3 shows that the marginal effect of relatedness on the probability of a female being targeted for eviction is positive for younger females and is significantly different from zero at ages less than 563 d. As age increases the marginal effect of relatedness becomes less positive (becoming negative for older females) but is not significantly different from zero (Fig. S3). We also performed a test of significance on the regression slopes of the effect of relatedness on the probability of a targeted female returning to the group following an eviction attempt for younger vs. older females to determine whether these slopes were significantly different from zero. Using noncentered variables and values of age plotted in Fig. 4B, the slope of regression for younger females was significantly different from zero (age at 25th percentile = 446 d, t₇₂ = 0.58, P = 0.026) and the slope of regression for older females was not significantly different from zero (age at 75th percentile = 922 d, t₇₂ = 2.27, P = 0.56). Similarly, using mean-centered variables, the slope of regression for younger females was significantly different from zero (age at mean − 1 SD, t₇₂ = 2.38, P = 0.0056) and the slope of regression for older females was not significantly different from zero (age at mean + 1 SD, t₇₂ = 0.85, P = 0.40).

Discussion

We have shown in very general terms that where recipients can offer resistance, individuals can gain from targeting selfish acts at closer, rather than more distant, relatives. In the particular case of violent eviction in banded mongooses, this model may therefore explain why dominant females target closer female relatives and why such discrimination is restricted to cases where recipients can offer most resistance. Patterns of resistance, particularly among younger females, deviated from the model predictions, as we discuss in more detail below. Further tests of the model could adopt an experimental approach to manipulate resistance or the costs and benefits of selfishness, which was not possible in our long-term field study.

Whereas our findings offer qualified support for the predictions of our model, it is important to consider alternative explanations for our results. For example, there has been much recent theoretical interest in the possibility that local competition among kin can erode selection for local helping and instead favor indiscriminate harming behavior (16, 17). A prediction of these models is that, across groups or species, rates of aggression may be independent of relatedness (17, 18). However, these models cannot explain the targeting of closer kin for aggression when less closely related, but otherwise equivalent targets are available. A second possibility is that relatedness is correlated with some other factor influencing aggression, such as resource holding potential (RHP) or the level of reproductive competition. For example, in sea anemones, higher aggression among closer relatives has been attributed to their greater similarity in RHP (5). In banded mongooses, there is no evidence that related females are of higher RHP or represent more of a reproductive threat. In fact, younger females (with lower RHP and who reproduce less often) are more likely to be targeted for eviction overall, regardless of relatedness (Fig. 4A). Moreover, our data show that dominant females do not suffer greater reproductive costs when they cobreed with more closely related females (Table S5). Our findings also cannot be explained as a nonadaptive side effect of selection to discriminate between species of heterospecific competitor, which has been suggested to explain negative kin discrimination in polyembryonic wasps (6).

Finally, it has been suggested that targeting relatives for eviction could be part of an adaptive forced dispersal strategy by breeders to maximize metapopulation fitness in a structured population (13). In a previous study we did not find support for this hypothesis as a predictor of eviction at a group level (13). Moreover, it is difficult to reconcile this idea with our observations of negative kin discrimination within a given eviction attempt. In classic models such as that of Hamilton and May (19), dispersal entails direct costs for individuals who leave their natal patch, but is nevertheless favored because it reduces local competition among kin. Because offspring value their own survival more than that of their siblings, whereas parents value all their offspring equally, offspring favor a lower dispersal rate than do their parents, and selection can therefore favor forced eviction of young (20–22). However, eviction by an adult of unrelated young offers equal benefits, in terms of reduced local competition, to eviction of related young, without inflicting the direct costs of dispersal on a relative. Hence, where adults can choose whom to evict, local kin competition alone cannot explain why they should preferentially target more related over less related young for expulsion. There may be other asymmetries associated with the forced dispersal of kin vs. nonkin, deriving, for example, from variation in local competitive ability or variation in the bet-hedging benefits of dispersal (23), but the effect of such variation on forced dispersal in heterogeneous groups has been little explored theoretically or empirically (13, 24). In banded mongooses, there is no evidence that closer kin compete more intensely (Table S5) or that forced dispersal of kin yields bet-hedging benefits.

We predicted that resistance to eviction should decrease with increasing relatedness to dominants. Contrary to this prediction, among younger females, closer relatives were more likely to regain entry to the group than older or less closely related females (Fig. 4B). This result runs directly counter to our assumption that these females are weaker and less able to force their way back into the group and suggests that factors other than strength or the costs of resistance may underlie the pattern by which younger females return to the group. For example, following eviction, dominants may voluntarily readmit closely related, younger females that would otherwise fare very badly outside the group. The negotiation process by which females regain entry to the group may thus be more complex than the simple two-step sequence of eviction and resistance assumed by our model. Whereas our analysis shows that even a two-step game can yield results that diverge from classical predictions, it is likely that many negotiations in family groups may be modeled better as a sequence of three or more steps, something we have not attempted here.

Negative kin discrimination was evident only in eviction attempts of females. In males we found no relationship between relatedness and the probability of being targeted for eviction. This difference between the sexes could reflect differences in the direct fitness incentive for males and females to retain group membership, which in our model is represented by the parameter b₂ (Fig. 1). Females gain greater direct fitness from group membership (i.e., higher b₂) than males because there is little or no reproductive suppression, and most females breed from the age of 10 mo (11, 25). In males, by contrast, most individuals are excluded from mating by the two or three oldest males within the group (10). In our model, low values of b₂ favor little or no kin discrimination (Fig. 2B). A relatively low value of b₂ in males compared with females may explain why males sometimes disperse voluntarily as a group, whereas females are invariably forced to leave after being subject to violent attack (7, 13).

More generally, our model shows that incorporating even very simple forms of behavioral anticipation can radically change the predictions of kin selection theory. Where such anticipation is possible, higher relatedness can lead to outcomes that are less favorable on average for all those involved, because the threat of resistance or punishment of selfish behavior is less credible between relatives than between unrelated individuals. Many empirical studies have shown that animals are in fact capable of adjusting their behavior according to the anticipated responses of their social partners in a range of contexts. Examples include signaling systems (26), negotiation over care of offspring (27), restraint in competitive growth (28), and audience effects (29). However, few have considered the possibility that this kind of anticipation might lead to less cooperative outcomes among closer kin. An example comes from economic studies of human behavior in the context of joint-liability group lending, which have found higher rates of loan default when there are more relatives within a group (30, 31), leading to barring of remaining group members from future borrowing. This pattern has been attributed to the difficulty of group members imposing penalties on relatives to enforce repayment (32, 33). Our results suggest that similar patterns might also occur in the behavior of other species and that the influence of kinship on aggression and cooperation within animal groups may be considerably more subtle and variable than predicted by classical kin selection theory.

Methods

Study Population and Data Collection.

Data were collected from 15 groups of banded mongooses living on the Mweya Peninsula, Queen Elizabeth National Park, Uganda (0°12′S, 27°54′E), between September 1997 and October 2015. For further details of habitat and climate, see ref. 8. Groups were visited every 1–3 d to record group composition, life history, and behavioral data. Individuals were easily identifiable by unique shave markings on their back and were regularly trapped to maintain these markings (34). On first capture a 2-mm skin sample was collected from the end of the tail for genetic analyses. For details of genetic analyses and calculating relatedness see SI Methods. Individuals were trained to step onto portable electronic scales to obtain weight measurements. The research was conducted with permission from Uganda Wildlife Authority and Uganda National Council for Science and Technology, and all methods were approved by the Ethical Review Committee of the University of Exeter.

We observed the attempted eviction of 405 individuals from eight groups in 44 eviction attempts. Eviction attempts were conspicuous, violent events and easy to recognize. We defined an eviction attempt to have occurred if one or more individuals left their group for at least 1 d following a period of intense aggression toward themselves or other group members (13, 35, 36). In 21 of 44 eviction attempts all targeted individuals rejoined their group; in 14 attempts some targeted individuals returned whereas others did not; and in 9 eviction attempts all targeted individuals dispersed.

Statistical Analyses.

Statistical analyses were performed in R 3.3.0 (37). We used GLMMs with a binomial error structure using a logit-link function, or a Poisson error structure using a log link function, in the “lme4” package (38). Poisson models were checked for overdispersion (39). In all analyses, we assessed the significance of each fixed effect by comparing the likelihood ratio of the maximal model to that of the model without the fixed effect (38). We present parameter estimates and SEs from maximal models, rather than removing nonsignificant fixed effects due to problems associated with stepwise model reduction (40). We did, however, remove nonsignificant interactions to allow the significance of the main effects to be tested (41).

i) Negative kin discrimination in banded mongooses.

Models were fitted to male and female data separately because not all eviction attempts involved males. We considered adult females over 10 mo old, because females younger than 10 mo are unlikely to be regular breeders and are rarely evicted (7, 11, 25). We fitted whether or not a female was targeted for eviction during an eviction attempt as the binomial response variable. We included mean pairwise relatedness to dominants in the group, which we defined as males and females over 3 y of age, as a fixed effect. We use this age criterion for social dominance throughout because, in both males and females, individuals over 3 y of age are more likely to breed, have higher fertility, and appear to be socially dominant (7, 10, 14, 42). In males there is a clear age-based dominance hierarchy, evident during estrus (10, 42). In females, experimentally suppressing reproduction in older females (>3 y) results in failure of the communal litter, whereas suppressing reproduction in younger females (<3 y) does not (14). Older females also breed more frequently (7, 11) and produce larger litters (43). Age (days), pregnancy status (pregnant or not pregnant), mean nonpregnant weight (grams) in the 60 d before the eviction attempt, mean rainfall (millimeters) in the 30 d preceding the eviction attempt, and group size (number of individuals over 6 mo) were included as additional fixed effects. We controlled for repeated measures of individuals, eviction attempts, and groups by including these terms as random intercepts and fitted the model to data on 207 females in 29 eviction attempts in five groups. To examine which males were targeted for eviction we considered adult males over 1 y old, because males under 1 y do not sire young (7, 42), and fitted whether or not a male was targeted for eviction during a mixed-sex eviction attempt as the binomial response variable. We included the same fixed and random effects as in the female model but, instead of pregnancy status, we included the male’s breeding status (whether or not the male had been observed mate guarding or had sired pups in the current breeding attempt) and fitted the model to data on 177 males in 15 eviction attempts in five groups.

Aggressive interactions between targeted individuals and other group members during eviction attempts were numerous, but systematic data on the identity of aggressors were difficult to record. However, since 2000 we have noted ad libitum the identity of individuals that were notably more aggressive than other group members toward potential evictees. Data on 86 of these primary aggressors were available for 26 eviction attempts. To investigate the relationship between the sex of primary aggressors and the sex of individuals targeted for eviction we fitted the number of primary aggressors in each eviction attempt as the Poisson response variable and included the sex of the primary aggressors, the type of eviction attempt (female only or mixed sex), and the interaction between these two variables as fixed effects. We included group identity and eviction attempt as random intercepts and fitted the model to 26 eviction attempts in six groups. See SI Methods for details of analyses of negative kin discrimination by primary aggressors, to avoid inbreeding or as a response to reproductive competition.

ii) Testing model prediction i: The selfish act will be directed preferentially toward closer relatives only when recipients can resist.

We repeated the original analysis investigating negative kin discrimination among females in eviction attempts, but included two-way interactions between female relatedness to dominants and age (days) and female relatedness to dominants and weight (grams). Other fixed and random effects were as in the original analysis. We fitted this model to data on 207 females in 29 eviction attempts in five groups.

To test further model prediction i, we examined kin discrimination in cases of infanticide of newborn pups. Infanticide is known to occur in this system, but is difficult to observe directly as it typically occurs in the den. In asynchronous litters, infanticide appears to be common because early life pup mortality is strongly dependent on the pregnancy status of other females in the group (14, 15). Pups that are born early in asynchronous litters almost always die in the first few days after birth, whereas pups born last almost always survive (15). Between November 1997 and October 2015, we recorded the order in which each female gave birth in an asynchronous litter (i.e., if she gave birth first, in the middle, or last) and whether any of her pups survived the first week after birth. Following ref. 15, we used the presence or absence of “babysitters” (adults left at the den to guard newly born pups) to measure patterns of early life litter mortality. Specifically, to determine the survival of an individual female’s pups, we considered only females who gave birth early relative to the rest of the breeding females and for which the failure of a specific female’s litter could be detected using cessation of babysitting (i.e., we did not consider females who gave birth when babysitting of other early-birthing females’ pups was still ongoing). A female’s litter was determined to have survived the first week after birth if there were still babysitters left 7 d after birth or if she was retrospectively assigned maternity to at least one emergent pup from the communal litter following genetic analysis. We observed 166 females that fitted the criteria outlined above, who gave birth to 120 asynchronous litters in 15 groups. Where none of the female’s pups survived the first week after birth, they were assumed to have been subject to an infanticidal attack. To test whether pups are more likely to be targeted for infanticide when mothers are less related to female dominants in the group, we fitted whether or not each female’s pups survived the first week after birth as the binomial response variable. We included the mother’s mean pairwise relatedness to female dominants older than 3 y of age, mother’s age (days), group size, and rainfall (millimeters) in the 30 d before birth as fixed effects. We controlled for repeated measures of mothers, litters, and groups by including these terms as random intercepts and fitted the model to data on 57 females giving birth to 50 communal litters in 11 groups.

iii) Testing model prediction ii: Resistance to the selfish act offered by recipients should decrease as their relatedness to the actor increases.

We fitted whether or not a female over 10 mo old that was targeted for eviction overcame efforts to permanently exclude her from the group as the binomial response variable. We considered only eviction attempts where some evictees were allowed to return and others were not due to problems with fitting a binomial model to outcomes that are exclusively successes or failures. We included mean pairwise relatedness to dominants in the group, age (days), and the interaction between these two variables as fixed effects. We were unable to include additional fixed effects in the model due to problems with model convergence. We controlled for repeated measures of individuals, eviction attempts, and groups by including these terms as random intercepts and fitted the model to data on 76 females in 14 eviction attempts in four groups.