Abstract
In transmission electron microscopy (TEM) the interaction of an electron beam with polymers such as P3HT:PCBM photovoltaic nanocomposites results in electron beam damage, which is the most important factor limiting acquisition of structural or chemical data at high spatial resolution. Beam effects can vary depending on parameters such as electron dose rate, temperature during imaging, and the presence of water and oxygen in the sample. Furthermore, beam damage will occur at different length scales. To assess beam damage at the angstrom scale, we followed the intensity of P3HT and PCBM diffraction rings as a function of accumulated electron dose by acquiring dose series and varying the electron dose rate, sample preparation, and the temperature during acquisition. From this, we calculated a critical dose for diffraction experiments. In imaging mode, thin film deformation was assessed using the normalized cross-correlation coefficient, while mass loss was determined via changes in average intensity and standard deviation, also varying electron dose rate, sample preparation, and temperature during acquisition. The understanding of beam damage and the determination of critical electron doses provides a framework for future experiments to maximize the information content during the acquisition of images and diffraction patterns with (cryogenic) transmission electron microscopy.
Introduction
Transmission electron microscopy (TEM) is one of the main tools to investigate the morphology of materials, from subnanometer to micrometer length scales. However, the interaction of electrons with materials, and especially beam sensitive structures such as polymers,1 biological materials,2,3 or zeolites,4 causes different types of radiation damage, e.g., atomic displacement, electrostatic charging, sputtering, radiolysis, and knock-on damage.5 These mechanisms operate at different length scales: At subnanometer length scales, knock-on damage and atomic displacement can result in distorted crystal lattices, while morphology changes due to heating, electrostatic charging and sputtering are visible at nanometer and micrometer length scales. Hence, for beam sensitive materials, beam damage constitutes a physical limit and determines the resolution that can be achieved in imaging, diffraction, and electron tomography.6 Therefore, it is important to analyze and understand beam damage to facilitate the study of these (beam sensitive) materials with a minimum amount of artifacts.
The degradation of crystal lattices, at subnanometer length scales, can be studied by electron diffraction. It is well established that electron beam damage causes the fading of diffraction spots and rings in protein crystallography,7 and it has been shown that it is affected by the temperature of the material, the electron flux through the material, and the accumulated amount of electrons transmitting the material.8−15 Furthermore, this effect is easily quantified by following the intensity of diffraction rings or spots as a function of accumulated dose.9,16−20
The effects of beam damage at nanometer and micrometer length scales are dependent on and specific to the utilized imaging mode but mainly relate to materials loss by sputtering, and shrinkage.21−24 The degradation of materials causes artifacts in the form of changes in contrast or local intensity, while mass loss will result in an increase in overall intensity.25 In the literature, this phenomenon is mostly studied by using the difference image of two images with different accumulated electron doses.26,27 These techniques, however, is not commonly used to follow beam damage over a multitude of images,25 which is essential for e.g. electron tomography.24,28
The analysis of organic photovoltaics (OPVs) is a good example where beam sensitivity plays an important part.28 OPVs contain a photoactive layer, which is composed of different organic molecules. Since the morphology of this photoactive layer, i.e., the distribution of molecules, including their nanoscale phase separation, has a large impact on the overall efficiency of OPVs, TEM has become a standard characterization tool. Common OPV materials are e.g. poly(3-hexylthiophene) (P3HT) and phenyl-C61-butyric acid methyl ester (PCBM). These materials show diffraction rings instead of diffraction spots, resulting from the random orientation of crystallites or the presence of amorphous phases. Therefore, radial averaging of diffraction patterns is a suitable way to record and analyze the intensity change of P3HT and PCBM diffraction signals29 upon electron beam damage.
In the analysis of OPVs, TEM samples are usually created by floating the photoactive layer on water from a water-soluble polymer film.30 The resulting water that is present in the sample might play a role in beam damage mechanisms as well, for example, by creating oxygen radicals. An oxygen- and water-free sample preparation method is therefore introduced to specifically study the influence of sample preparation.
In this paper, beam damage is studied in both diffraction and bright field imaging, investigating the effect of electron dose rate, temperature, and sample preparation. More specifically, (1) beam damage of the crystallinity is quantified via radially averaged diffraction patterns, (2) mass loss is assessed via changes in intensity and standard deviation of the mean intensity, and (3) shrinkage is determined by monitoring the movement of markers, while a method is introduced to determine shrinkage or expansion via the use of the normalized cross-correlation.
Materials and Methods
Materials
Poly(3-hexylthiophene) (P3HT, Plexcore OS2100) was supplied by Plextronics, while PCBM ((6,6)-phenyl-C61-butyric acid methyl ester, purity 99%) was purchased from Solenne B.V. and the solvent o-dichlorobenzene (oDCB) from Sigma-Aldrich. PEDOT:PSS (Clevios P VPAl 4083) was purchased from Heraues GmbH. TEM grids (Quantifoil, R2\2 200-mesh Cu) was purchased form Quantifoil Micro Tools GmbH. All materials were used as purchased.
Sample Preparation
P3HT and PCBM were dissolved in oDCB, resulting in a solution with 1 wt % P3HT and 1 wt % PCBM. The solution was stirred at 70 °C for 24 h to ensure complete dissolving of the materials.
A custom-made specimen holder was used to facilitate direct spin-coating on TEM grids. Four recesses were laser ablated (20 μm deep with a diameter of 3 mm) on 5, 10, 15, and 20 mm from the center of a 50 × 50 mm glass plate. A custom spring was designed to lock the TEM grids in the recesses, with minimal altering of flow behavior of the solution during spin-coating. Glass plates were cleaned by (1) ultrasonication in acetone for 30 min, (2) rubbing with soap and rinsing with demineralized water, (3) ultrasonication in isopropanol for 30 min, and (4) UV-ozone for 30 min.
The conventional sample preparation method proceeded via the following steps. First, PEDOT:PSS was spin-coated on 25 × 25 mm glass plates, at 3000 rpm for 60 s, resulting in a 50 nm thick water-soluble layer. The P3HT:PCBM solution was subsequently spin-coated at 2000 rpm for 120 s, which results in a 25 nm thick layer. The OPV thin films prepared on the PEDOT:PSS spin-coated glass plates were submerged in water to dissolve the PEDOT:PSS layer, resulting in an OPV thin film floating on a water surface. This film was picked up on a glow-discharged TEM grid, dried at room temperature, and subsequently annealed in air at 120 °C for 10 min. After floating of the OPV layer on water and pickup by the TEM grid, there is a small chance that some PEDOT:PSS will remain on the sample surface. However, due to the small surface-to-volume ratio, the diffraction and imaging experiments are dominated by the bulk information, including oxygen and water which can penetrate into the bulk. Furthermore, this adds a significant advantage to the new direct spin-coating method, since there certainly will be no PEDOT:PSS present during this method. In one of the conventional prepared samples, silver particles (∼10 nm diameter, dissolved in toluene with oleylamine as capping agent) were added to the P3HT:PCBM solution before spin-coating.
To exclude water and oxygen being present in the OPV thin film, another approach was followed. Here, the OPV thin film was directly spin-coated on a TEM grid inside a glovebox (M-Braun Labmaster Glove Box System) at 500 rpm for 10 min. The directly spin-coated samples were annealed at 120 °C for 10 min inside a glovebox. Note that the direct spin-coating method is not used as an alternative to OPV device fabrication but as an alternative TEM sample preparation method. It is not possible to achieve water- and oxygen-free TEM analysis by preparing a sample using the common floating method, hence the need for a direct spin-coating method. For clarity, the sample code used in the Results section is given in Table 1.
Table 1. Sample Code Used in the Results Section (x Represents the Electron Dose Rate Used in e/(Å2 s)).
| sample preparation | cryogenic conditions | room temperature |
|---|---|---|
| common floating approach | CF/Cryo/x | CF/RT/x |
| direct spin-coating | DS/Cryo/x | DS/RT/x |
TEM Acquisition
The samples were loaded into the TU/e Cryo Titan (FEI Company; now Thermo Fisher Scientific), which was operated at 300 kV and is equipped with a field emission gun. Diffraction patterns were acquired at dose rates of 0.1, 1, 10 e/(Å2 s), with exposure times of 5, 0.5, and 0.05 s (keeping the total dose per pattern constant), at a camera length of 1.15 m. For the bright field imaging experiments, the dose rates were set at 1, 10, and 100 e/(Å2 s), with exposure times of 5, 0.5, and 0.05 s (again, keeping the total dose per image constant), respectively, at a magnification of 18K. For high accumulated dose experiments, the screen was flipped down to realize constant irradiation and flipped up to acquire intermediate images.
Data Analysis
Diffraction patterns were radially averaged using an in-house Matlab script (details in the Supporting Information, section 1) and fitted by a nonlinear least-squares method using the lsqnonlin command in Matlab (details in Results section and Figure 1b). The signal intensities of P3HT (at 0.256 Å–1) and PCBM (at 0.217 Å–1) were normalized to their initial intensity and followed as a function of accumulated electron dose.
Figure 1.
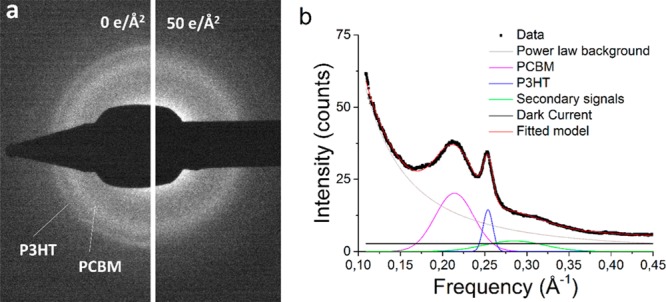
(a) Fading of diffraction rings of a P3HT:PCBM bulk heterojunction at room temperature, before and after exposure to 50 e/Å2. (b) Radial average of diffraction pattern as shown in (a) decomposed in its different components by least-squares fitting. The goodness of fit (R2) for the model is 0.9985.
Prior to further analysis, bright field images were aligned via cross-correlation to avoid processing artifacts from sample drift. The aligned data stack was cropped to the overlap area present in all images for analysis. From the resulting aligned stack of images, the average intensity, standard deviation, and the normalized cross-correlation coefficient with the first image of the series were measured as a function of accumulated electron dose.
Finally, to assess local deformations, the aligned stack was cut into 16 subareas of equal size. These subarea stacks were individually aligned via cross-correlation. From this alignment, the shift of each individual subarea with respect to the first image in the x and y direction was used to calculate the displacement of each subarea. Furthermore, the relative displacement from the center of the total image was calculated by measuring the distance between the center of the subarea and the center of the total image. More details can be found in the Results section and Supporting Information section 2.
Results
Figure 1a shows a diffraction pattern obtained from a typical P3HT:PCBM bulk heterojunction prepared via the conventional sample preparation (CF/RT/10), before and after exposure to 50 e/Å2 at room temperature. It is evident that the sharp outer ring, depicting the (020) lattice spacing in P3HT, is decreasing in intensity faster than the broad inner ring, characterizing PCBM nanocrystals, which is in agreement with previous studies.17 Since the PCBM is inherently broader than the P3HT ring, indicating a large part of PCBM being amorphous, a slower decrease in diffraction intensity for PCBM is expected.
In Figure 1b, the radially averaged diffraction pattern of the P3HT:PCBM bulk heterojunction is presented. To quantitatively analyze the decrease in intensity as a function of accumulated electron dose, it is necessary to separate neighboring peaks. Therefore, to independently address the intensity of the PCBM peak at 0.217 Å–1 and the P3HT peak at 0.256 Å–1, the spectrum was fitted to a model function by least-squares fitting. This function contains (in the same order as in eq 1) a Gaussian describing the PCBM peak, a Gaussian describing the P3HT peak, a Gaussian located between 0.285 and 0.323 Å–1 describing (inseparable) secondary components of both P3HT and PCBM,28,31 a power law to estimate the inelastic background, and a constant representing residual dark current in the diffraction patterns. The variables a1 and a2 describe the intensity of the PCBM and P3HT signal, respectively.
| 1 |
Effect of Dose Rate in Diffraction Mode
To study the effect of electron dose rate on the decrease of intensity of P3HT and PCBM diffraction rings, dose series were acquired at various dose rates, i.e., 0.1, 1, and 10 e/(Å2 s). The dose per image was kept constant at 0.5 e/Å2 by adjusting the exposure time accordingly. Because of differences in absolute peak height for PCBM and P3HT, and changes in PCBM/P3HT ratio in different regions of the sample, all peaks were normalized to the peak intensity of PCBM (a10) and P3HT (a2) of the initial diffraction pattern (a1,20).
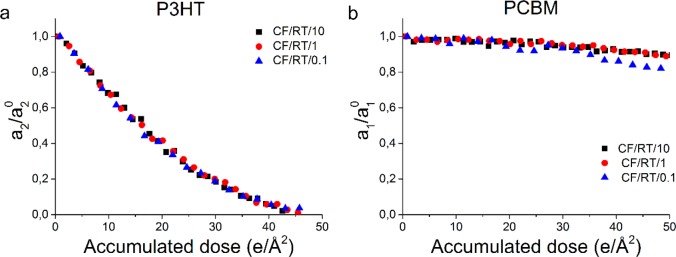
Figure 2 shows the decrease in relative intensity (a1,2i/a1,2) for P3HT (a) and PCBM (b) acquired at three different dose rates (CF/RT/x), in the presence of water and oxygen. The results confirm that the relative intensity of the P3HT diffraction ring decreases faster than the relative intensity of the PCBM diffraction ring, as seen in Figure 1a. In all three cases the critical dose for P3HT, which we define by the accumulated electron dose at which the relative intensity decreases to 1/e (∼37%), is about 16–19 e/Å2 (Table 2), as calculated from an exponential decay fit. Most notably, changing the electron dose rate from 0.1 to 10 e/(Å2 s) has no significant effect on the fading of the diffraction rings, i.e., the critical dose.
Figure 2.
Fading of relative diffraction intensity (a/a0) as a function of accumulated dose for P3HT (a) and PCBM (b) at different dose rates. For visibility reasons every third data point is shown.
Table 2. Critical Doses of P3HT and PCBM Diffraction Ring Intensity Fading to 1/e for Three Dose Rates, in e/Å2, Inter- or Extrapolated from an Exponential Decay Fit.
| signal | CF/RT/0.1 | CF/RT/1 | CF/RT/10 |
|---|---|---|---|
| P3HT | 18 ± 1 | 19 ± 1 | 16 ± 1 |
| PCBM | 265 ± 3 | 412 ± 5 | 392 ± 1 |
The critical dose of PCBM was obtained by an exponential decay extrapolation of the curves in Figure 2b (details are presented in the Supporting Information, section 3). Therefore, the critical dose for PCBM is less well-defined than the critical dose for P3HT. Table 2 shows that this critical dose is between 265 and 412 e/Å2. Despite the large error due to extrapolations, it is clearly shown that the critical dose of PCBM is more than 10 times larger than the critical dose of P3HT. Therefore, in this system, the stability of P3HT is the limiting factor. The results show that, using a dose of 0.1 e/Å2 per image, at least 160 diffraction patterns can be acquired, opening up the possibility of using high electron dose techniques such as electron diffraction tomography for organic crystals.29,32 To complement the presented results, studies on beam damage effects for each component individually and nanocomposites of different ratios should be considered. This is however beyond the scope of this paper.
In summary, dose rates between 0.1 and 10 e/(Å2 s) do not have an effect on the rate of relative intensity loss of both P3HT and PCBM. This is in agreement with previous studies on the decrease of features in the EELS spectrum of other organic materials,33−35 but in contrast with observations of Karuppasamy et al. in single-particle cryo-electron microscopy.25 Note that Karuppasamy et al. used an electron microscope operating at 120 kV, significantly decreasing the inelastic mean free path. At 300 kV, as in our experiments, changing the sample thickness or increasing the electron dose rate to values above 10 e/(Å2 s) might therefore cause an electron dose rate effect on sample damage. Nonetheless, this falls beyond the scope of this paper and is therefore not investigated.
As the decrease in diffraction intensity is related to the breaking of chemical bonds, beam damage will change the HOMO and LUMO levels of OPV materials, which can be measured with electron energy loss spectroscopy (EELS).17,36−38 Based on the low-loss EELS results presented in ref (17), a critical dose can be estimated which is similar to our diffraction results. This clearly illustrates the close relationship between diffraction intensities and energy levels in OPV materials with low-dose diffraction being somewhat simpler to carry out and more broadly available for critical dose measurements.
Effect of Temperature and Sample Preparation in Diffraction Mode
The above results were obtained with a standard OPV bulk heterojunction sample imaged at room temperature. Additional dose series were acquired in cryogenic conditions, as this has been shown to reduce beam damage in beam sensitive materials.10,12,27 We furthermore studied the effect of sample preparation using either the conventional sample preparation (CF) or by direct spin-coating (DS) on a TEM grid in a water and oxygen-free environment (glovebox), facilitated by a custom-made TEM specimen holder as described in the Methods section.
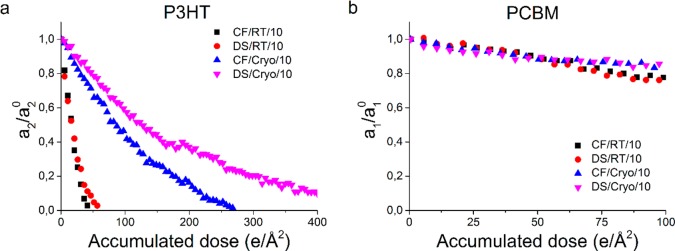
Figure 3 shows the influence of temperature and sample preparation on the decrease of relative intensity of the P3HT (a) and the PCBM (b) signal, with a dose per image of 0.5 e/Å2 acquired with a dose rate of 10 e/(Å2 s). It is clearly visible that the sample CF/Cryo/10 shows a slower fading of the diffraction signal for both the PCBM and the P3HT signal. The critical dose increases from ∼16 e/Å2 at room temperature to ∼108 e/Å2 at 80 K (Table 3). Hence, cryo-preservation is shown again to be essential in the analysis of beam sensitive materials.9,10,27 More importantly, having a quantitative criterion or threshold for determining exposure limits as presented here will provide a framework to maximize useful information before beam damage influences the validity of acquired data.
Figure 3.
Fading of relative diffraction intensity (a/a0) for P3HT (a) and PCBM (b) as a function of accumulated dose, showing the effect of sample preparation at room temperature (RT) and at 80 K (Cryo). A dose rate of 10 e/(Å2 s) was used. For visibility reasons, every fifth data point is shown.
Table 3. Critical Doses of P3HT and PCBM at a Dose Rate of 10 e/(Å2 s) at Room Temperature and Cryogenic Conditions Prepared by Either a Conventional Floating Approach or an Oxygen- and Water-Free Preparation Method.
| signal | CF/RT/10 | DS/RT/10 | CF/Cryo/10 | DS/Cryo/10 |
|---|---|---|---|---|
| P3HT | 16 ± 1 | 21 ± 1 | 108 ± 1 | 188 ± 1 |
| PCBM | 392 ± 1 | 372 ± 4 | 596 ± 4 | 766 ± 6 |
Sample preparation effects, i.e., the presence or absence of oxygen and water, are only minor at room temperature. However, at cryogenic conditions, the rate of relative intensity loss for P3HT (Figure 3a, purple triangles) is significantly decreased by a water- and oxygen-free sample preparation method (DS/Cryo/10), increasing the critical dose from ∼108 to ∼188 e/Å2 (Table 3). A detailed analysis of the significance of these results is presented in the Supporting Information, section 4.
The observed difference in critical dose for P3HT and PCBM with or without oxygen and water being present at low temperatures may be related to trapped oxygen and water molecules. These molecules will form radicals upon electron beam irradiation, thus decreasing the crystalline order at lower accumulated electron doses. Because of the fact that the samples have been in high vacuum for at least 30 min before imaging, it is expected that water and oxygen will diffuse out of the material at RT conditions and thus only be present in small amounts in the imaged thin film. This explains why sample preparation seems to have little influence when measuring at room temperature. For cryogenic conditions the exclusion of water and oxygen significantly improves the stability of P3HT exposed to an electron beam. Furthermore, for the room temperature experiments, annealing in air might cause minor damage. This also could explain the observed critical dose, causing the critical dose for the CF/RT/10 to be lower than the critical dose for DS/RT/10.
The values in Table 3 also suggest that a water- and oxygen-free method increases the critical dose of PCBM in cryogenic conditions. In this case, a linear extrapolation was used, since the adjusted R2 value for the exponential decay fits were too low (0.85 (exponential fit) compared to 0.95 (linear fit)). Since the PCBM intensity decay will probably not behave in a linear fashion, one could suggest that the difference between the PCBM critical doses at cryogenic conditions is therefore not significant. Since PCBM is more hydrophobic than P3HT, and it is known that P3HT forms a charge-transfer complex with oxygen,39 it can indeed be expected that the presence of water and oxygen has less influence on the decay of the PCBM diffraction ring.
Beam Damage As Observed during Imaging
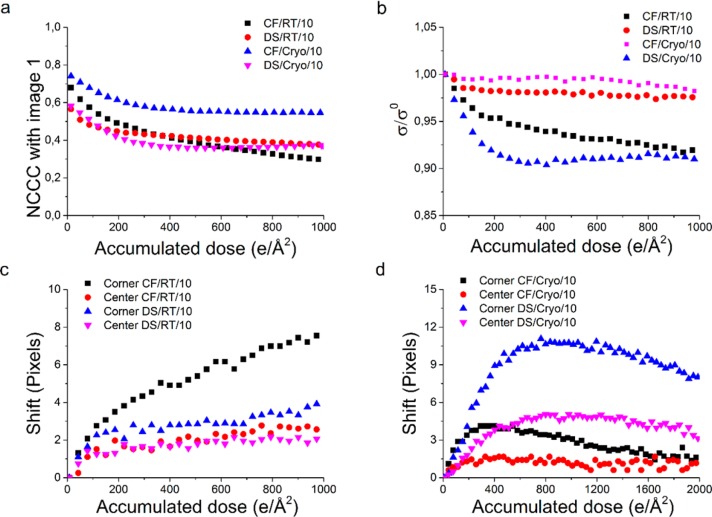
In imaging mode, beam damage can present itself as among others (1) shrinkage or expansion of an organic thin film40 and (2) sample thinning due to mass loss.24 Both effects were measured by acquiring dose series of samples prepared by CF and DS methods. These series of images were acquired at different dose rates and at either room temperature or cryogenic conditions. To study sample deformations, the normalized cross-correlation coefficient (NCCC) of an image with respect to the first image within the series was calculated. Sample thinning due to mass loss was assessed by the relative decrease in average pixel intensity and the accompanying standard deviation.
Effect of Dose Rate in Imaging Mode
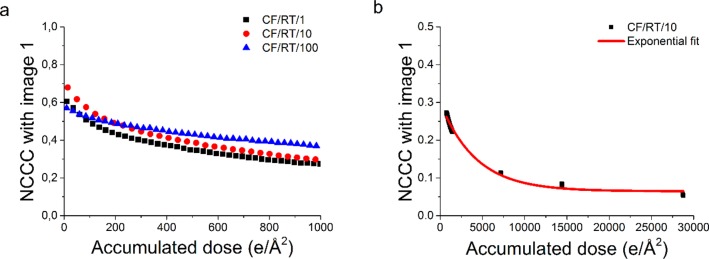
Figure 4a shows the decrease of the NCCC with respect to the original image as a function of accumulated dose at dose rates of 1, 10, and 100 e/(Å2 s) (CF/RT/x). Local differences in thickness, small deviations in intensity due to microscope instabilities, and high contrast contaminations cause the NCCC to start at different values for each series. Therefore, the trend of the curves is studies instead of the absolute NCCC values. It is clearly visible that the NCCC drops quickly before a more stable regime is reached after approximately 150–180 e/Å2, as calculated from the intersect of two linear fits: one fitted to the first 50 e/Å2 and one fitted between 750 and 1000 e/Å2 (for details, see Supporting Information, section 5). Identical fit regimes were chosen in every experiment to ensure a fair comparison between data sets, at room temperature and at cryogenic conditions.
Figure 4.
(a) Cross-correlation coefficient with respect to the first image of three dose series (1, 10, and 100 e/(Å2 s)) as a function of accumulated dose. For visibility reasons, every third data point is shown. (b) Cross-correlation coefficient with the first image of a dose series acquired at 10 e/Å2 at room temperature, starting at 750 e/Å2. An exponential fit is added to calculate the critical dose.
For CF/RT/100, the quick initial drop is less evident (a slope of (−6.73 ± 0.04) × 10–4 as compared to (−1.32 ± 0.04) × 10–3 and (−1.67 ± 0.05) × 10–3 for CF/RT/1 and CF/RT/10, respectively), which is likely caused by pre-exposure with a higher dose before starting the dose series. An exposure of 0.25 s to check that there was no carbon film in the entire field of view caused a pre-exposure of 0.25 and 2.5 e/Å2 for the CF/RT/1 and CF/RT/10 samples, respectively, which is small compared to the dose limit. However, for the CF/RT/100, this pre-exposure will be 25 e/Å2. This will cause significant damage, and therefore the NCCC for the last image will be higher, as the first image is already more damaged. After the cutoff dose is reached, a more stable second regime starts, as indicated by a much smaller slope (∼− 1 × 10–4). Since the cutoff dose and the slope of the second regime are fairly similar between dose rates of 1 to 100 e/(Å2 s), it is concluded that the dose rate effect is negligible, similar to the diffraction data.
Although the slope of the second damage regime is much smaller, beam damage still occurs. In a similar way as introduced for the diffraction data, a quantitative criterion can be set to calculate the critical dose, at which the initial NCCC decreases with a factor of e. To estimate this critical dose for imaging, a dose series is acquired at 10 e/(Å2 s), reaching an accumulated dose of 30 000 e/Å2. An exponential decay curve is fitted to the NCCC decay of this data set, starting at 750 e/Å2 to exclude effects from the first damage regime. Calculating the critical dose imaging results in a value of (2.6 ± 0.2) × 103 e/Å2 (for details, see Supporting Information, section 6).
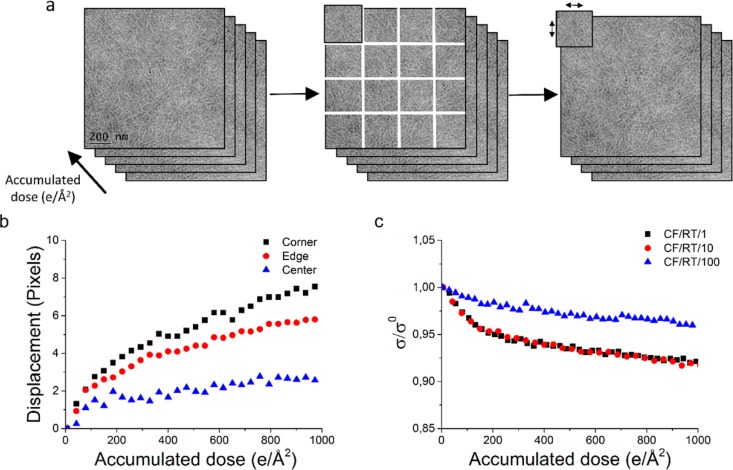
Since the NCCC is a measure of similarity, it will entail among others sample deformation and contrast loss or intermixing. To show that the initial drop in cross-correlation is caused by sample deformations, the stack of aligned images acquired at 10 e/(Å2 s) was cut into 16 equal subimages (Figure 5a), and these different subimages were aligned by the normalized cross-correlation to the next image of the dose series. This approach facilitates the measurement of displacement of each subimage, i.e., expansion or contraction of the thin film as a function of accumulated dose. The results of this analysis are plotted in Figure 5b. It is clearly visible that the displacement of the subimages at the corners and edges of the stack is larger than the displacement of the subimages at the center of the stack (Figure 5b), indicating movement to or from the center of the stack. Calculating the relative increase in distance between the center of each subimage and the center of the total image results in a shrinkage of 0.70 ± 0.14% at an accumulated dose of 1000 e/Å2.
Figure 5.
(a) Schematic representation of cutting a stack of images in 16 parts (left to middle) and using the cross-correlation to find the shift in 1 part of the image compared to the original image (right), as a representation of shrinkage or expansion. (b) The average shift of the 4 corner subareas, the 8 edge subareas, and the 4 center subareas, acquired at 10 e/(Å2 s). (c) Relative decrease in standard deviation of the mean intensity as a function of accumulated dose for samples prepared by the common floating approach at room temperature, at three different dose rates. For visibility reasons, every fifth data point is shown in (b) and (c).
The validity and accuracy of the method above has been proven against an approach that uses the movement of high contrast silver makers to determine shift, as presented in the Supporting Information, section 2.
As a different measure to assess beam damage, we quantify the change in average intensity that can be interpreted as a change in mass–thickness due to either mass loss or deformations of the thin film. To minimize the effects of microscope instabilities, two low-magnification overview images were taken, before and after the dose series. From these two images the intensity ratio of the nonilluminated and illuminated region before and after the series was calculated (Table 4). Because of the occurrence of lateral shrinkage, one would expect the sample to become thicker (assuming volume preservation), since material is moving toward the center. This would result in a lower average intensity. However, Table 4 shows an insignificant change in intensity, which can be explained by the fact that the relative shrinkage is small. Furthermore, thinning caused by mass loss will increase the average intensity, compensating for the thickening effect of shrinkage. Before and after images are shown in the Supporting Information, section 7.
Table 4. Relative Increase in Intensity Ratio between an Illuminated and a Nonilluminated Area before and after Imaging at Three Different Dose Rates at Room Temperature with Samples Prepared by the Common Floating Approach.
| CF/RT/1 | CF/RT/10 | CF/RT/100 | |
|---|---|---|---|
| intensity increase (%) | 0.57 ± 3.1 | 0.16 ± 2.6 | 0.22 ± 2.6 |
Last, Figure 5c shows the relative decrease in standard deviation of the mean intensity of the aligned images. Shrinkage would result in a higher standard deviation, since more data will move into the field of view. It is, however, clear that the standard deviation decreases, again pointing out that mass loss plays a significant role in beam damage processes. The fast drop in relative standard deviation at the onset of beam damage might be caused by quick mass loss of material at the surface of the sample removing sample roughness. After this initial drop, a more stable regime is reached where mass loss plays a less significant role since the sample has reached a more equilibrated state.
From this, we can again conclude that in imaging mode a dose rate between 1 and 100 e/(Å2 s) has a negligible effect on beam damage. Furthermore, we can conclude that the minimal pre-exposure of polymer thin films or microtome sections, often applied prior to acquiring electron tomography data sets,41 can now be quantified to limit artifacts in imaging. During this regime, mass loss and shrinkage occur, while after this regime, a second regime will set in, significantly reducing the rate of electron beam damage at higher doses. Furthermore, a critical dose in imaging is calculated, which results in a critical dose of more than 2500 e/Å2. Even when the cutoff dose of the first damage regime is subtracted, this leaves more than enough dose available for acquiring tomography data sets (e.g., tilting from −70° to +70° in 1° steps, with 10 e/Å2 per image results in a total dose of 1410 e/Å2).
Effect of Temperature and Sample Preparation in Imaging Mode
Figure 6a shows the decline of the NCCC with respect to the first image as a function of accumulated dose, for series acquired at room temperature and cryogenic conditions, and prepared by either the CF or DS methods. These series were acquired with a dose rate of 10 e/(Å2 s). Comparing the room temperature measurements, one can see that the decrease in NCCC in the first regime does not significantly change for DS method, as the calculated slope is (−1.57 ± 0.12) × 10–3 compared to (−1.67 ± 0.05) × 10–3 for the CF method. However, the cutoff between the two damage regimes decreases from 156 ± 9 to 96 ± 12 e/Å2. This indicates that the rate of damage is similar for both the CF and the DS method but that the total damage in the first regime will be smaller for the DS method (the relative decay of NCCC at the cutoff dose decreases from 24% for the CF method to 15% for the DS method), indicating a more stable system.
Figure 6.
(a) Decrease in NCCC with respect to the first image for dose series acquired at 10 e/(Å2 s), at room temperature and at cryogenic conditions, from samples prepared by either the conventional floating method or the oxygen- and water-free method. (b) Cross-correlation with the first image of a dose series acquired at 10 e/Å2 at room temperature of a sample prepared by the oxygen- and water-free method. An exponential fit is added to calculate the critical dose. (c) Mean-squared displacement of the 12 edge subareas and the 4 center subareas calculated by alignment via cross-correlation. The images were acquired at 10 e/Å2 at room temperature from a sample prepared by either the common floating approach or the oxygen- and water-free method. (d) See part c, but for images acquired at cryogenic conditions. For visibility reasons, every fifth data point is shown.
The second, more stable regime shows a relatively constant NCCC for the DS method, since the slope of this regime decreases from (−12.7 ± 0.3) × 10–5 for the CF method to (−6.9 ± 0.2) × 10–5 without water and oxygen present. The critical dose therefore increases from (2.6 ± 0.2) × 103 e/Å2 for the CF method to (5.0 ± 0.4) × 103 e/Å2 for the DS method (for details, see Supporting Information, sections 5 and 6). This again indicates that the DS method will create a more stable system during electron beam radiation.
Figure 6c shows the displacement of parts of the images acquired at room temperature by using the alignment method as described before. It is clearly visible that by using the DS method, the shrinkage of the thin film decreases significantly, from 0.70 ± 0.18% to 0.40 ± 0.14%. Figure 6b shows the decrease of relative standard deviation of the mean intensity. The sample prepared by the DS method is more stable, since it is clear that the absolute decrease in relative standard deviation is smaller for this method. Just as the NCCC behavior, a second more stable regime sets in. The smaller slope in this regime for the DS method (Figure 6b, black squares vs red circles) indicates a larger stability. All in all, this leads to the conclusion that at room temperature an oxygen- and water-free sample preparation method significantly enhances sample stability. After subtracting the initial pre-exposure regime, an electron dose of 5 × 103 e/Å2 is still available before reaching the critical dose imaging, which is about twice as much as for a sample prepared by the CF method. Furthermore, since the relative decay of NCCC at the cutoff dose is smaller for the DS method, the acquired data set in the second regime will show the most resemblance to the sample in the initial, nondamaged state. Figure 6a also shows the evolution of the NCCC as a function of accumulated dose in cryogenic conditions. Clearly, the two damage regimes remain visible. The slope of the first regime decreases from (−1.57 ± 0.12) × 10–3 for DS/RT/10 to (−9.25 ± 0.76) × 10–4 for DS/Cryo/10 and to a minimum of (−9.53 ± 0.57) × 10–4 for CF/Cryo/10. This indicates that cryo-preservation could be useful when acquiring small data sets with a low total dose, since the NCCC changes more slowly, and one can therefore acquire images as close as possible to the original, nondamaged state. The effect of water and oxygen seems minimal in this case.
The cutoff between the two damage regimes increases from 156 ± 9 e/Å2 for CF/RT/10 to 219 ± 19 and 271 ± 28 e/Å2 for CF/Cryo/10 and DS/Cryo/10, respectively. With a relative decay of 19% at the cutoff dose for CF/Cryo/10, in comparison to 37% for DS/Cryo/10, it can be concluded that for small data sets with relatively low doses a conventional floating method at cryogenic conditions is best applicable, since the NCCC decreases slowly over a larger amount of dose.
In cryogenic conditions, the second regime behaves differently in comparison to room temperature conditions, since the NCCC is increasing again. Therefore, it was impossible to determine a useful critical dose imaging, based on an NCCC decay by a factor of e. The increase in NCCC can be explained by an inversion of the displacement, i.e., initial shrinkage followed by expansion or vice versa. This is confirmed by the displacement of subareas, shown in Figure 6d. At an accumulated dose of 400 e/Å2, the relative shrinkage is calculated to be −0.39 ± 0.16% and −0.79 ± 0.42% for CF/Cryo/10 and DS/Cryo/10, respectively. This means that the sample will expand first, before it starts to shrink, in contrast to room temperature conditions where shrinkage occurs directly from the onset of beam damage. Whether a stable regime will appear after shrinkage in cryogenic conditions, just as in room temperature conditions, is not investigated.
Because of the initial expansion, one would expect an initial decrease in standard deviation, since the information on less material will be spread over the same amount of pixels. This effect is seen in Figure 6b. However, for the CF/Cryo/10 sample, this effect is minimal. Local mass loss, which is expected since oxygen and water can be removed easily, will increase the standard deviation, explaining the smaller decrease in relative standard deviation.
In cryogenic conditions, in contrast with room temperature conditions, the sample seems to be destabilized by an oxygen- and water-free sample preparation method. Furthermore, even without oxygen and water being present, the stability at high doses is less in cryogenic conditions than at room temperature. Further details on intensity changes of areas before and after exposure can be found in Supporting Information section 7.
Conclusions
By combining diffraction and imaging data, we have investigated electron beam damage effects in P3HT-PCBM thin films over multiple length scales. Analysis of the fading of electron diffraction rings allows us to quantify the beam sensitivity of each component of the nanocomposite individually. This shows that PCBM is 15 times more stable based on the criterion of the critical dose diffraction, i.e., the accumulated electron dose at which the intensity of the corresponding diffraction ring decreases with a factor of e. For electron dose rates between 0.1 and 10 e/(Å2 s), no dose rate effects are observed. Cryo-preservation increases beam stability of both materials with the critical dose for P3HT significantly increasing from 16 to 108 e/Å2, while the critical dose for PCBM increases from 392 to 596 e/Å2. Most importantly, it is shown that excluding water and oxygen during sample preparation further improves the beam stability of these materials, reaching a critical dose of 188 e/Å2 for P3HT, which corresponds to a 10-fold increase over conventional sample preparation and room temperature diffraction.
Beam damage in imaging mode was analyzed in terms of mass loss and thin film deformations. The normalized cross-correlation coefficient (NCCC) between images contains contributions from among others contrast loss and intermixing of phases. Here, the NCCC is used to assess sample deformation, as the NCCC is followed as a function of accumulated dose. First, it is shown that the dose rate effect is negligible for dose rates between 1 and 100 e/(Å2 s). Second, experiments at room temperature show a quick initial decrease in NCCC before a stable second regime is reached. In this first regime, shrinkage and mass loss occurs, as shown via the movement of subimages and changes in relative standard deviation. The second, more stable regime is used to calculate a critical dose imaging, defined by the dose at which the initial NCCC is decreased with a factor of e. An oxygen- and water-free sample preparation method increases this critical dose imaging from 2600 to 5000 e/Å2. Furthermore, since the relative decay of the NCCC at the cutoff dose is lowest in oxygen and water free conditions, data acquired in this second regime will be closest to the sample in a nondamaged state. In cryogenic conditions, the first regime shows a slower decrease of the NCCC, indicating that the first regime is more stable than in room temperature conditions. In the second regime, however, the NCCC increases again. This is due to the fact that after an initial expansion of the thin film the sample starts to shrink.
In summary, we suggest to use an oxygen- and water-free sample preparation method combined with cryogenic conditions in diffraction mode, while for imaging an oxygen- and water-free sample preparation method is best suited combined with data acquisition at room temperature (high total doses, large data sets) and a conventional floating method is best suited for cryogenic condition (small total doses, small data sets). We believe that the quantitative analysis of TEM beam damage as illustrated here will become a standard tool to optimize TEM imaging conditions and sample preparation protocols in the future.
Acknowledgments
We thank Arno van Hoof for providing the silver particles. We acknowledge financial support for this research from ADEM, A green Deal in Energy Materials of the Ministry of Economic Affairs of The Netherlands (www.adem-innovationlab.nl).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.7b01749.
Experimental details radial averaging, displacement calculation with silver particles; data fits: critical dose calculations in imaging and diffraction mode, calculating cutoff in imaging mode; intensity changes in imaging mode (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Ahn H.; Oblas D. W.; Whitten J. E. Electron Irradiation of Poly(3-hexylthiophene) Films. Macromolecules 2004, 37, 3381–3387. 10.1021/ma030589x. [DOI] [Google Scholar]
- Thach R. E.; Thach S. S. Damage to Biological Samples Caused by Electron Beam During Electron Microscopy. Biophys. J. 1971, 11, 204–210. 10.1016/S0006-3495(71)86208-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanc N. S.; Studer D.; Ruhl K.; Dubochet J. Electron Beam-Induced Changes in Vitreous Sections of Biological Samples. J. Microsc. 1998, 192, 194–201. 10.1046/j.1365-2818.1998.00420.x. [DOI] [PubMed] [Google Scholar]
- Treacy M. M. J.; Newsam J. M. Electron-Beam Sensitivity of Zeolite L. Ultramicroscopy 1987, 23, 411–419. 10.1016/0304-3991(87)90252-X. [DOI] [Google Scholar]
- Egerton R. F.; Li P.; Malac M. Radiation Damage in the TEM and SEM. Micron 2004, 35, 399–409. 10.1016/j.micron.2004.02.003. [DOI] [PubMed] [Google Scholar]
- Evans J. E.; Friedrich H.; Bals S.; Bradley R. S.; Dahmen T.; De Backer A.; de Jonge N.; Elbaum M.; Goris B.; Houben L.; et al. Advanced Tomography Techniques for Inorganic, Organic, and Biological Materials. MRS Bull. 2016, 41, 516–521. 10.1557/mrs.2016.134. [DOI] [Google Scholar]
- Hayward S. B.; Glaeser R. M. Radiation-Damage of Purple Membrane at Low-Temperature. Ultramicroscopy 1979, 4, 201–210. 10.1016/S0304-3991(79)90211-0. [DOI] [PubMed] [Google Scholar]
- Dubochet J.; Knapek E.; Dietrich I. Reduction of Beam Damage by Cryoprotection at 4K. Ultramicroscopy 1981, 6, 77–80. 10.1016/S0304-3991(81)80180-5. [DOI] [Google Scholar]
- Siegel G. Der Einfluss Tiefer Temperaturen Auf Die Strahlenschädigung Von Organischen Kristallen Durch 100 Kev-Elektronen. Z. Naturforsch., A: Phys. Sci. 1972, 27, 325–332. 10.1515/zna-1972-0219. [DOI] [Google Scholar]
- Knapek E.; Dubochet J. Beam Damage to Organic Material Is Considerably Reduced in Cryo-Electron Microscopy. J. Mol. Biol. 1980, 141, 147–161. 10.1016/0022-2836(80)90382-4. [DOI] [PubMed] [Google Scholar]
- Bammes B. E.; Jakana J.; Schmid M. F.; Chiu W. Radiation Damage Effects at Four Specimen Temperatures from 4 to 100 K. J. Struct. Biol. 2010, 169, 331–341. 10.1016/j.jsb.2009.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egerton R. F. Control of Radiation Damage in the TEM. Ultramicroscopy 2013, 127, 100–108. 10.1016/j.ultramic.2012.07.006. [DOI] [PubMed] [Google Scholar]
- Nord M.; Vullum P. E.; Hallsteinsen I.; Tybell T.; Holmestad R. Assessing Electron Beam Sensitivity for SrTiO3 and La0.7Sr0.3MnO3 Using Electron Energy Loss Spectroscopy. Ultramicroscopy 2016, 169, 98–106. 10.1016/j.ultramic.2016.07.004. [DOI] [PubMed] [Google Scholar]
- Fryer J. R.; Mcconnell C. H.; Zemlin F.; Dorset D. L. Effect of Temperature on Radiation-Damage to Aromatic Organic-Molecules. Ultramicroscopy 1992, 40, 163–169. 10.1016/0304-3991(92)90057-Q. [DOI] [Google Scholar]
- Fryer J. R. The Effect of Dose-Rate on Imaging Aromatic Organic-Crystals. Ultramicroscopy 1987, 23, 321–327. 10.1016/0304-3991(87)90242-7. [DOI] [Google Scholar]
- Glaeser R. M. Limitations to Significant Information in Biological Electron Microscopy as a Result of Radiation Damage. J. Ultrastruct. Res. 1971, 36, 466–482. 10.1016/S0022-5320(71)80118-1. [DOI] [PubMed] [Google Scholar]
- Guo C. H.; Allen F. I.; Lee Y.; Le T. P.; Song C.; Ciston J.; Minor A. M.; Gomez E. D. Probing Local Electronic Transitions in Organic Semiconductors through Energy-Loss Spectrum Imaging in the Transmission Electron Microscope. Adv. Funct. Mater. 2015, 25, 6071–6076. 10.1002/adfm.201502090. [DOI] [Google Scholar]
- Eggeman A. S.; Illig S.; Troisi A.; Sirringhaus H.; Midgley P. A. Measurement of Molecular Motion in Organic Semiconductors by Thermal Diffuse Electron Scattering. Nat. Mater. 2013, 12, 1045–1049. 10.1038/nmat3710. [DOI] [PubMed] [Google Scholar]
- Hayashida M.; Kawasaki T.; Kimura Y.; Takai Y. Estimation of Suitable Condition for Observing Copper-Phthalocyanine Crystalline Film by Transmission Electron Microscopy. Nucl. Instrum. Methods Phys. Res., Sect. B 2006, 248, 273–278. 10.1016/j.nimb.2006.04.168. [DOI] [Google Scholar]
- Koshino M.; Masunaga Y. H.; Nemoto T.; Kurata H.; Isoda S. Radiation Damage Analysis of 7,7,8,8,-Tetracyanoquinodimethane (TCNQ) and 2,3,5,6,-Tetrafluoro-7,7,8,8,-Tetracyanoquinodimethane (F(4)TCNQ) by Electron Diffraction and Electron Energy Loss Spectroscopy. Micron 2005, 36, 271–279. 10.1016/j.micron.2004.12.007. [DOI] [PubMed] [Google Scholar]
- Sarkar R.; Rentenberger C.; Rajagopalan J. Electron Beam Induced Artifacts During in Situ Tem Deformation of Nanostructured Metals. Sci. Rep. 2015, 5, 16345. 10.1038/srep16345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egerton R. F.; Wang F.; Crozier P. A. Beam-Induced Damage to Thin Specimens in an Intense Electron Probe. Microsc. Microanal. 2006, 12, 65–71. 10.1017/S1431927606060065. [DOI] [PubMed] [Google Scholar]
- Egerton R. F. Mechanisms of Radiation Damage in Beam-Sensitive Specimens, for TEM Accelerating Voltages between 10 and 300 kV. Microsc. Res. Technol. 2012, 75, 1550–1556. 10.1002/jemt.22099. [DOI] [PubMed] [Google Scholar]
- Aronova M. A.; Sousa A. A.; Zhang G.; Leapman R. D. Limitations of Beam Damage in Electron Spectroscopic Tomography of Embedded Cells. J. Microsc. 2010, 239, 223–232. 10.1111/j.1365-2818.2010.03376.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karuppasamy M.; Nejadasl F. K.; Vulovic M.; Koster A. J.; Ravelli R. B. G. Radiation Damage in Single-Particle Cryo-Electron Microscopy: Effects of Dose and Dose Rate. J. Synchrotron Radiat. 2011, 18, 398–412. 10.1107/S090904951100820X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehm G.; Nadarzinski K.; Ernst F.; Ruhle M. Quantification of Irradiation Damage Generated During HRTEM with 1250 keV Electrons. Ultramicroscopy 1996, 63, 49–55. 10.1016/0304-3991(96)00025-3. [DOI] [Google Scholar]
- De Carlo S.; El-Bez C.; Alvarez-Rua C.; Borge J.; Dubochet J. Cryo-Negative Staining Reduces Electron-Beam Sensitivity of Vitrified Biological Particles. J. Struct. Biol. 2002, 138, 216–226. 10.1016/S1047-8477(02)00035-7. [DOI] [PubMed] [Google Scholar]
- Wirix M. J. M.; Bomans P. H. H.; Hendrix M. M. R. M.; Friedrich H.; Sommerdijk N. A. J. M.; De With G. Visualizing Order in Dispersions and Solid State Morphology with Cryo-TEM and Electron Tomography: P3HTt:PCBM Organic Solar Cells. J. Mater. Chem. A 2015, 3, 5031–5040. 10.1039/C4TA05161K. [DOI] [Google Scholar]
- Wirix M. J. M.; Bomans P. H. H.; Friedrich H.; Sommerdijk N. A. J. M.; de With G. Three-Dimensional Structure of P3HT Assemblies in Organic Solvents Revealed by Cryo-Tem. Nano Lett. 2014, 14, 2033–2038. 10.1021/nl5001967. [DOI] [PubMed] [Google Scholar]
- van Bavel S.; Sourty E.; de With G.; Frolic K.; Loos J. Relation between Photoactive Layer Thickness, 3d Morphology, and Device Performance in P3HT/PCBM Bulk-Heterojunction Solar Cells. Macromolecules 2009, 42, 7396–7403. 10.1021/ma900817t. [DOI] [Google Scholar]
- Yang X. N.; van Duren J. K. J.; Rispens M. T.; Hummelen J. C.; Janssen R. A. J.; Michels M. A. J.; Loos J. Crystalline Organization of a Methanofullerene as Used for Plastic Solar-Cell Applications. Adv. Mater. 2004, 16, 802–806. 10.1002/adma.200306372. [DOI] [Google Scholar]
- Kolb U.; Gorelik T.; Kubel C.; Otten M. T.; Hubert D. Towards Automated Diffraction Tomography: Part I - Data Acquisition. Ultramicroscopy 2007, 107, 507–513. 10.1016/j.ultramic.2006.10.007. [DOI] [PubMed] [Google Scholar]
- Egerton R. F.; Lazar S.; Libera M. Delocalized Radiation Damage in Polymers. Micron 2012, 43, 2–7. 10.1016/j.micron.2011.05.007. [DOI] [PubMed] [Google Scholar]
- Egerton R. F.; Crozier P. A.; Rice P. Electron Energy-Loss Spectroscopy and Chemical-Change. Ultramicroscopy 1987, 23, 305–312. 10.1016/0304-3991(87)90240-3. [DOI] [Google Scholar]
- Martin J.; Beauparlant M.; Sauve S.; L’Esperance G. On the Threshold Conditions for Electron Beam Damage of Asbestos Amosite Fibers in the Transmission Electron Microscope (TEM). J. Occup. Environ. Hyg. 2016, 13, 924–935. 10.1080/15459624.2016.1191638. [DOI] [PubMed] [Google Scholar]
- Alexander J. A.; Scheltens F. J.; Drummy L. F.; Durstock M. F.; Gilchrist J. B.; Heutz S.; McComb D. W. Measurement of Optical Properties in Organic Photovoltaic Materials Using Monochromated Electron Energy-Loss Spectroscopy. J. Mater. Chem. A 2016, 4, 13636–13645. 10.1039/C6TA06201F. [DOI] [Google Scholar]
- Drummy L. F.; Davis R. J.; Moore D. L.; Durstock M.; Vaia R. A.; Hsu J. W. P. Molecular-Scale and Nanoscale Morphology of P3HT:PCBM Bulk Heterojunctions: Energy-Filtered TEM and Low-Dose HREM. Chem. Mater. 2011, 23, 907–912. 10.1021/cm102463t. [DOI] [Google Scholar]
- Pfannmoller M.; Flugge H.; Benner G.; Wacker I.; Sommer C.; Hanselmann M.; Schmale S.; Schmidt H.; Hamprecht F. A.; Rabe T.; et al. Visualizing a Homogeneous Blend in Bulk Heterojunction Polymer Solar Cells by Analytical Electron Microscopy. Nano Lett. 2011, 11, 3099–3107. 10.1021/nl201078t. [DOI] [PubMed] [Google Scholar]
- Bellani S.; Fazzi D.; Bruno P.; Giussani E.; Canesi E. V.; Lanzani G.; Antognazza M. R. Reversible P3HT/Oxygen Charge Transfer Complex Identification in Thin Films Exposed to Direct Contact with Water. J. Phys. Chem. C 2014, 118, 6291–6299. 10.1021/jp4119309. [DOI] [Google Scholar]
- Braunfeld M. B.; Koster A. J.; Sedat J. W.; Agard D. A. Cryo Automated Electron Tomography - Towards High-Resolution Reconstructions of Plastic-Embedded Structures. J. Microsc. 1994, 174, 75–84. 10.1111/j.1365-2818.1994.tb03451.x. [DOI] [PubMed] [Google Scholar]
- Johansen B. V. Bright Field Electron-Microscopy of Biological Specimens 0.5. Low-Dose Pre-Irradiation Procedure Reducing Beam Damage. Micron 1976, 7, 145–156. 10.1016/0047-7206(76)90058-3. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.