Noisy signal amplification in ultrasensitive signal transduction

Abstract

Because intracellular processes are inherently noisy, stochastic reactions process noisy signals in cellular signal transduction. One essential feature of biological signal transduction systems is the amplification of small changes in input signals. However, small random changes in the input signals could also be amplified, and the transduction reaction can also generate noise. Here, we show theoretically how the abrupt response of ultrasensitive signal-transduction reactions results in the generation of large inherent noise and the high amplification of input noise. The inherently generated noise propagates with amplification through intracellular molecular network. We discuss how the contribution of such transmitted noise can be shown experimentally. Our results imply that the switch-like behavior of signal transduction could be limited by noise; however, high amplification reaction could be advantageous to generate large noise, which would be essential to maintain behavioral variability.

Many cellular processes respond abruptly to internal and external variations by using networks of interacting molecules. One mechanism for sharpening the response is the cooperativity observed in hemoglobin (1–3). Response is also heightened when a messenger is activated and deactivated cyclically by a pair of opposing enzymes (4, 5), as observed in a combination of kinase and phosphatase reactions. In these reactions, the response is switch-like, with a threshold in the concentration of stimuli. In a cascade of such switch-like reactions, as observed in mitogen-activated protein kinase (MAPK) cascade, the amplification of the whole cascade can be much larger (6). Therefore, steep cellular responses may imply the often-adopted view that complicated combinations of those switches operate cellular behaviors. Is it more appropriate for the cellular system to have ultrasensitivity with higher Hill coefficients to have all-or-none behaviors? Because cellular processes are inherently noisy (7), such intrinsic cellular noise might affect the behavior of ultrasensitive signal transduction.

Recently, the existence of strong noise in biochemical reactions in cells has been demonstrated experimentally, particularly in gene expression (8–11). When such a noisy chemical component regulates a reaction, the noise seems to affect the behavior of the reaction. As the noise intensity of the regulating component increases, the noise intensity of the regulated component also appears to increase. This transmission of noise indicates that the following two distinct noise sources contribute to the noise of each component: the noise inherent in its own reaction (intrinsic noise) and the noise generated in other chemical components that affects the reaction (extrinsic noise). Elowitz et al. (10) pointed out and demonstrated this distinction experimentally in gene expression. A consistent view for previous experiments (8–11) on the noise in gene expression was provided by Paulsson (12), who analyzed the propagation of noise in a gene network theoretically. He showed a quantitative expression for both intrinsic and extrinsic noise based on a simple birth-and-death process of two chemical species.

The cellular signal transduction systems are also inherently noisy (13–15). How cells respond properly to noisy signals by using noisy molecular networks is an important problem in elucidating the underlying “design principle” of cellular systems. Oosawa (16, 17) discussed that such intracellular noise is hierarchically organized from thermal fluctuations to spike-like large fluctuations, which produce spontaneous signals to change the behavior of swimming cells such as bacteria and paramecia. Recently, the noise in signal transduction was discussed (18, 19), suggesting the large amplification results in the generation of strong random fluctuations in the output signal. As Elowitz et al. (10) and Paulsson (12) discussed in their studies on gene networks, the noise generated in a reaction propagates in signal transduction networks. The high amplification of input signals may imply the high amplification of the noise in input signals. Thus, the intrinsic and extrinsic noises are related to the amplification of signal-transduction processes.

Therefore, the problem that we address in this article is how intrinsic and extrinsic noises relate to the amplification of signals. We show the connection more clearly and systematically between the observable quantity such as gain, which quantifies the amplification, and both intrinsic and extrinsic noise intensities. We show that the intrinsic and extrinsic noises are described by the functions of the gain of signal-transduction reactions, summarized as the gain–intrinsic noise relation Eq. 8 and the gain–extrinsic noise relation Eq. 10. As the gain increases, the total noise in the output signal shows the crossover from the intrinsic-noise dominant regime to the extrinsic-noise dominant regime (Eq. 11 and Fig. 4). These gain–fluctuation relations are applicable to many types of reactions. In this article, the relations are studied for the three reactions that are always found in signal transduction cascades (1) (Fig. 1): the Michaelis–Menten-type reaction, and the ultrasensitive reactions such as the cooperative reactions in single proteins and the push–pull antagonistic reaction. Last, we propose criteria to verify experimentally which noise (intrinsic or extrinsic) is dominant in the cellular noise, and we discuss the biological relevance.

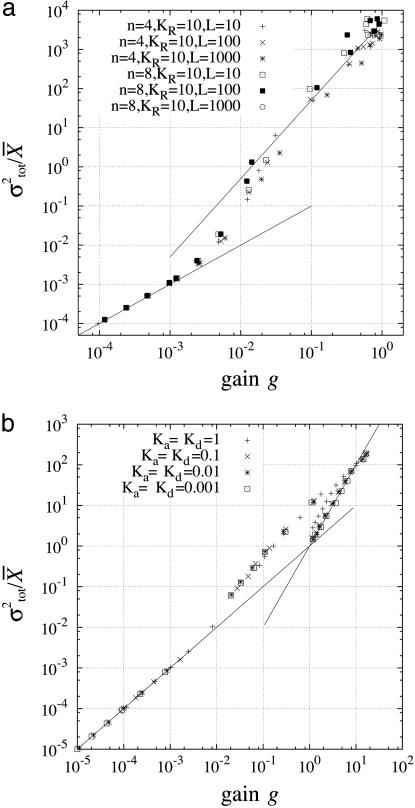
Fig. 4.

Amplification of noise in signal-transduction systems. To show the dependence of the total noise intensity σ_tot on the gain g, σ_tot/X̄ is plotted as a function of the gain g. Changing the average concentration of the input signal, g, σ_tot, and X̄ were obtained numerically. The numerical calculation was performed by using the Gillespie's algorithm (20), as in Fig. 3. In the present case, the concentration of the input signal also fluctuates in time, and the average concentration increases under the condition that the relative noise intensity is maintained to be constant. The following parameters are shown: the MWC model K_T = 1, K_R indicated in a; the push–pull reaction, V_a = V_d = 10, K_a and K_d indicated in b.

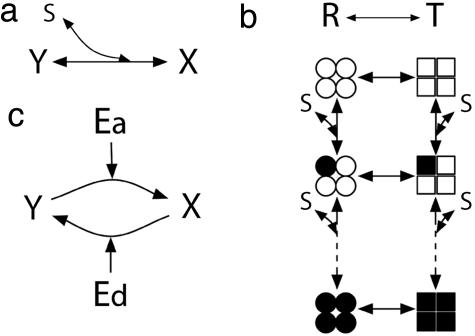
Fig. 1.

Three typical signal-transduction reactions. (a) The Michaelis–Menten-type reaction. (b) The Cooperative binding reaction. (c) The push–pull antagonistic reaction. The circle indicates the R state and the square is the T state. The subunits that are occupied by substrates are filled.

Signal-Transduction Reactions

The Michaelis–Menten-Type Reaction. The Michaelis–Menten-type reaction is the simplest signal-transduction reaction that behaves as a molecular switch.

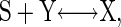[1]

where S is the signaling molecule that binds to the inactive state Y so that the protein is switched on to the active state X (Fig. 1a). This best-known reaction gives rise to the Michaelis–Menten kinetics (Fig. 2a).

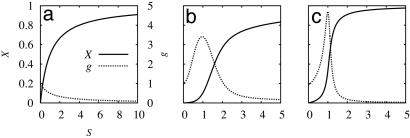
Fig. 2.

Ultrasensitive responses in signal-transduction reactions. The fractional concentration of the output signal X (left axis) and the gain g (right axis) are plotted as functions of the concentration of signal molecule. The Michaelis–Menten-type reaction (a), the MWC model (b), and the push–pull antagonistic reaction (c) are shown.

The Monod–Wyman–Changeux (MWC) (Concerted) Model. As an example of cooperative binding reaction, we study the MWC (concerted) model (1, 2), in which a number of identical subunits in a protein have two structural states, T and R (Fig. 1b). The state T shows a relatively low affinity for substrate, whereas the R state shows a higher affinity. The subunits in a protein are either all in the T state or all in the R state:

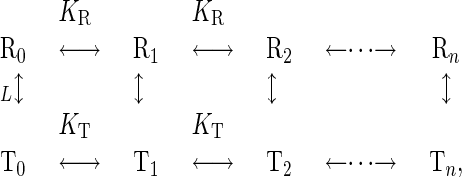[2]

where n is the number of subunits, and R_i and T_i indicate that i substrates bind to the molecule. L, K_R and K_T are the equilibrium constants. The subunits binding to the substrate transmit signals. Thus, the input signal S is the concentration of the substrate and the output signal X is the concentration of the subunits that bind to the substrates. Therefore, X is a linear combination of the concentrations of the states: X = [R₁] + [T₁] + 2[R₂] + 2[T₂] + · · · + n[R_n] + n[T_n]. The output signal can show a steeper response than that of the Michaelis–Menten kinetics (Fig. 2b).

The Push–Pull Antagonistic Reaction. The push–pull antagonistic reaction is the simplest example of a cyclic modification reaction that can also show sharp response (4, 5). In the push–pull reaction, the signaling molecule, which is an enzyme, switches its substrate protein from an inactive to an active state, whereas another enzyme switches the protein off (Fig. 1c). Each step is characterized by Michaelis–Menten kinetics:

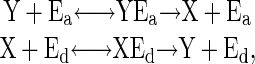[3]

where E_a is the signaling enzyme which switches inactive state Y to active state X, and E_d switches X off. Thus, the input signal is the concentration of E_a. If each Michaelis–Menten reaction works near saturation, sharp response is obtained (Fig. 2c).

Note that if K_T/K_R = 1 or L = 0 in the MWC model, or both of the Michaelis–Menten kinetics in the push–pull reaction work far from saturation, these reactions are reduced to the Michaelis–Menten-type reaction. Therefore, in the next section, we study the MWC model and the push–pull reaction.

Characterization of Signal Amplification

The amplification can be evaluated by changing the signal intensity S to S + ΔS and measuring the response ΔX in the output signal X from its stationary value X̄. The amplification can be quantified as follows by the gain g defined as the ratio between the fractional change in the output signal X and the fractional change in the input signal S:

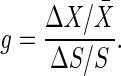[4]

In this article, we consider that there is only a small change in S. Then, the gain is rewritten as g = d log X/d log S. For the three reactions discussed in Signal-Transduction Reactions, the gain is shown in Fig. 2. Ultrasensitivity is defined as the response of a system that is more sensitive to change in S than is the normal hyperbolic response in Michaelis–Menten kinetics, in which the maximum gain g is unity. Thus, the maximum gain g of an ultrasensitive system is larger than unity.

Results and Discussions

Ultrasensitive Reactions Can Be Strong Noise Sources. First, we study how the gain is related to the intrinsic noise. In signal-transduction reactions, a modification or degradation reaction that switches the activated signal molecules off determines both the time constant of the output signal and the strength of the response. If the modification or degradation reaction rate Γ is small, the response to the change in the input signal may be large; conversely, if Γ is large, the response may be small. For a given value of the production reaction rate, with which the active signal molecules are produced, the gain is proportional to the inverse of the reaction rate Γ,

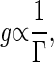[5]

if the change in the signal intensity is small.

The concentration of the output signal X fluctuates in time because of the intrinsic noise of chemical reactions, even if the input signal does not fluctuate in time. The variance of this intrinsic noise, σ²_in, is also determined by the rate Γ. The temporal evolution of X is a stochastic process. In such a process, the correlation between X at time 0 and at time t typically decays exponentially over time. Therefore, the information that a reaction takes place at a particular time disappears after the time constant τ = 1/Γ. Because the number X at a particular time is approximately given by integrating the stochastic change in X during the interval τ, the standard deviation σ_in in the distribution of such a number as X is proportional to 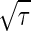, according to the central-limit theorem in the probability theory. Thus, the variance of the intrinsic noise σ²_in can be written as follows:

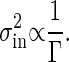[6]

From Eqs. 5 and 6, we conclude that the gain is proportional to the intrinsic noise,

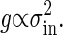[7]

This relation reveals that a high response that is characterized by high gain results in large intrinsic noise, whereas large intrinsic noise implies high gain. We can conclude at least that the gain and the intrinsic noise cannot be controlled independently. This gain–intrinsic noise relation in signal-transduction reactions, is exactly written as follows:

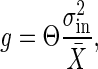[8]

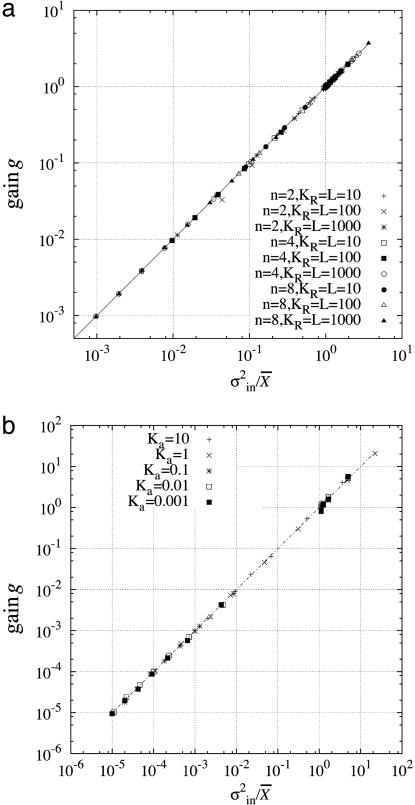
where X̄ is the average number of X before the change in the input signal and Θ is a particular constant depending on the reaction (see Appendix for the derivation). Note that Θ is not a dimensionless parameter and that it depends on the measurement of X. When we suppose that the output signal X is the number of the output molecule rather than the concentration, Θ is obtained as a simple number. In the reactions discussed in Signal-Transduction Reactions, we obtain Θ = 1. Stochastic simulations were performed for the MWC model and the push–pull reactions. The result, shown in Fig. 3, indicates clearly that the relation is satisfied in these reactions with Θ = 1.

Fig. 3.

The gain–intrinsic noise relation of signal transduction systems. The gain g is plotted as a function of the variance divided by the mean number. Changing the concentration of the input signal S, the gain, the variance, and the mean number are obtained by performing stochastic simulations of schemes, as shown in Eqs. 2 and 3, according to the Gillespie's numerical algorithm (20). (a) The MWC model. We used the parameter values: K_T = 1, and n, K_R, and L shown in the figure. The kinetic constants were arbitrarily chosen. (b) The push–pull reaction. The Michaelis constant is K_a for the activation reaction, as is indicated, and K_d = 1 for the deactivation reaction. The maximum velocities of activation and deactivation reactions are given by V_a = V_d = 100, respectively.

Single gene expression also follows the relation Eq. 8. When X is the number of protein products of a gene expression Θ = 1/(b + 1), where b is the translation efficiency defined as the average number of protein products produced from a single mRNA (see Appendix). Not only the reactions that we studied here, but also many other types of reactions, follow this reaction. For example, the ultrasensitive reactions such as the Koshland–Némethy–Filmer sequential model of allosteric enzymes (3), and the generalized model of allosteric enzymes (21, 22) follow the same relation.

However, in the case of the adaptive signal transduction reactions such as the kinetics of bacterial receptor responsible for chemotaxis (23, 24), the relation between the gain and the fluctuation could be more complicated than Eq. 8.

The Amplification of Noise in Input Signal Is Less than the Gain. If the signal-transduction reactions amplify the small changes in the input signal, the noise in the input signal may also be amplified. Here, we show how the amplification of input noise is related to the gain.

When the incoming signal contains noise with the standard deviation σ_s, the extrinsic noise contribution in the output signal is measured as the standard deviation of the extrinsic noise intensity σ_ex. The ratio between the relative noise intensities σ_ex/X̄ and σ_s/S gives the amplification rate of the noise λ, as follows:

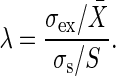[9]

As we will show, the amplification rate λ is determined by the time constant of the noise in the input signal, τ_s, and that of the signal-transduction reaction, τ, and the gain g.

First, we consider the case in which the time constant of the input noise, τ_s, is much larger than that of the transduction reaction, τ (i.e., τ_s >> τ). Then, such a noise is considered as slow modulation in the input signal, and thus, such a noise cannot be distinguished from an external systematic change in the input signal. The response of the change in an input signal is measured by the gain g. Therefore, in this case, the amplification rate λ is equal to the gain g and nothing else; i.e., λ = g.

Consider the other extreme case in which the time constant of the input noise, τ_s, is much smaller than that of the reaction, τ (i.e., τ_s << τ). The impact of the input noise on the output signal is evaluated by taking the temporal average of input noise during the time interval τ. The standard deviation of the temporal average is proportional to 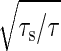. Consequently, the amplification rate λ in this regime is given by .

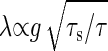Including the above two cases, the amplification rate λ is obtained by 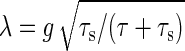. Thus, the gain–extrinsic noise relation is written as follows:

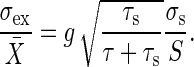[10]

The gain–extrinsic noise relation indicates that the amplification rate of the input noise is at most the gain g. When τ_s >> τ, the amplification rate λ approaches the gain g. When τ_s << τ, the noise in the input signal is averaged out and the amplification rate decreases proportionally to 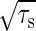as the time constant τ_s decreases. The derivation of Eq. 10 is shown in Appendix.

Both Intrinsic and Extrinsic Noises Contribute the Total Output Noise. From Eq. 10 the dependence of the extrinsic noise on the gain is given by 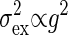. Remember that the variance of the intrinsic noise 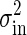is proportional to the gain g; i.e., 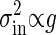, as shown in Eq. 8. Because the total noise is made up of the intrinsic and extrinsic noises, the dependence of the variance of the total noise is both linear and square on the gain g. In the MWC model and the push–pull reaction, it is numerically verified that 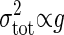when g is small, and 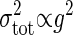when g is large (see Fig. 4). Therefore, if the gain g is small, the intrinsic noise is dominant in the total noise, whereas if the gain g is large, the extrinsic noise dominates (Table 1).

Table 1. Characteristics of intrinsic and extrinsic noises.

Characteristics	Intrinsic noise	Extrinsic noise
Noise to gain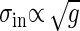
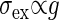Noise to output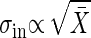
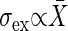Dominant frequency	Higher	Lower

The dependence of noise intensity on the gain and output signal intensity are shown in the first two rows. The intrinsic noise dominates higher-frequency noise, whereas the extrinsic noise dominates low-frequency noise, as shown in the third row.

Consequently, for the signal-transduction systems such as the three reactions introduced in Signal-Transduction Reactions and gene expression as well, the relative noise intensity of the total noise, σ_tot/X̄, in the stationary state is related to the gain g as the gain–fluctuation relation:

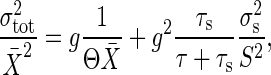[11]

where the first term on the right hand side is the intrinsic noise (Eq. 8), and the second term is the extrinsic noise (Eq. 10) (see Appendix for the derivation). Similar expression was derived by Paulsson (12) for the reaction noise of simple coupled chemical reactions to study gene-expression noise. Because the essential functioning of signal transduction is the amplification, we emphasize in our result based on Eq. 11 the connection between the noise intensity and the experimentally observable quantity gain g.

Transmitting Noise in Signal Transduction Cascades. The gain–fluctuation relation Eq. 11 is generalized in cascade reactions, such as the MAPK cascade. In a cascade, a signal-transduction system regulates another downstream signal transduction. Then, the fluctuation in the ith reaction is as follows:

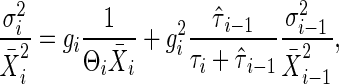[12]

where the subscript i indicates the reaction number in the cascade. In the case of MAPK cascade, when the ith reaction is a MAPK reaction, the i - 1th reaction is MAPK kinase reaction. In the second term, τ_i is the time constant of the ith reaction, and 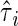is the time constant of the output noise of the ith reaction. In the second term, σ_i-1/X̄_i-1 is the total noise of the i - 1th reaction. The contribution of the intrinsic noise generated at a particular upstream reaction to the extrinsic noise of a downstream reaction is estimated as the product of the amplification rates λ of the reactions between them. Therefore, if the cascade consists of reactions with high gain, the extrinsic noise dominates the fluctuation in the output signal.

However, even when the cascade is made up of ultrasensitive reactions, if the downstream reactions work at almost saturation, the gains in these reactions can be much smaller than unity. As a result, the extrinsic noise contribution can be attenuated. Such an example was studied recently in a cascade of ultrasensitive reactions (25).

The Difference Between Dominating Extrinsic Noise and Dominating Intrinsic Noise. Which noise, intrinsic or extrinsic, dominates the cellular noise? How can we answer this question experimentally? In a gene network, Elowitz et al. (10) showed that the extrinsic noise contribution is dominant in the constitutive plasmid system. The question is also answered by measuring the dependence of the standard deviation on the average number. Suppose that the dependence of gain g on the output signal intensity X̄ is weak. Then, from Eq. 11, when the intrinsic noise is dominant, we have 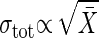. However, if the extrinsic noise dominates, it follows that 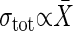(Table 1).

In gene expression, it was reported that when the expression levels of many genes are measured in different conditions in many kinds of species, the difference of the expression levels in each gene, ΔX, is in average linearly proportional to the expression level X̄ of each gene; i.e., 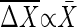(26). This experimental result, together with the definition of the gain, indicates that the expression levels move in the range where the gain g is almost constant against the change in the conditions. Then, the above criterion is applicable to gene expression. Ozbudak et al. (9) showed that the variance of expression noise is proportional to the expression level; 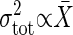, whereas Banerjee et al. (27) reported by using a different system that the standard deviation is proportional to the expression level; σ_tot ∝ X̄. Therefore, in these two different systems, the intrinsic noise is dominant in the former system, and the extrinsic noise is in the latter system.

Extrinsic Noise Dominates Low-Frequency Noise. For signal transduction systems, the ultrasensitive behavior of bacterial chemotaxis was reported (22, 28, 29). This ultrasensitivity suggests, from the viewpoint of the gain–fluctuation relation, that there is a strong underlying stochasticity in the network of chemotaxis responses. From our result, it can be further suggested that if the extrinsic noise dominates, the upstream reactions affect the fluctuation of the most downstream reaction, which determines the cellular behavior. As a result, the behavioral fluctuations are made up of the contributions of the fluctuations of several upstream reactions. On the other hand, if the intrinsic noise dominates, only the intrinsic noise of the most downstream reaction determines the behavioral fluctuations. As a result, the behavior could be simpler than the case in which extrinsic noise is dominant.

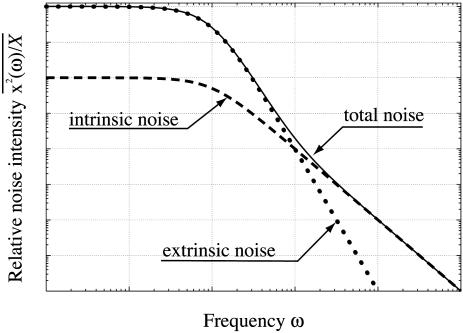
This distinction in the effects of the intrinsic and extrinsic noises on cellular behaviors can be clearly seen by performing a spectrum analysis of an output signal. The contributions of intrinsic and extrinsic noises to the total noise intensity depend on the frequency (see Eq. 20 in Appendix and Fig. 5). As the frequency ω increases, the intrinsic noise contribution σ_in is a constant up to the frequency τ^-1, and it then decreases proportionally to ω^-1. However, the contribution of extrinsic noise σ_ex is a constant up to the frequency 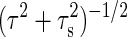, and for higher frequency ω, it decreases proportionally to ω^-2. Therefore, the low-frequency component can be dominated by the extrinsic noise if the gain g is large, whereas the high-frequency component is dominated by the intrinsic noise (Table 1). Consequently, the low-frequency modulations in the downstream reactions can be affected by the behaviors of upstream reactions, whereas the high-frequency modulations are expected to be independent of upstream reactions.

Fig. 5.

The frequency-dependent total, intrinsic, and extrinsic noise intensities, shown in Eq. 20, with particular parameter values plotted as functions of the frequency ω. The intrinsic noise (dashed line) is dominant in the higher-frequency region, whereas the extrinsic noise (dotted line) is dominated in the lower-frequency region.

Recently, Korobkova et al. (15) measured the stochastic behavior of chemotaxis network in a single bacterium and reported the complex temporal behavior. They reported that, as the concentration of an upstream molecule receptor methyltransferase CheR increased, the temporal behavioral variability was reduced and suppressed. The power spectrum intensity of the temporal behaviors decreased in the low-frequency region as the increase of [CheR], whereas the intensity in the high-frequency region was almost maintained. Because the low-frequency noise is dominated by the extrinsic noise, the experimental result suggests that, as [CheR] increases, whereas the intrinsic noise is unchanged, the extrinsic noise is suppressed and, as a result, the behavior becomes simpler. Therefore, the result implies that the extrinsic noise is essential to maintain the behavioral variability in wild-type bacteria.

Outlook. Our results imply that the signal transduction capacity can be limited by large noise of ultrasensitive reactions but, however, such reactions can be advantageous to generate large noise, which could be essential to maintain behavioral variability and spontaneous behaviors. Even though the three reactions discussed in this article include nonlinear reactions, our theoretical analysis describes well the behaviors obtained numerically. However, when a reaction works with strong nonlinearity, the effects of noise can be difficult to predict. In such cases, increasing the input noise can result in either enhancing or reducing the total noise of output signal, depending on the system (30). Nonlinearity also gives rise to a variety of phenomena, including multistabilities (31, 32) and temporal oscillations (33, 34). In these cases, the relation between the response and the fluctuations can be more complicated than the relations we studied. However, our present results would be the starting point for elucidating the role that the cellular noise performs for functioning of cellular systems.

Appendix

Deriving the Gain–Fluctuation Relation. To derive the gain–fluctuation relation Eq. 11, in this section, we mainly study the signal-transduction reaction, in which the chemical component Y is activated to X, and at the same time, X is deactivated to Y. This type of reaction includes many signaling reactions such as the Michaelis–Menten type reaction and push–pull reaction. The number of chemical component X and Y are X and Y, respectively, and the total number of X and Y is N = X + Y. If the number X is considered approximately as a continuous number, the temporal evolution of X is described by the chemical Langevin equation (19), given by the following:

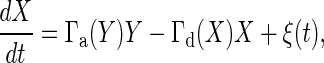[13]

where Γ_a(Y) and Γ_d(X) are the activation and deactivation reaction rates, respectively, which depend on the numbers X and Y. In the case of the push–pull reaction (19), the reaction rates are given by 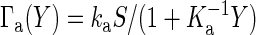, and 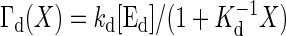, where S is the concentration of the input molecule E_a, K_a, and K_d are the Michaelis constants of each enzymatic reaction, and k_a and k_d are the kinetic constants. The last term ξ(t) is a white Gaussian noise with 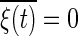and 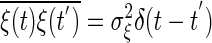. Because chemical reaction events take place in time as a Poisson process, the noise intensity 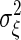is given by 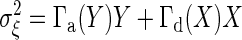(35).

To calculate the gain and the noise intensity, we study the linear response of X to the change in S. For such a linear response, the variance of the noise 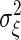is considered approximately as a constant in time. Therefore, substituting the stationary number X̄ and Ȳ for X and Y, 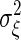is given by the following:

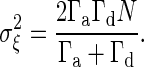[14]

The temporal evolution of the small deviations x and s from X̄ and S is described by the linearized Langevin equation of Eq. 13,

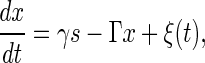[15]

where 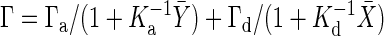and

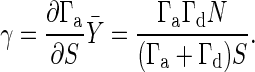[16]

First, we show the gain-intrinsic noise relation Eq. 8. We note that this relation is considered as a variant of the fluctuation–dissipation theorem in nonequilibrium statistical mechanics (36).

The gain is calculated from the mean response x̄ to the input change s as follows:

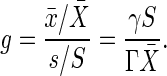[17]

To calculate the intrinsic noise intensity of the output signal X in the steady state, we solve Eq. 15 under the condition that s(t) = 0. Then, the intrinsic noise intensity 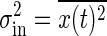is obtained by 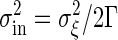. Consequently, the gain g is proportional to the intrinsic noise as follows:

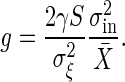[18]

Substituting Eqs. 14 and 16 into Eq. 18, the gain–intrinsic noise relation is obtained as Eq. 8 with Θ = 1.

Whereas the above reaction was described essentially by a single variable, the above derivation can be applied to the systems described by multiple variables, such as the MWC model and the Koshland–Némethy–Filmer model. In such cases, the intensity of the output signal X is a linear combination of the concentrations of n chemical components X₁,X₂,...,X_n. For example, in the case of MWC model, the intensity of the output signal is given by X = [R₁] + [T₁] + 2[R₂] + 2[T₂] + · · · + n[R_n] + n[T_n]. Even in such cases, the gain–intrinsic noise relation Eq. 8 holds between the gain and the variance of the output signal X, if the reactions satisfy the detailed balance condition for the steady state (35, 37). Note that this condition does not mean that the reactions must always be in the steady state. In fact, in the process of response, the reaction is away from the steady state. Moreover, the steady state is not necessarily thermodynamic equilibrium.

Next, we consider the case in which the number of input signal molecule is subjected to temporal stochastic fluctuations. Thus, suppose that the input modulation s(t) in Eq. 15 is a stochastic process, and for simplicity, the correlation of the fluctuation s(t) decays exponentially in time with the time constant τ_s. When s(ω) is the Fourier transform of s(t), the power spectrum density 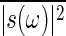is given by the following:

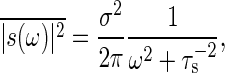[19]

where σ is a particular constant. Then, the variance of the noise in signal, 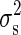, is calculated as .

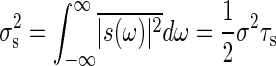Note that no correlation exists between s(t) and ξ(t). When x(ω) is the Fourier transform of x(t), solving Eq. 15 with Eqs. 8, 17, and 19, the power spectrum density 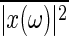is obtained by the following:

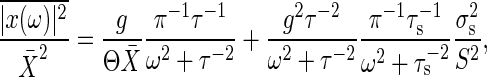[20]

where τ = Γ^-1 is the time constant of the signal transduction reaction. This expression gives the frequency-dependent total noise intensity. The total noise intensity 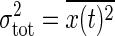is given by 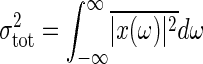. Therefore, the frequency integral of Eq. 20 gives the relative noise intensity of the total noise Eq. 11 with Θ = 1.

The Gain–Intrinsic Noise Relation in Gene Expression. Here, we calculate the parameter Θ in Eq. 8 for a single gene expression, which is modeled as follows:

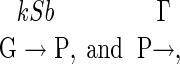in which G and P are the gene and its protein product, respectively. The transcription rate is k; the translation efficiency is denoted by b, which is defined as the translation rate divided by the degradation rate of mRNA; and the degradation rate of the protein product is Γ. In the present case, S is the gene activity, which is the fraction of the occupancy of the operator region by a regulatory protein that activates the transcription, and X is the number of protein products. Eq. 15 is applicable to this case, in which γ = kb, 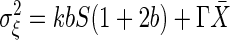(38). From Eq. 18, the parameter Θ is obtained as Θ = 1/(1 + b). This result is still valid for gene expression with autoregulation.